A Comprehensive, Non-Aggregated, Stochastic Approach to Loss Development

1. Introduction

Over the recent past, there has been much development and discussion of new stochastic models for loss development. These models apply a more scientific approach to the old problem of estimating unpaid losses, but most still stick with the same strategy of using aggregate losses. Some of these models work by fitting a curve to the aggregate development patterns, such as the inverse power curve (Sherman 1984), or the Hoerl curve (Wright 1990). Many approaches employ generalized linear models (GLMs), such as Barnett and Zehnwirth (1998), which looks at the trends in aggregate data, and Renshaw and Verrall (1998), which shows some of the statistical underpinnings of the chain-ladder method. Generalized additive models have been used as well (England and Verrall 2001), to smooth the curve in the development direction. There are many other approaches; this list is not meant to be comprehensive. Using aggregate losses, while simpler to deal with, discards much useful information that can be used to improve predictions.

The idea of separating out individual frequency and severity components is very common in other areas of actuarial practice, such as GLMs used for developing rating plans and for trend estimation, to name a few. But it is far less common for loss development. In a summary of the loss development literature (Taylor, McGuire, and Greenfield 2003), the authors, referring to using aggregated data, observe, “This format of data is fundamental to the loss reserving literature. Indeed, the literature contains little else.”

Even in the area of volatility estimation and predicting the distribution of loss payments, aggregated methods have dominated. The most common methods are the Mack and Murphy methods (Mack 1993; Murphy 1994), and the bootstrapping method (England and Verrall 1999), which involves bootstrapping the residuals from the aggregate loss triangle. There have been some recent Bayesian methods as well (e.g., Myers 2015). For a summary of methods, see England and Verrall (2002) and Myers (2015). It is difficult to say how accurate using aggregated data can be in producing an accurate distribution for loss payments, even more so when the data being worked with is sparse. While the primary focus of our paper is on estimating the mean of ultimate losses and loss reserves, our method is also well suited to estimating the distribution of loss payments, since it models the entire process from the ground up.

There have been a few approaches that use some of the more detailed data, but not all of it. Wright (1997) presents a loss development approach that looks at the development of frequency and severity separately. Another common practice is to use the projected ultimate claim counts as an exposure measure for each year to help with estimating ultimate aggregate losses. Guszcza and Lommele (2006) advocate for the use of more detailed data in the reserving process and draw an analogy to GLMs used for pricing that operate at the individual policy or claim level. Their approach still models on the aggregate development patterns, although it was only intended “in the spirit of taking a first step.” Zhou and Garrido (2009) also use GLMs and model on frequency and severity components separately. Meyers (2007) does this as well, but within a Bayesian framework. And recently, Parodi (2013) handles the frequency component of pure IBNR (incurred but not reported) by modeling on claim emergence times directly, one of the components of our model, but has more complicated formulas for handling the bias caused by data that is not at ultimate and also does not have a detailed approach for the other pieces. None of these methods uses all of the available information, such as the reporting times of unpaid claims, the settlement lags of closed claims, and how the probability of payment changes over time in a robust, comprehensive, statistical framework. The model presented in this paper also allows for expansion, such as controlling for different retentions, modeling claim state transitions as a Markov chain, or using a GLM to estimate claim payment probabilities from policy and claim characteristics while properly controlling for the bias caused from using data that is not at ultimate, and being able to correctly adjust these probabilities as the claim ages.

Despite our critique of aggregated methods, in many cases working with aggregate data may be satisfactory and the extra work involved in building a more detailed model may not justify the benefit. But for many other cases, such as those involving low-frequency/high-severity losses, where fine segmentations are desired, where there have been mix of business or attachment point changes, or when there are relatively fewer years of data available, this pushes the limits of what aggregate data can do, even with the most sophisticated stochastic models. In this paper we present a stochastic loss development model that analyzes all of the underlying parts of the claims process separately, while still keeping the model as simple as possible.

1.1. Objective

The goal of our method is to model the underlying claims process in more detail and to improve the accuracy of predictions. There are many benefits to individually modeling each component of the claims process separately. This can be compared to analyzing data for a trend indication. Combining frequency and severity information can often mask important patterns in the data, while separating them out usually yields better predictions. This is because when there are different underlying drivers affecting the data, it becomes harder to see what the true patterns in the data are. Take, for example, two incurred triangles for two different segments, in which the first segment has a slower reporting pattern, but more severe losses than the second. More severe losses tend to be reserved for sooner and more conservatively, and so this will make the aggregate loss development pattern faster. On the other hand, the slower reporting pattern will obviously make the pattern slower than the second. When comparing these two aggregate triangles, it may be difficult to judge whether the differences are caused mostly from volatility, or whether there are in fact real differences between these two segments. In contrast, looking at each component separately will yield clearer details and results. The example we gave applied to comparing two separate triangles, but this will also create problems when attempting to select development factors for a single, unstable triangle. High volatility compounds this issue.

Second, by looking at every component separately, we increase the data available to analyze, since, for example, only a fraction of reported claims end up being paid or reserved for. When looking at aggregate data, we only see the paid or incurred claims, but if we analyze the claim reporting pattern separately, we are able to utilize every single claim, even those that close without payment or reserve setup. When making predictions, we are also able to take into account the number and characteristics of claims that are currently open, which will add to the accuracy of our predictions.

Last, by separating out each piece, it becomes much easier to fit parametric models to the data that we can be confident in. Using aggregated data involves modeling processes that are more abstracted and removed from reality, which makes it harder to fit simple parametric models that can be used to smooth volatility and produce more accurate fits. It is difficult to find an appropriate curve that provides a good fit to the development patterns in aggregate data. But it is relatively easy to find very good fits for each of the individual pieces of the development process, such as the reporting and settlement times and the severity of each loss. Fitting parametric models involves estimating fewer parameters than relying on empirical data where every single duration needs to be estimated independently, and so helps lower the variance of the predictions, since prediction variance increases with the number of parameters being estimated.^[1] We show an example later based on simulated data that demonstrates that the prediction volatility can be cut by more than half by using this method over standard triangle methods. Fitting parametric models to each piece will also help us control for changes in retentions and limits, and also enable us to create segmentations in the data, as will be further explained in Sections 2.3 and 7.2.

1.2. Outline

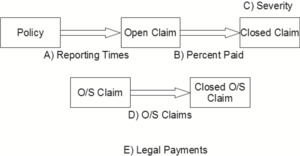
For this model, we break the claims process down into five separate pieces, as shown in Figure 1. Each piece will be discussed in more detail.

Figure 1.Claims process to be modeled

The five parts we will analyze are as follows:

1. The reporting time of each claim
2. The percent of reported claims that are paid, as well as the settlement times of reported claims
3. The severity of each paid claim
4. The final settlement amount of each claim that has outstanding case reserves
5. Legal payments

Section 2 will discuss fitting distributions when right truncation is present in the data, which will be used for some of these pieces; it will also discuss the fitting of hyper-parameters, which is not absolutely necessary to build this model, but can be used to make it more refined. Section 3 will then discuss each of these modeling steps in detail and Section 4 will discuss how to use each piece to calculate the unpaid and ultimate loss and legal estimates. Section 5 will show a numerical example of using this method on simulated data. Section 6 will discuss ways to check this model, and finally, Section 7 will discuss some alternatives and other uses of this model, such as to calculate the volatility of ultimate losses.

2. Technical background

Before we delve into the details of each piece, we first need to explain the process of right truncation and how to build a model when it is present in the data. This will be discussed in the first two parts of this section. It will also be helpful to understand the process of fitting hyper-parameters, which will be discussed in the third part of this section.

2.1. Maximum likelihood estimation with right truncation

When modeling insurance losses, we normally have to deal with left truncation and right censoring. Left truncation is caused by retentions where we have no information regarding the number of claims below the retention. Right censoring is caused by policy limits and is different from truncation in that we know the number of claims that pierce the limit, even if we still do not know the exact dollar amounts. Reported claim counts, for example, which we will be analyzing in this paper, are right truncated, since we have no information regarding the number of claims that will occur after the evaluation date of the data.

We will be using maximum likelihood estimation (MLE) to model reporting times, and MLE can handle right truncation similar to how it handles left truncation. To handle left truncation, the likelihood of each item is divided by the survival function at its truncation point; similarly, to handle right truncation, each item’s likelihood should be divided by the cumulative distribution function (CDF) at its truncation point.

We will illustrate this concept with a simple example using reporting lags. Assume that reporting lags follow an exponential distribution with a mean of one and a half years and that each claim arrives exactly as expected (so that we will receive claims at the 12.5%, 37.5%, 62.5%, 87.5% percentiles of the distribution). We receive exactly four claims each year, and the data evaluation date is 12/31/2014. For 2014, the latest accident year, we expect to receive four claims with the following reporting lags in years: 0.20, 0.71, 1.47, and 3.12. Since our data is evaluated at 12/31/2014 and the right truncation point for this accident year is one year, we will only actually see the first two of these claims. Similarly, for 2013, the next most recent accident year, we will see the first three of these claims, since the right truncation point for this accident year is two years. We will see the first three claims for accident year 2012, and we will see all of the claims for accident year 2011, which is the first year in our study. If we attempted to fit the theta parameter of the exponential distribution with maximum likelihood without any adjustment, we would get a value of 0.93, which equals the mean of the claim lags that have arrived before the evaluation date, and which is clearly incorrect. Fitting theta, now with taking the right truncation point of each accident year into account, yields a theta of 1.506, which is close to the correct value.

2.2. Reverse Kaplan-Meier method for right truncation

When fitting a distribution to data, it is a good idea to compare the fitted curve to the empirical to help judge the goodness of fit. Probably the most common method actuaries use to calculate the empirical distribution when dealing with retentions and limits (i.e., left truncation and right censoring) is the Kaplan-Meier method. Here, however, we have data that is right truncated, which is not handled by this method. We propose a modification to work with right truncated data that we will refer to as the reverse Kaplan-Meier method.

In the normal Kaplan-Meier method, we start from the left and calculate the conditional survival probabilities at each interval. For example, we may first calculate the probability of being greater than 1 conditional on being greater than 0, i.e., s(1)/s(0). We may then calculate s(2)/s(1), and so on. For this second interval, we would exclude any claims with retentions greater than 1, with limits less than 2, and with claims less than 1. To calculate the value of s(2), for example, we would multiply these two probabilities together, that is:

$$s(2)=\frac{s(1)}{s(0)} \times \frac{s(2)}{s(1)}.$$

To accommodate right truncation, we will instead start from the right and calculate the conditional CDF probabilities, e.g., F(9)/F(10), followed by F(8)/F(9), etc. To calculate the value of F(8) for example, we can multiply these probabilities together:

$$\frac{F(8)}{F(10)}=\frac{F(9)}{F(10)} \times \frac{F(8)}{F(9)}.$$

This is the value of F(8) conditional on the tail of the distribution at t = 10. We can plug in this tail value from the fitted distribution and use this empirical curve to test the goodness of fit of our fitted distribution. Using this method, all points of the calculated empirical distribution depend on the tail portion, which can be very volatile because of the thinness in this portion of the data. For the comparison with the fitted distribution to be useful, the right-most point should be chosen at a point before the data gets too volatile. It may be helpful to choose a couple of different right-most points for the comparison.

2.3. Hyper-parameters

This method can be used to help refine some pieces of the model, but it is not absolutely necessary. It involves fitting a distribution to data via MLE but letting one or more of the distribution parameters vary based on some characteristic of each data point. We refer to this technique as the hyper-parameters method, since the distribution’s parameters themselves have parameters, and these are known as hyper-parameters. This can be useful, for example, if we want our reporting times distribution to vary based on the retention.

To set this method up, each claim should have its own distribution parameters. These parameters are a function of some base parameters (that are common to all claims), the claim’s retention, in this example, and another adjustment parameter that helps determine how fast the parameter changes with retention. These base parameters can be the distribution parameters at a zero retention or at the lowest retention. Both the base parameters and the adjustment parameters are then all solved for using MLE. If there are different segments, each segment can be given its own base parameters but share the same adjustment parameters. One or more of the distribution’s parameters can contain hyper-parameters. It is also possible to reparameterize the distribution to help obtain the relationship we want, as will be shown in the following example.

In this example, we will assume that we are fitting a gamma distribution, with parameters alpha and beta, to the reporting times of all claims (which will be explained more later), and that we wish the mean of this distribution to vary with the retention, with the assumption that claims at higher retentions are generally reported later. The mean of a gamma distribution is given by alpha divided by beta, and so we need to reparameterize the distribution. We will reparameterize our distribution to have parameters for the mean (mu) and for the coefficient of variation (CV). The original parameters can be obtained by alpha = 1/CV², and beta = 1/(mu × CV²). Only the first parameter, mu, will vary with the retention.

The first step is to determine the shape of an appropriate curve to use for this parameter. For this, we fit the data with MLE allowing only one parameter for the CV, but having different parameters for the mean for each group of retentions. Plotting these points can help determine whether a linear of a logarithmic curve is the most appropriate. The final curve can then be plotted against these points to help judge the goodness of fit. After doing this, assume that we decided to use the equation, log(mu_r) = log(mu_base) + exp(theta) × log(r/base), where r is the retention of each claim, base is the retention of the lowest claim, and log(mu_base) and theta are parameters that are fit via MLE, in addition to the CV parameter which is common across all claims. We took the exponent of theta to ensure that the mu parameter is strictly increasing with retention. Once this is done, we have a distribution that is appropriate for every retention.

3. Modeling steps

The modeling of each of the five parts will now be explained in detail. Using all of these pieces for the calculation of the unpaid and ultimate projections will be discussed in the following section.

Table 1 shows the data that will be needed for each of the steps.

3.1. Part A: Reported times

In this section, we will explain how to model the reporting lag, that is, the time from the accident date of a claim to the report date. (If report date is unavailable, the create quarter can be used instead by using the first quarter that each claim number first appears.) This will be used to help estimate the pure IBNR portion of unpaid losses later. This data is right truncated since we have no information about the number of claims that will occur after the evaluation date. The right truncation point for each claim is the evaluation date of the data minus the accident date of the claim. We will use MLE to fit a distribution to these times. The exponential, Weibull, and gamma distributions all appear to fit this type of data very well. (A log-logistic curve may also be appropriate in some cases with a thicker tail, although the tail of this distribution should be cut off at some point so as not to be too severe.)

After this data is fit with MLE using right truncation, the goodness of fit should be compared against the empirical curve which can be obtained using the reverse-Kaplan-Meier method, all as described in the previous section. Using this approach, as opposed to using aggregate data, makes it much easier to see if the reporting lag distribution has any significant historical changes. There is also no need to estimate a separate tail piece, as this is already included in the reporting times distribution.^[2]

3.2. Part B: The likelihood of a claim being paid

The second component to be modeled is the percent of reported claims that will ultimately be paid. This can be done very simply by dividing the number of paid claims by the total number of closed claims, but this estimate may be biased if closed with no payment (CNP) claims tend to close faster than paid claims. If this is true and we do not take this into account, we will underestimate the percent of claims that are paid, since our snapshot of data being used will have relatively more CNP claims that would be present after all claims are settled. To give an extreme example to help illustrate this point, say there are two report years of data. All CNP claims settle in the first year, and all paid claims settle in the second year. There are 100 claims each year, and 50% of claims are paid. The evaluation date of the data is one year after the latest year. The first year will have 50 CNP claims and 50 paid claims. When looking at the second year, however, we will see 50 CNP claims and no paid claims, since all of the claims that will ultimately be paid are still open (and we do not know what their final state will be). When we calculate the percent of claims paid using the available data, we will get the following:

$$\frac{50 \text { paid claims }}{50 \text { paid claims }+100 \text { closed claims }}=\frac{1}{3}$$

which is less than the correct value of 50%.

Instead, we will suggest an alternative approach. For the first step, we fit distributions to all paid claims and to all CNP claims separately. (If the distributions do not appear different, then the paid likelihood can be calculated simply by dividing and there is no need to go further.) There will still be many open claims in the data that we do not know what their ultimate state will be, making the ultimate number of paid and CNP claims unknown, and so this data is right truncated. The right truncation point for each claim is equal to the reported date subtracted from the evaluation date. The exponential, Weibull, and gamma distributions all appear to be good candidates for this type of data.

The ultimate number of paid claims is equal to the following, where F(x) is the cumulative distribution function evaluated at x:

$$\sum_{i=\text {All Paid Claims}} 1 / F_{\text {Paid }}\left(\text {Evaluation Date}- \text {Report Date}_{i}\right) .$$

And the ultimate number of unpaid claims is equal to:

$$\sum_{i=\text {All CNP Claims }} 1 / F_{C N P}\left(\text{Evaluation Date - Report Date}_{i}\right) .$$

And so, the ultimate percent of claims that are paid is equal to:

$$\frac{\text {Ultimate Paid Claims}}{\text {Ultimate Paid Claims + Ultimate CNP Claims}} .$$

Dividing each claim by the CDF at the right truncation point is similar to performing a chain-ladder method. So, for example, if the settlement lag for CNP claims is uniform from zero to two years, and the settlement lag distribution for paid claims is uniform from zero to three years, the LDF to apply to CNP claims for the most recent year which has a right truncation point of one year equals 1/0.5 = 2, and the LDF to apply to paid claims for this year equals 1/0.333 = 3. The LDFs for the next most recent year with a right truncation point of two years are 1/1 = 1 and 1/0.667 = 1.5 for the CNP and paid claims, respectively. The paid claims will be developed more because of their slower closing pattern. Developing the CNP and paid claims to ultimate and then dividing will reflect the ultimate paid percentage that we expect to observe after every claim has been closed.

The most recent years may have high development factors and may be unstable. To address this, we can make the method more similar to a Cape Cod-like method by weighting each year appropriately according to the credibility of each year. To do this, the weight for each year can be set to the average of the calculated CDF values of each claim multiplied by the claim volume. The paid distribution or the CNP distribution can be used to calculate this CDF, or it can be taken as the average of the two. To give more recent, relevant experience slightly more weight, an exponential decay factor can be applied. Alternatively, the actual number of claims per year can be used instead. For this version, the ultimate claim counts for each year should be multiplied by the ratio of the actual claim count to the ultimate claim count for that year. Using this reweighting technique (that is, dividing by the CDF and then multiplying by an off-balance factor for each year) will not change the number of claims, but it still addresses the bias that is caused from our data being right truncated. Continuing our example, assume that there are six closed CNP claims and four closed paid claims in the most recent year, and nine closed CNP claims and six closed paid claims in the next most recent year. Our initial ultimate estimates for the most recent year equals 6 × 2 = 12 CNP claims and 4 × 3 = 12 paid claims. Our ultimate estimates for the next most recent year equals 9 × 1 = 9 and 6 × 1.5 = 9, for the CNP and paid claims, respectively. The off-balance factor for each year is equal to (6 + 4)/(12 + 12) = 0.4167 for the most recent year and (9 + 6)/(9 + 9) = 0.8333 for the next most recent year. So each CNP claim is counted as 2 × 0.4167 = 0.8333, and each paid claim is counted as 3 × 0.4167 = 1.25 for the most recent year. In the next most recent year, each CNP claim is counted as 1 × 0.8333 = 0.8333, and each paid claim is counted as 1.5 × 0.8333 = 1.25. The final ultimate number of CNP claims across both years is equal to 6 × 0.8333 + 9 × 0.8333 = 12.5, and the final ultimate number of paid claims equals 4 × 1.25 + 6 × 1.25 = 12.5, resulting in an ultimate likelihood of a claim being paid equal to one half. The probabilities are correct and the weights given to each year are appropriate. This approach gives more weight to the paid claims that typically close later to reflect the fact that we expect relatively more paid claims to close in the future. We will refer to this approach as right truncated reweighting. This approach will be used when building more complicated models on this type of data.

So far, we have calculated the total percentage of claims that will be paid; this will be used for the calculation of pure IBNR. We also need to determine how this percentage changes with duration to be able to apply this to currently open claims for calculation of IBNER (incurred but not enough reported). If paid claims have a longer duration than CNP claims, then it should be expected that the paid percentage should increase with duration, since relatively more CNP claims will have already closed earlier. So the longer a claim is open, the more chance it has of being paid. To calculate this, we can use Bayes’ formula as follows:

$$\begin{array}{l} P(\text { Paid } \mid t \geq x) \\ =\frac{P(t \geq x \mid \text { Paid }) \times P(\text { Paid })}{P(t \geq x \mid \text { Paid }) \times P(\text { Paid })+P(t \geq x \mid C N P) \times P(C N P)} \\ =\frac{s_{\text {Paid }}(x) \times P(\text { Paid })}{s_{\text {Paid }}(x) \times P(\text { Paid })+s_{C N P}(x) \times P(C N P)} \end{array} \tag{3.1}$$

where t is the time from the reported date of the claim and x is the duration for each year. It is also possible to calculate the paid likelihoods for claims closing at exactly a given duration (that is, not conditional, as in equation 3.1) by using the PDFs instead of the survival functions in formula (3.1). These values can then be used to compare against the actual paid likelihoods by duration as a sanity check. The conditional likelihoods cannot be used for this since these likelihoods represent the probability of a claim being paid given that it has been open for at least a certain number of years, but not exactly at that time.

A more detailed model that also incorporates outstanding claims can be built, where instead of just modeling the lags and probabilities of two states (paid and CNP), the outstanding state is modeled. Once claims are in the outstanding state, they can then transition to either the paid or CNP states. All of these states and transitions can be modeled using the same techniques discussed in this section. The ultimate probability of a claim being paid is then equal to the probability of a reported claim being paid (before transitioning to an outstanding state, that is) plus the product of the probabilities of transitioning to an outstanding state and of transitioning from an outstanding state to a paid state. This is a mini Markov chain model, with bias correction caused from the right truncation of the data. If open claims are assigned different “signal” reserves that represent information about the possibility of payment for each claim, then a more detailed Markov chain model can be built that incorporates the probability of transitioning to and from each of these “signal” states.

Another possible refinement is to have the paid (or other state) likelihoods vary by various factors, such as the type of claim or the reporting lag, by building a GLM on the claim data. To account for the bias caused from the data being at an incomplete state, right truncated reweighting can be used to calculate the weights for the GLM, and a weighted regression can be performed; this will account for the bias without altering the total number of observations. The settlement lag distributions can even be allowed to vary by different factors using the hyper-parameters approach. The resulting probabilities will be the paid (or other) likelihoods from time zero, which can be applied to new, pure IBNR claims. For currently open claims for calculation of IBNER, Bayes’ formula (3.1) should be used to calculate the conditional probabilities given that a claim has been open for at least a certain amount of time. If the settlement lag distributions were allowed to vary, the appropriate distribution should be used for this calculation as well.

We should note that using right truncated reweighting for the GLM and then again adjusting the resulting probabilities is not double counting the effects of development. The former is to account for the fact that the data used for modeling is not at ultimate, while the latter is needed to reflect how the probability of a claim being paid varies over time.

It may seem odd at first that the probabilities for open claims are developed and so will always be higher than the probabilities used to apply to new, pure IBNR claims (if this is how claims develop, which it often is). If everything develops as expected, the total predicted number of paid claims will not change, as will be illustrated. Using an example, there are 100 claims and half of these claims will be paid. All unpaid claims close in the first year and all paid claims close in the second year. The initial, unconditional probability to apply to new claims is 50%. After a year, we will assign 100% probability of being paid to all the remaining claims. Initially we predicted that half of the 100 claims will be paid, which is 50 claims. After a year, no actual claims were paid and we will predict that 100% of the 50 remaining claims will be paid, which also equals 50 claims. This estimate would be biased downwards if we did not apply this adjustment to calculate the conditional probabilities.

3.3. Part C: Severity portion

This portion involves fitting an appropriate severity distribution to the claim data. Before doing so, all losses should be trended to a common year. We will also need to take into account that more severe claims tend to be reported and settled later. It is technically possible to have the paid settlement time distribution vary with claim size and use right truncated reweighting here as well, but this approach will likely not be accurate, since only a few large claims may have settled earlier. Because this problem is also relevant to constructing increased limit factors in general, we will elaborate on this in detail. There are many ways that this can be accounted for, but we will only discuss a couple.

The first way is to use the hyper-parameters approach discussed earlier. Claim severity can be a function of the reporting lag, the settlement lag, both, or the sum of the two, which is the total duration of the claim. If these lag distributions were made to vary by retention or by other factors, it may be more accurate to model on the percentile complete instead of the actual lag. To give an example of using the hyper-parameters approach, if we allowed the scale parameter of our distribution to vary with duration, this would be assuming that each claim increases by the same amount on average, no matter the size of the claim. (Note that this may be a poor assumption, as it is more likely that the tail potential increases with duration, since the more severe claims tend to arrive at the later durations.) The limited expected value (LEV) at any lag can now be calculated. This LEV can be used directly if solving for ultimate losses by simulating claim arrival times. If using a closed-form solution, a weighted average of the LEVs can be calculated by using the (conditional) reporting times and/or settlement times distributions. If the total duration was used, the distribution for total duration can be obtained by calculating the discrete convolution of the reporting and settlement times distributions.^[3] If we wanted to calculate a single distribution that represents the expected amount of claims that will be settled in each duration, we can do the following. We will first note that if survival values are generated from a loss distribution, and these survival values are then converted into a probability density function (PDF) by taking the differences of the percentages at each interval, and then this data is refit via MLE using these PDF percentages as the weights (by multiplying each log-likelihood by its weight), the original distribution parameters will be produced. (This can be confirmed via simulation.) The values for each likelihood can either be the average of the two values for each interval, or more accurately, can be represented as a range. MLE can be performed using ranges by setting each likelihood to the difference of the CDFs at the two interval values. This can also be done by generating the PDF values from the distribution directly, but in order to be accurate, this would need to be done at very fine increments. Using this, we can generate a single distribution based on the percentages of claims expected to be settled in each duration by generating the PDF tables for each duration as mentioned, and then setting the total sum of the weights for each duration to equal the percentage of claims expected to be settled in each duration. (It is possible that this mixed distribution of durations may not be the same as the original distribution used to fit a single duration. If this is the case, parameters can be added by creating a mixed distribution of the same type as the original distribution. There is no fear of adding too many parameters and over-fitting here, since we are not fitting to actual data, but to values that have already been smoothed.) The survival percentages generated should start at and be conditional on the lowest policy retention and go up to the top of the credible region for the severity curve. This will make the mixing of the different duration curves more properly reflect the actual claim values and make the final fitted distribution more accurate.

Another way to account for the increasing severity by duration is to use a survival regression model called the Cox proportional hazards model. This model does not rely on any distribution assumptions for the underlying data, as it is semi-parametric. It can also handle retentions and limits, i.e., left truncation and right censoring. As opposed to a GLM that models on the mean, the Cox model tells how the hazard function varies with various parameters. The Cox model is multiplicative, similar to a log-link function in a GLM. The form of the model is $H_i(t)=H_0(t) \exp \left(B_{i 1} X_{i 1}+\right. \left.B_{i 2} X_{i 2}+\cdots\right)$, where H_i(t) is the cumulative hazard function for a particular risk at time t, H₀(t) is the baseline hazard, roughly similar to an intercept (although this is not returned from the model), and the B’s and X’s are the coefficients and the data for a particular risk, respectively. The cumulative hazard function, H(t) is equal to: H(t) = −ln[s(t)], and so s(t) = exp[−H(t)]. It can be seen from this formula that a multiplicative factor applied to the cumulative hazard function is equivalent to taking the survival function to a power.^[4] We will use this fact below. A full discussion of the Cox model is outside the scope of this paper.^[5]

Assuming that we are modeling on the total duration of each claim, with this approach we are assuming that the hazard function of the data changes with the duration. The hazard can be thought of very roughly as the thickness of the tail, and so we are assuming that the tail is what increases with duration.

Initially, a Cox model should be run on the individual loss data with a coefficient for each duration to help judge the shape of the curve for how the hazard changes with duration. Next, another model should be fit with a continuous coefficient either for the duration or the log of duration, or any other function of duration that is appropriate. Different segments that may be changing by year can also be controlled for with other coefficients.^[6]

Assuming the log of duration was used, the pattern for how the severity curve changes with duration, d, can be obtained from the results of the Cox model, as follows:

$$\begin{array}{l} \text{Relative Hazard}\ (d)\\ =\exp (\text {Cox Duration Coefficient} \times \log (d)) \\ =d^{\text {Cox Duration Coefficient }} \end{array} \tag{3.2}$$

There are two ways that will be discussed to create severity distributions using this information. Before we explain the first method, we first need to mention that if an empirical survival curve is generated from claim data using the Kaplan-Meier method, and this survival function is then converted to a PDF and fitted with MLE, as explained, the parameters will match those that would be obtained from fitting the claim data directly with MLE. (This can be confirmed via simulation as well.) The first way involves first calculating the empirical survival curve at the base duration, where the base duration is the duration that is assigned a coefficient of zero in the Cox model. To do this, instead of using the probably more familiar Kaplan-Meier method to calculate the empirical survival function, we use the Nelson-Aalen method to calculate the empirical cumulative hazard function. As a note on the Nelson-Aalen method, calculating the cumulative hazard and then taking the negative of the natural logarithms to convert to a survival function will produce very similar values to the survival values produced from the Kaplan-Meier method. The Nelson-Aalen estimate is equal to

$$H(t)=\sum_{i \leq t} \frac{d_{i}}{n_{i}},$$

where d_i is the number of events in each interval and n_i is the number of total risks that exist at each interval. To calculate the hazard at the base duration using the coefficients from the Cox model, the following formula can be used:

$$H_{0}(t)=\sum_{i \leq t} \frac{\sum_{E a c h R i s k} 1 / \exp \left(\operatorname{coefficient}\left(d_{i}\right)\right)}{n_{i}}. \tag{3.3}$$

The only difference from the normal Nelson-Aalen formula is that instead of counting all events the same, as one, each event is counted as the inverse of the exponent of the sum of its coefficients.

Using this, we can calculate the survival function at the base hazard by taking the negative of the natural logarithm of the cumulative hazard. With the base survival function, we can now calculate the survival function at any duration, d, using the formula

$$s_{d}(t)=s_{\text {Base }}(t)^{\text {Relative Hazard }(d)} \tag{3.4}$$

The survival functions at each duration can then be converted to probability distribution functions and then fit with MLE as shown above. Doing this will produce a distribution for each duration (or duration group, if durations were combined to simplify this procedure). A single distribution representing a weighted average of the expected durations can also be obtained by combining the data from multiple durations together and weighting each according to the expected percentage of claims expected to be settled at each duration. (Note that this new distribution may not be the same type as the original distribution as mentioned.) Alternatively, another way that does not require fitting a distribution at every duration is to only fit a distribution to the base duration. The fitted survival values can be produced at the base duration using this distribution, and the survival values at any duration can then be obtained by taking this base survival function to the appropriate power. The limited expected values can now be obtained by “integrating” the survival values at the desired duration, since

$$\operatorname{LEV}(\text { Retention,Policy Limit })=\int_{\text {Retention }}^{\text {Retention+PolicyLimit }} s(x) d x,$$

where by LEV(Retention, Policy Limit), we mean the limited expected value from the retention up to the retention plus the policy limit. To do this discretely, we can use this formula as an approximation:

$$\begin{array}{l} \text { LEV }(\text { Retention, Policy Limit }) \\ \quad=(\text { Width of } s(x) \text { Increments }) \times \sum_{\text {Retention }}^{\text {Retention }+ \text { Policy Limit }} s(x) . \end{array}$$

The thinner the increment width that the survival values are calculated at, the more accurate this will be. Putting this together, the formula to calculate the LEV at each duration d is

$$\begin{array}{l} L E V_{d}(\text { Retention, Policy Limit }) \\ \quad=\text { Width } \times \sum_{\text {Retention }}^{\text {Retention }+ \text { Policy Limit }} S(x)^{\text {Relative Hazard (d) }} \end{array} \tag{3.5}$$

The second method to construct distributions for each duration is similar except that it involves adjusting the actual claim values instead of the survival or hazard functions. We can use the well-known relationship for adjusting a distribution for trend, F(x) = F′(ax) (Rosenberg and Halpert 1981), where F(x) is the cumulative distribution function of the original distribution before adjusting for trend, F′(x) is the same after adjusting for trend, and a is the trend adjustment factor. Similarly here, using survival functions instead of cumulative distribution functions, we can solve for the adjustment factor for every value of x that satisfies, s(x) = s′(ax) = s(ax)^{Desired Adjustment}, or equivalently, s(x)^{1/Desired Adjustment} = s(ax), since the latter is computationally quicker to solve. The survival values can be determined from either the empirical Kaplan-Meier survival function or from a fitted survival function applied to the entire data set. This factor, a, can be determined for every claim amount and duration by backing into the value of a that satisfies the equality. Once this is done, all of the original loss data can be adjusted to the base duration, and then a loss distribution can be fit to this data. We can use this same method to adjust the claim data to any duration, or alternatively, any of the methods discussed in this section can be performed to derive LEVs at all of the durations.

If one is using a one- or two-parameter Pareto distribution, this process becomes simpler since taking the survival function to a power is equivalent to multiplying the alpha parameter by a factor. This can be easily seen by looking the Pareto formulas, which will not be shown here. Once the distribution is fit at the base duration using one of the methods discussed, the distribution for any duration can be obtained by adjusting the alpha parameter, as follows:

$$\alpha_{d}=\alpha_{\text {base }} \times \text { Relative Hazard }(d) \tag{3.6}$$

Similar methods can be used if using other types of regression models as well, such as a GLM or an accelerated failure time model, which will not be elaborated on here.

3.4. Part D: Outstanding reserved claims

This section explains the estimating of the ultimate settlement values of claims that currently have outstanding reserves. Note that this is different from open, non-reserved claims in that the reserve amounts here are significant. For example, some companies set up a reserve amount of one dollar or a similar amount to indicate that a claim is open, but that no real estimate of the claim’s ultimate settlement value is available yet.

To calculate the ultimate paid amounts, we will use a logistic GLM (that is a GLM with a logit link and a binomial error term) on all closed claims that have had an outstanding reserve set up at some point in the claim’s lifetime. We will model on the dollar amounts divided by the policy limits using the following regression equation:

$$\begin{aligned} \frac{\text { Paid }}{\text { Policy Limit }}= & B_{1} \frac{\text { Average } O / S}{\text { Policy Limit }} \\ & +B_{2} \exp \left(\frac{\text { Average } O / S}{\text { Policy Limit }}\right). \end{aligned} \tag{3.7}$$

We used the average outstanding value for each claim since the reserve amount of a claim may have changed over time.^[7] Note that this ratio can also be calculated directly by dividing the sum of ultimate paid dollars by the sum of outstanding reserves, but this result may be biased since the ultimate settlement values depend on the dollar amount of reserves setup, and this amount depends on the duration. It is also not as refined as it could be. CNP claims can be included or excluded from this model. If they are excluded, a separate model will need to be built to account for. If they are included, right truncated reweighting should be performed on the claims to avoid any bias.

Formula (3.7) seems to provide a very good fit to some types of data, although sometimes logarithms or other alternatives (such as splines) are more appropriate, depending on the book of business and the company. The logistic model will ensure that the predicted value is always less than one, since the claim cannot (usually) settle for more than the limit. (Some GLM packages may give a warning when modeling on data that is not all ones and zeros, but it should still return appropriate results.) Once again, the fit should be compared to the actual. This model will capture the fact that claims reserved near the policy limit tend to settle for lower on average (since they only have one direction to move), while claims reserved for lower amounts have a tendency to develop upwards, on average. It is also possible to add coefficients for the type of claim and other factors if desired.

3.5. Part E: Legal payments

The legal percentages should be calculated for each duration, since this percentage usually increases with duration. To address credibility issues with looking at each duration separately, a curve should be fit to this data. Once this is done, cumulative percentages should be calculated for each duration by taking a weighted average of the legal percentages from each duration until the last duration. The weights should be based on the expected amount of paid dollars per duration. This pattern can be obtained by looking at the aggregate data, or by using the model from this paper and simulating all years’ losses from the beginning. (This will be discussed a bit more, later, as well). These cumulative legal percentages will be applied to the unpaid losses for each accident year.

The approach we chose to use here is not as refined as it could be. It is also possible to build a more robust model that determines the legal payments separately for each of the parts from Table 1, and takes into account the number claims as well as the limits and retentions by year, etc. We used a simpler method here so as not to over-complicate our approach.

4. Calculation of unpaid losses

Each part of the unpaid loss plus legal expenses now needs to be calculated. Table 2 shows the data that is needed for each part that will be described in detail below. The right-most column also shows which parts of the modeling steps from Table 1 each piece depends on.

4.1. Part 1: Pure IBNR

For the calculation of pure IBNR, we will calculate the frequency of a claim for each policy using a Cape Cod-like method while also controlling for differences in retentions between policies. We will use the following formula to calculate the frequency per exposure unit:

$$\text { Frequency }=\frac{\text { Total Reported Claims }}{\text { Used Exposure Units }} \tag{4.1}$$

where F(x) and s(x) are the CDF and survival function, respectively, calculated at x and Used Exposures Units is defined as:

$$\begin{array}{l} \text{Exposure Units} \\ \times F_{\text{Report Time}}(\text{Eval Date}- \text {Avg Accident Date}) \\ \times s_{\text {Severity}}(\text {Retention}), \end{array} \tag{4.2}$$

The severity distribution should be detrended to the appropriate year before calculating this value. Doing this will take care of the frequency trend component that is a result of retention erosion. If there is a non-zero ground up frequency trend as well, this should also be accounted for. If using premiums, the exposure units can be the on-level premiums divided by the LEV for the policy layer. Dividing by the LEV takes the severity component out of the premium. Similar to the Cape Cod method, we multiply the exposures by the percentage of claims that were expected to have already been reported at this point in time. We obtain this percentage by applying the CDF of reported claim times (Part A) to the right truncation point for each group of policies. So as not give too much weight to older years, decaying weights can be used here as well. To take different retentions into account, we need to consider that a policy with a retention of $100,000 may only see 50% of the ground up claims while a policy with a retention of $200,000 may only see 20%. By multiplying the exposures by the survival function at the retention, we adjust for this. (The severity distribution that should be used should not be calculated at a specific duration, but should be the overall average distribution that would be used to price accounts.)

We then calculate the expected IBNR frequency per policy using this formula:

$$\begin{array}{l} \text{Frequency} \times \text{Exposures} \\ \times s_{\text{Report Time }}(\text{Eval Date}- \text{Avg Acc Date}) \\ \times s_{\text{Severity}}(R), \end{array} \tag{4.3}$$

where “Eval Date” is the evaluation data, “Avg Acc Date” is the average accident data, and “R” is the retention. The exposures times the survival function of the reported times represents the unused portion of the exposures. Once we have this, we can multiply the expected frequency per policy by the paid likelihood, obtained from Part B to get the expected number of paid IBNR claims. We then apply Part C to calculate the average severity for each paid claim by calculating the conditional severity of each paid claim above the retention, that is, LEV(Retention, Policy Limit)/s(Retention). The claim distribution should be detrended to the appropriate year if it is desired to have losses on a historical basis. Otherwise, if trended losses are needed for pricing or profitability purposes, no detrending is needed. The durations, reporting lags, and/or settlement lags should be taken into account if the severity distribution was made dependent on these, by using the appropriate conditional distributions given the current reporting lag of each claim.

4.2. Part 2: IBNER on non-reserved claims

For each open non-reserved claim, we need to calculate the probability of it being paid given its current duration using formula (3.1) from Part B above. Severities can be calculated taking into account each claim’s reporting lag and the conditional settlement times distribution given its current settlement lag. Multiplying these two pieces together yields the expected value of IBNER for each claim. Summing up all of these values will yield the total IBNER on opened, non-reserved claims for the entire book.

4.3. Part 3: IBNER on reserved claims

All that is needed for this part is to apply the model from Part D to all open reserved claims to produce the expected paid ratio to policy limit for each claim, and then multiply each percentage by the policy limit to obtain the dollar amount. Subtracting the total outstanding reserves from this number will yield the IBNER for these claims. Note that this amount can be both positive and negative.

4.4. Part 4: Legal payments

The appropriate cumulative legal percentage from Part E should then be applied to each accident year’s total unpaid losses to calculate the total expected legal payments, taking into account the age of each year. This part is only needed if legal payments are paid outside of the policy limits; otherwise, they should be included in Part C, in the average severity.

4.5. IBNR and ultimate losses

Taking the sum of the four parts above (sections 4.1–4.4) will yield the unreported loss plus legal estimates per year. Adding this to the incurred losses will produce the ultimate indications. It is also possible to calculate the losses for a prospective year of policies with the expected makeup of retentions and policy limits from the beginning to derive an estimate of the expected ultimate losses for the prospective period. This can be done for historical periods as a check as well.

5. Numerical example

We will now illustrate this method with an example using simulated data. To simplify, we will not include any outstanding claims or legal payments, so only Parts A (reporting times), B (percent of claims paid and settlement times), and C (claim severity) will be needed. We will also assume that the claim severity does not change with duration or year, and that all claims occur on the first day of each year. We first walk through an example using a particular simulation run chosen at random, and then discuss the results of running many simulations.

Claim reporting and settlement times were simulated from exponential distributions, with a mean of 2 years for reporting times, and means of 4 and 3 years for the settlement times of claims that end up being paid and unpaid, respectively. Claim frequencies were simulated from a negative binomial distribution having a variance-to-mean ratio of 2 and a frequency per policy of 0.5 (for claims above the retention). Each claim had a probability of 20% of being paid. Claim severity was simulated from a lognormal distribution with mu and sigma parameters of 9 and 2, respectively. All policies had a retention of half a million and a policy limit of one million. We simulated ten years of data, with 1,000 accounts each year. Tables 3 and 4 show what the aggregate loss triangle looks like for this simulation run, and the respective link ratios for that run. Note the large amount of volatility in the link ratios.

We will now use the method described in this paper. Following Part A, the first step is to fit an exponential distribution to the reporting times of all claims using MLE, taking the right truncation point of each year’s claims into account. Doing this yields a mean of 1.99, very close to the actual value of 2, which is not surprising given the large number of reported claims. Using this, we calculate the value of the CDF at the right truncation point for every policy (which is the evaluation date of the data minus the average accident data of each policy), and then multiply this by the number of exposures to produce the number of used exposures per year. Dividing the total number of claims by this number yields the excess claim frequency per policy. Normally, we would also multiply by the survival function at each claim’s retention to produce the ground up frequency, as in formula (4.2); we chose to skip this step for simplicity since all policies have the same retention in this example. The results are shown in Table 5. The bottom right of this table shows that the final calculated frequency per policy was 0.500, which matches the actual value used to simulate the data. Again, this accuracy is not surprising given the large number of total claims.

We now continue with Part B, and fit distributions to all of the paid and CNP claims separately, also with taking the right truncation point of each claim into account. The fitted means of the exponential distributions for the paid and CNP claims were 4.17 and 2.91, not far from the actual values of 4 and 3, respectively. We then develop each claim by taking the inverse of the CDF at the right truncation point, and add up all of these values to produce the ultimate number of paid and CNP claims per year as detailed in Section 3.2. We can then estimate the percentage of claims that are paid each year by dividing. To be more similar to a Cape Cod-like method, as mentioned, to calculate the weights given to each year, we first calculate the average of the paid and the CNP CDF values for each claim. We then take the average of these values across all claims for each year. Using this method, older, more mature years are given more weight and newer, greener years are given less. To place some more weight on the more recent experience, a yearly exponential decay factor can be applied, as mentioned above in Section 3.2, but we did not do so in this example for simplicity. The results are shown in Table 6. The final calculated value for the percent of claims paid was 21.2%, close to the true value of 20%.

Note how both the results in this table (minus the latest two years) as well as the previous table that shows claim frequency were relatively stable by year, even with volatile data such as this. This is usually not the case with loss development factors, as can be seen from the triangle in Table 4.

We then use formula (3.1) to solve for the conditional percent of claims paid given that a claim has been open for a certain amount of time. This percentage needs to be calculated for every open claim and depends on the evaluation date of the data and the report lag of each claim. The average percentages for each year are shown in Table 7. Note how the likelihood of being paid is higher for claims from older years which have been open for longer; this was expected since the average settlement time for paid claims was longer than that of unpaid claims.

The final piece is Part C, where we estimate the parameters of the severity distribution. Fitting a lognormal distribution to the data using MLE, taking the retention and limit of each claim into account produced mu and sigma parameters of 11.5 and 1.45, compared to the true parameters of 9 and 2. Using these parameters to calculate the average limited expected value for the appropriate retention and limit yields $479,726; the actual value was $469,588. (In practice, if all retentions and limits are the same and average severity does not appear to significantly change with the duration, it would be more efficient to calculate the average of the claim values directly, instead of fitting a distribution.)

We now use the results from steps A, B, and C to estimate the unpaid losses per year and calculate the pure IBNR and the IBNER per policy. Recall that pure IBNR is calculated at the policy level by multiplying the unused exposures by the claim frequency and multiplying that by the expected percentage of claims that will be paid and the claim severity (formula 4.3). IBNER is calculated at the claim level by multiplying the likelihood that each claim will be paid given its current duration (formula 3.1) by the severity. Results are then aggregated by year. Adding paid losses yields our ultimate projections. The results are shown in Table 8.

Table 9 shows how the results from this simulation compare to the actual.

Running many simulations confirms that this method is unbiased, even with a tail that extends for another 10 to 15 years past the evaluation date of the data. For comparison with a standard triangle method, we used the Cape Cod method with the modified Bondy method (Boor 2006) for estimating the tail, where the tail is set to the square of the latest loss development factor; this was about correct, although we did not penalize for any overall tail bias. Running 5,000 simulations showed a coefficient of variation for total unpaid losses for our method of 11.1% compared to 23.1% for the aggregate triangle method, meaning that in this example, our method cut the standard deviation down by more than half. The difference in the ultimate projections was a bit under 40%, also quite dramatic. As the data became sparser and we decreased the number of accounts per year, the benefit of our method over the triangle method became more pronounced, and it became smaller as we increased the number of years or accounts, both as expected. Any change that made the data more volatile, such as increasing the frequency variance-to-mean ratio, increasing the sigma parameter in the severity distribution, or extending the settlement times of claims, decreased the difference between the two methods, although not too significantly. At first, the direction of this change may seem surprising, but the fact is that as data becomes more volatile, there is less that can be done with it. As an extreme example, for data that is so volatile that has almost no credibility, any method used on it will perform just as poorly, since the volatility is coming from the data and not from the predictions.

We should mention that the differences in volatility mentioned are overstated since no human input was used for selecting the best loss development factors. On the flip side, though, no penalty was given for any inaccuracy of the tail estimate. But, regardless, it should not be surprising that this method can lower the volatility by a very large margin; each parameter needed for predicting ultimate losses is estimated using the entire data, as opposed to the triangle method where each “parameter” only uses data from a single duration. In addition, the estimated parameters from the latter part of the triangle are often very volatile and affect the entire estimate since they feed into all the earlier age-to-ultimate factors.

6. Checking

The most obvious way to check this model is to compare the ultimate results to that produced from a standard triangle analysis. Results are not expected to match, but this should still give some indication as to the appropriateness of the model.

If settlement times from Part B were calculated for times of paid claims only, that is, not including outstanding reserved claims, then paid loss development factors can be produced by starting each year from the beginning and calculating the expected losses at each duration. Loss development factors can then be calculated from these expected payments by duration, and these can then be compared to the factors obtained from a triangle method as a sanity check. It is also possible to use these paid loss development factors directly as an alternative. Producing incurred loss development factors is more complicated, as we would also need to take into account when reserves are set up, how they change, and when they will ultimately be paid.

7. Refinements and alternative models

7.1. Paid-only model

A simplified version of this model only uses paid losses and does not consider reported or reserved claims. With this approach, Parts B (percent paid and settlement times) and D (reserved claims) can be left out of the model since we are only interested in the settlement of paid claims. Part A (reporting times) will be modified to only include paid claims and will now model the complete reporting plus settlement duration of each claim. This approach does not take advantage of all of the data that the full model does, but is much easier to implement. With this version, we also do not have to worry about dependencies between reporting and settlement times, and so this can also serve as a test for the full version of the model.

With this paid-only model, more accurate modeling by retentions can also be performed. In the full model, we modeled on the retention of each policy, so for example, a 50 million dollar claim on a policy with a one million retention would only be considered under the one million retention group. With this new model, however, a Kaplan-Meier like approach can be used and this claim can be counted under all retentions up to 51 million, since this claim would still have occurred at all of these retentions. To model this, we would use the MLE hyper-parameters method, but claims can be counted multiple times in all of the retention groups that they could have occurred at. Normally, the Kaplan-Meier method is done at increments of every claim level, but this is clearly not possible here because of performance constraints. Instead, the method can be performed using wider intervals. This approach is not possible with the full version since the ultimate paid amounts for each claim in the model is unknown.

7.2. Segmentations using mixed models and Bayesian credibility

Our model consists of a bunch of different parametric distributions and GLMs. Each distribution can be broken into finer segments and incorporate credibility by building a Bayesian model. Similarly, instead of using GLMs, generalized linear mixed models (GLMMs) can be used to incorporate credibility by segment. To produce credibility weighted estimates, it is better to run a prospective year from the beginning instead of adding the credibility weighted unpaid estimates to actual losses. If this is not done, the unpaid portion may be credibility weighted, but the actual losses that already occurred still need to take credibility into account in order to be useful for a prediction. Alternatively, initial estimates can be produced without taking credibility into account, and these estimates can then be credibility weighted. Further discussion is outside the scope of this paper.

7.3. Differences by retention

All of the reporting and settlement time distributions can be made to vary with the retention of each claim by using the hyper-parameters approach discussed above in Section 2.3. This will take into account that larger claims, and thus policies with higher retentions, may have slower reporting and settlement of claims.

7.4. Copulas

As an alternative to using the hyper-parameters and the other approaches mentioned, normal or t copulas can be used instead to take into account the dependencies of the reporting, settlement, and claim severity distributions. A further discussion is outside the scope of this paper.

7.5. Calculation of volatility

This model can also be used to estimate the volatility in the IBNR or ultimate losses, either in closed form or via simulation. Alternatively, our framework can also be used to estimate the uncertainty in the loss predictions resulting from a regular triangle method. To do this, losses will need to be simulated and triangles can be generated from these losses. Simulating a paid triangle is relatively straightforward, but building a reported triangle is more difficult since it involves simulating the changes in each claim’s outstanding reserve values over time. The frequency of each claim having a reserve change per year or quarter can be calculated directly. For the average magnitude of each change, Part D above (Section 3.4) can be modified to model all reserve changes, instead of just changes from the outstanding amount to the paid amount. Now, given a starting reserve (as a percentage of the limit), we can calculate the expected reserve after the change. To be able to simulate, though, we need to build distributions around these expected values. To do this, a Beta distribution can be fit to the data using the hyper-parameters approach to set the mean equal to the predicted value from the GLM and allowing the volatility (that is the sum of the alpha and beta parameters) to be solved for using MLE. Once this is done, a Beta distribution will be available for each starting reserve amount that can be used to simulate the magnitude of the change. Once a triangle is simulated, LDFs can be calculated (and ideally smoothed) and a method similar to that used to calculate the actual IBNR and ultimate losses can be performed. Running many simulations will yield the distribution of the prediction errors, either on an absolute basis, or for a one-year time horizon, which is needed for Solvency II.

8. Conclusions

The goal of the frequency-severity development approach presented in this paper is improved accuracy and better segmentation. This model can also produce valuable information regarding the expected frequency and severity of individual policies, provide a better framework for investigating how the reporting and settlement patterns may be changing over time, and generate volatility estimates. A large loss load can be easily calculated as well using the severity distribution. All of the benefits of this model, however, need be evaluated against the additional effort involved. For cases involving very volatile or sparse data, including low frequency-high severity books of business, aggregate triangle methods start to struggle and their predictions can even become very questionable at times. In these scenarios, the case for building a more detailed model, such as the one presented in this paper, becomes even stronger. This model also takes many factors into account that triangle methods do not, such as the settlement lag of each claim and the outstanding amounts of each reserved claim, individually and not in aggregate, and so can be used to produce more accurate, refined estimates.