What Actuaries Should Know About Nonparametric Regression With Missing Data

1. Introduction

Consider a pair of variables (X, Y). Suppose that we are interested in prediction of Y given X = x. The optimal predictor m(x), which minimizes the conditional mean squared error {(Y − μ(x))²⏐X = x} among all possible predictors μ(x), is the conditional expectation:

$$m(x):=\mathbb{E}\{Y \mid X=x\}=\int y f^{Y \mid X}(y \mid x) d y \tag{1.1}$$

Here $f^{Y \mid X}(y \mid x)$ is the conditional density of Y given X. If no assumption about the shape of m(x) is made then (1.1) is called the nonparametric regression of response Y on predictor X. The familiar alternative to the nonparametric regression is the parametric linear regression when the actuary assumes that m(x) ≔ β₀ + β₁x and then estimates parameters β₀ and β₁. While classical parametric regression and its actuarial applications are well known (see Frees 2010; Frees, Derrig, and Meyers 2014; and Charpentier 2015), modern nonparametric regression is less familiar to actuaries. As a result, let us begin with presenting several examples that shed light on nonparametric methodology and a variety of casualty actuarial applications. A primer on nonparametric series estimation will be presented in Section 2.

Figure 1 presents two familiar datasets. For now let us ignore curves and concentrate on observations (pairs (X_l, Y_l), l = 1, 2, . . . , n) shown by circles. A plot of the pairs (X_l, Y_l) in the xy-plane (so-called scattergram or scatter plot) is a useful tool to get a first impression about a data at hand. Let us begin with analysis of the top diagram. The scattergram exhibits a portion of the automobile insurance claims data from a large midwestern (US) property and casualty insurer for a private passenger automobile insurance (Frees 2010, 16, 135). The dependent variable Y is the amount paid on a closed claim, in (US) dollars, and the predictor X is the age of the operator. Only claims larger than $10,000 are analyzed (two claims larger than $60,000 are omitted as outliers). Because the predictor is the random variable, the regression (1.1) may be referred to as a random design regression.

Figure 1.Linear and nonparametric regressions for two classical datasets. Observations are shown by circles, linear and nonparametric regressions by solid and dashed lines, respectively. Sample sizes in the top and bottom diagrams are 124 and 108, respectively.

An appealing nature of the regression problem is that one can easily appreciate its difficulty. To do this, try to draw a curve m(x) through the middle of the cloud of circles in the scattergram that, according to your own understanding of the data, gives a good fit (describes a relationship between X and Y) according to the model (1.1). Clearly such a curve depends on your imagination as well as your understanding of the data at hand. Now we are ready to compare our imagination with statistical estimates. The solid line shows us the classical linear least-squares regression. It indicates that there is no statistically significant relationship between the age and the amount paid on a closed claim (the estimated slope of 14.22 is insignificant with p-value equal to 0.7). Using linear regression for this data looks like a reasonable approach, but let us stress that this is up to the actuary to justify that the relationship between the amount paid on a claim and the age of the operator is linear and not of any other shape. Now let us look at the dashed line which exhibits the nonparametric estimate whose shape is defined by data. How this estimate is constructed will be explained in Section 2. The nonparametric regression exhibits a pronounced shape which implies an interesting conclusion: the amount paid on closed claims is largest for drivers around 68 years old and then it steadily decreases for both younger and older drivers. (Of course, it is possible that drivers of this age buy higher limits of insurance, or there are other lurking variables that we do not know. If these variables are available then a multivariate regression, discussed in Section 6, should be used.) Now, when we have an opinion of the nonparametric estimate, please look one more time at the data and you may notice that this conclusion has merit.

The bottom diagram in Figure 1 presents monthly housing starts from January 1966 to December 1974; this is the R test data. An interesting discussion of actuarial values of housing markets can be found in S. Wang and Chen (2014). While the top diagram presents a classical regression data of independent pairs of observations, here we are dealing with a time series where each response $Y_l$ is recorded at a specific time $X_l$, and $X_{l+1}=X_l+1$. The simplest classical decomposition model of a time series is

$$Y_{l}=m\left(X_{l}\right)+S\left(X_{l}\right)+\varepsilon_{l} \tag{1.2}$$

where $m(x)$ is a slowly changing function known as a trend component, $S(x)$ is a periodic function with period $T$ (that is, $S(x+T)=S(x))$ known as a seasonal (cyclical) component (it is also customarily assumed that the sum of its values over the period is zero), and $\varepsilon_l$ are random and possibly dependent components with zero mean; see a discussion in Chapter 5 of Efromovich (1999). While a traditional time series problem is to analyze the random components, here we are interested in estimation of the trend. Note that $\mathbb{E}\left(Y_l \mid X_l=x\right)=m(x)+S(x)$, by its definition the trend is a “slowly” changing (with respect to the seasonal component) function, and therefore the problem of interest is the regression problem with so-called fixed design (compare with the random design in the top diagram) when we are interested in a low-frequency component of the regression; see more in Section 5.1 of Efromovich (1999). Again, please use your imagination and try to draw the trend $m(x)$ via the scattergram. Note that the period of seasonal component is 12 months and this may simplify the task. Now look at the solid line (linear regression is a classical tool used for finding trends); it clearly does not fit the data. Then compare with the dashed line (nonparametric trend). The nonparametric trend clearly exhibits the famous boom and the tragic collapse of the housing market in the seventies, and it nicely fits the scattergram by showing two modes in the trend.

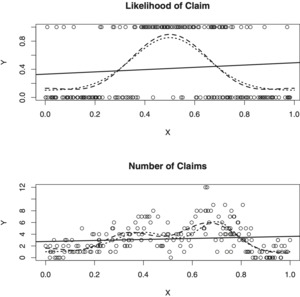
Unfortunately, analysis of real data does not allow us to appreciate how well a particular estimator performs. To overcome this drawback, statisticians use numerical simulations with a known underlying regression function. We are going to use this approach to shed additional light on nonparametric estimation and several attractive actuarial applications of the regression. We begin with the study of the likelihood (probability) of an insurable event, which may be a claim, payment, accident, early prepayment on mortgage, default on a payment, reinsurance event, early retirement, theft, loss of income, etc. Likelihood of an event is the most fundamental topic in actuarial science, and the likelihood may depend on observed variables; see chapter 9 in Klugman, Panjer, and Willmot (2012). Let Y be the indicator of an insurable event (claim), and X be a covariate which may affect the probability of claim; for instance, X may be general economic inflation, or deductible, or age of roof, or credit score, etc. We are interested in estimation of the conditional probability (Y = 1⏐X = x) = m(x). On first glance, this problem has nothing to do with regression, but as soon as we realize that Y is a Bernoulli random variable then we get the regression {Y⏐X = x} = (Y = 1⏐X = x) = m(x). The top diagram in Figure 2 illustrates this problem. Here X is uniformly distributed on [0, 1] and then n = 200 pairs of independent observations are generated according to Bernoulli distribution with (Y = 1⏐X) = m(X) and m(x) is shown by the short-dashed line (this function is a normal density). Because the regression function is known, try to recognize it in the scattergram. Linear regression, as it could be expected, gives us no hint about the underlying regression while the nonparametric estimate (which will be explained in Section 2) nicely exhibits the unimodal shape of the regression.

Figure 2.Linear and nonparametric regressions for simulated data, n = 200. Observations are shown by circles, underlying regression functions, linear and nonparametric regressions by short-dashed, solid and long-dashed lines, respectively.

Now let us consider our second simulated example where $Y$ is the number of claims (events) of interest, or it may be the number of noncovered losses, or payments on an insurance contract, or payments by the reinsurer, or defaults on mortgage, or early retirees, etc. For a given $X=x$, the number of claims is modeled by Poisson distribution with parameter $\lambda(x)$; that is, $\mathbb{P}(Y=k \mid X=x)=e^{-\lambda(x)}[\lambda(x)]^k / k!, k=0$, $1,2, \ldots$ The problem is to estimate $\lambda(x)$, and because $\mathbb{E}\{Y \mid X=x\}=\lambda(x)$ this problem again can be considered as a regression problem. A corresponding simulation with $n=200$ observations is shown in the bottom diagram of Figure 2. The underlying regression function is shown by the short-dashed bimodal line created by a mixture of two Gaussian densities. Again, try to use your imagination and draw a regression curve through the scattergram, or even simpler, try to recognize the regression function in the cloud of circles. The nonparametric estimate is shown by the long-dashed curve and it does exhibit two modes. The estimate is not perfect but it does correspond to the scattergram.

In summary, nonparametric regression can be used for solving a large and diverse number of actuarial problems. We will continue our discussion of the nonparametric regression in the next sections, and now let us turn our attention to the main topic of this paper—regression estimation with missing data when values of some responses and/or predictors are not available. Francis (2005, sec. 4.2), in the review of methods for dealing with missing data in insurance problems, writes that “. . . In large insurance databases, missing data is the rule rather than the expectation. It is also not uncommon for some data to be missed in database used for smaller analytical projects . . .” That review presents several methods that are used by actuaries to adjust for the missing values when performing an analysis:

1. The most common approach is referred to as a complete-case approach (case wise or list wise deletion is another name often used in the literature). It involves eliminating all records with missing values on any variable. Many statistical packages, including R, use this as the default solution to missing values. This method is the simplest, intuitively appealing and, as we will see shortly, for some settings it is even optimal but for others may imply inconsistent estimation.

2. Imputation is a common alternative to the deletion. It is used to “fill in” a value for the missing data using the other information in the database. A simple procedure for imputation is to replace the missing value with the mean or median of that variable. Another common procedure is to use simulation to replace the missing value with a value randomly drawn from the records having values for the variable. It is important to stress that imputation is only the first step in any estimation and inference procedure. The second step is to propose an estimator and then complement it by statistical inference about the properties of the estimator, and these are not trivial steps because imputation creates dependence between observations. Warning: the fact that a complete data is created by imputation should be always clearly cited because otherwise a wrong decision can be made by an actuary who is not aware about this fact. As an example, let us have a sample from a normal distribution (μ, σ²), of which some observations are missed. Suppose that an actuary is interested in the estimation of the mean μ, and an oracle helps by imputing the underlying μ in place of the lost observations. This is an ideal imputation, and then the actuary correctly uses the sample mean to estimate μ. However, if another actuary will use this imputed (and hence complete) sample to estimate the variance σ², the classical sample variance estimate will yield a biased estimate.

3. Multiple imputation is another popular method. It is based on repeated imputation–estimation steps and then aggregation (for instance, via averaging) of the estimates. Multiple imputation is a complicated statistical procedure which requires a rigorous statistical inference.

4. If the distribution of the data is known, then the maximum likelihood method may be used, and its numerically friendly EM (expectation-minimization) algorithm is convenient for models with missing data. Rempala and Derrig (2005) give a nice overview of the EM with applications to insurance problems.

A general discussion of statistical (primarily parametric) analysis with missing data can be found in Little and Rubin (2002) and Enders (2010). There are several classical scenarios for missing data, for which rather general conclusions are made:

1. If missing occurs purely at random then the missing mechanism (and the corresponding data) is called MCAR (missing completely at random). The complete-case approach is typically optimal for MCAR data.

2. If the probability of missing depends on always available (never missing) variable then the missing mechanism is called MAR (missing at random). Consistent estimation is possible and optimal estimation procedure depends on an underlying model.

3. In a general case, when the probability of missing may depend on the value of missing variable, the missing mechanism is called MNAR (missing not at random). Typically no consistent estimation is possible for MNAR data.

The context of the paper is as follows. Section 2 explains how to construct an optimal nonparametric regression estimator for the case of data with no missing values. Here an orthogonal series method, based on classical cosine basis, is explained because it implies best constant and rate of the risk convergence. The fact that the estimator attains the best constant is critical because MAR does not affect rate, hence we must explore the constant to point upon best estimator. Sections 3 and 4 discuss nonparametric regression estimation for MAR data with missing responses and predictors, respectively. Numerical analysis of real and simulated datasets complements theoretical results. Section 5 presents a discussion of results and some open problems.

2. Primer on nonparametric orthonormal series regression estimation for complete data

We are interested in estimating a regression function $m^{\prime}(x)$ on interval $x \in\left[b_1, b_1+b_2\right]$ using a sample $\left(X_1^{\prime}, Y_1\right), \ldots,\left(X_n^{\prime}, Y_n\right)$ from $\left(X^{\prime}, Y\right)$. It is assumed that $\left[b_1, b_1+b_2\right]$ is the support of $X^{\prime}$ and hence $b_1 \leq X_{(1)}^{\prime}$ $\leq X_{(n)}^{\prime} \leq b_1+b_2$ with $X_{(l)}^{\prime}$ being a traditional notation for ordered predictors. (If $\left[b_1, b_1+b_2\right]$ is a subset of the support then in what follows one may consider $Y_l I\left(X_l^{\prime} \in\left[b_1, b_1+b_2\right]\right)$ in place of $Y_l$ with no other changes in the proposed estimator. Here and in what follows $I(\cdot)$ is the indicator.) It is convenient to translate $\left[b_1, b_1+b_2\right]$ onto a standard interval, say $[0,1]$. We can always do this by defining $X:=\left(X^{\prime}-b_1\right) / b_2$ and then estimating $m(x):=m^{\prime}\left(b_2\left(x+b_1\right)\right)$. From now on we consider the pair $(X, Y)$, with $X$ being supported on $[0,1]$, and estimate the regression function $m(x)=\mathbb{E}\{Y \mid X=x\}$

Introduce a classical orthonormal basis $\varphi_0(x)=1$, $\varphi_j(x)=2^{1 / 2} \cos (\pi j x), j=1,2, \ldots$ on $[0,1]$. Note that $\int_0^1 \varphi_j(x) \varphi_i(x) d x=I(j=i)$. Then any square integrable function $m(x)$ that is a function satisfying $\int_0^1[m(x)]^2$ $d x<\infty$ can be written as a Fourier series

$$m(x)=\sum_{j=0}^{\infty} \theta_{j} \varphi_{j}(x) \tag{2.1}$$

In (2.1) the parameters

$$\theta_{j}:=\int_{0}^{1} m(x) \varphi_{j}(x) d x \tag{2.2}$$

are called Fourier coefficients of function m(x). Then the Parseval identity

$$\int_{0}^{1}[m(x)]^{2} d x=\sum_{j=0}^{\infty} \theta_{j}^{2} \tag{2.3}$$

allows us to write down the integral of a squared function via sum of its squared Fourier coefficients. For now this is all that we need to know about orthonormal basis and series expansion.

Our aim is to estimate the regression function m(x) via the expansion (2.1) where the infinite number of unknown Fourier coefficients should be replaced by their estimates. This explains the terminology “nonparametric series estimation.” There are two steps in nonparametric series estimation:

1. Suggest a reasonable estimator of $\theta_j$. Note that this is a traditional parametric problem.

2. Plug into the expansion (2.1) a finite (but possibly increasing with sample size n) number of estimated Fourier coefficients and set all others equal to zero.

We begin with the first step of estimating $\theta_j$. In what follows we present two popular methods of estimation. The former is the classical method of moments when the population mean is estimated by the sample mean. This method is convenient for a random design regression (the predictor X is a random variable with marginal density f^X(x)). In this case, using (1.1), the Fourier coefficient can be written as the expectation,

$$\begin{aligned} \theta_{j} & =\int_{0}^{1} m(x) \varphi_{j}(x) d x \\ & =\int_{0}^{1} \mathbb{E}\{Y \mid X=x\} \varphi_{j}(x) d x=\mathbb{E}\left\{\frac{Y \varphi_{j}(X)}{f^{X}(X)}\right\} \end{aligned} \tag{2.4}$$

Then the method of moments yields the estimator

$$\tilde{\theta}_{j}:=n^{-1} \sum_{l=1}^{n} \frac{Y_{l} \varphi_{j}\left(X_{l}\right)}{\tilde{f}^{X}\left(X_{l}\right)} . \tag{2.5}$$

Here $\tilde{f}^x$ is a series estimate of the marginal density. Namely, write $f^x(x)=\sum_{j=0}^{\infty} \kappa_j \varphi_j(x)$ where $\kappa_j=\int_0^1 f^x(x)$ $\varphi_j(x) d x=\mathbb{E}\left\{\varphi_j(X)\right\}$, and then method of moments yields the estimate $\tilde{\kappa}_j:=n^{-1} \sum_{l=1}^n \varphi\left(X_l\right)$. More about nonparametric density estimate can be found in Section 3.1 of Efromovich (1999), and we will see how it performs in Section 4.

Instead of using the method of moments, for regression problems a numerical integration approach is an attractive alternative. Remember that $\theta_j=\int_0^1 m(x)$ $\varphi_j(x) d x$, and we can evaluate this integral using the available observations. In particular, the following numerical integration is recommended in Section 4.2 of Efromovich (1999)

$$\hat{\theta}_{j}:=(2 s)^{-1} \sum_{l=1}^{n} Y_{(l)} \int_{X_{(l-s)}}^{X_{(l+s)}} \varphi_{j}(x) d x \tag{2.6}$$

where $Y_{(l)}$ are responses corresponding to $X_{(l)}$ and, to take care about boundaries, we define artificial $X_{(l)}:=$ $2 X_{(1)}-X_{(2+l)}$ for $l<1$ and $X_{(l)}:=2 X_{(n)}-X_{(2 n-l)}$ for $l>n$, and $s$ is the rounded-up $(1+\ln (\ln (n+20))) / 2$. The underlying idea of this special numerical integration is that $X_{(l+s)}-X_{(l-s)}$ is inversely proportional to $n f^X\left(X_{(t)}\right) /(2 s)$, and then the estimator is similar to (2.5). Furthermore, the numerical integration can be also used for a fixed-design regression such as in the time series example of monthly housing starts presented in the introduction. As a result, we get a universal estimator for both random and fixed designs.

To finish our discussion of the first step, we note that via a standard calculation (for details, see Section 4.2 in Efromovich 1999) we get for some constant d,

$$\mathbb{E}\left\{\left(\hat{\theta}_{j}-\theta_{j}\right)^{2}\right\}=d n^{-1}\left[1+o_{n}(1)+o_{j}(1)\right] \tag{2.7}$$

Here and in what follows we use a standard notation o_s(1) for vanishing sequences as s → ∞. For instance, if Y = m(X) + σ(X)ξ and ξ is independent standard normal random variable, then d = ∫¹₀[(σ(x))²/f^X(x)]dx. If one wants to estimate d, then this can be done either using a corresponding formula for d or using the universal method based on the following mathematical result.

Suppose that function g(x) is differentiable on [0, 1]. Using sin(jπ) = 0 for j = 1, 2, . . . we get via integration by parts,

$$\begin{aligned} \theta_{j} & =\int_{0}^{1} g(x) \varphi_{j}(x) d x \\ & =-j^{-1}\left[\pi^{-1} 2^{1 / 2} \int_{0}^{1}(d m(x) / d x) \sin (\pi j x) d x\right], j \geq 1 \end{aligned} \tag{2.8}$$

We conclude that Fourier coefficients of a differentiable function decrease and decrease fast. The interested reader can continue (2.8) for the case of twice-differentiable g(x) and check that in this case θ_j decreases proportionally to j⁻².

Now we can explain the universal method of the estimation of d which is based on (2.7) and (2.8). Consider two increasing sequences L_1,n and L_2n and define the universal estimate

$$\hat{d}:=n L_{2 n}^{-1} \sum_{j=L_{1 n^{+1}}}^{L_{1 n}+L_{2 n}} \hat{\theta}_{j}^{2} \tag{2.9}$$

Only the product d̂n⁻¹ is used by a series estimator, and this explains why the factor n in (2.9) does not “blow up” calculations. More about the universal method of the estimation of the parameter d and its statistical properties can be found in Efromovich and Pinsker (1996) and Section 4.1 in Efromovich (1999).

Now let us explain the second step of choosing a finite number of Fourier coefficients used by the series estimator. First of all, according to (2.8), an estimator should be based on low-frequency components. This leads us to a preliminary projection estimator $\tilde{m}(x, J):=\sum_{j=0}^J \hat{\theta}_j \varphi_j(x)$ where $J$ is called a cutoff. Its mean integrated squared error (MISE) can be expressed via Fourier coefficients using the Parseval identity (2.3),

$$\mathbb{E}\left\{\int_{0}^{1}(\tilde{m}(x)-m(x))^{2} d x\right\}=\sum_{j=0}^{J} \mathbb{E}\left\{\left(\hat{\theta}_{j}-\theta_{j}\right)^{2}\right\}+\sum_{j>J} \theta_{j}^{2} \tag{2.10}$$

Now we would like to find the optimal cutoff which minimizes the MISE. To do this we need to avoid an analysis of the infinite sum in the right side of (2.10), and this is possible to do. The Parseval identity allows us to write _j>J θ²_j = ∫¹₀ m²(x)dx − ^J_j=0 θ²_j, and then we can rewrite (2.10) as

$$\begin{array}{l} \mathbb{E}\left\{\int_{0}^{1}(\tilde{m}(x)-m(x))^{2} d x\right\} \\ \quad=\sum_{j=0}^{J}\left[\mathbb{E}\left\{\left(\hat{\theta}_{j}-\theta_{j}\right)^{2}\right\}-\theta_{j}^{2}\right]+\int_{0}^{1} m^{2}(x) d x \end{array} \tag{2.11}$$

Because the integral $\int_0^1 m^2(x) d x$ does not depend on $J$, we can use (2.7) and (2.9) to minimize the MISE with respect to $J$. It is possible to show that this simple procedure leads to rate but not sharp optimal estimation (the terminology will be explained shortly). To improve projection estimator and obtain a sharp estimator, we use “shrinked” estimates $v_j \hat{\theta}_j$, $v_j \in$ $[0,1]$. To understand why, let us remember a classical statistical assertion (it is verified straightforwardly using (2.7)),

$$\begin{array}{c} \mathbb{E}\left\{\left(\lambda_{j}^{*} \hat{\theta}_{j}-\theta_{j}\right)^{2}\right\} \leq \min _{\lambda} \mathbb{E}\left\{\left(\lambda \hat{\theta}_{j}-\theta_{j}\right)^{2}\right\}, \\ \lambda_{j}^{*}=\frac{\theta_{j}^{2}}{d n^{-1}+\theta_{j}^{2}}\left[1+o_{j}(1)+o_{n}(1)\right] . \end{array} \tag{2.12}$$

This result yields two popular methods of improving the projection estimator. The former is called universal thresholding where $v_j=I\left(\hat{\theta}_j^2 \geq 2 \ln (n) \hat{d} n^{-1}\right)$. The latter uses shrinking coefficients $v_j$ which mimic $\lambda_j^*$ defined in (2.12). It is also possible to combine these two methods as explained in Sections 3.3 and 4.2 of Efromovich (1999), and this is how the estimator supported by R-software of that book is constructed. For instance, estimates shown in Figure 2 are: (i) For the likelihood of claim $\hat{m}(x)=0.39-0.27 \varphi_3(x)+$ $0.18 \varphi_5(x)$; (ii) For the number of claims $\hat{m}(x)=3.17$ $-0.32 \varphi_1(x)-1.35 \varphi_2(x)+0.53 \varphi_3(x)-0.54 \varphi_4(x)+$ $0.17 \varphi_5(x)+0.49 \varphi_5(x)-0.52 \varphi_6(x)+0.19 \varphi_7(x)$. Corresponding $\hat{d}$ are 0.18 and 3.9 , so we can compare levels of difficulty for these two regressions.

Finally, let us finish this primer with a theoretical result which explains the notion of sharp-minimax nonparametric estimation. Introduce a class of α-differentiable on [0, 1] Sobolev functions

$$\mathcal{S}(\alpha, Q):=\left\{\begin{array}{l} m: m(x)=\sum_{j=0}^{\infty} \theta_{j} \varphi_{j}(x) \\ \sum_{j=0}^{\infty}\left(1+(\pi j)^{2 \alpha}\right) \theta_{j}^{2} \leq Q \end{array}\right\} \tag{2.13}$$

Consider a random design regression Y = m(X) + σ(X)ε with ε being standard normal and independent of X, σ(x) and f^X(x) being differentiable and f^X(x) > c > 0 on [0, 1]. Then the following lower bound for the MISE is valid,

$$\begin{array}{c} \inf _{\check{m}} \sup _{m \in S(\alpha, Q)} \mathbb{E}\left\{\int_{0}^{1}(\check{m}(x)-m(x))^{2} d x\right\} \\ \geq P(\alpha, Q)[n / d]^{-2 \alpha /(2 \alpha+1)}, \end{array} \tag{2.14}$$

where the infimum is taken over all possible estimators based on a sample of size n, d ≔ ∫¹₀[(σ(x))²/f^X(x)]dx and

$$P(\alpha, Q):=\left[\alpha /(\pi(\alpha+1)]^{2 \alpha /(2 \alpha+1)}[(2 \alpha+1) Q]^{1 /(2 \alpha+1)}\right. \tag{2.15}$$

Furthermore, there exists a series estimator (discussed earlier) whose MISE attains this lower bound. This is why (2.14) is called a sharp minimax lower bound, constant P is called sharp, and n^{−2α/(2α+1)} is called optimal rate of the MISE convergence. The interested reader can verify, using (2.7), (2.10) and (2.13), that a projection estimate with cutoff J = n^1/(2α+1) is rate optimal but not sharp. There are many different nonparametric estimators (kernel, spline, local polynomial, nearest neighbor) that are rate optimal but only a series estimator is known to be sharp minimax. As we shall see shortly, this property becomes important for the case of missing data.

For the case where the regression error ε is not normal, a similar lower bound exists with the coefficient d depending on a corresponding Fisher information (remember that 1/σ² is the Fisher information of normal random variable with variance σ²); see Efromovich (1996) and Chapters 3 and 7 in Efromovich (1999).

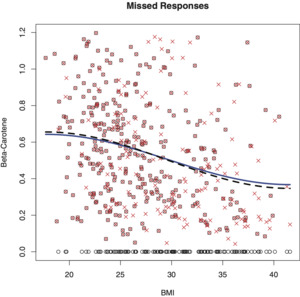
Remark 1 (Causality in Regression). Regression does not shed light on causality, and this is up to the actuary to resolve this issue. The latter is not an issue for all the above-presented examples where causality is plain. For instance, it is clear that the age of driver may be a predictor variable for a car accident and the corresponding loss amount, but not vice versa. On the other hand, there are many situations when we are dealing with a pair of random variables and each can be the predictor. Figure 3 presents such an example. Crosses show n = 441 pairs of observations from the WHEL study of women after breast cancer surgery (see Pierce et al. 2007). The left diagram shows the regression of beta-carotene (based on blood test) versus BMI (body mass index), while the right diagram shows the same data, only now for the regression of BMI on beta-carotene. Regression estimates are shown by solid lines. Note that a BMI of 18.5 to 25 may indicate an optimal weight, a number above 25 may indicate the person is overweight, and a number above 30 suggests the person is obese; at the same time an increase in beta-carotene decreases the likelihood of breast cancer relapse. The shown scattergrams are complicated: there is a huge variability (heteroscedasticity) in both variables and the marginal distributions are far from being homogeneous. Now let us look at the regression estimates. Overall they indicate a negative correlation between the variables (as may be expected) but the relationship is far from being obvious. Note that the curves resemble neither each other nor their inverse functions. The latter is typical for dependent random variables. As a result, it would be wrong to estimate {Y⏐X = x} and then try to use this estimate to infer about {X⏐Y = y}. This conclusion also holds for linear regression; see Casella and Berger (2002).

Figure 3.Nonparametric regression estimates for complete data. The same dataset of size n = 441 is shown in both diagrams by crosses, the solid lines show nonparametric regression estimates.

3. Regression with missing responses

The traditional model of regression with missing responses assumes that we observe a sample from a triplet (X, AY, A). Here the indicator A of availability of the response is the Bernoulli random variable which takes on values zero or one, and if A = 1 then the response is available (observed) and otherwise it is not available (missed). (The reader familiar with R-software can recall that it uses NA (not available) as a logical constant to denote a missing value.) In general there may be dire consequences of missing responses. For instance, suppose that the conditional probability of availability of the response depends on its value; that is,

$$\mathbb{P}(A=1 \mid X=x, Y=y)=h(y) \tag{3.1}$$

Let us show that in this case the regression function is not identifiable. Indeed, the joint (mixed) density of the triplet can be written as (here and in what follows a  {0, 1}),

$$\begin{array}{l} f^{X, A Y, A}(x, a y, a)=\left[h(y) f^{Y \mid X}(y \mid x) f^{X}(x)\right]^{a} \\ \times\left[\left(1-\int_{-\infty}^{\infty} h(y) f^{Y \mid X}(y \mid x) d y\right) f^{X}(x)\right]^{1-a} \end{array} \tag{3.2}$$

The joint distribution of the triplet, as a function in $y$, depends on the product $h(y) f^{Y \mid X}(y \mid x)$ and there is no way to estimate the conditional density $f^{Y \mid X}(y \mid x)$ (and, as a result, the conditional expectation) unless we know $h(y)$, and the latter is typically not the case. As a result, in general (3.1) precludes us from estimation of the regression function. Recall that in the introduction this setting was called missing not at random (MNAR), and more about MNAR can be found in Little and Rubin (2002) and Enders (2010). Discussion of MNAR is beyond the scope of this paper, and let us just mention that a possible solution is based on finding another always observed variable $V$ which makes setting MAR; that is, we get $\mathbb{P}(A=$ $1 \mid X, Y, V)=\mathbb{P}(A=1 \mid X, V)$

In what follows we restrict our attention to the case of MAR responses when

$$\begin{array}{l} \mathbb{P}(A=1 \mid X=x, Y=y) \\ \quad=\mathbb{P}(A=1 \mid X=x)=: h(x)>c>0 \end{array} \tag{3.3}$$

Note that if A = 0 then the response is missed, but the predictor is available and the probability of missing depends only on the value of the always observed predictor.

Let us show that in the MAR case the problem of nonparametric regression has a solution, and furthermore this solution can be based only on complete pairs. Write the joint (mixed) density of the triplet,

$$\begin{array}{c} f^{X, A Y, A}(x, a y, a)=\left[h(x) f^{Y \mid X}(y \mid x) f^{X}(x)\right]^{a} \\ \times\left[(1-h(x)) f^{X}(x)\right]^{1-a} . \end{array} \tag{3.4}$$

It follows from (3.4) that if we consider only complete pairs then the “new” design density (the probability density of predictors in complete pairs) is $g^x(x)=h(x) f^x(x) / q$, where $q:=\int_0^1 h(x) f^x(x) d x=$ $\mathbb{P}(A=1)$ is the probability of observing a complete pair (not missing the response); $q$ can be estimated by the sample mean estimate $\hat{q}:=N / n$ where $N:=\sum_{l=1}^n$ $A_l$ is the total number of complete pairs. This result immediately implies that Fourier coefficients $\theta_j$ in expansion (2.1) can be written as (compare with (2.4))

$$\theta_{j}=\mathbb{E}\left\{\frac{A Y \varphi_{j}(X)}{q g^{X}(X)}\right\} \tag{3.5}$$

Using the density estimator defined in the paragraph below line (2.5), we can use predictors in complete pairs and construct the estimator ĝ^X of g^X. Then the following method of moments estimate of Fourier coefficients (3.5) is proposed (compare with (2.5)),

$$\tilde{\theta}_{j}=\frac{\sum_{l=1}^{n} A_{l} Y_{l} \varphi_{j}\left(A_{l}\right) / \hat{g}^{X}\left(X_{l}\right)}{\sum_{l=1}^{n} A_{l}} \tag{3.6}$$

Note that the estimator (3.6) is based only on complete pairs. Further, because the universal estimator (2.6) is based on numerical integration, it also can be used here for complete pairs; recall that this estimator can be used for both random and fixed designs. More on technical details can be found in Efromovich (2011b).

As a result, we can always use a complete-case approach to solve the problem of MAR responses. Can this approach be improved by taking into account all predictors? There are a number of publications showing, both theoretically and empirically, that a complete-case approach can be improved via an appropriate imputation (recall our discussion of imputation in the introduction) and then using a standard nonparametric regression estimator. In particular, kernel smoothing is explored in Chu and Cheng (1995), nearest neighbor imputation is considered in Chen and Shao (2000), semiparametric estimation is discussed in Q. Wang, Linton, and Härdle (2004), nonparametric multiple imputation is discussed in Aerts et al. (2002), empirical likelihood over the imputed values in Wang and Rao (2002), local polynomials in Gonzalez-Manteiga and Perez-Gonzalez (2004), and local M-smoother in Boente, Conzalez-Manteiga, and Perez-Gonzales (2009). For instance, Boente, Conzalez-Manteiga, and Perez-Gonzales (2009) compared a simplified local M-smoother, based only on complete cases, with an imputed local M-smoother. The conclusion is that both estimators are consistent and robust, the imputed estimator is computationally more expensive but overall its performance is better. A similar approach is used in all above-mentioned research papers where a reasonable complete-case estimator is compared with a proposed estimator based on imputation.

To the contrary of the conclusion made in the above-cited literature, Efromovich (2011b) shows that the complete-case approach can perform on par or better than any other method based on all predictors. Let us explain how this result is established and why there is the controversy. It is known that missing responses do not affect the rate of the MISE convergence; hence to find an optimal estimator we need to find a sharp constant (remember our discussion about sharp constants in Section 2). Under the additional assumption that function h(x) is differentiable and h(x) > c > 0 on [0, 1], it is shown in Efromovich (2011b) that the lower bound (2.14), with m̆ based on a sample of size n from (X, AY, A), holds with new d = ∫¹₀[(σ(x))²/(h(x)f^X(x))]dx. Then it is established that the series estimator of Section 2, based only on complete pairs, is sharp minimax; that is, its MISE attains this lower bound and therefore the complete-case approach is sharp minimax (efficient). As a result, any other approach, based on imputation, multiple imputation, EM, etc., may match the performance of the complete-case approach but not dominate it.

But why do many publications assert that imputation implies better estimation? The answer is simple. Missing does not affect the rate of the MISE convergence, and hence only a sharp constant can point to the optimal solution. If the constant is unknown, then in the literature a reasonable complete-case estimator is compared with a proposed estimator based on imputation and then it is established, both theoretically and empirically, that the latter is better. Note that the root of the controversy is that a reasonable (but not optimal) complete-case estimator is used as a benchmark for the imputation estimator, and then any desired conclusion about superiority of imputation can be achieved.

One more remark about the above-discussed controversy. Until recently a similar situation has been known in parametric regression. Müller (2009), using a theoretical analysis of MAR responses, established a sharp lower bound and then suggested an estimator, based on a kernel imputation, which attains that sharp lower bound. At the same time, a reasonable complete-case estimator, considered in the paper, has been found to be not sharp minimax. This prompted the conclusion of superiority of the imputation for parametric regression. But later, Müller and Van Keilegom (2012) proposed a complete-case estimator which also attains the lower bound. This conclusion coincides with Efromovich (2011b).

Let us explain, using the likelihood approach, why ignoring incomplete pairs does not affect the quality of estimation. Consider (3.4) and the case $A=a=0$ when the response is missed. In this case the likelihood is $f^{x, A Y, A}(x, 0,0)=(1-h(x)) f^x(x)$ and it does not depend on $f^{Y X X}$. Hence, according to the likelihood principle, incomplete pairs contain no information about the parameters of interest and the corresponding Fisher information is zero.

The conclusion is that only pairs with available responses can be considered and then the same nonparametric regression estimator, suggested for the case of data with no missing observations, can be used. Furthermore, even if some predictors in incomplete pairs are also missed or corrupted (and the latter occurs in some datasets), this has no effect on the estimation.

Let us complement the theoretical discussion by several numerical examples. We begin with the WHEL data shown in Figure 3a. Let us simulate n = 441 observations of Bernoulli random variable A with h(x) decreasing in x. Figure 4 shows us the data: crosses and the solid line are the same as in Figure 3a, circles show realizations of (X, AY) with the number N = 312 of complete pairs shown by crossed circles. The dashed line is the nonparametric estimate based on complete cases (crossed circles). Note that not-crossed circles indicate cases with missed responses and observed predictors, while not-circled crosses show us missed responses that would not be available in a real dataset. As a result, Figure 4 is a good tool for understanding the problem, and it indicates that despite the complexity of the setting and losing 30% of responses, which is a rather large proportion even for parametric settings (Enders 2010), the nonparametric estimator based on complete pairs performs well.

Figure 4.Nonparametric regression for the case of missed responses. Crosses and the solid line are identical to ones in Figure 3a, that is, crosses are n = 441 realizations of (X, Y) for the WHEL breast-cancer data. Then a sample of size n = 441 from Bernoulli A is generated, and circles show realizations of (X, AY) with the number of complete pairs N = 312. As a result, for the case of missed responses, available complete pairs are shown by crossed circles, incomplete observations are shown by circles with the corresponding (unavailable for statistical analysis) complete pairs shown by crosses. The long-dashed line shows the nonparametric estimate based on complete pairs.

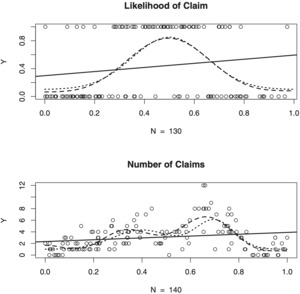
Our next example is based on two simulated datasets shown in Figure 2 where we know the underlying regression functions. Let us make responses available according to h(x) = 0.7 + 0.3 cos(πx). Complete pairs are shown in Figure 5. First of all, we see that the missing mechanism significantly affects the number of available complete pairs. The original n = 200 observations in two datasets are reduced to N = 130 and N = 140 observations, correspondingly (note that N is random and depends on a particular simulation from A). The loss of complete pairs is significant and this may force many statisticians and actuaries to think about imputation, because it is difficult to believe that nothing can be done and the information is completely lost, but as we now know, there is nothing that can be done about this loss. A silver lining is that optimal complete-case estimates, shown by long-dashed lines, are relatively (with respect to shown in Figure 2) good and exhibit unimodal and bimodal shapes of underlying regressions shown by the short-dashed lines.

Figure 5.Nonparametric regression, based on complete pairs, for the case of missed responses. Original data is shown in Figure 2. Number N of complete pairs is shown in the diagrams. The short-dashed, solid and long-dashed lines show underlying regression functions, linear and nonparametric regressions, respectively.

4. Regression with missing predictors

Here we are dealing with a sample from the MAR triplet (AX, Y, A) where

$$\begin{aligned} \mathbb{P}(A & =1 \mid X=x, Y=y)=\mathbb{P}(A=1 \mid Y=y) \\ & =\mathbb{E}\{A \mid Y=y\}=: h(y)>c>0 \end{aligned} \tag{4.1}$$

The Bernoulli random variable A is the indicator of availability (not missing) of the predictor X; in (4.1) the first equality is the assumption, the second equality is an identity, and the third equality is the definition of positive function h(y).

Statistical literature devoted to this case of missed predictors is practically next to none because the problem is dramatically more complicated than previously considered. Let us mention Nittner (2003) where imputation of predictors, based on the nearest neighbor method, is suggested and studied via numerical simulation. Another available publication, considered below, is Efromovich (2011a) where the optimal solution of this problem is proposed. (It is worthwhile to remind the reader that all regression settings with issues related to predictors are typically very complicated. For instance, if predictors are observed with measurement errors, then the regression problem becomes ill-posed and special estimators are required. See the discussion in Casella and Berger 2002 and in Section 4.11 of Efromovich 1999.)

To explain the solution, we begin with writing down the joint (mixed) density of the triplet,

$$\begin{array}{c} f^{A X, Y, A}(a x, y, a)=\left[h(y) f^{Y \mid X}(y \mid x) f^{X}(x)\right]^{a} \\ \times\left[(1-h(y)) f^{Y}(y)\right]^{1-a}, \quad a \in\{0,1\} . \end{array} \tag{4.2}$$

As we see, to identify the conditional density $f^{Y \mid X}(y \mid x)$, and therefore the nonparametric regression, we could use only complete pairs if we had known $h(y)$ and $f^X(x)$. Can these two functions be estimated from all available observations? The answer is “yes.” Indeed, according to the last equality in (4.1), $h(y)$ is the Bernoulli regression of $A$ on $Y$, and note that all $n$ realizations of pair $(Y, A)$ are available. We know from the introduction (recall the Bernoulli example in Figure 2) and Section 2 how to construct an estimate $\hat{h}(y)$ of $h(y)$; see also Section 4.5 in Efromovich (1999). Note that the estimate $\hat{h}(y)$ uses all $n$ responses, including those from incomplete pairs. To estimate an underlying design density $f^X(x)$ of the predictor $X$ we note that its Fourier coefficients $\kappa_j=\int_0^1 f^X(x) \varphi_j(x) d x$ can be written as

$$\kappa_{j}=\mathbb{E}\left\{A \varphi_{j}(A X)[h(Y)]^{-1}\right\} \tag{4.3}$$

This formula follows from (4.2). Then we can estimate $\kappa_j$ by the sample mean estimate

$$\hat{\kappa}_{j}=n^{-1} \sum_{l=1}^{n} A_{l} \varphi_{j}\left(A_{l} X_{l}\right)\left[\hat{h}\left(Y_{l}\right)\right]^{-1} \tag{4.4}$$

As was explained in Section 2, Fourier estimates (4.4) allow us to construct an estimate f̌^X(x) of the design density.

Now we can propose the following sample mean estimate of Fourier coefficients of the regression function,

$$\hat{\theta}_{j}=n^{-1} \sum_{l=1}^{n} A_{l} Y_{l}\left[\check{f}^{X}\left(A_{l} X_{l}\right) \hat{h}\left(Y_{l}\right)\right]^{-1} \varphi_{j}\left(A_{l} X_{l}\right) \tag{4.5}$$

These estimates of Fourier coefficients, according to Section 2, allow us to construct a nonparametric regression estimator m̌(x).

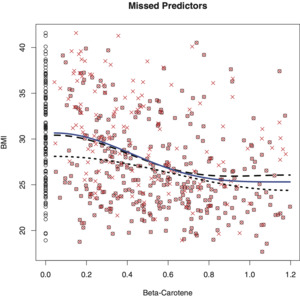
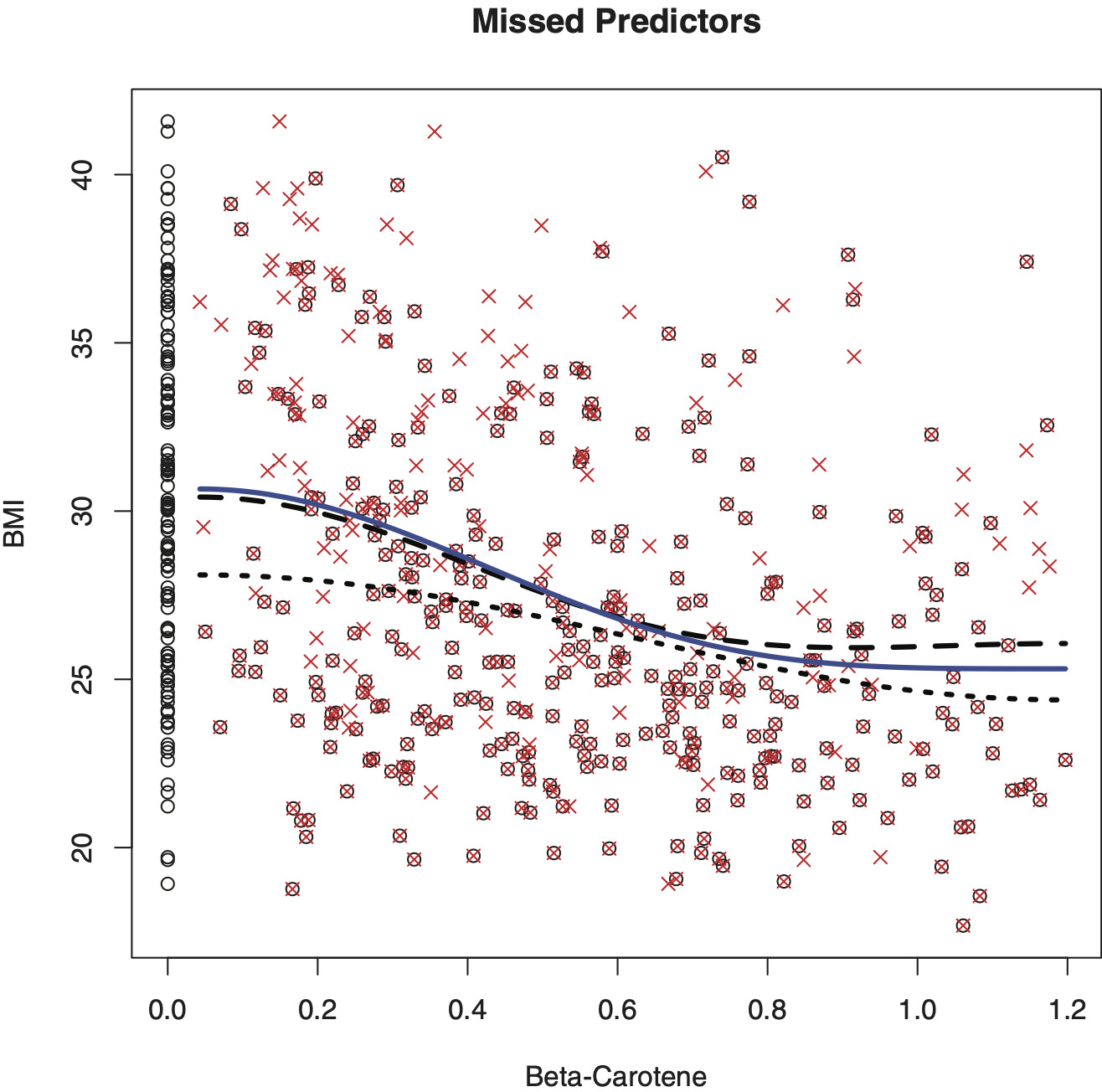
It is shown in Efromovich (2011a) that this method of estimation of regression function is optimal. Let us check how the estimator performs. Figure 6 exhibits the same data as in Figure 3. The solid line is the same as in Figure 3b; it is our nonparametric estimate based on all n = 441 underlying observations shown by crosses. It can be considered as an “oracle” regression for the case of observations with missed predictors. Now let us consider a naive approach when only complete pairs are used for estimation. Here we have N = 312 complete pairs, shown by crossed circles; this is a relatively large number but we know that a complete-case approach yields an inconsistent estimation, and hence it is of interest to look at the corresponding estimate. This estimate is shown by the short-dashed line. As we see, due to not taking into account incomplete pairs, the curve is significantly below the “oracle.” This is due to the fact that larger BMIs are missed, and we can see this via analyzing non-circled crosses that show underlying missed predictors. The long-dashed line is the recommended estimate. It is not perfect due to the right tail, but note that this is the area where we lost many observations. Overall, keeping in mind that 30% of predictors are missed, the outcome is good.

Figure 6.Nonparametric regression for the case of missed predictors. Observations, shown by circles and crosses, are the same as in Figure 3. The solid, long-dashed and short-dashed lines are: the estimate shown in Figure 3b which is based on all underlying observations shown by crosses; the recommended estimate based on data with missed predictors shown by circles; the estimate based on complete cases shown by crossed circles.

Now let us consider an analysis of other real data with missing predictors from a survey of college students published in Journal of American Statistical Association (Efromovich 2011a). One of the tasks of the survey was to understand how the credit score can predict the grade point average (GPA). Students were asked to get their current credit score on the Internet and then report it anonymously together with their GPA. Analysis of collected data revealed that all students who volunteered to participate in the survey reported their GPA, but many skipped reporting the credit score. (Reports indicating “no credit history” were excluded from the analysis and they were primarily from foreign students.) A discussion of results of the survey with students revealed that a missing credit score indicated that a student had no time and/or motivation to get the credit score, and the latter in no way was related to the value of the unknown credit score. As a result, the survey data fits the above-considered model of missing predictors. In what follows, observations are rescaled onto [0, 1]².

The top diagram in Figure 7 exhibits collected data for class . Ninety-two students provided GPA but among them only 41 provided their credit score. The solid line in the top diagram exhibits the estimated regression function that can be used for predicting the GPA for a known value of the credit score. We will return to this curve shortly, and now let us concentrate on estimated “nuisance” functions. The estimated density of the GPA is shown by the solid line in the second (from the top) diagram. The horizontal coordinates of circles indicate observed GPAs. Note that it is difficult to analyze the GPA in the traditional regression scattergram shown in the top diagram, and the second diagram dramatically improves the visualization. Note that no value of GPA is missed and thus the standard estimator of the R package is used here to estimate the density of GPA (Efromovich 1999). The third from the top diagram allows us to visualize the missing pattern of credit scores indicated by values of A. Remember that A = 1 if the credit score is available and A = 0 if not, and Y is the GPA. It is easy to see that students with lower GPA are less likely to provide their credit score. The estimated conditional probability h(y) = (A = 1⏐Y = y) is shown by the solid line. Note that the estimate does fit the data and corresponds to the visual analysis. The bottom diagram presents an opportunity to look at the available credit scores whose values are shown by horizontal coordinates of the circles. It is clear that circles are skewed to the right. Nonetheless, the above-proposed density estimate, shown by the solid line, is fairly symmetric. Let us explain this outcome. According to the estimated h(y), the lower the GPA, the larger the probability of a missing credit score. Now, if for a moment we return to the top diagram, then it indicates that the higher the credit score, the higher the GPA. Combining these two observations together, we conclude that students with a lower credit score (even if they do not know it) are more likely to not report it.

Figure 7.Analysis of (Credit Score, GPA) data for class A with n = 92 and N = 41.

Now let us return to the top diagram. If we look only on complete pairs (do not take into account circles with zero x-coordinates), then the solid line clearly does not go through the center of the cloud of circles as it would in a standard regression. Remember Figure 5, where we have seen a similar behavior in the simulated example.

The above-discussed nuisance functions in nonparametric regression with missing predictors may be of interest on their own. To understand why, let us look at Figure 8 presenting data for class which is another section of the same course. Here 72 students provided their GPA but only 50 provided their credit score. The structure of Figure 8 is identical to Figure 7. Let us examine estimated nuisance functions. The diagram second from the top shows the density of GPA. With respect to class , here more students have lower GPA and the density is no longer symmetric. This observation indicates that students in classes and are different. Now let us look at the diagram third from the top. This is where we observe the most striking difference between the two classes. In class students with a smaller GPA are more likely to report their credit score. This is a complete reversal from the missing pattern in class . At the same time, the estimated densities of credit scores in both classes look very similar (compare the two bottom diagrams in Figures 7 and 8). Finally, let us stress that the estimated regression functions, describing the relationship between the credit score and GPA, are very similar for the both classes (compare solid lines in the top diagrams in Figures 7 and 8). We may conclude that the proposed nonparametric regression estimator is robust.

Figure 8.Analysis of (Credit Score, GPA) for class B with n = 72 and N = 50.

5. Conclusions

1. Regression is the tool which allows the actuary to understand how one variable (the response) responds to changes in another variable (the predictor). Traditional regressions, like a linear regression, are based on a priori assumed shape of the regression. In other words, the actuary makes a decision about the shape of the regression. Nonparametric regression is based solely on data, requires no input from the actuary about the shape of an underlying regression, and for now it is one of the pillars of modern statistics. Methodology and methods of nonparametric estimation of regression functions are well developed for the case of complete data. The introduction presented a number of novel applications of nonparametric regression in casualty actuarial science, including nonparametric estimation of conditional likelihood of insurance event, conditional distribution of the number of insurance events, and the trend of a nonstationary time series.

2. A primer on nonparametric series regression estimation is presented in Section 2 and the method is illustrated via a number of real and simulated examples. Nonparametric series estimation is the simplest and most efficient method of estimation. Its underlying idea is based on the following 4 steps:

   a. Use an orthonormal basis, with cosine basis being the simplest and most convenient one.

   b. Approximate a known regression function by a truncated series.

   c. Estimate Fourier coefficients either via method of moments or via method of numerical integration.

   d. Choose only statistically significant estimated Fourier coefficients. Most popular methods of choosing are empirical risk minimization, shrinking and thresholding.

The series estimator adapts to unknown smoothness (number of derivatives) of an underlying regression function as well as to unknown design density. The estimator is also sharp minimax because its MISE attains the sharp minimax lower bound. Many other nonparametric estimators are proposed in statistical literature, like kernel, spline, nearest neighbor, etc., but only the series one is known to be sharp minimax.

3. In many actuarial applications it is typical to perform regression analysis with missed data. A thorough general discussion of the effect of missing data on regression estimation is presented. The actuary should be aware of several possible missing mechanisms. First of all, if the probability of missing a variable depends on its value (for instance, the probability of missing the amount paid on a closed claim depends on the amount) the missing precludes us from consistent estimation. If the latter is not the case, then optimal estimation is possible. For the case of a regression with missing at random responses, the optimal strategy is to simply ignore cases with missing responses. For a regression with missing predictors, a rather special estimation procedure, which includes estimation of nuisance functions, is optimal.

4. In this paper the case of a univariate predictor is considered; this is a prudent first step in any regression analysis. In some cases, like in the automobile insurance claims example, discussed in the introduction, univariate analysis raises questions about the effect of other covariates and the necessity to use a multivariate regression. The orthogonal series approach is easily expanded to a k-dimensional predictor X ≔ (V₁, . . . , V_k). The only difference is that now a k-dimensional basis ϕ_j(X) with j ≔ (j₁, . . . , j_k) is used; Section 6.1 in Efromovich (1999) explains how to construct the basis using the tensor-product of k univariate bases. Then the estimator (2.5) can be still used, and this is the main estimator for a multivariate problem. The estimator (2.6), which has been so successful for the univariate case, unfortunately has no multivariate analog. A discussion of sharp minimax estimation for the case of complete data can be found in Efromovich (1999, 2000). There is a specific difficulty in multivariate estimation, which is even referred to as the curse of multidimensionality. Namely, if a k-dimensional regression function is α-fold differentiable with respect to each variable, then the MISE convergence slows down to $n^{-2 \alpha /(2 \alpha+k)}$. Nonetheless, a reasonable estimation for small sample sizes is still possible and a number of elegant methods is proposed to overcome the curse; see Chapter 6 in Efromovich (1999). Optimal multidimensional regression with missing data is an open problem. Based on the presented univariate results, it is reasonable to conjecture that above-presented main conclusions will remain the same.

5. It is not unusual for actuarial data to be modified (incomplete) due to truncation and/or censoring. Most typical occurrences are due to deductibles and limits on payments. While such a modification leads to some missing information, truncation and censoring are treated by different methods and traditionally studied by a special branch of statistical science called survival analysis. To explain the difference, let us, for example, consider a regression of the amount of payment Y, which is subject to the limit on payment Z, on predictor X. This is the case of right-censored response and we observe realizations of the triplet (X, min(Z, Y), I(Y ≤ Z)) where I(·) is the indicator function. Now recall the “MAR-responses” setting of Section 3 where we observe realizations of the triplet (X, AY, A). Clearly we are dealing with different types of data. Furthermore, if the value of the response is not available due to right censoring, there is more information about its value (we do know that it is at least the limit on payment) than in the case of MAR response. It is an interesting and open problem to explore the case of modified (due to truncation and/or censoring) and then possibly missing data.

Acknowledgments

The research was supported in part by a grant from TAF/CAS/CKER, NSF Grants DMS-0906790 and DMS–1513461, and NSA Grant H982301310212. Suggestions of the Editor, Prof. Rick Gorvett, and four reviewers significantly improved the paper and are greatly appreciated. Special thanks go to Jerome Tuttle, FCAS for his very careful reading of the manuscript and a number of valuable remarks.