Rating Endorsements Using Generalized Linear Models

1. Introduction

It is common for insurance policies to contain optional insurance coverages, often referred to as endorsements or riders. These options may include alternative deductibles and coverage limits and they may also provide extensions to the type of peril (e.g., stolen jewelry in homeowners insurance) covered. Rate manuals provide guidance for the surcharge associated with these optional coverages. For example, Werner and Modlin (2010) describe processes of incorporating endorsement surcharges into rates. For the actuary who uses generalized linear model (GLM) techniques and is charged with developing an associated set of rates, how does one determine surcharges associated with endorsements?

There are several reasonable approaches for addressing this question. One approach is that endorsements form a relatively small fraction of the premium base and so only informal, ad hoc approaches are needed. Actuaries, of course, typically have substantial amounts of experience when ratemaking and this experience can be a guide to setting rates for such a relatively small part of the business. Another approach is to use information from an external agency for this set of relativities, even if GLM techniques are being using in conjunction with company data for the primary set of rates. A third approach, especially for large companies, is to treat endorsements as merely another type of coverage and use GLM techniques to determine this set of prices. This approach requires a substantial amount of data as well as claims that are identified by type of endorsement.

This paper is motivated by a rating study in which none of these approaches are appropriate. Our work makes three contributions. First, we consider the Wisconsin Local Government Property Insurance Fund and describe a process for determining intuitively appealing rates, for a political environment, based on GLM techniques. Second, we provide a detailed case study, so that other analysts may replicate parts of our approach. Through our use of GLM techniques, we provide relativities not only for our primary rating variables, but also for endorsements in a case when it is not known whether or not a claim is due to an endorsement. Third, we explore the use of shrinkage estimation in ratemaking, and demonstrate that little predictive ability is lost when the base rating variables are left stable.

1.1. Fund description

The Wisconsin Office of the Insurance Commissioner administers the Local Government Property Insurance Fund (LGPIF). The LGPIF was established to provide property insurance for local government entities, including counties, cities, towns, villages, school districts, and library boards. The fund insures local government property, such as government buildings, schools, libraries, and motor vehicles. The fund covers all property losses except those resulting from flood, earthquake, wear and tear, extremes in temperature, mold, war, nuclear reactions, and embezzlement or theft by an employee.

The fund covers over a thousand local government entities who pay approximately $25 million in premiums each year and receive insurance coverage of about $75 billion. State government buildings are not covered; the LGPIF is for local government entities that have separate budgetary responsibilities and who need insurance to moderate the budget effects of uncertain insurable events. Claims for state government buildings are charged to another state fund that essentially self-insures its properties.

The fund offers three major groups of insurance coverage: building and contents (BC), inland marine (construction equipment), and motor vehicles. For this paper, we focus on BC, as this was the primary motivation for developing the fund; coverage for local government property has been made available by the State of Wisconsin since 1911. However, even within this primary coverage, there are many optional coverages offered, including business interruption and fine arts endorsements.

In effect, the LGPIF acts as a stand-alone insurance company, charging premiums to each local government entity (policyholder) and paying claims when appropriate. Although the LGPIF is not permitted to deny coverage for local government entities, these entities may go onto the open market to secure coverage. Thus, the LGPIF acts as a “residual” market to a certain extent, meaning that other sources of market data may not reflect its experience.

1.2. Determining effective relativities

Although it is government insurance, because the LGPIF essentially acts as a stand-alone insurance company, many of its goals are similar to those of a private insurer. An analysis of LGPIF claims serves as important input for determining rates that the LGPIF charges its policyholders; these rates should reflect the appropriate level and amount of uncertainty of an insurance coverage. Particularly for a public entity such as the LGPIF, the ratemaking process should be transparent and seek to promote equity among policyholders.

Because the LGPIF has a moderate amount of exposure, as will be seen, there is little difficulty in using commonly accepted generalized linear modeling (GLM) techniques to determine rates that are unbiased and transparent for the primary building and contents coverage. However, the usual approaches for handling endorsements were deemed less than satisfactory for three reasons. First, as of this writing (2014–2015), the LGPIF is undergoing a major rate restructuring; due to the political environment, seemingly ad hoc adjustments, even if small, are deemed inappropriate. Second, information from external agencies is expensive and not particularly relevant; the LGPIF is a government entity and acts as a residual market, meaning that there is limited information on comparable risk pools. (See the Association of Government Risk Pools, http://www.agrip.org/, for one set of possible comparables.) Third, LGPIF data for optional coverages is limited, implying that the usual GLM techniques are not suitable for rating the optional coverages, such as endorsements.

To rate endorsements, this paper explores the use of GLM techniques with restrictions on the coefficients through shrinkage using well-known penalized likelihood methods (cf., Brockett, Chuang, and Pitaktong 2014). Analysts have vague knowledge and impressions about the size and magnitude of these coefficients, stemming from business practice, economic theory, and an understanding of general risk management practice. For example, if x is a binary variable representing the adoption of an alarm system (an “alarm credit”), then the analyst expects the associated coefficient to be negative in the neighborhood of 0 to −10%. That is, if a policyholder manages risk appropriately by introducing alarms, then resulting rates should be at least as low as without the adoption of an alarm system. Estimated alarm credit regression coefficients that are positive are not acceptable for rating purposes.

Compared to the traditional methods of simply including endorsements after the primary analysis has been done, our approach has two main advantages. First, we can use the data to suggest ways of introducing relativities for endorsements in a disciplined manner. Second, because we use GLM techniques, our approach is naturally multivariate and the introduction of endorsements accounts for the presence of other rating variables. Further, as we will see, the shrinkage methods used in this paper have the flexibility to also be used in other situations where the analyst wishes to moderate the effect of unreliable data.

The plan for the rest of the paper follows. We begin in Section 2 by giving more information about the data from the LGPIF as used in this study. Section 3 describes the shrinkage estimation techniques. Sections 4 and 5 describe the results of the model fitting from in-sample and out-of-sample perspectives, respectively. Section 6 provides concluding remarks, and alternative analyses are in the Appendix Section 7.

2. Data

2.1. Fund claims and rating variables

Building and contents is the fundamental coverage underpinning the LGPIF and is the focus of this paper. The claims may be a damage to the base property, content, or other properties covered by endorsements purchased by the policyholder. Hence, the observed claim amounts may vary according to specific terms of the endorsements, selected and purchased by the policyholder. The observed amounts reflect the total end result of each claim; however, the specific contribution by the endorsement is unobserved. Summary statistics of the data show that the average claim varies widely, especially with a high 2010 value due to a single large claim. The total number of policyholders is steadily declining and, conversely, the coverage is steadily increasing. Throughout this section, we summarize the distribution of average severity for policyholders; that is, for each policyholder, we examine total severity divided by the number of claims, i.e., the pure premium or loss cost. In our modeling sections, we appropriately weight by numbers of claims.

Table 1 shows policies beginning in 2006 because there was a shift in claim coding in 2005 so that comparisons with earlier years are not helpful. To mitigate the effect of open claims, we consider policy years prior to 2012. This means we have six years of data, years 2006, . . . , 2011, inclusive. We use a common strategy in predictive modeling where we split our data into a “training” and a “validation” sample. Specifically, we use years 2006–2010 inclusive (the training sample) to develop our rating factors. Then we apply these factors and 2011 rating variables to predict 2011 claims (the validation sample). Thus, henceforth our summary statistics refer to the 2006–2010 training data. Appendix 7.4 provides an alternative cross-sectional cross-validation.

For the training sample, Table 2 summarizes the distribution of our two continuous outcomes, frequency and claims amount. It is not surprising that the two distributions are right-skewed and correlated with one another. In addition, the table summarizes our continuous rating variables, (building and contents) coverage, and deductible amount. The table also suggests that these variables have right-skewed distributions. Moreover, they will turn out to be useful for predicting claims, as suggested by the positive correlations in Table 2 for coverage and deductible. We use a non-parametric (also known as “Spearman”) correlation due to the skewness of the data and the presence of zeros.

Table 3 describes the rating variables considered in this paper. To handle the skewness, we will henceforth focus on logarithmic transformations of coverage and deductibles. To get a sense of the relationship between the noncontinuous rating variables and claims, Table 4 relates the claims outcomes to these categorical variables. Table 4 suggests substantial variation in the claim frequency and average severity of the claims by entity type. It also demonstrates higher frequency and severity for the Fire5 variable and the reverse for the NoClaimCredit variable. The relationship for the Fire5 variable is counterintuitive in that one would expect lower claim amounts for those policyholders in areas with better public protection (when the protection code is five or less). Naturally, there are other variables that influence this relationship. We will see that these background variables are accounted for in the subsequent multivariate regression analysis, which yields an intuitive, appealing (negative) sign for the Fire5 variable.

The Appendix (Table 20) shows the claims experience by alarm credit. It underscores the difficulty of examining variables individually. For example, when looking at the experience for all entities, we see that policyholders with no alarm credit have on average lower frequency and severity than policyholders with the highest (15%, with 24/7 monitoring by a fire station or security company) alarm credit. In particular, when we look at the entity type School, the frequency is 0.422 and the severity 25,257 for no alarm credit, whereas for the highest alarm level it is 2.008 and 85,140. This may simply imply that entities with more claims are the ones that are likely to have an alarm system. Summary tables do not examine multivariate effects; for example, Table 4 ignores the effect of size (as we measure through coverage amounts) that affect claims.

2.2. Endorsements

As described in Section 2.1, we do not actually observe claims from an endorsement. For example, if a policyholder purchases a Golf Course Grounds endorsement and has a claim that is from this additional coverage, we are not able to observe this connection with our data. We do observe the additional claim, whether the policyholder has the endorsement, and the amount of coverage under the endorsement. In this sense, endorsements can be treated as another rating variable in our algorithms.

Table 5 describes endorsements, or optional coverages, that are available to LGPIF policyholders. Table 6 summarizes the claims experience by endorsement. Policyholders with the Zoo Animals endorsement experience an average annual claim frequency of 73.9. Presumably, policyholders paying for this extra protection would enjoy higher property claims and so should be charged additional premiums. The most frequently subscribed endorsement is the Monies & Securities, which covers monetary losses by theft, disappearance, or destruction. The average coverage and number of observations are over five years (2006–2010), the in-sample period. For example, the Zoo Animals coverage consists of 10 observations over five years and these were from the Henry Vilas Zoo in Dane County and the Milwaukee County Zoo in Milwaukee County.

Table 6 shows that a policyholder with any type of endorsement has a higher claims frequency compared to the total of all policyholders. Similarly, for most endorsements, policyholders have a higher average severity, with Pier and Wharf, Monies and Securities (limited term), and Other Endorsements being the exceptions. The effect of higher severity seems to be particularly large for certain endorsements, such as Zoo Animals, Golf Course Grounds, and Fine Arts.

To help establish the relationship between endorsements and claims outcomes, Table 6 also shows the average endorsement coverage (the average is over policyholders with some positive coverage). The table summarizes the Spearman correlation of the amount of endorsement coverage versus the frequency and severity of claims observed. It is not surprising that all of these correlations are positive, indicating that more coverage means both a higher frequency and severity of claims. In keeping with our frequency-severity approach to modeling, note that the claims severity correlations are calculated for observations with at least one claim.

3. Claims modeling

As described in Section 1, this paper uses generalized linear models, and following industry norms, employs logarithmic link functions that result in multiplicative relativities. We investigated both the frequency-severity approach as well as the Tweedie (“pure premium”) approach. Both models have strengths and weaknesses and, for our data set, predict claims on our holdout sample roughly equally well. See Frees (2014) for a comparison of these two modeling approaches. This section des-cribes estimation techniques employed and model specifications.

3.1. Shrinkage estimation

3.1.1. Linear model shrinkage

To introduce shrinkage estimation, we first provide a review in the context of the linear model; see, for example, Hastie, Tibshirani, and Friedman (2009) for further information. For notation, assume that y_i is the dependent variable and that x$_{i1}$, . . . , x_ik is the set of covariates (including coefficients for rating variables and endorsements). Then, the set of shrinkage estimators of β = (β₀, . . . , β$_k$)′ is determined by minimizing

$$\sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\sum_{j=1}^{k} x_{i j} \beta_{j}\right)^{2}+\lambda \sum_{j=1}^{k} \beta_{j}^{2} \tag{3.1}$$

Values of λ control the complexity of the model; smaller values mean less shrinkage. At one extreme, a value of λ = 0 reduces to ordinary least squares. At the other extreme, as λ approaches infinity, β approaches (or, is “shrunk towards”) 0, so the data becomes less relevant (has smaller weight) in determining values of β. Note that in equation (3.1) the intercept β₀ is typically not included, as this would make the procedure dependent on the origin of y; to illustrate, subtracting 250 (for example, for a deductible) from each value of y would substantially alter results.

Equivalent to equation (3.1), one could also determine β by minimizing the sum of squares

$$\sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\sum_{j=1}^{k} x_{i j} \beta_{j}\right)^{2}$$

but subject to a constraint of the form $\sum_{j=1}^k \beta_j^2 < c$. This formulation is desirable in that one can directly see how the β coefficients are being “shrunk” towards zero (as c becomes small). Thus, shrinkage estimation is a desirable intermediate device between (i) leaving a coefficient in the equation and (ii) removing it completely. Through shrinkage, we can include a rating variable but shrink its coefficient and hence reduce its effect on the predicted values.

After centering the y’s and x’s, we can also write the shrinkage estimators in the form

$$\hat{\boldsymbol{\beta}}_{\text {shrink }}=\left(\mathbf{X}^{\prime} \mathbf{X}+\lambda \mathbf{I}\right)^{-1} \mathbf{X}^{\prime} \mathbf{y} . \tag{3.2}$$

This equation has two appealing interpretations. First, even in the case when some of the rating variables are collinear so that X′X is no longer invertible, the matrix X′X + λI is invertible. Equation (3.2) was first known as a type of “ridge regression” to handle problems of collinearity.

Second, assuming normality of the outcomes and the regression coefficients, one can show that β̂$_{shrink}$ represents the posterior mean of β. Through this Bayesian context, one can think about the coefficients β having a distribution (centered about 0) and the analyst is allowed to incorporate his or her belief about the precision of the coefficient through a prior distribution.

3.1.2. Generalized linear model shrinkage

More generally, coefficients may be shrunk towards selected (possibly non-zero) values and we need not shrink all of them. In keeping with common statistical notation, we will make the term ⏐⏐Rβ − r⏐⏐² small, where Rβ represents sets of linear combinations of regression parameters (R is known) and r represents a vector of selected values.

For generalized linear models, the idea behind shrinkage estimation is to make a logarithmic likelihood large subject to requiring ⏐⏐Rβr⏐⏐² to be small. This naturally leads to the notion of a penalized likelihood of the form,

$$l(\boldsymbol{\beta})=\sum_{i=1}^{n} \log f\left(y_{i}\right)-\lambda\|\mathbf{R} \boldsymbol{\beta}-\mathbf{r}\|^{2}$$

where f() is a density or mass function. For example, for a Poisson distribution with mean _i exp(x$_i$β), we have $f_i\left(y_i\right)=\mu_i^{y_i} e^{-\mu_i} / y_{i}$! and

$$l(\boldsymbol{\beta})=\sum_{i=1}^{n}\left\{y_{i} \mathbf{x}_{i}^{\prime} \boldsymbol{\beta}-\exp \left(\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}\right)-\ln \left(y_{i} !\right)\right\}-\lambda\|\mathbf{R} \boldsymbol{\beta}-\mathbf{r}\|^{2}$$

For the application in this paper, we have

$$\mathbf{R}=\left[\begin{array}{ll} \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{I} \end{array}\right] \quad \boldsymbol{\beta}=\left[\begin{array}{l} \boldsymbol{\beta}_{1} \\ \boldsymbol{\beta}_{2} \end{array}\right] \quad \mathbf{r}=\left[\begin{array}{l} \mathbf{0} \\ \mathbf{0} \end{array}\right]$$

β₁ = coefficients for base rating variables

β₂ = coefficients for endorsements

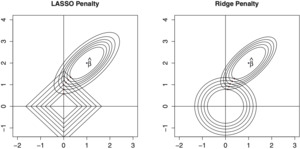
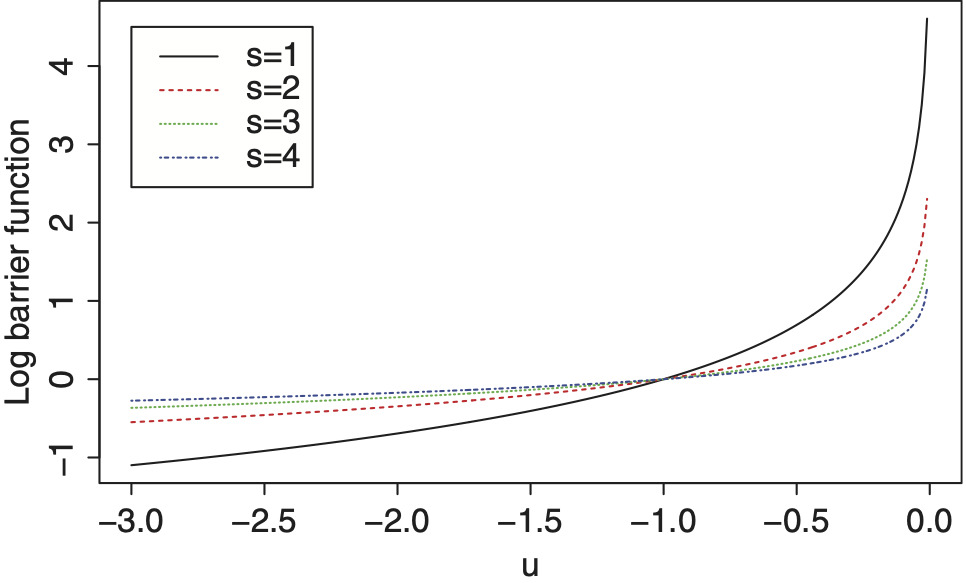
The shrinkage approach can be understood as a special case of constrained estimation, where the coefficient β is restricted to be within a neighborhood of r. By varying the shape of the constraint region, it is possible to obtain various properties of the resulting coefficient. We provide more details in Appendix Section 14 for the interested reader.

3.2. Offsets and endorsements

Variables described in Tables 3 and 5 were used to calibrate generalized linear models with logarithmic links and estimation methods outlined in Section 3.1. We also used the following offset variable

$$\begin{aligned} \text { offset }= & \ln (0.95) A C 05+\ln (0.90) A C 10 \\ & +\ln (0.85) A C 15 . \end{aligned}$$

Here, AC05 represents a binary variable to indicate the presence of a 5% alarm system, and similarly for AC10 and AC15. This seems a sound practice and so we retain this offset variable in our analysis.

When the LGPIF began capturing alarm system data, premium “credits” in the amount of 5% were given to those with AC05=1, and similarly for the other two categories. Alarm systems at the 5% level mean that automatic smoke alarms exist in some of the main rooms, those at the 10% level mean they exist in all of the main rooms. At the 15% level, facilities are monitored on a 24 hours per day, 7 days per week basis by a police, fire, or security company. The policyholder is eligible for a premium credit of an amount determined by the specified percentage, depending on the alarm credit amount. This section describes how alarm credit is used as an offset in our model. Table 20, in the Appendix, shows a summary of the claims with respect to different alarm credit categories.

Table 6 suggests that not only the presence of an endorsement but also its coverage amount may influence claims outcomes. To capture this, suppose that y_B represents claims from a base coverage with mean μ$_B$ = exp(x′β). Let y_E be the claims from an endorsement that we assume has mean μ$_E$. Then, the observed response y has the following mean structure

$$\mu=E y=\left\{\begin{array}{c} \mu_{B}=\exp \left(x^{\prime} \beta\right) \\ \text { endorsement not present } \\ \mu_{B}+\mu_{E}=\exp \left(x^{\prime} \beta+\beta_{E} x_{E}\right) \\ \text { endorsement present } \end{array} .\right.$$

We can readily accommodate this in a GLM structure using an interaction term of the presence of an endorsement with the variable x_E. We use

$$x_{E}=\ln \left(1+\frac{\text { Coverage }_{E}}{\text { Coverage }_{B}}\right) \text {, } \tag{3.3}$$

where Coverage_E and Coverage_B represent amount of coverage for the endorsement and base (building and contents), respectively. With this specification, we have

$$\begin{aligned} \mu_{E} & =\exp \left(\mathbf{x}^{\prime} \beta+\beta_{E} x_{E}\right)-\mu_{B} \\ & =\mu_{B}\left[\left(1+\frac{\text { Coverage }_{E}}{\text { Coverage }_{B}}\right)^{\beta_{E}}-1\right] \\ & \approx \mu_{B}\left[\left(1+\beta_{E} \frac{\text { Coverage }_{E}}{\text { Coverage }_{B}}\right)-1\right] \\ & =\beta_{E} \times \text { Coverage }_{E} \times\left(\frac{\mu_{B}}{\text { Coverage }_{B}}\right) \end{aligned}$$

using the approximation $(1 + z)^b \approx 1 + bz$. With this, we may think of the appropriate cost of the endorsement μ$_E$ as a factor times the endorsement coverage, rescaled by the overall cost per unit coverage. The factor, β$_E$, is estimated from the data.

For our data, some of the estimated coefficients associated with endorsement variables were insignificant and negative, making them unacceptable for rating purposes (this would mean that the policyholder electing the endorsement coverage would pay less premiums than otherwise). In particular, LnAccRecCovRat, LnPierWharfCovRat, and LnMoney SecCovRat were insignificant and negative, when included in the frequency model. One way to rate these variables is to include them in the severity model as covariates. An alternative is to include a binary variable to indicate having the endorsement, instead of using the log coverage ratios. Hence, we elect to use three indicator variables, AccRec, PierWharf, and MoneySec, in the frequency model.

In our model, another offset was used for VacancyPermit. In part, this was because interpretable coefficients could not be obtained for this endorsement variable from the given data, even when included as an indicator and shrinkage applied. Moreover, we had available prior information on the impact of this endorsement from historical precedence where the rate for VacancyPermit had been 0.4 times building rate. Therefore,

$$\text { offset }_{V P}=0.4 \times \ln \left(1+\frac{\text { Coverage }_{V P}}{\text { Coverage }_{B}}\right)$$

was added as an additional offset in the model.

3.3. Advantages of the shrinkage approach

The shrinkage approach provides a framework for controlling the coefficients of the endorsements, restricting them to be small, yet meaningful, values. Using a standard GLM, data-driven approach for rating endorsements can result in coefficients that cannot be interpreted in a meaningful way. For instance, the data may indicate that purchasing ZooAnimals coverage amounts to a seven-fold increase in premium. Applying shrinkage only to endorsements allows the base rating variables to remain at an actuarially fair level, while unreasonable behaviors of the endorsement coefficients are contained.

This approach is simple and flexible, and prevents the endorsement premiums from becoming unfair for those who hold only particular endorsements. For example, charging too much for ZooAnimals may result in unfair premiums for Milwaukee and Dane County, as these two policyholders are the ones who happen to have a public zoo endorsement coverage. In addition, the method allows for a sound risk management practice in a political setting, as the tuning parameter λ may be selected to accommodate the expectations of the environment in which the relativities are to be used. When the expectations regarding contributions from the endorsements are high, then the tuning parameter may be released to allow for an elevated premium level for the endorsements, while they could be shrunk to a small but still meaningful level when the contributions must remain low. In this process, the base rating variables remain stable, and hence ensure a steady outsample performance.

4. Results from the claims modeling

This section presents results using the frequency-severity approach as it provides more intuitive expressions for our parameter estimates. For comparison, we include the Tweedie model results in the Appendix Section 7.2 using the shrinkage approach with ridge penalty.

4.1. Frequency-severity modeling using shrinkage estimation

Table 7 provides fitting results for claims frequency, using the Poisson model. We incorporated base variables described in Table 3, and selected interaction terms and the offset variables described in Section 3.2. Estimation was conducted using shrinkage techniques in Section 3.1 but shrinking only the endorsement terms, not the base rating variables. For example, in Table 7, the covariate LnBusInterCovRat represents the business interruption endorsement variable given in equation (3.3). Parameter estimates for various values of the shrinkage parameter λ are given. Note that even though our shrinkage focuses on the endorsement variables, parameter estimates for other variables are affected due to the multivariate nature of the regression model.

Table 7 shows that Deductible and the interaction term between NoClaimCredit and lnCoverage display negative coefficients, as anticipated. It is notable that Fire5 also shows a negative coefficient, in contrast to the relationship suggested by the summary statistics in Table 4. This result is sensible, given that a low fire class represents higher public protection. Also, as anticipated, the coefficients for the endorsements are all positive and significant. The model is estimated with λ increasing from 0 (no shrinkage) to 1,000 (shrinkage). As λ increases, we observe the coefficients shrink towards zero.

Table 8 provides fitting results for claims severity, using the gamma model. Specifically, we used a logarithmic link function with the average claim as the dependent variable and the number of claims as the weight; cf. Frees (2014) for further discussions of this specification. As is common in severity modeling, there were fewer variables that were statistically significant when compared to the frequency model and so the model specification is much simpler. The coefficient for LnCoverage is negative; however, the coefficient in the frequency model is positive, and hence the overall effect is positive and interpretable. As shown in Table 4, cities and counties tend to have smaller average severities, and presumably the effect is due to such entities.

4.2. Parameter interpretation

The parameter estimates provided in Section 4.1 necessarily reflect the complexity of the system. To help interpret them, in this section we focus on a “typical” policyholder whose coverage is at the median of the distribution.

For our dataset, the median (50th percentile) BC coverage was $11.35 million, corresponding to 2.43 (= ln11.353,57 million) as shown in Table 9. Recall that LnCoverage is the total building and content coverage, in logarithmic millions of dollars.

Using this median coverage, Table 10 provides relativities for the rating factors. Table 10 shows that the entity “School” pays less, and that “City,” “County,” “Misc,” and “Town” pay more, all relative to the reference category “Village.” As we apply shrinkage to the endorsements, the relativity estimate for each entity type is smoothed, reflecting the change in the relativity estimates for the endorsements.

Note that the relativity of School is very small in comparison to other entity types; recall that relativities, like regression coefficients, summarize marginal changes in variables and may not capture all relevant data features. In this case, although 2.43 (ln11.353,57) is the median, it is only at the 11th percentile for Schools. So, if this example were focused on schools, then we would use a higher coverage amount to reflect the typical school coverage.

Table 10 also shows the relativity estimates for the three endorsement indicators. Note that AccRec, PierWharf, and MoneySec are used as indicators, while other endorsements are used as log coverage ratios in the frequency model. Because we have not applied shrinkage to the severity model, as λ is increased, the severity model remains the same. The final relativity estimate is obtained by multiplying the exponentiated estimates from the frequency model and the severity model. The reader may observe that having, say, ZooAnimalCov results in a seven-fold (7.220) increase in premium without shrinkage, while the effect is significantly mitigated after shrinkage is applied (1.296 with λ = 5 and as small as 1.004 with λ = 1,000). The effect of having GolfCourseCov results in a nearly three-fold (2.497) increase in premium without shrinkage, while the effect is mitigated to 1.252 with λ = 5 and as small as 1.001 with λ = 1,000.

A rating engine may be recommended using the relativities shown in Table 10. The final recommendation to the property fund consists of tabulated rating factors, which can be applied to the base premium in a multiplicative manner. The endorsement factors are then applied additively. Hence, the premium is calculated by the following rating formula:

$$\begin{aligned} \text { Premium }= & (\text { BasePremium }) \times(\text { NoClaimFactor }) \\ & \times(\text { AlarmCreditFactor }) \\ & \times(\text { DeductibleFactor }) \\ & +(\text { EndorsementRates }). \end{aligned}$$

The base premium is tabulated for the six different entities (including the base entity, Village), and two different fire classes. This base premium is adjusted for alarm credit, and a no-claims discount factor is applied depending on the policyholder’s experience. The deductible factor is selected and multiplied from a tabulated table of eleven deductible categories. Finally, the endorsement factors are added. Note that we could have also included endorsements multiplicatively based on the discussion in Section 3.2. We chose to use additive terms to be consistent with prior LGPIF practice.

5. Out-of-sample performance

The models described in Section 3 with fitted parameter values in Section 4 provide the basis for developing a rating algorithm. With this information, we can generate predictions based on 2011 (out-of-sample) rating variables. To assess the viability of these predictions, we compare them to 2011 out-of-sample claims. We also have available a Premium variable that was generated by an external agency (based on a very expensive process). For another comparison, we also generated scores for the Tweedie model based on the parameter results in the Appendix. This section compares our predictions with held-out claims and this premium score.

Table 11 reports correlations among scores and claims. For both the frequency-severity and the Tweedie model, there were very strong correlations between the scores from the usual unbiased methods without shrinkage (corresponding to λ = 0) and shrinkage-based scores (corresponding to λ = 1,000). Note, from Table 11, the outsample correlation for λ = 1,000 differs only by a little. Because of this strong relationship for these two extreme values of λ, we do not include scores for intermediate values of λ. Moreover, this means that at least for this data set, little predictive ability is lost by using shrinkage methods to give much more intuitively appealing relativities.

We note the strong correlation, nearly 94.29%, between the external agency Premium and the Tweedie model scores, as shown in Figure 1. This suggests that our analysis is able to reproduce (expensive) external agency scores effectively. Table 11 demonstrates that all three scoring approaches, the frequency-severity, the Tweedie, and the external agency premium score, fare about the same in predicting out of sample claims. The frequency-severity model does the best, while the Tweedie model shows the highest correlation with the external agency scores. Note that our frequency-severity scores outperform the external agency scores by a small amount.

Figure 1.Comparison of frequency-severity model scores and Tweedie model scores to external agency premium scores. The Spearman correlation coefficients are 74.87% and 94.29%

To get a better sense of the meaning of these correlations, Figure 2 shows the relationship between our frequency-severity (two-part model, or TPM) score and held out claims. The left-hand panel shows the relationship in terms of dollars and the right-hand panel gives the same data but using logarithmic scaling. For this figure, each plotting symbol corresponds to a policyholder and the overall Spearman correlation is a strong 43.30%.

Figure 2.Comparison of frequency-severity scores to out of sample claims for 2011. The Spearman correlation coefficient is 43.30%

We believe that our work is fairly typical of analyses of insurance company data. For statistical significance and interpretability of the coefficient estimates for the endorsements, we prefer the frequency-severity approach presented in Section 4.1. However, the Tweedie approach presented in the Appendix uses fewer parameters, and fares evenly when compared to the external agency premium scores. We think both approaches are sensible and the choice will ultimately depend on the actuary who is analyzing and making inferences from the data.

Appendix 7.4 shows an alternative robustness check, using a randomly selected cross-sectional sample of policyholders for out of sample validation. We further check the predictive ability of our claim scores using the Gini index. This is a newer measure developed in Frees, Meyers, and Cummings (2011). For our application, the Gini index is twice the average covariance between the predicted outcome and the rank of the predictor.

Table 12 summarizes these results. By inspecting the Gini indices, we observe only minute differences in the explanatory ability after applying the shrinkage technique. The Gini index is 70.05% using only the base rating variables, 69.66% with the endorsements, and 69.96% using shrinkage estimation. In the same way, the Pure Premium (Tweedie) scores show a 69.74% for the base score, 69.23% with endorsements in the model, and 69.77% using shrinkage estimation. For comparison, the Gini index of the external agency premiums turned out to be 72.69%.

In order to test the significance of the differences among these scores, we use Theorem 5 of Frees, Meyers, and Cummings (2011) which provides standard errors for the difference of two Gini indices. Table 13 shows that the differences among the scores are insignificant. For example, the difference between the frequency-severity score with λ = 1,000 and the external agency premiums is 0.027; however, the difference is within twice the standard error of the difference statistic. Further, Corollary 3 in Frees, Meyers, and Cummings (2011) established the asymptotic normality of the distribution of the difference statistic so that we can rely upon the usual normal-based rules for assessing statistical significance.

6. Concluding remarks

There are three main contributions of this paper. First, we have presented a detailed analysis of a government entity, the Wisconsin Local Government Property Insurance Fund. There is little in the literature on government property and casualty actuarial applications and we hope that this application will interest readers. Moreover, the LGPIF is similar to small commercial property insurance, making our work of interest to a broad readership.

Second, we have given a detailed analysis in the manner of a case study so that other analysts may replicate parts of our approach. Specifically, through our use of GLM techniques, we provide relativities not only for our primary rating variables but also for endorsements. We provided an approach for handling these optional coverages when it is not known whether or not a claim is due to an endorsement.

Third, we have explored the use of shrinkage estimation in ratemaking. Although applications can be general, we find them particularly appealing in the case of endorsements. For our data set, we found that little predictive ability was lost by using shrinkage methods and they gave much more intuitively appealing relativities. Particularly in a political environment such as that enjoyed by government insurance, it is helpful to have relativities that can be calibrated in a disciplined manner and are consistent with sound economic, risk management, and actuarial practice.

Acknowledgments

The authors acknowledge a Society of Actuaries CAE Grant for support of this work. The first author’s work was also supported in part by the University of Wisconsin-Madison’s Hickman-Larson Chair in Actuarial Science. We would also like to thank two anonymous reviewers for their helpful remarks.