Insurance Claims Fraud: Optimal Auditing Strategies in Insurance Companies

undefined

1. Introduction

Insurance claims fraud has been one of the major concerns in the insurance industry for a long time and has attracted much attention in both the scientific and firm-level environments. There exist many research papers and studies on the detection and deterrence of fraudulent activities and the optimal design of insurance contracts (see, e.g., Viaene and Dedene 2004; Picard 2009; Dionne, Giuliano, and Picard 2009; GDV 2011). Nevertheless, the Association of British Insurers (2012) reports the uncovering of 139,000 dishonest claims in the UK in 2011 alone, adding up to almost £1 billion in illegitimate loss reports; the estimated number of unrevealed cases is assumed to be substantially higher. In this study, we show that with the goal of minimizing insurance companies’ costs, the complete elimination of fraudulent activities is not always desirable. We derive acceptance ranges that comprise all valid fraud and auditing probability combinations under which contract conditions remain attractive enough for both insurer and policyholder to adhere to the insurance relationship. The actual strategies are chosen based on the respective market power.

Insurance claims fraud is a multi-layered phenomenon. While it is often associated with criminal activities, only a minority of illegitimate claims is said to contain outright fraud (see, e.g., Viaene and Dedene 2004; Tennyson 2008). This observation is probably due to the fact that for a case to be declared criminal fraud it needs to be proven that it is “a willful act of obtaining money or value from an insurer under false pretenses or material misrepresentations” (Derrig 2002). The more common and frequent type of insurance claims fraud is referred to as soft fraud. Even though there exists no clear definition of the term, it is generally associated with the attempt to exaggerate the magnitude of an otherwise legitimate claim (see, e.g., Weisberg and Derrig 1991; Viaene and Dedene 2004; Tennyson 2008). This form of inflation is also called build-up. In the context of our study, we use the term insurance claims fraud in the sense of soft fraud or build-up, i.e., fraud-prone policyholders claiming loss amounts exceeding their actual value.

The appearance of insurance claims fraud is based on information being asymmetrically distributed between the policyholder and the corresponding insurance company (e.g., Derrig 2002). Since the individuals observe the amount of loss privately after the time of occurrence, they may decide to misrepresent the magnitude. In a costly state verification environment as applied by researchers (e.g., Townsend 1979; Mookherjee and Png 1989; Bond and Crocker 1997; Picard and Fagart 1999), the insurer has the opportunity to perform verification processes to determine the truthfulness of an incoming claim. Any detected engagement in fraudulent activities can be charged with a penalty payment. However, since this auditing comes at some cost, the insurance company has to weigh the benefits against the accompanying expenses. Another component that needs to be considered in this calculation is the policyholder perspective. Viaene and Dedene (2004) found that policyholders who had negative experiences in the insurance relationship, such as delayed indemnifications or underpayment, were more likely to engage in fraudulent activities.

While costly state verification is based on the insurance company being able to detect attempts of misrepresentation, the costly state falsification approach focuses on the policyholder incurring some cost to manipulate the magnitude of loss such that it becomes unverifiable. The general setting was introduced by Lacker and Weinberg (1989) and transferred to the specific features of the insurance environment by Crocker and Morgan (1998) and Crocker and Tennyson (2002).

A different approach in the fight against insurance claims fraud was taken by Dionne and Vanasse (1992) and Moreno, Vzquez, and Watt (2006). Instead of engaging in cost-intensive auditing, the insurance company raised the insurance premium in the consecutive period whenever the policyholder filed some claim. This strategy is often applied in the automobile insurance sector where contract renewals are a common standard. As a result, illegitimate claims when no insured loss occurred may be prevented.

In this study, we consider an alternative approach on the subject of claims handling, especially when fraud is present. For this purpose, we focus on the parties’ behavioral strategies, i.e., from the insurance company perspective, we consider the verification scheme. It is characterized by the probability of performing an audit, whereas from the policyholder point of view, the defrauding strategy is taken into account as represented by the probability of engaging in fraudulent activities. The aim is to identify and analyze all conditions under which the insurance relationship is attractive for the insurance company and the policyholder, i.e., both stakeholders are willing to adhere to the insurance contract. Particularly, for any fraud strategy, i.e., the probability of filing an inflated loss amount, we determine the set containing all valid corresponding auditing probabilities, given some constant cost per audit and vice versa.

Previous research has focused on deriving optimal contracts such that at equilibrium, the policyholders have an incentive to always report their losses truthfully (e.g., Townsend 1979; Picard and Fagart 1999). However, the question arises as to how the two stakeholders representing two opposing groups of interest can be brought together in the first place. Which behavioral patterns, i.e., defrauding and auditing probabilities, is the respective other willing to accept without being worse off than in the situation when no insurance contract was signed prior to the occurrence of loss? From the insurance company perspective, one can assume that, given some fixed cost per audit, it is not appealing to enter an insurance relationship with individuals who engage in build-up on a large scale in terms of frequency and severity. From the policyholder point of view on the other side, it appears to be intuitive to assume that delayed or reduced indemnification due to extensive auditing might curtail the attractiveness of insurance.

In D’Arcy, Derrig, and Weisberg (2010), it is assumed that the behavior of competing insurance companies facing insurance fraud follows one of several Nash equilibria.^[1] If the insurance companies consider claims savings caused by their auditing strategy as a portion of the total claims, the authors can show that inefficiencies may arise. Beside a Nash equilibrium, the authors derive alternative cooperative and non-cooperative agreements between the insurance companies in order to reduce the mentioned incentives and inefficiencies in the insurance market. In addition, empirical results are provided for no-fault auto bodily injury liability claims from the state of Massachusetts.

Obtaining the resulting set of all acceptable fraud and auditing probability combinations, we make a crucial observation. In the context of cost-minimizing insurance companies, a mutual acceptance between both stakeholders can be reached for any fraudulent behavior the policyholder might exhibit. In particular, even in the case when the loss amount is inflated in most of the incoming claims, there may exist auditing strategies such that the insurer is willing to adhere to the insurance relationship and even be able to optimize its objective quantity. This result underlines the expectation expressed by Watt (2003) and shows that for cost-minimizing insurance companies it is not necessarily desirable to undercut all fraudulent activities.

Based on the results of the acceptance range, we analyze all valid fraud and auditing probability combinations with respect to their optimality for the stakeholders’ respective objective quantity. As expected, we are able to show that the best possible outcome can never be achieved for both the insurance company and the policyholder at the same time. Which one out of all valid behavioral strategy combinations they settle on depends on their respective market power.

We want to emphasize that the acceptance range is not to be understood as a cooperative agreement that both parties decide upon. It intends to demonstrate the range of all possibilities attractive enough so that both insurer and policyholder are willing to maintain the insurance relationship.

The model derived in this study is based on the costly state verification environment, considering the insurance company’s net present value of future cash flows and the policyholder’s expected utility of his terminal wealth position. To make sure that both stakeholders are willing to sign an insurance contract, we include participation constraints. We derive and analyze some analytical solutions to the optimization problems. Due to the complexity of the model, however, it is not always possible to obtain closed-form solutions. Therefore, we present a numerical approach using Monte Carlo methods. The simulation results and their implications for both stakeholders’ optimal strategies are discussed and illustrated graphically.

The remainder of this study is organized as follows: we start by presenting the model framework and first analytical results in Section 2. Thereafter, the numerical approach and the corresponding program are introduced in Section 3. In Section 4, we discuss the simulation results before concluding in Section 5.

2. Model framework

An individual with initial wealth W₀ is offered the possibility to sign an insurance contract with a fixed premium P due by the time of inception of insurance cover in t = t₀. At the same time, he faces some uncertain loss θ of stochastic amount which, by the time of occurrence t = t₁, is observed privately. In case he signed the insurance contract earlier, the policyholder can then choose to file a claim of some size θ̂. In the case of honest behavior, the amount of that claim will equal the actual loss, i.e., θ̂ = θ. If the policyholder decides to commit fraud, he reports some finite θ̂ > θ. The probability of the policyholder choosing to report a fraudulent claim is denoted by p.

In order to check if fraud takes place, the insurer audits incoming claims with some probability q and at the constant cost of k per audited claim (to be paid in t = t₁). Depending on whether auditing took place or not and the outcome in case of an audit, a payment R is made from the insurance company to the policyholder. Considering the different possible combinations of fraud and auditing probabilities p and q, the stochastic payment R in time t₁ can be defined as follows:

$$R(\theta, \hat{\theta})=(1-p) \theta+p[(1-q) \hat{\theta}+q(\theta-B)], \tag{1}$$

with B being the penalty payment deducted from the claim amount θ.

Equation (1) can be interpreted as an indemnity payment if R is positive, whereas a negative R represents the payment made from the insured to the insurance company in case of detected fraud when B > θ. There are several possible cases: if the reported loss is not checked, the insured receives the payment of θ̂. In the case of auditing, the payment depends on whether the policyholder committed fraud or not. Proven honesty leads to a payment of θ = θ̂. If a misrepresentation of loss is determined, the policyholder faces some penalty B. In our numerical example (reference setting), we choose B such that θ − B = 0.^[2] In this setting, we take audits to be perfect, i.e., if a fraudulent claim is made, it will surely be detected in the case of auditing.

In our analysis, we assume the fraud probability p to be constant for all policyholders in the portfolio. The insurer only knows the fraud probability p, which is an average figure for the (sub-)portfolio in focus. This figure may be based on the insurer’s past experience or results from general industry knowledge. The fraud probability p typically varies substantially between different lines of business and different sub-portfolios. The estimation of the fraud probability is not necessarily based on (a part of the) policyholders which are currently in the portfolio. Hence, even if the insurer provides no coverage for all policyholders that do possess a history of fraud, p would still be positive, as new policyholders typically have a tendency to commit fraud, too. The auditing probability q is a decision variable for the insurer and the optimal value for q results from the target functions and the optimization procedure shown in the next three sections. In this respect and taking the equal claims distributions for the policyholders into account, we refer to the homogeneous portfolio case only.

In Section 2.1 we introduce the setting as well as the objective quantity and the participation constraint from the insurance company perspective. The same is done from the policyholder point of view in Section 2.2. Based on this information, we state the resulting optimization problems for both stakeholders in Section 2.3. Assumptions about the distribution of information among the policyholder and the insurance company are given in Section 2.4 before presenting analytical results in Section 2.5.

2.1. Insurance company: Cash flow, net present value and participation constraint

In the framework introduced above, we observe the future cash flows from the insurance company perspective at the time of insurance inception in t = t₀ and the time of loss realization and settling in t = t₁ and analyze their resulting present value. In the case of an insurance contract coming into existence, the insurance company receives the premium payment P in t = t₀. An incoming claim in t = t₁ that is audited with probability q and at some given cost k(> 0) per analyzed claim, results in −R(θ, θ̂) − qk.

The insurance company’s net present value NPV of its future incoming and outgoing cash flows is denoted by

$$N P V=P-P V(R(\theta, \hat{\theta}))-P V(q k), \tag{2}$$

where PV stands for the present value of the cash flows payable in t = t₁ and R(θ, θ̂) denotes the indemnity payment as defined in (1). Assuming a risk-neutral insurance company and a risk-free interest rate r_f = 0, PV can be replaced by the expected value in (2).

Condition 1. The insurance company is willing to participate in an insurance contract if its net present value is positive. Hence, one obtains the following participation constraint:

$$N P V \geq 0. \tag{3}$$

Applying Equation (2), participation constraint (3) can be formulated as

$$P \geq \mathbb{E}(R(\theta, \hat{\theta}))+q k. \tag{4}$$

Apparently, the expression on the right-hand side represents a lower bound for the premium payments the insurance company is willing to accept. Its value depends on the expected value of the indemnity payments that will be made and a loading that reflects the auditing effort.

2.2. Policyholder: Wealth position, utility function and participation constraint

From the policyholder perspective, we analyze his wealth position and the corresponding expected utility at the time of inception of insurance cover t = t₀ and the time of loss realization and claiming t = t₁ for the framework introduced above.

An individual initially owns some wealth W₀. Its consecutive development depends on whether he signs an insurance contract prior to the occurrence of loss or not. In a situation without an insurance contract, the individual holds the unchanged wealth position

$$W_{0}^{B}=W_{0} \tag{5}$$

at time t = t₀. At the time of loss occurrence in t = t₁, this amount decreases to

$$W_{1}^{B}=W_{0}^{B}-\theta=W_{0}-\theta. \tag{6}$$

The decision to sign an insurance contract is accompanied by the payment of an insurance premium P. Consequently, when signing the contract at time t = t₀, the individual owns the wealth position

$$W_{0}^{A}=W_{0}-P. \tag{7}$$

Assuming a loss θ of some stochastic level occurs and therefore a claim is filed at time t = t₁, the policyholder’s wealth at that point in time is denoted by

$$W_{1}^{A}=W_{0}^{A}-\theta+R(\theta, \hat{\theta})=W_{0}-P-\theta+R(\theta, \hat{\theta}) \tag{8}$$

with R(θ, θ̂) as defined in (1).

We assume the policyholder’s utility being described by a standard mean-variance utility function of his individual wealth. For a given wealth position W and the risk aversion parameter a(≥ 0) of the individual, this utility function is given by

$$U(W)=\mathbb{E}(W)-\frac{a}{2} \operatorname{Var}(W), \tag{9}$$

where (W) denotes the expected value of the stochastic variable W.

In the case where no insurance contract was signed prior to the occurrence of loss, using Equation (6) and definition (9), the final utility is written as

$$\begin{aligned} U\left(W_{1}^{B}\right) & =\mathbb{E}\left(W_{0}-\theta\right)-\frac{a}{2} \operatorname{Var}\left(W_{0}-\theta\right) \\ & =W_{0}-\mathbb{E}(\theta)-\frac{a}{2} \operatorname{Var}(\theta). \end{aligned} \tag{10}$$

For the setting in which an insurance contract was signed by applying the definition in (9) to Equation (8), we obtain

$$\begin{aligned} U\left(W_{1}^{A}\right)= & \mathbb{E}\left(W_{0}-P-\theta+R(\theta, \hat{\theta})\right) \\ & -\frac{a}{2} \operatorname{Var}\left(W_{0}-P-\theta+R(\theta, \hat{\theta})\right) \\ = & W_{0}-P-\mathbb{E}(\theta-R(\theta, \hat{\theta})) \\ & -\frac{a}{2} \operatorname{Var}(\theta-R(\theta, \hat{\theta})). \end{aligned} \tag{11}$$

Comparing Equations (10) and (11), one sees the difference in influencing factors for the final expected utility for each situation. In a setting without the existence of an insurance contract, the final expected utility U(W^B₁) solely depends on the extent of the actual loss θ and the policyholder’s risk aversion parameter a. However, in a situation in which insurance coverage exists, the value of the corresponding expected utility U(W^A₁) is not only influenced by θ, P and a. In addition, the policyholder’s fraud strategy p and the insurer’s auditing strategy q have an impact on that value due to the payment of R (see (1)). Moreover, if the insured decides to commit fraud, the size of θ̂ that he chooses to claim is relevant, as well as the enforced penalty payment B (see (1)), in case the fraudulent claim gets detected.

Condition 2. The individual’s decision to get insurance coverage in the first place depends on whether his utility by the time of loss occurrence is greater with having insurance than without it. In other words,

$$U\left(W_{1}^{A}\right) \geq U\left(W_{1}^{B}\right). \tag{12}$$

Using (11) and (10), this participation constraint (12) can be written as

$$\begin{array}{c} -P+\mathbb{E}(R(\theta, \hat{\theta}))-\frac{a}{2} \operatorname{Var}(\theta-R(\theta, \hat{\theta})) \geq-\frac{a}{2} \operatorname{Var}(\theta) \\ \Leftrightarrow P-\mathbb{E}(R(\theta, \hat{\theta})) \leq-\frac{a}{2} \operatorname{Var}(R(\theta, \hat{\theta})) \\ +a \operatorname{Cov}(\theta, R(\theta, \hat{\theta})). \end{array} \tag{13}$$

Based on the representation P ≤ E(R(θ, θ̂)) − $\frac{a}{2}$ Var(R(θ, θ̂)) + a Cov(θ, R(θ, θ̂)), the inequality in (13) can be interpreted as an upper bound for the insurance premium the potential policyholder is willing to pay for his insurance coverage. It depends on the utility of the payment R and the covariance between actual loss θ and R. Furthermore, the individual’s risk aversion parameter a has an influence on his willingness to pay.

2.3. Optimization of positions

So far, the model framework and the participation constraints for both the policyholder and the insurance company have been presented. Based on this information, we state the corresponding optimization problems.

The insurance company is aiming to maximize the net present value of the incoming and outgoing future payments with respect to its audit strategy such that both stakeholders are still willing to participate, i.e., Equations (12) and (3) hold. Again, it is assumed that the other parameters are given. This objective function can be written as:

$$\begin{aligned} & \textbf{Insurance company's optimization problem}\\ & \text{Find the audit strategy }q\text{ s.t. }N P V\text{ is maximized and}\\ & \text{Equations (12),(3) hold.} \end{aligned}\tag{14}$$

At the same time, the policyholder’s aim is to maximize his final expected utility with respect to his fraud strategy such that both participation constraints (12) and (3) hold, i.e., an insurance contract exists. It is assumed that all the other parameters are given. We will denote this optimization problem by:

$$\begin{aligned} & \textbf{Policyholder's optimization problem}\\ & \text{Find the fraud strategy }p\text{ s.t. }U\left(W_{1}^{A}\right)\text{ is maximized} \\ & \text{and Equations (12),(3) hold.} \end{aligned}\tag{15}$$

Both stakeholders try to optimize their own respective position. Our aim is to analyze these conflicting objectives and participation constraints from both the insured’s and insurer’s perspective and find a common acceptance range for the resulting fraud and auditing strategies.

Given a particular fraud probability p for the portfolio in focus, the insurer can calculate a) auditing probabilities q that are acceptable for the policyholder and b) an optimal value for q in order to maximize his NPV. For instance, if q = 10% is a valid outcome of the optimization procedure, the insurer should audit every 10th claim; the auditing costs for checking this particular claim are given by k.

Under the target function assumed for the insurer and the policyholder respectively, we show later that in general no p − q combination exists that maximizes the position of both stakeholder groups, i.e., the insurer’s NPV and the policyholder’s utility. Even though q cannot be freely chosen by the insurer for a given value of p, the concrete value of q finally depends on the market conditions (competition/market power) of the two stakeholder groups. If the market power would be solely by the policyholders, q should be a value that maximizes policyholder’s utility; the insurer’s NPV, however, would be non-negative.

In addition, it should be noted that the insurer could improve the optimization procedure described in this section. For instance, the insurer could derive an optimal threshold value for the claim amount θ̄. Claims handed to the insurer below θ̄ would not be subject to fraud auditing; claims exceeding θ̄ should be checked with probability q. In this context, θ̄ depends strongly on the auditing costs k. However, the problem with such a procedure is that the auditing strategy becomes very ineffective if the policyholder or a third party (like a car repair station in the case of motor insurance) receives some knowledge about the trigger value (see Müller, Schmeiser, and Wagner 2015).

2.4. Assumptions about the distribution of information

Before presenting the results of our analytical analyses, we summarize the assumptions regarding the distribution of information among the stakeholders.

2.4.1. Insurance company perspective

The choice of the insurance company’s feasible auditing strategies depends on the policyholder’s prevalent defrauding behavior, i.e., the potential fraud amount and the probability of an incoming claim to be inflated. The insurance company is assumed to have full information about the distribution of the reported losses θ̂ due to having observed incoming claims to date. In particular, this information can be specified for each insurance segment or even loss type. Furthermore, we expect that it has an adequate estimate for the distribution of the actual losses θ based on the outcomes of previous auditing processes. Consequently, the insurer is able to deduce the deviation from the magnitude that is to be expected for the particular loss type α ≔ θ̂/θ, i.e., the potential fraud amount in case fraudulent behavior occurs. Since the optimal auditing strategy also depends on the second component of the policyholder’s defrauding strategy, the prevalent fraud probability p, the insurance company has to estimate this value as well. For this purpose, whole catalogs consisting of criteria, so-called red flags, have been derived and implemented, aiming to estimate the probability of a claim being illegitimate as accurately as possible (see, e.g., Belhadji, Dionne, and Tarkhani 2000 and Bermúdez et al. 2008). Such indicators can be targeted at the individuals’ characteristics, such as gender, nationality or place of residence, as well as the attributes associated with the loss event. Combining this information, one is able to obtain a precise predictor for the fraud probability p (e.g., Dionne, Giuliano, and Picard 2009). It then chooses the corresponding optimal audit probability that maximizes its NPV in response.

2.4.2. Policyholder perspective

We assume that fraud-prone policyholders do not have sufficient information about the insurance company’s auditing process itself, i.e., he or she does not know the exact criteria for a claim to undergo verification. As a consequence, the individual cannot manipulate the claim in a way such that the insurer would not be able to identify the fraud attempt. This assumption is essential and not unrealistic. Waiving it would make auditing of any kind redundant, since the insurance company would never be able to detect loss inflation or other kinds of manipulation regardless of how the verification process is designed.

For the purpose of our analysis, we assume the policyholder to be able to estimate the probability of being audited by the insurance company when submitting a claim. This assumption is not in conflict with the one made before. The knowledge of the probability of one’s claim being audited does not imply an ability to manipulate the verifiability. Rather, it provides the policyholder with the possibility to become aware of which fraud behavior is advantageous in this particular situation and maybe choose the optimal one.

In the context of our study, we consider one observation period and determine all potentially feasible behavioral strategies from both the insurance company and the policyholder perspectives. Based on their decisions, however, other behavioral strategies may become more favorable for one or the other party in the consecutive periods. Therefore, the potential behavioral options need to be reconsidered by both stakeholders at the beginning of each observation period.

2.5. Analytical results

In the course of this subsection, we derive analytical results for the presented optimization problems assuming different conditions. The proofs can be found in the Appendix.

In the first proposition, we derive fraud and auditing strategies p and q for a special setting of the model framework. The crucial assumption in this case is concerning the policyholder’s risk aversion parameter a that is set a = 0, i.e., we assume the policyholder to be risk-neutral. This implies optimizing the insured’s objective function from a present value perspective.

Proposition 1. For a = 0 and θ, θ̂ such that 0 ≤ θ θ̂, the optimal fraud and auditing strategies from both stakeholders’ perspectives are p = 1 and q = 0. This results in P = E(θ̂).

This proposition implies that, under the given assumptions, the insurance company should waive auditing incoming claims and allow fraudulent behavior instead. In return, the expected amount of fraud will be added to the insurance premium. Furthermore, the proposition confirms a characteristic behavior that risk-neutral policyholders show. They are assumed to have no interest in insuring a potential loss at a premium which exceeds its expected value.^[3] Since in this specific setting all policyholders claim the fraudulent amount θ̂ at all times, the premium cannot be set higher than the expected value of θ̂. On the other hand, for the insurance company to be willing to participate in the insurance relationship, this premium must be below this value. Hence, the insurance premium equals exactly (θ̂). If administration and/or frictional costs need to be taken into account, Proposition 1 can (even for risk-neutral insurers) not be fulfilled.

In the remainder of this subsection, optimal fraud and auditing strategies will be derived for the policyholder and insurance company respectively in a more general setting. First of all, the policyholder is assumed to be risk-averse, i.e., the risk aversion parameter a is strictly positive, a > 0. This means his objective function is actually given as an expected utility function, i.e., the variance of the difference between indemnity payment R(θ, θ̂) and actual loss θ, denoted by Var(θ − R(θ, θ̂)), has an impact on the final result.

Furthermore, whenever the policyholder decides to make a fraudulent claim, he reports θ̂ = αθ for some given finite α ≥ 1 to the insurance company. This setting implies that the relative amount of fraud is constant. We deem it likely to assume that fraud-prone policyholders take the actual loss amount into consideration when trying to inflate it, i.e., they regard the relative fraud amount as a percentage surcharge. In this way, the filed claim does not deviate substantially from the loss amounts that can be expected related to the corresponding loss type. Consequently, the inflated claim is not perceived as illegitimate by the insurance company, which makes it less probable to undergo verification. This assumption is in line with the observations stated by Viaene and Dedene (2004). They found that in the context of soft fraud, the excess amounts tend to be relatively small.

We will derive fraud and auditing strategies, namely p^opt and q^opt, for the setting introduced above. Other than in Proposition 1, the potential policyholder is assumed to be risk-averse.

Proposition 2. Assume p, q to be in the acceptance range, i.e., an insurance contract exists. For $a>0$, $B=\theta$, $\hat{\theta}=\alpha \theta$ with some given 1, the respective optimal strategies p^opt, q^opt are given by:

i. Insurance company perspective

Let some p be given. In order for the net present value NPV to be maximized, choose

$$q^{o p t}=\left\{\begin{array}{ll} \text { as large as possible if } & p>p^{*} \\ \text { as small as possible if } & p \leq p^{*} \end{array},\right. \tag{16}$$

where p* ≔$\frac{k}{\alpha \mathbb{E}(\theta)}$

ii. Policyholder perspective

Let some q be given. In order for the final expected utility U(W^A₁) to be maximized, choose

$$p^{o p t}=\left\{\begin{array}{l} \text { as large as possible such that } \\ \frac{-\mathbb{E}(\theta)}{\text { ap }(1-\alpha(1-q)) \operatorname{Var}(\theta)} \geq 1 \\ \text { as small as possible such that } \\ \frac{-\mathbb{E}(\theta)}{\text { ap }(1-\alpha(1-q)) \operatorname{Var}(\theta)} \leq 0 \end{array} .\right. \tag{17}$$

For the case 0 $\frac{-\mathbb{E}(\theta)}{a p(1-\alpha(1-q)) \operatorname{Var}(\theta)}$ 1 no general statement can be made.

Proposition 2(i) looks at the optimization problem from the insurance company perspective. It states the optimal auditing strategy with respect to a given fraud probability. The insurance company has two general strategies to choose from. It can either decide to audit the incoming claims with the maximal probability possible, i.e., such that the participation constraints of both policyholder and insurance company hold true, or the auditing probability can be chosen as small as possible. This decision depends on an estimate of the policyholder’s behavior p. Based on whether it exceeds or falls short of the threshold $\frac{k}{\alpha \mathbb{E}(\theta)}$, the insurance company opts for a high or low auditing probability, respectively. According to Proposition 2(i), the exceed of the threshold is influenced by the costs per audit k. The lower these are, given some fixed α and θ, the more likely it is for the fraud probability to exceed the resulting threshold. In this case, it becomes optimal for the insurance company to verify the incoming claims with a high probability. The opposite relationship holds true for the expected loss amount θ and the degree of fraud that is represented by α. The higher their values are, the lower the threshold becomes and the more likely it is for the estimated fraud probability to exceed the latter. For the insurance company, this implies auditing the incoming claims with the highest probability possible as well. For an illustration of the results obtained in Proposition 2(i), see Figure 1(a) and the discussions in Section 4.1.

Proposition 2(ii) considers the policyholder point of view in this optimization problem. In this case, the decision whether to choose the fraud probability as large or small as possible, given a certain auditing strategy, is not as clear as in the previous situation described in Proposition 2(i), especially since there are situations for which no forecast can be made. Furthermore, difficulties arise when trying to interpret the impact of single model parameters on the value of the threshold that determines the optimal auditing behavior in the known cases. However, see Figure 1(b) and the discussions in Section 4.1 for an illustration of the optimal fraud probability from the policyholder perspective.

The challenges that occur with finding a closed-form analytical solution to the introduced maximization problem emphasize the need for a numerical approach. In Section 3, we therefore present a method for deriving the acceptance range for both policyholder and insurance company. Furthermore, the impact of valid p − q combinations on the objective quantities U(W^A₁) and NPV is analyzed and illustrated.

3. Computational aspects

As discussed in the previous section, simple analytical solutions to the optimization problem cannot be derived for all general settings. Moreover, the results may be hard to interpret both graphically and economically. In this section, we will approach these challenges by using numerical methods and Monte Carlo simulation. The aim is to compute the acceptance range with respect to the fraud and auditing strategies for various parameterizations of the model. After having introduced the procedure, the results of the simulations will be analyzed and presented graphically.

3.1. Monte Carlo simulation and numerical methods

We use the Monte Carlo technique to find the optimal acceptance range regarding the fraud and auditing strategies of the policyholder and the insurance company, respectively. The main idea behind this approach is to generate a sufficiently large number of loss realizations N (we will use N = 100,000) of the random variable θ. Furthermore, we consider all fraud and auditing probabilities p and q that are represented by $l \cdot \frac{1}{M}$ for l = 0, 1, . . . , M where M denotes the number of discretization points on the interval [0, 1]. Based on these assumptions, the resulting indemnity payments R, the policyholder’s wealth positions with and without having signed the insurance contract W^A₁ and W^B₁ and the insurance company’s value V are calculated for each outcome of the simulation and each fraud and auditing probability combination.

Using Equations (1), (6) and (8) for R, W^B₁ and W^A₁ respectively, this can written as follows:

$$\begin{aligned} R[n, i, j]= & (1-p[i]) \theta[n] \\ & +p[i]\left(\begin{array}{c} (1-q[j]) \alpha \theta \\ +q[j](\theta[n]-B[n]) \end{array}\right) \end{aligned} \tag{18}$$

$$W_{1}^{B}[n, i, j]=W_{0}-\theta[n] \tag{19}$$

$$W_{1}^{A}[n, i, j]=W_{0}-P \theta[n]+R[n, i, j], \tag{20}$$

where θ[n] denotes the nth realization of the random variable θ and p[i] and q[j] are the considered fraud and auditing probability represented by $i \frac{1}{M} \text { and } j \frac{1}{M}$ for i, j = 0, 1, . . . , M, respectively. Consequently, the term [n, i, j] indicates for which combination of loss realization and fraud and auditing probabilities the quantities R, W^B₁ and W^A₁ are evaluated.

The next step to determining the acceptance range is to derive the objective quantities, i.e., the policyholder’s final utility depending on whether he signed the insurance contract prior to the loss or not and the insurance company’s present value based on the corresponding wealth and value positions calculated before. For this purpose, we use arithmetic averaging with respect to the realizations of the random variable θ for each possible combination of p and q. Regarding the individual’s final utility when having decided against insurance coverage, we use the following formula, derived from Equation (10):

$$\begin{aligned} U\left(W_{1}^{B}\right)[i, j]= & \hat{\mu}_{n}\left(W_{1}^{B}[n, i, j]\right) \\ & -\frac{a}{2} \hat{\sigma}_{n}^{2}\left(W_{1}^{B}[n, i, j]\right), \end{aligned} \tag{21}$$

where $\hat{\mu}_n$ denotes the estimator for the expected value with respect to all realizations n = 1, . . . , N and $\hat{\sigma}_n^2$ the estimator for the variance with respect to all realizations n = 1, . . . , N. The same procedure applies for the case when an insurance contract was signed, this time using Equation (11):

$$\begin{aligned} U\left(W_{1}^{A}\right)[i, j]= & \hat{\mu}_{n}\left(W_{1}^{A}[n, i, j]\right) \\ & -\frac{\alpha}{2} \hat{\sigma}_{n}^{2}\left(W_{1}^{A}[n, i, j]\right) . \end{aligned} \tag{22}$$

From the insurance company point of view, the net present value of its future incoming and outgoing cash flows depending on the fraud and auditing probability can be derived as follows, based on Equation (2):

$$N P V[i, j]=P-\hat{\mu}_{n}(R[n, i, j])-q[j] k. \tag{23}$$

We are now in the position to check for the participation constraints of both the policyholder and the insurance company. Only if this holds true, an insurance contract will be offered by the insurance company and purchased by the policyholder. In addition, our optimization problem is only well defined under these conditions. The idea here is to systematically analyze the participation constraints given in Equations (12) and (3) for each combination of fraud and auditing probabilities. In case these are verified, we consider the corresponding p − q combination as valid. At the end of this procedure, we obtain the acceptance range.

The actual aim is to find the optimal strategies p and q such that the objective quantities, i.e., the policyholder’s final wealth position U(W^A₁) and the present value of the insurance company’s future incoming and outgoing cash flows NPV, are maximized from each of the participants’ perspectives. For these to be determined, we calculate the results for U(W^A₁) and NPV evaluated with respect to the valid p − q combinations, respectively. Once the maximal values have been found, we can retrace the corresponding fraud and auditing probabilities under which the maximum was attained. This procedure is performed separately for the two participants.

3.2. Choice of parameters

We analyze the implementation of the model for different parameterizations. The aim here is to study the influence of certain model parameters on the acceptance range regarding the valid fraud and auditing probabilities.

We make assumptions concerning the distribution of the loss variable θ, the policyholder’s initial wealth position W₀ and the penalty payment B that remain fixed throughout the whole analysis. For instance, the policyholder’s wealth position is set to W₀ = 0. Since his participation constraint that is given by Equation (12) is independent of this parameter, our choice will not have any influence on whether he signs the insurance contract or not. Furthermore, we assume the random variable θ to follow a log-normal distribution. This assumption is commonly used, as mentioned in Marlin (1984), since it guarantees positive values for the realizations of the random variable. In particular, the parameters of the log-normal distributed random variable θ are set such that (θ) = 1 μ and Var(θ) = 0.4² σ².

This entails that the parameters for the log-normal distribution are 0.0742 and 0.3853 (for the mean and standard deviation of the distribution on the log scale). Regarding the penalty payment B, we take it to be of the same value as the corresponding realization of the loss θ such that in the case of detected fraudulent behavior the indemnity payment is 0. Additionally, we will not consider exogenously given penalties. Viaene and Dedene (2004) claim that in practice insurance companies tend to negotiate with allegedly suspicious policyholders since substantial legal evidence is needed to prosecute insurance claim fraud successfully.

In this subsection, we analyze the influence of the policyholder’s risk aversion a, the amount of fraud that is represented by α, the insurance premium P and the cost per audit k on the acceptance range, respectively. For this purpose, we use the ceteris paribus assumption in the analysis, i.e., we study the change in the acceptance range caused by one isolated factor while keeping all the others constant. Unless noted otherwise, the policyholder is taken to be risk averse. Hence, to start with, his risk aversion parameter a is set 6. Furthermore, we first assume that in the case of fraudulent behavior the policyholder always decides to claim an amount that is 20% higher than the actual loss. According to Derrig, Johnston, and Sprinkel (2006), this value seems reasonable. In an auto injury insurance claim study from 2002, they revealed that the average payments that were made related to bodily injury claims added up to approximately $7,872 if no buildup or fraud was detected, whereas in cases where fraudulent behavior appeared, the amount rose up to $9,559 on average. The last assumption that we have to make concerns the insurance premium. It can be split up into the fair premium and an appropriate loading factor. The fair premium corresponds to the expected loss. Hence, having set the expected value of the loss variable θ to μ = 1, it implies a fair premium of 1 as well. However, the loss ratio in the automobile insurance in many industrialized countries over the last years averaged out to approximately 70%.^[4] Using this observation and the assumption of μ = 1, we set the fair premium to 1.4. Furthermore, since the insurance company faces additional costs due to the auditing process with positive probability, it will add a corresponding loading factor to the fair premium. However, as mentioned in Cummins and Mahul (2004), the loading factor cannot be chosen too big since potential policyholders would not sign the insurance contract under such conditions. For the purpose of starting our analysis, we will assume the total insurance premium to be P = 1.45. The last parameter whose influence on the acceptance range will be analyzed is the cost per audit k. It is set k = 0.1 which corresponds to 10% of the expected value of the loss θ. For the purpose of our analysis and in order to keep focused, we will disregard costs other than the ones due to auditing.

The multiplicative relationship θ̂ = αθ for fraud-prone policyholders accounts for the built-up case only. Hence, the variable θ needs to be positive in this context. However, an extension of the model setup could be provided for fraud cases where no claim had occurred or a claim has taken place which is not covered by the policyholder’s policy. For such a case, an additive relationship and information about the average distribution of the two fraud cases—“build-up” fraud and fraud without an underlying claim—within the portfolio is needed.

Table 1 sums up the choices for the input parameters for the reference setting as introduced. In the course of this study, we base our simulations and studies on these values.

Unless otherwise noted, the simulation results are based on N = 100,000 realizations of the loss variable θ and M = 50 discretization points in the interval [0, 1].

4. Simulation results

This section contains the results based on the numerical simulation. First, we discuss the reference setting and the impacts on the objective quantities and the corresponding optimal strategies. Furthermore, a sensitivity analysis of the relevant parameters is performed.

4.1. Reference setting

Before discussing the effects of different parameterizations regarding the policyholder’s risk aversion, the amount of fraud, the insurance premium and the cost per audit on the acceptance range, we will first illustrate the results given the input parameters as summarized in Table 1.

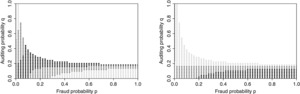
Figure 1 shows the acceptance range from both the policyholder and the insurance company perspective based on the values for the input parameters that were presented above. Each point in the graphic represents a valid fraud and auditing probability combination.

To illustrate the dimension of the objective quantities U(W^A₁) and NPV that result from the current parameter choice and a certain p − q combination, the points in Figure 1 are displayed in different shades according to the value. For this purpose, given that the input parameters are fixed, the p − q combinations that lead to the lowest third of outcomes are presented in the lightest shade, whereas those combinations that result in the highest third of outcomes are shown in the darkest shade. The remaining points are displayed in a medium shade. This implies that the darker the shade of a point, the higher is the relative value of the corresponding U(W^A₁) or NPV.

4.1.1. Insurance company perspective

From the insurance company point of view, we are interested in deriving all feasible and, in particular, the optimal verification strategies characterized by the probability of auditing q when the prevalent defrauding probability p is known.

For this purpose, let some constant fraud behavior that is characterized by p be given. The choice regarding the optimal corresponding auditing strategy q from the insurance company perspective depends on the value of the fraud probability p. As already proven in Proposition 2, there exists a threshold p* that determines whether it is optimal to audit the incoming claims with the highest probability possible or the lowest valid probability, i.e., the highest and lowest q respectively contained in the acceptance range. Considering the choice of the input parameters for the reference setting, the value of this threshold is given by $p^*=k / \alpha \mathbb{E}(\theta)$ = 0.083. This implies that in the case p > 0.083, it is best for the insurance company to audit the incoming claims with the highest valid probability, whereas if p ≤ 0.083, the optimal strategy is to chose q as small as possible. These relationships can be observed in Figure 1(a).

Another interesting observation can be made when considering p = 1. In this specific setting, the fraud-prone policyholders decide to inflate their claims by 20% each time they incur an insured loss. Intuition would tell us that such an extensive case of build-up cannot be acceptable from the insurance company point of view, i.e., it would not be possible to find feasible auditing strategies in this context. However, we are able to observe the opposite in our analyses due to the circumstance that the insurer in our reference setting has to incur relatively low costs to detect fraudulent attempts. Additionally, in the case of proven build-up, no indemnity payments are made to the policyholder, i.e., neither the excess nor the loss amounts are paid out. As a consequence, it is possible to have the savings from detected fraud outweigh the additional costs from indemnifying inflated losses such that the net present value NPV is positive. Thereby, the best result from the insurance company point of view is achieved when performing audits with the highest feasible probability q.

4.1.2. Policyholder perspective

Similarly to the case above, we determine all acceptable and especially optimal defrauding strategies p from the policyholder perspective, given that they have knowledge of the current insurance company’s auditing scheme q. The former are defined by the probability of filing an inflated loss amount.

Hence, we assume the insurance company to be committed to some constant auditing strategy q. From the policyholder perspective, it is always optimal to correspond with reporting fraudulent claims at the highest valid probability p. Figure 1(b) supports this result.

This finding appears to be rather intuitive. The premise in this context is the insurance company having committed itself to some constant verification scheme expressed by some constant probability q. However, this implies that the share of incoming claims that does not have to undergo the auditing process remains constant as well. In this case, it is advisable for the policyholder population to increase the probability p of exaggerating their loss amounts, i.e., the share of build-up among the claims that are indemnified instantly rises as well, leading to higher payouts for the individuals.

Figure 1(b) can be interpreted in the following way too: If we have some fixed level for p (with 1 > p > 0) within the portfolio, the utility of the fraudulent acting policyholders will ceteris paribus be reduced if q increases, because such policyholders get caught more often and need to pay the penalty B (> 0). Since we have no utility change for those policyholders that are honest in respect to different levels of q, the overall utility level of the group of policyholders in the portfolio is reduced if q increases. As p denotes the (ex-ante) probability that a policyholder in the portfolio will commit an insurance fraud and the utility is measured for the group of policyholders (and not on the individual level), we can see that for a positive value of p one can derive levels for q, resulting in a situation in which the policyholders are not willing to purchase insurance any more. However, there could be some “educational effects” if the policyholders assume that for some level of p the insurer may choose an auditing probability q leading to a situation in which the policyholders would be better off without insurance. Acting in a rational way, the policyholders should rather reduce p, expecting the insurer via signaling to reduce q to a level that results in a valid p − q combination. However, the insurer has a strong incentive, too, to choose only levels of q which are acceptable for the policyholders in order to be able to sell insurance and hence achieve a positive NPV.

As indicated in Section 1, Figure 1 illustrates that in the setting of our model framework, it is impossible to find a feasible p – q combination that maximizes the objective quantities of both stakeholders at the same time. The prevalent behavioral strategies result in an optimum of either the insurance company’s net present value NPV or the policyholder’s utility U(W^A₁) of having signed an insurance contract prior to the occurrence of loss. Which one of these events will be observed depends on the market power of the respective parties. Assuming a highly competitive market, it is likely for those defrauding and auditing probability combinations to be applied that maximize the policyholders’ objective while the insurer is still willing to adhere to the insurance relationship. However, if the insurance company is in the position of possessing the position of power, other probability combinations become of interest, since the insurer will be able to maximize its own objective while making sure to keep contract conditions attractive enough for its policyholder population.

Furthermore, it seems possible for defrauding and auditing strategies that have once been optimal for the respective stakeholder to become unattractive in the consecutive observation period. Consequently, the insurance company and the policyholders need to identify all acceptable probability combinations p − q at the beginning of each period, and possibly realign their strategies on this basis.

4.2. Sensitivity analysis of relevant parameters

In the remainder of this section, we present and discuss the resulting acceptance ranges, i.e., all valid p − q combinations based on different choices regarding the input parameters of risk aversion a, fraud amount α, insurance premium P and cost per audit k. Since the effects of the different valid p − q combinations on the policyholder’s final utility position U(W^A₁) and on the insurance company’s present value NPV have been presented and analyzed, we restrict ourselves to showing the acceptance range itself without the impacts on the objective quantities.

4.2.1. Influence of policyholder’s risk aversion

In this subsection, we will analyze the impact of different risk aversion parameters on the acceptance range of the fraud and auditing probabilities. For this purpose, we chose different values for a while keeping all the other input parameters as given in Table 1. In particular, Figure 2 shows the acceptance range for the risk aversion parameters a = 5 and a = 10.

Comparing the two graphics for the acceptance range, we find that the upper bound shifts in an upward direction when increasing the policyholder’s risk aversion parameter. This implies that the higher the risk aversion of the policyholder is, the broader the acceptance range becomes, assuming all the other input parameters to be constant.

In other words, the more risk averse the policyholder is, the higher the auditing probability q can be chosen for each fraud strategy p while the policyholder is still willing to participate in the insurance contract.

It seems reasonable to assume that policyholders’ risk aversion a and the fraud probability p are not independent from each other. In particular, we would assume that very risk-averse policyholders (cf. Figure 2(b) with a = 10) would rather exhibit a lower fraud probability p compared to policyholders with a lower degree of risk aversion (cf. Figure 2(a) with a = 5). However, for both cases in our numerical example, there still exist acceptable p − q combinations for the policyholders and the insurer.

4.2.2. Influence of fraud amount

In Figure 3, the acceptance range is displayed for the fraud amounts α = 1.1 and α = 1.8, i.e., in the case of fraudulent behavior, the claimed loss is given by θ̂ = 1.1 · θ or θ̂ = 1.8 · θ. Again, the remaining input parameters are chosen as displayed in Table 1.

Comparing the graphics for the different choices of α, we find that the upper bound of the acceptance range as well as part of the lower bound shift in an upward direction when increasing the fraud amount. To be more precise: while the number of valid p − q combinations with high auditing probabilities q increases for all fraud strategies p, the change in the lower bound occurs only in the area of high fraud probabilities p. Summing up these effects, we can state that the higher the amount of fraud, the wider the acceptance range becomes. However, a change from α = 1.2 in the reference setting to α = 1.1 results in marginal modifications within the acceptance range.

This outcome can be interpreted in the following way: the higher the amount of fraud α per claim, the more likely it is for the policyholder to accept higher auditing probabilities q, given that his own fraud probability p is fixed. In these cases, even though the auditing activity increased, the gain in final utility U(W^A₁) due to excessive claiming is still positive, despite the higher chance of being convicted and imposed with a penalty payment. On the other hand, it becomes unattractive from the insurance company perspective to audit the incoming claims with a low probability q when the amount of fraud is increased, assuming a high fixed fraud behavior p. Such a strategy would imply that the majority of fraudulent claims remained undetected, which consequently leads to an increase in outgoing cash flows due to excessive fraud amounts. This increase, however, is not covered by incoming positions like insurance premiums or penalty payments. Therefore, if the fraud amount α goes up, p − q combinations with higher values for q become acceptable to both stakeholders, whereas no insurance contract will come into existence with individuals who are expected to commit excessive fraud frequently.

4.2.3 Influence of insurance premium

Insurance premiums are another common way to influence the willingness of both the potential policyholder and the insurance company to participate in an insurance contract. In Figure 4, the acceptance range is presented for two different values of the insurance premium, i.e., P = 1.35 and P = 1.55, while the other input parameters are chosen as in the reference setting.

A comparison of the acceptance ranges when choosing P = 1.35 and P = 1.55 shows that the upper bound shifts in a downward direction when increasing the value of the insurance premium. This means that the higher the insurance premium is, the smaller the acceptance range gets while keeping the remaining input parameters unchanged.

In other words, the lower the insurance premium P is, the more willing the policyholder is to accept higher audit probabilities q when keeping his own fraud probability p constant. However, if the insurance premium is set too high, i.e., it exceeds the expected loss amount by far, potential policyholders will have no benefit from signing such an insurance contract.

The effect of shrinking acceptance ranges due to high insurance premiums can be weakened by offering such contracts to potential policyholders whose risk aversion is assumed to be high as well. As we have seen in Figure 2, the increase in risk aversion has the opposite effect on the acceptance range as the choice of the insurance premium.

It needs to be pointed out that the insurance premium seems to have a significant impact on the acceptance range. Even though the values of P have been varied only marginally throughout the analysis, i.e., ±7% of the reference level, the resulting number and positions of the valid p − q combinations differ markedly.

4.2.4. Influence of cost per audit

The last input parameter that can be adjusted easily is the cost per audit k. Its value can give an indication of what type of auditing is being performed by the insurance company. Auditing procedures in which standard techniques are applied require minor costs, whereas investigative processes that are initiated to verify major claims result in high costs.

Figure 5 displays the acceptance ranges when the cost per audit is chosen to be k = 0.01 and k = 1.0, respectively, while keeping the remaining input parameters as in the reference setting.

When comparing the graphic where the cost per audit is set k = 0.01 to the one with k = 1.0, we find that the upper boundary of the acceptance range shifts in a downward direction in the case of low fraud probabilities p while there appears to be no change in the remaining valid p − q combinations. This implies that the higher the cost per audit, the smaller the acceptance range becomes when keeping the other input parameters constant. However, only marginal changes within the acceptance range can be observed when choosing k = 0.01 instead of k = 0.1 as given in the reference setting.

This observation can be explained in the following way: the higher the cost per auditing process, the less willing the insurance company becomes to verify those incoming claims for which a low fraud probability is assumed. Such a strategy would lead to high expenses for the insurer that are not likely to be covered. The policyholder rarely commits fraud and even in case he does, the additional amount claimed is not excessive. Therefore, relatively high auditing costs and comparably low expenses resulting from undetected fraudulent claims are opposing each other. As a consequence, no insurance contracts will come into existence with policyholders whose fraud probability p and amount α are expected to be low while the cost per audit k is set at a high level.

A way to avoid this effect is to adjust the effort put into the auditing process to each specific case.

Depending on the type of loss and the corresponding amount claimed, the insurance company can decide whether to apply a basic procedure at low cost or an extensive process that leads to high expenses.

As indicated by the very extreme choice of the parameters, i.e., in the first case k = 0.01 corresponds to 1% of the expected loss and in the second one k = 1.0 equals the expected loss, the cost per audit k does not have a significant influence on the acceptance range. However, the results imply that extensive auditing in the form of high values for q is not sustainable for the insurance company if the cost per audit k is high.

For simplification reasons we decided to assume that any detection is successful from the point of view of the insurance company. In practice, this is generally not the case. However, the introduction of non-successful detections is comparable with additional auditing costs k and hence lead to the effect shown above.

4.2.5. Influence of the penalty

In our basic setting we assumed that B = θ. However, B strongly depends on the concrete jurisdiction in force. In Germany, e.g., the penalty is typically much larger than the pure fraudulent add-up θ̂ − θ. The reason for this is that in the case of a detected fraud, the insurer is allowed to charge the policyholder the auditing and administration costs coming along with this particular fraud case. In addition, the policyholder may face court and further law costs and will often not get insurance coverage at that particular insurer again. In any case, we would expect B to be positive. This is due to the fact that for B = 0, at least rational policyholders would always commit fraud because they could never be worse off compared to the situation without fraud. In our sensitivity analysis in Figure 6 we reduced the penalty to B = 0.5 · θ and B = 0.1 · θ, respectively. We can see that one gets a larger range of acceptable p − q combinations if the penalty is reduced. The interpretation is straightforward: policyholders would accept an increase of the auditing probability, because the penalty is less severe whenever a fraud is detected.

4.2.6. Influence of the loss size standard deviation

In Figure 7 we illustrate the influence of an increase of the standard derivation of the loss size distribution on the range of acceptable p − q combinations. Again, we used a ceteris paribus analysis. Therefore, we assumed in particular that the same premium is charged for the different cases (the influence of different premium levels has been analyzed in Figure 4). Hence, the insurer does not consider the individual loss size volatility for pricing purposes in these examples. This is—for instance—the case, if an expected premium principle is used (in this case, the premium loading is a percentage of the expected indemnity payment). The interpretation of the results can be done in the following way: For risk-averse policyholders, insurance coverage gets more attractive giving an increasing loss size volatility if everything else stays unchanged. Hence, policyholders would accept higher auditing probabilities leading to an increasing range of acceptable p − q combinations.

5. Conclusive remarks and outlook

In this study, we build and analyze a model framework that depicts the handling of insurance claims fraud based on a costly state verification approach. We present analytical solutions as well as numerical methods for solving the resulting optimization problems that take both the insurance company and the policyholder perspectives into account. Our focus is set on deriving an acceptance range consisting of all valid fraud and auditing probability combinations and analyzing their optimality regarding both stakeholders’ objective quantities. In addition, we discuss the impact of different relevant input parameters on the size of the acceptance range. Furthermore, we are able to calculate a threshold value for incoming claims based on which the insurance company can decide whether to perform auditing or not.

One of our main findings is the derivation of optimal auditing and fraud strategies from the stakeholders’ perspectives. Especially from the insurance company point of view, it seems intuitive: the optimal answer to low fraud probabilities is to perform auditing with a small probability as well, whereas medium and high fraud probabilities require the largest valid audit probability to maximize the net present value. An interesting observation in this regard is that the insurance company benefits from the existence of insurance contracts (almost) regardless of the policyholders’ defrauding strategy. This finding demonstrates that in the context of cost-minimizing insurers, it is not essential to completely prevent all defrauding attempts ventured by the policyholder population.

Based on our numerical approach, we present and analyze the acceptance range for different parameterizations as well as the optimality of different auditing and fraud probability combinations regarding the stakeholders’ respective objective quantities. While a relatively high risk aversion, a high relative amount of fraud, and low insurance premiums result in broadening the acceptance range, the latter becomes smaller whenever the value of these input parameters is chosen the opposite way. We also find that the cost per audit merely influences the number of valid fraud and auditing probability combinations. Furthermore, the simulation results support and illustrate our analytical findings regarding optimal fraud and auditing strategies.

The model that we present in this study can be extended for future research. On the one hand, another type of auditing could be introduced that, while less costly than the perfect one, detects fraud only with some probability less than one. On the other hand, insurance premiums could depend on the auditing probability, since more strict auditing policies require a longer period to process incoming claims and policyholders might not be willing to pay the original insurance premium due to possible delays in indemnity payments. Another topic for further research is to back test the results derived in this study with insurance company data and profiling experience.

Our model is in many ways a simplification of real auditing processes in the insurance industry. We assume that all other indicators for fraudulent policyholders’ behavior—e.g., individual claims history or loss description—had been used already and particular risks that are suspicious had been selected and reviewed separately. Hence, we are left with an approximately homogeneous (sub-)portfolio with no particular indication for fraud. In this respect, the insurer auditing procedure is rather a multilayered process.

However, we do know that this portfolio still faces on average a positive fraud probability denoted by p. The insurer can only perform one auditing process with fixed costs k; the auditing process is thereby certain to determine a fraud. Both aspects are simplifications of real-world behavior. In general, the insurer can perform different costly auditing processes and a less expensive monitoring will typically be less accurate in respect to policyholders’ fraudulent activities. In the context of a homogeneous portfolio, however, only one auditing process (of a finite number of different monitoring activities with different costs and efficiencies) with costs k and a given probability of a “false positive” / “false negative” would be optimal for the insurer to use. A combination of different monitoring activities can be expected in the context of a heterogeneous portfolio. From the modelling point of view, it would be possible to introduce an additional variable indicating the probability of a “false positive.” However, the results are quite straightforward: the effects on the outcomes are ceteris paribus, very similar to an increase in the auditing costs k (which is shown via numerical examples in the sensitivity analysis in Section 4.2).

In our model setup, insurance fraud is carried out by the policyholder. This is not necessarily the case in insurance practice. In motor insurance, it is often the repair station that provides very costly and extensive repairing (at least on the invoice) whenever the claim is insured. The optimization procedure derived in this paper needs to be revised if a second party can commit fraud, too. This is due to the fact that the participating constraint by the policyholder will in general be influenced by the behavior of an additional group (for instance, a repair station in the case of motor insurance).