Counterfactual Disaster Risk Analysis

1. Introduction

Whenever disasters occur, there are often many lessons to be learned by the communities and industries affected and their insurers. Investigations may be undertaken, public inquiries may be established, technical reports written, and recommendations made for disaster risk reduction. The greater the disaster, as measured in terms of casualties, damage, and economic loss, the more lessons that risk managers will seek to learn. Conversely, as the human, societal, and insurance loss measures associated with an event decrease, so also is the amount of attention usually given. In the limit that no actual loss is associated with an event occurrence, few long-term lessons may ultimately be learned, and a timely opportunity for future disaster risk reduction may be lost.

The origin of the word “disaster” is based on the ancient belief in an astrological cause, as if the clockwork motions of the stars predetermined their dates as precisely as eclipses. Except for those who read horoscopes, we now know that disaster history is not preordained. Because history cannot be changed, it is typically treated as fixed. However, disaster occurrence has complex dynamics, in which randomness and dynamical chaos play a substantial part. There are numerous situations in history where a system was close to disaster, which never quite materialized. Fortunately, there was no untimely dynamic perturbation that might have edged the system to disaster.

The statistical foundation of quantitative disaster analysis is the database of actual loss experience. Any disaster that occurs without apparent historical precedent is liable to be received with some degree of surprise. Since the start of the millennium, there have been numerous costly surprises for the insurance industry, affecting both assets and liabilities—so much so that a special glossary of evocative terms has emerged to describe surprising catastrophes: black swans (Taleb 2007), dragon kings (Sornette and Sanchev 2009), unknown unknowns, etc. Knightian uncertainty is often cited to explain the limits of risk analysis and excuse surprise as almost inevitable. But beyond adopting a new vocabulary to cover unforeseen disasters, actuaries can be better prepared to anticipate and cope with such extreme rare events.

Counterfactual disaster risk analysis has a contrasting focus on the past, exploring the depths of counterfactual history to identify and assess previous situations where a disaster might have occurred, but was averted or otherwise failed to materialize. Specifically, the following two questions are raised. First, what perturbation to the historical context might have edged a system towards disaster? Second, what was the likelihood that such a critical change might have happened?

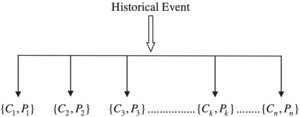
Answers to these questions facilitate counterfactual risk evaluation (Balke and Pearl 1994), informing decisions on catastrophe insurance risk management. Importantly, they provide sense checks of estimates of probable maximum loss (PML) that may be associated with substantial epistemic uncertainty, risk ambiguity, and diversity in expert judgement. Suppose that the historical record for a particular peril spans a period of N years. Within this observation period, only M events have occurred. Counterfactual analysis of the j’th event might be undertaken with a moderate effort, and would generate a table of counterfactual losses C₁(j), C₂(j), C₃(j) . . . , with associated probabilities p₁(j), p₂(j), p₃(j). . . . Each historical event spawns an ensemble of counterfactual realizations, which may be envisioned in Figure 1 as a building block of a basic catastrophe model.

Figure 1.Counterfactual losses and probabilities for a historical event

These results could be used to calculate various PML risk metrics to compare with existing standard PML estimation methods. As another application, counterfactual disaster analysis could be used as a technique in reverse stress testing. Given a specified catastrophe insurance loss, the various pathways by which such an extreme loss might materialize could be explored counterfactually by selecting some actual historical events, and perturbing them to generate the target extreme loss.

The practical need and rationale for counterfactual disaster risk analysis emerges from the social psychology of disasters. Complacency tends to become entrenched amongst those who have experienced an event that has caused little or no damage. Compounding a public attitude of complacency is the sociological principle of social proof: people tend to do what others like them are doing. According to Lindell and Perry (1992), the interpretations of the outcomes of prior disasters and why these outcomes unfolded will influence subsequent perceptions of future disaster events. If an event passes with few negative outcomes, there is a natural inclination to move on, rather than look back and take note of what actions might be warranted.

A counterfactual risk perspective is useful for many government and corporate stakeholders apart from insurers. Assessment of the counterfactual disaster risk can guide safety authorities in commissioning disaster mitigation projects to reduce future losses, and help prioritize them according to urgency. The insurance industry stands to benefit from lower claims, sounder risk management, and enhanced underwriting risk awareness.

1.1. Alternative realizations of history

From a scientist’s perspective, history is not inevitable, but is just one possible realization of what might have happened. Indeed, in his discussion of the logic of counterfactuals in causal inference, Pearl (2000) has emphasized that counterfactuals carry as clear an empirical message as any scientific laws, and indeed are fundamental to them.

Major surprises may be discovered lurking in alternative realizations of historical experience. To quote Philip Roth (2004), an eminent American author of counterfactual fiction: "History, harmless history, where everything unexpected in its own time is chronicled on the page as inevitable. The terror of the unforeseen is what the science of history hides." All manner of unforeseen, surprising catastrophes were close to occurring, but ultimately did not materialize, and hence are completely absent from the historical record, and therefore remain hidden from actuarial view.

Disaster events are typically chronicled and analyzed as if they were inevitable. Such determinism is far from reality. A salient example of how a minor, random perturbation to the system state can have a massive impact on insurance loss is provided by the Al Qaeda attack on the In-Amenas gas plant in Algeria in January 2013. In the annals of insurance claims, this event is recorded as a hostage crisis, not a major international petrochemical plant disaster. This is because a stray terrorist bullet accidentally caused a power blackout that automatically shut down the plant (Statoil 2013). This stroke of good fortune prevented the terrorists from achieving their goal of setting off a massive gas explosion.

Another notable illustration is 9/11, which is the classic paradigm of an unforeseeable Black Swan event. However, a hijacked passenger jet might have been flown into an iconic structure before 9/11. The Algerian terrorist organization GIA planned to destroy the Eiffel Tower in Paris in this way in December 1994. Fortunately, French intelligence discovered from an informant that this was the hijackers’ intent. Accordingly, French commandos stormed the plane. Without the intelligence on the hijackers’ true intent, the French authorities might have been coerced by continued hostage shooting to allow the plane to fly on to Paris. From a risk perspective, the chance of informant failure would have been at least 10%, so there was a significant counterfactual probability that the Eiffel Tower would have been attacked.

Crucially, because there was no impact on the Eiffel Tower, international aviation policy on dealing with hijack situations was not revised, as it most surely would have been had the terrorist plot been successful. Given the non-trivial probability of plot success, the IATA protocol for dealing with hijackings might have been altered six years before 9/11 to prevent unauthorized cockpit control. This never happened; neither was there any impact on U.S. terrorism insurance.

Another aviation example where safety policy might have changed earlier involves criminal pilot action. A Germanwings Airbus 320 was intentionally crashed into a French mountainside on March 24, 2015. There was a precedent for this malevolent pilot action. On November 29, 2013, a Mozambique Airlines plane flying from the Mozambican capital Maputo to Luanda in Angola crashed: the pilot had locked out the copilot. Relevant for risk analysis, there may have been some previous situations where a pilot was minded to take similar action, but was thwarted by lack of opportunity. Following the Airbus 320 crash, codes of practice have been revised to ensure at least two flight crew are in the cockpit. However, a counterfactual analysis would have earlier highlighted an exceptional aviation risk that might have been addressed before, to the benefit of flyers and aviation insurers.

2. System state representation

Catastrophe insurance risk modeling focuses on the probability of an event occurring, and the conditional loss probability given an event occurrence. More fundamentally, the hazard state of the whole system can be described as a complex, time-dependent function of a number n of underlying hazard variables, some of which may be hidden and not directly observable: S = f[X(1), X(2), . . . X(n)].

At various times t, a particular domain D(t) of the space of underlying hazard variables becomes immediately dangerous to an insurance risk portfolio in that the hazard state changes from passive to active, and some external agent of physical force strikes the portfolio. Such an agent might be earthquake ground shaking, volcanic flow, landslide debris, wind pressure of a tropical cyclone or tornado, water breach of a flood or tsunami defence, toxic release from an industrial installation, terrorist bomb blast, etc.

As observed by an insurer, a hazard event occurs at time t causing loss L(t) to the insured portfolio. From an actuarial perspective, the historical time series of occasional losses L(t) can be analyzed by an array of statistical techniques. However, given the rarity of extreme catastrophe insurance losses, and the sparseness of the loss time series, any statistical analysis just relying on loss experience is fraught with huge uncertainty, the size of which is appreciated by actuaries (Nicholson and Smith 2013).

Fortunately, loss statistics are far from being the only source of useful information and knowledge about a hazard. Indeed, it is the catastrophe modeler’s task to understand, measure and chart the extent of the dangerous domain of hazard variables D(t). In particular, there are combinations of the input variables {X(1), X(2), . . . X(n)} which lie just outside this dangerous domain, but which may be dynamically perturbed to fall within the dangerous domain (Figure 2). Furthermore, there are zones within the interior of the dangerous domain itself that can be perturbed into very much more dangerous regions of high loss amplification.

Figure 2.Perturbation of a system state into the dangerous domain D(t)

The future stochastic event datasets constructed within catastrophe risk models explore and chart the dangerous domain of hazard variables D(t). These stochastic datasets are constructed to span the realm of possibility as thoroughly as is currently feasible, but their completeness is an open hypothesis, subject to potential refutation by surprising events. Interesting new insights into D(t) can be gained from revisiting and rewriting virtual history (Ferguson 2000). In particular, salutary lessons may be learned from the counterfactual insurance losses that were narrowly averted because of the haphazard absence of the necessary dynamic perturbations. Stochastic datasets might be further augmented by scenarios inspired and constructed from detailed stochastic modeling of past historical events. Spatial resolution might be enhanced significantly in this way, especially in event regions of high population density and complex geography. However, the past cannot be changed, and it is not customary for catastrophe modelers to undertake detailed stochastic modeling of past historical events, which are generally treated as fixed given data.

For some specific selected historical events, retrospective probabilistic assessments have been undertaken. A prime example is a reassessment of the volcanic crisis on the French Caribbean island of Guadeloupe in 1976 (Hincks et al. 2014). A Bayesian belief network was constructed to estimate the counterfactual probability of the major eruption that never ultimately materialized. A mass evacuation has long been criticized for being unnecessary, but this retrospective analysis indicates that the hazard level warranted this safety precaution, notwithstanding the severe island economic disruption.

For any hazard, valuable lessons may be learned from the counterfactual losses that were narrowly averted or diminished because of the haphazard absence of the necessary dynamic system perturbations. Explorative study is required of the types of perturbation that might have triggered a disaster, and how likely they were. Insights into the geometrical configuration of the dangerous domain emerge from considering the circumstances under which organizational system defense counters the reducing safety margin of a physical hazard variable. Marginal parameter variations that significantly amplify catastrophe loss are important to tabulate. There are numerous explicit and implicit sources of nonlinear loss amplification, corresponding to tipping points in hazard, vulnerability, and loss aggregation.

2.1. Wildfire spread

A wide range of natural and man-made catastrophes are available to illustrate how counterfactual disaster risk analysis can promote disaster risk reduction. To start, consider wildfire risk to an urban environment. Three generic classes of fire risk variables are the number of fresh ignitions X(1); wind strength and direction X(2); and fire-fighting capacity X(3). Because of fire-fighting crew fatigue and resource limitations, the disaster domain can be breached if there is a sufficient supply of ignitions (either accidentally or maliciously generated), and a runaway disaster may develop if strong hot dry winds persist in an unfavorable direction.

As a notable historical example, consider the 1991 East Bay Hills, California, wildfire storm. The fire started on October 19, and by nightfall was being brought under control. However, a new ignition the following morning rapidly spread the wind-driven fire, overwhelming the fire-fighting crews. More than 3,800 homes were destroyed and 25 people were killed. The FEMA (1991) report on the wildfire noted candidly that the fire was beyond the capability of fire suppression forces to control. As long as the Diablo wind was present, the fire was going to spread, no matter what strategy and resources were used. The fire was contained only when the wind changed.

A counterfactual analysis of this major U.S. wildfire loss is illuminating. Fire losses will depend mainly on the fuel that is downwind from the fire and the length of time that the wind continues to push the fire in that direction. The hot, dry wind persistence risk can be estimated from decades of Californian meteorological observation. There was a counterfactual probability of a few percent that the wind might have persisted for another half-day. This system perturbation might have triggered a complete failure of wildfire control, and driven the fire insurance loss way beyond the $2.7 billion that stands as a record to the present day.

Recognizing the likelihood of an uncontrolled wildfire, significant measures to mitigate the regional wildfire hazard would have been warranted by the reduction in future property loss. Almost a quarter of a century later, in the summer of 2015, civic approval was finally given to cut down highly flammable oil-laden eucalyptus trees in the Oakland Hills. This decision might have been hastened by earlier counterfactual disaster risk analysis.

3. Counterfactual perspective on disaster heuristics

The degree of surprise and astonishment that extreme events generate depends in part on the underlying human perception of extreme events. This perception is naturally anchored to observations made about hazards. Below are listed seven observations on the historical record that influence and guide common, but potentially misleading, heuristics about extreme events. These events are identified here as A, B and C. A counterfactual perspective can serve as a useful corrective to intuitive heuristics that might lead actuaries astray (Kahneman 2011).

1. Lack of Precedent: Event A has never happened before.

2. Pattern Regularity: There has been a regular pattern to event A occurrence.

3. Sound Operational Record: Past operational experience has so far been sound.

4. Weather Crises Averted: Past weather crises have been satisfactorily averted.

5. Contingent Necessity: Event B has always preceded event A.

6. Decoupled Events: Events A and B have never occurred together.

7. Cascading Losses: Cascade loss sequence C has never been observed.

A counterfactual perspective on these heuristics, and their pitfalls for actuaries, will be considered in turn. For any peril and territory, such a perspective can be explored, identifying dynamic system perturbations for which these heuristics are violated. Here, the principles of counterfactual thinking are explained by way of some particularly salient examples, associated with catastrophe insurance losses.

3.1. Lack of precedent

If there is no historical precedent for an extreme event, preparation for such an event may not seem justified. This may lead to risk oversight. With the current state of historical and scientific knowledge, there are very few hazard events that should take risk analysts by surprise. Almost all either did happen before in some guise, or, taking a counterfactual view, might well have happened before.

Take, for example, the magnitude 9 Japanese earthquake and tsunami of March 11, 2011. The influential Japanese seismologist, Hiroo Kanamori, had estimated the maximum regional earthquake magnitude to be much lower, around 8.2. However, a counterfactual review of regional earthquake history would have questioned this assertion. The Jogan earthquake of 869 generated a tsunami impacting an extremely broad area, including not just two but all three main prefectures of northeast Japan. Even if the 869 event magnitude had been somewhat below 9, there is a counterfactual argument that future fault slip might exceed whatever it was in 869. Indeed, it has been common practice in seismic hazard assessment to add half a unit of magnitude to the largest historical event to define maximum magnitude.

3.2. Pattern regularity

Historical evidence may indicate a regular pattern to the occurrence of event A, which informs preparedness and response decisions. For example, there may appear to be a periodic or quasi-periodic frequency to the occurrence of event A. Expectation of such regularity can be a source of dangerous unexpected surprise. Unseasonal extreme weather is a prime cause of surprising natural disasters, such as flash floods, violent convective storms, late season tropical cyclones, etc. From a counterfactual perspective, a dynamic meteorological perturbation could delay a late season storm into a hazardous out-of-season shock.

With regard to earthquake hazard, wariness is needed over the concept of seismic cycles, and the appealing but simplistic notion that there is some notable regularity in the recurrence time intervals between major earthquakes. This may result in the misleading perception that after a major earthquake, seismic risk mitigation may become less urgent and that insurance risk is necessarily reduced.

To illustrate the degree of randomness in earthquake recurrence, consider the sequence of six earthquakes at Parkfield, Central California from 1857 to 1966. Based on the approximately regular time intervals between these characteristic events, which averaged 22 years, a prediction was made for the next event after 1966 to fall in 1988. Surprisingly to seismologists, it was 16 years later in 2004 that the next characteristic event occurred. Counterfactually, this can be interpreted in terms of the randomness of each past event recurrence. The 1966 event was not inevitable in that year—it might have happened a number of years earlier or later. Seismologists making the prediction were fooled by randomness (Taleb 2001). If this randomness had been accounted for in the previous event dates, there would have been much less confidence in the predictability of the date of the next event.

3.3. Sound operational management

Critical industries have a predominantly sound operational record. But there is a substantial database of near misses and close calls (Hopkins 2010), from which safety lessons should be learned, if statistics other than actual incidents and casualties are taken into account. In the interest of promoting safety within industry and reducing the prevalence of accidents, near-miss management systems have been advocated by Kleindorfer et al. (2012), following on from studies at the Wharton Business School, including operational risk (Muermann and Oktem 2002). Regrettably, the warnings afforded by near misses are often disregarded. Part of the risk management value of counterfactual disaster analysis is the capacity to identify potential prospects for mitigating future disasters, even where the historical evidence is very sparse or completely nonexistent.

Near-miss examples in transportation provide some of the most graphic scenarios. For example, in attempting to land at Heathrow, London, in thick fog on November 21, 1989, a Boeing 747 cleared the roof of an airport hotel by just twelve feet (Macrae 2010). This was, of course, not intentional. But consider the maritime insurance example of the Costa Concordia cruise ship which sailed up the northwest coast of Italy, past the island of Giglio. One of the key hazard variables determining the ship’s hazard state was its distance from the navigational safety contour around the island. This might be designated as X(1). The official scheduled route of the cruise ship gave the island an abundantly wide berth, with X(1) > 10 kilometers. Given the terrestrial accuracy of GPS expressed within meters, the dangerous domain should never have been close to being breached, even allowing for gross human navigational error.

However, a tradition had developed for the Costa Concordia to be steered intentionally very close to the safety contour to maximize the spectacle for islanders and cruise passengers alike, so that X(1) ∼ 0. This then left virtually no margin for the navigational failings that would take the Costa Concordia within the dangerous sinking domain, as happened on the fateful evening on January 13, 2012. With the heavy costs of the lengthy engineering salvage operation, this became the worst maritime insurance loss, exceeding $2 billion. A counterfactual analysis of past cruises would have warned of the risk of such a catastrophe.

3.4. Weather crises averted

Weather is a universal peril. When an extreme weather crisis passes, the very act of survival may lead to complacency rather than urgency to mitigate the weather risk. Even if historical experience has been benign in managing severe weather, important lessons may yet need to be learned. On January 27, 2015, a Nor’easter winter storm, Juno, knocked out both of the high voltage transmission lines connecting the Pilgrim nuclear power plant in Plymouth, Mass. The reactor automatically shut down when the second offsite power line was lost. When equipment problems and operator errors complicated the intended response, the Nuclear Regulatory Commission investigated, and found a failure to open the valve supplying cooling water. Counterfactually, a serious nuclear incident might have occurred, with a likelihood that could be gauged from the site probabilistic safety assessment fault tree.

Amongst meteorological loss amplifiers, a sensitive system state variable is the state of the tide. Consider coastal flooding. The state of the tide is a key variable for coastal flooding from a storm surge or tsunami. Overtopping of a coastal sea defence defines a key boundary of the dangerous domain. The historical record provides numerous examples of calamitous coastal flooding being averted, or the loss severity being considerably mitigated, by a combination of stout sea defences—and luck that the highest storm surge level did not coincide with high tide.

In October 2012, Superstorm Sandy struck Boston at low tide, but up to 6% of Boston could have been flooded if Sandy had arrived at high tide (Douglas, Kirshen, and Wormser 2013). Four months later, a four-foot storm surge hit Boston, fortunately again at low tide, not high tide. With the high tide already a foot higher than average because of the new moon, coincidence of the storm surge with this high tide would have given rise to the 100-year flood, as designated on flood maps. A counterfactual analysis would have provided a sense check on the extreme flood return period.

A year earlier, in August 2011, Hurricane Irene made landfall as a tropical storm in the New York City area, which narrowly avoided the flooding that accompanied Superstorm Sandy. The sparse historical catalogue of hurricane losses in New York belies the serious danger posed by threatening events in the 2011 and 2012 hurricane seasons. At one point along Hurricane Irene’s track towards New York, there was a counterfactual 1% probability of a catastrophe insurance loss in excess of $50 billion.

3.5. Contingent necessity

It may emerge from historical experience that if event A does happen, then event B would happen beforehand, and this sequence might be relied upon to provide sufficient warning. In a volcanological risk context, this precept of contingent necessity may be expressed in the belief that, in the event of a major eruption of a designated volcano, there would be ample precursory observations that would warn of an impending major eruption early enough for those at risk to be safely evacuated.

A probabilistic framework is best for clarifying the predictive role of precursory activity. Consider a simple case where the output response Y (e.g., eruption) is a binary function of another binary precursory event indicator Z (e.g., presence of volcanic tremors), and a complex set of other variables U that may influence Y. We write y = f(z, u). For any given condition U, the relationship between Z and Y must be one of only four binary functions (Pearl 2000):

$$f_{0}:\{Y(0)=0 \& Y(1)=0\} ; f_{2}:\{Y(0)=1 \& Y(1)=0\}$$

$$f_{1}:\{Y(0)=0 \& Y(1)=1\} ; f_{3}:\{Y(0)=1 \& Y(1)=1\}$$

As u varies, the only effect is to switch the (Z, Y) relationship among these four functions. The probability P(u) thus induces a probability function over the possible response pairs {Y(0), Y(1)}. U could be an external forcing factor causing a sudden dynamic perturbation to a volcanic system. Triggers include regional earthquake occurrence, hydrological and meteorological disturbance, and landslides.

Consider Mount St. Helens in Washington State in May 1980. Earthquakes under the volcano had intensified over a few weeks. On the morning of May 18, a larger earthquake with a magnitude of 5.0 triggered a landslide. This landslide sent layers of rock tumbling down the mountain, so the magma underneath was suddenly relieved of the pressure above it. An enormous lateral blast ensued and Mount St. Helens erupted violently. Looking back over past volcanic crises, the impact of external dynamic triggers can be explored, and the risk of their occurrence assessed.

In volcano catalogues of eruptions, it has not been routine to include periods of unrest, such as seismic activity. This incompleteness of information reflects the traditional view that such data are of scientific interest, but inessential for hazard estimation, which is primarily dependent on the time series of the actual eruption events themselves. However, for volcanoes with a low frequency of eruption, occasional periods of unrest may be important indicators of failed eruptions which should be taken into account in volcano hazard assessment.

Soufrière Hills on the Caribbean island of Montserrat is a prime example. Until 1995, this volcano had not erupted since 1630, yet had given rise to three periods of significant unrest over the previous century. These might be interpreted as failed attempts at eruption. In the authoritative Smithsonian Institution catalogue of volcanoes of the world (Simkin and Siebert 1994), which was published shortly before the eruption in 1995, the 1630 eruption is included as the sole entry for Montserrat—but none of the unrest history is listed. Yet there were three distinct episodes of unrest in the 1890s, 1930s and 1960s.

Key system state variables X(t) for volcano hazard include those governing the subterranean dynamics, e.g., the influx of magma feeding the volcano. Periods of unrest may correspond to intermittent intrusions of magma which are insufficient to lead to eruptive activity. For any historical period of unrest, a Bayesian belief network of the underlying geophysical, geochemical and geodetic causal factors could generate an estimate of the counterfactual likelihood Pr(E|U) that the unrest U might lead to an eruption E. With this likelihood evaluated, the annual probability of an eruption can be calculated in terms of the frequency of unrest periods f(U) as: Pr(E) = f(U) * Pr(E|U).

For Montserrat, a baseline annual eruption frequency would have been about 1%, which is higher than using the elapsed time to the last eruption in 1630, and so would have yielded a more pessimistic, and ultimately much more realistic, assessment of volcanic hazard at the island capital, Plymouth, which was destroyed in 1997. The risk blindness of insurers is reflected in the absence of policy wording for volcanic eruption.

3.6. Decoupled events

The resilience of society can be severely strained by any major disaster. Stress analysts would inquire what if the societal system state is perturbed by another major event that can compound human and economic losses. A geological hazard example is the dynamic triggering of a volcanic eruption by a large earthquake. This is a dual scenario for Tokyo, given the active volcanic status of Mt. Fuji. Insight into what other event combinations should be of concern as societal stress tests may be gained from a counterfactual disaster analysis. Where events A and B have never occurred together historically, it is often presumed that there is no need to consider what would happen if they did. This may be poor risk management procedure.

A tipping point in health risk can arise from the occasional confluence of two independent risk factors. As a natural hazard affecting the health of the U.K. population, a sustained volcanic eruption in Iceland, generating vast quantities of toxic gases, can have serious consequences for those with respiratory problems. The Laki eruption in Iceland of 1783 persisted for eight months. The resulting acid fog dispersed over Europe caused more than 10,000 excess deaths in England. But it could have been much worse. In the previous year, 1782, a pandemic originating in China spread westwards into England and Scotland. Had the pandemic occurred a year later (or Laki erupted a year earlier), the double perils of influenza and acid fog would have elevated the death toll to catastrophic levels.

This counterfactual perfect storm scenario almost happened with the arrival of the swine flu pandemic from Mexico in 2009. Had it occurred a year later (for which there was a few percent chance), it would have coincided with the eruption of the Iceland volcano Eyjafjallajōkull in 2010, the ash cloud from which closed down U.K. airspace for days. Based on previous history, there is a causal linkage between eruptions of Eyjafjallajōkull and of its more fearsome neighbor Katla. In 2010, there was a counterfactual probability well in excess of 10% that a major eruption of Katla might have been triggered and magnified the regional societal dislocation and insurance loss.

3.7. Cascading consequences

Even though the multidimensional space of risk variables has a complex geometry, important insight can be gained from the marginal variation of an individual or several variables. Thus the binary switch of on-site power could leverage loss at a petrochemical plant by orders of magnitude. Power outage is well appreciated to be a key variable for estimating the scale of business interruption, especially where industries lack supply chain resilience against external hazards. The Rome blackout on September 17, 2003, was a classic cascading process, which started with a windstorm causing a tree to fall on a power line several hundred miles away on the Swiss border. All types of natural hazards can trigger cascading disaster. After the Chi-Chi earthquake in Taiwan of September 21, 1999, power loss was a major factor impeding the 24-hour production schedule of computer microchips.

The October 2011 Thailand floods generated insurance losses approaching $15 billion, which came as a financial shock and costly surprise to the developing Asian insurance markets. In estimating probable maximum loss, an exploratory search should be conducted for risk variables that have the capacity to leverage large losses. For Bangkok flood risk, a key risk variable was the volume capacity of dam reservoir storage. A government decision to keep the water levels high before and during the summer rainy season resulted in the dams being full in late September 2011, and large amounts of water had to be released. The discharge of water from dam reservoirs defines a literal tipping point for the amplification of catastrophe loss in Thailand. The extra water resulted in the failure of dikes that were intended to prevent flooding of important facilities owned by Japanese manufacturing companies.

This 2011 disaster might have been foreseen from a counterfactual perspective. Very similar rainfall conditions were observed historically in 1995 as in 2011, but many of the regional facilities that were flooded in 2011 did not flood in 1995, even though the rainfall conditions were comparable. This was because, during the 1995 flood, much of the runoff was stored in two dams. As an exacerbating factor in mid-October 2011, the tides were very high. Perturbing the 1995 system state with marginal adjustments to the tide level and the release of dam reservoir water would have moved the system deep into the disaster zone. This counterfactual insight might have challenged the policy to keep water levels high in the dam reservoirs in September 2011, and so mitigate the consequent flood insurance losses.

4. Terrorism

Following the Al Qaeda attack on 9/11, counterterrorism security and intelligence resources have been ramped up steeply across the countries of the western alliance: the United States, Canada, Western Europe, Australia, and New Zealand. The balance between the privacy and public safety shifted to make such coordinated attacks very much harder to organize, plan, resource, and perpetrate.

Terrorism is subject to control by Western civil authorities in a way that natural hazards are not. As a consequence of having highly capable and empowered counterterrorism forces, despite there being numerous plots, there have been only a handful of successful notable terrorist attacks against the Western alliance since 9/11. Even in these cases, at least one of the terrorists was previously known to the national security services. In the Western alliance since 9/11, terrorism insurance is effectively insurance against the occasional failure of counterterrorism.

The various links between members of a social network provide key insight into the involvement of an individual in a terrorist plot. The singular achievement of the Western security services in interdicting the great majority of the significant plots since 9/11 is evidence of their command of terrorist communications networks. A key part of the interdiction process is the dragnet of contact chaining: the contacts of terrorist suspects are tracked; then the contacts of these contacts are tracked, etc. (Harding 2014). Through this enveloping international surveillance process, many terrorists have been brought to justice, including Osama bin Laden himself.

The process of contact chaining is a major social network constraint on large conspiracies. The more operatives are engaged in a plot, the greater is the chance that one of them will be caught within a contact chain under counterterrorism surveillance. Terrorist social network and contact chaining analysis (Woo 2015) has shown that the probability of a plot being interdicted in the Western alliance [Int-Prob] by contact chaining increases with the number of active cell operatives, as indicated in Table 1:

Highly elaborate ambitious plots capable of inflicting catastrophic insurance loss would typically involve so many operatives as to have a very high likelihood of interdiction. This would be wasteful of terrorist resources. Discouragement of jihadi plots involving double-digit operative numbers has come from Osama bin Laden himself in a message from his Abottabad hideout: “For a large operation against the US, pick a number of brothers not to exceed ten.” The more operatives there are, the greater is the chance that one of them will compromise the terrorist venture, either by his own actions or communications, or through some branch of his network of social contacts.

For any significant terrorist plot to succeed, it must avoid interdiction as well as technical malfunction. Taking both factors into account, the counterfactual probability of success for any past plot can be estimated. One of the most notorious plots since 9/11 was the liquid explosives plot of 2006, which the Al Qaeda chief strategist boasted would be bigger than 9/11. The ambitious plot to bring down as many as seven transatlantic aircraft was interdicted. Given the number of operatives involved, the counterfactual probability of success was about 8%; high enough to warrant the airport security restrictions on liquids imposed ever since 2006.

4.1. Cyber terrorism

The 2006 liquid explosives plot required terrorists to bring liquids on board aircraft. Another class of plot where terrorists could attack remotely involves operations in cyberspace. By hacking control or monitoring systems, terrorists could trigger industrial disasters. The fact that hackers may be foreign and well beyond the jurisdiction of where a disaster takes place makes cyber terrorism a topical cause for concern to Western security officials and insurers.

Where disasters have actually occurred, a counterfactual perspective can yield important insights into alternative future pathways to disaster that might be surprising and alarming, and for which further risk mitigation is required. One such counterfactual analysis is to substitute alternative disaster agents in historical events. Historical disasters need not necessarily have had their specific set of predetermined causes, but might have occurred counterfactually through other agents or factors. Exploring these alternatives can guide catastrophe risk management and reduce future surprise and loss.

There are numerous possibilities to reflect upon. First, any accidental human error might potentially have been deliberate. Any historical control system failure due to human error might in future be intentional. If a control system is internet-enabled, failure might be induced through cyber crime. Take as an example the natural-gas pipeline explosion in San Bruno, California, in 2010. The explosion occurred after maintenance on what should have been an uninterrupted power supply. The maintenance caused electricity to the Supervisory Control and Data Acquisition (SCADA) system to be lost. A control valve on the pipeline was programmed to open automatically if the SCADA system lost power. As a consequence, gas flowed into the pipeline in an uncontrolled way, causing a pressure surge that burst the pipe. Counterfactually, the agent for disrupting the power supply might well have been a cyber criminal attacking the SCADA control system, rather than the unforeseen consequence of maintenance. Crucially, the risk management response to the disaster should have included a tightening of cyber security.

Another counterfactual prospect is of industrial sensor failure being substituted by a cyber attack. The Buncefield U.K. explosion of December 2005 originated with the failure of the gauge monitoring the fuel level in a storage tank. Overflow of the tank led to formation of a vapor cloud, which eventually exploded. Counterfactually, the gauge might have functioned normally until it ceased to operate due to a cyber attack. Another U.S. example is the collapse of a dike in Missouri, also in December 2005. Sensors failed to detect when the dam’s 1.5 billion gallon water reservoir was full. A fail-safe shutdown mechanism also failed, so an overflow developed and a 60-foot section of parapet wall gave way.

The operability of sensors is crucial to many industrial and infrastructure facilities. Whatever the likelihood is estimated to be of accidental sensor failure, it is augmented by the likelihood of malevolent action by cyber vandals and cyber terrorists. A future sensor failure disaster caused by cyber attack may well have some similar historical precedent, where the failure was induced accidentally through malfunction or error. The broadening of historical experience to include scenarios with substitute disaster agents yields a fuller risk perspective. In particular, consideration of additional malevolent modes of loss may elevate the probability of failure beyond what is actuarially perceived.

5. Conclusions

The past is what it was; but it is nevertheless instructive to ask questions about the past. One of the most insightful questions that was asked of 9/11, and might be asked of any disaster is this: Why didn’t this happen before? Historical investigation may reveal that it did, or might have happened before with an estimated likelihood, but there was limited risk awareness and insufficient action taken to mitigate the potential loss. Actual loss experience has always been the foundation for actuarial risk analysis. Where losses are frequent, the actual database of losses is large enough to encompass most of the domain of realistic possibility. Risk insights can then be gained through extensive statistical data mining. However, especially for rare risks, actual catastrophe loss experience, especially when it has been light or even nonexistent, may be very misleading, and engender risk perception bias.

There is an intrinsic optimism bias which leads people, not least insurers, to underestimate risks if large losses have yet to materialize. As a consequence of optimism bias, when a catastrophe loss does occur, it often catches people by surprise. The degree of surprise would be lessened if emerging risks were tracked early and managed well in advance of any catastrophe event. Counterfactual analysis of emerging risks would be helpful in this tracking and risk management process. To enlarge the historical event dataset of emerging risks, a retrospective stochastic analysis of historical events can be undertaken to explore the range of possible catastrophe losses that might have arisen before, could still happen, and should be mitigated in the future.

The greatest U.S. catastrophe insurance loss was caused by Hurricane Katrina in August 2005. During Hurricane Katrina, more than half of the 3,500 miles of levees that protect Greater New Orleans were damaged, breached, or destroyed. The infrastructure failures observed in the Greater New Orleans area were partly man-made and might have been prevented. A combination of engineering errors and political indecision weakened the hurricane protection system.

Analytical methods have been devised to address issues of hurricane uncertainty. For estimating uncertainty in extreme value analysis of hurricanes and other weather hazards, the use of statistical resampling methods, such as the bootstrap, was advocated by Coles and Simiu (2003). But no amount of resampling of the hurricane wind speed database before 2005 could have forewarned of the catastrophe loss of Hurricane Katrina in August 2005. However, a counterfactual analysis of Hurricanes Georges in 1998 and Ivan in 2004 would have been more effective for anticipating the record-breaking losses to come.

In the hurricane season just before Katrina, Hurricane Ivan, a category 4 hurricane with 140 mph winds, was slowly moving directly toward New Orleans. Fortunately for New Orleans, the storm veered away to the north and made landfall east of Mobile Bay, Alabama. But forecasters at one stage were predicting a 25% probability that Ivan would remain on track to strike New Orleans as an extreme storm, and dire forecasts of the flooding loss implications were issued (Laska 2004). Such counterfactual probabilities are useful to insurers for benchmarking their return period loss estimates, and gauging a better sense of the robustness of their models, in particular for detecting indications of the underestimation of some extreme risks.

Counterfactual analysis of historical events is an important supplementary tool for uncertainty assessment and disaster preparedness, as well as for catastrophe insurance risk management such as the estimation of probable maximum loss. The past cannot be changed, but counterfactual disaster analysis can change the future.

Acknowledgment

Part of this work was undertaken at the Institute of Catastrophe Risk Management, Nanyang Technological University, Singapore.