A Comparison of Resampling Methods for Bootstrapping Triangle GLMs

undefined

1. Introduction

Several authors have described the use of bootstrapping in the context of GLM-based stochastic reserving models for property and casualty loss development triangles; e.g., England and Verrall (2002), Pinheiro, Silva and Centeno (2003), and Hartl (2013). A more general textbook treatment of the bootstrapping procedure for GLMs can be found in Davison and Hinkley (1997, Section 7.2). While alternative approaches are mentioned, practical examples that are based on linear rescaling of Pearson residuals are often presented. This approach has the appeal of straightforward mathematics: all you need is one addition and one multiplication. As a result, it can be implemented with relative ease in a spreadsheet.

For real data, however, the linear rescaling of Pearson residuals often leads to negative values in the resampling distribution for smaller data values, thus violating the model assumptions of the GLM we started with. In other words, the bootstrapping procedure fails. Both the details of this breakdown and the alternative method of deviance residual resampling are discussed in Hartl (2010). Other authors, e.g., Gluck and Venter (2009), employ parametric resampling and thus sidestep the problem. While parametric resampling circumvents the issue of negative values in the resampling distribution, there is an increased computational cost because generating pseudo-random variates from typical exponential family distributions requires the evaluation of logs, exponentials or even more computationally intensive functions. As mentioned above, linear rescaling of Pearson residuals, by contrast, only requires one addition and one multiplication.

In this paper we propose two alternative methods for generating pseudo data: split-linear rescaling and sampling from a limited and shifted Pareto distribution. During the time-critical Monte Carlo iteration phase of the bootstrapping procedure, both of the proposed alternative methods are about the same or better in terms of computational cost than linear re-scaling of Pearson residuals. In Section 2 we describe basic mathematical properties of split-linear rescaling, and sampling from a limited and shifted Pareto distribution. Proofs of some key formulas from this section are given in Appendix A. Section 3 is more technical in nature and can be skipped on a first reading, but it does contain information of interest to readers who want to implement the proposed methods themselves. The algorithms and memory requirements needed for linear rescaling, split-linear rescaling, and sampling from a limited and shifted Pareto distribution are discussed. We present performance comparisons based on a VBA for Excel implementation, and thus demonstrate that the new methods are computationally as efficient as linear rescaling. The VBA application is available from the author on request. Conclusions are discussed in Section 4.

2. Two schemes for generating pseudo data

Before delving into the mathematical properties of the proposed methods, we briefly review resampling for bootstrapping purposes and introduce the notation used in this paper.

2.1. Resampling basics

Bootstrapping is a Monte Carlo simulation technique that is employed to approximate the sampling distribution of a quantity that is estimated from a data sample. To do so, one repeatedly generates pseudo data and re-estimates the quantity in question.

The key idea of non-parametric bootstrapping is to sample the standardized observed residuals relative to the stochastic model that is assumed to generate the original data. The sampled standardized observed residuals are then used to generate the pseudo data. As pointed out in Davison and Hinkley (1997), due to the non-unique definition of residuals for GLMs, there are multiple non-parametric residual resampling methods. We also observe that the various residual standardization schemes typically fail to strictly standardize the residuals.^[1] To proceed with the bootstrap we therefore we must consider the iid assumption for the standardized residuals as being “approximately” true.

How these ideas are applied to GLM-based stochastic reserving is described in England and Verrall (2002) and Pinheiro, Silva, and Centeno (2003). An alternative to non-parametric bootstrapping is parametric resampling, where the pseudo data are generated by sampling from an assumed parametric distribution. One version of this approach is used in Gluck and Venter (2009). In either case, pseudo data are repeatedly generated and the model is refitted to the pseudo data. In this way, one generates a Monte Carlo sample of the distribution of fitted parameters or other derived quantities, such as the projected reserve.

2.2. Notation

In the context of our discussion we will have to refer both to individual values and to collections of similar values. To do so we follow the convention that boldface symbols refer to vector quantities while non-boldface symbols refer to scalar quantities. For example, the symbol y refers to a generic element of y. Where we do need to distinguish between different elements of y, we will employ subscripts such as y_i and y_j.

More specifically, y refers to the vector of original data. The hat symbol, as in ŷ or ŷ, indicates that we are talking about fitted values. The asterisk symbol, finally, is used to refer to a full set of pseudo data, y*, or an individual pseudo datum, y*.

For residual-based bootstrapping, we need a set of standardized residuals, which we denote by s. To avoid bias as a result of the resampling process, we require the mean of s to be exactly zero. This is in addition to the usual requirement that the variance of s equals one. It is useful to think of a standardized residual as a function of an original data value and the fitted value predicted by the GLM

$$s=H_{\hat{y}}(y) \text {. } \tag{2.1}$$

The function H_ŷ(·) depends on the definition of residual and the standardization procedure employed. This is discussed in detail in McCullagh and Nelder (1989), Davison and Hinkley (1997), or Pinheiro, Silva, and Centeno (2003). For residual-based bootstrapping, obtaining a pseudo datum (a.k.a. resampled data value) is a two-step process: we randomly sample from the standardized residuals, and then solve the following equation for y*

$$\operatorname{Rnd}(s)=H_{\hat{y}}\left(y^{*}\right)$$

Note that the function Rnd(s) denotes the operation of randomly sampling from the set of standardized residuals. We summarize the resampling procedure for an individual data point as

$$y^{*}=H_{\hat{y}}^{-1}(\operatorname{Rnd}(s)) \tag{2.2}$$

For a concrete example, we consider Pearson residual resampling for an over dispersed Poisson model. In this case equation (2.2) becomes

$$y^{*}=\hat{y}+\sqrt{\phi \hat{y}} \cdot \operatorname{Rnd}(s) \tag{2.3}$$

where φ is the dispersion factor. From this equation, one can easily see how a negative standardized residual and sufficiently small values of ŷ will lead to negative resampling values. This breakdown is frequently encountered when using Pearson residuals for bootstrapping triangle GLMs. A more detailed discussion and examples of this can be found in Hartl (2010). As noted in subsection 2.1, non-parametric residual resampling relies on the assumption that standardized residuals are “approximately” iid. When the described breakdown of linear Pearson residual rescaling occurs, we can interpret this as saying that this approximation is not good enough for this data set, prompting one to look for alternatives.

2.3. Split-linear rescaling

Our goal is to avoid the breakdown of the resampling scheme that results from zero or negative pseudo data being generated. To this end we introduce a new parameter, π$_{min}$, that defines the smallest allowable pseudo data values as a percentage of the expected mean. Conceptually this could be different for each data point, but we use a ratio that is uniformly applied to all data points. One might argue that just requiring the pseudo data to be positive is sufficient, and that introducing π$_{min}$ is overly restrictive. At the same time, since we are dealing with finite precision computer- based simulations, we may get into numerical trouble if we get too close to zero. Practitioners who want to explore what happens at the limits are welcome to choose very small values for π$_{min}$.

The intuitive idea behind split-linear rescaling is as follows: if the standard Pearson residual rescaling procedure results in resampling values that are below π$_{min}$ times the expected mean value, we split the standard Pearson residual resampling values into a lower set and an upper set. Next we “squeeze” the lower resampling values together, so that they no longer dip below π$_{min}$ times the expected mean value. The “squeezing” operation does preserve the mean, but it will lower the variance of the resampling distribution. To offset this, we apply a mean preserving “expansion” operation to the upper resampling values.

We proceed by defining what we mean by “squeezing” and “expanding.” Given any set of values, z, with mean μ, we can obtain a new set of values, z′, that has the same mean. This is accomplished by applying the following linear transformation to each element z of z

$$z^{\prime}=\mu+c(z-\mu) \tag{2.4}$$

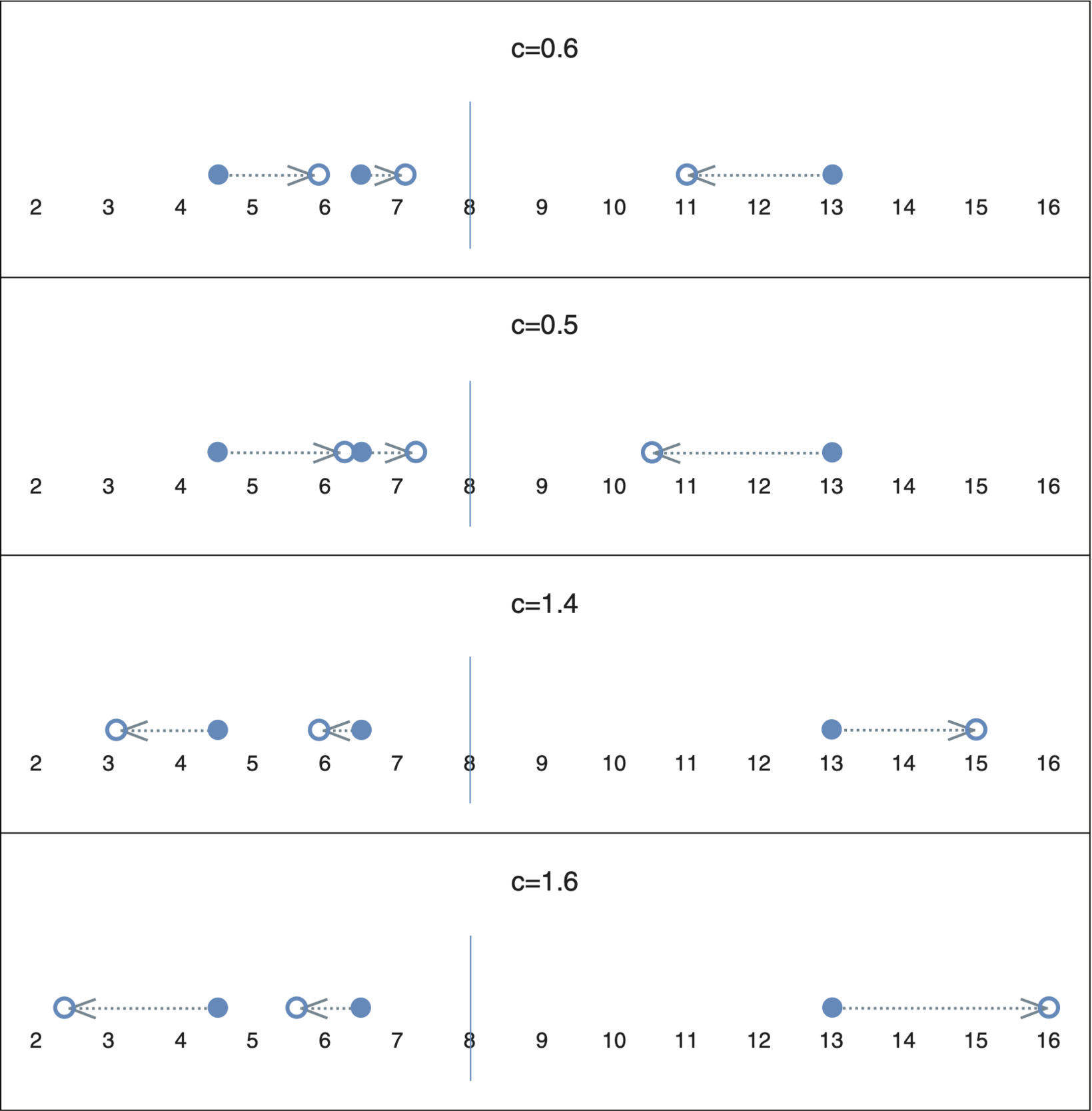
where the scaling factor, c, is a positive constant. If c 1, we end up “squeezing” the values. If c > 1, the values are “expanded.” The proof that transformation (2.4) preserves the mean is left as an easy exercise for the reader. Figure 1 graphically represents the impact of different values of c on a set of data points with values of 4.5, 6.5, and 13 and a mean of 8.

If $\boldsymbol{\sigma}^2_{z}$ denotes the variance of z, it is also easy to show that

$$\boldsymbol{\sigma}_{z^{\prime}}^{2}=c^{2} \boldsymbol{\sigma}_{z}^{2} \tag{2.5}$$

So we can see that if we “squeeze” a set of values, we will reduce the variance. Conversely, if we expand the values, we will increase the variance. For split-linear rescaling, however, we apply transformation (2.4) to two disjoint subsets of the original data set, so we need to consider the impact on the overall variance resulting from the transformation on each subset.

To be specific, let us assume that the original resampling distribution, y*, has m data values and mean μ. Let us furthermore assume that we have partitioned y* into two subsets, y_l* and y_u*, with q and r data values, respectively. The corresponding means are μ$_l$ and μ$_u$. For convenience we will assume that the values in the lower subset are less than the values in the upper subset. Furthermore, we can assume without loss of generality that the original data set and both subsets are indexed in ascending order. In particular, the first element of each subset can be assumed to be the smallest element. The split-linear transformation can be summarized by the following equation,

$$y^{* \prime}=\left\{\begin{array}{l} \mu_{l}+c_{l}\left(y^{*}-\mu_{l}\right), \text { if } y^{*} \in y_{l}^{*} \\ \mu_{u}+c_{u}\left(y^{*}-\mu_{u}\right), \text { if } y^{*} \in \boldsymbol{y}_{u}^{* \prime} \end{array},\right. \tag{2.6}$$

where c_l and c_u, are the scaling factors for the lower and upper subset. Since transformation (2.4) preserves the mean of each subset, the overall mean is also preserved. In A.1 we show that the variance of the transformed resampling distribution can be expressed as

$$\sigma_{y^{*}}^{2}=\frac{1}{m}\left(\begin{array}{c} q\left(\mu_{l}-\mu\right)^{2}+q c_{l}^{2} \sigma_{y_{l}^{*}}^{2} \\ +r\left(\mu_{u}-\mu\right)^{2}+r c_{u}^{2} \sigma_{y_{u}^{*}}^{2} \end{array}\right) \text {. } \tag{2.7}$$

In practice we proceed by finding a suitable partition of y* and a value of c_l such that we satisfy the condition that no value of y*′ drops below _min. To get a variance preserving split-linear transformation we then set the right-hand side of equation (2.7) equal to the variance of y* and solve the resulting equation for c_u. We summarize the general procedure for split-linear rescaling as follows.

• Step 0 Generate y* using Pearson residual rescaling. If y₁* ≥ π_minμ, use y*—there is no need to use split-linear rescaling.

• Step 1 Find a suitable partition of y* such that μ_l > π$_{min}$μ.

• Step 2 Calculate c _l using the following formula

  $$c_{l}=\frac{\mu_{l}-\pi_{\min } \mu}{\mu_{l}-y_{l_{1}}^{*}} .$$

• Step 3 Calculate c _u according to

  $$c_{u}=\sqrt{1+\left(1-c_{l}^{2}\right) \frac{q \sigma_{y_{l}^{*}}^{2}}{r \sigma_{y_{u}^{*}}^{2}}}$$

• Step 4 *Generate y*′ by applying transformation (2.6)

  $$y^{* \prime}=\left\{\begin{array}{l} \mu_{l}+c_{l}\left(y^{*}-\mu_{l}\right), \text { if } y^{*} \in \boldsymbol{y}_{l}^{*} \\ \mu_{u}+c_{u}\left(y^{*}-\mu_{u}\right), \text { if } y^{*} \in \boldsymbol{y}_{u}^{*} \end{array}\right. \text {. } \tag{2.8}$$

Proofs for the formulas given in equation (2.8) can be found in A.2 and A.3. The condition in Step 1 that μ$_l$ > π$_{min}$μ is necessary because the smallest value in the lower set, y₁*, gets “squeezed” towards μ$_l$, so the transformed value y₁*′ can only reach π$_{min}$μ if μ$_l$ > π$_{min}$μ.

We also observe that for Step 1 there can be more than one of partition of y* such that μ$_l$ > π$_{min}$μ. So, which one should we choose? One strategy might be to simply take the first one that comes along, with the smallest number of elements in y_l*. The strategy we are employing is to find the partition that makes c_u² − 1 as close to 1 − c_l² as possible, by minimizing the absolute difference between $q \sigma_{y_l^*}^2$ and $r \sigma_{y_u^*}^2$. This heuristic decision is motivated by a notion that the adjustment should be as evenly spread over the entire distribution as possible, rather than just “bunching” values in the left tail. Tracking $q \sigma_{y_i^*}^2$ and $r \sigma_{y_u^*}^2$ proved to be convenient because they can be updated recursively as we move values from the upper set to the lower set, and the optimal partition can be determined without testing all possible partitions.

Finally, we note that there are two situations in which the split-linear rescaling procedure does not work: breakdowns may occur during Step 3 or during Step 4. For Step 3 the breakdown happens if $\sigma_{y_u^*}^2=0$. This means that all the values in y_u* are the same (including the degenerate case where there are no values in y_u*). In this case we cannot expand the upper subset. Passing the $\sigma_{y_u^*}^2>0$ hurdle, however, still leaves open the possibility that the procedure breaks down in Step 4 because $y_{u_1}^{*^{\prime}}<\pi_{\min } \mu$. This means that the smallest value in y_u* gets mapped to a value below π$_{min}$μ, thus violating the very constraint we wanted to satisfy by using split-linear rescaling. Working with real data we have encountered both of the breakdowns discussed, but we also have found that split-linear resampling succeeds in many cases where linear Pearson resampling fails.

2.4. Sampling from a limited and shifted Pareto distribution

We briefly discuss the justification for the method, before presenting the mathematical properties of the distribution.

2.4.1. Rationale for parametric resampling

The original idea of bootstrapping is that that the residuals can be interpreted as a sample from the error distribution, and that we can therefore use it to approximate the error distribution itself. In the context of development triangle GLMs, where we only have one data point for each combination of covariate levels, this assumption may be a little shaky. To see why bootstrapping seems to work anyway, we note that from a pseudo likelihood perspective (see chapter 9 in McCullagh and Nelder 1989), the fitted values of the GLM only depend on the assumed relationship between the fitted means and the corresponding expected variances. I.e., the specific shape of the error distribution beyond the second moment assumption does not affect the fitted parameter values, and we are dealing with a semi-parametric model for the data. The residual rescaling procedure ensures that for each data point we sample from a distribution with the correct mean-variance relationship. Viewed this way, residual bootstrapping is just one way to run a Monte Carlo simulation to determine the shape of the sampling distribution of the model parameters.

Unless we strongly believe that the observed residuals contain good information about the error structure (beyond a way of estimating the dispersion parameter), it seems equally valid to perform the Monte Carlo simulation using another resampling distribution that satisfies the mean-variance relationship, and is thus consistent with the semi-parametric model assumption for the data that the original model fit is based on. A more detailed discussion of the case for parametric resampling in the context of development triangle GLMs can be found on pages 16 and 17 of Hartl (2010). In this subsection we present one such resampling scheme that is efficient from a computational point of view and works well for small fitted values and large dispersion factors.

2.4.2. Properties of the limited and shifted Pareto distribution

We are only considering distributions with a Pareto index of one. The cumulative distribution function is given by

$$\mathrm{F}(x)=\left\{\begin{array}{ll} 0 & x+c<a \\ 1-\frac{a}{x+c} & a \leq x+c<b \\ 1 & b \leq x+c \end{array}\right. \tag{2.9}$$

where 0 a b, and c . Note that this is a mixed distribution with P(X = b − c)= a/b. The following formulas for the expectation and variance are derived in A.4:

$$\begin{array}{c} \mathrm{E}(X)=a\left(1-\ln \frac{a}{b}\right)-c \\ \operatorname{Var}(X)=2 a b-a^{2}-a^{2}\left(1-\ln \frac{a}{b}\right)^{2} \end{array} \tag{2.10}$$

This distribution has three parameters, which generally allows us to match the required mean and variance, while maintaining the minimum percentage of mean condition. Actually we employ two strategies.

First, we argue heuristically that it is desirable that a/b is small, but not too small. This ensures that the distribution is largely continuous, while there is also a reasonable chance that the maximum value is predictably attained during a 10,000 or 50,000 run simulation. By setting a/b = 0.001 (any other small, but not too small value would do, as well) we end up with

$$\hat{y}=7.908 a-c, \quad V(\hat{y})=1,936.467 a^{2} \tag{2.11}$$

so the parameters a, b, c can readily be calculated in closed form (each fitted data point has its own set of parameters). Often the distribution obtained using this strategy will satisfy the minimum percentage of mean condition (i.e. a − c ≥ π*_minŷ*).

Second, if the first strategy fails to satisfy the minimum percentage of mean condition, we solve the following system of equations:

$$\begin{aligned} a-c & =\pi_{\min } \hat{y} \\ a\left(1-\ln \frac{a}{b}\right)-c & =\hat{y} \\ 2 a b-a^{2}-a^{2}\left(1-\ln \frac{a}{b}\right)^{2} & =V(\hat{y}) . \end{aligned} \tag{2.12}$$

It is not possible to solve this non-linear system of equations in closed form, but it can be reduced to the following equation with one unknown

$$1+\gamma+\frac{1+k}{2} \gamma^{2}-e^{\gamma}=0 \tag{2.13}$$

where k = V(ŷ)(1 − π$_{min}$)⁻²ŷ⁻². A derivation of equation (2.13) is provided in A.5.

In A.6 we show that equation (2.13) has a unique positive solution for all k > 0. For a brief discussion on how to find the solution the reader is referred to A.7. While it is always possible to use parametric resampling from a limited and shifted Pareto distribution, we caution that the distribution may become nearly degenerate for small values of k (P(X = b − c) goes to 1) or nearly unlimited for large values of k (b − c becomes large, and P(X = b − c) goes to 0).

3. Relative performance

When considering the code needed to implement a bootstrapping scheme, one can distinguish three phases: initialization, Monte Carlo phase, and processing of output. During initialization we perform the initial model fit and create the data structures needed to efficiently execute the resampling and refitting during the Monte Carlo phase. Typically we perform a bootstrapping simulation to get a robust measure of the variance or a tail index such as TVar. So, as a general rule, we want to run as many Monte Carlo iterations as possible (given time and memory constraints). For this reason the time spent during initialization and processing of output is small compared to the time spent during the Monte Carlo phase. Therefore we restrict ourselves to analyzing performance during the Monte Carlo phase.

3.1. Pseudo code for resampling step

For all our methods we assume that the resampling parameters were pre-computed and stored during the initialization phase. Furthermore we assume that there are m data points and r standardized residuals.

The memory requirements for linear Pearson residual resampling are

Dim Residual(1 To r) As Double
Dim Base(1 To n) As Double
Dim Scale(1 To n) As Double

The pseudo code for resampling the ith data point is

Function ResampleLinearPearson
    (i As Integer) As Double
Dim j As Integer
j = 1 + int(RandUniform(0,1) * r)
    ` RandInteger(1,r) 
Result = Base(i) + Scale(i) * Residual(j)
End Function    (3.1)
                    

The memory requirements for split-linear residual resampling are

Dim Residual(1 To r) As Double
Dim FirstUp(1 To n) As Integer
Dim BaseLow(1 To n) As Double
Dim BaseUp(1 To n) As Double
Dim ScaleLow(1 To n) As Double
Dim ScaleUp(1 To n) As Double

The pseudo code for resampling the ith data point is

Function ResampleSplitLinear
    (i As Integer) As Double
Dim j As Integer
j = 1 + int(RandUniform(0,1) * r)
    ` RandInteger(1,r) 
If j  FirstUp(i)
    Result = BaseLow(i) + ScaleLow(i)
    * Residual(j)
Else
    Result = BaseUp(i) + ScaleUp(i)
    * Residual(j)
End If 
End Function    (3.2)
                    

Note that by precomputing BaseLow, ScaleLow, BaseUp, and ScaleUp we are effectively combining the original linear Pearson rescaling with the split-linear transformation (2.6) into one linear transformation (technically one transformation for the lower set and one for the upper set). Details can be found in A.8. We observe that only one line of code from the If . . . then . . . else block will actually be executed for any given data point, so the executed operations for split-linear resampling are almost the same as linear Pearson resampling, except for the comparison and branching operation needed for the If . . . then . . . else block.

The memory requirements for limited Pareto sampling are

Dim a(1 To n) As Double
Dim bmc(1 To n) As Double ` bmc = b minus c
Dim c(1 To n) As Double
Dim p(1 To n) As Double

The pseudo code for resampling the ith data point is

Function ResampleLimitedPareto(i As Integer)
    As Double
Dim u As Double
u = RandUniform(0,1)
If u = p(i) Then
    Result = bmc(i)
Else
    Result = a(i)/u – c(i)
End If
End Function    (3.3)
                    

This formula is simply the inverse transform method applied to the CDF given by (2.9).

Note that a typical random number generator will produce a uniform random number between 0 and 1. Generating a random integer (between given bounds) is usually accomplished as indicated in the pseudo code above, even if a particular implementation may hide this from the user by providing a RandInteger function. For our operation counts in Table 1 we will exclude the addition in RandInteger, because this can be avoided by using 0-based instead of 1-based arrays.

3.2. Performance comparisons

Table 1 summarizes the memory requirements and provides operation counts for each of the three methods. Please note that in the case of limited Pareto sampling, the operation counts depend on the random number generated, and therefore two columns of operation counts are provided. With probability (1 − p) the first column applies, and with probability p, the second column applies. The “int()” row refers to the truncation of the fractional part used in RandInteger; the “comparison” row refers the If . . . then . . . else block. For the memory row, dbl refers to a 64 bit floating point number, and int refers to a 32 bit integer (some systems may allocate 64 bits for an integer).

The computational cost for the various operations does depend on the programming language and platform used. However, we can unambiguously conclude that split-linear rescaling requires slightly more operations (one additional array access, and one comparison) than linear Pearson rescaling. Comparing linear Pearson rescaling to limited Pareto sampling, we note that linear Pearson rescaling requires an additional multiplication operation, while limited Pareto sampling involves an additional comparison. The complexity of the comparison is similar to a subtraction operation, so we expect that on most platforms, limited Pareto sampling will perform slightly better than linear Pearson rescaling. Limited Pareto rescaling additionally benefits from the reduced complexity in case we sample the upper limit.

To provide some concrete examples, we have tested the methods on two actuarial development triangles. The first data set (A) is a US Industry Auto paid loss triangle taken from Friedland (2010, 107). This triangle was chosen because all three methods work, allowing us to benchmark them against each other. The second data set (B) is taken from the appendix to Taylor and Ashe (1983) and has been used by a number of authors to demonstrate stochastic reserving models. Data set (B) is presented in the triangle form familiar to P&C actuaries in Pinheiro, Silva, and Centeno (2003). Both triangles are included in appendix B for reference purposes. Linear Pearson rescaling fails for this second triangle (see Hartl 2010 for a detailed discussion). We are using it to demonstrate that the two alternative methods proposed in this paper do extend the applicability of the bootstrapping approach to triangle GLMs. To further demonstrate the flexibility of the GLM approach, the second model is fitted to the last five diagonals of the triangle (instead of the full triangle). Note that for data set B we only have 40 data points vs 55 data points for data set A (because we are only using the most recent five diagonals). In each case we are also sampling 45 future cells to simulate the process error component.

All the test results cited in this paper were produced with a VBA for Excel application that is available from the author on request. Because VBA for Excel is an interpreted language that is embedded in a complex environment, reliably testing the performance is not straightforward. Since we cannot control for the variation in the environment, we have used a randomized sampling scheme, where we executed a fixed number of test runs and randomly chose which particular method to use for each test run. We ran two different test scripts for each triangle. The first test script (sampling) tested the resampling operation in isolation. Given our total number of test runs, we expect about 3,333 runs for each method, where each test run consists of resampling the triangle and simulating the reserve runoff 100 times. The second test script (full) tested the resampling methods in the context of the full bootstrapping simulation (i.e., including refitting the model, projecting the reserve based on the refitted model, and simulating the runoff of the reserve). Again, we expect about 3,333 test runs for each method, with 100 bootstrapping iterations each. The scripts were run on the author’s Lenovo X230 tablet (Intel Core i5, 2.6GHz, 4GB ram), under Windows 7(64 bit), with Excel 2010.

Table 2 summarizes the average run time and the standard deviation for 100 iterations, for each data set and test script. All run times are in seconds and pertain only to the Monte Carlo phase.

The VBA for Excel based performance comparison confirms the relative performance we expected based on our operation counts in Table 1.

4. Conclusions

We presented two new methods for generating pseudo data for bootstrapping a GLM. Split-linear rescaling is a residual based resampling technique that extends the class of triangle GLMs that can be bootstrapped, but it can fail for specific triangles. Sampling from a limited and shifted Pareto distribution is always possible (subject to practical limitations when the distribution becomes almost degenerate or effectively unlimited). Both methods are computationally inexpensive and comparable to linear Pearson residual rescaling. Further research is needed to explore the sensitivity of bootstrapped confidence intervals or tail measures to the resampling distribution employed.

---

Acknowledgments

This paper was written and revised while the author worked as an Assistant Professor at Bryant University, RI. The author is also grateful for the constructive comments from the anonymous reviewers.

---