Credibility Prediction Using Collateral Information

1. Introduction

Dating back at least to papers by Mowbray (1914) and Whitney (1918), credibility has enjoyed a long history in actuarial science. As seen in the Mowbray and Whitney papers, credibility helps to address two important problems:

• Sharing of information among risk classes. It is common for a distinct risk class to lack information or exposure upon which the insurer can adequately base prices. When developing a rate for a specific risk class, it is naturally desirable to use information from related risk classes.

• Infusing collateral information into resulting rates. At times, an insurer may not have sufficient information from a specific risk class nor from related risk classes and so wishes to incorporate external (“collateral”) information.

A natural tool for incorporating collateral information in a disciplined manner is through the use of Bayesian methods (cf. Norberg 1979, 202, and Jewell 1975). Bailey (1950a, 1950b) introduced the Bayesian model into credibility theory and showed the equivalence between the Bayesian predictive mean and traditional credibility pricing formulas in specific cases. As noted by these authors, the Bayesian paradigm not only readily permits the sharing of information among risk classes but also allows the analyst to incorporate collateral information.

This result was considerably generalized by Jewell (1974), who showed that linear credibility estimators can be achieved through the use of conjugate priors in linear exponential families. Subsequently, Dannenburg, Kaas, and Goovaerts (1996) demonstrated how to incorporate variable weights and Ohlsson and Johansson (2006) extended it to allow parameters to vary by policyholder as one would observe in an insurance portfolio. Moreover, Ohlsson and Johansson (2006) gave specific results for the Tweedie family, a special case of considerable interest in insurance applications and this study. In this work, we also incorporate collateral information in a GLM context and so extend this line of research. In some sense, this paper is a dual application to that of Ohlsson (2008), who also relied on Ohlsson and Johansson (2006) but focused on the risk sharing aspects of credibility.

The rest of the paper is structured as follows: Section 2 motivates our modeling framework and Section 3 introduces the closed-form credibility predictors. A simulation study is performed in Section 4. We demonstrate the value added by the collateral information in a variety of hypothetical scenarios, such as different types of score, sample size, and data variability. Section 5 applies the proposed approach to an automobile insurance dataset from Massachusetts. Section 6 concludes the paper and technical details are summarized in the Appendix.

2. Motivation

In this paper, we consider cross-sectional sampling. So, think of each policyholder being observed once and policyholders’ claims experience as being unrelated. (In the Appendix, we more precisely assume that claims are independent, conditional on uncertainties in the collateral information introduced in the following.) For the ith policyholder, use y_i to denote the dependent variable (claim) and $\mathbf{x}_i$ to denote a vector of explanatory (covariate) variables that provide rating information about the policyholder. For this sampling scheme, the information for the model development or training data set is ${(y_i,\mathbf{x}_i), i = 1, \ldots, n}$ that we label as $Y_{Train}$. In a similar way, the information for the model validation set is ${(y_i,\mathbf{x}_i)}, i = n + 1, \ldots, n + n_{Valid}\}$ that we label as $Y_{Valid}$.

2.1. Base case—No covariate information

In the base model, the insurer’s ith policyholder has claim y_i with mean $\mu_i$. The mean is not observed and may be estimated by policyholder covariates. Before introducing covariates, we assume that the insurer has available an observed score or “manual premium” that is provided by an external agency. Denote the score as μ_α,i and relate it to the mean as a multiplicative effect

$$\mu_{i}=\alpha \times \mu_{\alpha, i} \text {. }$$

The external score is an estimate of the true mean and we use α to denote the corresponding relative error. The variable α may vary by policyholder or risk class. For the moment, we omit the subscript on this term.

From a frequentist perspective, one can think about the term α as a measurement error induced by the score. It is well known in the statistical literature that ignoring this aspect can induce bias in all model coefficients; cf. Carroll et al. (2006). We utilize a Bayesian framework and interpret the distribution of {α} as representing the knowledge that the actuary has of the score. Before seeing any data, we assume unbiased scoring and so the mean of the prior distribution is one. This distribution may be subjective and allows the analyst a formal mechanism to inject his or her assessments into the model.

With the training sample Y_Train, it will be straightforward to use Bayesian procedures to directly form an estimate of the scoring procedure bias as E(α|Y_Train). Then, for a new policy in Y_Valid, we are able to form a prediction using E(y_i|Y_Train) = μ_α,i × E(α|Y_Train) for i in {n + 1, . . . , n + n_Valid}.

Of course, it is certainly possible to focus on the random mean $\mu_i$, that is, using Bayesian procedures to update $\mu_i$ directly. As will be seen, creation of a new variable α allows us to decompose the random aspect of the uncertainty from other portions, such as covariate information. Moreover, this decomposition will facilitate interpretability as we seek to combine different categorical (factor) random effects.

2.2. Introducing covariates

As a next step, we assume that the insurer has one or more covariates that could be included in the model. For example, thinking of y_i representing the claim on the ith personal automobile policy, the insurer knows whether or not the policyholder also owns a homeowners policy (x_i = 1 if yes and = 0 otherwise). The insurer could incorporate this information into the collateral score model using the representation

$$\ln \mu_{i}=\ln \alpha+\ln _{\alpha, i}+x_{i} \beta$$

where β is a parameter to be estimated. For this motivation section, we use a logarithmic link function. More generally, the insurer could have a set of covariates that could be included through the representation

$$\ln \mu_{i}=\ln \alpha+\ln \mu_{\alpha, i}+\mathbf{x}_{i}^{\prime} \boldsymbol{\beta} \tag{1}$$

Here, $\mathbf{x}_i^{\prime}=\left(x_{i 1}, \ldots, x_{i K}\right)$ represents a set of K explanatory variables and β is the corresponding set of parameters. We interpret the term $\mathbf{x}_i^{\prime} \beta$ as representing the effects of the insurer’s portfolio on claims (e.g., insurer underwriting standards).

Similar to the base case, the training sample Y_Train is $\left\{\left(y_i, \mathbf{x}_i\right), i=1, \ldots, n\right\}$ and Section 3 will show how to use Bayesian procedures to estimate E(α|Y_Train). Based on Y_Train, we may estimate the regression coefficients β (say, b). Then, we will be able to form a prediction using $\mathrm{E}\left(y_i \mid Y_{\text {Train }}\right)=\mathrm{E}\left(\alpha \mid Y_{\text {Train }}\right) \times \mu_{\alpha, i} \times \exp \left(\mathbf{x}_i^{\prime} \mathbf{b}\right)$ for i in {n + 1, . . . , n + n_Valid}.

2.3. Multiple scores

As a variation, we can imagine a situation where there is more than one set of collateral information. Suppose that we have two sets of collateral scores with their associated uncertainties, $\alpha_1 \times \mu_{1, \alpha, i}$ and $\alpha_2 \times \mu_{2, \alpha, i}$. If we are unsure how to combine them in our claims model, then it would be sensible to use (unknown) scaling factors γ₁ and γ₂ and consider a variation of equation (1),

$$\begin{aligned} \ln \mu_{i}= & x_{i 1} \beta_{1}+\cdots+x_{i K} \beta_{K}+\gamma_{1} \ln \left(\alpha_{1} \mu_{1, \alpha, i}\right) \\ & +\gamma_{2} \ln \left(\alpha_{2} \mu_{2, \alpha, i}\right) \\ = & x_{i 1} \beta_{1}+\cdots+x_{i K} \beta_{K}+\gamma_{1} \ln \mu_{1, \alpha, i} \\ & +\gamma_{2} \ln \mu_{2, \alpha, i}+\gamma_{1} \ln \alpha_{1}+\gamma_{2} \ln \alpha_{2} \\ = & \tilde{\mathbf{x}}_{i}^{\prime} \tilde{\beta}+\ln \tilde{\alpha}, \end{aligned}$$

where $\tilde{\mathbf{x}}_i^{\prime}=\left(x_{i 1}, \ldots, x_{i K}, \ln \mu_{1, \alpha, i}, \ln \mu_{2, \alpha i,}\right)$ is a set of known covariates, $\widetilde{\boldsymbol{\beta}}=\left(\beta_1, \ldots, \beta_K, \gamma_1, \gamma_2\right)^{\prime}$ is a set of variables to be estimated, and $\ln \tilde{\alpha}=\gamma_1 \ln \alpha_1+\gamma_2 \ln \alpha_2$ is a random source of uncertainty. In a similar way, incorporating multiple sets of collateral scores is simply a special case of equation (1).

If the scaling factors γ₁ and γ₂ are known, then we can again use equation (1) but with uncertainty $\ln \tilde{\alpha}=\gamma_1 \ln \alpha_1+\gamma_2 \ln \alpha_2$ and offset $\ln \mu_{\alpha, i}=\gamma_1 \ln \mu_{1, \alpha, i} +\gamma_2 \ln \mu_{2, \alpha, i}$.

2.4. Introducing multiple sources of collateral information

The collateral information may also contain multiple sources, each representing a different type of uncertainty. For example, returning to the personal automobile example, one can imagine one set of uncertainties (α₁) for retirees and another set (α₂) for all other drivers. In general, we will assume that there are q sets of uncertainties represented as $\alpha^*=\left(\ln \alpha_1, \ldots, \ln \alpha_q\right)^{\prime}$ that feed into a claims model as

$$\ln \mu_{i}=\ln \mu_{\alpha, i}+\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}+\mathbf{z}_{i}^{\prime} \boldsymbol{\alpha}^{*} \tag{2}$$

Here, $\mathbf{z}_i^{\prime}=\left(z_{i 1}, \ldots, z_{i q}\right)$ represents a set of q explanatory variables for a linear allocation of the appropriate sources of collateral information to the ith policyholder.

2.5. Factor random effects

To further develop intuition, think of the special case where we have split up the rating schedule into q categories, where q may range in the hundreds (for example, in personal auto, one can think of many combinations of age, gender, territory, and so forth). Now, α* represents a categorical factor so that each z_ij is a binary variable assigning the ith observation to the jth level of the factor. Standard mappings (e.g., Frees 2010, section 4.7) allow one to readily go from regression notation, where we distinguish observations using i, to a one-factor notation, where we distinguish observations using ij. In the one-factor notation, there are i = 1, . . . , c factors, and, for the jth factor, there are j = 1, . . . , n_j observations, for a total of n₁ + . . . + n_c = n observations. Henceforth, we use the factor notation.

3. Credibility prediction

To recapitulate, we assume that the claims distribution is a component of a generalized linear model (GLM). For the ith policyholder that is in the jth level of the factor, we specify a conditional mean

$$\mathrm{E}\left(y_{i j} \mid \boldsymbol{\alpha}\right)=\boldsymbol{\alpha}_{j} \times \mu_{\alpha, i j} \times \exp \left(\mathbf{x}_{i j}^{\prime} \boldsymbol{\beta}\right) \tag{3}$$

where $\alpha_j$ reflects the uncertainty about the score, $\mu_{\alpha,ij}$ is the (externally) provided score, and $\exp \left(\mathbf{x}_{i j}^{\prime} \boldsymbol{\beta}\right)$ represents insurer-specific adjustments reflecting covariate effects. Our prior belief is that the scoring procedure is unbiased and so we assume that $E(\alpha_j) = 1$. Thus, the (unconditional) mean is $\mu_{ij} = \mu_{\alpha, i j} \exp \left(\mathbf{x}_{i j}^{\prime} \boldsymbol{\beta}\right)$. Although our theory allows $\mu_{ij}$ to be a (smooth) nonlinear function of covariates, in practice we often specify a logarithmic link function used in equation (3).

We next specify a prior distribution to reflect the uncertainty of the collateral information summarized in $\alpha_j$. Fortunately, modern-day computational methods permit a wide scope of alternative choices using, for example, Markov chain Monte Carlo (MCMC) methods (see, for example, Hartman 2014). With a prior distribution, it is straightforward to calculate the marginal distribution of y by integrating over the prior and then use maximum likelihood to estimate the parameters of the conditional outcome distribution that include β.

Although it is possible to calculate posterior means using MCMC techniques for general prior distributions, it is also desirable to specify distributions where closed-form expressions are available. In the Appendix, we consider several exponential families, including the normal, Poisson, gamma, inverse Gaussian, and Tweedie. This section generalizes the work of Ohlsson and Johansson (2006), who focused on the Tweedie distribution (that includes the Poisson and gamma cases). For each family, we specify a natural conjugate prior density in Appendix equation (9) with mean $E \alpha_j=1$ and dispersion parameter $\phi_\alpha$. For example, in the case of the Tweedie distribution, the dispersion parameter associated with the natural conjugate prior is $\phi_\alpha=\operatorname{Var}\left(\alpha_j\right) / E \alpha_j^p$.

In these special cases, we have an explicit expression for the posterior mean of the form

$$\mathrm{E}\left(\alpha_j \mid Y_{\text {Train }}\right)=\zeta_j+\left(1-\zeta_j\right) \overline{(y / \mu}_{W j},\tag{4}$$

where $\zeta_j$ is a credibility factor

$$\zeta_{j}=\frac{\phi}{\phi+\phi_{\alpha} W_{j}} \tag{5}$$

that is determined by the sum of weights within the jth factor $W_j=\sum_{i: z_y=1} b_2\left(\mu_{i j}\right)$, and $\overline{(y / \mu)}_{W j}=\sum_{i: z_j=1}\left(y_{i j} / \mu_{i j}\right) b_2\left(\mu_{i j}\right) / W_j$, a weighted average. Here, z_ij is a binary variable that is one if the ith policyholder is in the jth risk category. The parameter φ and the function b₂(•) depend on the choice of the outcome (claims) distribution. For example, Table 9 in the Appendix shows that $b_2\left(\mu_{i j}\right)=\mu_{i j}^{2-p}$ for the Tweedie distribution.

Equations (4) and (5) have pleasing interpretations that are common in credibility expressions. On the one hand, the credibility factor $\zeta_j$ tends to one as either φ_α → 0 or φ → ∞. In either case, we think of the uncertainty associated with the score being very (increasingly) small relative to the dispersion in the outcome distribution. On the other hand, the credibility factor $\zeta_j$ tends to zero as either φ → 0 or W_j → ∞. Intuitively, the credibility (of the score) is small with high precision data or as the number of observations in the jth level of the factor becomes large, indicating substantial information content in the data. Additional details are in the Appendix.

As yet another special case, suppose that the uncertainty grouping is sufficiently refined so that the covariates are constant within the uncertainty group. In this case, $\mu_{ij}$ is a constant over the set {i:z_ij = 1} and equal to, say, $\mu_j$. Then, the weight is a constant times the number of observations in group j, $W_j=n_j \times b_2\left(\mu_j\right)$, the weighted average becomes a simple average $\overline{(y / \mu)}_{W j}=\sum_{i: z, j=1} y_{i j} /\left(n_j \mu_j\right)=\bar{y}_j / \mu_j$, and the credibility factor reduces to

$$\zeta_{j}=\frac{\phi}{\phi+\phi_{\alpha} n_{j} b_{2}\left(\mu_{j}\right)} \tag{6}$$

For predicting claims from the validation sample, we can calculate an estimator of $\mathrm{E}\left(y_{i j} \mid Y_{\text {Train }}\right)$ for i in n + 1, . . . , n + n_Valid. Using estimates based on Y_Train, the predictor for the ith policyholder in the validation sample is

$$\left(\zeta_j+\left(1-\zeta_j\right) \overline{(y / \mu)}_{w j}\right) \mu_{\alpha, i j} \exp \left(\mathbf{x}_{i j}^{\prime} \mathbf{b}\right).\tag{7}$$

3.1. Illustration

To get a better handle on the credibility factors, assume that you wish to apply the credibility factors in equation (5). How does one think about the distribution of the uncertainty of scores, $\alpha_j$? We know that the expected uncertainty is one $\left(\mathrm{E} \alpha_j=1\right)$ and that the dispersion parameter, at least in the Tweedie case, is close to the variance of $\alpha_j$ (specifically, $\phi_\alpha=\operatorname{Var} \alpha_j / E \alpha_j^p$).

To give a better sense of the dispersion parameter prior distribution, Figure 1 compares prior distributions over different values of dispersion parameters. This prior distribution corresponds to a Tweedie distribution with shape parameter p = 1.5. From the figure, we see that large values of φ_α mean that the distribution is fatter tailed and right-skewed. Conversely, a relatively small value of φ_α (equal to 0.01) gives a distribution that appears to be approximately normally distributed.

Figure 1.Prior distributions for different dispersion parameters φ_α

How does the prior distribution affect the credibility factor? To give insights into this question, we turn to the special case in equation (6) where covariates are constant within the uncertainty group. As a benchmark, we consider the parameters of a Tweedie regression model that will be described in detail in Section 4. Specifically, we assume a Tweedie distribution with parameters p = 1.5, φ = 1,087.709 and μ = 211.87.

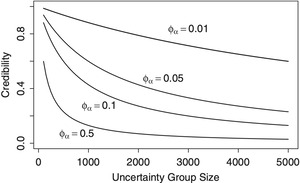
For these parameter choices and the credibility factor in equation (6), Figure 2 compares credibility factors over several dispersion parameters and group sizes. As anticipated, smaller values of φ_α mean that we have more confidence in the (external) score and so the credibility factor is closer to one. Further, larger group sizes mean that we have more confidence in the posterior mean so that the credibility factor is lower. Note that in this paper, the credibility factor measures the amount of belief in the prior mean, not in the data. We could have easily defined the credibility factor in terms of its complement (1 − ζ); however, our goal is to emphasize the credibility of the collateral (prior) information, not the data.

Figure 2.Credibility factors by uncertainty parameters φ_α and group size

4. Simulation study

4.1. Simulation design

For the simulation study, we consider a situation where an insurer has a portfolio of policies in a ratemaking development year. The insurer has policyholder characteristics (xs) and claims (ys) upon which rating predictors can be developed. The insurer also contacts an external agency that provides one or more scores based on the characteristics in the insurer’s portfolio in the development year. These scores can be used by the insurer to produce modified rating predictors. An insurer then compares the alternative predictors using a new data set, “out-of-sample testing.” As part of the testing procedure, the external agency also provides scores based on the characteristics of the new out-of-sample policyholders.

Prior to giving the comparison results, this section describes the data generating process, alternative scores provided, and the rating predictors.

4.1.1. Data generating process

We simulated a portfolio of policies and claims experience based on a sample of Massachusetts automobile experience reported in Frees (2014). Table 1 provides the policyholder distribution by two rating factors, an age-based rating group and territory. Thinking of an insurer’s experience in a specific state or province, we consider sample sizes of 2,000 and 10,000 policyholders. For each situation, we generated a portfolio of policyholders using the distribution reported in Table 1 for the model or ratemaking development (in-) sample, and another data set of the same size for out-of-sample testing.

For each policyholder, we simulated claims using the Tweedie distribution with parameters reported in Table 2. We used a logarithmic link function with scale parameter p = 1.5 and initial choice of a dispersion parameter φ = 250. For example, suppose that we wish to estimate expected claims for an Adult driver in Territory 6. Because these are the reference levels, the estimate is exp(5.356) = 211.87. The corresponding probability of zero claims is $\exp \left\{-\mu_{i j}^{2-\mathrm{p}} /(\phi(2-\mathrm{p}))\right\}=89.0 \%$. Use β₀ to denote the vector of parameters in Table 2.

4.1.2. Alternative scores

A score is provided by an external agency that is based on policyholder characteristics. The best (although unattainable in practice) score is the mean, exp(x′β₀), that we label ScoreTrue.

To derive alternative scores, we assume that the external agency has other data that follows the same distribution as in Section 4.1.1. Ideally, the analyst for the external agency (i) works with a large data set, (ii) employs an extensive set of covariates, and (iii) uses modern (appropriate) statistical methods. To assess these alternatives, we provide eight alternative scores that vary by:

• sample size, either a relatively large sample size (LS) 100,000 or a small sample size (SS) 10,000;

• number of covariates, either including both age and territory (Full) or a reduced set, only age (Red); and

• statistical methods, either a GLM using a Tweedie distribution (GLM) or a linear model (LM).

Thus, for example, LS_Full_GLM denotes a score that the analyst derives using a sample size of 100,000, both age and territory covariates, and a GLM representation. As another example, SS_Red_LM denotes a score derived using a sample size of 10,000, only the age covariate, and a linear model.

Scores are calibrated from data and so are subject to estimation error. To generate the scores, we used q = 6 risk categories corresponding to different territories. We use the conjugate prior distribution described in the Appendix with parameter φ_α = 0.01. This corresponds to a standard deviation of $\alpha_j$ of approximately 0.1.

4.1.3. Rating predictors

The analyst for the insurer has many choices of rating predictors. First, one option is to use only company experience, ignoring any scores provided by an external agency. We will assume that the insurer analyst is only using GLM representations but, like the external analyst, may be working with a limited set of covariates. Specifically, we distinguish between the cases when the analyst has a full set of covariates, including both age and territory (Full), and a reduced set, only age (Red).

Second, another option is to use only the score provided by the external agency, ignoring company information. As described in Section 4.1.2, there are eight such scores available, in addition to the baseline true score.

A third option is for the analyst to use the externally provided score as an offset in a GLM model and then incorporate additional company covariates as available. We also considered including the externally provided score as a variable in a GLM model together with company covariates. No real insights were garnered from this alternative option and so we do not describe results here.

Fourth, the analyst may incorporate the externally provided score as an offset, use company covariates, and modify the predictors based on the insurer’s belief in the scores using the predictors described in Section 3. For our work, we allow the belief parameter to vary over φ_α = 0.5,0.1,0.01,0.

4.1.4. Out-of-sample summary measures

We choose seven criteria to measure how each model performs in terms of out-of-sample prediction. The first three statistics are standard out-of-sample validation statistics, e.g., Frees (2010); they measure how far away the predicted values deviate from the observed values in the hold-out sample. Thus, the smaller the numbers, the better the predictions. The mean absolute (percentage) error computes the average of the (percentage) absolute error between the prediction and the observed value; the root mean square error is the square root of the average squared distance between the prediction and the observed values.

The next three statistics measure the correlation between predicted values and observed values in the hold-out sample. The larger the numbers, the better are the predictions. Recall that the Pearson correlation is obtained by dividing the covariance of two variables by their standard deviations and the Spearman correlation is defined as the Pearson correlation coefficient of the ranked variables. That is, the original values need to be converted to ranks, and Spearman correlation is less sensitive than Pearson correlation to outliers in the tails of both samples. The Gini coefficient is a newer measure developed in Frees, Meyers, and Cummings (2013). It measures the correlation between the rank of predictor and the corresponding outcome from a hold-out sample. The seventh statistic is a Gini index that corresponds closely to the correlation coefficient. This Gini index is twice the average covariance between the the outcome in the hold-out sample and the rank of the predictor. All correlations are reported on a percentage scale, that is, multiplied by 100.

4.2. Simulation results

Table 3 summarizes the out-of-sample statistics for our credibility rating predictors. For ease of comparison, Panel A presents the results in the case φ_α = 0.0 so there is no presumed uncertainty associated with the score. Even in Panel A we see that the mean absolute error and the mean absolute percentage error give non-intuitive results. In each case, going from the “Full” set of covariates to the “Red” (reduced), they actually increase, indicating a poorer ability to predict. The root mean square error statistic fares better, although it still does not provide the type of separation that one would like to see. Although useful for many applications, because our outcome claims variable contains many zeros and, when positive, has a skewed distribution, these traditional measures are less useful for rating analyses.

Panels B, C, and D of Table 3 present results as the analyst changes his or her belief about the score’s precision. As one increases the value of φ_α, one places less credibility on the score and more on the data. Interestingly, when even acknowledging a small imprecision in the score, the case φ_α = 0.01, the Gini correlation increases from approximately 5.22 to 7.48, even for scores that use only a reduced set of covariates. This is because we selected the risk classes to correspond to the set of information, territory, that is “missing” in both the company’s covariates and external agency covariates. By averaging over these risk classes in one period, the insurer has a very useful nonparametric predictor of claims in the next period. Results for the traditional Pearson and Spearmen coefficients are consistent with the newer Gini correlations. Because of the literature cited above, we focus henceforth on the newer Gini measure.

Tables 4 and 5 present out-of-sample summary statistics for small sample and small dispersion cases. For these alternative cases, we focus on the Gini correlations. Table 4 provides similar information compared to Table 3, except we now assume that the insurer has 2,000 policyholders for in-sample analysis and out-of-sample testing. The scoring procedures by the external agency remain the same. The table shows that the results for this smaller sample size are consistent with those in Table 3, except that now the belief parameter φ_α must be larger, placing more emphasis on the data, in order to overcome a poor score.

Table 5 returns to the scenario of 10,000 policyholders available in- and out-of-sample, yet now consider the case where the outcome dispersion parameter φ reduces from 250 to 100. Because of this reduction in dispersion, all correlations are larger than the corresponding elements in Table 3, yet the conclusions remain essentially the same.

5. Massachusetts automobile claims

In this example, we consider a database of personal automobile claims from the Commonwealth Automobile Reinsurers (CAR) in Massachusetts, described in Ferreira and Minikel (2010). The CAR is a statistical agent for motor vehicle insurance in the Commonwealth of Massachusetts and collects insurance data for both private passengers and commercial automobiles in the state. In Massachusetts, individuals who drive a car must purchase third-party liability (property damage and bodily injury) and personal injury protection (PIP) coverage for their personal vehicle.

The database summarizes experience of over three million policyholders in year 2006. For each policy, we observe the number of claims, the type of claim for each accident, and the total payments associated with each type during the year. Besides the claim information, the data also contain basic risk classification variables. Because the dataset represents experience from several insurance carriers, we only have access to a limited number of common rating variables reported to the bureau.

We take a random sample of 100,000 policyholders for this study. The first 50,000 observations are used as training data to develop the model, and the rest are reserved as hold-out for validation. Table 6 displays the description and summary statistics of the rating factors for the training data. As described in Ferreira and Minikel (2010), Rating Group indicates policyholder characteristics and Territory Group indicates the risk level of the driving area defined by the garage town. Rating Group is constructed from finer-grained driver classes. Territory Group is constructed based the Automobile Insurance Bureau’s relativities estimated for the 351 Massachusetts towns and the 10 state-defined regions within the city of Boston. These geographical units are ranked by the estimated risk and then grouped into six territories. Table 6 shows that 77% policyholders are adult drivers and 11% are from the most risky driving territory. The last two columns present the average liability and PIP claims.

To illustrate the value added by the collateral information from external sources, we consider scores produced by ISO Risk Analyzer—a commercial predictive model from Verisk Analytics. Specifically, two sets of scores are used in the credibility prediction, the relativities from the vehicle module for liability and from the environmental module. The former is based on vehicle characteristics and is the focus of this example. The latter captures the effects of granular environmental factors instead of the crude location of garage town indicated by the territory group.

We use the same out-of-sample statistics as introduced in the simulation section. The results for the liability and PIP coverage are reported in Tables 7 and 8, respectively. We compare the credibility predictions with (Panels B–E) and without (Panel A) collateral information—the vehicle module liability score.

In Panel A, the insurer only uses rating variables as covariates in the prediction. We consider three base scenarios representing a range of complexity of predictive models employed by the insurer.

1. A naive insurer, relying on the principal of parsimony, could use a reduced set of covariates—rating group only.

2. A more knowledgable insurer might consider a full set of covariates, including both rating and territory groups in the prediction.

3. In addition to the rough territory information, a sophisticated insurer might incorporate the more detailed address-specific risk factors, which could be the relativities from the environmental module.

In Panels B–E, the insurer combines the vehicle liability score with each of the three basic models introduced in Panel A. Consistent with the simulation study, we include the vehicle module relativity as an offset in the Tweedie GLM. We further assume that the measurement error in this external score varies by territory group, i.e., credibility predictions are calculated according to equation (4) where the subscript j refers to territory. The confidence in the score is reflected by parameter φ_α with a larger value indicating higher uncertainty. Predictions for φ_α = 0, 0.01, 0.1, and 0.5 are reported.

We observe similar patterns in both tables and, in general, the out-of-sample statistics suggest that collateral information could improve prediction. First, Panel A suggests that geographic information is an important predictor for this data set. For example, if the insurer is knowledgeable enough to use territory group in the prediction, the Gini index increases from 17.36 to 41.33. By further incorporating granular information from the environmental module, one could improve the Gini index to 46.59. Consistent results are also observed in Panels B–E.

Second, the credibility prediction in Panels B–E for the naive insurer reinforces the results observed in Table 3 in the simulation study. Specifically, when even allowing for a small imprecision (φ_α = 0.01) in the score, the Gini index increases from 31.79 to 45.83. This is because the territory group, as suggested by Panel A, is an important risk class indicator for the portfolio of policyholders. Although the naive insurer is not knowledgeable to use territory as a covariate, the territory information is brought into the prediction through the factor random effect specification. However, this difference between Panel B and Panels C–E is less prominent for more sophisticated insurers, because including territory group as a predictor reduces the effect of averaging over these risk classes.

Third, comparing Panels B–E with Panel A, one finds that regardless of the complexity of the predictive model used by the insurer, using the vehicle liability score further improves the prediction. One notices that higher lift is provided by the external score for less sophisticated insurers. For example, the Gini index increases approximately from 41 to 47 for a knowledgeable insurer, and from 46 to 49 for a sophisticated insurer. This observation is anticipated because the score is likely to contain more relevant information that is missing in the reduced set of covariates.

6. Conclusion

This study was motivated by a practical problem in property casualty insurance ratemaking: How can individual insurers blend external information with their own rating variables to improve prediction? We answered this question by developing credibility predictions in a GLM context using Bayesian methods and hence contributed to the credibility literature on incorporating collateral information.

Collateral information can take different forms. We think of them as a single or multiple scores obtained from external agencies, be it a rating bureau or a proprietary entity. Such a score is conceptually attractive because it could incorporate rating information not available to the insurer or it could be generated through advanced predictive models that the insurer could not afford in house. To adapt the external score to the insurer’s own rating scheme, we introduced the uncertainty in the score that is allowed to vary across different risk classes and made statistical inference for the bias from the data. We employed a Bayesian approach. The advantage of this approach is that it provides a mechanism for the analyst to incorporate his or her prior belief about the uncertainty of the score into the prediction.

Using conjugate priors, we derived close-form credibility predictors for a variety of distributions in the exponential family, with a focus on the Tweedie family in the simulation study and the application of Massachusetts automobile insurance. The Tweedie GLM is commonly used in modeling pure premiums in property-casualty insurance and thus is a natural choice for incorporating external scores such as manual rates or ISO Risk Analyzer relativities. For validation, we noted that the traditional out-of-sample statistics are less useful and emphasized recently developed Gini statistics for measuring the predictive performance.

Acknowledgment

We gratefully acknowledge the financial support for this study by Insurance Services Offices, Inc. Support for revisions was provided by a Society of Actuaries Center of Actuarial Excellence grant. We thank editor and anonymous reviewers for helpful comments.