1. Introduction
The theory tested in this paper involves the environmental processes inseparably tied to the obsolescence of the ordered investments of material, time, and energy that we call physical assets. These exogenous processes, such as advancing technology, changing energy costs, changing costs of capital, increasing costs of labor, or emerging government incentives to adopt new technology, act in the aggregate over time to render some types of infrastructure capital obsolete. Although mechanical wear on physical assets is an important endogenous influence on asset mortality, we are speaking equally of quantifiable socioeconomic processes that drive obsolescence; therefore, the role of actuarial science cannot be abrogated.
1.1. The role of the actuary
The subject of this paper may push the boundaries of what is considered actuarial science, particularly if one’s definition is limited only to activities associated with existing insurance products. Nevertheless, as this paper deals with populations of mortality risks, it is no wonder that the vocabulary of actuarial science is the most apt at defining obsolescence and exposing never-before-seen optimization relationships at the portfolio level. Only actuaries possess the specific training to reveal this kind of phenomenon.
The processes that drive obsolescence of infrastructure assets are primarily socioeconomic, not physical. Without actuarial science, balancing the costly activities of manufacturing and operation in the face of the uncertain future forces of advancing technology, changing energy and labor costs, and even regulation is often pragmatically dealt with through simple deferral of the replacement decision, which leads to the systematic destruction of resources and wealth and an enormous opportunity for their recovery.
By defining this problem in the context of insurance, the industry’s full actuarial talent could be brought to bear on what would essentially become a ratemaking and reserving exercise to assure the appropriate portfolio treatment of pooled, homogeneously grouped physical assets treated as mortality risks. Underwriting, reinsurance, and other industry resources could further assure the most efficient allocation of capital, while simultaneously providing a cheaper and less volatile risk-financing delivery method for the replacement of aging infrastructure.
It is incumbent on actuaries to use their special knowledge of risk outside the strict context of existing insurance practices, and this is the whole point of enterprise risk management. The basic CAS education provides an ample toolkit that, if applied fundamentally in other industries, might result in new stem areas of practice where property and casualty actuaries could provide new insights to old problems outside of insurance that currently lack theoretical foundation.
1.2. Physical assets
Physical assets in the sectors of transportation, power, water supply, healthcare, and communications make up the infrastructure that allows society to thrive. Machines, vehicles, buildings, and structures are manufactured at great expense; then, as they age, they run at an ever-increasing cost relative to advancing replacement technology. Eventually the economic advantages of a newer machine become so cogent that they inevitably force a replacement decision, even under the most austere budget management. Is there a best time that organizations are missing to take this action?
Resources to manufacture and operate physical assets are scarce, yet they represent the vast proportion of all materials and energy consumed by society. The optimization theory tested in this paper suggests that potentially significant creation and destruction of wealth are at stake in the critical timing of infrastructure replacement and that life cycle costs of aging infrastructure can be minimized by handling obsolescence as an insurable event.
Obsolescence can be thought of as a state, or as a temporal transition to a state, of an asset when it should be replaced. In this state, the asset may still be in good working order yet be obsolete. In industry, obsolescence can occur because a like replacement becomes available that is economically superior in some way. A replacement asset may have comparative advantages to the existing asset, such as superior energy usage or comparatively reduced losses due to increasingly frequent unplanned failures of the old asset. Obsolescence may also be due to the availability of more advanced technology, changing energy costs, lost tax shelters from expired depreciation, the physically aging condition of the asset itself, or, more likely, the sum of all these factors working together. What is important in defining the state of obsolescence is the existence of a transition from a state of non-obsolescence and the fact that this transition may occur at a localized time.
A major assumption of this theory is that there exist aggregate processes of obsolescence that may differ greatly among different classes of assets but that remain relatively stationary over time. Processes of obsolescence, such as those manifested by Moore’s law for computing hardware or by the U.S. Department of Transportation’s data on vehicle longevity, are evidence of stable forces of mortality on physical assets.
1.3. Infrastructure service contracts
Contracts that contain provisions requiring the replacement of aging physical assets over long periods were first referred to as infrastructure service contracts (ISCs) in volume 8, issue 2 of Variance. In practice, such contracts require the service provider to replace a physical asset, such as underground piping, a machine, or a vehicle, when its life is deemed to have expired. Such contract provisions exist only in a very small percentage of infrastructure services, usually as a part of an alternative delivery method such as a design, build, operate contract, in which a contractor is responsible not only for the design and construction of infrastructure but also for its long-term operation for several decades. ISCs also exist in military utilities privatization, where whole bases may be turned over to a private contractor for management of such utilities as water, power, sewage, and steam systems for up to 50-year terms.
A good part of Wendling (2015) discussed the absence (in industry) of an objective definition of when this expiration of life occurs in a physical asset. Machines have no vital signs that would make such a determination easy, and any machine can always be repaired or refurbished ad nauseam to the point of immortality. The ISC today exists in a vacuum of theoretical understanding about objective criteria that constitute the end of life of a physical asset or why the timing of this replacement should matter.
Although ISCs are relatively obscure, Wendling (2014) argued that if they are modified with a definition of obsolescence based on the portfolio theory of that paper, the humble ISC would transform into a powerful tool for optimizing life cycle costs and creating wealth in the form of prospectively valued operating costs savings. Furthermore, underwriting ISCs as insurance could provide added benefits in the form of tax deductions and reinsurance.
1.4. M(t)
The subject theory is ontological in that it provides a fundamental explanation of why a phenomenon—the periodic replacement of physical assets—occurs in the first place. A fundamental investigation into this phenomenon uncovers and lays bare the structure of its underlying causes. We will find in this investigation that the phenomenon itself invokes the ontic existence of cyclical costs M(t) that drive it; in addition, only these cyclical costs, treated statistically, can ground the familiar phenomenon of asset mortality, much of which we already think we understand through pseudo-conceptions, which only seem to have been demonstrated. Since we already know that physical assets exhibit mortality with certain characteristics, we then invent the underlying concept of M(t)—a time-dependent function equal to the rising, cyclical, calendar-year opportunity costs of not substituting an old asset with a new replacement asset—to explain the observed features of this mortality.
M(t) captures anything that creates an opportunity cost in an existing physical asset through the existence of a substitute asset, such as energy savings; lower staffing needs; lower maintenance costs associated with new assets; and all other quantifiable calendar-year costs of time, energy, and materials needed above and beyond those of owning the newest, latest like asset. Such costs, by definition, begin at zero when the asset is new and then generally increase as the asset ages. These costs are an abstraction (a model) and are not usually recorded, though they can be tracked in real time if necessary. We ask the reader to take a leap of faith in accepting that such costs exist, so that we can proceed to arguments illustrating their hypothetical utility.
In some cases, these costs may indeed be comprised mostly of unscheduled repair costs, such as the ever-increasing cost of maintaining line breaks in a length of underground pipeline. In such a case, M(t) quantification is more of an accounting exercise than one involving an engineering evaluation of competing replacement technologies. In other cases, the analysis may be much more complex and involve costs that are not as easy to objectively quantify.
Even the expected value of a catastrophic loss is, in theory, a constituent of M(t). The chance of some mechanical failure causing loss of life, property, or revenues, such as in the case of a communications satellite or a mission-critical component of a manufacturing process, has been studied in other fields through the analysis of endogenous, mechanical aging processes of the machine itself. Great advances in reliability have been made through this kind of analysis and have even given a stochastic explanation of machine mortality. Yet these traditional theories of machine component failure do not begin to explain why some assets, such as certain pumps or bridges, never need to be replaced or why some fleet assets with a fluid resale market have a better chance of continued survival if they are very old rather than newer assets in the same fleet. These latter phenomena beg for a better understanding of why managers must choose between keeping an existing asset and replacing it with an expensive new one.
By condensing all the opportunity costs that could possibly motivate a manager to make an expensive replacement into a single, measurable quantity called M(t), we are using an aggregate approach to obsolescence risk management, much like combining all possible causes of mortality into a life table or including the whole field of causes of liability claims into an incurred loss triangle to aggregate all effects into one quantitative bulk measurement. It is like measuring the force of a fluid on a surface area to measure pressure instead of having to calculate the trajectory and momentum of every molecule in a volume to achieve the same. In our analysis, M(t) is the rising needle on the gauge of obsolescence. Knowing the point on the gauge’s scale when action must be taken and whether this matters are questions that we will explore; they can be answered by applying actuarial science to engineering data.
1.5. Criticism: Parsimony versus black box
We often want a simpler model involving fewer variables instead of a black box predictor involving them all. Wendling (2014) required estimating an error term β that may not be as trivial as it was described. The model also involved considerable judgment that was not transparent and was possibly inaccurate. That paper also emphasized the use of empirical asset mortality data. Such data—essentially, the distributions of ages of assets at mortality—were meant to create life tables for homogeneous groups of assets susceptible to similar forces of mortality and to be input into an algorithm that would determine the appropriate threshold of M(t) to cull and replace an asset. However, asset mortality data are not readily available, and there are usually no accurate records of physical asset longevity. In addition, the algorithm was iterative and required a calibration period that would not allow immediate projection of costs. For these reasons, the experiment and reserving method described in this paper will emphasize the use of empirical M(t) data instead of asset mortality data; it will also attempt to eliminate actuarial judgment entirely.
Although M(t) data are typically not recorded, they can be analyzed using existing engineering data and economic analysis of replacement technologies. Such data are cross-sectional in time and therefore do not require historical records, which were never established in the first place. We can also work with relatively sparse amounts of M(t) data to completely characterize an asset class.
2. Simulation experiment
Wendling (2014) inductively arrived at the principles that form the hypotheses of this experiment—that is, (1) there is only one instant in time when an asset must be replaced in order to optimize the present-value cost impact to the enterprise, (2) this instant can be observed at a threshold value of M(t) at which to execute the replacement, and (3) the present-value cost impact of the timing of this action is significant.
The method of this simulation experiment will be not only to prove these hypotheses but also to understand what would happen if we randomly sampled M(t) in the real world using a small, realistically obtainable set (n = 10) of M(t) measurements within a homogeneous group of like assets—for example, similar vehicles or comparable wind turbine components, such as blades, nacelles, or generators—and then applied statistical learning techniques to extrapolate mortality characteristics for a class of assets and reserves for long-term service contracts covering these assets. We want to know what kind of modeling fidelity can be attained using a very limited amount of data.
At the start of the experiment, we will simulate reality with an M(t) time series to calculate “true” values of interest; we will then learn from a small sampling of that reality to calculate the analogous modeled values. At the end of the experiment, we will compare the “true” results against the modeled results.
The code used to test our hypotheses, provided in Appendix 2, is divided into subroutines labeled modules A through J for easy reference. The code was written using RStudio. Proponents of efficient code may be dismayed that many of the subroutines have repeated lines, including loops that create the time series projections of M(t). Many of these modules could have been combined to create an abbreviated, elegant program that runs faster, but then the functioning of the code would have become opaque, because the density of assumptions would have undermined the pedagogic clarity we are trying to achieve. The main goal in writing this code was transparency of the underlying computations to someone reading it, not speed or minimizing the number of lines. For this reason, we have spaciously spread out the program and provided ample comments to explain what is happening.
2.1. Simulating “true” M(t)
Module A generates a time series of “true” costs, such as shown in Figure 2.1. The plot in Figure 2.1, which is the foundation of the experiment, consists of generating projections of stochastically rising M(t) costs for an asset, which are occasionally interrupted when M(t) crosses some predetermined threshold that triggers the replacement of an asset. When a replacement occurs, a replacement cost of $10,000 is added to the time series. Once a replacement takes place, M(t) begins again at zero and increases stochastically until the threshold is exceeded once again, resulting in the next replacement, and so forth. A typical time series thus generated looks like what is shown in Figure 2.1. This simulation will test hundreds of trials at different replacement thresholds. The horizon of 100 years is sufficiently long so that the present value of the most distant costs will gradually converge to zero. There is no escalation of costs over time, since a real discount rate will be used in the subsequent present-value calculation. The real discount rate also incorporates the chance that ownership of the infrastructure asset will possibly end at some point in the distant future. We will incorporate shorter contract terms of 50 years or less later when calculating contract reserves.
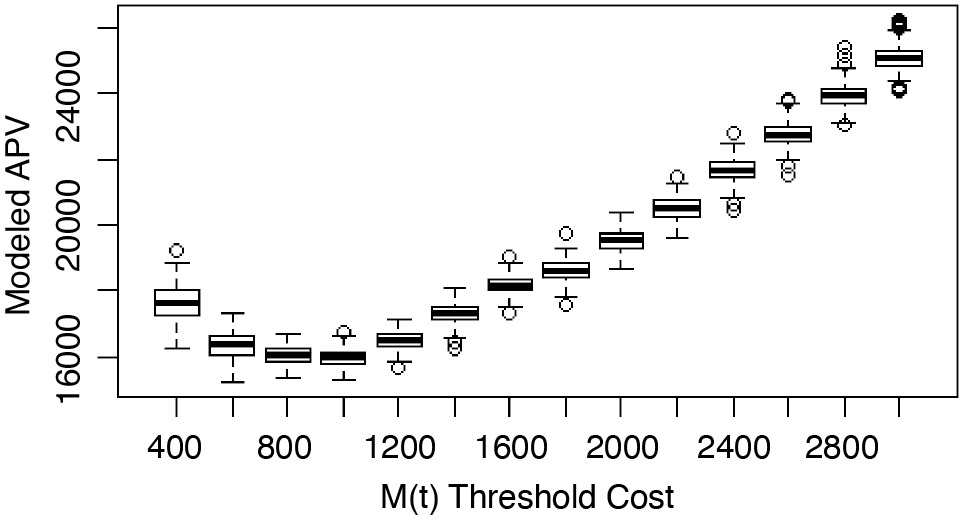
The code then calculates the present value of each time series generated in Figure 2.1 and performs this calculation N.Sim = 200 times at each of multiple thresholds of M(t) to generate the box plot shown in Figure 2.2. The data points in Figure 2.2 are the present values of hundreds of random trials of the time series of the kind shown in Figure 2.1 at various threshold values of M(t). The median bars in Figure 2.2 are close proxies for the expected values of the present values—the actuarial present values (APVs)—of all future costs for a specific threshold replacement cost, which happens to be minimized at M(t) = $1,000 in Figure 2.2.
These data points are all generated using a single real discount rate (3.1%), which is derived in Appendix 1 using the example of a large power utility company. The shape in Figure 2.2 is very common for typical discount rates and demonstrates that there is indeed an optimum threshold to replace an asset if it is part of a fleet or portfolio of similar assets. Figure 2.2 also shows how deviating too low from the optimum threshold is less forgiving than erring with too high a threshold. This plot reveals a kind of optimization problem in which the selection of the optimum replacement threshold of M(t) can create important valuation differences in the APV of all future costs associated with an asset and its future replacements.
Figure 2.2 was generated by module A for a range of threshold costs ranging from $200 to $3,000 in increments of $200 for an asset with a replacement value of $10,000. This calculation was done N.Sim = 200 times at each threshold tested; it was then plotted in box plot form. The 200 samples allow extraction of a statistically significant mean value of M(t) threshold, which illustrates why this is a portfolio capital management approach. If N.Sim = 1, then the noise of the process would make it impossible to recognize the optimum mean in Figure 2.2, and the optimum threshold would not be statistically significant to the manager making a decision to replace only one asset isolated from the whole fleet.
Figure 2.2 is a plot of the “true” APV, since we are using this simulated data as the control against which the success of our experiment will be measured. In module B, we find the minimum median value of the box plot in Figure 2.2 and match it with the corresponding optimum replacement threshold. This threshold value is then recorded in an array, which will later be compared to the modeled result. Module C finds the minimized APV median value of the box plot of Figure 2.2. This value is also stored in an array that will later be compared to the modeled result.
2.2. Plotting the lifespan distribution
Since we are analyzing a mortality problem, it is appropriate to ask what kind of time to replacement (obsolescence) distribution the process in Figure 2.1 creates. Module K creates a histogram in Figure 2.3 for the M(t) process used in Figures 2.1 and 2.2, using a replacement threshold of 800 for an asset with replacement value of $10,000 (8% replacement threshold). We generated 5,000 trials in module J to produce this distribution. It is important to note that the distribution will not be the same for each threshold of M(t) used. As the threshold selected increases, the distribution will shift to the right because the time to replacement will be longer with M(t) having to reach ever higher levels before triggering a replacement decision.
The time to obsolescence histogram in Figure 2.3 underscores the life contingency nature of the problem. However, unlike human mortality, these distributions are not objectively fixed across different owners, since obsolescence is subjectively defined by factors unique to the owner of the asset. The theory suggests that determination of obsolescence is influenced by the owner’s real cost of capital; in addition, the life distribution can shift in either direction for different owners, even for otherwise identical cohorts of assets. The life distributions can also shift over time because of environmental changes simultaneously affecting the entire population of assets in a class, such as technology advances or changes in energy costs.
2.3. Sampling and fitting “true” M(t)
In module D, we randomly select n = 10 samples of the same M(t) process that was used to create the “true” plots in Figures 2.1 and 2.2. This is analogous to randomly selecting 10 like assets in the field, such as industrial blowers of a particular class, such that their ages are random. Each asset would then undergo an engineer’s analysis to quantify M(t) costs.
The data in Figure 2.4 are then fitted using a second-order polynomial in module E. This fitting process is automatic, with no constraints around the form of the polynomial as long as it is the least squares fit. Polynomial coefficients are extracted and saved for use in modeling the M(t) time series in module G.
The residuals of the polynomial fit are then fitted using a normal distribution in module F. There may be better distributions than this, as the noise about the polynomial should never result in negative values of M(t), but it is a close approximation of what we are trying to model in the simulation.
In fitting both the polynomial and the noise to the M(t) sample, we have created an automatic process based only on R’s lm function that does not use human judgment to aid selection. No goodness of fit diagnostics are evaluated or used to reject the fitted form of M(t) at any time. For this reason, the code does not always generate the ideal plots shown in this paper. Some of the outliers in the simulated data can be explained by a bad fit of the polynomial that resulted in obviously anomalous results such as inflected polynomials with negative values or concavity, which are unlikely in reality; these outliers could have been prevented if human judgment had been applied.
2.4. Generating the modeled values with the fitted M(t)
Once the sample of “true” M(t) has been fitted, the routine executed in module A is repeated again in module G to generate an analogous box plot, but this time using the modeled M(t) process.
As in modules B and C, we extract from the box plot the threshold that minimized the modeled APV in module H and the modeled minimum APV in module I. Also, as in module A, we can set N.Sim as high as we want to fit as many simulated points into each threshold box as needed to aid in selecting a statistically significant optimum threshold of M(t). It costs nothing but computer time to run these trials once the “true” M(t) has been sampled, but it does increase precision.
In module I (bis), the first correlation plot to test our modeled results against the “truth” is for only one point, as shown in Figure 2.6. Because this is only one trial, it does not give a true appreciation of potential biases or accuracy at higher discount rates. The real discount rate used in this example was 3.01%.
Figure 2.7 was generated by going through 80 iterations of modules A through I, with the real discount rate incrementing by 0.2% with each new point generated. This created a range of r = 3.01% to 19.01%. As the discount rate increased, the optimum threshold became larger and the accuracy of prediction became worse. The greater thresholds were more difficult to predict using this code only because the difference between adjacent APVs became less significant at higher discount rates and because it was harder for the code to discern the differences. A higher number of trials in the N.Sim variable in modules A and G could have helped increase precision, but this divergence took place for unrealistically high real discount rates of greater than 15%, which is much higher than what is usually expected for owners of infrastructure.
In Figure 2.7, the red line represents perfect correlation between the modeled thresholds and the “true” threshold. The data on optimized APV at these thresholds were gathered simultaneously and are compared in Figure 2.8.
What is interesting about the data in Figure 2.8 is that there does not seem to be any particular bias of the modeled results compared to the “true” results in determining both the optimum threshold and the minimized APV. This is notable given that both the “true” M(t) process and the fitted M(t) process were generated differently and were arbitrarily selected. The red line represents perfect correlation between true and modeled results. The objective of showing the two correlation plots in a side-by-side comparison, as in Figure 2.8, is to show how there is room for error in selecting the critical replacement threshold of M(t), which has little impact on the accuracy of the APV and, consequently, on the calculation of reserves, which follows the same calculation method with only slight modifications.
2.5. “True” versus modeled reserves
Once the optimum threshold of M(t) that minimizes the APV has been determined, the reserve can be calculated by generating the M(t) and replacement cost curves once again, though for the shorter terms more typical of the ISCs—say, 20 to 50 years. The latter term is typical for military utilities privatization contracts. The future cash flows, once projected this way, can be discounted using a different discount rate more appropriate for an insurance company’s reserve calculation, or they can be left undiscounted, as in the examples that follow. We use the “true” M(t) process and optimum threshold; we then repeat the same calculations for the modeled M(t) process and optimum threshold. As a reminder, the reserve we are calculating is only for a single asset of replacement value $10,000. The following plots were generated in module J.
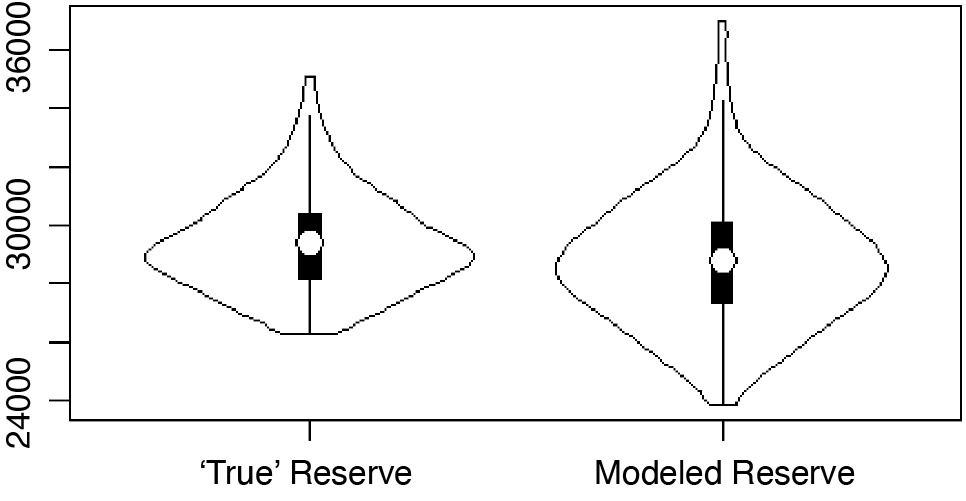
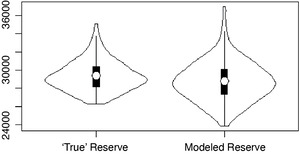
Figure 2.9 is a violin plot of “true” versus modeled reserves. A violin plot is a combination of a box plot and a rotated kernel density plot to each side of the box plot, giving an appreciation of the variability of the reserve outcomes around its mean.
The reader should be aware that Figure 2.9 is probably a better modeling result than usual. The means of the reserve violins can be expected to be in agreement only to the same extent as the APVs of Figure 2.8, which can create somewhat less-perfect-looking plots in this side-by-side comparison. Even if the means are nearly equal, the fitted result may fail to accurately duplicate the distribution of values about the mean. This is partly due to the previously mentioned lack of actuarial judgment in the automated fitting of M(t) in this experiment; it is also partly due to a distortion that happens at certain contract lengths. We use violin plots, instead of box plots, to compare reserves because an unusual phenomenon happens around shorter contract terms that are near to low multiples of the asset’s average lifespan. This phenomenon creates distortions in the distribution of outcomes, which cannot be observed in a simple box plot.
Figure 2.9 shows a reserve for a 50-year contract and a faithfully modeled reserve both in the expected value and in the description of the variability around that value. However, for the 40-year contract in Figure 2.10, which has a term close to twice the average lifespan of the asset, the distribution begins to exhibit a barbell-like behavior because the threshold value of M(t) may be attained for the second time with about an even probability. The asset will be replaced, or not, for a second time with more or less the same chance, though modeling this accurately is especially difficult. The larger white dot in the violin in Figure 2.10 represents the mean, while the smaller dot represents the median. There is considerable distortion on the predicted median as the potential outcomes “squeeze through the aperture,” and it becomes difficult to model this phenomenon accurately, as can be seen by the difference in the two shapes of Figure 2.10. The distortion on the mean is not as acute as on the median, and the median is no longer as good a proxy for the mean for reserve calculations as it was in the box plots for the APV calculations. The impact on modeled distribution of outcomes around the mean is worse than on the mean itself.
We are calling these values reserves, because we wish to embrace the financial reporting context in this hypothetical exercise. ISCs are not yet managed as insurance and do not yet require the establishment of reserves in their accounting. However, the theory suggests that obsolescence may be best treated as an insurable contingency, thus creating the need to demonstrate that such future expenditures can be accounted for as reserves under an extended service contract and that such costs are reasonably estimable.
Expected future costs should be perceived as a liability on the balance sheet, even if there is not yet a statutory requirement to report it. We will show that the magnitude of this invisible liability is significant for certain kinds of companies and can be minimized to increase the firm’s equity.
There are also elements of M(t) that would not usually be covered under a service contract (essentially, anything that is not an unscheduled repair); these elements would have to be removed from the reserve value calculation. For the sake of simplicity, however, this adjustment was not done in the code. In theory, all the constituents of M(t) plus the asset replacement could be covered under the ISC.
The mean in these violin plots is what would be recorded as a liability, and virtually all of it would be recorded as unearned premium reserve. When the asset is deemed obsolete during the term of the contract (that is, when its M(t) crosses its contractual threshold), settlement of the claim would be so rapid compared to the contract term (1 year compared to 50 years) that only a very small portion of the unearned premium reserve would become a loss reserve for any amount of time.
2.6. Magnitude of efficiency gains
The impact of obsolescence management of physical assets on firm valuation will next be demonstrated using a concrete example of a major power utility, NextEra Energy, which relies heavily on its physical infrastructure to generate revenues. The following data are taken from page 74 of the NextEra 10K statement for the fiscal year ended December 31, 2014:
From the property, plant, and equipment category at the top of the balance sheet, we know that the replacement value of NextEra’s fixed capital assets is equal to $68.042B. This is replacement value, because depreciation and amortization are listed as a separate line item. This replacement value is the company’s single largest asset category, with total assets equaling $74.929B. Total equity is $20.168B, of which nearly all is common shareholders’ equity at $19.916B. We will use the ratio of replacement value of fixed assets to shareholder equity in order to demonstrate the sensitivity of firm valuation to changes in the management of the obsolescence of physical assets. This ratio will naturally be higher for companies such as utilities, which have mostly fixed capital assets.
In Figure 2.2, we see that the APV associated with our $10,000 test asset can vary from about $14,000 to $22,000, depending on the selection from a common range of replacement thresholds of M(t). This equals 1.4 to 2.2 times the replacement value of the modeled asset, or a range equal to 2.2 – 1.4 = 0.8 times the replacement value. In reality, NextEra has dozens of different classes of assets with many different replacement values to analyze, not just the one of our simulation. For simplification, however, if we generalize this range to the entire enterprise fixed asset replacement value, the range of value at stake is 0.800 x $68.042B = $54.434B. In terms of shareholder value, the range that can be created or destroyed through portfolio obsolescence management is $54.434B/$19.916B = 2.733, or a stake approaching nearly three times the common shareholder equity.
3. Conclusion
This simulation experiment may not have provided rigorous proof of the hypotheses, since the M(t) process used in the code was arbitrary and cannot represent all the possible ways that M(t) costs might actually evolve over time in reality. Nevertheless, for this one arbitrary example, the impact of the M(t) threshold on prospectively measured valuations was found to be significant.
There is no way of knowing whether owners of infrastructure are not already achieving the optimum level of efficiency depicted in Figure 2.2 indirectly through other methods. However, as described in Wendling (2012), managers who do not take a portfolio view of physical assets and who make replacement decisions in isolation may have incentives to defer asset replacements past the optimal time indicated by the portfolio theory. They may act independently and rationally according to their own self-interest but behave contrary to the interests of the owner of the entire asset portfolio by managing the turnover of assets at some point other than at the optimum time, thus depleting the shared resources symbolized by Figure 2.2.
As was mentioned in Section 2.6, the actuary would need samples of M(t) for dozens of different asset classes grouped according to their mortality characteristics. Classification of assets would involve yet other methods and would be an additional source of modeling imprecision. Such a level of analytical work is unprecedented in the management of infrastructure asset mortality but might be well worth the effort if the valuation impacts mentioned in Section 2.6 are true and manifest themselves over time through more traditional measures of financial performance.
_and_replacement_costs_for_a_single_asset.png)

_or_time_to_obsolescence)_distribution.png)
_costs_among_a_set_of_like_assets.png)

_thresholds_and_minimized_apvs_for_*r*___3.01___*n*___10.png)
_thresholds_for_*r*___3.01__to_19.01___*n*___10__generated_throu.png)
_thresholds_and_minimized_apvs_for_*r*___3.01__to_19.01___*n*___.png)

_and_replacement_costs_for_a_single_asset.png)

_or_time_to_obsolescence)_distribution.png)
_costs_among_a_set_of_like_assets.png)
_thresholds_and_minimized_apvs_for_*r*___3.01___*n*___10.png)
_thresholds_for_*r*___3.01__to_19.01___*n*___10__generated_throu.png)
_thresholds_and_minimized_apvs_for_*r*___3.01__to_19.01___*n*___.png)