An Alternative Approach to Credibility for Large Account Pricing

undefined

1. Introduction

This paper illustrates a comprehensive approach to utilizing and credibility weighting all available information for large account pricing. The typical approach to considering the loss experience above the basic limit is to analyze the burn costs in these excess layers directly (see Clark 2011, for example). Burn costs are extremely volatile in addition to being highly right skewed, which does not perform well with linear credibility methods, such as Buhlmann-Straub or similar methods (Venter 2003). Additionally, in the traditional approach, it is difficult to calculate all of the variances and covariances between the different methods and layers, which are needed for obtaining the optimal credibilities. It also involves developing and making a selection for each layer used, which can be cumbersome.

An alternative approach is shown that uses all of the available data in a more robust and seamless manner. Credibility weighting of the account’s experience with the exposure cost^[1] for the basic limit is performed using Buhlmann-Straub credibility. Modified formulae are shown that are more suitable for this scenario. For the excess layers, the excess losses themselves are utilized to modify the severity distribution that is used to calculate the increased limit factors. This is done via a simple Bayesian credibility technique that does not require any specialized software to run. Such an approach considers all available information in the same way as analyzing burn costs, but does not suffer from the same pitfalls. Another version of the model is also shown that does not differentiate between basic layer and excess losses. Last, it is shown how the method can be improved for higher layers by leveraging Extreme Value Theory.

1.1. Research context

Clark (2011) as well as Marcus (2010) and others develop an approach for credibility weighting all of the available account information up an excess tower. The information considered is in the form of the exposure cost for each layer, the capped loss cost estimate for the chosen basic limit, and the burn costs associated with all of the layers above the basic limit up to the policy layer. Formulae are shown for calculating all of the relevant variances and covariances between the different methods and between the various layers, which are needed for calculating all of the credibilities.

This paper takes a different approach and uses the excess losses to modify the severity distribution that is used to calculate the ILF; this is another way of utilizing all of the available account information that does not suffer from the pitfalls mentioned.

1.2. Objective

The goal of this paper is to show how all available information pertaining to an account in terms of the exposure cost estimate and the loss information can be incorporated to produce an optimal estimate of the prospective cost.

1.3. Outline

Section 2 provides a review of account rating and gives a quick overview of the current approaches. Section 3 discusses credibility weightings of the basic layer loss cost, and section 4 shows strategies for credibility weighting the excess losses with the portfolio severity distribution. Section 5 shows an alternative version of this method that does not require the selection of a basic limit, and section 6 shows how Extreme Value Theory can be leveraged for the pricing of high up layers. Finally, section 7 shows simulation results to illustrate the relative benefit that can be achieved from the proposed method, even with only a small number of claims.

2. A brief overview of account rating and the current approach

When an account is priced, certain characteristics about the account may be available, such as the industry or the state of operation. This information can be used to select the best exposure loss cost for the account, which is used as the a priori estimate for the account before considering the loss experience. The exposure loss cost can come from company data by analyzing the entire portfolio of accounts, from a large, external insurance services source, such as ISO or NCCI, from public rate filing information, from publicly available or purchased relevant data, or from judgment.

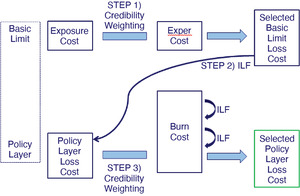
Very often, individual loss information for the account being priced is only available above a certain large loss threshold. Below this threshold, information is given in aggregate, which usually includes the sum of the total capped loss amount and the number of claims. More or less information may be available depending on the account. A basic limit is chosen, usually greater than the large loss threshold, as a relatively stable point in which to develop and analyze the account’s losses. Once this is done, if the policy is excess or if the policy limit is greater than the basic limit, an increased limit factor (ILF) is applied to the basic limit losses to produce the loss estimate for the policy layer. It is also possible to look at the account’s actual losses in the policy layer, or even below it but above the basic limit, which are known as the burn costs, as another alternative estimate. The exposure cost is the most stable, but may be less relevant to a particular account. The loss experience is more relevant, but also more volatile, depending on the size of the account. The burn costs are the most relevant, but also the most volatile. Determining the amount of credibility to assign to each estimate can be difficult. Such an approach is illustrated in Figure 1 (where “Exper Cost” stands for the Experience Cost). The exact details pertaining to how the credibilities are calculated vary by practitioner.

As an example, assume that an account is being priced, with the information available shown in Table 1. Other pricing and portfolio information are shown in Table 2.

The total loss cost for the basic layer would be calculated as $2,568.90 × 100 exposures = $256,890. The actual capped losses for the account are $900,000. Assuming that 40% credibility is given to these losses, the selected loss cost estimate for this layer is 0.4 × $900,000 + 0.6 × $256,890 = $514,136. Applying the ILF of 0.1193, the estimated policy layer losses are $61,336. The only actual loss that pierced the policy retention of $500,000 is the $1M loss, so the burn cost in the policy layer is $500,000. Assuming that 5% credibility is given to these losses, the final loss cost estimate for the account would equal 0.05 × $500,000 + 0.95 × $61,336 = $83,269.

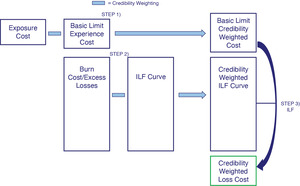
Clark (2011) developed a comprehensive approach to utilizing all of the data. For the basic limit, a selection is made based off of a credibility weighting between the exposure cost and the loss rating cost. For each excess layer, a credibility weighting is performed between the exposure cost (which is the basic layer exposure cost multiplied by the appropriate ILF), the actual loss cost in the layer (i.e., the burn cost), and the previous layer’s selection multiplied by the appropriate ILF. Formulas are shown for calculating all relevant variances and covariances, which are needed for estimating the optimal credibilities for each method in each layer, although obtaining everything required for the calculations is still difficult. For further details on this method, refer to the paper. This approach is illustrated in Figure 2.

Using the same example, Table 3 shows the calculations for Clark’s method. The assumed credibilities for each method in each layer are shown in Table 4. In reality, they would be calculated using the formulas shown in the paper. The final indication from this method is $88,913.

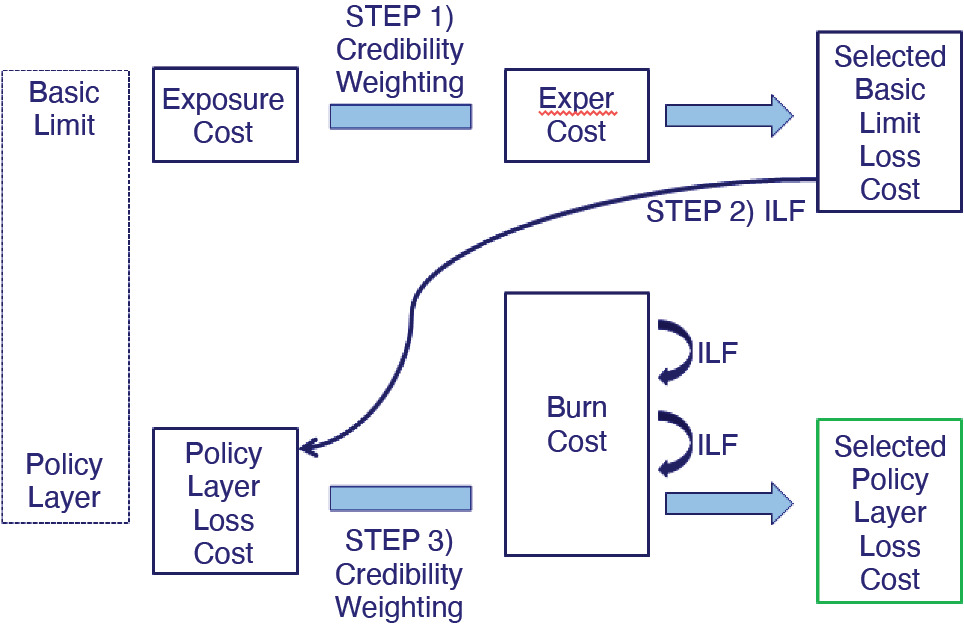
The proposed approach that will be discussed in this paper is illustrated in Figure 3. It can be seen that all of the data that is used in Clark’s approach is used here as well. The basic layer losses are credibility weighted with the exposure estimate using Buhlmann-Straub credibility (with modified formulae, as is shown in section 3). Next, the excess losses are credibility weighted together with the ILF curve to produce a credibility weighted ILF curve, as shown in section 4. A credibility weighted ILF is then produced and multiplied by the basic layer losses to produce the final policy layer loss cost selection. Further details are discussed in the remainder of the paper.

3. Credibility weighting the basic layer

3.1. Using Buhlmann-Straub credibility on the basic layer

Before illustrating the method for considering the excess losses, a quick discussion of how Buhlmann-Straub credibility can be applied to the basic layer losses is shown first. Credibility for account pricing on the basic layer losses is different from the typical credibility weighting scenario since each item being credibility weighted has a different a priori loss cost (since the exposure costs can differ based on the class, etc.), that is, the complements are not the same. This also puts each account on a different scale. A difference of $1,000 may be relatively large for one account, but not as large for another. To deal with this issue, the Buhlmann-Straub formulas can be modified to take into account the expected variance-to-mean relationship. If credibility weighting an account’s frequency, it is assumed that the variance is proportional to the mean (as in the Poisson and negative binomial families used in GLM modeling). For severity, the variance is proportional to the square of the mean (as in the gamma family), and for aggregate losses, the variance is proportional to the mean taken to some power between one and two (as in the Tweedie family, although these equations are less sensitive to the power used than in GLM modeling; a common assumption is to set this power to 1.67 (Klinker 2011)). The variance components in the formulas (that is, the sum of squared errors) can be divided by the expected value for each account taken to the appropriate power. The formulas are shown below. (These formulas would be calculated on a sample of actual accounts. For further discussion, see Korn 2017.)

$$\widehat{E P V}=\frac{\sum_{g=1}^{G} \sum_{n=1}^{N_{g}} e_{g n}\left(l_{g n}-\bar{l}_{g}\right)^{2} / \bar{L}_{g}^{p}}{\sum_{g=1}^{G}\left(N_{g}-1\right)} \tag{3.1}$$

$$\widehat{V H M}=\frac{\sum_{g=1}^{G} e_{g}\left(\bar{l}_{g}-\bar{L}_{g}\right)^{2} / \bar{L}_{g}^{p}-(G-1) \widehat{E P V}}{e-\frac{\sum_{g=1}^{G} e_{g}^{2}}{e}} \tag{3.2}$$

where EPV is the expected value of the process variance, or the “within variance,” and VHM is the variance of the hypothetical means, or the “between variance.” G is the number of segments, which in this case would be the number of accounts used, N is the number of periods, e is the number of exposures, l_gn is the loss cost (per exposure) for group g and period n, l_g is the average loss cost for group g, L_g is the expected loss cost for group g using the exposure costs,^[2] and p is the selected variance/Tweedie power. It can be seen that if the exposure loss cost L_g is the same for every account, these terms will cancel out in the resulting credibility calculations and the formulae will be identical to the original.

Once the within and between variances are calculated, the credibility assigned to an account can be calculated as normal.

$$k=\frac{\widehat{E P V}}{\widehat{V H M}} \tag{3.3}$$

$$Z=\frac{e}{e+k} \tag{3.4}$$

3.2. Accounting for trend and development in the basic layer

Accounting for trend in the basic layer losses is relatively straightforward. All losses should be trended to the prospective year before all of the calculations mentioned above. The basic limit as well as the large loss threshold are trended as well, with no changes to procedure due to credibility weighting.

To account for development, a Bornhuetter-Ferguson method should not be used since it pushes each year towards the mean and thus artificially lowers the volatility inherent in the experience. Instead, a Cape Cod-like approach^[3] can be used, which allows for a more direct analysis of the experience itself. This method compares the reported losses against the “used” exposures, which results in the chain ladder estimates for each year, but the final result is weighted by the used exposures, which accounts for the fact that more volatility is expected in the greener years (Korn 2015b). The total exposures for each group should be the sum of the used exposures across all years.

4. Credibility weighting the excess losses

4.1. Introduction

Another source of information not considered in the basic layer losses are the excess losses, that is, the losses greater than the basic limit. The normal way of utilizing this data is to calculate burn costs for some or all of the layers above the basic limit. After applying the appropriate ILF, if relevant, these values can serve as alternative loss cost estimates as well. In this type of approach, each of these excess layers needs to be developed separately, and credibility needs to be determined for each, which can be cumbersome. Calculating an appropriate credibility to assign to each layer can be difficult.

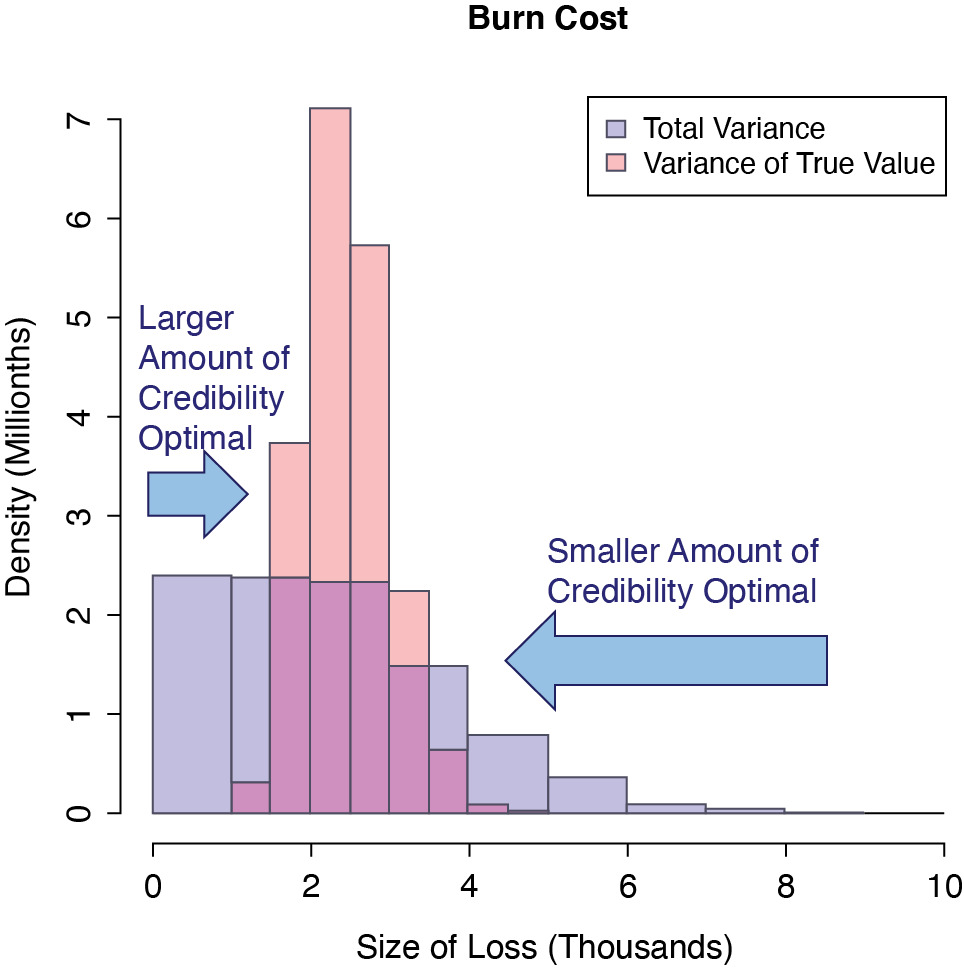
Burn costs are also right skewed, which do not perform well with linear credibility methods, as mentioned. To get a sense of why this is so, consider Figure 4, which shows the distribution of the burn cost in a higher layer (produced via simulation). The majority of the time, the burn cost is only slightly lower than the true value (the left side of the figure). A smaller portion of the time, such as when there has been a large loss, the burn cost is much greater than the true value (the right side of the figure). For cases where the burn cost is lower than the true value and not that far off, a larger amount of credibility should be assigned to the estimate on average than when it is greater than the true value and is very far off. That is why linear credibility methods that assign a single weight to an estimate do not work well in this case.

The problem with credibility weighting burn costs is illustrated.

As an alternative, instead of examining burn costs directly, the excess losses can be leveraged to modify the severity distribution that is used to calculate the increased limit factor. Such an approach is another way of utilizing the excess loss data and is more robust.

The remainder of this section discusses an implementation of this method and addresses various potential hurdles.

4.2. Method of fitting

The first question to consider is what is the best fitting method when only a small number of claims, often only in summarized form, are available. To answer this question a simulation was performed with only 25 claims and a large loss threshold of $200,000. See the following footnote for more details on the simulation.^[4] For the maximum likelihood method, the full formula shown later that utilizes the basic layer losses (Formula 5.1) was used but without the credibility component, which is discussed later. The bias and root mean square error (RMSE) was calculated by comparing the fitted limited expected values against the actual. The results are shown in Table 5.

CSP stands for conditional survival probability. The methods that utilized this sought to minimize the errors between these actual and fitted probabilities. The method labeled “CSP Binomial” sought to maximize the likelihood by comparing these actual and fitted probabilities using a binomial distribution. The method labeled “LEV Error Percent Squared” sought to minimize the squared percentage errors of the fitted and actual limited expected values. The method labeled “Counts Chi-Square” compared the number of actual and expected excess claims in each layer and sought to minimize the chi-squared statistic. It can be seen that the maximum likelihood method (“MLE”) has both the lowest bias and the lowest root mean square error. (Note that applying credibility would further reduce this bias to a minimal amount.) It is also the most theoretically sound and the best for incorporating credibility, as is explained in the following section. For all of these reasons, maximum likelihood is used as the fitting method for the remainder of this paper.

Before deriving the likelihood formula for aggregate losses, first note that instead of applying an ILF to the basic limit losses, it is also possible to simply multiply an account’s estimated ultimate claim count by the expected limited average severity calculated from the same severity distribution. The advantage of using an ILF is that it gives weight to the basic limit losses, as shown below, where N is the estimated claim count for the account and LEV(x) is the limited expected value calculated at x:

$$\begin{array}{l} \text {Capped Losses} \times \text {ILF (Policy Layer}) \\ \quad =N \times L E V_{\text {Account }}(\text {Loss Cap}) \\ \qquad \times \frac{L E V_{\text {Porfolio }}(\text {Policy Layer})}{L E V_{\text {Porfolio}}(\text {Loss Cap})} \\ \quad \left.=N \times L E V_{\text {Porffolio}} \text { (Policy Layer}\right) \\ \qquad \times \frac{L E V_{\text {Account }}(\text {Loss Cap})}{L E V_{\text {Porfolio}}(\text {Loss Cap})} \\ \end{array} \tag{4.1}$$

So applying an ILF is the same as multiplying an account’s claim count by the portfolio estimated limited expected value at the policy layer, multiplied by an experience factor equal to the ratio of the account’s actual capped severity divided by the expected. This last component gives (full) credibility to the account’s capped severity. (Because full credibility is given, in a traditional setting, it is important not to set the basic limit too high.)

If individual claim data is only available above a certain threshold, which is often the case, there are three pieces of information relevant to an account’s severity: 1) the sum of the capped losses, 2) the number of losses below the large loss threshold, and 3) the number and amounts of the losses above the threshold. If the ILF method is used, the first component is already accounted for by the very use of an ILF and including it in the credibility calculation would be double counting. Therefore, only the two latter items should be considered.^[5] The claims below the threshold are left censored (as opposed to left truncated or right censored, which actuaries are more used to), since we are aware of the presence of each claim but do not know its exact value, similar to the effect of a policy limit. Maximum likelihood estimation can handle left censoring similar to how it handles right censoring. For right censored data, the logarithm of the survival function at the censoring point is added to log-likelihood. Similarly, for a left censored point, the logarithm of the cumulative distribution function at the large loss threshold is added to the log-likelihood. This should be done for every claim below the large loss threshold and so the logarithm of the CDF at the threshold should be multiplied by the number of claims below the threshold. (If the claim count given in the submission data is deemed to be unreliable, a similar formula that uses left truncation can be used instead.) Expressed algebraically, the formula for the log-likelihood is

$$\sum_{x=\text {Claims }>L L T} \log (P D F(x))+n \times \log (C D F(L L T)), \tag{4.2}$$

where LLT is the large loss threshold, PDF is the probability density function, CDF is the cumulative density function, and n is the number of claims below the large loss threshold. The number of claims used in this calculation should be on a loss-only basis and claims with only legal payments should be excluded from the claim counts, unless legal payments are included in the limit and are accounted for in the ILF distribution. If this claim count cannot be obtained directly, factors to estimate the loss-only claim count will need to be derived for each age.

4.3. Method of credibility weighting

Bayesian credibility will be used to incorporate an account’s severity information. This method performs credibility on each of the distribution parameters simultaneously while fitting the distribution and so is optimal to another approach that may attempt to credibility weight already fitted parameters. It is also able to handle right skewed data.

This method can be implemented without the use of specialized software. The distribution of maximum likelihood parameters is assumed to be approximately normally distributed. A normally distributed prior distribution will be used (which is the complement of credibility, in Bayesian terms), which is the common assumption. This is a conjugate prior and the resulting posterior distribution (the credibility weighted result, in Bayesian terms) is normally distributed as well. Maximum likelihood estimation (MLE) returns the mode of the distribution, which will also return the mean in the case, since the mode equals the mean for a normal distribution. So, this simple Bayesian credibility model can be solved using just MLE (Korn 2015a). It can also be confirmed that the resulting parameter values are almost identical whether MLE or specialized software is used.

To recap, the formula for Bayesian credibility is f(Posterior) ∼ f(Likelihood) × f(Prior), or f(Parameters | Data) ∼ f(Data | Parameters) × f(Parameters). When using regular MLE, only the first component, the likelihood, is used. Bayesian credibility adds the second component, the prior distribution of the parameters, which is what performs the credibility weighting with the portfolio parameters. The prior used for each parameter will be a normal distribution with a mean of the portfolio parameter. The equivalent of the within variances needed for the credibility calculation to take place are implied automatically based on the shape of the likelihood function and do not need to be calculated, but the between variances do, which is discussed in section 4.4. This prior log-likelihood should be added to the regular log-likelihood. The final log-likelihood formula for a two-parameter distribution that incorporates credibility is as follows:

$$\begin{array}{c} \sum_{x=C l a i m s>L L T} \log (\text {PDF }(x, p 1, p 2)) \\ +n \times \log (C D F(L L T, p 1, p 2)) \\ +\log (\operatorname{Norm}(p 1, \text {Portfolio } p 1, \text {Between Var } 1)) \\ +\log (\text {Norm }(p 2, \text { Portfolio } 22, \text {Between Var } 2)), \end{array} \tag{4.3}$$

where PDF(x, p1, p2) is the probability density function evaluated at x and with parameters, p1 and p2; CDF(x, p1, p2) is the cumulative density function evaluated at x and with parameters, p1 and p2; and Norm(x, p, v) is the normal probability distribution function evaluated at x, with a mean of p, and a variance of v. n is the number of claims below the large loss threshold. Portfolio p1 and Portfolio p2 are the portfolio parameters for the distribution and Between Var 1 and Between Var 2 are the between variances for each of the portfolio parameters.

As an example, use the information from Tables 1 and 2 and assume that the standard deviation of the portfolio severity lognormal distribution parameters are 0.5 and 0.25 for mu and sigma, respectively, and that the selected basic limit loss cost is the same as calculated in the examples above ($514,316). The log-likelihood formula is as follows:

$$\begin{array}{c} \log (\operatorname{lognormal-pdf}(200,000, \text {mu, sigma})) \\ +\log (\operatorname{lognormal-pdf}(500,000, \text {mu}, \text { sigma})) \\ +\log (\operatorname{lognormal-pdf}(100,000, \text {mu, sigma})) \\ +7 \times \log (\operatorname{lognormal-cdf}(100,000, \text {mu, sigma})) \\ \quad+\log (\text {normal-pdf }(\text {mu}, 8,0.5)) \\ +\log (\text {normal-pdf }(\text {sigma}, 2,0.25)), \end{array} \tag{4.3a}$$

where lognormal-pdf(a, b, c) is the lognormal probability density function at a with mu and sigma parameters of b and c, respectively, and lognormal-cdf(a, b, c) is the lognormal cumulative density function at a with mu and sigma parameters of b and c, respectively. A maximization routine would be run on this function to determine the optimal values of mu and sigma. Doing so produces the values 8.54 for mu and 2.22 for sigma, indicating that this account has a more severe severity distribution than the average. Using these parameters, the revised, credibility weighted ILF from the basic layer to the policy layer is 0.3183, which produces a final loss cost estimate of $163,660.

Taking a look at the robustness of the various methods, assume that the one million dollar loss in the example was $500,000 instead. Recalculating the loss cost for the first method shown produces a revised estimate of $58,269, which is 43% lower than the original estimate. Doing the same for Clark’s method produces a revised estimate of $63,913, which is 39% lower than the original. In practice, the actual change will depend on the number of losses as well as the credibilities assigned to the different layers. Clark’s method should also be more robust than the traditional, as it uses the losses in all of the layers and so would be less dependant on any single layer. But this still illustrates the danger of looking at burn costs directly. In contrast, making this same change with the proposed approach produces a loss cost of $153,361, which is only 7% lower than the original. (Increasing the credibility given to the losses by changing the prior standard deviations of the mu and sigma parameters to 1 and 0.5, respectively, increases this number to 10%, still very low.) Even though the burn cost in the policy layer changes dramatically, the proposed method that looks at the entire severity profile of the account across all excess layers simultaneously does not have the same drastic change.

The robustness of the various methods are compared by changing the amount of one of the losses from one million to 500 thousand.

4.4. Accounting for trend and development in the excess losses

Both the losses and the large loss threshold should be trended to the prospective year before performing any of the above calculations. Using Formula 4.3, it is possible to account for different years of data with different large loss thresholds by including the parts from different years separately. Or alternatively, all years can be grouped together and the highest large loss threshold can be used.

There is a tendency for the severity of each year to increase with time since the more severe claims often take longer to settle. The claims data needs to be adjusted to reflect this. A simple approach is to apply the same amount of adjustment that was used to adjust the portfolio data to produce the final ILF distribution, whichever methods were used. With this approach, the complement of credibility used for each account should be the severity distribution before adjustment, and then the same parameter adjustments that were used at the portfolio level can be applied to these fitted parameters.

Another simple method is to assume that severity development affects all layers by the same factor. The severity development factor for each year can be calculated by dividing the (uncapped) LDF by the claim count development factor, or it can be calculated directly from severity triangles. Each claim above the large loss threshold as well as the threshold itself should then be multiplied by the appropriate factor per year before performing any of the credibility calculations mentioned. Many more methods are possible as well that will not be discussed here. (See McNulty 2017 and section 3.3 of Korn 2016, for example.)

4.5. Calculating the between variance of the parameters

Calculation of the variances used for the prior distributions can be difficult. The Buhlmann-Straub formulae do not work well with interrelated values such as distribution parameters. MLE cannot be used either as the distributions of the between variances are usually not symmetric and so the mode that MLE returns is usually incorrect and is often at zero. A Bayesian model utilizing specialized software can be built if there is sufficient expertise. Another technique is to use a method similar to ridge regression which estimates the between variances using cross validation.

This method is relatively straightforward to explain and is quite powerful as well.^[6] Possible candidate values for the between variance parameters are tested and are used to fit the severity distribution for each risk on a fraction of the data, and then the remainder of the data is used to evaluate the resulting fitted distributions. The between variance parameters with the highest out-of-sample total likelihood is chosen. The calculation of the likelihood on the test data should not include the prior/credibility component. The fitting and testing for each set of parameters should be run multiple times until stability is reached, which can be verified by graphing the results. The same training and testing samples should be used for each set of parameters, as this greatly adds to the stability of this approach. Simulation tests using this method (with two thirds of the data used to fit and the remaining one third to test) on a variety of different distributions are able to reproduce the actual between variances on average, which shows that the method is working as expected. K-fold cross validation can be used as well, but will not be discussed here.

4.6. Distributions with more than two parameters

If the portfolio distribution has more than two (or perhaps three) parameters, it may be difficult to apply Bayesian credibility in this fashion. The method can still be performed as long as two “adjustment parameters” can be added that adjust the original parameters of the severity distribution. For a mixed distribution, such as a mixed exponential or a mixed lognormal, one approach is to have the first adjustment parameter apply a scale adjustment, that is, to modify all claims by the same factor. The second adjustment parameter can be used to shift the weights forwards and backwards, which will affect the tail of the distribution if the individual distributions are arranged in order of their scale parameter. (To explain the scale adjustment, most distributions have what is known as a scale parameter, which can be used to adjust all claims by the same factor. For the exponential distribution, the theta parameter is a scale parameter, and so multiplying this parameter by 1.1, for example, will increase all claim values by 10%. For the lognormal distribution, the mu parameter is a log-scale parameter, and so to increase all claims by 10%, for example, the logarithm of 1.1 would be added to this parameter.) For a mixed distribution, the scale parameter of each of the individual distributions should be adjusted.

One way to implement this is as follows, using the mixed exponential distribution as the example:

$$\theta_{i}=\theta_{i} \times \exp (A d j 1) \tag{4.4}$$

$$R_{i}=W_{i} \times \exp (i \times \operatorname{Adj} 2) \tag{4.5}$$

$$W_{i}=R_{i} / \sum R \tag{4.6}$$

where Adj1 and Adj2 are the two adjustment parameters, i represents each individual distribution within the mixed exponential ordered by the theta parameters, R is a temporary variable, and W are the weights for the mixed distribution. Adjustment parameters of zero will cause no change, positive adjustment parameters will increase the severity, and negative adjustment parameters will decrease the severity.

4.7. Separate primary and excess distributions

Sometimes a separate severity distribution is used for the lower and upper layers and they are then joined together in some fashion to calculate all relevant values. One way to join the distributions is to use the survival function of the upper distribution to calculate all values conditional on the switching point (that is, the point at which the first distribution ends and the second one begins), and then use the survival function of the lower distribution to convert the value to be unconditional again from ground up. The formulae for the survival function and for the LEV for values in the upper layer, assuming a switching point of p are as follows:

$$S(x)=S_{U}(x) / S_{U}(p) \times S_{L}(p) \tag{4.7}$$

$$\begin{aligned} \operatorname{LEV}(x)= & {\left[L E V_{U}(x)-L E V_{U}(p)\right] / } \\ & S_{U}(p) \times S_{L}(p)+L E V_{L}(p) \end{aligned} \tag{4.8}$$

where U indicates using the upper layer severity distribution and L indicates using the lower layer severity distribution. More than two distributions can be joined together in the same fashion as well.

Using this approach, both the lower and upper layer severity distributions can be adjusted if there is enough credible experience in each of the layers to make the task worthwhile. When adjusting the lower distribution, values should be capped at the switching point (and the survival function of the switching point should be used in the likelihood formula for claims greater than this point). When adjusting the upper distribution, only claim values above the switching point can be used and so the data should be considered to be left truncated at this point. Even if no or few claims pierce this point, modifying the lower layer severity distribution still affects the calculated ILF and LEV values in the upper layer since the upper layer sits on top of the lower one.

4.8. When maximum likelihood cannot be used

Depending on the environment a pricing system is implemented in, an optimization routine required to determine the maximum likelihood may be difficult to find. An alternative is to calculate the log-likelihood for all possible parameter values around the expected using some small increment value, and then to select the parameters with the maximum value.

5. An alternative version without a basic limit

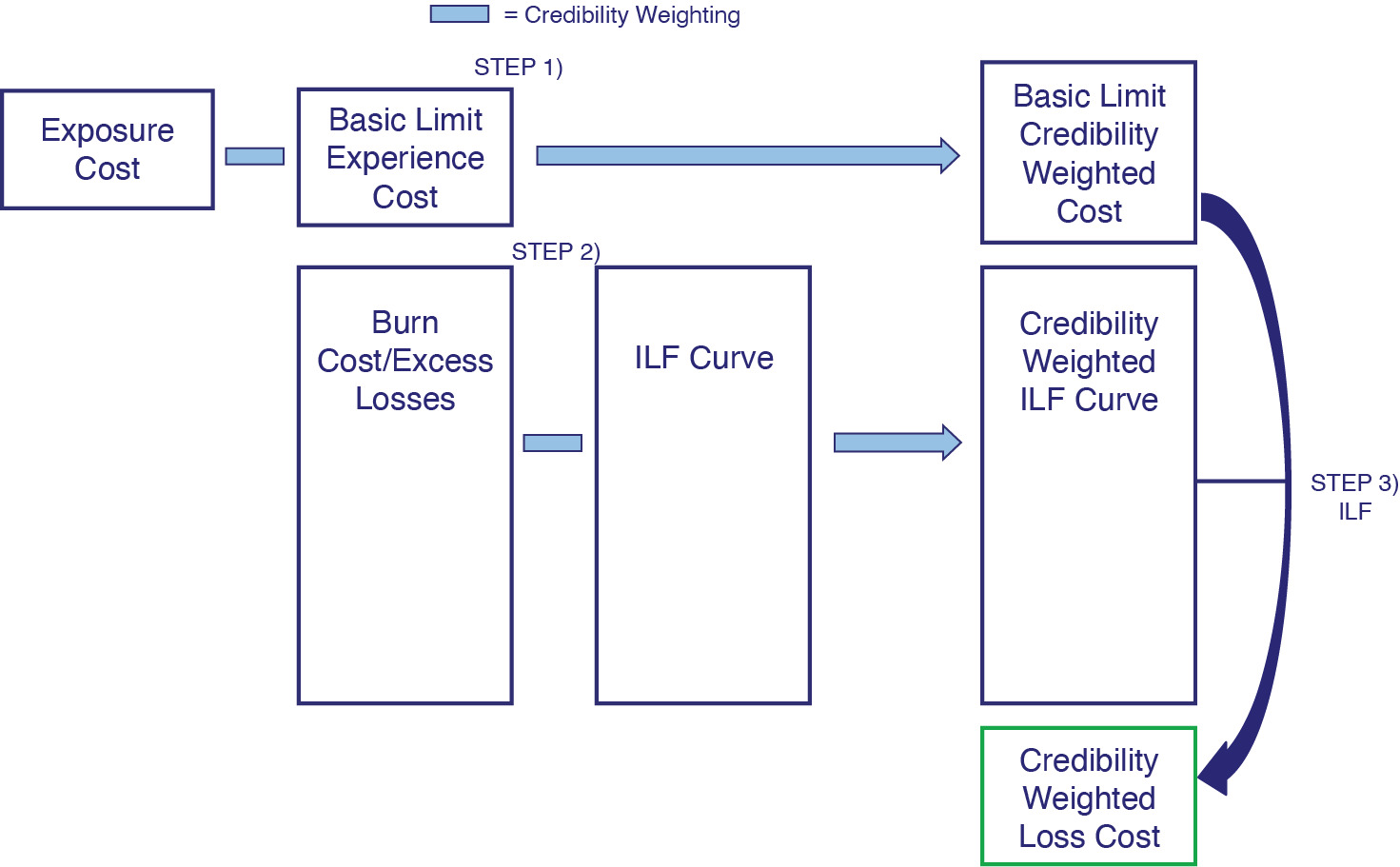
Using the approach mentioned thus far, the basic limit losses are credibility weighted using the Buhlmann-Straub method and the excess losses are credibility weighted using Bayesian credibility. It is possible to simplify this procedure and incorporate both the basic limit severity as well as the excess severity in the same step. This can be accomplished by adding the average capped severity to the likelihood formula used to fit and credibility weight the severity curve. Once this is done, there is no need to use ILFs, since the basic layer severity is already accounted for, as explained in section 4.2. Instead the expected average severity of the policy layer can be calculated from the (credibility weighted) severity curve directly, and this amount can be multiplied by the (also credibility weighted) frequency to produce the final loss cost estimate. This approach is illustrated in Figure 5.

Utilizing central limit theorem, it can be assumed that the average capped severity is approximately normally distributed. (Performing simulations with a small number of claims and a Box-Cox test justifies this assumption as well.) For a very small number of claims, it is possible to use a gamma distribution instead, although in simulation tests this does not seem to provide any benefit. The expected mean and variance of this normal or gamma distribution can be calculated with the MLE parameters using the limited first and second moment functions of the appropriate distribution. The variance should be divided by the actual claim count to produce the variance of the average severity. For a normal distribution, these parameters can be plugged in directly; for a gamma distribution, they can be used to solve for the two parameters of this distribution. The likelihood formula for this approach, including the credibility component, is as follows:

$$\begin{array}{c} \sum_{x=\text { Claims }>L L T} \log (\text { PDF }(x, p 1, p 2)) \\ +n \times \log (C D F(L L T, p 1, p 2)) \\ +\log \left(\text { Norm }\left(\text { Average Capped Severity, }, \sigma^{2}\right)\right) \\ +\log (\text { Norm }(p 1, \text { Portfolio } p 1, \text { Between Var } 1)) \\ +\log (\text { Norm }(p 2, \text { Portfolio } p 2, \text { Between Var } 2)) \end{array} \tag{5.1}$$

where µ and σ² are calculated as:

$$\begin{array}{c} =L E V(\text {Basic Limit, } p 1 p 2) \\ \sigma^{2}=\begin{array}{c} \text { LEV2 }(\text {Basic Limit }, p 1, p 2) \\ -L E V(\text {Basic Limit, } p 1, p 2)^{2} \end{array} / m \text {. } \end{array} \tag{5.1a}$$

Average Capped Severity is the average severity at the basic limit calculated from the account’s losses, n is the number of claims below the large loss threshold, m is the total number of claims, and LEV2 is the second moment of the limited expected value. As above, PDF, CDF, and Norm are the probability distribution function, cumulative distribution function, and the normal probability density function respectively.

Using the same pricing data shown in Tables 1 and 2, the log-likelihood formula is:

$$\begin{array}{l} \mu=\text { lognormal-lev }(100,000, \mathrm{mu}, \text { sigma}) \\ \sigma^{2}=\left[\begin{array}{c} \operatorname{lognormal}-\operatorname{lev} 2(100,000, \mathrm{mu}, \text { sigma})\\ -\log \text { normal-lev }(100,000, \mathrm{mu}, \text { sigma})^{2} \end{array} \right] / 10 \\ \text {log-likelihood }= \\ \quad \log (\operatorname{lognormal-pdf}(200,000, \text { mu, sigma})) \\ \quad +\log (\log \text { normal-pdf }(500,000, \text { mu, sigma}) \text { ) } \\ \quad + \log (\log \text { normal-pdf }(1,000,000, \text { mu, sigma})) \\ \quad +\ 7 \times \log (\operatorname{lognormal-cdf}(100,000, \mathrm{mu}, \text { sigma})) \\ \quad +\log \left(\text {normal-pdf }\left(90,000, \mu, \sigma^{2}\right)\right) \\ \quad +\log (\text {normal-pdf }(\mathrm{mu}, 8,0.5)) \\ \quad +\log (\text {normal-pdf }(\text {sigma, } 2,0.25)) \text {. } \\ \end{array} \tag{5.1b}$$

Where everything is as mentioned above, lognormal-lev(a, b, c) is the lognormal limited expected value and lognormal-lev2(a, b, c) is the second moment of the lognormal limited expected value at a with mu and sigma parameters of b and c, respectively.

Maximizing the log-likelihood of this formula results in mu and sigma parameters of 9.84 and 2.26, which produces an estimated average severity for the $500,000 xs $500,000 policy layer of $26,413. The number of actual losses was 10 while the exposure estimate is 20. Giving 50% credibility to the experience yields an estimated frequency of 15. Multiplying frequency by severity yields a final loss cost estimate for the policy layer of 15 × $26,413 = $396,192.

Looking at the robustness of this approach, changing the one million dollar loss in the example to $500,000, as was done previously (in section 4.3), produces a revised estimate of $385,339, which is only 3% lower than the original estimate. (Increasing the credibility given to the losses by changing the prior standard deviations of the mu and sigma parameters to 1 and 0.5, respectively, increases this number to 10%, still very low.) This shows that this method is robust to changes in the value of a single loss.

6. Using extreme value theory for high up layers

A common question that comes up when pricing higher layers is the relevance of smaller claims to the loss potential of the higher up layers, since, quite often, completely different types of loss may be occurring in each, having completely different drivers. A large account may have an abundance of tiny claims, for example, making the basic limit loss cost very large. But this may have no bearing on the possible occurrence of a large loss. An alternative approach for high up layers is illustrated in this section where only losses above a certain threshold are used. Judgement is needed for deciding how high up a layer should be to warrant the use of this method.

Such a method requires a framework for determining which claims to include, as well as a technique for extrapolating an account’s severity potential, since extrapolating with most distributions is not recommended.^[7] Exteme Value Theory provides both and will be illustrated.

Using the Peak Over Threshold version of Extreme Value Theory, a Generalized Pareto Distribution (GPD) is used to fit the severity distribution using only losses above a chosen threshold. A GPD contains a threshold parameter for the minimum value to include and two other parameters that are fit via maximum likelihood estimation. (See McNeil 1997 for application to estimating loss severity.) Unlike other distributions, it is acceptable to extrapolate this curve when fit in this manner. (Note that a single parameter Pareto is a subset of a GPD and so can be extrapolated as well.) According to the theory, a GPD will be a better fit to data that is further into the tail, and so a higher threshold is expected to provide a better theoretical fit. But there is a tradeoff, since selecting a higher threshold causes less data to be available, which will increase the prediction variance. Looking at graphs of fitted versus empirical severity is the typical way to analyze this trade off and to select a threshold, although other methods are available. (See Scarrott and MacDonald 2012 for an overview.) These techniques can be used for deciding which losses to include for account rating. As a practical test, looking at a bunch of actual accounts in different commercial lines of business, the GPD provides a good fit to accounts’ losses above a selected threshold, even where the GPD may not be the ideal loss distribution for the portfolio at that point.

To fit a GPD, the likelihood formulas shown above do not need to be used, since only losses above the large loss threshold will be included, and so the likelihood function is simply the probability density function. Setting the threshold parameter of the GPD automatically takes the left truncation of the included data into account, and the fitted distribution will be conditional on having a claim of at least that threshold. Multiplying the calculated severity at the policy layer obtained from the fitted GPD (which is the severity conditional of having a loss of at least the threshold) by the expected (credibility weighted) excess frequency at the threshold yields the final loss cost.

However, implementing this method with credibility weighting would be tricky since the portfolio severity distribution may not be a GPD. And even if it is, it becomes difficult to compare GPDs fitted at different threshold values.^[8] A trick is shown here to allow for any type of distribution to be used for the portfolio.

Recall that Bayes’ formula is being used for credibility: f(Parameters | Data) = f(Data | Parameters) × f(Parameters). Credibility is performed by calculating the prior likelihood on the parameters. It is also possible to reparameterize the distribution and use other new parameters instead. In this case, the logarithm of the instantaneous hazards (that is, f(x)/s(x)) will be used for the new parameters at different points, the same number as the number of parameters in the portfolio distribution. These were chosen since they are approximately normally distributed, work well in practice, and are also not dependent on the selected threshold as they are conditional values. If the values of these instantaneous hazard functions are known, it is possible to solve for the parameters of the original distribution since there are the same number of unknowns as equations. And once the original distribution parameters are known, they can then be used to calculate any required value from the distribution, such as PDF and CDF values. This being the case, the instantaneous hazard values can be thought of as the new parameters of the distribution, and the prior likelihood can be calculated on these new parameters instead. To simplify this procedure, instead of actually solving for the original parameters, we can effectively “pretend” that they were solved for. Now, the original parameters can still be used as the input to the maximum likelihood routine but the prior likelihood can be calculated on the logarithm of the instantaneous hazard values, since the results will be exactly the same. In practice, it is suggested to use the differences in the hazard values for each addition parameter since it makes the parameters less correlated and seems to work better in simulation tests. In summary, the likelihood equation is as follows, assuming a two parameter distribution:

$$\begin{array}{c} p 1=\log \left(f\left(t_{1}\right) / s\left(t_{1}\right)\right) \\ p 2=\log \left(f\left(t_{1}\right) / s\left(t_{1}\right)-f(t 2) / s\left(t_{2}\right)\right) \\ \log l i k=\sum_{i} \log \left(G D P\left(x_{i}, \alpha, \beta, \text { threshold}\right)\right) \\ \quad \qquad +\log (\operatorname{Norm}(p 1, h 1, v 1))+\log (\operatorname{Norm}(p 2, h 2, v 2)) \end{array} \tag{6.1}$$

where GPD is the PDF of the GPD distribution, Norm is the normal PDF, t1 and t2 are the two points chosen to calculate the instantaneous hazards at, x are the claim values, α and β are the fitted GPD parameters, threshold is the selected threshold, h1 and h2 are the credibility complements for the logarithm of the hazard functions, which can be calculated from the portfolio severity distribution, and v1 and v2 are the between variances of these values.

Simulations were conducted using this method. A lognormal distribution^[9] was used to simulate values instead of a GPD so as to test the robustness of this method. The results are shown in Table 6.

7. Simulation

A simulation was conducted to help demonstrate the benefit the method presented in this paper can provide even with only a small number of claims. The results are shown in Tables 7 through 11. Results of using aggregate claim data with the likelihood formulae discussed in this paper as well as using the individual claim data were both calculated for comparison purposes. Both versions of the aggregate likelihood method, the ILF approach with the basic limit and the frequency/severity approach, were used. The errors were calculated on the total estimated losses for the policy layer. Tables 7 through 9 show the results of using a lognormal severity distribution: the first shows a lower excess layer, the second shows a higher excess layer, and the last shows a primary layer with a self insured retention. Table 10 shows the results for a mixed exponential and Table 11 shows the results for a mixed lognormal. (Simulations were also conducted with gamma and Pareto distributions as well with similar results, but are not shown here for the sake of brevity.) Refer to the following footnote for more details on how the simulation was conducted.^[10] All simulations used only 25 ground up claims.

As the results show, this method is able to provide substantial benefit over the basic approach of applying an ILF to the capped loss estimate, even with only a small number of claims. The biases are very low as well.^[11] For the lognormal distributions, the sigma parameter was multiplied by n/(n – 1), where n is the claim count, which is a well-known adjustment for reducing the MLE bias of the normal and lognormal distributions.^[12] (The biases are slightly larger for the higher excess accounts, but are within an acceptable range for these layers, given the high estimation volatility.) (To further reduce the bias, it is possible to conduct a simulation to estimate the approximate bias factor and then divide out this bias factor from each account’s loss cost estimate, although this should not be necessary most of the time.)

As expected, the LEV method (with the aggregate losses) is able to perform better than the ILF method (without the aggregate losses), since it also takes into account the credibility of the basic limit losses. Also, the LEV method performs best when taking into account the basic limit losses, since more information is being included. The ILF method performs better when this is not included, since this information is already captured from applying an ILF, and including it in the likelihood double counts this piece of information. However, the difference is not dramatic.

8. Discussion and conclusion

An alternative technique of looking at an account’s loss information was shown in this paper where, instead of looking at burn costs in a specific layer directly, the information is used to modify the severity curve instead. Three versions were shown. The first still followed the traditional structure of dividing up basic layer losses from the excess layers. The second was a frequency-severity approach that treated all severity information the same. The third approach was also frequency-severity based but only used the excess frequency and severity information and utilized Extreme Value Theory to extrapolate the severity curve to high up layers.

All of the methods discussed are more theoretical in nature than the existing techniques in that they take an indirect approach to measuring an account’s severity potential. This may make the results more difficult to interpret and explain than the traditional methods. Also, one of the main problems pointed out with the traditional methods was their use of burn costs with volatile data. In scenarios having more data with less volatility or skewness, this becomes less of an issue. Also, the ease of implementing each approach will depend on the specific expertise of the practitioner as well as what information and data are available. Deciding on the best method for a given situation should take all of these factors into account.

---

1. Throughout this paper, the following definitions will be used:

   Exposure cost: Pricing of an account based off of the insured characteristics and size using predetermined rates

   Experience cost: Pricing of an account based off of the insured’s actual losses. An increased limits factor is then usually applied to this loss pick to make the estimate relevant for a higher limit or layer.

   Burn cost: Pricing of an excess account based off of the insured’s actual losses in a non-ground up layer.

2. If the exposure frequency used comes from an external source, it can be seen that any overall error between it and the actual loss experience will increase the between variance and will thus raise the credibility given to the losses, which is reasonable. If this is not desired, the actual average frequency from the internal experience can be used instead in the formulae even if it is not used during the actual pricing.

3. For those unfamiliar with this method, the “used” premium is first calculated by dividing the premium by the LDF for each year. Dividing the reported (or paid) losses by the used premium in each year would produce results equivalent to the chain ladder method. Dividing the total reported losses by the total used premium across all years produces an average of these chain ladder loss ratios that gives less weight to the more recent, greener years.

4. A lognormal was simulated with mean mu and sigma parameters of 11 and 2.5, respectively. The standard deviation of the parameters was 10% of the mean values. The policy attachment point and limit was both 10 million.

5. Note that even though there may be some slight correlation between the sum of the capped losses and the number of claims that do not exceed the cap, as mention by Clark (2011), these are still different pieces of information and need to be accounted for separately.

6. One advantage of this approach over using a Bayesian model is that this method works well even with only two or three groups, whereas a Bayesian model tends to overestimate the prior variances in these cases. Though not relevant to this topic, as many accounts should be available to calculate the between variances, this is still a very useful method in general for building portfolio ILF distributions.

7. Note that this is less of an issue when credibility weighting with the portfolio severity curve, assuming that this curve has losses near the layer being priced. However, it would be nice to better extend the severity potential of the actual account as well.

8. Theoretically, once the threshold is far enough into the tail, the alpha parameter should remain constant as the threshold increases, but this is only theoretical. In practice, it often continues to change.

9. Claims were simulated from a lognormal distribution with parameters 11 and 2.5, respectively. 1000 iterations were performed. The between standard deviation of the lognormal parameters was 1 and 0.5, respectively. This was used to calculate the between standard deviations of the transformed parameters, that is, the hazard functions. 50 claims were simulated, a threshold of 250 thousand was used, and there was an average of 14.5 claims above the threshold.

10. For the lognormal distribution, mean mu and sigma parameters of 11 and 2.5 were used, respectively. The standard deviation as well as the prior standard deviation assumed was 10% of the mean parameter values. The large loss threshold was 200 thousand, which translated to an average of 8.1 claims above the threshold. For the mixed exponential, the following mean mu values were used: 2863.5, 22215.7, 89355.0, 266664.3, 1108333.2, 3731510.8, 9309907.8, 20249975.1, 51141863.9, 230000000.0 and the following weights were used: 0.378297, 0.327698, 0.19941, 0.080178, 0.012106, 0.001764, 0.000362, 0.000125, 0.000048, 0.000012. The large loss threshold was 30 thousand, which translated to an average of 8 claims above the threshold. The standard deviation of the adjustment parameters was 1 and 0.5. For the mixed lognormal, the mu parameters were 8 and 12, the sigma parameters were 2.5 and 2.7, and the weights were 75% and 25%. The large loss threshold was 25 thousand, which translated to an average of 8.7 claims above the threshold. The standard deviation of the adjustment parameters was 1 and 0.5. Simulating with certain mean parameter values and standard deviations would result in an average policy layer LEV that differed from the LEV calculated from the mean parameters, and so using these mean parameter values as the complement of credibility would cause a bias. Using prior values that result from fitting all of the data together would also not be exact, as the data from multiple draws of a certain distribution with different parameter values would not necessarily be a perfect fit to that distribution, and a bias would show up as well. Instead, the prior parameters used for credibility weighting were adjusted together so that the result from using the average LEV would be unbiased. This is only an issue for simulation and would not be an issue in practice.

11. The slight positive bias comes from the transformation involved in the LEV or ILF calculation, since even if the parameter mean value estimates are unbiased, applying a function to these estimates can create some bias, as Jensen’s inequality states. For most distributions, this bias happens to be positive. As long as the parameter errors are not too great, the bias will remain small. The credibility weighting being performed reduces the parameter errors, and as a result, the bias as well.

12. This adjustment cancels out most of the negative parameter bias. In this case, not applying this adjustment would have probably resulted in a lower overall bias.