A Model for Policy-Size and Diversification Discounts

undefined

1. Introduction

The primary function of insurance is to transfer risk from consumers, who are not well-equipped to tolerate it, to insurance corporations, which can draw upon large amounts of capital and which benefit from the uncertainty-mitigating effect of diversification. This diversification places the insurer in a unique position for bearing relatively high levels of risk. To further encourage this diversification for its book (as well as more complete buy-in from folks who may be considering insuring additional items or purchasing additional coverages), an insurer may find it advantageous to offer premium discounts for policies that present a high level of diversification in themselves.^[1] For example, even if four quarter-million-dollar homes spread over a large geographic area present roughly the same loss expectation as a single million-dollar home, the associated risk level is lower for the geographically diverse homes since it is unlikely all four would experience a total loss during a short window of time.

Perhaps the best candidate for a geographic diversification discount is a homeowners or farmowners (HO/FO) policy because buildings are relativity easy to geocode^[2] with today’s technology. In order to calculate a geographic diversification relativity for such a policy, we first must know the location and risk-free premium^[3] (or, alternatively, the limit of insurance) of each insured building. Ideally, the geocode should be at the rooftop level. If possible, latitude and longitude coordinates^[4] should be obtained for a position near the center of each building.

But how does one construct a diversification discount that is actuarially sound, given that diversification does not reduce loss expectation but only loss variation and uncertainty? If the insurer maintains an explicit premium provision for any kind of risk margin, a more diverse book of business can help reduce it. And even if there is no explicit risk margin, one can argue that a risk margin is still being carried implicitly—buried inside the target underwriting profit—because if an adverse scenario develops, the required funds will come out of surplus.

The current practice is for insurers to bake a risk margin direction into their base rates by adjusting the permissible loss ratio. This means that the company risk margin is being allocated to policyholders in proportion to their premium. It also means that every policy gets exactly the same uprate in order to fund the risk margin. This approach fails to recognize the outsized contribution of more diverse policies toward reducing the company risk margin. A better approach would be to calculate risk margins at the policy level and allocate the company risk margin to policies not by premium, but by policy risk margin. This would result in more tempered risk-loading uprates for diverse policies, and steeper ones for less diverse policies.

To illustrate this, consider a simple example. Imagine a book of business involving just three policies (A, B, and C) with an aggregate risk-free premium of $1,000—$100 from Policy A, $200 from Policy B, and $700 from Policy C. If the insurer requires a $100 risk margin, the current method would result in a 10% uprate for each policy. So $10 would come from Policy A, $20 from Policy B, and $70 from Policy C to fund the company risk margin. The proposed approach would result in a different allocation—perhaps $20 from Policy A, $30 from Policy B, and just $50 from Policy C. Instead of a 10% risk-loading uprate for everyone, this means a 20% uprate for Policy A, 15% for Policy B, and just over 7% for Policy C.

A diversification relativity can then be calculated for each policy by dividing the uprate using the new allocation method by what it would have been under the old method.^[5] In the example case, the relativities for the three policies are: 1.091 (a 9.1% surcharge^[6]) for Policy A, 1.045 (a 4.5% surcharge) for Policy B, and 0.974 (a 2.6% discount) for Policy C.

The objective of this paper is to develop the mathematical model for calculating diversification relativities like these from geocode information in an actuarially sound way. A concise summary of the approach to be developed is as follows:

1. Distance is calculated between each pair of buildings on a policy using a formula that converts two pairs of latitude/longitude coordinates into a distance. This formula is robust to curvature effects of Earth over large distances. (See Section 2.1.)

2. The correlation between loss distributions for each pair of buildings on a policy is estimated from the separation distance using a distance-correlation model we develop. (See Section 2.2.)

3. The variance of the loss distribution is estimated at the policy level as a multiple of the variance for an individual building.^[7] This multiple is given by a weighted sum of elements in the correlation matrix. (See Section 2.3.)

4. Risk margin is estimated at the policy level from the estimated variance using the upper half of a pre-selected confidence interval. In this way, it is designed to supplement risk-free premium (which is based on the expectation value) in order to protect against the most adverse results that fall within the selected confidence interval. This results in a policy risk margin that is proportional to the standard deviation of the policy loss distribution. The constant of proportionality depends on the size of confidence interval that is selected. (See Section 2.4.)

5. The diversification relativity is calculated at the policy level from the risk margin using the ratio of risk factors (or risk-loading uprates) under (1) policy-risk-margin-based allocation of the company risk margin to (2) premium-based allocation. (See Section 2.5.)

An instrumental quantity that is calculated during this process is the CV ratio, which is the ratio of the coefficient of variation for an aggregate loss distribution (like for a policy, or for the company as a whole) to that for an individual building (or insured item). This CV ratio quantifies the degree of diversification inherent in a group of insured items. By definition, the CV ratio is 1 for a single item (no diversification), and we’ll see that it approaches 0 in the limit as the number of uncorrelated items in a group grows without bound (maximum diversification).^[8]

Section 3 illustrates how one can scale the magnitudes of the diversification discounts calculated in Section 2, and Section 4 presents various alternative formulations that broaden the potential application to non-geographic types of diversification. Each formulation of the method is, by design, revenue neutral.

2. The geographic diversification model

Each of Sections 2.1 through 2.5 is dedicated to one of the five primary steps in this method. An example is developed in parallel to the theory as it is presented, and this example is revisited in each subsection.

2.1. Measuring distances

Ideally, for this technique to work as intended, latitude and longitude coordinates should be available at (or near) the rooftop level for each insured building. If geocodes are only available at a lower level of precision (like street level), then the method can still be used, but correlations estimated (in Section 2.2) between nearby buildings will also be less precise. Correlations between more distant buildings should be unaffected by anything other than major geocoding errors.

The following geometric formula converts the geocodes for two locations into a separation distance (as measured in miles along a great circle on the surface of the Earth). It assumes that Earth is a perfect sphere. Technically, this is not quite true,^[9] but our mechanism for converting distances to correlations will not be sufficiently precise as to be adversely impacted by this assumption.

$$\begin{aligned} d_{i j}= & 3,959 \\ & \times \operatorname{acos}\left[\begin{array}{c} \cos \theta_{i} \cos \theta_{j}\left(\cos \varphi_{i} \cos \varphi_{j}+\sin \varphi_{i} \sin \varphi_{j}\right) \\ +\sin \theta_{i} \sin \theta_{j} \end{array}\right] \end{aligned} \tag{2.1}$$

where the leading factor of 3,959 is the average radius of Earth (in miles), “acos” refers to the arccosine (or inverse cosine) function, and

$$\begin{array}{c}\theta=\frac{\pi}{180^{\circ}} \times \text {latitude}\\ (\text{as measured in decimal degrees}),\end{array} \tag{2.2}$$

$$\begin{array}{c} \varphi=\frac{\pi}{180^{\circ}} \times \text {longitude}\\ (\text{as measured in decimal degrees}).\end{array} \tag{2.3}$$

These formulas assume that the application performing the calculations will apply the trigonometric functions in radian mode. If degree mode is used instead, then the meridianal angle θ and the azimuthal angle φ will not need the π/180° conversion factor, but will directly equal the latitude and longitude, respectively. Instead the final output for d_ij will need to be multiplied by this conversion factor.

Example

Consider the following four historical sites: the Ulysses S. Grant Memorial outside the U.S. Capitol building, the nearby Peace Monument, the President John F. Kennedy Gravesite at Arlington National Cemetery, and the Statue of Liberty. The latitude and longitude coordinates for these sites are shown in Table 1. Using Equations (2.2) and (2.3) to convert these coordinates to radians, and plugging them into Equation (2.1) in pairs, we obtain the following matrix of distances. To give a sense of scale, the separation calculated between the first two sites translates to 361 feet.

$$\begin{array}{c} \text{Separation distance (in miles)}\\ \text{between pairs of sites in Table 1}\\ \\ \begin{gathered} \\ 1 \\ 2 \\ 3 \\ 4\end{gathered}\left(\begin{array}{cccc}1 & 2 & 3 & 4 \\ 0 & 0.0684 & 3.2009 & 200.7262 \\ 0.0684 & 0 & 3.2435 & 200.6633 \\ 3.2009 & 3.2435 & 0 & 203.5320 \\ 200.7262 & 200.6633 & 203.5320 & 0\end{array}\right)\end{array}$$

Because four digits are carried on the Earth radius used in Equation (2.1), we can expect our calculated distances to be accurate to about the fourth significant digit (assuming our geocodes are sufficiently accurate). One can corroborate these distances by right-clicking in Google maps to measure distance between pairs of points. Keep in mind that results will vary when measuring distance, depending on where exactly the user clicks.

2.2. Estimating correlations between buildings

Now that we have separation distances between each pair of buildings on a policy, we consider a couple models that express correlation (of loss distributions) as a function of distance, $\rho_{i j}=\rho\left(d_{i j}\right)$. The following assumptions underlie both distance-correlation models.

1. Two buildings separated by a great distance are effectively independent.

2. Two buildings separated by a small distance have a strong correlation.

3. As the distance between two buildings increases, the correlation between them decreases.

These assumptions imply that (d) must start at 1, and decrease asymptotically to 0 with increasing separation. The question remains: “How quickly does the correlation decrease as the distance between two buildings increases?” There likely is not a single objective answer to that question. And any answer will depend on what types of perils we’re considering. Perhaps correlation is inversely proportional to distance—or inversely proportional to the distance raised to some power.

The problem with this idea is that as d becomes very small, the correlation grows without bound. Since a correlation greater than 1 is not meaningful, this correlation model would need to be capped.

$$\begin{array}{c}\text{Power model for correlation}\\ \\ \rho(d) \stackrel{?}{=} \min \left(\kappa d^{-\alpha}, 1\right) ; \quad \kappa>0, \quad \alpha>0 \tag{2.4}\end{array}$$

An alternative for the distance-correlation function that does not require capping is a decaying exponential. As long as we don’t scale the exponential itself (but only the distance inside the exponential), it already has the appropriate values in the limits when d is large and small. We can also continue to allow the distance to be taken to some power without affecting the limiting values.

$$\begin{array}{c}\text{Exponential model for correlation}\\ \\ \rho(d) \stackrel{?}{=} \exp \left(-\kappa d^{\alpha}\right) ; \quad \kappa>0, \quad \alpha>0 \tag{2.5}\end{array}$$

In order to determine which model would be better, and to guide our selections of the corresponding κ and α parameters, we give some thought to what values of ρ would be reasonable for various distances d. Buildings separated by a few miles should probably be assigned a correlation in the vicinity of 5% since they could both be impacted by a single event (storm, wildfire, earthquake, flood, etc.), but likely only if it’s a catastrophe-type event. Even neighboring buildings are not likely to be perfectly correlated, though the correlation should be much higher—maybe something around or just above 50%—since even an isolated claim could impact both buildings. The values I selected are shown in Table 2, as well as in Figure 1, which also shows the power and exponential models that fit^[10] them best.

The plot in either panel of Figure 1 compares the results of the power model (dotted curves) and the exponential model (solid curves) with the selected correlations (crosshairs) from Table 2. The panel on the left is linear in separation distance, while the one on the right provides a logarithmic scale on the horizontal axis.

Even with correlation capped in the power model, treating two buildings as perfectly correlated probably doesn’t make much sense unless they are essentially on top of each other. The version of this model that best fits the selected points (κ = 0.16 and α = 0.30) requires capping for anything closer than 0.0022 miles (12 feet). This seems reasonable, but the exponential model does a much better job hovering close to our expectations at all distance ranges. Its best-fit parameters are κ = 1.99 and α = 0.31.

If d is expressed in units of miles, the two suggested correlation models with best-fit parameters (rounded to the second decimal place) are

$$\begin{array}{c}\text{Best-fit power model}\\ \\ \rho(d) \stackrel{?}{=} \min \left(0.16 d^{-0.30}, 1\right), \tag{2.6}\end{array}$$

$$\begin{array}{c}\text{Best-fit exponential model}\\ \\ \rho(d) \stackrel{?}{=} \exp \left(-1.99 d^{0.31}\right). \tag{2.7} \end{array}$$

It appears that the exponential model is the better of the two, at least for the values selected and shown in Table 2. (The sum of the squared residuals for this model is more than ten times smaller than for the power model, the root mean square is more than three times smaller, and the general shape of the exponential curve can be seen to follow the points much more closely, especially when distances are plotted logarithmically.) By the same token, other practitioners may come to other reasonable conclusions about what correlations would make sense at various distances for their books of business. Selecting different values for Table 2 would result in different best-fit parameters. In Appendix A, we show how to tailor the parameters for these two models to an arbitrary list of selected correlations.

Example

Returning to our four example sites, and plugging the separation distances obtained at the end of Section 2.1 into Equations (2.6) and (2.7), we find that the two models result in the following correlation matrices, rounded to the fourth decimal place.

$$\begin{array}{c} \text{Correlations between pairs of sites in Table 1}\\ \\ \text{Best-fit power model}\\ \\ \begin{gathered} \\ 1 \\ 2 \\ 3 \\ 4 \end{gathered}\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 0.3577 & 0.1129 & 0.0326 \\ 0.3577 & 1 & 0.1124 & 0.0326 \\ 0.1129 & 0.1124 & 1 & 0.0325 \\ 0.0326 & 0.0326 & 0.0325 & 1 \end{array}\right)\\ \\ \text{Best-fit exponential model}\\ \\ \begin{array}{c} \\ 1 \\ 2 \\ 3 \\ 4 \end{array}\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 0.4204 & 0.0576 & 0.0000 \\ 0.4204 & 1 & 0.0569 & 0.0000 \\ 0.0576 & 0.0569 & 1 & 0.0000 \\ 0.0000 & 0.0000 & 0.0000 & 1 \end{array}\right) \end{array}$$

For future calculations, we will stick with the correlations estimated using the exponential model.^[11]

2.3. Estimating variance at the policy level

This is the most statistically intense step in calculating a diversification relativity. The basic idea behind this section is to use the variance to explore how the coefficient of variation (CV) for a policy shrinks as exposures with varying degrees of correlation are aggregated into the policy. Policies with many buildings spread over a geographically diverse area will tend to have smaller CVs than those with fewer buildings or a more concentrated collection of buildings.

In order to account for expenses in all subsequent calculations, whenever we refer to the loss distribution, we will mean the expense-loaded loss distribution. And whenever we refer to expected losses, we will mean expected losses plus expenses. So the mean of the loss distribution will equal the expense-loaded policy premium,^[12] and not just the pure premium.

We need a formula to calculate the variance of a sum of random variables, where each random variable corresponds to the loss distribution of one specific building. This formula could be used to aggregate the loss distributions of all the buildings on a policy in order to calculate policy variance, or it could be used to aggregate the loss distributions of every building insured by the company in order to calculate company-level variance. We will need it for both applications.

It would be convenient if we could assume that the random variables are identically distributed, but in fact, they don’t even have the same expected value (since expected losses vary by building). The next-simplest assumption we can make is that each distribution has the same shape and differs from the others only by a scale factor. That scale factor is the expected loss (or premium) for the building. If each distribution has the same shape, then its mean and standard deviation will be proportional, and it will have the same CV. We’ll call this the base CV.

We can pull the scale factor by which the distributions differ outside the random variable and, instead, think of it as a weight.^[13] In that way, we’re back to a sum of identically-distributed random variables; it’s just that now we’re talking about a weighted sum.^[14]

We stand to gain more intuition into the aggregation process if we first imagine how things would be without the weights. So we’ll develop the formula we need without weights, and then show how the result is impacted by including the weights.

Let X_i be the random variable associated with the prospective loss distribution for Building i, and let P_i be its mean—the risk-free premium. Without weights, the loss distribution is identical for every building, so

$$X_{i}=X_{0} \quad \text { and } \quad P_{i}=P_{0} \text {, } \tag{2.8}$$

where the nought subscripts refer to a base exposure, such as a particular type of building insured over a policy period. Similarly, let X₊ be the random variable from the aggregate loss distribution, and let P₊ be the aggregate premium.

Of course, the aggregate premium is just the sum of individual building premiums since the mean of a sum of random variables is the sum of the means.

$$P_{+}=\mathrm{E}\left[X_{+}\right]=\mathrm{E}\left[\sum_{i=1}^{n} X_{i}\right]=\sum_{i=1}^{n} \mathrm{E}\left[X_{i}\right]=n \mathrm{E}\left[X_{0}\right]=n P_{0}, \tag{2.9}$$

where n is the number of buildings we’re aggregating over (e.g., the number of buildings on a policy, or the total number of buildings insured by the company).

The aggregate variance, on the other hand, depends on the degree of correlation between buildings. Buildings could be mutually independent, they could be perfectly correlated, or anything between those two extremes.^[15] In general, these correlations can be represented by a correlation matrix with elements $\rho_{i j}$, each somewhere between 0 and 1. We saw examples of such a correlation matrix in Section 2.2.

A little algebra shows that the aggregate variance is proportional to the sum of all the elements inside the correlation matrix, which is symmetric and has 1’s down the diagonal since each variable is, by definition, perfectly correlated with itself.

$$\begin{aligned} \sigma_{+}^{2} & =\operatorname{Var}\left[X_{+}\right]=\operatorname{Var}\left[\sum_{i=1}^{n} X_{i}\right]=\sum_{i=1}^{n} \sum_{j=1}^{n} \operatorname{Cov}\left[X_{i}, X_{j}\right] \\ & =\sum_{i=1}^{n} \sum_{j=1}^{n}\left[\operatorname{Corr}\left[X_{i}, X_{j}\right] \sqrt{\operatorname{Var}\left[X_{i}\right] \operatorname{Var}\left[X_{j}\right]}\right] \\ & =\left[\sum_{i=1}^{n} \sum_{j=1}^{n} \rho_{i j}\right] \operatorname{Var}\left[X_{0}\right]=\left[\sum_{i=1}^{n} \sum_{j=1}^{n} \rho_{i j}\right] \sigma_{0}^{2} \\ & \left.=\left[\begin{array}{ccccc} 1 & \rho_{12} & \rho_{13} & \cdots & \rho_{1 n} \\ \rho_{12} & 1 & \rho_{23} & \cdots & \rho_{2 n} \\ \rho_{13} & \rho_{23} & 1 & \cdots & \rho_{3 n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \rho_{1 n} & \rho_{2 n} & \rho_{3 n} & \cdots & 1 \end{array}\right)\right] \sigma_{0}^{2} \end{aligned} \tag{2.10}$$

This result is consistent with what we would expect to find in the two limiting cases.

1. If all the variables are mutually independent, then the correlations off the diagonal become 0 and the correlation matrix becomes the identity matrix.^[16] In this case, the correlation elements sum to n. This is consistent with the fact that the variance of a sum equals the sum of the variance when the underlying variables are independent and identically distributed.

2. If all the variables are perfectly correlated, then every element of the correlation matrix is 1, so they sum to n². This is consistent with the fact that n perfectly correlated and identically-distributed random variables are equivalent to a single random variable scaled up by a factor of n, and that results in the variance being scaled up by a factor of n².

In the general case where the correlations can vary from element to element, they could sum to any value not less than n and not more than n².

One important consequence of less-than-perfect correlation between buildings is a decrease in the aggregate coefficient of variation,

$$v=\frac{\sigma}{P} \tag{2.11}$$

and a relative narrowing of the confidence interval. This narrowing is characterized by the ratio of the aggregate CV to the CV for a base exposure.

$$\tag{2.12}$$

This “CV ratio” is never larger than 1 (perfect correlation) and never smaller than $1 / \sqrt{n}$ (mutual independence). Here is our first glimpse at the role diversification plays because a narrower confidence interval means less uncertainty—less risk.

Now, consider what happens when we incorporate weights and allow the premiums to vary by building. The random variable and premium for Building i become

$$X_{i}=R_{i} X_{0} \quad \text { and } \quad P_{i}=R_{i} P_{0} \tag{2.13}$$

where R_i = P_i/P₀ is the premium relativity-to-base for Building i.

While we don’t show the intermediate steps,^[17] the aggregate premium generalizes to

$$P_{+}=\left(\sum_{i=1}^{n} R_{i}\right) P_{0}, \tag{2.14}$$

and the aggregate variance to

$$\sigma_{+}^{2}=\left[\sum_{i=1}^{n} \sum_{j=1}^{n} R_{i} R_{j} \rho_{i j}\right] \sigma_{0}^{2} \tag{2.15}$$

Aggregate variance is now proportional to the sum of elements in the correlation matrix, each weighted by both the relativity corresponding to the matrix row and the one corresponding to the column. So the correlation between two buildings is being weighted by the premium relativity of each building.

As for the CV (and CV ratio), we can replace the newly appearing relativities with the slightly-more-intuitive premiums as weights.^[18]

$$\frac{v_{+}}{v_{0}}=\frac{\sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} P_{i} P_{j} \rho_{i j}}}{\sum_{i=1}^{n} P_{i}} \tag{02.16}$$

The upper bound for the CV ratio is still 1 (perfect correlation), and the lower bound (mutual independence) is now /(P₁ + P₂ + . . . + P_n).

Example

The variance and CV ratio for a hypothetical policy composed of buildings at the four example sites both depend on the expected losses of the individual buildings. In order to evaluate the performance of Equations (2.15) and (2.16) in various situations, we consider three scenarios with different premium weightings (shown in Table 3). First we consider the situation where each building is equally weighted, then a scenario where a single dominant building is isolated from the others, and finally one where it’s close to most of the others. While the base premium is open to arbitrary selection, the base CV is a fundamental characteristic of the loss distribution for a building, and it needs to be estimated. Let’s use a base premium of $1,000 and assume a base CV of 0.3 for our example. The reader is encouraged to reference Table 4 while reading through the example for a more clear comparison between scenarios.

Scenario 1

Before we apply the correlation matrix we found with the exponential distance-correlation model at the end of Section 2.2, it’s worth considering what the policy variance would be in each of the two special cases of mutual independence (buildings all far apart) and perfect correlation (buildings all close together).

In the first case, Equation (2.15) says we should take the sum of squared premium relativities to get the policy variance in units of the variance of a base exposure. This works out to be 4. Because the exposures are perfectly independent, their variances add. Meanwhile, the CV ratio (obtained by dividing root variance by the count of exposures) comes out to 0.5, so we know there is a moderate amount of narrowing going on.

In the second case, we square the sum of premium relativities^[19] and get 16. The higher variance means a greater degree of uncertainty in prospective losses because the individual losses all swing together. Consequently, the CV ratio is 1, and there is no narrowing.

The difference between the two extremes is large in Scenario 1 because the weights are evenly distributed. When the weights are far from being evenly distributed, diversification is hampered because large dominant weights are mathematically equivalent to multiple smaller weights that are perfectly correlated. We’ll see this effect with Scenarios 2 and 3.

The actual variance in Scenario 1, obtained by plugging the correlation matrix into Equation (2.15), is 5.0701, and the CV ratio is 0.5629. The diversification has a significant impact, even though two of the sites are only a few hundred feet apart. Because the Statue of Liberty site is effectively independent of the other three, and the Arlington Cemetery site is almost independent of the remaining two, the variance and CV ratio are only slightly higher than they would have been in the case of mutual independence.

Scenario 2

We again consider the maximum and minimum variances produced by the two special cases of independence and perfect correlation. Evidently, regardless of their geographic positioning, four buildings with the weightings shown in Scenarios 2 and 3 have a minimum variance of (3 × 0.5²) + 2.5² = 7 and a maximum variance of (3 × 0.5 + 2.5)² = 16, in units of the base variance. The minimum CV ratio is 0.6614. The maximum variance has not changed from Scenario 1, but the minimum variance has almost doubled. This is due to the nonuniform distribution of weights. It’s not possible to separate (or uncorrelate) the 2.5 units of exposure in the building with the dominant weight, no matter how far apart the four sites are.

In this case, the actual variance is 7.2677 times the base variance, and the CV ratio is 0.6740, only slightly higher than the minimum for buildings with these weightings. This is undoubtedly because the dominant exposure is isolated from the others, while those that are partially correlated are more minor exposures.

Scenario 3

The maximum and minimum variances (and CV ratios) are the same as they were under Scenario 2 because both scenarios used the same weightings (just in different orders). But now the variance obtained from the actual correlation matrix is 8.2237 times the base variance, and the CV ratio is 0.7169. These don’t sound much larger than the Scenario 2 values, but consider the fact that they’re both about four and a half times farther from the minimum values of 7 and 0.6614, respectively. The higher variance in this case is due to the fact that the dominant exposure is at one of the partially correlated sites rather than the isolated site.

2.4. Defining a risk margin

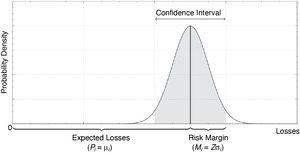
There are many ways that a risk margin can be defined. Perhaps the simplest meaningful definition is as the upper half of a confidence interval. In that way, the risk-free premium is a provision for expected losses and the risk margin serves as an additional buffer to protect against the possibility that losses turn out to be worse than expected. The extent of the protection depends on the size of the confidence interval used to define the risk margin. The critical value Z is the number of standard deviations that the confidence interval extends on either side of the distribution mean µ. The relationship between risk margin M and premium P is illustrated in Figure 2.

There are many ways that a risk margin can be defined. Perhaps the simplest meaningful definition is as the upper half of a confidence interval. In that way, the risk-free premium is a provision for expected losses and the risk margin serves as an additional buffer to protect against the possibility that losses turn out to be worse than expected.

Because of the central limit theorem (or “law of large numbers”), the loss distribution over a large number of exposures is likely to be approximately normal.^[20] The premium is a provision for expected losses, which equals the mean of the loss distribution, while the risk premium (or risk margin) is a contingent provision for losses exceeding expectations. In Figure 2, we model it as the difference between the upper bound of a confidence interval and the mean of the aggregate loss distribution. Consequently, the ratio of risk margin to expected losses is proportional to the CV of the loss distribution. And the constant of proportionality Z determines the width of the confidence interval.

The relationship between risk margin M and premium P is summarized by Equation (2.17).

$$Z v=\frac{M}{P} \tag{2.17}$$

This idea behind the risk margin can be applied to both the company as a whole, and to individual policies. So let M be the company risk margin (which may be calculated as shown here or by some other method) and let $M_{\{k\}}$ be the individual policy risk margin for Policy k. (The curly brackets around the subscript are to remind us that this is for a collection of exposures; we’ll express the risk margin for a single exposure i as M_i, while company-level variables will not have subscripts at all.) Combining this definition of risk margin with the formula for aggregate variance, given by Equation (2.15), we obtain the following formulas for the company and policy risk margins.

$$M \equiv Z \sigma=Z \sigma_{0} \sqrt{\sum_{i \in \text { comp }} \sum_{j \in \text { comp }} R_{i} R_{j} \rho_{i j}} \tag{2.18}$$

$$M_{\{k\}} \equiv Z \sigma_{\{k\}}=Z \sigma_{0} \sqrt{\sum_{i \in\{k\}} \sum_{j \in k\}} R_{i} R_{j} \rho_{i j}} \tag{2.19}$$

If the insurer is including a risk margin^[21] in the actual premiums charged, then it should reflect the impact of diversification over the insurer’s entire book. By combining many (independent or partially correlated) policies into its book, the company is able to achieve a level of diversification beyond that presented by individual policyholders. Due to this additional diversification, the company’s CV will necessarily be smaller than any individual policy’s, so the company risk margin is much smaller than the sum of individual policy risk margins. In other words, consumers are already benefitting from the insurer’s ability to diversify. This benefit can be expressed as the ratio of the insurer’s aggregate risk margin to the sum of individual policy risk margins. We’ll call this the book diversification ratio D. And its role will become clear in Section 2.5 when we build the diversification relativity out of the risk margins we have developed.

$$D \equiv \frac{M}{\sum_{k \in \text { comp }} M_{\{k\}}} \tag{2.20}$$

It is useful to re-express D in terms of CVs, using Equation (2.17).

$$D=\frac{Z v P}{\sum_{k \in \text { comp }} Z v_{\{k\}} P_{\{k\}}}$$

The Z factors out of the sum in the denominator and cancels with the Z in the numerator, and we divide top and bottom by P.

$$D=\frac{v}{\left(\sum_{k \in \text { comp }} v_{\{k\}} P_{\{k\}}\right) / P}$$

Because the individual policy premiums sum to the company premium, the denominator is just a premium-weighted average CV across all policies on the book (each of which is larger than the company CV).

$$D=\frac{v}{v_{\text {avg }}} \tag{2.21}$$

We see that the book diversification ratio reflects the degree to which the company CV is smaller than that of the average policy. This supports our original claim that D indicates how much additional diversification is achieved by aggregating policies into a book.

Example

If we select a 95% confidence interval on which to base the risk margin, then the upper bound of that confidence interval is at the 97.5 percentile. So if we assume the aggregate loss distribution is approximately normal, then Z = N⁻¹(0.975) ≈ 1.9600. The policy risk margin, given by Equation (2.19), is 1.9600 times the square root of the variance we calculated in Section 2.3.

If we carry forward the results of Scenario 2, the risk margin is $(1.9600 \times \$300) \sqrt{7.2677} \approx \$1,585$, where we have used σ₀ = v₀P₀ = 0.3 × $1,000 = $300. This aggregate risk margin over the exposures at each of our four example sites is about 2.7 times the risk margin for a base exposure (which is $588). Here the impact of diversification crystalizes. These exposures present 4 times the expected losses of a base exposure but require only 2.7 times the risk margin. The ratio of these two numbers (inverted) equals the CV ratio, 0.6740. These relationships are shown in Table 5 for each scenario.

Next, we consider calculating D. We can do this either as a ratio of risk margins (Equation 2.20) or as a ratio of CVs (Equation 2.21). Either way, we may run into trouble with the numerator. A large insurer could provide coverage for upward of a million buildings, so calculating the numerator could involve a correlation matrix with more than a trillion elements. This may not be feasible from a computational standpoint.

We’ll see in Section 3 that we can get away without calculating D. But D has an insightful interpretation, so it may still be worth developing a method to estimate it. A reasonable first-order estimate can be produced based just on the policy count by assuming that each policy looks like an average policy and that each insured item looks like an average item.

Let n be the number of policies on the book and m the average number of items per policy. An estimate of the average correlation between items on a policy—call it γ—must also be provided, as well as an estimate for the average correlation between items on separate policies—call that β. One example of potentially reasonable estimates for γ and β may be in the neighborhood of 0.4 and 0.0005, corresponding to average separations between buildings on the order of 500 feet and 100 miles, respectively (using the exponential distance-correlation model presented in Section 2.2).^[22]

As shown in Appendix B, these assumptions lead to the following estimate for the book diversification ratio.

$$D \approx \sqrt{\frac{[1+(m-1) \gamma]+m(n-1) \beta}{n[1+(m-1) \gamma]}} \tag{2.22}$$

So if there is an average of three items per policy and there are 50,000 policies, for example, and if the estimates of γ and β above are deemed appropriate, this works out to be D ≈ 0.0292. So in this situation, the company risk margin is just less than 3% what it would need to be in aggregate if each policy were self-insured.

This is the benefit of insurance. While overhead causes premium to exceed pure losses, the needed risk margin is much less than it would be using self-insurance.^[23]

2.5. Calculating the diversification relativity

The approach to calculating a diversification relativity r can be understood by considering the way the company risk margin is incorporated into the rates. And this is likely done through an adjustment to base rates—possibly by application of a multiplicative factor to base rates. The problem with applying the adjustment directly to base rates is that this allocates the company’s risk margin in proportion to policy premium. Every policyholder receives the same benefit from the insurer’s diversification. Under premium-based allocation, risk-loaded premium $\tilde{P}_{\{k\}}^{\text {(prem) }}$ for Policy k becomes^[24]

$$\tilde{P}_{\{k\}}^{(\text {prem })}=P_{\{k\}}+\frac{P_{\{k\}}}{P} M=\left(1+\frac{M}{P}\right) P_{\{k\}} \equiv F P_{\{k\}}, \tag{2.23}$$

thereby defining a company risk factor F . The company risk factor^[25] that is applied to premium is the same for all policies:

$$F=1+\frac{M}{P}=1+Z v \tag{2.24}$$

The way to credit policyholders for their contributions to the book’s diversification is to allocate the company risk margin in proportion to policy risk margins (instead of premium). In this way, larger, more diverse policies will experience a smaller risk charge per premium dollar.

Under policy-risk-margin-based allocation, Policy k’s share of the company risk margin changes from

$$\left(\frac{P_{\{k\}}}{P}\right) M \text { to }\left(\frac{M_{\{k\}}}{\sum_{k \in \text { comp }} M_{\{k\}}}\right) M.$$

This new allocation results in a risk-loaded premium of

$$\begin{aligned} \tilde{P}_{\{k\}}^{\text {(risk) }} & =P_{\{k\}}+\frac{M_{\{k\}}}{\sum_{k \in \text { omp }} M_{\{k\}}} M \\ & =\left(1+\frac{M}{P_{\{k\}}} \frac{M_{\{k\}}}{\sum_{k \in \text { oomp }} M_{\{k\}}}\right) P_{\{k\}} \equiv F_{\{k\}} P_{\{k\}}, \end{aligned} \tag{2.25}$$

thereby defining a risk factor specifically for Policy k.

$$F_{\{k\}}=1+\left(\frac{M_{\{k\}}}{P_{\{k\}}}\right)\left(\frac{M}{\sum_{k \in \text { omp }} M_{\{k\}}}\right)=1+Z v_{\{k\}} D \tag{2.26}$$

So the policy risk factor can be seen to equal 1 plus the product of three component factors:

1. The critical value for the confidence interval selected to define risk margins,

2. The CV for Policy k’s loss distribution, given by Equation (2.16), and

3. The book diversification ratio, given by Equation (2.20).

Equivalent to just using policy-risk-margin-based allocation, the original company risk factor can be used to achieve overall rate adequacy on a risk-loaded basis, and a diversification relativity can be applied at the policy level. Since this relativity is designed to simulate policy-risk-margin-based allocation, it divides out the company risk factor and multiplies in the individual policy risk factor. Consequently, it must equal the ratio of the policy risk factor to the company risk factor.

$$r_{\{k\}}=\frac{F_{\{k\}}}{F}=\frac{1+Z v_{\{k\}} D}{1+Z v}=\frac{1+Z v_{\{k\}} D}{1+Z v_{\text {avg }} D} \tag{2.27}$$

In the final step, we have used Equation (2.21) to express ν in terms of D. Since we’re not changing the total amount of premium collected but just the way we allocate it among policies, we’re guaranteed that the approach is revenue neutral.

Note that, when calculating a diversification relativity for some policy, it’s not enough to have information about the diversification of the policy itself. We also need to know about the average level of policy diversification for the company. A policy that qualifies for a diversification discount with one company may need to be assessed a surcharge with another company. Only if the policy is more diversified than the average for a particular company will it qualify for a discount.

And whenever new policies are written or current policies are amended, the company-level variables will shift slightly in response, so the average policy CV will be fluid. But we assume that the number of policies on the book is significant so that the company values are effectively unchanged when one policy is amended. In practice, an insurer would need to periodically update its company CV and book diversification ratio, but this can be done either annually or in conjunction with the regular implementation of rate changes.

Example

Suppose the example book diversification ratio we estimated in Section 2.4 were applicable to the company insuring our imaginary policy. If the average policy CV ratio for that company turns out to be 0.75, then the example policy (with the 0.6740 CV ratio we calculated in Section 2.4) will certainly qualify for a discount.

The CV for this example policy is v_{Ex.} ≈ 0.6740 × 0.3 ≈ 0.2022, while the one for the average policy is v_avg ≈ 0.75 × 0.3 ≈ 0.225.

$$\begin{aligned} r_{\{\mathrm{Ex}\}\}} & \approx \frac{1+1.9600 \times 0.2022 \times 0.0292}{1+1.9600 \times 0.225 \times 0.0292} \approx \frac{1.0116}{1.0129} \\ & \approx 0.9987 \end{aligned}$$

This is indeed a discount, but it’s awfully tiny (∼0.1%). To get a better idea of what’s going on here, let’s consider two other (very distinct) policies—the first with a single insured item (a base exposure) and an annual premium of P_{4} = $1,000, and the second with 25 identical insured items (but not necessarily base exposures) spread over a large geographic area and a total premium of P_{5} = $12,500. Let’s call these Scenarios 4 and 5.

We’ll need to find the CV for each policy. The summations in Equation (2.16) go away for the first policy since it contains a single item. Consequently, its CV ratio is just 1, and the CV equals the base CV.

$$v_{\{4\}}=v_{0}=0.3$$

As for the second policy, each item must have a premium equal to $12,500 / 25 = $500, and the mutual (or off-diagonal) correlations among them must be very small since we’re told they’re geographically diverse.

Ignoring the off-diagonal terms in the numerator’s summation, we have

$$v_{\{5\}}=\frac{\sqrt{25 \times \$ 500 \times \$ 500 \times 1}}{25 \times \$ 500} v_{0}=0.2 v_{0}=0.06$$

We now have all the needed pieces to calculate the two policy diversification relativities, but before we actually do that, it’s worth taking a look at the various allocations of the company risk margin as they relate to these two policies. And for that, we also need to know the total company premium. So let’s say that’s $300 million. We can use Equation (2.21) to calculate the company CV: v = v_avgD ≈ 0.225 × 0.0292 ≈ 0.00657. We can then calculate the company-level risk margin and the sum of policy risk margins.

$$\begin{aligned} M & =Z v P \approx 1.9600 \times 0.00657 \times \$ 300 \text { million } \\ & =\$ 3,863,160 \\ \sum_{k \notin \text { comp }} M_{\{k\}} & =\frac{M}{D} \approx \frac{\$ 3,863,160}{0.0292}=\$ 132.3 \text { million } \end{aligned}$$

Under premium-based allocation, the risk-loaded premiums from Equation (2.23) for these two policies become

$$\begin{aligned} \tilde{P}_{\{4\}}^{(\text {prem })} & \approx \$ 1,000+\frac{\$ 1,000}{\$ 300 \text { million }} \$ 3,863,160 \\ & \approx \$ 1,012.88 \\ P_{\{5\}}^{(\text {prem })} & \approx \$ 12,500+\frac{\$ 12,500}{\$ 300 \text { million }} \$ 3,863,160 \\ & \approx \$ 12,660.96 \end{aligned}$$

Each of these corresponds to a company risk factor of $F=\tilde{P}_{\{k\}}^{(\text {prem })} / P_{\{k\}} \approx 1.0129$.

But the two policy risk margins are

$$\begin{aligned} M_{\{4\}}^{(\text {risk })} & \approx Z v_{\{4\}} P_{\{1\}} \approx 1.9600 \times 0.3 \times \$ 1,000 \approx \$ 588, \\ M_{\{5\}}^{(\text {risk })} & \approx Z v_{\{5\}} P_{\{2\}} \approx 1.9600 \times 0.06 \times \$ 12,500 \\ & \approx \$ 1,470 . \end{aligned}$$

These can be used to calculate the risk-loaded premium under policy-risk-margin-based allocation, given by Equation (2.25).

$$\begin{aligned} \tilde{P}_{\{4\}}^{(\text {risk })} & \approx \$ 1,000+\frac{\$ 588}{\$ 132.3 \text { million }} \$ 3,863,160 \\ & \approx \$ 1,017.17 \\ \tilde{P}_{\{5\}}^{(\text {risk })} & \approx \$ 12,500+\frac{\$ 1,233.75}{\$ 132.3 \text { million }} \$ 3,863,160 \\ & \approx \$ 12,542.92 \end{aligned}$$

So the policy risk factors are

$$\begin{array}{l} F_{\{4\}}^{\text {(risk })} \approx \frac{\$ 1,017.17}{\$ 1,000} \approx 1.0172, \\ F_{\{5\}}^{(\text {risk })} \approx \frac{\$ 12,542.92}{\$ 12,500} \approx 1.0034 . \end{array}$$

We now proceed to calculate the policy diversification relativities using Equation (2.27) and the various factors we calculated before looking at the company risk margin allocation.

$$\begin{aligned} r_{\{4\}} & \approx \frac{1+1.9600 \times 0.3 \times 0.0292}{1+1.9600 \times 0.225 \times 0.0292} \approx \frac{1.0172}{1.0129} \\ & \approx 1.0042 \\ r_{\{5\}} & \approx \frac{1+1.9600 \times 0.06 \times 0.0292}{1+1.9600 \times 0.225 \times 0.0292} \approx \frac{1.0034}{1.0129} \\ & \approx 0.9907 \end{aligned}$$

As expected, Equation (2.27) produces results that equal the ratio of the policy risk factors to the company risk factor. These results, along with their analogs for the three scenarios discussed earlier and a sixth scenario representing a policy with the average CV, are shown in Table 6.

What’s alarming, however, is that these diversification relativities constitute a mere 0.4% surcharge and a 0.9% discount, respectively. This should immediately raise a concern. Because no policy can be less diversified than the first policy, and few policies would be more diverse than the second, we can conclude that the variation in possible diversification relativities for this example company is quite small.

This is a valid concern. As currently prescribed, the diversification relativities generally have little impact on final premiums, and that makes it difficult to justify the effort to implement them. Most would find it desirable to find a way to magnify their impact while maintaining overall revenue neutrality. In Section 3, we show that this can be done without modifying our approach.

3. Increasing the impact of the diversification relativity

First, we need to understand why the diversification relativities are so muted. The reason has to do with the book diversification ratio. Because a company with a large book is able to achieve a high degree of diversification, the required risk margin may be small compared to the risk-free premium. And since the diversification relativity is a reallocation of just the risk margin (and not the rest of the premium), only a small fraction of the total risk-loaded premium is impacted.

So one way to magnify the impact is to increase the size of the risk margin relative to risk-free premium. While the magnitude of the required risk margin is already determined in part by the degree of diversification, it is also influenced by the width of the confidence interval that risk margins are based on. In other words, we can simultaneously increase all risk margins by increasing Z. And this will increase the portion of total risk-loaded premium that gets reallocated. The result is that diversification discounts and surcharges will be more pronounced. As a collective, we can dial their magnitude up and down at will simply by adjusting the parameter Z in Equation (2.27).

Consider the mathematical impact of varying Z. At one extreme, if Z = 0, the risk margin vanishes entirely, so there’s nothing to reallocate and all diversification relativities go to 1. Diversification has no influence on premium in this case. At the other extreme, in the limit as Z → ∞, effectively all of the risk-loaded premium is risk margin, so everything gets reallocated. The 1’s in both the numerator and denominator of r become insignificant and can be neglected. Consequently, the Z’s and D’s cancel. We find that the diversification relativity approaches the ratio of the CV for Policy k to the average policy CV. So a policy with the average CV experiences no premium adjustment (as is the case for any value of Z), while one with half the average CV ends up paying only half the pre-discounted premium. Once again, we see that the coefficient of variation plays the starring role. These limiting cases are summarized in Table 7.

Adjusting Z for the purpose of tweaking the impact of the diversification relativity can be done independently of adjusting any actual provision that the company carries for risk. That is, if the company carries an explicit risk margin based on a 95% confidence interval, but wants to offer more significant diversification discounts than those produced with Z = 1.96, they can select a higher value of Z (like 10 or 100) within the diversification relativity model for equitability/classification purposes while maintaining the appropriate risk load (based on their selected 95% confidence interval) for overall premium adequacy. Analogously, if a company carries no explicit risk margin, that doesn’t mean it’s unable to use the diversification relativities we have developed here. It just means that the actual risk margin selected is based on a 0% confidence interval, while the diversification relativities will be based on some other interval.

Bottom line: The Z selected for classification does not necessarily need to be tied to the Z used for adequacy.

3.1. Selecting the right value for Z

One way to pick Z is by observing how the extremal values for the diversification relativity (the maximum surcharge and discount) depend on Z. The maximum surcharge occurs for a policy with no diversification—just a single insured item. The CV ratio for such a policy is 1 (regardless of the premium). No policy will achieve the maximum discount (because you can always add more items to further increase the diversification), but there is a limit to how big the discount could ever get for a given value of Z. This can be calculated in association with a hypothetical policy having an infinite number of mutually independent items. The CV ratio for this policy is 0.

Plugging these extreme values for the CV ratio into Equation (2.27), we obtain the extreme values for the diversification relativity as a function of Z.

$$r_{\max }(Z)=\frac{1+Z v_{0} D}{1+Z v_{\text {avg }} D} \tag{3.1}$$

$$r_{\min }(Z)=\frac{1}{1+Z v_{\text {avg }} D} \tag{3.2}$$

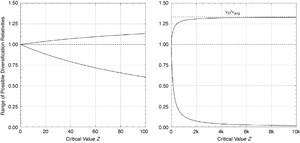
These functions are illustrated visually in Figure 3. Both panels show the potential range of the diversification relativities as a function of the critical value Z for our example company. But the panel on the left is constrained to values of Z that produce ranges that might be considered reasonable in various circumstances, while the panel on the right extends to larger values of Z (where the κ appearing in the axis labels stands for thousands), and shows the global behavior of the relativity range. In particular, we see that the lower bound eventually approaches 0 from above, and the upper bound approaches v₀/v_avg (which is the reciprocal of the average CV ratio) from below. These represent an absolute limit on the possible range of diversification relativities allowed by Equation (2.27) for this example company.

A desired relativity value for one of these extremes could be selected, allowing us to back into the corresponding value for Z. Because the lower bound (maximum discount) is based on a hypothetical policy with an infinite number of diverse items, no actual policies will receive a discount this big. But the upper bound (maximum surcharge) is based on any policy with a single insured item, and there are probably many of these. So it may be advisable to select Z based on a desired value for the maximum surcharge rather than the maximum discount, as basing Z on a selected maximum discount may have unexpected results.^[26] It’s interesting to note that, either way, one can take advantage of the fact that we’re adjusting Z in order to avoid having to calculate the book diversification ratio.^[27]

Alternatively, one could identify a hypothetical policy with a high degree (but finite amount) of diversification, like the one from our example with 25 geographically diverse buildings. A reasonable diversification discount could be selected for this policy, and then Z could be backed into based on that constraint. This is the approach we’ll take with our example. We’ll set the diversification discount to 20% for our diverse policy and solve for Z.

$$0.8=\frac{1+Z \times 0.06 \times 0.0292}{1+Z \times 0.225 \times 0.0292} \Rightarrow Z \approx 57$$

Then for the example policy that was based on the four historic sites, the diversification relativity becomes

$$r_{\text {\{Ex.\} }} \approx \frac{1+57 \times 0.2022 \times 0.0292}{1+57 \times 0.225 \times 0.0292} \approx \frac{1.3365}{1.3745} \approx 0.9724.$$

So adjusting the value of Z has caused the discount for this policy to increase from the 0.1% we originally saw in Section 2.5 to 2.8%. This has indeed produced a much wider range of relativities, corresponding to a 9.1% surcharge for the single-item policy and the 20% discount we selected for the geographically diverse policy. We can also calculate the largest discount theoretically possible for this value of Z using Equation (3.2), and that turns out to be a 27.2% discount.

These and the corresponding results for the scenarios discussed throughout the latter half of Section 2 are presented in Table 8.

Here, it also becomes evident just how big a role policy size can play in the diversification discount. Since small policies have little diversification in themselves, they will experience a surcharge, while larger policies are more likely to receive a discount. This is the sense in which the diversification discount can also be viewed as a policy-size discount.

4. Non-geographic forms of diversification

The diversification relativity discussed in this paper hinges on quantifying the degree of correlation among exposures. In Section 2.2 we showed how to model correlation based on physical separation. But there are other forms of diversification that do not involve a physical separation distance, such as diversification over multiple lines of business. We’ll refer to these forms of diversification collectively as “coverage-type” diversification. And we discuss two possible approaches toward incorporating them into a model.

The first approach models different types of correlation separately and brings them together at the end. The second models them jointly and is more precise, but more computationally intensive. Which approach is more appropriate will depend on whether geocode information is available for items insured under lines of business other than HO/FO (like personal liability, auto, inland marine, workers compensation, umbrella, etc.).

4.1. Homogeneous distribution of geographic diversification across lines

If geocodes are only available for HO/FO, then it will be necessary to make an assumption about the degree of geographic diversification for each additional line of business, compared to HO/FO. If we believe it’s reasonable to assume that the degree of geographic diversification is similar for all lines of business on a policy, then we can apply the geographic diversification relativity from the HO/FO line of business to all lines. We will need to make an additional assumption about policies that exclude HO/FO coverage. (Perhaps we could assume, for example, that an “auto only” policy has no geographic diversification, in which case v_{k} would equal v₀.)

With separate models for both geographic and coverage-type diversification, the homogeneous-distribution analog of Equation (2.27) is

$$r_{\{k\}}=r_{\{k\}}^{(\text {geo })} r_{\{k\}}^{(\text {covg })}=\left(\frac{F_{\{k\}}^{(\text {geo })}}{F^{(\text {geo })}}\right)\left(\frac{F_{\{k\}}^{(\text {covg })}}{F^{(\text {covg })}}\right) \tag{4.1}$$

The only difference is the appearance of the second ratio of risk factors. The CVs buried inside each geographic risk factor will be based on the modeled geographic correlations among HO/FO items, while those inside the coverage risk factors will be based on correlations between lines of business. These will need to be judgmentally selected. The practitioner may, for example, select the line correlations shown in Table 9.

Before we look at an example, it’s worth pointing out that the book diversification ratio will behave very differently in the coverage-type diversification model. It may actually turn out that some policies have more coverage-type diversification than the company does as a whole! (Consider a policyholder with equal amounts of premium in two lines of business, but a company with an 80/20 split.) This suggests that the D related to coverage type will be much larger than the one related to geography; in fact, it’s conceivable that it could be greater than 1. This fundamental difference between geographic and coverage-type diversification owes to the fact that items on different policies are predominantly in different places, but not in different lines of business.^[28]

Example

Assume now that in addition to the HO/FO policy from Scenario 2 with buildings at each of the four example sites, the policyholder has an auto policy (with the same company) for a vehicle with a $1,000 annual premium.

We’ll use Equation (4.1) to capture both geographic and business-line diversification. The ratio of geographic risk factors will be exactly the same as it was in the Section 3.1 example. But we will need to calculate the ratio of business-line risk factors, and that will require determining business-line counterparts for each variable that goes into the ratio.

Premiums are aggregated over all items in a line of business, so we have the following correlation matrix and associated premiums.

$$\begin{array}{c} \text{Business-line correlation matrix}\\ \\ \begin{gathered}\\ \text{HO} \\ \text{Auto}\end{gathered} \left( \begin{array}{cc} \text{HO} & \text{Auto}\\ 1.000 & 0.500\\ 0.500 & 1.000 \end{array} \right) \end{array} \qquad \begin{array}{c} \text{Premium}\\ \\ \\ \left( \begin{array}{r} \$4,000\\1,000 \end{array} \right) \end{array}$$

We again use Equation (2.16) to find the CV ratio and get 0.9165. This is much higher than the geographic CV ratio was (0.6740) because the vast majority of business on this example policy is in the HO line. The insured vehicle does produce a little coverage diversification, but not as much as it would if there were similar amounts of business in each line.

As we discussed before returning to the example, the coverage-based book diversification ratio will be much higher than the geography-based one. We’re about to see that the same is true for the company CV. Of the $300 million in total company premium, suppose $100 million is for HO and $200 million is in auto. Then the business-line company CV ratio is

$$\begin{aligned} \frac{v^{(\text{covg})}}{v_0^{(\text{covg})}} & = \frac{\sqrt{\begin{array}{c}1 \times (\$100 \text{ million})^2 + 2 \times 0.5\\ \times (\$100 \text{ million}) \times (\$200 \text{ million})\\ + 1 \times (\$200 \text{ million})^2\end{array}}}{\$100 \text{ million} + $200 \text{ million}} \\ & \approx 0.8819. \end{aligned}$$

(For comparison, the geographic company CV ratio was only 0.75 × 0.0292 = 0.0219.)

Let’s say that the business-line average policy CV ratio is 0.9, then we can calculate the book diversification ratio using Equation (2.21).

$$D^{(\text {covg})}=\frac{0.8819}{0.9} \approx 0.9799$$

The base CV that is used to convert a CV ratio into a full-fledged CV is independent of the model type, so it will still be 0.3 for this example. Consequently, the policy CV is 0.9165 × 0.3 ≈ 0.2750, and the company CV is only slightly lower at 0.8819 × 0.3 ≈ 0.2646.

The value of Z that was selected in Section 3.1 to calibrate the geographic diversification relativities will not be appropriate for business-line diversification. So we’ll need to repeat that analysis for the business-line relativities. If doing so suggests Z^(covg) = 15, then the business-line diversification relativity will work out to

$$\begin{aligned} r_{\{\text {Ex.}\}}^{(\text {covg})} & \approx \frac{1+15 \times 0.2750 \times 0.9799}{1+15 \times 0.2646} \\ & \approx \frac{5.0421}{4.9690} \approx 1.0147 . \end{aligned}$$

This just needs to be multiplied by the geographic diversification relativity, 0.9724, to get the combined diversification relativity, 0.9867.

In this case, we see that the benefit of geographic diversification was tempered by the relative lack of business-line diversification for this policy.

4.2. Combined diversification relativity

If exposures under all lines of business (not just HO/FO) have been geocoded, then both types of diversification can be treated within the same model. The correlations appearing in Equation (2.16) will just need to be reduced by an additional factor reflecting business-line (or coverage-type) differences.^[29]

If exposures under all lines of business . . . have been geocoded, then both types of diversification can be treated within the same model. The correlations appearing in Equation (2.16) will just need to be reduced by an additional factor reflecting business-line (or coverage-type) differences.

$$\frac{v_{+}}{v_{0}}=\frac{\sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} P_{i} P_{j} \rho_{i j}^{(\mathrm{geo})} \rho_{i j}^{(\mathrm{covg})}}}{\sum_{i=1}^{n} P_{i}} \tag{4.2}$$

The coverage-related correlations $\rho_{i j}^{(\text {covg) }}$ will be the correlations between lines of business (like those shown in Table 9) corresponding to insured items i and j. Once v_{k} and v have been adjusted to reflect coverage correlations, we can return to Equation (2.27) for the diversification relativity.

Example

Taking the auto to be garaged at Site 1, and using the business-line correlations shown in Table 9, we now have two correlation matrices: one for geographic correlation, and one for business-line correlation.

$$\begin{array}{c} \text{Geographic correlation matrix}\\ \\ \begin{gathered} \\ 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{gathered}\left(\begin{array}{ccccc} 1 & 2 & 3 & 4 & 5 \\ 1 & 0.4204 & 0.0576 & 0.0000 & 1 \\ 0.4204 & 1 & 0.0569 & 0.0000 & 0.4204 \\ 0.0576 & 0.0569 & 1 & 0.0000 & 0.0576 \\ 0.0000 & 0.0000 & 0.0000 & 1 & 0.0000 \\ 1 & 0.4204 & 0.0576 & 0.0000 & 1 \end{array}\right)\\ \\\text{Business-line correlation matrix}\\ \\ \begin{gathered} 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{gathered}\left(\begin{array}{ccccc}1 & 2 & 3 & 4 & 5 \\ 1 & 1 & 1 & 1 & 0.5 \\ 1 & 1 & 1 & 1 & 0.5 \\ 1 & 1 & 1 & 1 & 0.5 \\ 0.5 & 0.5 & 0.5 & 0.5 & 1\end{array}\right)\end{array}$$

Rather than matrix multiplying them (as is common in linear algebra), Equation (4.2) indicates that we should multiply out the two matrices element-by-element to get the following combined correlation matrix. The vector of premiums is also shown for convenience.

$$\begin{array}{c} \text{Combined correlation matrix}\\ \\ \begin{gathered} \\ 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{gathered}\left(\begin{array}{ccccc} 1 & 2 & 3 & 4 & 5 \\ 1 & 0.4204 & 0.0576 & 0.0000 & 0.5 \\ 0.4204 & 1 & 0.0569 & 0.0000 & 0.2102 \\ 0.0576 & 0.0569 & 1 & 0.0000 & 0.0288 \\ 0.0000 & 0.0000 & 0.0000 & 1 & 0.0000 \\ 0.5 & 0.2102 & 0.0288 & 0.0000 & 1 \end{array}\right)\\ \\ \text{Premium}\\ \\ \left(\begin{array}{rr} \$ \quad 500 \\ 500 \\ 500 \\ 2,500 \\ 1,000 \end{array}\right)\end{array}$$

Next, Equation (2.16) tells us in order to get the CV, we need to take the square root of the sum of all the elements of the correlation matrix (weighted by the appropriate premiums), and divide it by the sum of the premiums. Doing so results in a CV ratio of 0.5878. This is a bit smaller than the 0.6740 CV ratio we originally obtained in Section 2.3, so adding coverage for the auto has increased the impact of diversification for this policy. However, the other multiline policies on the book will also benefit from including coverage-type diversification. So the company’s average policy CV will be less than it was when we considered only geographic diversification.

If we had actual data for this example company, we would apply the techniques demonstrated throughout Sections 2 and 3 to that data in order to calculate the company CV, the book diversification ratio, and an appropriate critical value for calibration, all based upon the combined correlations. Instead, we’ll have to take reasonable values for them as givens. So let the company CV be 0.004 (instead of 0.00657), the book diversification ratio be 0.08 (instead of 0.0292), and the selected critical value be 25 (instead of 57). Then we can work out the combined diversification relativity.

$$\begin{aligned} r_{\{\mathrm{Ex}\}} & \approx \frac{1+25 \times(0.5878 \times 0.3) \times 0.08}{1+25 \times 0.004} \\ & \approx \frac{1.3527}{1.1} \approx 1.2297 \end{aligned}$$

The higher relativity under this approach is due to the company parameters we selected. Evidently, the average policy using these selected values is significantly more diversified than the example policy.

Accommodating differences among perils

The current approach can also be used to accommodate different distance-correlation relationships by peril. This is good because it may not be reasonable to utilize a single distance-correlation relationship for all perils. Geographic correlation for the earthquake peril, for example, likely persists out to much greater distances than it does for the fire peril.

. . . it may not be reasonable to utilize a single distance-correlation relationship for all perils. Geographic correlation for the earthquake peril, for example, likely persists out to much greater distances than it does for the fire peril.

Premium would need to be allocated by peril, and the geographic correlation $\rho_{i j}^{(\mathrm{geo})}$ would also need to be estimated separately for each peril, using the corresponding selected by-peril distance-correlation relationships. A different correlation matrix, analogous to the one presented in Table 9, would be required to replace $\rho_{i j}^{\text {(covg) }}$ with $\rho_{i j}^{\text {(peril) }}$. The practitioner would need to select the correlation between each pair of perils. For example, the wind and hail perils may be highly correlated, while the water and theft perils may be independent. Negative correlations may even exist between perils. Consider, for example, the freezing and rioting perils. Rioting is more likely to happen in large cities which tend to be built in valleys, whereas freezing would be more common in mountainous areas. (Construction practices may or may not fully address expected temperature differences.)

The sums in the CV formulas would then be over each peril-specific exposure—that is, over each building/peril combination.

Example

For this example, consider an HO policy with two insured buildings, one at Site 2 with a premium of $500, and the other at Site 3 also with a premium of $500. And let this policy contain coverage against two perils: fire and earthquake. Suppose that, after taking the “fire following earthquake” phenomenon into account, the peril correlation between fire and earthquake is estimated to be 0.3, and that 80% of the premium for each building is associated with the fire peril.

We’ll use the exponential distance-correlation model given by Equation (2.7) for the fire peril, and the same model but with the κ parameter adjusted from 1.99 down to 1.00 for the earthquake peril. This results in correlations that extend outward approximately ten times as far for the earthquake peril. We first work out the fire and earthquake geographic correlation matrices for these sites.

$$\begin{array}{c} \text{Fire peril}\\ \\ \begin{gathered}\\ 2 \\ 3 \end{gathered} \left( \begin{array}{cc} 2 & 3 \\ 1 & 0.0569 \\ 0.0569 & 1 \end{array} \right) \end{array} \qquad \begin{array}{c} \text{Earthquaker peril}\\ \\ \begin{gathered}\\ 2 \\ 3 \end{gathered} \left( \begin{array}{cc} 2 & 3 \\ 1 & 0.2369 \\ 0.2369 & 1 \end{array} \right) \end{array}$$

As anticipated, the correlations are much higher for the earthquake peril.

The full geographic correlation matrix will be a 4 × 4 matrix with one column and one row for each building/peril combination. The geographic correlation between two items that are associated with separate perils can be estimated as the geometric average of the values produced by the distance-correlation model for each peril. So, for example, the geographic correlation of fire coverage at Site 2 and earthquake coverage at Site 3 can be estimated as = 0.1161.

$$\begin{array}{c} \text{Exposure description}\\ \\ \begin{array}{l}\text{1: Site 2—Fire}\\ \text{2: Site 2—Earthquake}\\ \text{3: Site 3—Fire}\\ \text{4: Site 3—Earthquake}\\ \end{array}\\ \\ \text{Full geographic correlation matrix}\\ \\ \begin{gathered} \\ 1 \\ 2 \\ 3 \\ 4 \end{gathered} \left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 1 & 0.0569 & 0.1161 \\ 1 & 1 & 0.1161 & 0.2369 \\ 0.0569 & 0.1161 & 1 & 1 \\ 0.1161 & 0.2369 & 1 & 1 \end{array}\right)\\ \\ \text{Premium} \\ \\ \left(\begin{array}{r} \$ 400 \\ 100 \\ 400 \\ 100 \end{array}\right)\end{array}$$

Because it doesn’t try to marry two separate correlation models, the peril correlation matrix (analogous to the coverage or business-line correlation matrix) is much simpler to construct. Correlation elements associated with the same peril in both row and column are 1, while those associated with fire in one and earthquake in the other are 0.3. The result is shown next, and we multiply it element-by-element into the full geographic correlation matrix to get the combined correlation matrix, shown afterward.

$$\begin{array}{c} \text{Peril correlation matrix}\\ \\ \begin{gathered} \\ 1 \\ 2 \\ 3 \\ 4 \end{gathered}\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 0.3 & 1 & 0.3 \\ 0.3 & 1 & 0.3 & 1 \\ 1 & 0.3 & 1 & 0.3 \\ 0.3 & 1 & 0.3 & 1 \end{array}\right)\\ \\ \text{Combined correlation matrix}\\ \\ \begin{gathered} \\ 1 \\ 2 \\ 3 \\ 4 \end{gathered} \left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 0.3 & 0.0569 & 0.0348 \\ 0.3 & 1 & 0.0348 & 0.2369 \\ 0.0569 & 0.0348 & 1 & 0.3 \\ 0.0348 & 0.2369 & 0.3 & 1 \end{array}\right)\end{array}$$

From this, we calculate the CV ratio from Equation (2.16), and get 0.4165. Using the same book diversification ratio and company CV as used in the previous example in this section, and using the same value for Z, the diversification relativity works out to

$$\begin{aligned} r_{\{\text {Ex. }\}} & \approx \frac{1+25 \times(0.4165 \times 0.3) \times 0.08}{1+25 \times 0.004} \\ & \approx \frac{1.2499}{1.1} \approx 1.1363 . \end{aligned}$$

5. Conclusions

Historically, any premium provision for a risk margin has been allocated to policies in proportion to risk-free premium. This has resulted in a situation where every policy incurs the same risk factor—or ratio of risk-loaded premium to risk-free premium. In other words, customers bringing highly diversified exposures pay the same amount of risk premium per risk-free premium dollar as those with highly concentrated exposures.

We have shown that this situation can be resolved by allocating risk premium in proportion to a policy’s own risk margin, so that customers insuring highly diverse exposures pay less risk premium per risk-free premium dollar.

Alternatively, a company can continue to use premium-based allocation but include a diversification relativity in the premium calculation. This diversification relativity has the effect of replacing the risk-loaded premium with what it would have been had policy-risk-margin-based allocation been used in the first place. It does this by dividing out the uniform company risk factor and multiplying in the policy risk factor. So the diversification relativity is defined as the ratio of the policy-to-company risk factors.

In order to calculate the policy risk margins, we constructed a simple model that takes the distance between two insured items and converts it to an estimated loss correlation. We concluded that the exponential model with parameters given by Equation (2.7) was appropriate for a book characterized by the distance-correlation relations selected in Table 2. We also provided formulas, Equations (2.1) through (2.3), for calculating the distance between two insured items once they’ve been geocoded.

There are a number of mathematical properties that we would like our geographic diversification factor to satisfy.

1. Multiple buildings at the same exact location would be equivalent to a single building at that location with a premium equal to the sum of the premiums of the original buildings.

2. The greater the distance between two buildings, the greater their geographic diversification.

3. A situation involving two buildings separated by some distance will result in greater diversification if the premium is approximately the same for each building. If one premium is significantly smaller than the other, the situation is only slightly different from one in which only the building with the larger premium is insured.

And indeed, our model satisfies each of these requirements.

We also addressed the fact that the company risk margin tends to be small compared to expected losses and expenses. This means the diversification relativities tend to be very close to 1, thereby falling short of our objective to develop impactful diversification discounts. So we demonstrated that increasing the critical value Z (upon which confidence intervals are based) produces more widely distributed diversification relativities, while preserving revenue neutrality.

Finally, we showed how the concepts in this paper could be applied to non-geographic forms of diversification, including diversification by peril and across lines of business, and we showed how the model formulas would be impacted by these generalizations.

---

Acknowledgments

The potential application of this work was broadened due to a suggestion from my company’s Actuarial Director, Randy Nordquist, FCAS, MAAA. Thank you for recommending that I include a discussion about accommodating both diversification across perils and differences in the distance-correlation relationship by peril.

This paper was also improved thanks to helpful reviews from the editor and referees, and due to observant comments from attendees of the 2017 Farm Bureau Actuarial Conference in Coeur d’Alene, Idaho.

Finally, this project would not have been possible without the support of my wife Amber, and our children, Susan, Benjamin, and Caleb. Thank you for your patience and for your insights.