Do Underwriting Cycles Matter? An Analysis Based on Dynamic Financial Analysis

1. Introduction

Underwriting cycles, i.e., the cyclical patterns of insurance prices and profits, have been extensively researched for the United States and to some degree for Europe and Asia. Although there is ongoing academic dispute with regard to their causes, the existence of underwriting cycles is broadly accepted in academia and practice. Underwriting cycles are incorporated into enterprise risk management and solvency models such as dynamic financial analysis models (Kaufmann, Gadmer, and Klett 2001). Findings on insurance cycles are also used in forecasting and scenario analysis of hard and soft market phases, which is particularly crucial, e.g., for market entry and exit strategies of insurance companies (Chen, Wong, and Lee 1999).

In this paper, we investigate whether underwriting cycles substantially affect the risk and return of non-life insurance companies. For this purpose, we integrate empirically observed underwriting cycles in a dynamic financial analysis framework using an Ornstein-Uhlenbeck process and analyze their impact on risk and return under different scenarios. The key question is whether underwriting cycles substantially affect risk and return or whether their impact is negligible. Substantial impact would confirm the importance of modeling underwriting cycles in enterprise risk management; minor impact, although of academic interest, would throw some doubt on the relevance of these cycles in practice. Most practitioners would confirm that underwriting cycles have a substantial effect on insurance company profitability; however, their impact on risk is not often discussed in practice and thus might be of special interest to practitioners. A typical question would be, for example, whether an insurer could be more or less vulnerable to insolvency due to cyclicality of underwriting premium levels. Given the broad discussion of underwriting cycles both in academia and in practice, we expect a substantial impact and a high relevance, but we are not aware of any research that has systematically illustrated the impact of these cycles in an enterprise risk management framework.

Our paper builds on two branches of literature—dynamic financial analysis (DFA) and underwriting cycles. Since their introduction in the late 1990s (CAS 2010), several surveys and applications of DFAs have been published. Lowe and Stanard (1997) focus on property-catastrophe reinsurance and develop a model for the underwriting, investment, and capital management process. Kaufmann, Gadmer, and Klett (2001) focus on non-life insurance companies and also provide an up-and-running model. Those papers introduce basic DFA models; Blum et al. (2001), D’Arcy and Gorvett (2004), and Eling, Parnitzke, and Schmeiser (2008) use DFA to examine specific decision-making situations. Blum et al. (2001) analyze the impact of foreign exchange risks on reinsurance decisions and D’Arcy and Gorvett (2004) search for an optimal growth rate in the property-casualty insurance business. Eling, Parnitzke, and Schmeiser (2008) concentrate on how management strategies influence a non-life insurer’s risk and return position. Recently, Eling and Toplek (2009) integrated copulas in DFA to assess the impact of nonlinear dependencies on a non-life insurer’s risk and return profile. DFA is thus well suited for analyzing how changes in the business environment influence risk and return of insurance companies, and in this paper we use it to study the impact of underwriting cycles.

Empirical work analyzes underwriting cycles for a broad range of countries and for many lines of business. Among the most important studies are Cummins and Outreville (1987) (covering 13 countries), Lamm-Tennant and Weiss (1997) (12 countries), Meier and Outreville (2006) (three countries), Meier (2006) (four countries), and Swiss Swiss Re (2001) (seven countries). Some studies focus on regions, such as Asia (Chen, Wong, and Lee 1999) or Europe (Meier and Outreville 2006). For a recent critical discussion of the empirical properties of underwriting cycles, see Boyer (2012). Another important stream of literature analyzes the causes of underwriting cycles, looking at naïve ratemaking methods (Venezian 1985), competition-driven prices (Wilson 1981; Stewart 1981; Harrington and Danzon 1994), capacity constraints (Winter 1988, 1991, 1994; Niehaus and Terry 1993; Cummins and Danzon 1997), institutional intervention (Cummins and Outreville 1987), the general business cycle (Grace and Hotchkiss 1995; Chen, Wong, and Lee 1999), and interest rates (Wilson 1981; Doherty and Kang 1998; Fields and Venezian 1989).

Given this broad empirical evidence and the vast literature on the causes of underwriting cycles, it is surprising that underwriting cycles have not yet been the focus of enterprise risk management models. This paper thus contributes to both streams of literature by evaluating underwriting cycles’ impact on the insurer’s risk and return position, building on the DFA model presented by Eling and Toplek (2009). We find that underwriting cycles have a substantial influence on risk and return measures.

Our results have important implications for managers of insurance and reinsurance companies because they indicate that it is crucial to consider underwriting cycles in risk management. Understanding the nature and characteristics of underwriting cycles in enterprise risk management will make the industry and individual companies aware of the magnitude of the effects of future underwriting cycles (see Chen, Wong, and Lee 1999). Furthermore, our findings with regard to different risk measures are important for regulators and rating agencies that rely on measures such as the ruin probability and the expected policyholder deficit when calculating risk-based capital. These measures are also the foundation of internal risk models, again emphasizing the relevance of the results for insurers and reinsurers.

The rest of the paper is organized as follows. In Section 2, we present the DFA framework, which follows Eling and Toplek (2009) and contains the essential elements of a non-life insurance company. In Section 3, we describe the considered underwriting cycles and how they can be integrated in a DFA model. In Section 4, we conduct a DFA simulation study to examine the effects of underwriting cycles on risk and return. Section 5 concludes.

2. DFA model

We rely on the DFA model presented in Eling, Parnitzke, and Schmeiser (2008) and further developed in Eling and Toplek (2009) to illustrate the impact of underwriting cycles on risk and return of insurance companies. We provide a brief review of the model here; full details can be found in those papers. The insurer’s equity capital is projected into the future taking into consideration asset returns, claims, and different types of costs. EC_t denotes the insurer’s equity capital at the end of period t (t ∈ {1, . . . , T}) and E_t the company’s earnings in t. Simulation is discontinued for scenarios in which the insurer defaults and thus has negative or zero equity capital. Development of the equity capital over time can be written as

$$E C_{t}=E C_{t-1}+E_{t},$$

with E₀ as the starting equity capital. The earnings E_t in year t consist of the investment result I_t and the underwriting result U_t; taxes (with tax rate tr) are paid on positive earnings:

$$E_{t}=I_{t}+U_{t}-\max \left(t r \cdot\left(l_{t}+U_{t}\right), 0\right) .$$

The investment return I_t in year t is given as

$$I_{t}=r_{p t} \cdot\left(E C_{t-1}+P_{t}-E x_{t}^{P}\right) .$$

Here, r_pt is the total return on the investment portfolio, P_t the premium earnings throughout year t, and Ex_t^P the up-front costs to be paid. The investment portfolio is comprised of all available funds (equity capital plus premiums less up-front costs) and the investment return is obtained by multiplying the portfolio return with these funds. The portfolio return in year t is calculated as $r_{p t}=\alpha_t \cdot r_{1 t}+\left(1-\alpha_t\right) \cdot r_{2 t}$, with $r_{1 t}$ as the (random) return of high-risk investments (e.g., stocks), $r_{2 t}$ as the (random) return of low-risk investments (e.g., bonds), and $\alpha_t$ as the share of high-risk investments.

The underwriting result U_t in year t is calculated as insurance premiums P_t less claims C_t less costs (up-front costs Ex_t^P and claim settlement costs Ex_t^C). The claims in year t are the sum of (random) non-catastrophe losses and (random) catastrophe losses (C_t = C_t^Cat + C_t^Non–Cat). U_t is then given by

$$U_{t}=P_{t}-C_{t}-E x_{t}^{P}-E x_{t}^{c} .$$

The premium income P_t depends on the underwriting market volume accessible to the insurer (MV_t), its share of the relevant market ($\beta_t$), and a premium rate level ($\Pi_t$). The market volume is obtained by inflating last year’s market volume by the rate i (to represent average market growth and compensate for inflation):

$$P_{t}=\Pi_{t} \cdot \beta_{t} \cdot M V_{t-1} \cdot(1+i),$$

with MV₀ as the starting market size. The premium rate level $\Pi_t$ reflects the influence of the underwriting cycle and is described in detail in the next section.

To appropriately interpret results of the simulation model, we briefly discuss some aspects of the premium and reserving process of the DFA model. No explicit ratemaking models are employed, as this would require the implementation of management rules and an exogenous market environment, including consideration of competitors and their actions. Instead, we rely on a passive ratemaking mechanism and assume that the expected premium earnings and the expected base claims grow with the overall market size, i.e., with inflation. This results in an almost constant expected combined ratio. Thus, we implicitly assume that the insurer’s underwriting, in a situation without underwriting cycles, can match the overall market trend and the insurer thus can charge an adequate, in terms of expected loss and cost ratio, premium rate level. For the sake of simplicity, no reserving process is included in the model. We consider yearly contracts with premiums paid at the beginning of each year. All claims resulting from these contracts are assumed to be entirely settled at the end of the year.

Also, the insurer’s market share $\beta_t$ is assumed to remain constant for all simulation years so that its insurance portfolio only grows with overall market inflation. Otherwise, the model would need to include an exogenous market environment as well as management rules, which are not considered in order to isolate effects of the underwriting cycles. For an application of management rules in DFA models, see Eling, Parnitzke, and Schmeiser (2008).

Two types of costs are integrated in the model, the up-front costs (Ex_t^P) and claim settlement costs (Ex_t.^C). The claim settlement costs are given as a portion δ of the total claims, i.e., Ex_t^C = δC_t. The up-front costs depend linearly on the level of written market volume (modeled with the factor γ), and quadratically on the change in written market volume (modeled with the factor η, e.g., due to increased advertising and promotion efforts). The up-front costs Ex_t^P are thus calculated as

$$E x_{t}^{P}=\gamma \cdot \beta_{t} \cdot M V_{t}+\eta \cdot\left(\left(\beta_{t}-\beta_{t-1}\right) \cdot M V_{t-1}\right)^{2} .$$

DFA modeling is always a tradeoff between accuracy and complexity. Although the presented model is far too simple to accurately reflect reality, increased model complexity is not always an advantage. The increased number of parameters that influence model results could possibly mask the effects of underwriting cycles, which are the focus of our study. We thus restrict ourselves to the standard components necessary in DFA.

3. Integrating underwriting cycles in DFA

3.1. Overview of modeling options

In our model, the premium income P_t in year t is dependent on the premium rate level $\Pi_t$, which is a factor representing the attainable premium level subject to the underwriting cycle. Several options for integrating underwriting cycles in DFA are found in the literature.

According to D’Arcy et al. (1998), the premium rate level may be modeled using a discrete Markov process of order 1. Relying on this type of process requires setting predefined states of the underwriting cycle: one application of Markov processes in DFA (Eling, Parnitzke, and Schmeiser 2008) uses three market states: weak, moderate, and strong. In the real world, there is a much wider range of possible states; indeed, Kaufmann, Gadmer, and Klett (2001) state that calibration of the required transition matrix is a delicate task and therefore propose that it should be based on personal experience rather than on empirical data. Such Markov chains may be suitable for benchmarking purposes in an academic setting, but they are not readily calibrated to empirical data.

Cummins and Outreville (1987) empirically estimate underwriting cycles using an autoregressive process of order 2. This AR(2) process can be integrated in a DFA simulation and thus employ past information (such as premium rate levels or the combined ratio) to simulate future premium rate levels. Autoregressive processes are the most widespread approach for modeling cyclical patterns of premium rate levels over time (for an overview, see Venezian 1985; Niehaus and Terry 1993; Daykin, Pentikäinen, and Pesonen 1994; Lamm-Tennant and Weiss 1997; Fung et al. 1998; Chen, Wong, and Lee 1999; Meier 2006) and have been used in a variety of DFA models such as Eling and Toplek (2009) and Kaufmann, Gadmer, and Klett (2001).

While the AR(2) process can be calibrated to empirical data and does not require setting of predefined market states as in the Markov chain approach, for the purpose of this analysis an approach is required that allows for direct control of the main process drivers, the long-term premium rate level, and the process variance. This is necessary in order to analyze the sensitivity of simulation results with respect to these parameters. A continuous-time alternative that fulfills these requirements is the Ornstein-Uhlenbeck process.

3.2. Ornstein-Uhlenbeck process

To integrate underwriting cycles in our analysis, we rely on the continuous-time Ornstein-Uhlenbeck (OU) process.^[1] The OU process for the premium rate level $\Pi_t$ follows the stochastic differential equation

$$d \Pi_{t}=\lambda\left(\mu-\Pi_{t}\right) d t+\sigma d W_{t},$$

with some starting value Π₀. The process is mean-reverting with stability level µ, which, in our context, can be interpreted as the long-term premium rate level. The strength of reversion toward µ is described by the reversion parameter λ > 0. The stochastic element is a standard Wiener process W_t, scaled by the standard deviation parameter σ > 0. The parameter σ thus controls (in combination with λ) the process variance, as for higher values the influence of the random process W_t, and thus overall process variability, increases. The OU process can be interpreted as the limiting case of an AR(1) process, which allows estimation of the process parameters using linear regression. In our context, the OU process is evaluated at discrete time steps and since our DFA model is set up on a yearly basis, each time step is interpreted as one year.^[2]

4. Simulation analysis based on empirical data

4.1. Model and calibration

To assess the impact of underwriting cycles on risk and return of insurance companies, we analyze the DFA model introduced in Eling and Toplek (2009) and consider different parameterizations of the OU process. For process calibration we rely on Swiss Re sigma premium growth data for the worldwide non-life market for the years 1980 to 2010. We also employ country-specific non-life insurance premium growth data for Australia, Canada, Germany, Japan, Switzerland, and the United Kingdom between 1984 and 2010, as reported in the OECD statistics database.^[3],[4] In relying on premium growth data for calibration of the OU process, which describes the achievable premium level in our model, we implicitly assume that years with positive premium growth rates represent a hard market phase and vice versa.

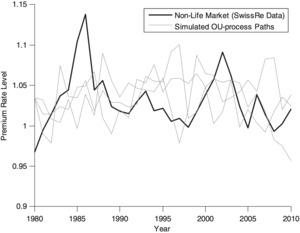
Figure 1 shows the actual development of the premium rate level for the worldwide non-life insurance market from 1980 to 2010. Also included in this figure are three paths simulated according to the estimated OU process. This figure highlights that the simulated process variance is comparable to the observed variance.

Figure 1.Observed non-life market premium rate level and simulated paths

Our analysis proceeds in three steps. (1) The parameter estimates derived from the empirical data described above are used for a market-specific analysis. (2) We systematically vary the process parameters to analyze the impact these parameters have on simulation results. (3) To analyze the robustness of our findings, we vary the dependence structure among the assets, the liabilities, and between assets and liabilities: in the main analysis we assume independence among the assets, the liabilities, and between assets and liabilities, while in later robustness tests we consider both nonlinear dependence structures. Furthermore, we vary the asset allocation, which can be a main driver for investment results and, thus, the financial stability of insurance companies.

For each simulated scenario, the model is initialized using the same state of the random number generator, so that differences in simulation results can be exclusively ascribed to the varying properties of the underwriting cycle or model parameterization. As the starting value for the processes, we choose the respective average premium level µ. Calibration of the DFA model, aside from the underwriting cycle, is based on Eling and Toplek (2009) and reported in Appendix A.

The impact of the underwriting cycle is identified using the geometric growth rate of the insurer’s equity capital and two risk measures: ruin probability and expected policyholder deficit. We rely on these two risk measures because they are widespread in academia and practice and are typically considered in a DFA context (see Eling and Toplek 2009). Results for other popular risk measures, such as value at risk and tail value at risk (see Dowd and Blake 2006) are available upon request. The geometric equity growth rate is defined as

$$G E G=\left(\frac{E\left(E C_{T}\right)}{E C_{0}}\right)^{1 / T}-1,$$

with T as the total number of simulation years. The ruin probability is given by

$$R P=P(\tau \leq T),$$

with τ = inf{t|t > 0, EC_t 0} being the year of ruin. The expected policyholder deficit relative to the initial capital is

$$E P D=\left(\Sigma_{t-1}^{T} E\left(\max \left\{-E C_{t} ; 0\right\}\right) \cdot\left(1+r_{f}\right)^{-t}\right) / E C_{0} \text {, }$$

with r_f as the risk-free interest rate (the equity capital is set to zero the year after insolvency).

4.2. Simulation analysis based on empirical data

In a first step, we calibrate the DFA model with underwriting cycles fitted to the empirical premium growth data from Swiss Re and OECD. The fitted process parameters are reported in the first three columns of Table 1, while the according simulation results are reported in the last three columns.

The simulation results without underwriting cycle are reported in the first row of Table 1 (GEG = 23.74%, RP = 0.016%, EPD = 0.002%) and can be considered as a benchmark case for the scenarios with a cycle. The values for GEG indicate that on average the equity capital of the insurer grows by 23.74% per year. The calibration used in this paper thus reflects the situation of a relatively profitable insurance company (as mentioned, we rely on the calibration used in Eling and Toplek 2009).

Generally, the underwriting cycle adds uncertainty to the premium rate level that the insurer can charge. Consequently, the effects of hard and soft insurance markets are reflected in the variation of the considered risk measures. The process parameter σ represents the influence of the stochastic error process W_t and thus affects the level of variation inherent in the underwriting cycle. Higher values are associated with stronger expected changes in the chargeable premium rate level. It is especially noteworthy that the process variance is much lower for the worldwide non-life market than for single countries. For the non-life market, the standard deviation (of the stationary process, i.e., $\sqrt{\sigma^{2} / 2 \lambda}$), is 3.16%, while in Germany and Japan it is 15.94% and 18.65%, respectively.

As shown in Table 1, the equity growth rate increases in all cases when an underwriting cycle is introduced. This can be explained by the process stability level µ being larger than 1 in all cases. For our model, this means that insurers can, on average and over time, charge higher prices for the same coverage, resulting in a capital inflow for the insurer.

Higher volatility of the underwriting cycle is in general associated with higher risk as measured by RP and EPD. For example, the parameterization for the total non-life insurance market provides the lowest overall risk and also has the lowest process variance, while the opposite is true for Japan.^[5] However, some of the effects of higher process variation are compensated for by the overall process mean and the strength of mean reversion. The parameters µ and σ for Germany and Switzerland are very comparable, but the German cycle exhibits higher downside risk. This can be explained by the higher mean-reversion rate of the Swiss cycle, which results in faster recovery when premiums are low. The ruin probability for Switzerland (0.127%) is therefore lower than the ruin probability for Germany (0.172%). This aspect will be discussed in the next section as well. Also, the ruin probability for Japan is much higher than that for Germany and Switzerland.

The differences found in the equity growth rate and downside risk document that underwriting cycles have an important influence on DFA results. The results are especially relevant for regulators and policyholders who are interested in limiting default risk, compared to other stakeholders who might be more interested in the return situation of the insurance company. Overall, higher volatility and thus higher chances for sudden changes in the short-term achievable premium level are strong drivers of the downside risk of insurance companies.

In non-life insurance, most contracts are renewed after one year. Consequently, insurers should take precautions in regard to absorbing drops in the premium rate level, especially if the market is highly competitive, as is, e.g., the German automobile insurance market. Adverse period-to-period effects should also be guarded against by appropriate pricing methodologies. Another important finding is that the underwriting cycle of the aggregate market induces lower levels of risk than those of single countries. Therefore, insurers may consider diversification over several countries to reduce their exposure to adverse short-term effects of the underwriting cycle in one country.

4.3. Systematic variation of process parameters μ, σ, and λ

To achieve a clearer sense of how underwriting cycles affect insurance company risk, we systematically vary the process parameters µ, σ, and λ, and focus on the ruin probability as a measure of risk. The country-specific analysis highlighted the relevance of the process calibration for simulation results. While the parameter µ determines the expected value, the process variance depends on the parameters σ and λ. We use the German underwriting cycle, as reported in Table 1, as the basis for this analysis. We vary the respective parameters over a range of ±10%, considering 250 model points, and rerun the simulations with 250,000 iterations. Results are shown in Figure 2.

Figure 2.Ruin probability for varying values of the parameter μ

As expected, the relationship between the long-term premium level µ and the ruin probability is negative. A decrement in the premium rate level, ceteris paribus, increases the risk of insolvency and vice versa. However, this relationship is not linear and has a decreasing slope. Thus, once a certain security level is reached, additional capital inflows due to hard underwriting markets have only a minimal positive effect on the stability of insurance companies.

In Figure 3, the process parameters that determine the process variance are varied. The left-hand side of this figure shows the simulation results for varying levels of σ. The higher σ, i.e., the influence of the error term W_t, the higher the ruin probability. This effect is almost linear, so that increased uncertainty in achievable premium levels always poses a risk, regardless of whether this uncertainty is already high. The relationship between the strength of mean reversion to the long-term stability level, i.e., λ, and risk is shown on the right-hand side of Figure 3. A stronger mean reversion rate is negatively associated with risk, indicating that time until premium level recovery can be achieved is also very relevant to the downside risk of insurance companies. This explains the relatively high levels of risk found for Japan in Table 1. The effects on the considered risk measures, however, are slightly smaller than for variation of σ.

Figure 3.Ruin probability for varying values of the parameters σ and λ

As both λ and σ affect process variance, this analysis confirms that period-to-period variance is a significant driver of insurance company risk. In this analysis we vary the parameters by only ±10%, but estimation results in Table 1 show that the empirically observed variation can be much higher.

4.4. Robustness of findings

There are various possibilities for testing the robustness of our findings. One central aspect considered in Eling, Parnitzke, and Schmeiser (2008) was the variation of the dependence structure in the DFA model. To this point, our focus has been on uncorrelated risks, i.e., we assume independence among assets, among liabilities, and between assets and liabilities. We now abandon this assumption and model dependence structures according to the Gauss and the Clayton copula.^[6] We thus consider nonlinear dependence and intend to analyze whether the results found for the underwriting cycles are substantially affected by a variation of the dependence structure. As in the main part of the analysis, 500,000 simulation runs are considered. The results are reported in Appendix B.

While the actual risk and return figures vary, the insights from the main analysis remain unchanged. We see that the long-term stability level drives the growth of the equity capital and period-to-period variance is a major driver for downside risk. The dependence structure affects the risk situation more strongly than the return situation. As shown by Eling and Toplek (2009) the dependence structure induced by the Clayton copula leads to higher values for ruin probability and expected policyholder deficit than the Gauss copula’s due to higher tail dependence.

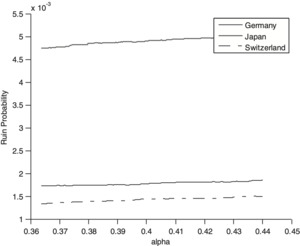
As a second robustness test we vary the insurer’s asset allocation, specifically, the share invested in risky assets (e.g., stocks). The initial asset allocation for the risky assets (α = 40%) is varied by ±10% over 250 model points. We consider three different parameterizations of the underwriting cycle, namely, for Japan, Germany, and Switzerland. The results, using 250,000 simulation runs, are shown in Figure 4.

Figure 4.Ruin probability for varying asset allocations

This test has several interesting results. First, the ruin probability increases with the riskiness of the overall asset allocation. Moreover, the impact of this variation on the risk measure is smaller than that of a ±10% change in the corresponding underwriting cycle’s parameters. Thus the underwriting cycle is an important element and determines the risk situation of insurance companies. Finally, these results are robust for varying underwriting cycles, as the findings from the main analysis (i.e., that Japan has a higher ruin probability than Germany, which, in turn has a higher ruin probability than Switzerland) are confirmed.

5. Conclusion

The aim of our paper is to enhance the understanding of underwriting cycles in an enterprise risk management context by systematically analyzing them in a DFA framework. Understanding the nature and characteristics of underwriting cycles in enterprise risk management will make individual companies, and the industry as a whole, aware of the magnitude of the effects these cycles can have (Chen, Wong, and Lee 1999). Moreover, prospective insurance entrants should find the timing and causes of underwriting cycles highly relevant. Our main findings can be summarized as follows:

1. Underwriting cycles have a substantial influence on both risk and return. The main driver of insurance company risk is the variance of the underwriting cycle, or uncertainty in achievable premium levels. In our context, the relationship between ruin probability and process variance is nearly linear.

2. The existence of underwriting cycles makes possible efficient diversification against adverse effects of sudden premium rate drops in single countries. In this context, we find the cycle variance and resulting risk for aggregated markets to be smaller than for single countries.

3. Our results indicate that the inclusion of different dependence structures will mainly affect risk, and only marginally the return situation.

Given the substantial differences in risk and return numbers found in our model, it seems crucial to take underwriting cycles into account in risk modeling. However, it is important to keep in mind that the simulation results depend on the model and cycle calibration. We consider the Ornstein-Uhlenbeck process and calibrate it to data from several countries. However, the results should not be misinterpreted to mean, for example, that German insurers are more risky than Swiss insurers. Rather, the results show the range of potential outcomes in a specific situation and thus illustrate the variability of risk and return introduced by underwriting cycles that must be taken into consideration by insurance managers.

The approaches to modeling underwriting cycles presented in this paper are, like the DFA framework itself, only models, and thus simplifications of reality. Moreover, the data used to estimate cycle parameters are partly aggregated over different lines of business. Integrating underwriting cycles calibrated according to different lines of business and applying these to different risk positions separately would be a useful extension of the work presented here, e.g., in discovering additional diversification effects. Such an undertaking could investigate in more detail the effects of different business types, such as long- or short-tail business, on corporate success. Also, this type of analysis might be especially relevant for multinational insurers already active in several countries, or for insurers planning market entry and exit strategies. Future research could also include the implication of these cycles in other established DFA models, such as Dynamo, a publicly available DFA model developed by a working party in the Casualty Actuarial Society.