An Analysis of the Market Price of Cat Bonds

undefined

1. Introduction

Describing the market price of property catastrophe (“cat”) bonds is important on two planes: the practical and theoretical. On the practical plane, firms desire to know how prices have behaved in the past, how prices vary by type of risk, and, potentially, how prices will behave in the future. Moreover, a model that accurately describes prices would be valuable when evaluating the price of a potential transaction: if the price is higher than the model’s prediction then the price could be considered expensive, and vice versa. On the theoretical plane, describing the market price of cat bonds illuminates the more general question of risk pricing, which relates to reinsurance contracts, corporate bonds, and other risk-bearing transactions.

1.1. Research context

Cat bond pricing has been investigated in Lane (2000); Gatumel and Guégan (2008) have reviewed Lane’s model as well as other models of risk pricing. Since first writing this paper, we also found the new work of Lane and Mahul (2008).

1.2. Objective

Our objective is to propose a model that describes the market clearing price of cat bonds. We propose a model that builds on theory, parsimoniously conforms to empirical data, and accentuates practicability.

2. Background

Insurance and reinsurance companies have used “cat bonds” to hedge, for a price, the risk of property catastrophe (“cat”) loss.^[1] Essentially, investors supply capital equal (usually) to the amount of the bond; the capital is then available to pay any covered losses from property catastrophe as defined in the bond. The insurance and reinsurance companies who sponsor the bonds thus hedge their exposure to cat risk, while investors earn return on capital via the coupon payments on the bonds.^[2] If no cat event takes place, the investors receive all the coupon payments and return of principal, whereas if a cat loss does occur, the investors will typically lose out on some coupons and also sustain loss of principal.

The coupon rate received by the investors is usually split into two components. First, because the investors contribute money for one (or more) years, the investors receive interest payments for the time value of their money, which is usually based on an ultra-low-risk investment rate.^[3] In addition, the investors are subject to a potential cat loss, so they receive an additional coupon rate for taking on this risk; this additional coupon rate, quoted as a percentage of the amount of the bond, can be referred to as “risk premium,” “risk spread,” “spread over risk-free,” and “spread.” In this paper, we will use the term “spread.” Thus, we can say that

$$\begin{array}{l} \text{Total coupon rate }\%\text{ to investors} =\\ \quad \text{ultra-low-risk investment rate }\%+ \text{spread }\%. \end{array}\tag{2.1}$$

The ultra-low-risk investment rate is intended to compensate investors primarily for the holding of their money but not for cat risk; thus, the spread is the component of the coupon rate that relates to the event risk of a cat loss. Therefore, we will generally use the spread to measure the “price” of hedging the cat risk:

$$\text {Price of hedging the risk of cat }=\text{ spread } \%. \tag{2.2}$$

While the spread represents the price of issuing the bond, it does not measure the “net cost” to the sponsor of the bond. After all, the sponsor has a mathematical expectation of receiving some cat loss recoveries from the bond; the “annual average loss” (“AAL”) or “expected loss” measures this quantity. In fact, as part of the bond issuance process, the sponsor will typically hire a third-party cat modeling firm to estimate the expected loss (which is then usually expressed as a percentage of the amount of the bond, a convention we follow in this paper). Usually, the spread should exceed the modeled expected loss, because the spread should be large enough to provide for the mathematically average loss and still provide some additional rate of return (above zero). Thus, we can say:

$$\begin{aligned} \text { Spread } \%= & \text { expected loss } \% \\ & + \text { additional rate of return } \% . \end{aligned} \tag{2.3}$$

$$\text { Spread } \%=\text { expected loss } \%+\text { margin } \% . \tag{2.4a}$$

$$\text { Margin } \%=\text { spread } \%-\text { expected loss } \% . \tag{2.4b}$$

Generally, these values are quoted as percentages of the amount of the bond; thus, in this paper the terms “spread,” “expected loss,” and “margin” will typically be used in the context of “as a percentage of the bond amount.” We also note that the bond amount is analogous to the occurrence limit and the aggregate limit of a property cat reinsurance contract; we will therefore use the term “limit” interchangeably with “bond amount.”^[4]

The question we investigate in this paper relates to the market pricing of cat bonds: how can we explain and predict the spreads of cat bonds? Do models of spread behavior conform to conceptual frameworks and also conform to empirical evidence? How does a theory of risk pricing inform our choice of model? Simultaneously, how does our inspection of empirical data affect our theory of risk pricing? These are the themes we explore in this paper.

3. Models of cat bond prices

Each buyer and seller in the market uses his own risk preferences to evaluate price. Models of cat bond prices do not necessarily attempt to replicate the exact risk preferences and decisions of each market participant; rather, using a macro-level perspective, they describe the observed market clearing price, which is the outcome of all the risk preferences of all the individual buyers and sellers.

Before proceeding with our analysis, we discuss several pre-existing models of cat pricing and describe what motivates us to find an alternative model. Because the issue of pricing for cat risk arises in both the cat bond market and also the traditional reinsurance market, we discuss models of cat risk pricing that derive from both sources.

3.1. Some existing models

One existing model of spreads is “multiple of expected loss.” Practitioners in the cat bond market often measure, report, and benchmark cat bond spreads as a “multiple of expected loss.”^[5] Implicitly, they espouse a model such that

$$\text { Spread } \%=\text { expected loss } \% * \text{multiple}. \tag{3.1}$$

In this model, the parameter “multiple” must vary quite significantly, because empirical data shows that when expected loss is large, the multiple is small, and when expected loss is small, the multiple is large. As a result, the “multiple of expected loss” model is neither an accurate model nor a particularly useful model. Thus, one of our central motivations is to find an alternative model that better describes spread behavior, yet preserves the ease of use of the “multiple of expected loss” model.

A different class of existing models focuses on some form of volatility metric or risk measure of the individual bond (or layer or “tranche”) in order to model the spread. Thus,

$$\text{Spread }\%= \text{expected loss }\%+ \text{margin }\% \text{ based on standalone risk}. \tag{3.2}$$

This family of models includes

1. Margin % = function of standalone standard deviation.^[6]

2. Margin % = function of conditional expected loss (i.e., conditional severity).^[7]

One problem with using standard deviation is that for highly skewed distributions, which are prevalent in property cat reinsurance, standard deviation is not an accurate description of extreme downside risk; rather, the skewed downside risk must be measured using other metrics.^[8] Thus we hypothesize that the following model, which focuses on the extreme downside of total amount of capital at risk, might be a suitable candidate:

$$\text{Spread }\%= \text{expected loss }\% +\frac{\binom{\text { amount of capital at risk } * \text { required rate }}{\text { of return on capital } \%}}{\text { amount of the bond }}. \tag{3.3}$$

For typical cat bonds, a severe downside loss can wipe out the entire principal; so the amount of “capital at risk” equals the full amount of the bond. Returning to Equation (3.3), if we replace the term “amount of capital at risk” with “amount of the bond” and cancel the term in the numerator and the denominator, we derive

$$\begin{aligned} \text{Spread }\%= & \text{ expected loss }\%\\ & + \text{required rate of return on capital }\%. \end{aligned}\tag{3.4}$$

Another problem with the standalone standard deviation and conditional severity models is that they violate a key principle of risk pricing: that one ought to measure risk not on a standalone basis but rather in a portfolio context. Thus, the standard deviation or conditional severity of a particular bond should be much less important in a portfolio context—what matters is the bond’s contribution to the total risk of the portfolio, which may differ from its standalone volatility.^[9]

What attribute of a cat bond can approximately indicate its contribution to the risk of the overall portfolio?^[10] In the context of property catastrophe risk, it seems that different perils ought to behave independently of one another; thus, we would expect virtually no connection or correlation between losses on a bond covering Southeast USA Hurricane and losses on a bond covering California Earthquake. At the same time, two bonds that both cover California Earthquake would likely tend to be correlated—if there’s a loss on one bond, there will likely be a loss on the second bond as well. So a bond’s covered “peril and geographical zone” (often “peril” for short), such as Southeast USA Wind, California Earthquake, etc., ought to be important for understanding a bond’s contribution to the risk of the total portfolio.

3.2. Initial hypothesis

As a result of the discussion above, our initial hypothesis is that cat bond pricing ought to conform to the following model:

$$\begin{aligned} \text{Spread } \%= & \text{ expected loss }\%\\ & + \text{peril specific required rate of return on capital }\%. \end{aligned}\tag{3.5}$$

$$\begin{aligned} \text { Spread } \%= & \text { expected loss } \% \\ & + \text { peril specific margin } \% . \end{aligned} \tag{3.6}$$

Such a model states that a bond’s spread must be large enough to cover the expected loss and also provide an “additional rate of return on capital” to compensate for the bond’s contribution to total portfolio risk, which varies based upon the covered peril. One advantage of this type of model, in which the compensation for risk is expressed as an additional rate of return, is its similarity to other bond market models.^[11] In addition, such a model would satisfy the intuition of practitioners that

1. If a bond’s expected loss is small, then the spread’s “multiple of expected loss” is relatively high.

2. If a bond’s expected loss is large, then the spread’s “multiple of expected loss” is relatively low.

3.3. Revised hypothesis

A review of cat bond market prices, however, shows that this model (Equation (3.6)) does not accurately describe the data. Rather, as the expected loss % increases, not only does the spread % increase, but the margin % itself (which equals spread % minus expected loss %) tends to increase as well.^[12]

We need to revise our hypothesis and propose a new model to better fit the empirical data. In proposing a revised model, we chose not to pursue various models that would describe the spread of a cat bond as an exponential function or log function of expected loss. The reason we made this decision is to ensure that our proposed model satisfies the criteria of “no arbitrage pricing” described in Venter (1991). A model that satisfies the principle of no arbitrage is laudable on the theoretical plane and also valuable on the practical plane. The practical value derives from the attribute that the price of one large layer (or “tranche”) will be the same as the sum of two smaller layers that comprise the larger layer. In essence, the price of the sum is the same as the sum of the prices. In contradistinction, models that do not satisfy “no arbitrage pricing” will calculate a price for one large layer that is different (either larger or smaller) than the sum of the prices of two layers that comprise the larger layer.^[13]

We therefore propose the following model:

1. Spread % = expected loss % + peril specific margin %.

2. Peril specific margin % = increasing function of expected loss %.

To describe margin as an increasing function of expected loss, we begin with a basic model, a linear relationship:

$$\begin{aligned} & \text{Peril specific margin }\%= \text{peril specific flat margin }\%\\ & \qquad + \text{peril specific factor} * \text{expected loss }\%. \end{aligned}\tag{3.7}$$

Combining all the pieces of Equations (3.6) and (3.7), we obtain:

$$\begin{array}{l} \text {Spread } \%=\text { expected loss } \% \\ \qquad \text { + peril specific flat margin } \% \\ \qquad \text { + peril specific factor } * \text { expected loss } \%. \end{array} \tag{3.8}$$

Or, more concisely, we have a straightforward linear function to describe spread:

$$\begin{array}{l} \text{Spread }\%= \text{peril specific flat margin }\%\\ \qquad + \text{expected loss }\% *(1+ \text{peril specific factor}).\end{array}\tag{3.9}$$

Or, for each peril, we can say

$$\begin{aligned} \text { Spread } \% = &\text { constant } \% \\ & + \text { loss multiplier } * \text { expected loss } \% . \end{aligned} \tag{3.10}$$

Because the variables of “spread,” “constant,” and “expected loss” are defined as “% of bond amount,” we also wish to show the equation in dollar terms. Multiplying both sides of the equation by “bond amount,” we obtain

$$\begin{aligned} \text { Spread } \$= & \text { bond amount } \$ * \text { constant } \% \\ & + \text { loss multiplier } * \text { expected loss } \$ . \end{aligned} \tag{3.11}$$

Equation (3.11) clarifies that the total dollar price of risk hedging in the cat bond market, according to this model, is a linear function of expected loss and bond amount.

Similarly, we note that we can rewrite Equation (3.11) in the terminology of traditional reinsurance:^[14]

$$\begin{aligned} \text { Premium } \$= & \text { aggregate limit } \$ * \text { constant } \% \\ & + \text { loss multiplier } * \text { expected loss } \$ . \end{aligned} \tag{3.12}$$

Equation (3.12) clarifies that the total dollar price of risk hedging in the reinsurance market, according to this model, is a linear function of expected loss and aggregate limit.

One favorable aspect of this type of model, as described in Equations (3.10), (3.11), and (3.12), is that it satisfies the “no arbitrage principle of pricing” as described by Venter (1991). In contradistinction, many other proposed models violate the principle of “no arbitrage.”

3.4. Conjecture on revised hypothesis

Why does the original hypothesis, “spread % = constant % + expected loss %,” fail? Why do we need the revised model, “spread % = constant % + loss multiplier * expected loss %”? Why does the expected loss need to be multiplied by a factor to obtain a viable model for spread? What does the “loss multiplier” represent? On one hand, we do not strictly need to answer these questions; so long as one model does a superior job of approximating, describing, and predicting reality, we should generally choose the better model (all else equal). On the other hand, formulating a reasonable conjecture about why a promising initial model fails, and why a modified model works better, can provide insight and potentially assist us in our later analysis.

As indicated earlier, this question also arises with corporate bond spreads and is known as the “credit spread puzzle.” As a result, various explanations offered for corporate bonds might be relevant for our discussion of cat bonds.

Hull, Predescu, and White (2005) describe several ideas to explain the excess spreads observed in corporate bonds; each one implies a different result when extrapolated from corporate bonds to cat bonds.

One explanation for the excess spreads in corporate bonds is that systematic risk is in fact prevalent in corporate bonds, especially high-yield bonds of companies of lower credit rating whose bonds behave somewhat like equities. This explanation works well for bonds below investment grade but does not work as well for investment grade bonds; similarly, since cat bonds should have virtually zero systematic risk, this hypothesis does not explain well the empirical observations that cat bond margins increase as the expected loss increases.

A second explanation suggests that non-systematic risk, aka diversifiable risk, requires a margin because portfolio managers of corporate bonds cannot fully diversify away all of the diversifiable risk in a corporate bond portfolio. This rationale would seem, at first, to carry over very well to cat bonds, since many players in the cat bond market are specialists who might be concentrated in cat bonds, thus requiring additional margin for the diversifiable but ultimately remnant risk. If this were true, however, then we would observe that the cat bonds covering non-peak risks, which diversify a cat bond portfolio, would have persistently low margins; yet, even for non-peak risks we observe the phenomenon that the margin increases as the layer expected loss increases.

The third explanation states that the credit spread puzzle observed in the corporate bond market arises mainly because market participants have forward-looking estimates of expected loss that might differ from the published statistical estimates of the expected loss. This explanation would transplant very well into the world of cat bonds because the statistical estimates of expected loss calculated by the cat modeling firms might not necessarily conform to the views of expected loss that market participants will use when pricing a bond.^[15]

After reviewing Hull’s analysis of the excess spreads in the corporate bond market, and in conjunction with our prior discussion in Sections 3.1, 3.2, and 3.3 of pricing models for cat risk, we can return to our question of Section 3.4: in the revised model “spread % = constant % + loss multiplier * expected loss %,” why do we need a loss multiplier and what does the loss multiplier represent? Our conjecture is that the “loss multiplier” parameter relates to uncertainty in the expected loss estimate.

Recall that we do not actually know the true underlying value of expected loss; rather, cat modeling firms, using computer software, provide values that are merely estimates of the true expected loss. Perhaps if we knew the precise value of expected loss, then we could say that a reasonable model is “spread % = constant % + expected loss %.” But given the uncertainty in the estimated expected loss, we must amend the model to say that “spread % = constant % + loss multiplier * expected loss %.”^[16] Meanwhile, Equations (3.5) and (3.10) remind us that the peril-specific “constant %” derives from a “required rate of return on capital” for cat risk.

4. Analysis of empirical data

In this section, we discuss the underlying data that we use in our analysis and investigate the results of fitting parameters of our proposed model to the empirical data.

4.1. Data and limitations

When investigating the price of risk in the cat bond market, we can analyze the spreads of bonds “when issued” (when they are first bought by investors in the “primary market”) and also later on when the bonds are resold and traded in the “secondary market.” Although trading in the secondary market has become more active, many initial investors prefer to buy and hold their bonds to maturity. Thus, we view the pricing of “when issued” bonds to be more informative and robust, whereas the secondary market, still in its formative stages, may not be sufficiently reliable (yet) for analyzing the price of risk. As a result, we use only the data points for cat bonds in the primary market, when they are originally issued.

The data for this study comprises various tranches of bonds, their expected loss, spreads, and the perils they cover, for the years 1998–2008. Before proceeding to analyze the data, we applied a number of filters to the data. First, because we describe cat bond spreads with peril-specific parameters, we could use only single peril bonds; we excluded from this analysis any bonds that covered more than one peril.^[17] This initial filtering left us with approximately 150 useable data points. Next, some bonds can be issued for a longer duration than the time that they are exposed to property cat risk; thus, the published spread, which corresponds to the entire lifespan of the bond, does not correspond to the time that the bond is “on risk.” To avoid this problem, we excluded any bonds whose issuance date preceded the inception date by more than 30 days. A similar complication arises when the bond covers a seasonal risk such as Wind: because the risk of cat loss is not uniform throughout the year, there can be a difference between the lifespan of the bond and the amount of time it is “on risk.” To deal this problem, we excluded any bonds whose covered peril was Wind and whose duration exceeded a whole number of years by more than 30 days. After applying the various data filters, we began the analysis with 115 data points. We also mapped the data to “issuance year” based on a 12-month period ending June 30; thus, the “2008 issuance year” comprises bonds issued between July 1, 2007, and June 30, 2008.^[18]

4.2. Results

In this section we use the empirical data to fit the parameters of our proposed model:

$$\begin{aligned} \text { Spread } \%= & \text { constant } \% \\ & + \text { loss multiplier } * \text { expected loss } \% . \end{aligned} \tag{4.1}$$

4.2.1. Wind: USA

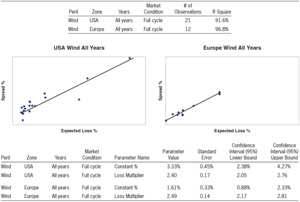
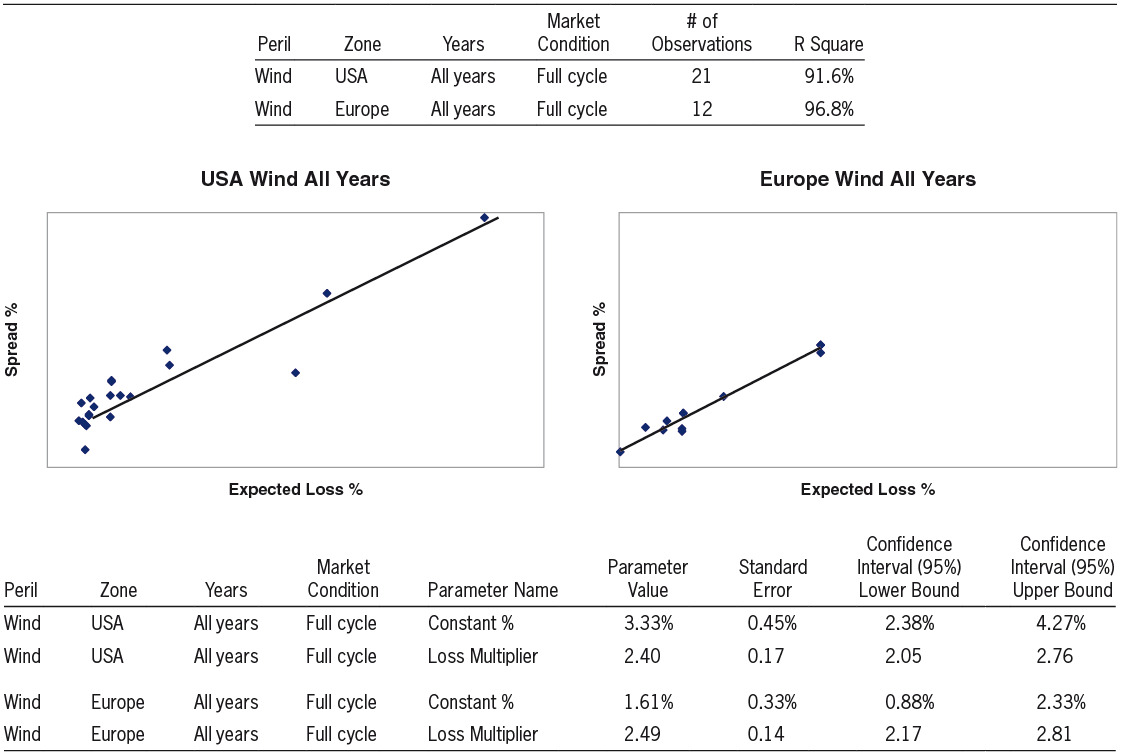
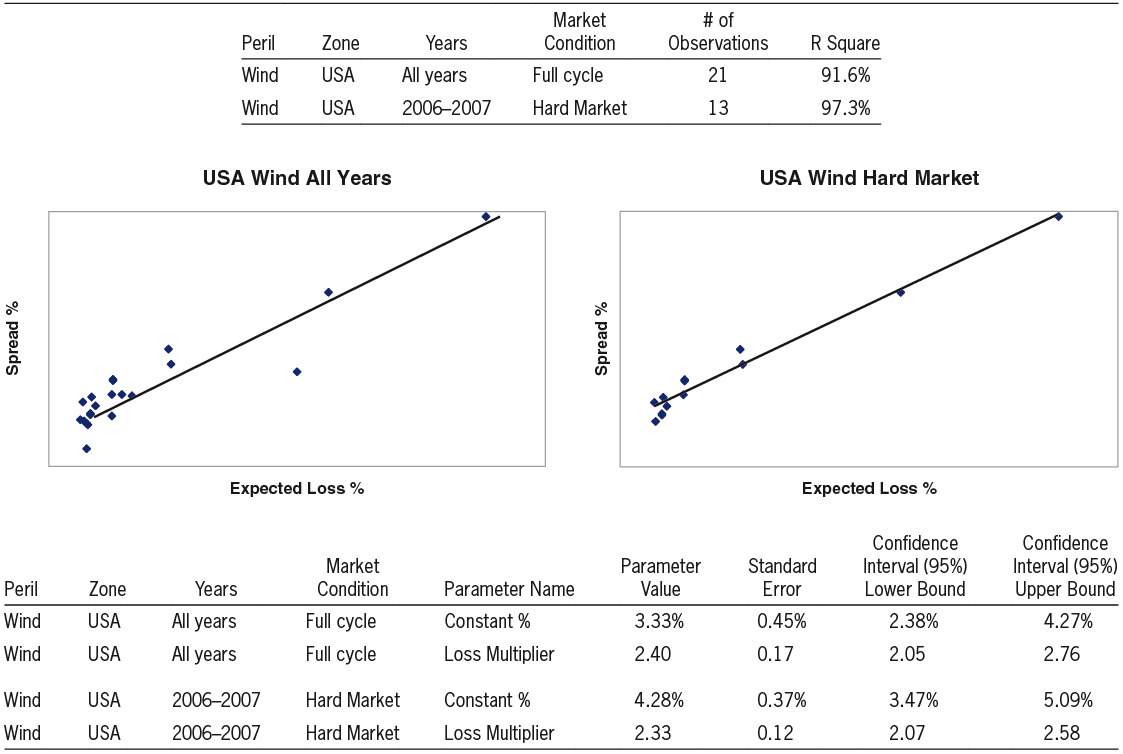
We begin by inspecting results for USA Wind.^[19] Exhibit 1 shows the fitted parameters.

The parameters in Exhibit 1 show that we can approximate the spread (when issued) of any cat bond that covers USA Wind as follows:

$$\text { Spread } \%=3.33 \%+2.40 * \text { expected loss } \% \text {. }$$

The model provides an approximation for describing spread; one can use expert judgment to refine the modeled spread by incorporating the many additional factors that influence the actual issuance spread (market conditions, trigger type, etc.).

As noted in Exhibit 1, the regression applies to USA Wind, using all years of data (1998–2008); the time horizon of the historical data covers market conditions ranging from the high prices of a “hard market” to the low prices of a “soft market.” We note that the model’s intercept (“Constant %”) and slope (“Loss Multiplier”) are significant variables.

One benefit of having a mathematical model of cat bond pricing is that it allows us to take the wide array of cat bond prices and summarize them in compact form (2 variables). Such a model also enables us to compare and contrast price behavior for various different perils, zones, time periods, and market conditions.

4.2.2. USA Wind vs. Europe Wind

We now inspect the results for the peril Wind in two different geographical zones: USA and Europe.

We note that the parameter “Constant %” for Wind is significantly higher for USA than for Europe. Given the very large accumulation of exposure in USA, it is reasonable that USA Wind contributes much more than Europe Wind to the total risk of an overall portfolio; thus the higher value of “Constant %” for USA is consistent with our hypothesis that this parameter relates to the “peril specific required rate of return on capital.” We also note that the second parameter, “Loss Multiplier,” is significantly different than unity. Interestingly, the “Loss Multiplier” for Wind does not vary much between USA and Europe. This may suggest a similar magnitude of uncertainty for expected loss estimates for USA Wind and Europe Wind, or it may be just a coincidence. Exhibit 2 shows the output.

4.2.3. USA Wind All Years vs. USA Wind Hard Market

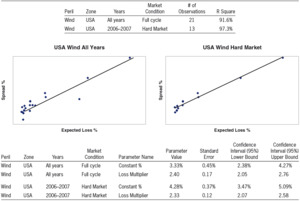
Having inspected data relating to two different zones, we now turn to analyzing data arising from two different definitions of the relevant time period to inspect.

Exhibit 3 shows results for the peril Wind and the zone USA on 2 bases:

1. Using all years of data across a full cycle of market conditions.

2. Using the 2006 and 2007 years of data, which correspond to a “hard market,” a time period of increased risk aversion and higher prices.

We note that the calculated value for “Constant %” tends to be significantly higher when using data restricted to the hard market years in comparison to using data from all years. This behavior conforms to our expectations that the market’s required rate of return on capital is higher than average during a hard market. In contrast, the fitted value for “Loss Multiplier” for USA Wind using hard market data does not differ much from the fitted value using all years’ data. Thus, the data and calculated parameters for this peril show a specific type of hard market phenomenon in which the price function’s intercept is higher than average but the slope is not higher than average.

4.2.4. Earthquake: California vs. Japan

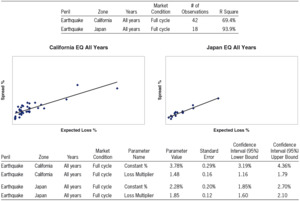
We now turn to the other major catastrophic peril, Earthquake (EQ). Exhibit 4 shows a comparison between California EQ and Japan EQ.

California, with its peak level of exposure accumulation, has a significantly higher “Constant %” than Japan. The value of the parameter “Loss Multiplier” does vary between USA and Japan, although the difference is not as significant as the difference in the “Constant %” parameter.

4.2.5. California EQ All Years vs. California EQ Hard Market

We now analyze EQ pricing during different time periods.

Exhibit 5 shows that for California Earthquake, the “Constant %” and the “Loss Multiplier” both differ significantly when using data from the hard market of 2006–2007 versus when using all years’ data. Thus, the data and calculated parameters for this peril show a specific type of hard market phenomenon in which the price function’s intercept is higher than average and also the slope is higher than average.

4.2.6. Wind and EQ, USA and Europe, California and Japan

We now examine our results for Wind and EQ in one combined context.

Exhibit 6a displays the critical parameters that summarize the behavior of four major peril/zone combinations: USA Wind, Europe Wind, California EQ, and Japan EQ. Each unique combination of peril and zone contributes in a different way to the risk of the total portfolio; thus, each peril/zone requires its own linear model with different parameters.

Despite the differences in the models, however, there appear to be some similarities. We begin by focusing on the “Constant %” parameter of the linear models.

Exhibit 6b shows that for the parameter “Constant %,” which is the intercept of the linear models, the values for the “peak” perils/zones of USA Wind and California EQ are quite similar. Additionally, the values for the significant yet “non-peak” perils of Europe Wind and Japan EQ are similar to each other and also are dissimilar to the values for the two peak perils.^[20] This phenomenon is consistent with our hypothesis that the “Constant %” relates to the “required rate of return on capital”: peak zones have the largest accumulation of exposure, tend to contribute the most to the total portfolio risk, and thus ought to have the highest required rate of return on capital; non-peak zones have less acute accumulation of exposure, tend to correlate less directly with the overall portfolio, receive some credit for their diversification effect, and have lower required rate of return on capital.

We now turn to the second parameter of the model, “Loss Multiplier.”

In Exhibit 6c, parameter values are similar not based on “peak” and “non-peak,” but rather they are similar based on geophysical peril. The value for Loss Multiplier for the peril Wind hardly varies, whether in the USA zone or in the Europe zone. In addition, the value for Loss Multiplier for the peril Earthquake for the California zone is somewhat similar to its value for the Japan zone; moreover, these values for Earthquake are dissimilar to the values for Wind. Returning once again to our conjecture: if the Loss Multiplier is greater than 1.0 because of the uncertainty in the cat model’s estimated expected loss, then this uncertainty might be similar within a common physical peril (Wind) and might be dissimilar across different physical perils (Wind vs. EQ).^[21]

Until now we have advocated the use of an individual linear model for each unique combination of major peril and zone, as described in Exhibit 6a; using 2 parameters to describe each major peril/zone combination, we have a total of 8 parameters to describe cat bond pricing for these major perils. In many cases, this approach will be the recommended framework for estimating parameters of the models of cat bond spreads.

In certain other times, there may be a need or opportunity for a more parsimonious model. Our discussion of the partial similarities of the linear models (the intercept is similar by zone, the slope is similar by peril) suggests the possibility of combining the various peril/zone combinations into one single linear model. We’ve seen that the Loss Multiplier varies by peril (Wind versus EQ) and that the Constant % varies by zone (peak USA Wind and California EQ versus non-peak Europe Wind and Japan EQ). So a single linear model combining all the individual linear models might look as follows:

$$\begin{array}{l} \text{Spread }\% = \text{Contant}_{\text{All}}\%\\ \quad + \text{Additional Constant}_{\text{Peak}}\% * \text{Peak Peril Indicator}\\ \quad + \text{Loss Multiplier}_{\text{EQ}} * \text{Expected Loss}_{\text{EQ}} \%\\ \quad + \text{Loss Multiplier}_{\text{Wind}} * \text{Expected Loss}_{\text{Wind}} \%. \end{array}\tag{4.2}$$

For this model, we assign each data point’s expected loss to either EQ or Wind. We also use an indicator variable to classify the data point as peak or non-peak (1 or 0). Now we can include all data points from single-peril bonds covering USA Wind, California EQ, Europe Wind, and Japan EQ in one model and fit the parameters.

Exhibit 7a shows how the cat bond spread tends to vary based upon expected loss, peril (Wind vs. EQ), and zone (Peak vs. Non-Peak). The intercept of the line for a non-peak zone is Constant_All %, whereas the intercept for a peak zone is the sum of Constant_All % and Additional Constant_Peak %; thus, peak zones have a larger intercept value. The slope of the line depends upon the Loss Multiplier, which varies by peril; thus, the slope of the line is steeper for Wind than for Earthquake.

We can also examine such a model for a restricted time period, when market conditions are more homogeneous.

Exhibit 7b, together with Exhibit 7a, shows that when using the data of the hard market years of 2006–2007, the parameters of the linear model are different than when using all years’ data; the differences are manifest in various ways. The parameter “Additional Constant_Peak %,” which reflects the incremental additional price for peak zones, roughly doubles, from a 1.17% all years’ average to a hard market value of 2.30%; meanwhile, the parameter “Constant_All %,” which serves as the intercept for non-peak zones, hardly changes. The parameter “Loss Multiplier_Wind,” which already has a high value for the all years’ data, does not differ when fitted to the hard market data; “Loss Multiplier_EQ,” which has a lower prevailing value for the all years’ data, differs significantly when fitted to hard market data.

4.2.7. All perils

When we describe bond spreads using individual linear models, there are certain peril/zone combinations that will not have sufficient data to support reliable parameters. For example, Australia EQ, Mexico EQ, Mediterranean EQ, and Japan Wind are some of the perils for which we do not have enough data points to support standalone linear price functions. However, one of the advantages of a combined model such as Equation (4.2) is the ability to include many of these ancillary perils in one overall linear function. In order to do so, we first note that these ancillary perils are likely less correlated with the overall portfolio than peak and non-peak perils; as a result, they ought to have a lower required rate of return on capital and thus a materially different value for “Constant %.” We thus expand our categories to 3 buckets:^[22]

1. Peak (USA Wind, California EQ)

2. Non-peak (Europe Wind, Japan EQ)

3. Diversifying (Japan Wind, Australia EQ, Mexico EQ, Mediterranean EQ, Central USA EQ, and Pacific Northwest USA EQ)

We now can augment Equation (4.2) to apply to all peril/zone combinations, as follows:

$$\begin{array}{l} \text{Spread }\% = \text{Constant }\% \\ \quad + \text{Additional Constant}_{\text{Peak}} \% * \text{Peak Peril Indicator}\\ \quad + \text{Additional Constant}_{\text{Diversifying}} \% * \text{Diversifying Peril Indicator}\\ \quad + \text{Loss Multiplier}_{\text{EQ}} * \text{Expected Loss}_{\text{EQ}}\%\\ \quad + \text{Loss Multiplier}_{\text{Wind}} * \text{Expected Loss}_{\text{Wind}}\%. \end{array} \tag{4.3}$$

In Equation (4.3), the slope of the linear price function depends on whether the covered peril is EQ or Wind; the intercept depends upon the peril/zone being peak, non-peak, or diversifying.

For a diversifying peril, the intercept is the sum of “Constant_All %” and “Additional Constant_Diversifying %.” We expect that the parameter value for “Additional Constant_Diversifying %” should be negative, because a diversifying peril should have a lower required rate of return on capital and thus a lower intercept than other perils.

Exhibit 8a shows the results of fitting parameters to the model in Equation (4.3), using data from bonds covering all perils/zones.

The parameters displayed in Exhibit 8a describe the spreads of property cat bonds covering all perils and zones. They tell us that one can approximate the spread of any “single peril” cat bond by taking the product of the expected loss and a “Loss Multiplier” (which depends on whether the peril is Wind or EQ) and then adding a “Constant %” (which depends upon the whether the covered peril/zone is “peak,” “non-peak,” or “diversifying”).^[23] Exhibit 8a also confirms our expectations that the linear function for a diversifying peril has a significant additional negative parameter (“Additional Constant_Diversifying %”) and thus a lower intercept than other perils.

We now inspect the results of fitting parameters to the same model but using the more homogenous market conditions prevalent during the hard market years of 2006–2007.

Exhibit 8b, together with Exhibit 8a, shows that when using the data of the hard market years of 2006–2007, the parameters of the model differ in various ways. The parameter “Additional Constant_Peak %,” which reflects the incremental additional price for peak zones, is significantly higher. The parameter “Constant_All %,” which serves as the intercept for non-peak zones, hardly changes. Finally, the parameter “Additional Constant_Diversifying %” becomes even more negative when using hard market data, implying that the required rate of return for a “diversifying peril” is lower when the additional cost of peak perils is higher; stated differently, the “benefit” of a diversifying peril is larger when the incremental cost of peak perils is larger. However, the large standard error for this negative parameter indicates that this change may not be significant and requires further investigation. Finally, we note that the parameter “Loss Multiplier_EQ” is larger when fitted to hard market data, while the parameter “Loss Multiplier_Wind” does not change. While the future seldom duplicates the past, these results may provide some hints about how key pricing parameters might behave during future hard markets.

5. Areas for further research

Some areas for further research are as follows:

1. Our analysis uses simple regression, which weights all squared errors equally. Future research may consider a linear model that allows for varying weights on the squared error terms when fitting parameters.

2. Because of data limitations, we included only single-peril bonds in our analysis. For multi-peril bonds, one requires information about the amount of expected loss that various perils and zones contribute to the total expected loss. With such data, one can include price information from multi-peril bonds when selecting models and fitting parameters.^[24] In addition, one could then quantify to what extent (if any) a multi-peril bond suffers a price penalty relative to what the price “should have been” based on the contribution of various covered perils to its expected loss. Such a model could help quantify the tradeoff of sponsoring several bonds that each cover a single peril (e.g., better price but higher transactional costs) versus the advantages of sponsoring one bond covering multiple perils (e.g., worse price but lower transactional costs).

3. The parameters of the proposed linear model tend to be different based on market conditions, which are constantly changing. With sufficient data, one might be able to fit parameters to many incremental time periods and produce a time series of fitted parameters; such a data set would allow one to analyze how the parameters drift over time. If one could identify the catalysts that drive the changes in the parameters over time, one could develop a forward-looking model that predicts the likely changes in the values of the key parameters of the price function for the next time period.

4. Our focus thus far has been on the price of hedging cat risk via the cat bond market. What about the price of hedging cat risk in the traditional reinsurance market? We note that reinsurance contracts, which typically have reinstatable limit and premium, have different contractual features than cat bonds. Still, would some form of linear model adequately capture the market price of reinsurance contracts? Would such a model for the price of reinsurance contracts be similar or dissimilar to the model for cat bond prices? What would the similarity or dissimilarity of these models tell us? What would these models tell us about which types of cat risk are best handled via balance sheet equity capital, reinsurance capital, and cat bond capital? For example, our analysis suggests that two forces affect the price of cat risk in the cat bond market: the first factor is required rate of return on capital, and the second factor is uncertainty in the estimate of expected loss. The broad asset portfolios that hold cat bonds may provide better diversification than traditional reinsurers, which may lower the component of price that derives from the required rate of return on capital, yet the uncertainty in the estimated expected loss may exert counter-pressure and raise the price of cat bonds. As a result, cat bonds may be relatively attractive in situations in which the layer price is mostly influenced by the “required rate of return” factor, but not in situations in which price is mostly influenced by the “uncertainty in the expected loss” factor. This hypothesis suggests that cat bonds will likely continue to be relevant mainly for cat layers that have low expected loss and cover peak perils, whereas reinsurance capital or equity capital may be preferable in other situations. The implication is that insurers may be able to enhance their capital structure by mixing together equity capital, reinsurance capital, and cat bond capital in an optimal combination.

6. Conclusions

In this paper, we describe the market clearing price of cat bonds by modeling cat bond spreads as a linear function of the bonds’ expected loss. This relationship between spread and expected loss, however, differs by cat peril and geographic zone; each unique combination of peril and zone sports its own “price line” with a different intercept and slope. We also present an approach which combines these individual models into one unified model. Whether using individual models or a combined model, the parameters differ over time as market conditions change. We hypothesize that the key parameters in the linear models relate to two main drivers of price: required rate of return on capital and uncertainty of the expected loss. These two factors provide a roadmap for indentifying situations that are most suitable for reinsurance versus cat bonds and vice versa. We also note that the factor relating to uncertainty of the expected loss may help explain the broader issue of the “credit spread puzzle,” which is an unresolved question about the corporate bond market.

Using the proposed linear models for cat bond prices, we can compute the market clearing price functions for various perils and zones, how they compare and contrast to each other, and how they change over time. Such models help us understand the drivers of the price of cat risk and help us describe how prices have behaved in the past and, potentially, how they might behave in the future.

---

Acknowledgment

The authors thank all those who commented on earlier drafts of this paper.

---

1. This section serves as basic introduction and background for the purpose of discussing the market price of cat risk. It is not intended as a comprehensive text on the cat bond market. Therefore, we caution the reader that some statements that are generally true may have caveats and exceptions, which we typically choose not to highlight because our concerns are materiality and brevity.

2. We caution the reader that this section serves as a streamlined background and does not address all the various technicalities of cat bonds. One example of a technicality is that an insurance company typically uses a Special Purpose Vehicle (SPV) to “issue” the bond; the company only “sponsors” the bond. In this paper, we use the terms “sponsor” and “issue” interchangeably.

3. Prior to the financial crisis of 2008, cat bonds usually used the LIBOR rate as a benchmark, which is higher than the risk-free rate and incorporates some credit risk as well. After this arrangement proved problematic, the market switched to other approaches; now treasuries or other ultra-low-credit-risk investments are often used.

4. Where “limit” is the “100% limit” reduced for “co-participation” or “coinsurance.”

5. Similarly, Lane and Mahul (2008, 5) describe observed spread as “it was 2.7 times the expected loss.”

6. See Kreps (1999); this model enjoys widespread popularity in the traditional reinsurance market.

7. See Lane (2000). Although Lane also uses the probability of loss, here we specifically focus on the choice of conditional expected loss because, according to Lane, “we believe that one way to capture the asymmetric nature of loss distribution is to measure the ‘conditional expected loss’ (CEL). . . .” Thus the choice of conditional expected loss is emblematic of the family of models that assert that spread is related to standalone volatility and standalone risk.

8. See Kozik and Larson (2001).

9. Indeed, Kreps (1999) states quite explicitly that a price based on standalone standard deviation should be viewed only as an upper bound of the price, whereas the actual market price should be lower.

10. This “overall portfolio” could theoretically be as diverse as the portfolio of all investments opportunities, but we note that taking cat risk may require critical mass of time, money, and expertise, which implies an “overall portfolio” that is concentrated in cat bonds. At the same time, cat bond pricing can be influenced by pricing in the traditional reinsurance market. So the “overall portfolio” in which we evaluate the risk of a cat bond may range from the portfolio of all investment opportunities to the portfolio of all cat bonds to the portfolio of all reinsured exposures; or it may reflect a mixture of these various perspectives. This issue requires further research.

11. Hull, Predescu, and White (2005).

12. This surprising phenomenon occurs in the corporate bond market as well, where it is sometimes referred to as the “credit spread puzzle”; see Hull, Predescu, and White (2005). Thus pricing models of corporate bond market spreads might be able to shed light on cat bond spreads, and vice versa.

13. This was a drawback of various models we reviewed in the literature.

14. Here the “spread” is the “price” (or “premium”) and the “bond amount” is the aggregate limit. This analogy holds for reinsurance contracts that have no reinstatement premium and no reinstatement of limit. We require further research to determine how to adapt the cat bond pricing formula for a reinsurance contract with reinstatable limit and premium.

15. In addition to uncertainty in the expected loss estimate, there is also the statistical downward bias arising from the sponsor’s prerogative to choose which modeling firm will forecast the expected loss for the bond.

16. An interesting test case arises when a modeling firm makes systematic changes to its model and to its loss cost estimates; if the overall effect is to consistently and multiplicatively increase the expected loss estimates then, all else equal, the loss multiplier that is observed in the market should decrease in magnitude.

17. With sufficiently detailed information, one could include multi-peril bonds in the analysis; however, because we could not obtain reliable data quantifying how much the various perils contributed to the total expected loss of multi-peril bonds, we could not include these bonds in our analysis.

18. This mapping is used in AON Capital Markets (2008).

19. The bonds in this category generally cover some combination of Florida, Southeast USA, and/or Northeast USA. We could not split this large category into more granular subcategories.

20. See MMC Securities (2006), which categorizes perils/zones into 3 major buckets:

    1. “Peak” (USA Wind and USA EQ)

    2. “Non-Peak” (Europe Wind and Japan EQ)

    3. “Pure Diversifying Perils” (other perils such as Australia EQ, Mexico EQ, and Japan Wind)

21. This hypothesis is speculative because the wind peril’s behavior and the commercial models that estimate the expected loss and the calibration data that they use are different across geographical zones (e.g., USA vs. Europe) as well.

22. See MMC Securities (2006).

23. The equation should be extendable to apply to multi-peril bonds as well.

24. In fact, since first writing this paper, an analysis by Lane and Mahul (2008) has included multi-perils bonds; one drawback of their multi-peril bond analysis is that it does not define the intercept term as the weighted average of the intercepts of the covered single perils (despite using a weighted average approach for the slope).