Bayesian Claim Severity with Mixed Distributions

1. Introduction

Actuaries find per-claim loss severity distributions useful for several purposes, including computing increased limit factors (ILFs), pricing excess of loss (XOL) reinsurance contracts, and stochastic risk modeling. This paper presents a method for computing a severity distribution in the mixed exponential family.

When claim data is abundant, a severity distribution can be easily computed using empirical methods, non-parametric statistics, or maximum likelihood methods (Klugman, Panjer, and Willmot 2009). When no data is available, actuaries use a default distribution, perhaps from a statistical agency or from a different book of business. Our technique is designed to compute a severity distribution for the awkward middle ground where data is partially credible: some claims have been observed, but the default distribution is still considered informative.

Intuitively, the claim severity distribution should morph from the default distribution into some fitted distribution as more and more claims are observed. This paper uses Bayesian statistics to achieve this “morphing” in a principled and mathematically correct way.

Here are some advantages of the technique presented in this paper:

1. The default severity distribution is mixed exponential and thus is compatible with many severity distributions supplied by Insurance Services Office (ISO). Other mixed distributions should work with minor modifications.

2. In the limiting condition where there are no claims, the method produces the default distribution—having too few claims is never an issue.

3. In the other limiting condition (abundant observed claims), the method is equivalent to fitting a mixed exponential via maximum likelihood.

4. The uncertainty about the default severity distribution is supplied by a single parameter, which can be estimated in a straightforward way.

5. Truncated and censored data (as caused by limits and deductibles) are handled correctly. Adjustments such as the Kaplan-Meier estimator are not required.

6. The posterior distribution is computed using standard Bayesian updating on observed claim severities. This is usually considered the most principled way of analyzing partially-credible data.

7. Trend can be a chicken-and-egg problem: claim severity depends on trend, but the estimation of trend depends on the credibility of observed claim severities. Here trend and severity are estimated simultaneously.

8. The technique quantifies uncertainty about the severity distribution. In other words, it analyzes “parameter risk” and not just “process risk.”

9. The resulting posterior predictive severity distribution is easy to work with analytically because it is a mixed exponential with the same means as the default severity distribution.

The numerical results of this technique can be computed quickly using the Markov chain Monte Carlo (MCMC) method. Below we will use this method on some sample data to compute the posterior distribution. Later the paper discusses two possible applications: pricing excess of loss reinsurance and generating ILFs.

2. Required input data

We need four pieces of input data to use the technique to compute a posterior severity distribution:

1. the observed claim data: a per-claim list of severity, age, deductible, and whether or not each claim was capped by a policy limit,

2. the means and weights of the default mixed exponential severity distribution,

3. the prior severity uncertainty, as represented by Dirichlet parameter α₀, and

4. the prior trend mean and standard deviation.

The first, claim data, is straightforward. The other inputs are more subjective. The remainder of this section discusses each of these and gives some examples.

2.1. Claim data

Table 1 shows the format of the necessary claim data. The Amount column contains the total claim size (this could include or exclude loss expense, depending on what’s being modeled). In this example, we are using closed claims only, so no development is necessary. If development is required, claims should be developed prior to the application of this method.

The Age column is used for trending and indicates years before the desired trend endpoint. Fractional ages are allowed. The capped column indicates whether the claim was capped by policy limits. The deductible column indicates the deductible that the claim was subjected to. If the deductibles were non-zero, the indicated amount would be the loss net of the deductible.

2.2. Mixed exponential

The second piece of data required by this method is the mixed exponential severity distribution that would be used if no claim data were available. Here we use a Bayesian framework, where it is called the prior predictive distribution. Table 2 shows the means and weights of an example mixed exponential distribution. Common sources for this data are statistical organizations such as ISO or analysis of a similar book of business. For weights a_j and means $\mu_j$, the probability density function of a mixed exponential is

$$f(x)=\sum_{j=1}^{m} \frac{a_{j}}{\propto_{j}} e^{-\frac{x}{\alpha_{j}}}.$$

This paper focuses on the mixed exponential distribution because that is the prior severity distribution most familiar to the author. However, this paper’s techniques should apply to mixtures of other distributions (e.g., an Erlang mixture as developed by Lee and Lin 2010) with modifications. The main computational requirement is that the distribution’s density and cumulative distribution function should be calculable.

2.3. Dirichlet uncertainty

Although the means and weights of the mixed exponential distribution determine the severity distribution, we also need to know how certain we are that these parameters are accurate. Are they just a rough estimate that may be far off, or are we sure that the true distribution is very similar? The more confidence we have in our a priori distribution, the longer we will stick with it as more claims are observed. This uncertainty can be summarized as α₀, the sum of the Dirichlet parameters. Here we picked a value of 20. See Section 3.3 for guidance on choosing this parameter.

2.4. Trend

Finally, we need the prior trend rate distribution. The trend is applied to each ground-up claim by age. For instance, if the trend rate is 7%, then claims of age 2.5 are expected to be 1.07^−2.5 times as severe as claims of age 0.

We assume trend is constant over time, and the parameter uncertainty is modeled as a gamma distribution, shifted so that the zero point indicates −100% trend. Choosing a mean and standard deviation suffices to determine the gamma parameters via method of moments. These constants can be based on a statistical agency, another book of business, economic indicators, or actuarial judgment. In this paper, the example trend mean is 0.05 and the trend standard deviation is 0.01.

3. Bayesian model

The expressions below formally describe the assumed Bayesian model. See Hoff (2009) for a basic introduction to Bayesian methods.

$$x_{i} \mid b_{i}, r \sim \min \left(\operatorname{Exponential}\left(\frac{r^{t}}{\mu_{b_{i}}}\right), l_{i}\right). \tag{1}$$

$$b_{i} \mid w_{1}, \ldots, w_{m} \sim \text { Categorical }\left(g_{d_{i}}\left(w_{1}\right), \ldots, g_{d_{i}}\left(w_{m}\right)\right). \tag{2}$$

$$w_{1}, \ldots, w_{m} \sim \operatorname{Dirichlet}\left(\boldsymbol{\alpha}_{1}, \ldots, \boldsymbol{\alpha}_{m}\right). \tag{3}$$

$$r \sim \operatorname{Gamma}(k, \theta). \tag{4}$$

x_i, b_i, w_b, and r are all real random variables, while $\mu_b$, m, t_i, d_i, l_i, $\alpha_j$, k, and θ are real numbers. Index i ∈ {1, . . . , n} ranges over the number of observed claims n; x_i are the claims’ severities, l_i are their limits, and d_i are their deductibles. m is the number of mixed exponential buckets; b_i ∈ {1, . . . , m} represents the bucket that produced the ith claim, and $\mu_b$ is the mean of each bucket b. Functions $g_{d_{i}}$ adjust the weights for each claim’s deductible d_i; they are defined by Equation (24) in Section 5. Finally, t_i is the age of the ith claim and r is the trend factor. Random variables are independent unless the dependence is expressed in the equations above.

Intuitively, Equations (1) and (2) express the process risk and (3) and (4) express the parameter risk. They basically say that each claim is independent and is produced by a (possibly capped) mixed exponential distribution. Moreover, we know for certain the exponential means µ₁, . . . , $\mu_m$. However, the trend rate and mixed exponential weights are uncertain. All claims share the same trend factor r and mixed exponential weights w₁, . . . , w_m but these are themselves random variables, generated by the gamma and Dirichlet distributions. Sometimes $\alpha_j$, k, and θ are called hyperparameters because they generate parameters (w_b and r) used in other distributions.

3.1. The categorical distribution

Actuaries know and use the categorical distribution but perhaps do not bother naming it. This distribution simply chooses a number from 1 to m with specified probabilities. For instance, if y ∼ Categorical (.5, .3, .2) then y = 1 with probability 0.5, y = 2 with probability 0.3, and y = 3 otherwise. Equations (1) and (2) imply that x_i is a capped and trended mixed exponential distribution, conditional on weights w₁, . . . , w_m.

3.2. The Dirichlet distribution

The exponential, categorical, and gamma distributions are familiar to actuaries, the Dirichlet perhaps less so. The Dirichlet distribution is the multidimensional analogue of the beta distribution. Just as the beta distribution can be used to express uncertainty about two numbers that must sum to 1, the Dirichlet can express uncertainty about m positive numbers that must sum to 1. And just as the beta distribution can parameterize a Bernoulli distribution, the Dirichlet is natural for parameterizing a categorical distribution. This property makes it popular in Bayesian analysis (see Mildenhall 2006, for an example of the Dirichlet applied in an insurance context).

Here are some useful properties of the Dirichlet distribution (Wikipedia, n.d.). If w₁, . . . , w_m ∼ Dirichlet $\left(\alpha_1, \ldots, \alpha_m\right)$ and $\alpha_0=\sum_{j=1}^m \alpha_j$, then

$$\sum_{j=1}^{m} w_{j}=1. \tag{5}$$

$$E\left[w_{j}\right]=\frac{\alpha_{j}}{\alpha_{0}}. \tag{6}$$

$$\operatorname{Var}\left[w_{j}\right]=\frac{\alpha_{j}\left(\alpha_{0}-\alpha_{j}\right)}{\alpha_{0}^{2}\left(\alpha_{0}+1\right)}=\frac{E\left[w_{j}\right]\left(1-E\left[w_{j}\right]\right)}{\left(\alpha_{0}+1\right)}. \tag{7}$$

$$\begin{array}{r} \operatorname{Cov}\left[w_{j}, w_{k}\right]=\frac{-\alpha_{j} \alpha_{k}}{\alpha_{0}^{2}\left(\alpha_{0}+1\right)}=\frac{-E\left[w_{j}\right] E\left[w_{k}\right]}{\alpha_{0}+1} \\ \text { for } j \neq k . \end{array} \tag{8}$$

Because we are given the initial default weights a_j = E[w_j], the choice of α₀ will uniquely determine $\alpha_1, \ldots, \alpha_m$ by (6). As in the beta distribution, the larger the sum of the parameters α₀, the more certain we are of the true weights.

3.3. Choosing α₀

In the input data section, the parameter α₀ was used to summarize our uncertainty around the mixed exponential prior distribution. Sometimes this parameter is thought of intuitively as the number of claim observations equivalent to the information encapsulated by our Bayesian prior. In this case, however, that intuition is of limited help in selecting a particular value. Instead we will use this result:

Suppose that X is a mixed exponential distribution (with fixed means) depending on weights w₁, . . . , w_m, and that h(x) is a real function. Define h_j = E[h(x)|b = j] and $a_{j}=\frac{\alpha_{j}}{\alpha_{0}}$ Then

$$\begin{array}{l} \operatorname{Var}\left[E\left[h(x) \mid w_{1}, \ldots, w_{m}\right]\right]=\sigma^{2} \\ =\operatorname{Var}\left[\sum_{j=1}^{m} w_{j} E[h(x) \mid b=j]\right] \\ =\operatorname{Var}\left[\sum_{j=1}^{m} w_{j} h_{j}\right] \end{array} \tag{9}$$

$$=\sum_{j=1}^{m} h_{j}^{2} \operatorname{Var}\left[w_{j}\right]+\sum_{j \neq k} h_{j} h_{k} \operatorname{Cov}\left[w_{j}, w_{k}\right] \tag{10}$$

$$=\sum_{j=1}^{m} h_{j}^{2} \frac{a_{j}\left(1-a_{j}\right)}{\alpha_{0}+1}+\sum_{j=k} h_{j} h_{k} \frac{-a_{j} a_{k}}{\alpha_{0}+1}, \tag{11}$$

hence

$$\alpha_{0}=\sigma^{-2}\left(\sum_{j=1}^{m} h_{j}^{2} a_{j}\left(1-a_{j}\right)-\sum_{j \neq k} h_{j} h_{k} a_{j} a_{k}\right)-1 . \tag{12}$$

Above, (9) follows from (1) and (2), (10) from the variance sum formula, and (11) from (7) and (8).

We can now use (12) to choose a value for α₀. For instance, suppose the actuary feels that the there is about $50,000 of uncertainty around the expected value of the actual ground-up mixed exponential claim distribution capped at $1M, where uncertainty is measured by the standard deviation. Then, by setting h(X) = min(X, 1Mil), $h_{j}=\mu_{j}\left(1-e^{-\frac{1 M i l}{\mu_{j}}}\right),$ and σ = $50,000, the above result can be used to calculate α₀.

In our sample input data, we assumed that the standard deviation of expected loss in the first million layer was 65770. Applying (12), α₀ = 20.

3.3.1. Other metrics

Although (12) gives us a quick way to estimate α₀ from prior uncertainty about the standard deviation of expected loss, the actuary’s prior may be couched in different terms. For instance, he or she may instead have an intuition about a 90% confidence interval around expected loss, or even a 90% confidence interval around the 95% percentile of loss.

A simple simulation can be used to infer α₀ from this type of information:

1. Using a candidate value of α₀, simulate 500 draws from the Dirichlet distribution.

2. For each of the draws in (1), simulate 1000 claims, applying deductibles or limits as desired.

3. For each draw in (1), compute the statistic (e.g., expected loss) on the 1000 claims generated in (2).

4. Compute the summary statistic (e.g., standard deviation) on the 500 statistics computed in (3).

Modern computers are fast enough that the above procedure may just take a split second per α₀ value. It is thus practical to evaluate a range of values and choose one based on an arbitrary metric.

3.4. Matching the prior predictive severity distribution

In the introduction, we mentioned that the model matches the prior predictive mixed exponential severity distribution before any claims are observed. This is demonstrated below, by showing that our model’s CDF is equal to the CDF of the desired default mixed exponential. For simplicity we will assume here that there are no limits or deductibles—if two distributions are the same gross of limits and deductibles, they will also be the same net of those policy terms.

$$F(c)=\operatorname{Prob}\left[x_{i}<c\right] \tag{13}$$

$$=\sum_{j=1}^{m} \operatorname{Prob}\left[x_{i}<c \mid b_{i}=j\right] \operatorname{Prob}\left[b_{i}=j\right] \tag{14}$$

$$\begin{array}{c} =\sum_{j=1}^{m} \operatorname{Prob}\left[x_{i}<c \mid b_{i}=j\right] \\ \int \operatorname{Prob}\left[b_{i}=j \mid w_{j}\right] f\left(w_{1}, \ldots, w_{m}\right) d w \end{array} \tag{15}$$

$$=\sum_{j=1}^{m} \operatorname{Prob}\left[x_{i}<c \mid b_{i}=j\right] E\left[w_{j}\right] \tag{16}$$

$$=\sum_{j=1}^{m}\left(1-e^{-\frac{c d^{i}}{m_{j}}}\right) a_{j} \tag{17}$$

$$=\sum_{j=1}^{m} a_{j}\left(1-e^{-\frac{c}{m_{j}}}\right) \tag{18}$$

$$=1-\sum_{j=1}^{m} a_{j} e^{-\frac{c}{m_{j}}} . \tag{19}$$

Steps (13) to (17) follow from simple probability and the model specification. Step (18) holds because our default distribution is taken to cover the current time, so t_i = 0. Finally, $\sum_{j=1}^m a_j=1$ implies (19), the CDF of our default mixed exponential distribution.

3.5. Deductibles

This subsection will describe how this method accounts for deductibles and explain how the g functions mentioned in Section 3 are derived. The main result will be that a mixed exponential ground-up severity distribution implies that losses net of any deductible level are also mixed exponential with the same means.

Suppose a claim has a mixed exponential ground-up severity distribution represented by random variable X. Then its probability density function is

$$f_{X}(x)=\sum_{j=1}^{m} \frac{a_{j}}{\mu_{j}} e^{-\frac{x}{\mu_{j}}}$$

for means $\mu_j$ and weights a_j. The loss net of deductible d is distributed as Y = (X − d)|{X >= d}. Its density function is

$$f_{Y}(x)=\frac{f_{X}(x+d)}{1-F_{X}(d)} \tag{20}$$

$$=\frac{\sum_{j=1}^{m} a_{j} \frac{\mu_{j}}{-\frac{x+d}{\mu_{j}}}}{\sum_{j=1}^{m} a_{j} e^{-\frac{d}{u_{j}}}} \tag{21}$$

$$=\frac{\sum_{j=1}^{m} \frac{a_{j} e^{-d / \mu_{j}}}{\mu_{j}} e^{-\frac{x}{\mu_{j}}}}{\sum_{j=1}^{m} a_{j} e^{-\frac{d}{\mu_{j}}}} \tag{22}$$

$$=\sum_{j=1}^{m} \frac{a_{j}^{\prime}}{\mu_{j}} e^{-\frac{x}{\mu_{j}}}, \tag{23}$$

and therefore the new distribution is also mixed exponential with means $\mu_j$ and new weights a_j′ where $a_{j}^{\prime}=\frac{a_{j} e^{-\frac{d}{\mu_{j}}}}{\sum_{k=1}^{m} a_{k} e^{-\frac{d}{\mu_{k}}}}$.

By defining

$$g_{d}\left(w_{j}\right)=\frac{w_{j} e^{-\frac{d}{\mu_{j}}}}{\sum_{k=1}^{m} w_{k} e^{-\frac{d}{\mu_{k}}}} \tag{24}$$

we adjust the mixed exponential weights to reflect the deductible d. From this definition we can make two observations:

1. If there is no deductible, then $g_{0}\left(w_{j}\right)=\frac{w_{j} \times 1}{\sum_{k=1}^{m} w_{k} \times 1}$= w_j. Thus, we can simply ignore the g functions in this case.

2. The larger the deductible d, the more the weights of the mixed exponential are skewed to the larger means by the $e^{-\frac{d}{\mu_{j}}}$ term. This is intuitive because exponentials with larger means tend to generate more severe claims.

This method correctly adjusts each claim’s severity distribution to account for its deductible. However, it suffers from two limitations when claims are subject to different deductible levels. First, it assumes that claims subject to different deductible levels are generated from the same underlying ground-up distribution. In reality, policyholders’ perceptions of their risk influence their deductible choices. Second, it only takes into account per-claim severity data. Frequency data along with exposure information per deductible level (e.g., a deductible profile) may yield additional information about ground-up severity.

3.6. Why not vary the means?

It may seem more practical to allow the means of the exponential distributions to vary with observed claims. The reason this paper only adjusts the weights is that this allows the correct default distribution to be used when there are no claims. As shown in the previous section, the prior predictive severity distribution will correctly equal the default distribution as long as the expected weights are equal to the desired default weights. However, there is no similar way to do this by varying the means.

For example, suppose desired claim severity is an equally-weighted mixed exponential of means 100 and 300:

$$p(x)=0.5 \frac{e^{-x / 100}}{100}+0.5 \frac{e^{-x / 300}}{300} .$$

Then p(x) can be expressed as the weighted mixture of various other mixtures of exponentials with means 100 and 300, such as

$$\begin{aligned} p(x)= & \frac{1}{2}\left(0.25 \frac{e^{-x / 100}}{100}+0.75 \frac{e^{-x / 300}}{300}\right) \\ & +\frac{1}{2}\left(0.75 \frac{e^{-x / 100}}{100}+0.25 \frac{e^{-x / 300}}{300}\right). \end{aligned}$$

However, it is impossible to express p(x) as a (positive) mixture of exponentials with means other than 100 or 300. Thus, the method used in this paper to add uncertainty to a mixed exponential’s weights cannot be used to add uncertainty to its means instead.

4. Computation and results

The posterior distribution of the probabilistic model specified in Section 3 is probably not analytically soluble because of the interaction of the Dirichlet and gamma distributions. Interestingly, the model does permit an analytic solution if we omit trend uncertainty, but the number of terms in the analytic solution is exponential in the number of claims and thus is computationally intractable.

However, a Markov chain Monte Carlo (MCMC) technique can be used to quickly compute the posterior distribution. We recommend Just Another Gibbs Sampler (JAGS), which can create an MCMC algorithm given a succinct description of a Bayesian model (Plummer 2003). It is also cross-platform, open source, actively maintained, and easily integrated into R code. Here is JAGS code that expresses the model specified in Equations (1)–(4).

model {
    weights ~ ddirch(alpha)
    trend.factor ~ dgamma(trend.shape, trend.rate)
    
    for (i in 1:n) {
        bucket[i] ~ dcat(weights)
        is.capped[i] ~ dinterval(claim[i], limit[i])
        claim[i] ~ dexp(1 / (means[bucket[i]] / trend.factor^ages[i]))
    }
}

Above, is.capped is a boolean vector that indicates whether each claim is capped at policy limits. Complete documented R code, without the ability to handle adjustable deductible levels, is available in an easy-to-use format from FAViR (n.d.). Because the example data set was from a casualty line and had no deductible, the above omits deductible handling code for speed. Appendix A contains the full JAGS model.

Appendix A also discusses code to implement the same model written in Stan (Stan Development Team 2013), an alternative to JAGS.

4.1. Example MCMC results

The model was run based on the input data in Section 2, i.e.:

1. The observed 10 claims x_i as shown in Table 1.

2. The default mixed exponential means $\mu_j$ and weights a_j as shown in Table 2.

3. The severity uncertainty from Section 3 represented by α₀ = 20.

4. The trend mean and standard deviation, chosen in Section 2.4 to be 5% and 1%, respectively.

A few results of the MCMC simulation, samples from the posterior distribution of the bucket weights w_i, are shown in Table 3. Table 4 summarizes all the results.

The required time of the MCMC simulation will increase linearly with the number of claims n, the number of exponential means m, and the number of samples. In this example, 80,000 samples were produced in total. The runtime was quick on a Intel i5 CPU because there were only 10 claims being analyzed. In practice, the runtime of this model does not seem to be a large practical problem—if the number of claims is large enough that the model runs slowly, the number of claims is also large enough that the data has full credibility and a (faster) maximum likelihood technique, as in Keatinge (1999), would reach the same answer.

Table 4 compares the prior and posterior marginal expected weights. The error column is an estimate of the standard error in the expected value of the MCMC method. This can be decreased through running more simulations. Because the error is estimated using time-series methods, it takes autocorrelation into account. The other exhibits assume this error is acceptably small and can be ignored. The coda package of R is compatible with JAGS and includes more tools for MCMC error-testing and diagnostics.

Because data from only 10 claims were available, the expected prior and posterior weights are very similar. However, the weights for the $5M and $20M buckets have increased. In general, each claim will nudge up the weights of the high likelihood means. The probability of a sample severity from an exponential distribution being capped at $1M, $e^{-\frac{1 M i l}{\mu}}$, increases with the distribution’s mean µ. Thus, a claim getting capped at policy limits is evidence in favor of the larger exponential means; conversely, a small claim is evidence in favor of the smaller means. Two of our 10 claims were capped, so our larger means ($5M and $20M) have gotten more posterior weight. The posterior expected trend (not shown in the table) is still 5.0%; this is also not surprising because only a few claims per year were available.

4.2. Sensitivity testing

The results in the previous section depended on the selection of α₀ = 20 in Section 3. Because α₀ is proportional to σ⁻² by Equation (12), a doubling of uncertainty is associated with a fourfold decrease in α₀. Table 5 shows the results of the simulation with α₀ equal to 5 and 80. As α₀ increases, the initial uncertainty decreases and the posterior weights approach the prior weights. The autocorrelation-adjusted error for every reported weight percentage was less than 0.1%.

5. Applications

The output of this method is a mixed exponential posterior severity distribution and can be used like any other severity distribution. For instance, it can help with pricing excess of loss reinsurance layers, for producing ILFs, or for stochastic risk simulation. The first two applications will be illustrated in this section.

5.1. Reinsurance XOL pricing

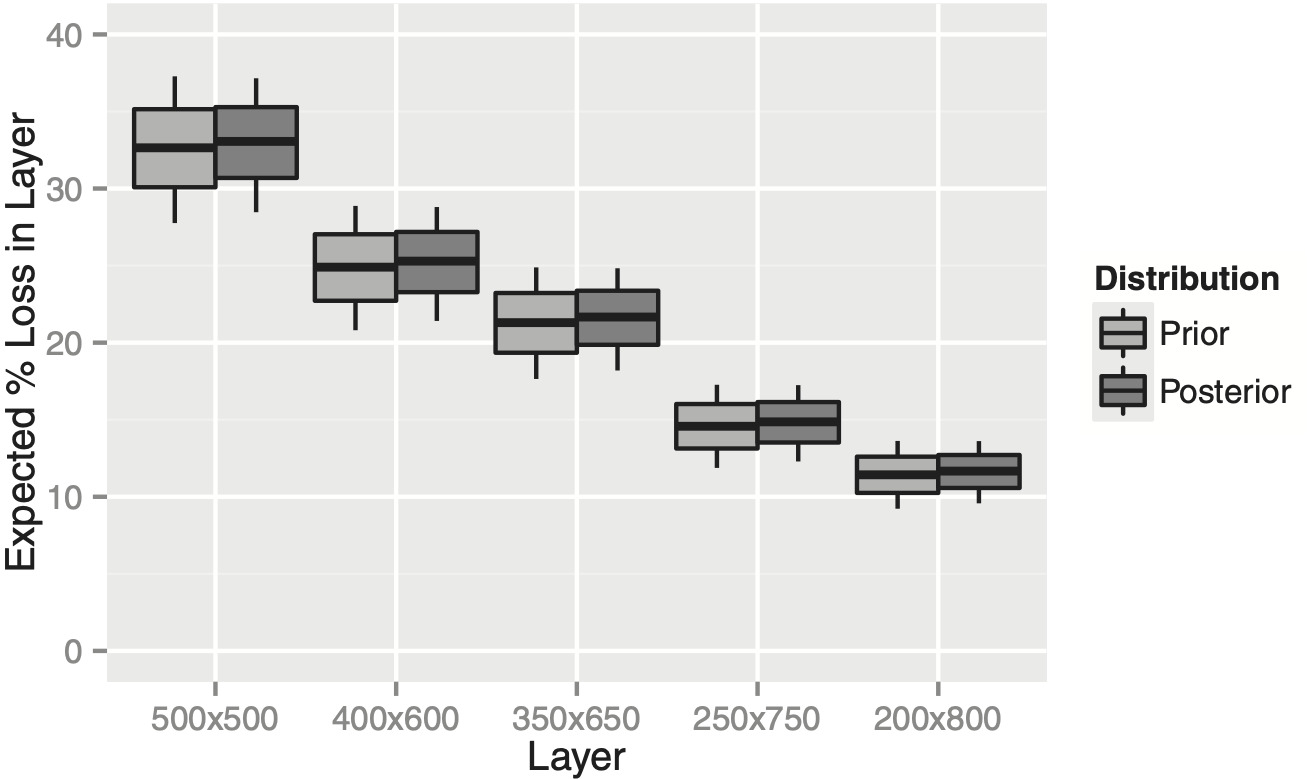
Consider a company that only writes $1M limits and is evaluating the purchase of an excess of loss reinsurance layer. Several options are available: $500K xs $500K, $400K xs $600K, $350K xs $650K, $250K xs $750K, and $200K xs $800K. One way to price these layers that is popular with reinsurers is to compute the percentage loss in each of these layers relative to direct loss.

This ceded loss percentage can be computed by iterating through the sampled weights as in Table 3 and integrating the mixed exponential distribution implied by each set. The results in our example are shown in Figure 1. Each boxplot shows the 10th, 25th, 50th, 75th, and 90th percentiles of the corresponding distribution. Note that these boxplots represent uncertainty about the distribution of claim severities (“parameter risk”).

Figure 1.Prior vs. posterior loss in layer

The boxplots do not show the uncertainty caused by whether individual claims fall into the layers (“process risk”), which would depend on the claim frequency distribution. A high anticipated volume of claims would diversify away the process risk, but not the uncertainty shown by the boxplots.

The ceded losses per layer could then be computed by multiplying the calculated percentage loss in each layer by the direct loss ratio and dollars of direct premium. This ceded loss could then be grossed up for reinsurer expenses and profit load to determine the price of the reinsurance contract.

5.2. ILFs

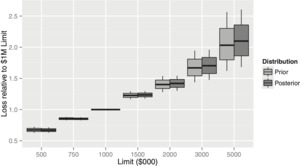
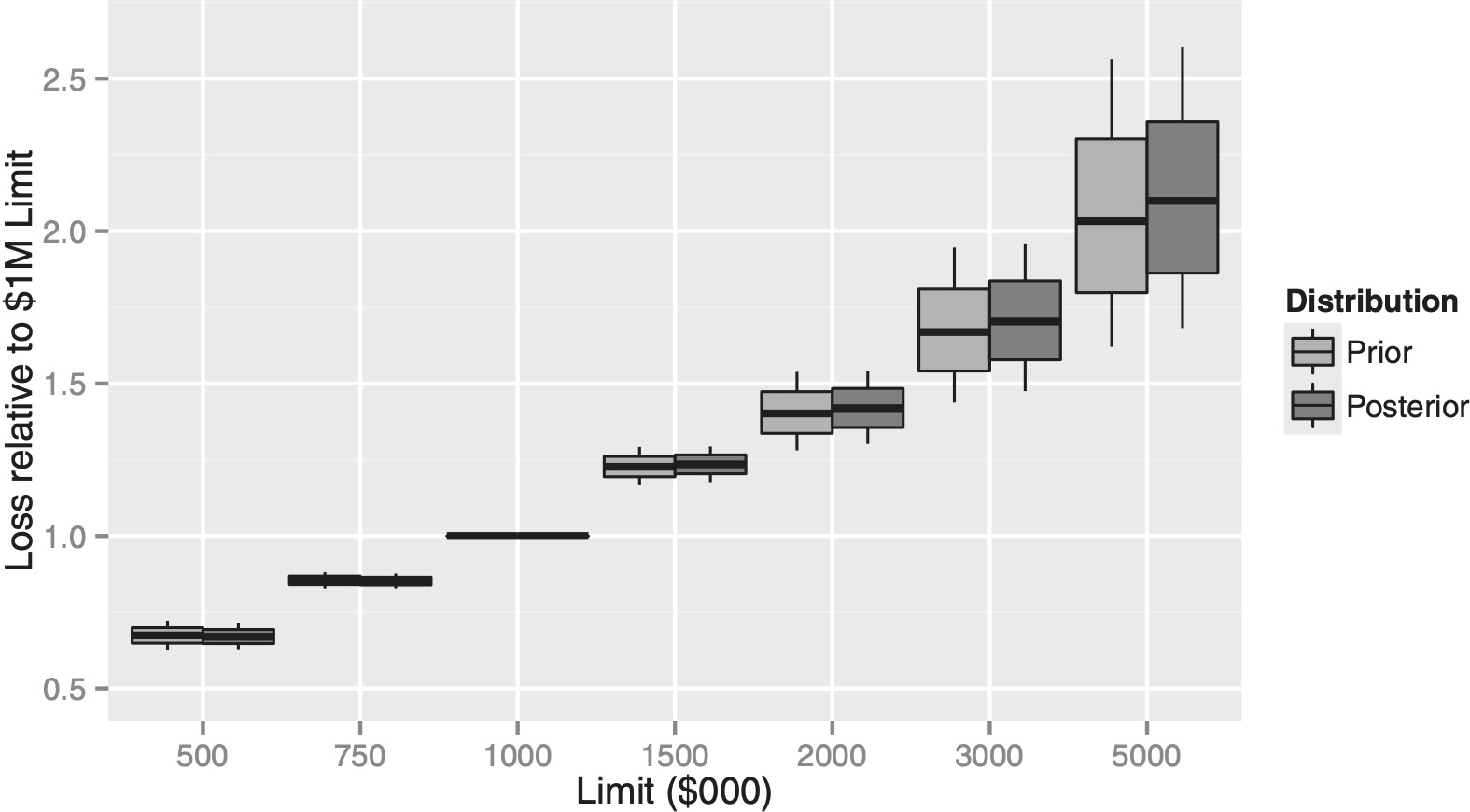
Another application of a claim severity distribution is calculating increased limits factors. Suppose our company, which currently only writes $1M limits, wants to write policies with a variety of other limits. Just as in the previous section, for each sampled weight distribution we can compute the ratios of expected loss relative to a $1M policy by integrating each specified mixed exponential. The results are shown in Figure 2.

Figure 2.Loss relative to $1M limit

As expected, the uncertainty about loss increases as the limit increases. Because our data set included some claims capped at $1M, the posterior distribution predicts a greater increase in loss for limits above $1M. As before, these boxplots do not include “process risk,” only the remaining uncertainty about the underlying claim severity distribution.

The loss relativities in Figure 2 should not be used as ILFs directly because they are not loaded for expense and risk. Another issue not considered here is whether policies with different limits will really be generated by the same severity distribution. Table 6 compares ILFs based purely on expected loss with risk-loaded ILFs based on expected loss plus twice the standard deviation of loss. The additional parameter risk associated with the higher limits leads to more leveraged ILFs.

6. Conclusion

This paper describes a technique for estimating claim severity distributions based on partially credible data and a mixed exponential prior predictive severity distribution. Conceptually the technique is straightforward—we specify a Bayesian model compatible with the prior severity distribution and our uncertainty about that distribution, and then conditionalize on the observed data to find the desired posterior distribution.

The main idea of the Bayesian model is the use of a Dirichlet distribution to parameterize the mixed exponential weights. The Dirichlet distribution only requires one extra parameter, which represents uncertainty about the prior predictive severity distribution. The posterior distribution is computed numerically using MCMC implemented by JAGS.

Once computed, the posterior severity distribution is easy to work with and can be used for such typical applications as pricing XOL reinsurance or computing ILFs.

Acknowledgments

Thanks to Steve Mildenhall, Paul Eaton, and the editors at Variance for comments on earlier versions of this paper.