Tail-Related Risk Measures of Extreme Value Distribution

1. Introduction

Many countries are regularly hit by natural disasters that cause significant damage to crops. Rice is the world’s most important staple food crop, and it feeds more than half of the world population (Luo et al. 1998; Bakker et al. 2005; Aggarwal et al. 2006; Storkey and Cussans 2007; Lai 2010). World rice production in 2007 was estimated to be 652 million tons, of which 90% came from Asia (FAO 2008). Major studies show that extreme weather events have a great effect on rice production (Lansigan, De los Santos, and Coladilla 2000; Yamamoto and Iwaya 2006). Among these weather phenomena, typhoons or tropical cyclones are the most destructive. Catastrophic events are not frequent but cause massive destruction. The annual aggregate rice damage caused by typhoons can be ascribed to a combination of two random variables: the annual frequency and the severity of losses when they occur. Based on fitted annual frequency and loss distributions, this paper attempts to develop a collective risk model^[1] (Klugman, Panjer, and Willmot 2004) for typhoon damage to rice. The current task is to develop appropriate annual frequency and loss distributions for typhoon losses. Moreover, in actuarial science, the aggregate claims are obtained by summing up all the policies in the portfolio (Boland 2007). To make the collective risk model tractable, major studies usually make two fundamental assumptions: (1) the individual claim amounts are independent and identically distributed (i.i.d.) random variables, and (2) the random variables of the number of claims and the individual claim amounts are mutually independent (Bowers et al. 1997). As typhoons generally strike areas only once, they are not correlated to one another. In this paper, we will try to test statistically the independence of annual frequency and severity relating to rice-loss data. Most empirical studies find sufficient evidence of skewness and kurtosis in their yield data (Babcock and Hennessy 1996; Hennessy, Babcock, and Hayes 1997; Coble et al. 1996; Nelson and Preckel 1989). As a consequence, evidential support for abnormality of crop yield has become a major issue in agricultural economics (Just and Weninger 1999; Atwood, Shaik, and Watts 2002, 2003). The fitted loss distribution shows more skewness because losses in crop yields are related to natural disasters. In most countries with developed crop insurance programs, insured-loss calculation in the form of excess probability curves can enable risk managers to decide high excess loss layers for private or governmental crop risk-management and insurance programs (Rosenzweig et al. 2002). Estimating the number of exposures needed to exceed the economic damage threshold from a model (Hansen 2004; Muralidharan and Pasalu 2006) would be more accurate, and the choices of the threshold value above which losses are retained by government also become a critical decision (Hansen 2004; Larsson 2005). However, the extreme value theory (EVT) methods and the generalized Pareto (GP) distribution (GPD) (McNeil 1997; McNeil and Saladin 1997; Cebrian, Denuit, and Lambert 2003; Brabson and Palutikof 2000; Embrechts, Resnick, and Samorodnitsky 1999) have been considered in the study of trends of the extreme losses to get an appropriate assessment and decision.

In the past three decades, typhoons caused losses of up to USD 67.333 billion to Taiwan’s crops. Over a 37-year period, approximately two-thirds (63%) of all natural disaster damage to rice was caused by typhoons. On average, each typhoon causes rice damage estimated at USD 5.57 million (COA 2013). To ease the effect of natural disasters on agriculture and to the farmers, many countries have implemented agriculture insurance plans or set up disaster relief systems. For example, Taiwan’s agricultural natural disaster assistance program (TANDAP) was approved and implemented in 1991. This program provides farmers with financial assistance, including cash relief, subsidies, and low-interest loans, to compensate for yield loss caused by natural disasters. However, rice losses of farmers are actually higher than what is provided in the government budgets due to underestimation and budget limits. For example, the Council of Agriculture (COA)^[2] budgeted USD 36.17 million for TANDAP annually, starting in 2004. This budget appears insufficient for specific years when huge agriculture losses are incurred. For example, there was an estimated loss of USD 366.67 million in 2007. Consequently, an accurate estimation of annual rice damage would not only be a critical task for TANDAP to budget compensation plans, but would also significantly affect its future research in agricultural risk-management and insurance plans.

Based on EVT, we attempt to fit these extreme losses using the peak-over-threshold (POT) approach and see how these extreme losses affect the tail behavior of the rice-loss distribution. This paper aims to estimate the tail quantile risk measures using EVT and estimate the expected annual aggregate rice losses using a collective risk model. Its main objectives are: (1) to fit the annual frequency and severity distributions of rice-loss data; (2) to estimate the quantile risk measures, e.g., value-at-risk (VaR), expected shortfall (ES), and expected annual aggregate losses (EAAL) or expected aggregate losses (EAS), in the example of extreme losses based on EVT modeling; and (3) to estimate the expected annual aggregate rice losses using a collective risk model. In addition, we know that the relationship between natural disasters and rice yields is a complex issue. This paper only discusses the risk analysis of a collective risk model for rice damage due to extreme events. Assessment of rice damage must be appropriately implemented in order to objectively account for morphological developmental criteria brought about by technological change over time. Finally, the results we obtained can be used in estimating the risk of rice damage due to flood, and our algorithm can be applied to other disasters and in other countries.

This paper is organized as follows. Section 2 summarizes the basic theories concerning the independent test, the loss distribution fitting, the expected annual aggregate loss (EAAL) estimation, and the estimated quantile risk measures from extreme observations. Section 3 interprets the empirical results. Conclusions are drawn in Section 4.

2. Models and methods

For rice damage due to typhoons, we denote the annual loss frequency as N, the individual losses as X_js, and the annual aggregate losses as S. Two hypotheses are made: H1: N and ($X_1, X_2, \ldots$) are independent random variables, and H2: $X_1, X_2, \ldots$ are i.i.d. random variables.

2.1. Independence of annual frequency and losses

To examine the independence of the annual frequency and loss variables caused by every single typhoon, the N and X_js data are summarized into an 8 × 10 contingency table, with the row variable denoting annual frequency and the column variable denoting severity. To understand these differences, categorizing the loss maps into major groups would be helpful. The loss frequency variables are classed into eight ordinal groups, from lowest to highest. The loss severity variables are categorized into 10 ordinal groups, i.e., from very small (10th percentile) to very large (90th percentile). As the two variables are ordinal, we use the Goodman and Kruskal’s gamma test for independence distribution. Generalization of the Goodman and Kruskal’s gamma statistic^[3] γ is used for the measurement of the strength of dependence (association) between two categorical variables with ordered categories. The Goodman and Kruskal’s gamma statistic γ ranges between −1 and 1. Values close to an absolute value of one indicate a strong relationship between the two variables, whereas values close to zero indicate little or no relationship.

2.2. Annual frequency distribution

Frequency distribution is usually represented by one of the standard discrete statistical distributions. We now consider that two frequency models exist in this paper: the Poisson distribution and the binomial distribution. The Poisson distribution is one of the most common distribution methods used for modeling loss/claim frequency (Klugman, Panjer, and Willmot 2004; Promislow 2006). The Poisson distribution requires only a single parameter. To estimate the parameter of annual frequency, the maximum likelihood estimation (MLE) is used. Let n_k denote the number of years in which a frequency of exactly k losses occurred. The maximum likelihood estimate of the Poisson parameter is

$$\hat{\lambda}=\frac{\sum_{k=0}^{\infty} k n_{k}}{n}, \tag{1}$$

and this may be estimated by the sample mean of 3.324. Note that the maximum sample frequency is 7 and this would be the lowest choice for n. If n is known, then only p needs to be estimated. Various combinations of estimates of n and p can be tried subject to the condition that n × p = 3.324, the sample mean.

The binomial distribution is another counting distribution that arises naturally and frequently in claim number (or loss number) modeling, as the mean of sample exceeds the variance (Klugman, Panjer, and Willmot 2004). The binomial distribution has two parameters, n and p, where n is the number of trials and p is the probability of a success from each of the n independent trials. The binomial distribution can be calculated from the formula as $P(X-x)= ^n C_x p^x (1-p)^{(n-x)}, x=0,1,2, \ldots, n$. Note that we say X follows a binomial distribution with parameters, n and p.

The chi-square statistic of goodness-of-fit test is computed as a quantitative measure for the overall fit of the selected distribution. The test statistic is

$$Q=\sum_{k=0}^{\infty} \frac{\left(n_{k}-E_{k}\right)^{2}}{E_{k}}, \tag{2}$$

where E_k is the expected number of counts. The number of degrees of freedom for this test statistics is given by d = (# of cells) − (# of estimated parameters) − 1.

The null hypothesis is that the underlying distribution is the Poisson distribution. If the value of Q is less than $\chi_{d, \alpha}^2$, where $\alpha$ is the significance level of the test, we do not reject the null hypothesis (Klugman, Panjer, and Willmot 2004).

To further analyze the models, we also present the probability difference graph to determine how well the theoretical distribution fits with the observed data and compare the goodness-of-fit of several fitted distributions. The probability difference graph is a plot of the difference between the empirical and the theoretical cumulative distribution functions (CDFs).

$$\operatorname{Diff}(x)=F_{n}(x)-F(x) \tag{3}$$

where $F_{n}(x)=\frac{1}{n} \times[\text { Number of observations } \leq x]$ denotes the empirical CDF of the data and F(x) is the theoretical (fitted) CDF.

2.3. Loss distribution

Several different distributions can often fit to the same data set.

2.3.1. Classical loss distribution

Since the histogram of rice losses indicates a right-skewed data set, the recommended right-skewed distribution such as gamma, log-normal, and log-gamma distributions will be tested in this paper. To estimate the parameters of loss distributions, the maximum likelihood estimation is used. Furthermore, the Kolmogorov-Smirnov (K–S) statistic is then computed as a quantitative measure of the overall fit of the selected distribution to the empirical distribution. The K–S test has the advantage of making no assumption about the distribution of data. K–S is based on the largest vertical difference between the theoretical and the empirical cumulative distribution function. The detailed process is as follows:

Let X = (X₁, . . . , X_n) be a random sample from some distribution with the cumulative distribution function [F_n(x), F(x)]. The K–S statistic (K) is based on the largest vertical difference between the theoretical and the empirical cumulative distribution function (Bain and Engelhardt 1991).

$$K=\max _{1 \leqslant i s n}\left(F\left(x_{i}\right)-\frac{i-1}{n}, \frac{i}{n}-F\left(x_{i}\right)\right) . \tag{4}$$

If the test statistic, K, is greater than the critical value obtained from a table, we reject the data following the specified distribution.

For testing the appropriateness of the selected distribution, a Q–Q plot is used for comparing the estimated quantiles of the fitted distribution with the quantiles of a theoretical distribution. To further analyze the models, we also present the probability difference graph to determine how well the theoretical distribution fits the observed data and compare the goodness-of-fit for several fitted distributions.

2.3.2. Extreme value distribution

The Q–Q plot is a strong evidence of deviation from a straight line at the large observations, even though K–S tests suggest the selected models fit well. This inappropriate fitting of tail behavior of loss distribution suggests using extreme value distribution for fitting. Estimation of an extreme loss severity distribution from historical data is an important activity in risk assessment. EVT provides methods for statistically quantifying such events and their consequences (Embrechts, Kluppelberg, and Mikosh 1997; Reiss and Thomas 1997; De Haan and Ferreira 2006). Generally, two related ways of identifying extremes in real data are used. Two models of the generalized extreme value distribution (GEVD) and the generalized Pareto distribution (GPD) are introduced that are central for the statistical analysis of maxima or minima and of excess over a higher or lower threshold. It is critically important to determine if using GPD from EVT results in an adequate fit. In the following sections, the fundamental theoretical results underlying the block maxima and the threshold method are summarized.

2.3.3. Generalized Pareto distribution (GPD)

In some instances, the attendant exposures exceeded the expectations of local specialists and government authorities in managing extreme loss. Extreme value with GPD plays an increasingly important role in natural disaster analysis. If we consider an unknown distribution function F of a random variable X, we will be interested in estimating the distribution function F_u of variable x above a certain threshold u. The distribution function F_u is called conditional excess distribution function and is defined as

$$F_{u}(y)=P(X-u \leq y \mid X>u), \quad 0 \leq y \leq x_{F}-u, \tag{5}$$

where X is the random variable, u is the given threshold, y = x − u are the excesses, and x_F is the right endpoint of F. We verify that F can be written as

$$F_{u}(y)=\frac{F(u+y)-F(u)}{1-F(u)}=\frac{F(x)-F(u)}{1-F(u)} . \tag{6}$$

Pickands (1975) and Balkema and de Haan (1974) suggest that, for a large class of underlying distribution function F, the conditional excess distribution function is F_u(y). When the value of the threshold is large, the function is well approximated by

$$F_{u}(y) \approx G_{\xi, \sigma}(y), \quad u \rightarrow \infty$$

where

$$G_{\xi, \sigma}(y)=\left\{\begin{array}{ll} 1-\left(1+\frac{\xi}{\sigma} y\right)^{-1 / / 5} & \text { if } \xi \neq 0 \\ 1-e^{-y / \sigma} & \text { if } \xi=0 \end{array}\right. \tag{7}$$

for y ∈ [0, (x_F − u)], if ξ ≥ 0 and for $y \in\left[0,-\frac{\sigma}{\xi}\right],$ if ξ 0. G_ξ,σ is the so-called GPD, with σ > 0 as the scale parameter and ξ as the shape parameter. Here, ξ is the shape parameter that determines the speed at which the tail disappears. This distribution is defined as the GPD because it subsumes other known distributions, including the Pareto and normal distributions, as special examples. The normal distribution corresponds to ξ = 0, where the tails in the example disappear at an exponential speed (Jorion 2007). By supposing x = u + y, the GPD can also be expressed as a function of x, i.e., G_ξ,σ(x) = 1 − (1 + ξ(x − u)/σ)^−1/ξ.

2.3.4. Tail-related risk measures of extreme value distribution: VaR and ES of GPD

Measures, such as skewness and kurtosis, can be used to quantify the risk not adequately described by variance alone (Rosenberg and Schuermann 2005). An alternative approach is to examine the percentiles of the distribution to provide useful information in the high quantiles of the loss distribution. Some of the most frequent questions concerning risk management in many fields involve extreme quantile estimation, which determines the value of a given variable that exceeds a given probability. Typical examples of such measures are VaR, ES, and EAAL. A measure that provides useful information for risk management is the high quantile of the distribution of losses. VaR is broadly defined as a quantile of the distribution of returns or losses of the concerned portfolio (Jorion 2007). We let 0.95 ≤ q 1 as an example. VaR is the qth high quantile of distribution F:

$$\operatorname{VaR}_{q}=F^{-1}(q) \tag{8}$$

where F⁻¹ is the inverse of F.

Artzner et al. (1997) demonstrated that VaR is not a coherent risk measure. To remedy the problems inherent in VaR, they proposed the use of ES as an alternative, a risk measure using conditional tail expectation, also called tail VaR. ES is the expected value of the loss in those examples where it exceeds the predefined confidence level. Thus, ES is equal to the average loss rice crops will suffer under the example of extreme situations where the losses exceed the predefined confidence level. ES is the expected loss size given that VaR is the threshold value level

$$\mathrm{E}(\mathrm{S})_{q}=E\left(X_{i} \mid X>\operatorname{VaR}_{q}\right) . \tag{9}$$

In practice, the EVT estimators can be derived as follows. We propose to evaluate VaR at the 1% confidence level. We then choose a cutoff point u such that the right tail contains a small percentage of the data. The EVT distribution then provides a parametric distribution of the tails above this level. We first need to use the actual data to compute the ratio of observations in the tail beyond u or N_u/n, consistent with the unity sum of the tail probability. Given these parameters, the tail distribution and density functions are, respectively,

$$F(x)=1-\left(\frac{N_{u}}{n}\right)\left[1+\frac{\xi}{\sigma}(x-\mu)\right]^{-1 / \xi} \tag{10}$$

$$f(x)=\left(\frac{N_{u}}{n}\right)\left(\frac{1}{\sigma}\right)\left(1+\frac{\xi}{\sigma}(x-\mu)\right)^{-(1 / \xi)-1} . \tag{11}$$

The quantile at the qth level of confidence is obtained by setting the cumulative distribution as F_u(y) = q, where y = x − u, and solving for x, which yields

$$\hat{V a} R_{q}=u+\frac{\hat{\sigma}}{\hat{\xi}}\left\{\left[\left(\frac{n}{N_{u}}\right)(1-q)\right]^{-\hat{\xi}}-1\right\}, \tag{12}$$

where N_u is the number of losses above the threshold u, n is the total number of losses, and q is a given probability. This equation provides a quantile estimator of VaR based not only on the data but also on our knowledge of the parametric distribution of tails. Such an estimator has a lower estimation error than the ordinary sample quantile, a nonparametric method (Jorion 2007). Furthermore, we can obtain the ES estimate or the average beyond VaR using the following formula (Jorion 2007):

$$E \hat{(S)_{q}}=\frac{\operatorname{VaN}_{q}}{1-\hat{\xi}}+\frac{\hat{\sigma}-\hat{\xi} u}{1-\hat{\xi}}. \tag{13}$$

2.3.5. EAAL or EAS estimation

Let N denote the annual loss frequency of rice damage due to typhoon in a given time period. Note that X₁ denotes the first loss, X₂ as the second loss, and so on. In the collective risk model, the random sum (Bowers et al. 1997) represents the aggregate losses generated by the portfolio for the period under study.

$$S_{N}=\sum_{j=1}^{N} X_{j} . \tag{14}$$

The number of losses N is a random variable and is associated with the frequency of loss. The individual losses X₁, X₂, . . . are also random variables and are said to measure the severity of losses. In the collective risk model, we model the annual aggregate rice loss S as a compound distribution in the form S = X₁ + X₂ + . . . + X_N. When N is a Poisson distribution, S has a compound Poisson distribution (Promislow 2006; Boland 2007). The mean and variance of the aggregate losses (AS) are well known by actuaries. The moment equations for aggregate losses are expressed as

$$E(A S)=E_{N}(E(S \mid N)) \tag{15}$$

and

$$V(A S)=\operatorname{Var}_{N}(E(S \mid N))+E_{N}(V(S \mid N)). \tag{16}$$

We will calculate the independence test of the annual frequency and losses, annual frequency distribution fitting, and classical and extreme loss distribution fittings associated to the different distributions, i.e., GEVD and GPD. Our purpose is to determine the best-fitting distribution of crop damage due to extreme events in a collective risk model. In addition, we aim to discuss the difference between the values of VaR and ES in the tail-related risk measures of the GPD model, the EAAL or EAS estimation, and the analysis of the annual aggregate loss based on a selected distribution. Note that from E(AS) and V(AS), we can consider different types of the simplest premium calculation principles with the tail-related risk measures, characterized by mean of some elementary properties, and some other principles will be given a statistical justification.

3. Results

3.1. Data

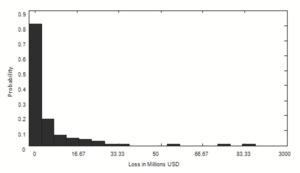
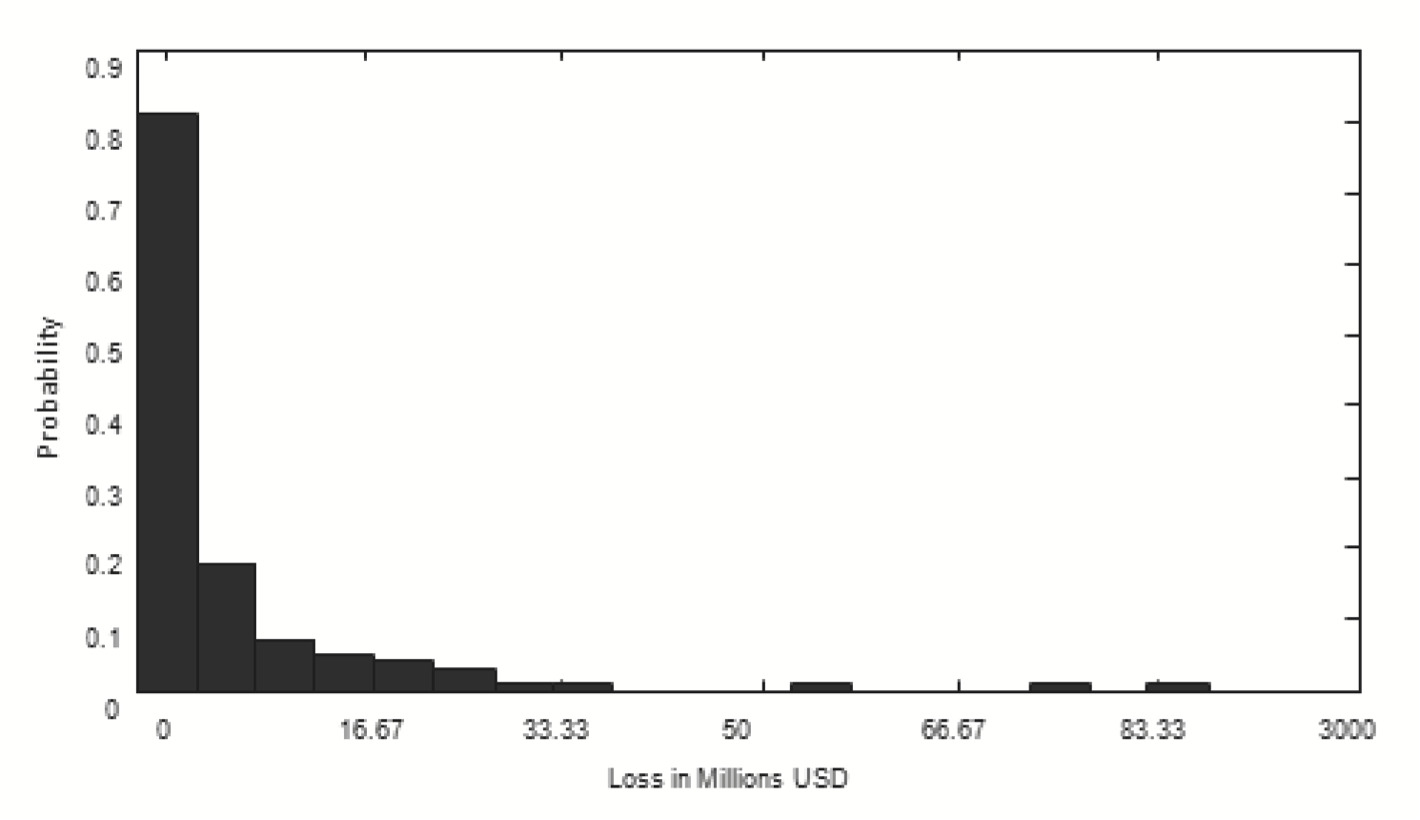
The data used in the current work are obtained from Taiwan’s Agriculture Yearbook, provided by the Council of Agriculture (COA) of Taiwan. Adjusting for inflation, 123 instances of estimated rice losses caused by typhoons from 1971 to 2007 are summarized in Table 1 and shown in Figure 1. The sample mean and variance of the frequency distribution are 3.3 and 2.3, respectively. The sample mean and standard deviation of the severity distribution are approximately USD 5.57 million and USD 12.59 million, respectively. On average, 3.3 typhoons hit Taiwan’s rice crops annually, and the average rice loss in this small country caused by each typhoon is USD 5.57 million. During the preceding 37 years, typhoons hit Taiwan’s agriculture, causing tremendous losses of over USD 33.33 million in four years: 1975, 1986, 1998, and 2007. Moreover, eight years incurred extreme rice losses of over USD 16.67 million. The coefficients of skewness and kurtosis are 4.2 and 20.7, respectively. Consequently, the Jarque–Bera test shows a corresponding p value of 0.0000 from 1971, which means that the fitted loss data were not normally distributed. Figure 1 shows the annual frequency and the rice damage caused by typhoons. This chart shows no particular pattern in the loss series, and the annual frequency and the severity of rice damage are not related.

Figure 1.Taiwan’s 123 instances of rice losses caused by typhoons in 1971–2007

3.2. Results of independence test of annual frequency and losses

In Table 2, if “increasing loss frequency N leads to increasing levels of loss severity X_js,” a tendency for large losses is predicted to occur with high annual frequency. The Goodman and Kruskal’s gamma statistic in the previous example will be close to one. In the present example, γ̂ is 0.07, with a corresponding p value of 0.665, indicating a very weak relationship between the two variables. We do not reject the fact that N and X₁ are independent random variables. We further check the independence between N and X₂. The Goodman and Kruskal’s gamma statistic is 0.066, with a corresponding p value of 0.684. Consequently, we do not reject the fact that the annual frequency and severity are independent random variables.

3.3. Results of the annual frequency distribution fitting

Panel A of Table 3 shows the annual frequency distribution of the 123 typhoons observed during the 37-year period in 1971–2007. The sample mean and variance of this frequency distribution are 3.324 and 2.281, respectively. Figure 2 shows no particular trend of the annual frequency. The maximum likelihood estimate of the Poisson parameter λ̂ is 3.324. Various combinations of the condition where n × p = E(N) are also considered. We interpret this given n as the theoretical maximum number of typhoons during a year. Panel A of Table 3 shows the observed frequencies against a set of fitted frequencies based on the Poisson distribution (null hypothesis). The parameter estimation and chi-square goodness-of-fit test are also given. However, some of the expected frequencies are less than five. For the chi-square approximation to be valid, the expected frequency should be at least five. Therefore, we need to combine some cells in the tails in Panel B of Table 3. The Poisson distribution can approximate the observed frequency distribution reasonably well. Moreover, the Poisson parameter λ̂ = 3.324, and the chi-square statistic χ²₃ is 1.415 with a corresponding p value of 0.7020, suggesting a good fit for the Poisson distribution.

Figure 2.Annual frequency (1971–2007)

To examine the appropriateness of the fitted distribution, a probability difference graph is used to compare the goodness-of-fit of the two fitted distributions. Figure 3 shows that the Poisson distribution with parameter λ̂ = 3.3 is still better than the binomial distribution with two parameters n̂ = 7 and p̂ = 0.47 in the fitted model.

Figure 3.Probability difference graph of the comparison between the Poisson(3.3) and the fitted binomial(7, 0.47) distributions

3.4. Results of loss distribution fitting

In Panel B of Table 1, the sample mean and standard deviation of the severity distribution are approximate USD 5.57 million and USD 12.59 million, respectively. The inter-quartile range is large (about USD 5.33 million), and the data contain a significant number of very high losses (the maximum loss observed is USD 84.05 million). The distribution of rice losses due to typhoons is considerably skewed to the right (the skewness coefficient is equal to 4.2). The histogram of losses shows a long-tailed behavior of the underlying data in Figure 4. The Jarque–Bera test applied to rice-loss data leads to a clear rejection of the null hypothesis of normality, with a corresponding p value of zero. Hence, we consider a right-skewed distribution set, and the recommended right-skewed distribution, such as gamma, log-normal, and log-gamma distributions, will be tested in the next context.

Figure 4.Histogram of losses

3.5. Classical loss distribution fitting

Table 4 summarizes the maximum-likelihood estimation (MLE.) parameters of loss distribution. The goodness-of-fit test of the log-normal, log-gamma, and gamma distributions is also included. The K–S goodness-of-fit test of the log-normal distribution with estimated location parameter µ̂ = 10.079 and estimated scale parameter σ̂ = 2.37 does not reject the null hypothesis. A similar conclusion favors the log-gamma distribution. Therefore, we conclude that both log-normal and log-gamma distributions fit the sample data well enough to be acceptable models, but the gamma distribution does not.

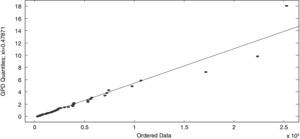
The log-normal distribution fits the sample data and has a mean of USD 13.17 million and a standard deviation of USD 218.40 million. The probability of exceeding USD 3.33 million is 0.27, clearly too low compared with the probability of 0.32, or 39 events out of 123. This result indicates that the log-normal distribution does not fit the tail behavior well, although it fits the whole distribution well. Figure 5 shows the Q–Q plot of the log-normal and log-gamma fits. If the sample observations match the theoretical one, the plot will be on a straight line. Both plots show theoretical models that do not fit well at the tail part of the loss distribution. More attention is required for the tail (extreme values) of the loss distribution.

Figure 5.Q-Q plot of log-normal (left) and log-gamma (right) distributions

3.6. Extreme value distribution fitting

We are interested in the severe losses and now try to capture the behavior of the loss tail using the extreme value distribution model. We analyze the tail region, instead of the center region, of the distribution of rice damage, as suitable estimates for the tails of loss severity distributions are essential for risk financing or positioning of high excess loss layers in private or government insurance and disaster risk-management programs (Rosenzweig et al. 2002). Hence, estimating the number of events that exceed the economic damage threshold from a model will be more accurate (Hansen 2004; Muralidharan and Pasalu 2006). The choice of the threshold value above which losses are insured or retained by the government also becomes a critical decision (Hansen 2004; Larsson 2005).

3.7. Results of GPD fitting

In Sections 3.4 and 3.5, the log-normal and log-gamma distributions did not fit well through the entire data, particularly at the tail of the loss distribution. The mean excess plot is sometimes used to identify a likely loss distribution. Figure 6 shows the mean excess function for loss estimations. The linear trend line is fitted to the losses of over USD 0.97 million and indicates that a GPD may provide a reasonable fit to the losses in excess of this threshold value. Hence, our present analysis is based on a set of 56 largest rice losses over a threshold value of USD 0.96 million. Then, we have a two-parameter representation of GPD: scale σ̂ (132,349) and shape ξ̂ (0.4625). For typical financial data, ξ > 0 implies a heavy tail or a tail that disappears more slowly than the normal. Note that the size of the shape parameter is the most important. Higher shape parameters can be generated, which results in a thicker tail and more losses. It is an important key issue in comparing the fitted shape parameter with the change in threshold. In this case, the K–S test statistic is 0.0518 with a corresponding p value of 0.9964, suggesting that GPD is a good fit for the 56 extreme losses. The data, MLE, and K–S test are summarized in Table 5. In Figure 7, the Q–Q plot shows an approximate linearity, which indicates that GPD is a correct model for the 56 extreme losses. In the next section, we will use GPD to calculate some risk-related measures, such as VaR, ES, and E(AS), which could be helpful as a reference for some disaster-assistance problems.

Figure 6.Mean excess plot of loss distribution

Figure 7.Q–Q plot of GPD.

3.8. Tail-related risk measures of GPD: VaR and ES

Equations (12) and (13) provide a quantile estimator of VaR based not only on the data but also on our knowledge of the parametric distribution of tails. Such an estimator has a lower estimation error than the ordinary sample quantile, a nonparametric method (Jorion 2007). The 90th, 95th, and 99th percentile of VaR and ES are shown in Table 6. These high-quantile measures can provide useful information to authorities and risk managers for checking applicable loss compensation regulations and for adjusting a relief threshold or a natural disaster relief budget plan. For example, ES_0.90 is computed as the average of the losses that exceed VaR_0.90, i.e., we can have a rice loss of USD 10.94 million with a 10% chance of a next typhoon damage to rice, and the expected loss exceeding USD 10.93 million will be USD 27.73 million. Referring to the relief threshold criteria of TANDAP, the criterion threshold for granted cash relief is USD 6 million, implying that the criterion threshold of the recent policy relieves severe damage to rice farmers with a probability of only about 0.15.

3.9. Results of the EAAL estimation

In previous sections, we concentrated on the risk measures of extreme rice losses caused by typhoons. In this section, we estimate the EAAL or EAS of rice damage due to typhoons using a collective risk model. Based on collective risk model views, aggregate (total) losses as a compound distribution are a compound Poisson distribution in rice-loss data. We have two models for estimation in Table 7. Model I is a compound Poisson distribution with parameter λ̂ = 3.3, where the losses are log-normal distribution with two parameters µ̂ = 10.079 and σ̂ = 2.37. Model II is a compound Poisson distribution with parameter λ̂ = 3.3, where the losses are GPD with two parameters ξ̂ = 0.4625 and σ̂ = 132,349. Table 7 summarizes the annual aggregate losses based on a selected distribution. Model I has an EAAL of USD 43.5 million, larger than that of Model II (USD 30.27 million), but Model II has a smaller variance. The log-normal distribution is 50 times the variance of GP, leading to an incredible expectation of aggregate losses. For practical reasons, we consider Model II to be a reliable result. Compared with the annual budget (USD 36.17 million) of TANDAP, we find that the annual budget is insufficient for compensating the losses of farmers because the above expectation is only for rice. Obviously, expected loss is an important element that affects retention ability for the non-insurance plan (relief program) and insurance pricing. Thus, accurate estimates of expected aggregate losses can help authorities determine whether a cash relief program/risk premium of crop losses can meet the need for farmers or insurance coverage under extreme events.

4. Conclusion

Unusual climate and weather have caused substantial damage to agricultural sectors in many areas of the world. These events cause very heavy losses. This paper discusses the independence between annual frequency and severity due to individual typhoons. A collective risk model is a feasible scheme for estimating the annual aggregate losses. This paper uses EVT, and the modeling strategy focuses on the POT approach to fit GPDs. Rice damage due to typhoons was calculated because many observations can have a substantial effect on the heavy-tailed distribution using traditional estimation procedures. The loss distribution process is heavy-tailed, implying that it is also not normal; using normality results in large underestimation of the threshold value of rice losses. In modeling a loss, a notable concern about the chances and sizes of extremely large losses is usually considered, in particular, the right tail of the distribution. Examining the distribution percentiles can provide useful information regarding the high quantiles of the loss distributions. Typical examples of such measures, such as VaR, ES, and EAS or EAAL, were presented, which are useful to authorities and risk managers studying applicable loss compensation regulations and adjusting relief threshold or natural disaster relief budget plans. Overall, the analyses performed in these examples provide insight on several aspects of estimating rice losses. The conclusions are as follows.

(1) The annual frequency of rice damage caused by typhoons is fitted well by the Poisson distribution with one parameter. The loss distribution of rice damage caused by typhoons is fitted by log-normal distribution with two parameters. However, the log-normal distribution badly fits the tail of rice-loss distribution. We suggest an alternative distribution called GPD to fit the losses with extreme values. GPD with two parameters outperforms the log-normal fit, especially at the tail behavior fitting. GPD allows easy estimation of the high quantiles and the maximum probable loss from the data. These loss distributions are useful for reviewing loss compensation regulations and relief fund (non-insurance project) applicability and can be used as a reference for planning future crop insurance.

(2) The threshold value can be used as reference in decision making for setting grant-in-cash relief.

(3) We consider tail-related risk measures, e.g., VaR, ES, and EAS, of GPD. Given different confidence intervals, these high-quantile measures can provide useful information in reviewing the applicable loss compensation regulations and for adjusting the relief threshold or natural disaster relief budget plans.

(4) A compound Poisson distribution is applicable for estimating annual aggregate rice losses. Obviously, expected loss is an important element that affects the retention ability of the non-insurance plan (relief program) and insurance pricing. For further research, we can apply countrywide rice-loss data to examine the appropriate grant-in-cash relief threshold for each typhoon event. Moreover, we can apply agricultural loss data to a model, including product loss (crop, forestry, livestock, and fishery), cultivated land loss, and irrigation facility loss, and some climatic variables, such as precipitation, strength of typhoon, and maximum wind speed, to forecast the losses caused by typhoons. The results we obtained are useful in loss assessment of crops in decision making regarding national capacities for risk financing of major agricultural disasters and disaster risk-management programs.

Acknowledgments

The author is grateful to the two anonymous Variance reviewers for their comments on an earlier version of this paper.