A Flexible Framework for Stochastic Reserving Models

undefined

1. Introduction

Traditional approaches to estimating unpaid claim liabilities, an exercise often referred to briefly as “reserving,” have usually been deterministic in nature and allowed for the exercise of the practitioner’s judgment in arriving at estimates. In the end, an honest practitioner recognized that his or her final estimates were just that, and that final payments would likely differ, potentially materially. The loss process under consideration is generally too complex to be adequately described by a single deterministic forecasting method. Typically, practitioners have used more than one forecasting method in reserving exercises and in fact, in the United States, Actuarial Standard of Practice Number 43 states “The actuary should consider the use of multiple methods” in estimating unpaid claim liabilities. The divergence of forecasts among various methods indicated that the underlying loss process violated the assumptions inherent in one or more of the forecast methods. This provided the practitioner indications of further qualitative or quantitative investigation needed to better understand the underlying loss process. Conversely, if different methods provided reasonably similar forecasts, then the practitioner took some comfort that his or her methods captured the critical characteristics underlying the loss process.

There has long been interest in quantifying the uncertainty inherent in these traditional estimates. Traditional practitioners would often get a qualitative sense of the uncertainty in their estimates by reviewing both the volatility of the data used for forecasting and the range of estimates provided by the various forecast methods used. However, practitioners have sought ways to better describe and quantify this uncertainty inherent in reserving projections and have turned to statistical approaches for the answer.

Probably the most commonly used of all the traditional reserving methods is the development factor approach, commonly referred to as the chain ladder method. This method is straightforward to describe, flexible, and easy to implement computationally. It is not surprising, then, that it would be one of the first methods to be considered in a stochastic framework.

Here we would like to make a clear distinction between a stochastic model and a non-stochastic or deterministic model. In this paper, we will use the term method to denote specific description of a process underlying the emergence of amounts over time which allows a practitioner to extrapolate from historical experience. For example, the chain ladder method assumes that cumulative amounts at one age will be a specified percentage of cumulative amounts at the immediate prior age. The implementation of the method involves studying the triangle of development factors sometimes referred to as “link ratios,” the ratios of the cumulative amounts at one age to the cumulative amounts at a prior age, selecting a representative factor for each age, then computing a forecast from the product of the cumulative amounts to date with the appropriate selected factors.

By a stochastic reserving model, we mean a mathematical statement describing how amounts emerge over time along with an explicit statement regarding the uncertainty or variability of the corresponding amounts. For example, the statement of a method may be that amounts at 24 months will be the amounts at 12 months times a fixed factor. A stochastic model based on that statement would be as follows: amounts at 12 and 24 months are random variables A₁₂ and A₂₄, respectively, with distributions such that E(A₂₄) = cE(A₁₂) for some constant c.

In principle, stochastic models describe the full probability distribution of possible future claim payments. However, such models are often too complex to allow closed-form calculation of even key quantities such as the expected value or standard deviation. Instead, the widespread availability of inexpensive computing power has enabled the use of a number of simulation approaches to estimate uncertainty. Probably the most common tool currently employed is the bootstrap applied to the chain ladder model as discussed by England and Verrall (1999), which provides an estimate of the uncertainty of estimates resulting from the chain ladder model.

When reviewing uncertainty in a reserving framework, it is important to recognize precisely what sources of uncertainty are being addressed and what sources are not. From the reserving point of view, total uncertainty can be thought of as having contributions from three sources:

• Process uncertainty—random fluctuations inherent in any stochastic process, even if the process and all its related parameters are known with certainty;

• Parameter uncertainty—the possibility that the parameters of the selected model are estimated incorrectly, even if the selected model is correct; and

• Model uncertainty—the possibility that the amounts to be modeled do not arise from the model assumed.

Works such as England and Verrall (1999) consider only a single model, so even though they may appropriately take into account process and parameter uncertainty, they cannot even begin to account for model uncertainty. Just as practitioners applying traditional reserving methods need to apply a variety of methods to assess uncertainty, those using stochastic approaches should not ignore model uncertainty.

In this paper, rather than relying on linear or generalized linear models, as do many of the papers using the bootstrap method, we take advantage of the broad availability of relatively cheap computing power to look directly at non-linear reserving models and make use of the maximum likelihood estimators (MLEs) to derive estimates of both process and parameter uncertainty. We will also use this same framework to consider a range of different models and begin to explore ways we can at least start to recognize model uncertainty in our estimates.

2. Maximum likelihood estimators

Klugman, Panjer, and Willmot (1998) present a very clear and concise discussion of the MLE approach. Rather than repeating that exposition here, we will briefly summarize the concept of maximum likelihood estimate and the principle conclusions of the primary theorem appearing on page 62 of Klugman, Panjer, and Willmot (1998). We will refer to this result as Theorem 1 in what follows.

Suppose we have a sample drawn from a distribution whose general form is known and described by a set of parameters, but the values of those parameters are themselves unknown. The task then is to estimate those parameters given the sample drawn. One approach to this problem is based on the relative likelihood of drawing the sample X given a particular choice of the parameters θ, calling this likelihood L(X|θ). The maximum likelihood estimator or MLE is the value of θ that gives the largest value for L(X|θ) over all possible choices for θ. Under some mild regularity conditions on the distribution under consideration, the MLE has the following asymptotic properties as the sample size grows to infinity:

1. It asymptotically tends to the true value of the unknown parameters.

2. Its variance asymptotically tends to a value that is no larger than the variance of any other estimator of those parameters.

3. It asymptotically approaches a Gaussian distribution.

The asymptotic Gaussian distribution has mean θ and covariance matrix equal to the inverse of the Fisher information matrix, which has elements given in (2.1).

$$\mathbf{I}(\boldsymbol{\theta})_{i j}=\mathrm{E}_{\mathbf{x}}\left(\frac{\partial^{2}}{\partial \theta_{i} \partial \theta_{j}}-\ln (\mathrm{L}(X \mid \boldsymbol{\theta}))\right) \tag{2.1}$$

In practice, both the mean and covariance matrix of the limiting Gaussian distribution are calculated assuming that the actual parameter values are equal to the MLE. We will use this property in incorporating parameter uncertainty in the stochastic models we present here.

3. General stochastic reserving model

We will focus on the usual triangular array of amounts, where the amount could be claim counts, paid losses, or case-incurred losses (paid losses plus claim adjuster estimates of outstanding losses). In the remainder of this paper we will use the term “payments” for simplicity, but do not intend any loss of generality. If we are interested in incurred losses then “payments made” during a time span would translate to “change in incurred losses” during that time. Similar adaptations can be made for claim counts or other amounts of interest.

We will denote by C_ij payments made for exposure period i during development period j. Here the time spans are unspecified and can represent quarters, half years, years, or other time spans of interest. Similarly, the exposure period could represent a policy period, accident period, underwriting period, or other span of interest. As with payments, we will simply refer to accident years and annual development in what follows.

We will assume that the time span of interest covers m accident years and n years of development. We will denote by n_i the age of the most recent available experience for accident year i. In the case of a square data set with m = n accident years and development years, then n_i = n − i + 1.

In addition to the basic paid amount data, we will assume we have some measure of exposure for each accident year, either an exposure count, premium amount, or an estimate of ultimate claim counts. We note that ultimate claim counts often cannot be known with certainty and as such should be treated as random variables. We will not make that generalization here but rather leave it as a future project. In any event, we will denote this measure of relative exposure as W_i for accident year i. We will thus focus on the incremental averages A_ij defined by Equation (3.1).

$$A_{i j}=\frac{C_{i j}}{W_{i}} . \tag{3.1}$$

The incorporation of this additional exposure information widens the variety of methods available for analysis. We can now move beyond the simple chain ladder to include others, such as a version of the Cape Cod variant of the Bornhuetter-Ferguson method, an incremental severity method discussed by Berquist and Sherman (1977), and a variant of the Hoerl curve method discussed by Wright (1992).

At this point, we will assume that the reserving method can be expressed as a matrix-valued function of a parameter vector θ, as expressed in (3.2).

$$A_{i j}=g_{i j}(\boldsymbol{\theta}). \tag{3.2}$$

We will turn this simple method or “recipe” into a stochastic model by introducing random variables with specific probability distributions. It is not unusual to assume that the variances of the incremental amounts are proportional to a power of their expected values (for example, see Venter 2007). We will take this same approach. However, since we will allow the expected values to be negative, we will, without loss of generality, take the variance to be proportional to a power of the square of the mean. Also, we are taking the constant of proportionality among the variances as an exponential, thereby allowing the parameter to take on any value. In addition, we note that the variance of an average of a sample independently drawn from a population with a finite variance will be inversely proportional to the number of items in the sample, so we will take the constant of proportionality to also vary inversely to the number of exposures.

Following the notation in Venter (2007), we will state our stochastic model as shown in (3.3), suppressing subscripts for the moment and letting w denote the natural log of the exposure measure for an accident year.

$$\begin{array}{c} \mathrm{E}(A)=\mu , \\ \operatorname{Var}(A)=\frac{e^{\mathrm{\kappa}}\left(\mu^{2}\right)^{p}}{W}=e^{\mathrm{\kappa}-w}\left(\mu^{2}\right)^{p} \end{array} \tag{3.3}$$

Note that this model includes an implicit structural heteroscedasticity. The expected values will differ by accident year and development year. Since the variance is a function of the expected value, it will likewise differ by accident and development year. By combining this structure with two variance parameters, κ and p, that can be fit to the data, we provide a mechanism for the variance structure of the model to approximate the variance structure of the data without over-parameterizing our model. We note, though, that the formulae we present here can very easily be modified to allow κ to vary by development period if additional control over the heteroscedasticity is desired.

We note the incremental amounts A under consideration are averages of a number of observations. If we assume the observations are themselves independent, then the central limit theorem would imply that they have asymptotically Gaussian distributions. For this reason, we will assume that the A variables are all independent and have Gaussian distributions given in (3.4), again suppressing subscripts for the moment.

$$A \sim \mathrm{N}\left(\mu, e^{\kappa-w}\left(\mu^{2}\right)^{p}\right). \tag{3.4}$$

Since we are concerned with MLEs, the negative log likelihood for this distribution will be key to our analysis. The likelihood function for a Gaussian distribution is given by (3.5).

$$\mathrm{f}(x ; \mu, \kappa, p)=\frac{1}{\sqrt{2 \pi e^{\kappa-w}\left(\mu^{2}\right)^{p}}} e^{-\frac{(x-\mu)^{2}}{2 e^{x-m(\mu)^{p}}}} . \tag{3.5}$$

This gives a negative log likelihood for a single variable given in (3.6).

$$\begin{array}{l} 1(x ; \mu, \kappa, p)=-\ln (\mathrm{f}(x ; \mu, \kappa, p)) \\ \quad=-\ln \left(\frac{1}{\sqrt{2 \pi e^{\kappa-w}\left(\mu^{2}\right)^{p}}} \exp \left(-\frac{(x-\mu)^{2}}{2 e^{\kappa-w}\left(\mu^{2}\right)^{p}}\right)\right) \\ \quad=\frac{1}{2}\left(\kappa-w+\ln \left(2 \pi\left(\mu^{2}\right)^{p}\right)\right)+\frac{(x-\mu)^{2}}{2 e^{\kappa-w}\left(\mu^{2}\right)^{p}} . \end{array} \tag{3.6}$$

Using the relationships in (3.2) and (3.4), we have the stochastic statement of our reserving model as shown in (3.7).

$$A_{i j} \sim \mathrm{N}\left(g_{i j}(\boldsymbol{\theta}), e^{\mathrm{k}-w_{i}}\left(g_{i j}(\boldsymbol{\theta})^{2}\right)^{p}\right) . \tag{3.7}$$

In formula (3.7) the added constants w_i are included to reflect the fact that the variance of an average of a sample is dependent on the number of elements composing that sample. At this point, if we wanted the constant of proportionality to vary by development lag we would simply substitute a vector for the constant parameter κ.

With observations in a typical loss triangle, we get the negative log likelihood function given in (3.8).

$$\begin{array}{l} \ell\left(A_{11}, A_{12}, \ldots, A_{m 1} ; \boldsymbol{\theta}, \kappa, p\right) \\ \quad = \frac{1}{2} \sum_{(i, j \in \in} \kappa-w_{i}+\ln \left(2 \pi\left(g_{i j}(\boldsymbol{\theta})^{2}\right)^{p}\right) \\ \qquad +\frac{\left(A_{i j}-g_{i j}(\boldsymbol{\theta})\right)^{2}}{e^{\kappa-w_{i}}\left(g_{i j}(\boldsymbol{\theta})^{2}\right)^{p}} . \end{array} \tag{3.8}$$

The set S in (3.8) denotes the set of all index pairs for which data are available. We denote by T the index pairs over which we want forecasts. If the data were available in a full triangle, with n rows and n columns, then S and T would follow the form given in (3.9).

$$\begin{array}{l} S=\{(i, j) \mid i=1,2, \ldots, n, j=1,2, \ldots, n-i+1\} \\ T=\{(i, j) \mid i=2, \ldots, n, j=n-i+2, \ldots, n\} \end{array} \tag{3.9}$$

However, we do not need to restrict ourselves to this regular case and will use the more flexible notation.

We select the values of the parameters to be the MLEs, the values that minimize the negative log likelihood function in (3.8). Let us denote these estimates by θ̂, κ̂, and p̂. In practice there are a number of tools available to estimate these parameters. We have used the nlminb function in the package MASS written for the statistical programming language and environment R (R Core Team 2012) for this purpose, though other tools might be just as useful. We used analytic rather than numeric representations for the various derivatives to increase the accuracy and speed of the calculation.

If we assume that there is no model or parameter uncertainty, so that the model parameterized with the MLEs gives an exact description of the true loss emergence process, then it is straightforward to obtain estimates of the distribution of outcomes. We have assumed that, for fixed values of the parameters, the variables A_ij are independent. Thus, in the absence of parameter or model uncertainty that could introduce correlations between the variables, we can conclude that the distribution of average future payments for each year is given by (3.10) and that the distribution of total future payments is given by (3.11).

$$R_{i} \sim \mathrm{N}\left(W_{i} \sum_{\{j(L i, j) \in T\}} g_{i j}(\hat{\boldsymbol{\theta}}), W_{i}^{2} \sum_{\{j(i, j) \in T\}} e^{\hat{\boldsymbol{\alpha}}-w_{i}}\left(g_{i j}(\hat{\boldsymbol{\theta}})^{2}\right)^{\hat{p}}\right) . \tag{3.10}$$

$$R_{T} \sim \mathrm{N}\left(\sum_{i=1}^{m} W_{i} \sum_{\{j(i, i, \in \in\}} g_{i j}(\hat{\boldsymbol{\theta}}), \sum_{i=1}^{m} W_{i}^{2} \sum_{\{j(i, j) \in T\}} e^{\hat{\alpha}-w_{i}}\left(g_{i j}(\hat{\boldsymbol{\theta}})^{2}\right)^{\hat{p}}\right) . \tag{3.11}$$

This then gives the effect of process uncertainty on the total forecast incremental averages by accident year. This does not, however, address the issue of parameter uncertainty.

Just as the standard error provides insight into parameter uncertainty in usual regression applications, the information matrix can be helpful in estimating the variance-covariance matrix of the parameters. Since we have based our model on a Gaussian distribution, the conditions of Theorem 1 will be met as long as the functions g_ij are sufficiently regular, which will be the case for the examples we will consider. Thus, to estimate the variance-covariance matrix for the parameters, we first define the Fisher information matrix as the matrix of expected values of the Hessian of the negative log likelihood function.

First, the Hessian is the matrix whose element in the ith row and the jth column is the second derivative of the negative log likelihood function, once with respect to the ith variable and once with respect to the jth as shown in (3.12), assuming the vector θ has k elements.

$$\text { Hessian } \ell=\left(\begin{array}{ccccc} \frac{\partial^{2} \ell}{\partial \theta_{1}^{2}} & \cdots & \frac{\partial^{2} \ell}{\partial \theta_{1} \partial \theta_{k}} & \frac{\partial^{2} \ell}{\partial \theta_{1} \partial \kappa} & \frac{\partial^{2} \ell}{\partial \theta_{1} \partial p} \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ \frac{\partial^{2} \ell}{\partial \theta_{k} \partial \theta_{1}} & \cdots & \frac{\partial^{2} \ell}{\partial \theta_{k}^{2}} & \frac{\partial^{2} \ell}{\partial \theta_{k} \partial \kappa} & \frac{\partial^{2} \ell}{\partial \theta_{k} \partial p} \\ \frac{\partial^{2} \ell}{\partial \kappa \partial \theta_{1}} & \cdots & \frac{\partial^{2} \ell}{\partial \kappa \partial \theta_{k}} & \frac{\partial^{2} \ell}{\partial \kappa^{2}} & \frac{\partial^{2} \ell}{\partial \kappa \partial p} \\ \frac{\partial^{2} \ell}{\partial p \partial \theta_{1}} & \cdots & \frac{\partial^{2} \ell}{\partial p \partial \theta_{k}} & \frac{\partial^{2} \ell}{\partial p \partial \kappa} & \frac{\partial^{2} \ell}{\partial p^{2}} \end{array}\right) \tag{3.12}$$

Thus the information matrix, which is the expected value of this Hessian, evaluated at the parameter estimates is given in (3.13).

$$\mathbf{I}(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})=\left(\begin{array}{ccccc} \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \theta_{1}^{2}}\right) & \cdots & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \theta_{1} \partial \theta_{k}}\right) & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \theta_{1} \partial \kappa}\right) & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \theta_{1} \partial p}\right) \\ \vdots & \ddots & \vdots & \vdots \\ \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \theta_{k} \partial \theta_{1}}\right) & \cdots & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \theta_{k}^{2}}\right) & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \theta_{k} \partial \kappa}\right) & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \theta_{k} \partial p}\right) \\ \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \kappa \partial \theta_{1}}\right) & \cdots & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \kappa \partial \theta_{k}}\right) & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \kappa^{2}}\right) & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial \kappa \partial p}\right) \\ \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial p \partial \theta_{1}}\right) & \cdots & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial p \partial \theta_{k}}\right) & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial p \partial \kappa}\right) & \mathrm{E}\left(\frac{\partial^{2} \ell(\hat{\boldsymbol{\theta}}, \hat{\kappa}, \hat{p})}{\partial p^{2}}\right) \end{array}\right) \tag{3.13}$$

We show these expectations, along with both the elements of the gradient and the Hessian of the negative log likelihood function in terms of the general model functions g_ij in Appendix A to this paper. The inverse of the information matrix is then an approximation for the variance-covariance matrix for the parameters. In particular, then, an estimate of the standard error of the various parameters is given by the square root of the diagonal of that matrix, that is by $\sqrt{\operatorname{diag}\left(\mathbf{I}(\hat{\boldsymbol{\theta}}, \hat{\boldsymbol{\kappa}}, \hat{p})^{-1}\right)} .$ If we are willing to assume, by virtue of Theorem 1 above, that the parameters asymptotically have a multivariate Gaussian distribution with expected value (θ̂, κ̂, p̂) and covariance matrix l(θ̂, κ̂, p̂)⁻¹, then the problem of estimating the distribution of reserve forecasts reduces to estimating the distribution of a random variable whose parameters have a known distribution, a classical problem of estimating a posterior distribution.

There are a number of approaches that can be applied to that problem. Given that we have not placed any real restrictions on the general expected value model, other than having the second derivatives existing, an analytic solution is not easy to obtain. A Markov chain Monte Carlo (MCMC) method such as the Gibbs sampler as discussed by Scollnik (1996) or the Metropolis-Hastings algorithm as discussed by Meyers (2009) could be used for this purpose. However, our assumption that the parameters have a multivariate Gaussian distribution makes a more straightforward approach available. We use direct Monte Carlo simulation to estimate the reserve distribution. We first randomly select a parameter vector (θ*, κ*, p̂*) from a multivariate Gaussian distribution with expected value (θ̂, κ̂, p̂) and covariance matrix l(θ̂, κ̂, p̂)⁻¹ and then randomly select Gaussian variables R_i* from Gaussian distributions with mean $E_{i} \sum_{\{j(i, j, j \in T\}} g_{i j}\left(\boldsymbol{\theta}^{*}\right)$ and variance $E_{i}^{2} \sum_{\{j(x, j) \in\}\}} e^{k^{*}-w_{i}}\left(g_{i j}\left(\boldsymbol{\theta}^{*}\right)^{2}\right)^{2}$ for each value of i.

At this juncture, if we wished to assume that claim counts were stochastic but independent of the incremental severities, we could simulate the ultimate number of claims by exposure year to add a provision for uncertainty in those estimates in the final forecast.

This then sets a general framework that can be applied to any loss model that is sufficiently differentiable. The next section of this paper will look at five specific examples of commonly applied reserving methods adapted to this framework.

4. Example models

In this section we will show how five commonly used reserving methods can be readily adapted to stochastic models in this framework. The five models we select are a variant of the Bornhuetter-Ferguson method that is akin to the Stanard-Buhlmann or Cape Cod method, a variation of the incremental severity model presented by Berquist and Sherman (1977), two variations of the Hoerl curve models presented by Wright (1992), and a formulation of the traditional chain ladder or development factor method.

We will show the application of these five models to aggregate commercial automobile liability paid loss and defense and cost containment expenses, net of reinsurance, as reported in the 2010 Schedule P by ten U.S. insurers all writing $50 million or more in net premiums for that line in 2010, as shown in Table 1. We used a standard chain ladder applied to reported counts for these carriers to derive the claim count estimates.

4.1. Cape Cod model

Bornhuetter and Ferguson (1972) estimate the future incurred losses for an accident year as a percentage of an a priori estimate of ultimate losses for that year. The percentage is based on historical incurred loss development patterns, and the a priori estimate is based on a selected loss ratio times the premiums for that year. The distinguishing feature of the Cape Cod variant of this method, as presented, for example, by Stanard (1985), is that it derives the a priori loss estimates directly from the data. We will use the term “Cape Cod” in this paper to refer to an approach that has the same general structure of the Bornhuetter-Ferguson approach but derives its a priori ultimate estimates by accident year from the loss and exposure data alone, without reference to outside information. The specific model we use may not necessarily correspond to others used that are also called Cape Cod.

To this purpose, then, we will assume that the incremental average amounts are the product of two different factors, one representing the accident year influence, usually taken as the ultimate losses for the year, and the other corresponding to the lag, usually taken as the percentage of losses emerging that year. With this simple formulation, there are infinitely many sets of parameters that give the same model, since multiplying all the accident year parameters by a constant and dividing all the development year parameters by the same constant gives the same result. For that reason we selected the slightly more complicated parameterization for this model shown in (4.1) with a total of m + n − 1 parameters.

$$g_{i j}(\boldsymbol{\theta})=\left\{\begin{array}{l} \theta_{1} \text { if } i=j=1 \\ \theta_{1} \theta_{i} \text { if } j=1 \text { and } i>1 \\ \theta_{1} \theta_{m+j-1} \text { if } i=1 \text { and } j>1 \\ \theta_{1} \theta_{i} \theta_{m+j-1} \text { if } i>1 \text { and } j>1 \end{array}\right. \tag{4.1}$$

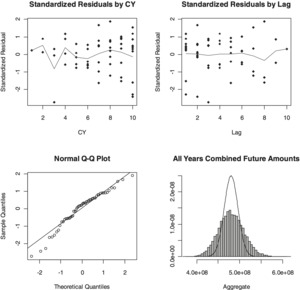
Just as with the usual Cape Cod method, this model uses the data to determine the accident year expected loss rather than basing those estimates on sources outside the data as in the Bornhuetter-Ferguson method. It therefore allows a separate loss level for each accident year. Table 2 shows the parameter estimates for this model.

In addition to the parameter estimates, Table 2 shows estimates of the standard error of the parameters, taken as the square root of the diagonal of the covariance matrix for the parameters. The standard error is a measure of the standard deviation of particular parameters given the observed data. A large standard error relative to a parameter estimate may indicate significant uncertainty around that estimate.

We would also like to be able to compare the fits of different models to get an assessment of which models seem to better reflect patterns in the observed data. One measure that is comparable among models is the likelihood of the data given the fitted model. However, one can often increase this likelihood by adding parameters to a model, so a useful comparison should also take into account the number of parameters necessary to obtain a particular fit. The Akaike Information Criterion (AIC; see, for example, Venables and Ripley 2002), is one such statistic that addresses both of these points, particularly when comparing models with the same underlying probability structure as we are doing here. As used in these calculations the AIC is twice the negative log likelihood valued at the selected parameters plus twice the number of parameters estimated. Thus a smaller value of the AIC tends to indicate a better fit.

Table 3 shows the expected average cost forecasts as well as indicated standard deviations by cell implied by the model, but ignoring parameter uncertainty.

As mentioned above, we make use of the Fisher Information Matrix to estimate covariance among the parameter estimates. Thus the distribution of forecasts from the Cape Cod method reflects both the process uncertainty shown in Table 3 and the parameter uncertainty captured by the Fisher information matrix. Table 4 summarizes the forecasts for total future payments, both by accident year and in total as well as forecasts for the next calendar year. In this table we show the total estimated future loss payments and standard deviation by accident year and in total for all accident years implied by the model, both with and without consideration of parameter uncertainty. Also shown are the results of our simulation of the effects of parameter uncertainty on those amounts along with the 90% confidence interval implied by that simulation. The lower half of Table 4 shows the same information for the payments estimated to be made in the next year. This information can provide a test for how well emerging data fits the model. If payments next year fall outside the range indicated, then there may be cause to question whether the Cape Cod model is the appropriate one for this data set.

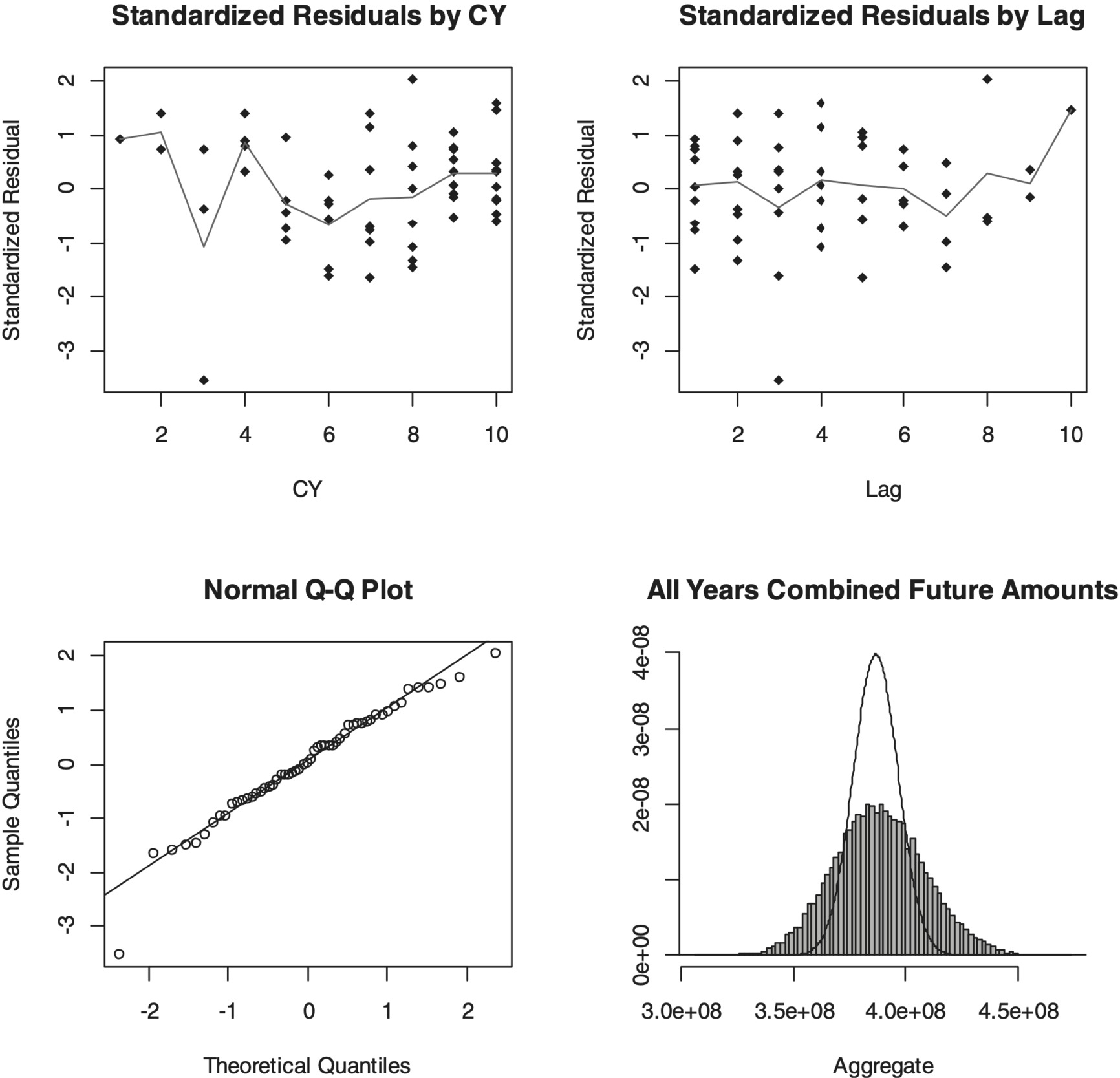
As with other stochastic models, it is often helpful to visualize the model’s fit both in terms of standardized residuals and Q-Q plots. The former help inform if the model is missing significant patterns in the data, while the latter test how well the model captures the statistical characteristics of the data. Generally, a Q-Q plot that follows a straight line indicates that the actual variability observed in the data is consistent with the form of the model. Deviation from a straight line may indicate the actual data have different “tail” characteristics than what is assumed in the model. Figure 1 gives four different charts resulting from our Cape Cod model fit. Calendar year influences may show in the Standardized Residuals by CY plot, while tests of how well the model fits in the tail are shown in the Standardized Residuals by Lag plot. The normal Q-Q plot shows how close to a Gaussian (straight line) the standardized residuals fall. Finally, the distributions of total reserve forecasts both with (histogram) and without (line) parameter uncertainty are shown graphically.

Appendix B shows the derivatives for this formulation of the Cape Cod model.

All these calculations were carried out using the open-source statistical package R. The code used is shown in Appendix G of this paper.

4.2. Berquist-Sherman incremental severity model

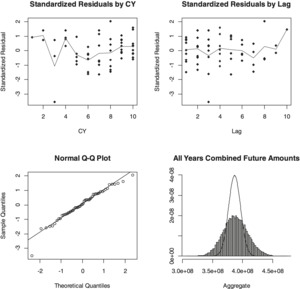
The Cape Cod model has the largest number of parameters of the five models we discuss here. Berquist and Sherman (1977) recognized that average costs may exhibit a reasonably predictable trend over the experience period in question. They developed methods to model incremental severities that allowed for not only different loss levels by lag, as in the Cape Cod model, but also different trends by payment lag as well. We simplify their approach here somewhat and replace the separate loss levels for each accident year by a single parameter, trend from one accident year to the next, and assume that this trend is constant through the entire time frame to be modeled, effectively replacing the m accident year parameters by a single trend parameter for a total of n + 1 parameters to be estimated using the data. We thus use the formulation in (4.2) for the Berquist-Sherman incremental severity model.

$$g_{i j}(\boldsymbol{\theta})=\theta_{j} e^{i \theta_{n+1}}, i=1,2, \ldots, m, j=1,2, \ldots, n \tag{4.2}$$

Table 5 through Table 7 and Figure 2 show the results for this model, similar to Table 2 through Table 4 and Figure 1.

Appendix C shows the derivatives for this formulation of the Berquist-Sherman incremental severity model.

4.3. Wright’s model

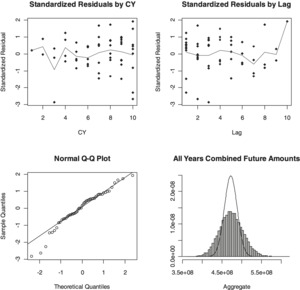
The Berquist-Sherman model presented here replaced the Cape Cod’s accident year level factors with a uniform annual trend. That model still maintained separate parameters for each development lag. Just as fitting a line replaces a number of points with a line defined by two parameters, Wright (1992) made use of a curve to replace the multiple lag parameters with a fixed number of parameters. Wright considered two similar curves representing loss volume as a year aged, using the variable τ to represent what he calls “operational time.” Two of the curves he considered are shown in (4.3).

$$\begin{array}{l} \exp \left(\beta_{0}+\beta_{1} \tau+\beta_{2} \ln (\tau)\right) \\ \exp \left(\beta_{0}+\beta_{1} \tau+\beta_{2} \tau^{2}\right) \end{array} \tag{4.3}$$

Both of these are special cases of the form shown in (4.4).

$$\exp \left(\beta_{0}+\beta_{1} \tau+\beta_{2} \tau^{2}+\beta_{3} \ln (\tau)\right) \tag{4.4}$$

Incorporating this curve with separate level parameters by accident year, we call the function in (4.5) Wright’s model.

$$\begin{array}{r} g_{i j}(\theta)=\exp \left(\theta_{i}+\theta_{m+1} j+\theta_{m+2} j^{2}+\theta_{m+3} \ln (j)\right), \\ i=1, \ldots, m, j=1, \ldots, n \end{array} \tag{4.5}$$

We note that, in contrast to the prior two models, this requires that the expected losses be positive in all cells. We also note that we use the formulation from England and Verrall (2001), which uses the age directly rather than the operational time variant used by Wright (1992). If we wished to replace the parameter j in (4.5) by a more general operational time independent variable $\tau_{i j}$, the formulae in Appendix D still hold with $\tau_{i j}$ replacing j.

Table 8 through Table 10 and Figure 3 show the results for this model similar to Table 2 through Table 4 and Figure 1.

Appendix D shows the derivatives for this formulation of Wright’s model.

4.4. Generalized Hoerl curve model

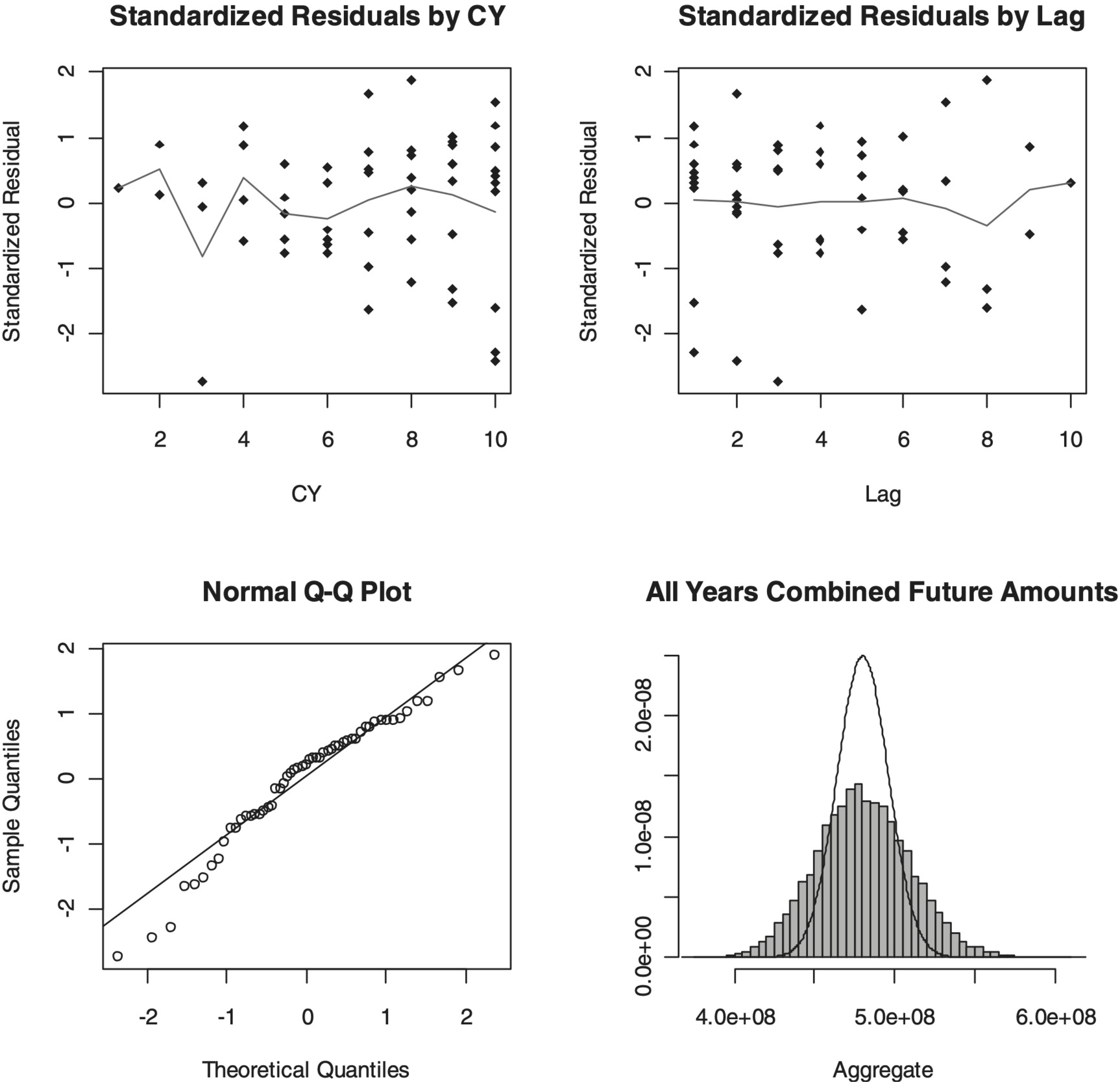
Just as the Berquist-Sherman model presented here replaced the Cape Cod’s accident year level factors with a uniform annual trend, we can further refine Wright’s model and replace separate accident year levels by an expected trended amount. We will use the four-parameter curve in (4.4) and incorporate trend as well in the model that we call a generalized Hoerl curve model shown in (4.6).

$$\begin{array}{r} g_{i j}(\boldsymbol{\theta})=\exp \left(\theta_{1}+\theta_{2} j+\theta_{3} j^{2}+\theta_{4} \ln (j)+i \theta_{5}\right), \\ i=1, \ldots, m, j=1, \ldots, n \end{array} \tag{4.6}$$

We note that, as with the last model, this requires that the expected losses be positive in all cells. Again, if we wished to replace the parameter j in (4.6) by a more general operational time independent variable $\tau_{i j}$, the formulae in Appendix E still hold with $\tau_{i j}$ replacing j.

Table 11 through Table 13 and Figure 4 show the results for this model similar to Table 2 through Table 4 and Figure 1.

Appendix E shows the derivatives for this formulation of the generalized Hoerl curve model.

4.5. Chain ladder model

The fifth model we will consider here is the chain ladder. In contrast to England and Verrall (1999), our purpose is to state the classical method in a general stochastic framework and we are not interested in reproducing the selection of classic weighted average development factors. We note that the chain ladder method is equivalent to assuming the incremental amounts at a particular age are equal to some factor times the aggregate amount for the accident year. So far, this is precisely the formulation of the Cape Cod model above. That model has m + n − 1 parameters. What sets the chain ladder apart, though, is the additional constraint that the expected amounts to date equal the actual amounts to date for each accident year. In effect, this constraint fixes m of the parameters that reflect accident year levels, reducing the remaining model to n − 1 parameters. The implication of this formulation is that the risk that the actual and expected amounts to date differ is not captured in process or parameter uncertainty but rather remains in the realm of model uncertainty.

Thus, we formulate the chain ladder model here using (4.7). Here we denote the actual average amount paid to date per unit of exposure for accident year i by P_i and denote by n_i the age of the most mature available entry for that accident year. For example, in a complete “square” triangle with annual development for m accident years through m years of development we have n_i = m − i + 1.

$$g_{i j}(\boldsymbol{\theta})=\left\{\begin{array}{l} P_{1} \theta_{j} \text { if } j<n \text { and } i=1 \\ P_{1}\left(1-\sum_{k=1}^{n-1} \theta_{k}\right) \text { if } j=n \text { and } i=1 \\ \frac{P_{i} \theta_{j}}{\sum_{k=1}^{n_{i}} \theta_{k}} \text { if } j<n \text { and } i \neq 1 \\ \frac{P_{i}}{\sum_{k=1}^{n_{i}} \theta_{k}}\left(1-\sum_{k=1}^{n-1} \theta_{k}\right) \text { if } j=n \text { and } i \neq 1 \end{array}\right. \tag{4.7}$$

Table 14 through Table 16 and Figure 5 show the results for this model, similar to Table 2 through Table 4 and Figure 1.

Appendix F shows the derivatives for this formulation of the chain ladder model.

5. Some other MLE applications

This is not the only paper to discuss the use of MLEs in the context of actuarial projections. Weisner (1978) shows the use of MLEs in fitting probability distributions to the emergence of reported claims over time, similar to the Hoerl curve model presented here, but limited to a single accident year. Clark (2003) also used parametric curves to model emergence of losses but in the context of loss triangles. In the models presented here, the Berquist-Sherman model can be seen as a special case of the Cape Cod where accident year variations are replaced by trend. Wright’s model can be seen as another special case of the Cape Cod where the development year variations are replaced by a smooth curve. The Hoerl curve model can be seen as a special case of both of these, with both development variations and accident year variations replaced by parametric curves. Wright’s model most closely tracks the approach taken in Clark (2003).

Instead of a Hoerl curve, Clark considers the log-logistic curve and the Weibull curve as cumulative emergence patterns. Clark also presents another model, labeled as “Cape Cod,” which assumes constant expected accident year loss ratios. In terms of the models we have here, this is quite similar to the Hoerl curve model, with the assumption of no trend and using premiums as an exposure measure in the denominator.

Instead of allowing the variance of incremental amounts to be proportional to a power of the square of their mean, Clark requires them to be proportional to the mean, resulting in the selection of the overdispersed Poisson as an underlying statistical model. Given the general framework presented in this paper, it would not be difficult to include additional example models here. All that would be necessary would be to appropriately define the various functions corresponding to (3.2). In the implementation we would need to derive the Hessian of those expected value functions and to incorporate them in the R code in Appendix G.

6. Observations and conclusions

As with traditional analyses, the various stochastic models considered here give different estimates of expected total future payments, ranging from $388 million for Wright’s model to $480 million for the Berquist-Sherman model, and AIC values ranging from 643 for the Berquist-Sherman model to 599 for the chain ladder model. Comparing the total indicated distributions of projected future payments, as shown in Figure 6, provides valuable information.

Figure 6 shows that not only are the expected amounts different among the various models but so are the underlying distributions of forecast outcomes. Under the Hoerl and Berquist-Sherman models, there is little likelihood for the bulk of the potential forecasts from the Cape Cod, Wright, and chain ladder models and the converse is also true. In short, differences in the forecasts are likely not due to random fluctuations or even parameter uncertainty but to differences among the models themselves. This is model uncertainty. Although the chain ladder model shows the tightest distribution and lowest AIC value, care should be taken in jumping to conclusions. As mentioned before, the formulation of the chain ladder has the requirement that the expected amount to date equals the actual amount for each accident year, a restriction that the other three models presented do not have.

Reviewing the data in Table 1 gives some insight as to the reason for the differences among the models. We see average costs steadily increasing through accident year 2008 and then dropping off in the most recent two accident years. Both the Berquist-Sherman incremental severity and the generalized Hoerl curve models shown here assume a uniform trend throughout. The drop-off in the last two accident years increases the errors for these two models and hence the standard deviation of the forecasts. The Cape Cod, Wright, and chain ladder models all key on the amounts to date for the more recent accident years and thus their forecasts react to the change in the pattern. The fundamental question then becomes whether this drop-off is due to some characteristic of the underlying data or random noise. If the former is the case, then the uniform trend assumption of the Berquist and Hoerl models would be violated. If the latter is the case, then the Cape Cod and chain ladder models will be fitting to noise and not signal. The data alone as presented does not answer this question.

In spite of the additional information provided by stochastic models, the practitioner is faced with the same question that the practitioner of traditional methods faced: the applicability of a particular model or method to a particular data set. Unfortunately, a single data set probably is not sufficient to answer the question in either situation. This is a significant drawback to this or any frequentist statistical approach.

This entire discussion goes to probably the greatest source of uncertainty in reserving projections—the question of model uncertainty. We hope the greater ease that the approach outlined in this paper gives to considering a range of models in reserving exercises will make it easier to explore and quantify the issue of model uncertainty in the future.

These models applied to a single data set may not give insight into model uncertainty. However, successive applications of these models over time might give additional insight. One significant advantage these stochastic models have over their non-stochastic counterparts is the ability to assess new data. Table 4, Table 7, Table 13, and Table 16 show not only estimates and statistics on total future payments by accident year, but also estimates and statistics on forecast payments during the next year. If emerging losses deviate significantly, say outside the 90% confidence interval shown, then one might come to suspect that a particular model may not be capturing what is actually going on in the underlying data. This observation also opens the way toward a potential weighting of the various models as time progresses. If we assess that none of these models are better than any of the others in deriving an ultimate loss forecast, then a Bayesian outlook would say that the model that is a straight average of the five might in some sense be better than any of the models alone. As losses emerge next year, this same Bayesian approach would indicate how to modify those a priori weights to reflect how well or how poorly a particular model performed in forecasting the future. If one applied such a Bayesian evolution to a broad stable of models, possibly incorporating some not shown here, it is likely that the resulting blend could produce forecasts most consistent with the underlying data. Models that have a good track record of predicting the next diagonal receive increasing weight while those with poor records receive decreasing weight.

There is still much work to be done. At least until the loss-generating process in insurance is understood and can be adequately and accurately modeled, there continues to be the need to look at a range of potential loss emergence models, not just the results from a single one. There also continues to be the need to find a way to sort through all those various models to best track and predict future payments or claims. Frequentist approaches such as those presented here by their nature are limited to observed data. They can, however, form the basis for a richer analysis, incorporating not only data specific to a particular situation but also experience from similar situations using Bayesian methods.