Actuarial Portfolio Management of Infrastructure Service Contracts

1. Introduction

This paper predicts the existence of potentially substantial economic inefficiencies borne by organizations that are not detectable through examination of data created by currently configured accounting systems. Its conclusions are predicated on assumptions about the nature of a function called M(t), which defines the size and timing of opportunity costs unique to individual physical assets. Certain gross characteristics of M(t) will be described, and are simply assumed for the purpose of building a theoretical argument which could form the basis for an enterprise policy to manage physical assets.

The physical assets referred to in this paper are fixed assets that are not expended during operations, and are used to produce revenues. They do not include cash or inventories, which might sometimes be included under a broader definition. They comprise the plant, property, and equipment line item on the balance sheet. These assets are sometimes collectively referred to as plant. Many physical assets will eventually be replaced with like or similar assets that perform the same mission within the plant. The process of replacing physical assets when they have reached the end of their useful lives is often referred to as renewal.

The value of physical assets in the economy is vast. Of particular interest in this paper is capital equipment. According to the United States Census Bureau (USCB 2012), $7.212T of capital equipment was purchased between 2001 to 2010 in the United States alone. Much of it will be replaced in the future when it becomes obsolete. Subsequent years will probably show increasing levels of investment in capital equipment.

For some companies, physical asset expenditures, including not only repairs and replacements, but also other operating costs, are significant when compared to net earnings. Efficiency gains in these expenditures may have a material impact on their market valuations. Oil and gas companies, electrical power producers, airlines, public utilities, transportation authorities, and manufacturers are all sectors that rely heavily on physical assets, and may benefit from a management approach realistically addressing their mortality. According to Evans and Annunziata (2012) a one-percent efficiency savings applied across these specific global industry sectors could result in an addition of $15.3T to global GDP by 2030.

Matziorinis and Rowley (1993) describe the magnitude of physical asset expenditures and some of the shortcomings in the way they are accounted for on a macroeconomic level. They focus on repair and replacement expenditures only, and express the opinion that these do not receive much attention in the theory and econometrics of investment, despite their importance. They also describe the effect of the level of aggregation of physical assets in the accounting of such expenditures as a reason they cannot be consistently measured. For example, is an airplane a single physical asset, or is it composed of the airframe, engines, and interior fittings as separate assets?

Work has been done attempting to explain the economic reasons for replacement investment. Eisner (1972), Feldstein and Foot (1971), and Feldstein (1974) have studied statistical correlations in empirical data classified into different candidate determinant variables, including a firm’s liquidity, cost of capital, level of sales, level of expansion investment, level of capacity utilization, business expectations, rate of change in capital goods prices, the average age of capital goods, tax factors, and technology change. Interesting correlations among these variables were discovered by these authors, and subsequent works which cite them have used their findings to address the accuracy of macroeconomic measures, such as gross fixed capital expenditure or gross fixed capital formation. These authors also considered behavioral effects implicit in these explanatory variables, which we intend to filter out by articulating a purely rational enterprise policy for the replacement of physical assets.

2. Infrastructure service contracts (ISCs)

In enterprise risk management, there is usually a lack of appropriate risk transfer mechanisms for operational risks. In this paper, we will suggest the deliberate creation of volatile, risky cash flows resulting from asset replacements in order to achieve a higher level of operational efficiency. Fortunately, there already exists an institution for transferring such risks. Extended service contracts can be used to implement physical asset replacement policies. This section serves as an introduction to such contracts for facilities and infrastructure, and intends to provide some historical background on the environment in which the theory described in this paper was conceived.

As there are extended service contracts for homes and vehicles, so there are long duration repair and replacement agreements for whole industrial facilities and public infrastructure. Unlike their home and vehicle counterparts, such extended warranties for facilities and infrastructure do not exist as stand-alone products. Rather, they are underwritten in the limited context of non-insurance entities providing entire railways, water treatment plants, power plants, or other large ensembles of physical assets.

Contracts in which single entities provide integrated engineering, procurement, construction, operations, routine maintenance, repair and replacement services to deliver and run new facilities and infrastructure may have first come into existence in the 1980s, and possibly much earlier if one includes public-private partnerships for public utility infrastructure which date back to the late nineteenth century. Companies specializing in one or more of the above services usually must form consortia to meet the wide scope of responsibilities required under such contracts. Contract terms can be as long as 50 years, and entities providing these services assume most of the functional roles of the owner of the facility.

This integrated suite of services, including repair and replacement, is not the usual way to deliver infrastructure. In the United States, it applies to less than 1% of new facilities. However, useful principles regarding planning of capital expenditures and methods for projecting losses and expenses associated with repair and replacement obligations have been developed during negotiations among parties seeking to transfer these uncertain cash flows, and these principles and methods apply to all physical assets, whether or not covered by such contracts.

We refer to the entities described above as service providers. They have a direct contractual relationship with the facility owner to provide a wide range of services, including repair and replacement of capital assets. The facility owner is the contract holder, and is usually a utility, municipality, or transportation authority. Replacement of physical assets usually refers to the replacement of a whole item of capital equipment or a structure, such as machinery or a building.

Service providers are responsible for complete facility maintenance, including routine maintenance, repairs, and replacements of physical assets. The agreement to provide repair and replacement services is a part of a larger offering of services, and is now often set forth in distinct articles within such contracts. In the past, these obligations were informally agreed to and not meticulously documented. Recently, as this infrastructure delivery method has gained traction in the United States, attorneys have attempted to formalize physical asset replacement obligations. Spelling out these obligations has forced negotiating parties to explicitly consider the economic aspects that the contract must capture for an equitable transfer of risk and fair pricing.

In this paper, only the long duration repair and replacement obligations under such contracts are referred to as infrastructure service contracts (ISCs). This definition, unique to this paper, allows us to separate and focus only on the services that are a very near counterpart to home and vehicle extended service contracts with which they share many similarities.

Manufacturers of capital equipment have also provided extended service contracts covering repairs and replacements associated with their products. This is partly in response to the needs of service providers who wish to transfer these risks, and manufacturers’ willingness to assume such risks as a value added service in order to sell capital equipment. A manufacturer will often provide an extended service contract which matches the duration and requirements of the service provider’s contract with facility owners.

As with their home and vehicle counterparts, the exposure to risk in ISCs varies significantly during the contract period, and pro rata earning of service fees does not provide a match between income and liabilities. In addition, service fees are not always received in proportion to the level of exposure to risk. Unlike their home and vehicle counterparts, earning patterns are not easily predicted by traditional property and casualty methods using data triangles. There is little historical loss data, and the tails for such coverage can be far longer than these contracts have been in existence.

The entities that underwrite ISCs are not insurance companies. To our knowledge, insurers are not involved in underwriting long duration repair and replacement risks associated with industrial and public infrastructure. There are several reasons for this, which will be discussed later. Facility owners transfer these risks to service providers. Then service providers transfer some of these risks to manufacturers. In both of these transactions, the underwriting of repair and replacement losses is always only a portion of the total services rendered. Beyond the service provider and manufacturer, there is no further place to transfer this risk.

2.1. Typical features of the ISC

In an ISC, the service provider agrees to replace physical assets during the term of the contract. Because of the long term of these contracts, a large proportion of the covered capital equipment in a facility may be replaced, perhaps multiple times. Repairs are an important part of the scope of an ISC, but the majority of losses and expenses arise from the contract’s replacement obligations.

The timing of replacement decisions is critical to projecting loss costs for this coverage. In some ISCs, the language controlling timing of equipment replacement is very prescriptive. In others, the service provider is essentially a concessionaire (owner) of the facility during the term of the contract, and since maintenance costs are fully internalized by the service provider, the decision of when to replace an item of capital equipment is left at the service provider’s discretion.

Some contracts stipulate a required physical condition of the facility at the end of the contract term. This can be specified as a threshold minimum weighted average useful life of covered facility capital equipment at the end of the contract term, in which estimated equipment replacement costs weight estimates of remaining useful equipment life, as determined by a facility condition assessment conducted by a third-party evaluator.

Some contracts use verbal thresholds to describe the minimum required physical condition of equipment and structures at the end of the term. If the facility does not meet these qualitative descriptions, then the service provider must make all repairs, replacements, or cash payments necessary to remedy the deficiencies.

The service provider usually cannot terminate the contract for convenience, nor modify the service fee during the term of the contract. The service fee can be automatically indexed for inflation. An indexing formula is usually a pre-negotiated part of the contract, not subject to modification after the contract is executed. Common indexes used are a weighted combination of Consumer Price Index (CPI), Employment Cost Index (ECI), and other indexes published by the Bureau of Labor Statistics (BLS).

As with their automobile and home counterparts, ISCs are secondary to short-term warranties against defects in workmanship provided by the equipment manufacturer (original equipment manufacturer or OEM) or equipment seller. However, this is small comfort to the service provider who essentially provides a warranty many times longer than the OEM warranty. OEM warranties for capital equipment can typically last 18 months from delivery or 12 months from time of use, whichever comes first. This period is small compared to the 10- to 50-year terms of ISCs.

Some contracts also include a negotiated list of major equipment subject to replacement obligations. Each item of equipment may have a cap for replacement cost reimbursement to the service provider, but replacement obligations are limited to those items on the list.

ISCs usually do not have explicit service fees. Coverage is often bundled as a part of a larger service fee for ongoing operations and maintenance services, which can include consumables, power, labor, and scheduled maintenance. Fees can be paid as a level monthly amount (subject only to indexing as described above) over the contract term. Alternatively, some fee payment structures separate the ISC (repair and replacement) component from the total service fee, and try to match fee payment with the expected emergence of losses. The latter payment method implicitly recognizes that new infrastructure will probably not incur significant repair and replacement losses until decades after the beginning of the contract. The contract holder usually requests this, since ISCs normally do not have provisions for the refund of unearned services fees should the owner decide to cancel the contract prematurely.

ISCs also exist for older facilities in military utilities privatization. These contracts are riskier for service providers, since the condition of the facility is difficult to assess without a costly inspection that must be conducted prior to bidding on such services. Unlike service contracts for new facilities, these are usually underwritten only by companies providing complete operations and maintenance services.Manufacturers will seldom underwrite unscheduled maintenance obligations on old capital equipment that has been in operation for a while.

Level service fees are usually charged throughout the life of the contract, indexed for inflation, but with no other modification. Because the fees associated with ISCs can be high (ranging from $100,000 per year for a small water treatment plant to $25,000,000 per year for a city light rail system), the considerable time and expense of underwriting, which involves item-by-item estimation of asset repair and replacement costs, is justified.

2.2. Projecting future losses of ISCs

One of the key issues to whether or not such future expenditures can be accounted for as loss reserves under an extended service contract is whether or not such amounts are reasonably estimable. The necessity of pricing such contracts has resulted in several methods for forecasting future losses associated with these contracts. Under FAS 5, if the amount is not reasonably estimable, then no accrual of a liability is necessary. Since no standard actuarial method for estimating such unpaid liabilities exists, they might be deemed as not reasonably estimable.

The difficulty in projecting capital equipment repair and replacement losses stems from a lack of recorded historical experience. Owners of physical assets keep maintenance records, but they are incomplete, without standard format, often proprietary, and have not been around for very long. There is no central repository for this data, nor are there vital statistics on the longevity of capital equipment. Contract conditions are extremely varied, and service providers have such sparse information individually that the usual actuarial methods would not be useful to produce projections of loss emergence over the life of the contract.

Furthermore, since we are addressing the subject of mortality, the actuarial nature of this analysis more closely resembles a life contingency problem for which an approach using customary data triangles may not be appropriate. Unlike death benefits, however, repair and replacement liabilities under ISCs are distant future property losses, and are inflation sensitive.

Central to estimating loss costs due to equipment replacements are estimates of equipment longevity. However, there are no life tables for the diverse types of capital equipment used in widely varying industries. A gas turbine will not have the same expected lifespan as a dump truck, or even another gas turbine in a different industry. There are published accounting guidelines on useful life of physical assets, but they follow very broad classifications, and are used mostly for depreciation purposes. There are also manufacturer’s claims of equipment longevity, but these may be biased. Even though these guidelines have some basis in reality, they are only point values with no information on the variance of asset lifespan.

The method employed to project losses and expenses must take into account the life contingency nature of this problem, but must also work with the limited amount of data available on equipment longevity. The method should not entrain superfluous assumptions due to the absence of data. If an assumption must be made, then the results should be compared to those from other alternative assumptions. Wendling (2011) outlines a simulation method for estimating future asset replacement costs as a stochastic process.

3. An economic model for physical asset replacement

Regardless of the level of asset aggregation, accountants describe a physical asset as having a useful life. FASB Statement of Financial Accounting Standards No. 5 states that “the eventual expiration of the utility of an asset is not uncertain” (FASB 1975). However, what does utility mean in the context of lifespan? If a machine fails due to the failure of a discrete component, it can always be repaired (the component can be replaced) to return it to its useful state. Indeed, any physical asset that is an aggregation of components can be repaired indefinitely to maintain its usefulness. A physical asset that is an aggregation of components never has to reach the end of its useful life. It can be immortal with respect to utility. Nevertheless, we know that companies do replace physical assets at all levels of aggregation, and accountants have used the concept of utility to represent this phenomenon. We will focus on an economic, rather than accounting, understanding of why physical assets are eventually replaced.

It is useful to look at the motivations for replacement of physical assets under most types of extended service contracts to gain insight. Such contracts provide for either repair or replacement of an asset, such as capital equipment. If it were less expensive to replace an item of equipment than to repair it, then the party paying for the repair or replacement would naturally prefer to replace it. However, in the case of most capital equipment, replacement is usually not an immediate alternative to an expensive repair. Under an extended service contract for a home, it is easy to purchase a water heater at the hardware store as an immediate alternative to an expensive repair. In contrast, in an industrial setting, it is not so easy, for example, to purchase a locomotive as an immediate alternative to repairing one. The procurement process from requisition to commissioning can last years. Even prior to such a requisition, the decision to replace a major item of capital equipment is the result of a lengthy process, which begins with the gradual (and often delayed) recognition of the economic benefits of replacement, and is often deferred due to management incentives and the lack of availability of scarce funds for asset replacements.

Capital equipment seldom generates repair costs from a single mechanical failure close to the all-in replacement cost of the equipment. Therefore, the repair versus replacement rationale described at the beginning of the last paragraph may hold for home, vehicle, or appliance service contracts, but it has little application with capital equipment.

Repairs are triggered when equipment or components fail. Repairs cannot be deferred, since they are required to restore equipment to functionality, which can be critical from the standpoints of safety, reliability, availability, or lost revenues. However, replacement of a physical asset is deferrable, in favor of continued repairs, even though it may not always be economically efficient to do so.

And what of the role of technological obsolescence in a replacement decision? Obsolescence is the state of a fixed asset, service or process when it becomes unwanted or should no longer be used. However, the asset may still be useful (and usually is) in good working order. In industry, obsolescence is thought to occur because a like replacement is available that is economically superior in some way. A replacement asset may have comparative advantages to the existing asset, such as saving time or reducing energy usage, potential costs of downtime, or consumption of scarce resources. Obsolescence may be due to the availability of new technology or the aging condition of the asset itself.

Few actions have as powerful an impact on the operating costs of an individual physical asset as its complete and utter replacement with a new one. Few actions are as expensive. To understand the reasons for replacement, it is useful to remember that the opportunity costs associated with keeping an old asset (not having the newer version of the like asset) usually rise as the asset ages. This is the natural consequence of aging machinery components and environmental factors, such as energy costs and advances in technology. At some threshold of these costs, a decision to replace an entire asset may be preferable to one of continuing to pay for rising opportunity costs. We will initially focus only on unscheduled repair costs, in keeping with our service contract analogy, but will then show that our models encompass any actual expenses and opportunity costs that influence the replacement decision.

Let us initially define M(t) only as the variable cost of repair at time t. M(t) is the annual variable repair cost in calendar year t. Later, we will expand this definition to mean all the opportunity costs associated with an individual asset that are above and beyond the operating costs of having the latest, newest, like asset. These variable costs are the additional costs for a company to repair an item of equipment beyond its fixed costs. Variable costs vary with the frequency of equipment failures, but fixed costs do not. An example of a variable cost of repair is the cost of new components and labor to install them, and is contingent on the occurrence of an equipment failure. An example of fixed costs is the cost of routine, scheduled, preventive maintenance.^[1]

A company may also have lower variable costs for a given level of repairs because of its degree of dependence on fixed costs to accomplish the same repairs—for example, the level of on-the-job training given to its maintenance staff, or the investment in permanent tools needed to perform maintenance functions. We loosely define these differences in variable cost to achieve a given level of repair as an organization’s marginal cost of repair.

We define C as the all-in loss and expense to replace an item of equipment, including the costs of the new equipment and installation, less any salvage recoveries. T is the average inter-replacement time, or average time between replacements, calculated over many replacements occurring over a long period.

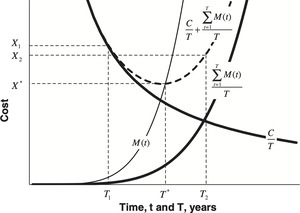
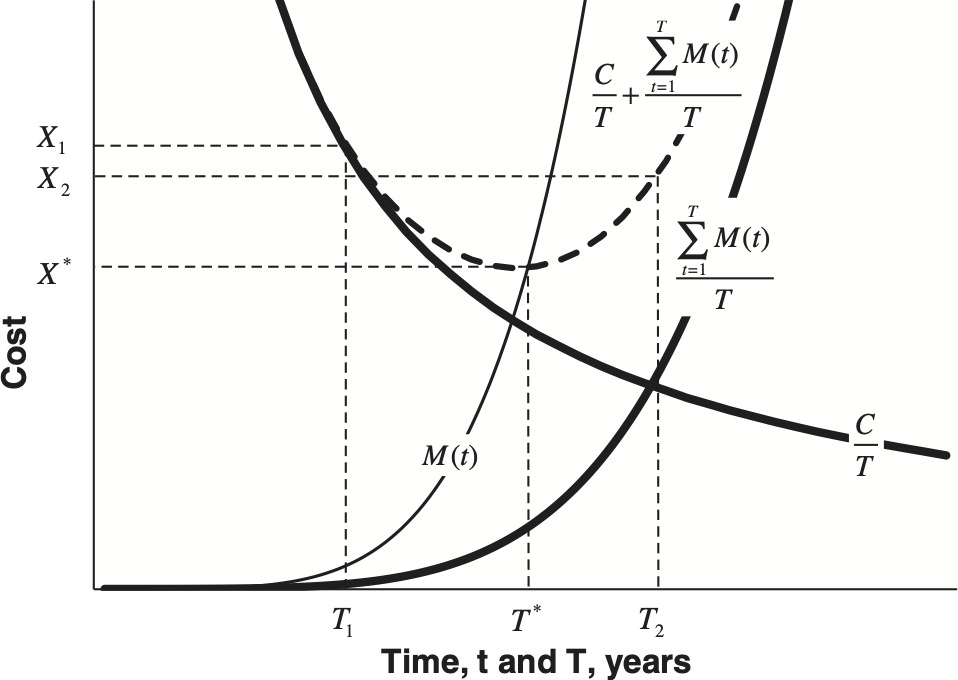
Figure 1 is a conceptual model of average costs familiar to economists. The downward sloping dark curve is the average cost of replacement, which decreases with T. The upward sloping dark curve is the average cost of repairs, which increases with T. The dotted curve is the total average cost of repair and replacement, which is the sum of the two dark curves. Unlike M(t), these curves represent averages over a long period of time, and over a large number of replacements. The formulae shown on the graph show the algebraic relationships of these curves to M(t), C, and T. We use summations rather than integrals due to the fact that M(t) would probably be measured in discrete annual amounts.

Figure 1.Replacement optimization theory

The most important feature of this graph is that for increasing M(t), the total average cost of repair and replacement (the dotted curve) is minimum at T*, which corresponds to a total average cost of repair and replacement of X*. It also illustrates that if times other than T* are chosen for replacement, that total average costs will be higher. The efficient time for replacement is at T*. Any other replacement time is not efficient.

This figure illustrates the effects of a repair versus replacement policy. If replacements occur before T*, at T₁, then the total average repair and replacement cost will be higher than X*, at X₁. This results from a surplus of M(t) under M(T*). If replacements occur after T*, at T₂, then the total average repair and replacement cost will also be higher than X*, at X₂. This results from a deficit of M(t) over M(T*).

Efficient repair versus replacement policy may have a material impact on the earnings of organizations that rely heavily on physical equipment to generate revenues. For example, a power utility with $20 billion in machinery and equipment with an optimal lifespan of 20 years would pay 1/20th × $20 billion each year in replacements, and perhaps an additional 15% of this amount in repairs, or $1.15 billion. If an inefficient repair versus replacement policy resulted in an additional 10% in excess of X* in total average repair and replacement costs, then this would add $115,000,000 to the organization’s annual operating costs. If earnings were on the order of $1 billion, then this inefficiency could be material to such an enterprise’s market valuation. This is a hypothetical example, and we do not have documented accounting evidence of the inefficiencies predicted by Figure 1. However, the dollar values and the potential loss of efficiency (see section 6.2) described in the example are realistic.

Figure 1 has two important implications. First, it illustrates the existence of an optimal inter-replacement time. The second implication is the causal relationship between repairs and optimal replacement timing, since the evolution of M(t) determines T*.

This conceptual model is useful to illustrate these two implications, but it does not take into account time value of money when calculating averages of repair and replacement costs, which are really perpetuities, spread over time. Therefore, we cannot use the principle in Figure 1 to precisely calculate values such as X*, or M(t) evaluated at T*.

4. A financial model for physical asset replacement

A second conceptual approach is to think of replacement as an option that should be exercised at the optimal time, T*. In this model, we compare the present value of M(t) evaluated at T* in perpetuity, to the present value of all future repair and replacement costs, resulting from a replacement at T*, in perpetuity. Repair and replacement are mutually exclusive and complementary options. By deciding to not replace a physical asset today, one is deciding to continue to repair it. By deciding to not continue repairs, one is deciding to replace the asset. For a going concern, there is no third exclusive option. There is also no “do nothing” option with respect to these two alternatives. Therefore, the decision must be exercised relative to each physical asset, individually.

If the variable cost of repairs is increasing, it will cross a certain threshold at time T* at which the present value of continued repairs at that threshold will exceed the present value of an immediate replacement with all its attendant future repairs and replacements. Optimal replacement occurs at this threshold value of M(t).

The two first terms on the right side of equation (4.1) represent the present value at replacement time of a perpetuity (due) of replacements costing C occurring every T* years. The third term on the right of equation 4.1 represents the present value at replacement time of a perpetuity of all repair costs repeating every T* years. The time value of money is represented by a discount rate, i.

$$\frac{M\left(T^{*}\right)}{i}=C+\frac{C}{i s_{\overline{T^{*}}}}+\frac{(1+i)^{T^{*}} \sum_{t=1}^{T^{*}} M(t) v^{t}}{i s_{\overline{T^{*}}}} . \tag{4.1}$$

Multiplying both sides of equation (4.1) by i gives

$$M\left(T^{*}\right)=i C+\frac{C}{s_{T \uparrow \mid}}+\frac{(1+i)^{T *} \sum_{t=1}^{T *} M(t) v^{t}}{s_{T T^{*}}} . \tag{4.2a}$$

The continued derivation beyond equation (4.2) is provided in the Appendix, but for M(t) exhibiting the kind of convexity shown in Figure 1, most values of T* typical of capital equipment (i.e., T* > 10 years), and for typical values of i, the right term of equation 4.2 becomes very small, and equation (4.2) can be approximated by^[2]

$$M\left(T^{*}\right) \cong i C+\frac{C}{S_{T^{*}}} \tag{4.3}$$

As T* becomes very large (i.e., T* > 75 years), equation (4.3) can be further reduced and approximated by equation (4.4).

$$M\left(T^{*}\right) \cong i C . \tag{4.4}$$

Equation (4.4) is simply the discount rate multiplied by the all-in cost of replacement and represents an observable threshold of increasing M(t) at which the replacement decision is optimal. The equation becomes an equality as T* or i, or both, become large. Equations (4.3) and (4.4) are very handy rules of thumb, and are reasonably accurate for replacement decisions for most types of physical assets with lifespans longer than 10 years. In equation (4.3), T* is an a priori estimate of the expected useful life of the physical asset. Equation (4.4) requires no such estimate of the expected lifespan of the physical asset, but would not be appropriate for short-lived assets, such as information technology or vehicles.

This conceptual model has its own interesting implication. If M(t) never exceeds this threshold, then replacement will never occur. In such a situation, there will never be a rational time in which the enterprise should replace the physical asset. This may be the case for an enterprise with a very low marginal cost of repair. It is also the case for many types of assets with low repair costs (relative to replacement), such as buildings or concrete structures, which explains why most of our discussion on replacement of physical assets focuses on capital equipment.

Since we know little about the function M(t), apart from some gross characteristics discussed below, it is a boon to our analysis that it can be dropped from our determination of the appropriate asset replacement time. Decisions for the efficient replacement of physical assets can be based on a simple trigger that is easily articulated in policy, or as a contractual performance obligation.

If i = 0, then equation (4.2) reduces to equation (4.5):

$$M\left(T^{*}\right)=\frac{C}{T^{*}}+\frac{\sum_{i=1}^{T^{*}} M(t)}{T^{*}} . \tag{4.5}$$

The first term on the right side of equation (4.5) equals the average cost of replacement in Figure 1, and the second term on the right side of this equation equals the average cost of repairs in Figure 1, both evaluated at the optimal replacement time, T*. Therefore, the financial model described in equations (4.1) through (4.4) converges with the economic model described in Figure 1, if we ignore the time value of money in both models.

The curves in Figure 1 can be adjusted for the time value of money to obtain the same result as in equations (4.1) to (4.4), but then Figure 1 would lose its simplicity and illustrative power as an economist’s tool for understanding the minimization of average costs. This adjustment would also not affect the two important implications of Figure 1 discussed in section 3. If this adjustment were graphed, we would notice that M(t) still intersects the minimum point of the adjusted average cost of repair and replacement (the dotted curve), just as it does in Figure 1. All curves of Figure 1, except for M(t) would move upward and to the right with an increasing (nonzero) discount rate. We will not create such graphs here, but simply note that equations (4.1) to (4.4) provide the correct threshold values of M(T*), because of their inclusion of the time value of money.

Another way to approach this problem derives from personal experience. A few years ago, I replaced an old car. It had been in the shop several times that year for unrelated repairs, and seemed to continue a trend of increasing costs that had begun a few years earlier. The maintenance costs, I reasoned, were becoming a significant fraction of what I would pay annually for a loan on a new car, and without all the hassle. Of course, the annual amount of such an imaginary loan would depend on its term, but the number I had in mind for comparison was for the longest possible loan, perhaps approaching the amount of time I might own the next car. My annual maintenance costs were becoming an ever-increasing proportion of the annual amount that would be paid for this loan (equation (4.6) below).

$$\text { Amount }=\frac{C}{a_{\overline{T^{*}}}} \tag{4.6}$$

Then, with some algebra:

$$=\frac{C}{v^{T^{*}} S_{\overline{T^{* *}}}} \tag{4.7}$$

$$=\frac{C(1+i)^{T^{*}}}{s_{T^{*}}} \tag{4.8}$$

$$=C\left(\frac{i \frac{\left[(1+i)^{T^{*}}-1\right]}{i}}{s_{\overline{T \Downarrow}}}+\frac{1}{s_{\overline{T \Downarrow}}}\right) \tag{4.9}$$

$$=C\left(i+\frac{1}{s_{T^{\Psi}}}\right)=i C+\frac{C}{s_{T^{\Psi}}} \tag{4.10}$$

Equation (4.10) is the same result as in equation (4.3). The personal experience described above is a third, separate philosophical approach to the problem of asset replacement, but it is mathematically equivalent to the first two. It also shows that the horizon of the decision does not have to be infinite. In other words, the cash flows under consideration only have to be as long as the expected lifespan of the replacement asset, not in perpetuity, in order for the trigger expression in equation (4.10) to be true.

For typical asset lifespans, the threshold value of M(t) is most sensitive to estimates of the discount rate and the all-in replacement cost (which are easily estimable), less sensitive to errors in the a priori estimate of lifespan, and virtually insensitive to the (unknown) form of the function M(t).

4.1. A broader interpretation of M(t)

In the above conceptual models, M(t) was defined as the calendar year variable cost of repairs for a physical asset at time t. This interpretation is usually consistent with the scope of responsibility in an extended service contract. The service provider for such a contract is usually not obliged to replace an item of capital equipment simply because a newer, more efficient version of the same capital equipment emerges in the market. However, the owner of the asset internalizes all economic costs associated with it, and may wish to expand the definition of M(t).

A more general interpretation of M(t) would be that it represents the calendar year cost (in year t) of holding an old physical asset. By holding an old physical asset (instead of replacing it) the enterprise may pay not only for increasing repairs, but expected revenue losses due to increased frequency of downtime of aging equipment, or for the opportunity cost of lower operating expenses associated with new, more technologically advanced replacement equipment. Such opportunity costs can be objectively quantified as savings in operating and routine maintenance costs. Since technology generally improves, these opportunity costs increase, which is consistent with our assumption of increasing M(t) in our model.

For those replacement assets that are capitalized, even the opportunity cost of not realizing the tax shelter from depreciation of a new asset can also be considered a constituent of M(t).

There are probably potential constituents of M(t) that are impossible to measure objectively. For example, how does one put a value on “new car smell” when making a decision to buy a new car? In an industrial setting, these constituents are, or at least should be, selected on a more rational basis. Having the flexibility to explicitly define the constituents of M(t) actually allows elimination of subjective, even behavioral, constituents that have the potential to contribute to decisions that are irrational with respect to the goal of maximizing enterprise value. An example of this would be deferral of replacements for the sake of short-term profitability or a manager’s bonus.

There are probably also constituents of M(t) that are difficult to quantify. For example, the expected revenue lost due to increasing downtime of an aging physical asset. These costs, although difficult to measure, still exist. Such obstacles are also present in traditional capital expenditure planning methods often used in an asset replacement decision.

In theory, any calendar year cost of not replacing old equipment that would be considered under a traditional capital budgeting method could be monitored as a constituent of M(t). Because of the increasing prevalence of individual physical asset accounting systems, repair costs of individual assets are now being regularly tracked and updated. Such information systems can easily be adapted to include current opportunity costs, and any other objectively measurable economic constituents of M(t). Such costs can be monitored by engineers, and the accuracy and documentation of that information could become an increased focus of their expertise.

By broadening the definition of M(t), we expand our theory to balance all possible operating expenditures against replacement costs or capital expenditures.

4.2. The random nature of M(t)

In reality, M(t) does not increase smoothly over time as depicted in Figure 1, but sporadically as it approaches the threshold cost from beneath it. For example, variable repair costs, although increasing in t, are random. Repair costs are fortuitous by virtue of their causation by random physical factors, such as breaking, snapping, short-circuiting, wearing, rupture, or fouling. The very propensity of a physical asset to require repairs (a measure of its quality) is a function of factors beyond the enterprise’s control. For example, was the physical asset produced during a labor strike at the factory? Technology change, reflected as opportunity cost in M(t), is an uncontrolled external factor, which can also trigger the replacement decision. The rising opportunity cost created by unforeseen technology advances is fortuitous and beyond the control of the enterprise pursuing a policy of efficiency.

Since replacement times are determined by a stochastically increasing M(t), and the optimal replacement time depends on a threshold of M(t), then the time until that threshold is crossed is also random. Because the constituent costs of M(t) are fortuitous, efficient replacement costs are also fortuitous in a sense similar to the fortuity of death benefits. Repairs and replacements, if executed efficiently, are both examples of unscheduled maintenance. Any attempt to schedule or plan replacements will generally not be efficient.

M(t) increases and approaches a threshold from underneath much in the same way that an aggregate excess of loss treaty attachment point might be approached over time. Measuring M(t) and knowing when it crosses the threshold value can be difficult, particularly if we wish to use equation (4.3) as a contractual trigger for replacement. The use of moving averages of M(t), in order to dampen observed fluctuations, and avoid making premature replacement decisions, can solve this problem.

The perpetuity equations above assumed that replacements are evenly spaced apart in time, but the random nature of M(t) invalidates this assumption. Since inter-replacement time is a random variable, replacements are a stochastic stream of events. The present value of a stochastic stream of cash flows is not equal to the present value of a regularly spaced (scheduled) stream of cash flows, as was assumed in our financial model. However, the impact of this idealization on the accuracy and implications of the equations above is minimal, and merely represents a further refinement of our analysis to be handled below.

4.3. Ever-increasing M(t)

Figure 1 shows that M(t) increases, and is assumed to never return to a level below M(T*). This assumption simplifies the financial model described earlier in this section 4, and is based on historical experience that all of the so-far mentioned constituents of M(t) generally increase over time. There may be exceptions to this. Repair costs, for example, can decrease after a period of high frequency of repairs. This is especially true for arrays of identical components that comprise a single physical asset, which can create periodic concentrations of repair costs over time, or for relatively simple machines. However, rising opportunity costs associated with advancing technology are usually not reversible.

4.4. The convexity of M(t)

In Figure 1, M(t) is shown to have convexity. That is, costs seem to increase at an increasing rate over time. This is largely anecdotal, but there is a theoretical basis for this. Since most equipment components follow time to failure distributions that have an increasing force of mortality over time (i.e., the Weibull distribution), one would expect an aggregation of such components to exhibit the same progression of repair frequency, thus convexity, as that seen at the lower percentiles of such a distribution. Equipment that requires repairs at an evenly increasing rate over time would be considered to be of very poor quality.

Unforeseen advances in technology will result in step increases of the opportunity costs of holding old physical assets, which can occur at any time. Such changes invalidate the assumption of convex M(t) because they can occur with equal probability at any point in the asset’s life. However, advances in technology that create such opportunity costs are exceptional events, and not regular phenomena that occur over the lifespans of each replacement.

The assumption of convexity in M(t) as depicted in Figure 1 is important, since it means that most of the M(t) costs occur late in the life of a physical asset, and therefore are heavily discounted in equation (4.2). Convexity in M(t) is what helps us to easily drop it from the determination of the approximate replacement threshold value of M(t) in equation (4.3).

4.5. The nature of i

By broadening the definition of M(t) in section 4.1, the trigger for economically optimal replacement of a physical asset given by equation (4.3) now resembles the usual process of capital expenditure planning in which the net present value of all future costs operating old physical assets are compared to that of new ones.

Since we now understand the preceding equations to be an expression of the traditional capital budgeting process in the context of renewal, and we are considering alternative uses of a firm’s free cash flow, we can conclude that the discount factor used in the above perpetuities is the (real) cost of capital of the entity making the replacement decision.

4.6. Summary of assumptions concerning M(t)

The assumptions concerning M(t) were made in order to create an argument from which to draw useful conclusions. The assumptions are summarized as follows:

• M(t) is comprised of variable repair costs, but must also include opportunity costs of improved technology, expected loss costs due to downtime, and any other cost that would normally be considered under a traditional capital budgeting method when making a replacement decision.

• M(t) increases, and does not return to a value below the threshold value at which replacement is required, once this threshold is crossed.

• M(t), although increasing, is random, and approaches the threshold value requiring replacement, much the same way in which the attachment point of an aggregate excess of loss treaty is approached.

• M(t) has convexity, as depicted in Figure 1.

These idealizations broadly describe the time-dependent nature of factors usually considered in a replacement capital budgeting exercise. They are not always true, but experience has shown that they are usually the rule rather than the exception. These assumptions are probably always true for a large subset of physical assets, such as capital equipment.

4.7. Stochastic considerations of the model

Expressions (4.1), (4.2), and (4.3) do not provide guidance for when to replace individual assets, since they assume that all assets have identical lifespans. As we have described in section 4.2, assets (locomotives, wind turbines, vehicles, etc.) are not replaced punctually at some average lifespan.

First, let us show Equation (4.2) as an inequality, since we are really concerned with timing a decision with the rising M(t), so anytime M(t) is greater than (or equal to) the right side of the equation is when to replace the asset. When the following inequality is satisfied, we must replace the asset in order to minimize the present value of all future costs associated with the asset:

$$M(t) \geq i C+\frac{C}{s_{\overline{T^{*} \mid}}}+\frac{(1+i)^{T^{*}} \sum_{t=1}^{T^{*}} M(t) v^{t}}{s_{\overline{T^{*} \mid}}} \tag{4.7.1}$$

Then, since the time to replacement is random, we take the expected value of the right side of expressions (4.1) and (4.2). We want to do this, since we are interested in minimizing the expected value of the present value (the actuarial present value) of all future costs associated with each individual asset and its successors.

$$M(t) \geq E\left[i C+\frac{C}{s_{T^{*} \mid}}+\frac{(1+i)^{T^{* *}} \sum_{t=1}^{T^{*}} M(t) v^{t}}{s_{T^{*}}}\right] \tag{4.7.2}$$

$$M(t) \geq i C+E\left[\frac{C}{s_{T^{*}}}+\frac{(1+i)^{T^{*}} \sum_{t=1}^{T^{*}} M(t) v^{t}}{s_{T^{*} \mid}}\right] \tag{4.7.3}$$

The phenomenon of M(t) intersecting the minimum is also preserved for the actuarial present value as it was for the dotted curve in the Figure 1. This is because it is possible to capture the randomness of the replacement time simply with a risk-adjusted cost of capital instead of i, and we have already determined that the phenomenon of M(t) intersecting the minimum is preserved for equation (4.2).

Approximation 1:

As we first noted after equation (4.2), the right-most term inside the brackets is then assumed to equal zero.

$$M(t) \geq i C+E\left[\frac{C}{s_{\text {Tभ⿱ }}}+0\right] \tag{4.7.4}$$

We do this only to get rid of that term, since it cannot be easily evaluated using objective data, and since its value is very small compared to the other terms in the equation. M(t) does not follow a deterministic process as depicted in the above graphs; rather, it follows a stochastic process, and the eliminated term would require considerably more historic data to evaluate than can be reasonably obtained in practice. A possible range of values of this term can be obtained through scenario testing, and since the values are usually very small compared to the other terms, this approximation slightly understates the right side of the inequality.

Then, dividing both sides by C,

$$\frac{M(t)}{C} \geq i+E\left[\frac{1}{s_{T^{\star}}}\right] \tag{4.7.5}$$

Approximation 2:

$$E\left[\frac{1}{s_{T_{\Psi}}}\right]=\sum_{i=1}^{N}\left[\frac{1}{s_{\overline{T_{i}}}}\right] / N \tag{4.7.6}$$

where T₁, T₂, . . . , T_N, are empirical ages at the time of replacement (asset mortality data) from a homogeneous class of assets.

This assumes that the expected value of the above term is simply equal to the average of the term evaluated over N empirical observations of time to replacement of similar assets. Although a close approximation, it is really the interreplacement time at each future replacement that is random, not an identical value of interreplacement time for all future replacements. This approximation tends to slightly overstate the right side of the inequality.

The inequality now looks like this:

$$\frac{M(t)}{C} \geq i+\sum_{i=1}^{N}\left[\frac{1}{s_{T_{i}}}\right] / N . \tag{4.7.7}$$

Considering the two approximations we have made so far,

$$\begin{array}{l} \quad \text{Approximation 1}(\text{slightly understates the right side})\\+ \text{Approximation 2} (\text{slightly overstates the right side})\\=\beta \end{array}$$

The errors due to Approximations 1 and 2 are small, and occur in opposite directions. They approximately cancel each other out, but we will call their sum β, and include it in the model. This value is a small error term that can be evaluated through simulation and judgment. The appropriateness of these two approximations will require further analysis on a case-by-case basis.

The model now looks like this, and can be broken down into these parts:

$$\overbrace{\overbrace{\frac{M\left(T^*\right)}{C} \geq}^\text{Individual Asset} i+ \overbrace{\sum_{i=1}^N\left[\frac{1}{s_{\overline{T_{i}|}}}\right] / N}^\text{Entire Class}}^\text{Objective (Empirical)} + \overbrace{\overbrace{\beta}^\text{Error}}^\text{Subjective}\tag{4.7.8}$$

where T₁, T₂, T₃, . . . , T_N, are empirical ages at the time of replacement of assets from a class (asset mortality data), such as locomotives, gas turbines, or even better, a homogeneous ensemble of similar vehicles in a fleet owned by the same enterprise. As soon as this inequality is satisfied for an individual asset, one must replace the asset in order to minimize costs for the entire class of assets.

It is important to note here that, since the sampled empirical ages affect the calculation of the threshold value, they also affect the values of newly generated empirical ages. Asset mortality data generated by the model is also fed back into the model, since it newly characterizes the mortality of the class. Therefore, this model is iterative. The model will converge to a steady state, but the selection of seed values for T₁, T₂, T₃, . . . , T_N should be done with the goal of shortening the calibration period.

4.8. Principles of physical asset replacement

The conclusions from the application of simple financial mathematics to the above assumptions about the nature of M(t) can be summarized by the following three principles:

1. There is only one instant in time that an asset must be replaced in order to minimize the present value cost impact to the enterprise.

2. This efficient instant is observable, and a function of both the owner’s cost of capital and readily obtainable current calendar year information.

3. The time to this efficient instant is random. It may be infinite.

The above principles imply that efficient physical asset replacement is a life contingency problem. The advantage of having an easily calculable and objective trigger for economically optimal replacement is manifested by the ability to make prompt decisions that are ruthless with respect to the goal of minimizing the overall net present value cost impact to the enterprise. A threshold value, based on readily observable calendar year information, makes it possible to base contractual replacement obligations on events that cannot be manipulated by either party to such a contract. The advent of individual physical asset accounting systems makes it easy to track all types of costs associated with individual physical assets, and makes enforcement of such a policy or service contract feasible.

4.9. Model interpretation

Because of its iterative nature using feedback, the model of equation (4.7.8) is a process control algorithm, and the process in question is the mortality within entire ensembles, fleets, or homogeneous classes of physical assets. Decisions on individual assets depend on aggregate information (asset mortality data) from the fleet to optimize the performance of the entire fleet. One can imagine that the random life distribution defining mortality of a class of assets will not remain stationary, but will migrate in shape and form over time as distributional changes caused by environmental factors, such as advancing technology or changing energy costs, work their way through an asset population of mixed ages. As these distributional changes occur, the model follows them with the singular goal of minimizing the actuarial present value of all future costs, both capital and operational.

The structure of this model shows that even if the accuracy on the right side of the inequality is not perfect, the left side always provides a way to prioritize the assets for replacement in order to achieve the minimum of average total cost.

Most of this model is based on objective data that can be easily obtained in practice. M(t) is simply the engineering data which ordinarily goes into this type of analysis, such as energy costs, repair costs, expired depreciation, potential loss costs, potential down time costs, etc. The model also separates the data obtained from the individual asset from the asset mortality data obtained from the entire class of assets. There is a clear role for the art of classification of assets into homogeneous groups with similar characteristics that affect their mortality.

5. Comparison with other capital budgeting methods

The trigger expression in (4.7.8) suggest a new way of renewal capital budgeting at the operating level that can be implemented through an enterprise wide policy or contractually. Other capital expenditure decision making tools, such as payback period, internal rate of return (IRR), and net present value (NPV), are described in introductory finance texts. Often, the authors of those texts express a preference for the NPV method. The equivalent annual cost (EAC) method also incorporates the time value of money, and is used as a means of comparing investments with different time horizons, such as asset lifespans.

These are all excellent tools for evaluating new capital investments or projects. They are flexible, and can be used to simultaneously evaluate multiple capital investments, particularly those with a finite horizon. However, in our situation, the initial capital investment is a sunk cost, and the asset is already on the balance sheet generating revenue. Physical asset renewal is distinct from initial capital investment in that there are always the same two mutually exclusive options (see beginning of section 4) under consideration, and timeliness of the decision between these two options is important.

An enterprise-wide policy based on the triggers described by equation (4.7.8) recognizes the importance of timeliness in the asset replacement decision. However, other capital budgeting methods are used in a manner consistent with planning for new capital investment. These traditional methods are purely prospective in that they only recognize that the time to replace an asset has arrived, but fail to account for the fact that the best time to replace the asset may have long passed.

Traditional capital budgeting tools are also relatively cumbersome and haphazard tools. They depend on the initiative of line managers, must be created for each project, and are subject to review, second-guessing, and deferral. In the situation of long-lived assets for a going concern, equation (4.7.8) reduces the capital budgeting process to monitoring a predetermined set of current calendar year M(t) constituents, and regular comparison to threshold values. Decisions are made by policy. The only input needed in such a system is the continual data entry of calendar year M(t) information, with the decision itself being automated. The increased usage of individual physical asset accounting systems make this a practicable reality today.

6. Value impact to an owner

6.1. Measurability

Asset renewal is generally the result of a traditional capital budgeting process, and, as we have already noted, planned replacement timing generally is not efficient. However, we cannot estimate the magnitude of that inefficiency for any company simply by examining its financial statements, or even from detailed existing accounting data. To the extent that M(t) is not being continuously monitored, and managers are not aware of the threshold indicated by equation (4.7.8), the efficient replacement policy of Figure 1 will generally not be realized.

Although there are now individual physical asset accounting systems which can digitally track all kinds of cost data at the individual asset level, they are not presently being used to record all the constituents of M(t) described in section 4.1, hence the losses in efficiency that are predicted by Figure 1 are not being monitored (continuously or otherwise). Once M(t) is defined and continuously monitored, it would be possible to measure existing deficits of M(t) over M(T*) and any surpluses of M(t) under M(T*) for assets about to be replaced. This would allow approximation of the present value cost impact of a policy that aims to eliminate such deficits and surpluses.

6.2. Magnitude

Earlier, we used an example of a power utility that might be experiencing 10% excess costs associated with machinery and equipment. In that example, we referred only to repair and replacement costs, but we now know that the inefficiency affects any operational costs associated with physical assets. The following analysis provides some basis for that 10% assumption.

In equation (4.2), we equated the calendar year value of M(t) with a set of terms at the efficient replacement time T*:

$$M\left(T^{*}\right)=i C+\frac{C}{s_{T \uparrow \mid}}+\frac{(1+i)^{T *} \sum_{t=1}^{T *} M(t) v^{t}}{s_{T T^{*}}}. \tag{4.2}$$

In this section, we introduce another interpretation of the terms on the right side of equation (4.2). The sum of these terms represents an equivalent annual level amount in perpetuity, which is minimized at the efficient time T*. For other values of T, the equality in equation (4.2) is not true. In other words, this equivalent annual amount, let us call it A(T), is not equal to M(T) for values of T other than T*. Equation (4.2) is generalized as follows:

$$A(T)=i C+\frac{C}{s_{\bar{T} \mid}}+\frac{(1+i)^{T} \sum_{t=1}^{T} M(t) v^{t}}{s_{\bar{T} \mid}}. \tag{6.1}$$

Now we can say that the present value of an efficient enterprise policy based on equation (4.2) is equal to M(T*)/i, and that the present value of an (inefficient) enterprise policy based on equation (6.1) (where T is not T*) is equal to A(T)/i. The present value impact of a transition from an inefficient policy to an efficient policy would be the difference between the present values of these two perpetuities.

We then assume that a firm is using a 5-year payback approach to justify the replacement of the physical asset, which corresponds to M(t) 0.2C at replacement time, and if we let i 4.5%, C 1000, and describe M(t) using the following polynomial^[3]

$$M(t)=a t+b t^{2}+c t^{3}+d t^{4}+e t^{5} \tag{6.2}$$

where the coefficients equal:

$$\begin{aligned} a \qquad &0.000000000067\\ b \qquad &0.000000001696\\ c \qquad &0.000000037193\\ d \qquad &0.000000780821\\ e \qquad &0.000016087092 \end{aligned}$$

One can plot equations (4.2) and (6.1) to show that T* = 22 years, M(T*) = 83 and A(T) = 89 at T = 26 years where M(26) = 200. This represents about a 7% increase in the present value cost impact due to the inefficient 5-year payback replacement policy. Because of the extreme convexity of M(t) in this example, a 5-year payback policy that is not prompt, resulting in an additional deferral of only 4 more years (to T = 30), would result in A(T) = 104, which represents about a 25% increase in the present value cost impact due to an inefficient replacement policy.

If we replace the polynomial used for M(t) by a straight line (no convexity):

$$M(t)=3.882 t. \tag{6.3}$$

Performing the same calculations based on equations (4.2) and (6.1), we show that T* = 23 years, M(T*) = 90 and A(T) = 121 at T = 51 years where M(51) = 200. This represents about a 34% increase in the present value cost impact due to an inefficient replacement policy. Because there is no convexity of M(t) in this example, a policy resulting in additional deferral of a few more years would not result in a significant increase in the present value cost impact due to an inefficient replacement policy.

In this example, the functions used to model M(t) in equations (6.2) and (6.3) were selected to create reasonable values of T* at typical values of i, and because they represent extremes of convexity in M(t) with which to bracket a range of potential present value cost impacts. Convexity is the one characteristic of M(t) for which we have the least obtainable information. The value of C is arbitrary. A firm using a 5-year payback approach for asset renewal decisions realizes a present value cost impact that is from 7% to 34% higher than the efficient level. This excess would be only for costs associated with physical assets that are susceptible to replacement, such as capital equipment. Since many of the constituents of M(t) are not being continuously monitored, the 5-year payback approach used in this example is not likely to be prompt, even with respect to its own benchmark. The 10% inefficiency assumption used in the power utility example is at the lower end of this range, and may be generous.

7. Distortions on incentives in ISCs

The conceptual models of sections 3 and 4 try to approach capital planning associated with repair and replacement from the rational perspective of the facility owner. Care must be taken in the contract language to insure that the incentives of the service provider enhance and protect the interests of the facility owner.

7.1. Finite term of ISCs

The discussion so far has focused on an analysis of cash flows in perpetuity. This may be true for the owner who views the facility as a going concern. However, ISCs have finite terms, and service providers do not expect to continue repair and replacement obligations past the end of those terms. In many cases, the contract term is only about as long as, or low multiples of, the average expected life of capital equipment in a facility.

The finite planning horizon of the service provider could encourage behavior, near the end of a contract term, to defer expensive replacements in favor of continued repairs. These repairs may be less costly to the service provider who is planning to leave the facility soon. The owner may be left with a facility that is functional, but obsolete. In other words, at the end of the contract term, the owner may be left with a facility full of old equipment that needs replacement.

7.2. Whose cost of capital?

In section 4 we derived a rule that tells us that the optimal time for replacement for most types of capital equipment is when increasing M(t) crosses a threshold proportional to the product of the cost of capital and the all-in cost of replacement (iC). However, if the cost of capital for a contract holder, who issues municipal bonds, is around 4.5%, the cost of capital for a service provider is 7%, and the cost of capital for a manufacturer who relies mostly on equity capital is 10%, then there is clearly a mismatch of optimal replacement timing implied by equations (4.3) or (4.4). Entities with the higher cost of capital will rationally defer replacement decisions, compared to those with the lower cost of capital. Unless there is an objective contractual trigger for replacement that explicitly recognizes which cost of capital to use, this mismatch may have a deleterious impact on the contract holder’s interests.

Although we believe that a replacement trigger based on equation 4.7.8 is the more practical way to protect an owner’s interests, ISCs can have provisions to stipulate a required physical condition of the facility at the end of the contract term. This is an attempt to force repair versus replacement decisions to be made in a way so that the facility, at the end of the contract, would be in a condition identical to that had the owner been in charge of all such decisions.

7.3. Systematic incentive to defer replacement

Wendling (2012) outlines a simulation experiment to demonstrate how managers, who consider the retirement and replacement of individual assets in isolation, may have rational incentives, due to risk aversion and uncertainty, to defer the replacement of assets past a time optimal from the perspective of the shareholder who owns the entire portfolio of such assets.

8. Managing capital expenditures

If replacement timing is not optimal in practice, then the excess amounts paid above X* (Figure 1) are a real cost of not managing the risks and uncertainties associated with the unscheduled expenditures of physical assets. ISCs, because of their extreme duration, have forced the creation of a risk management approach to capital expenditure planning that solves this problem. ISCs provide both the contractual trigger for efficient replacement timing, and the mechanism to insure that funds are available at the optimal replacement time.

The very existence of ISCs creates a precedent. It demonstrates that it is possible to transfer the risk of uncertain future capital expenditures associated with new or existing facilities between entities. The demand for ISCs stems from the following reasons:

• A desire to assign unpredictable long-term repair and replacement costs to the party that has the greatest ability to control them, namely, the builder and operator of the facility.

• To assure that needed funds are promptly made available for repairs when machinery breaks down.

• To accelerate the timely repair or replacement of equipment from the standpoints of safety and reliability.

Although not the original intent, extended service contracts for facilities and infrastructure have achieved the following collateral purposes:

• As a mechanism to save earnings during an initial period of low maintenance costs (and higher profitability) on new facilities, for a later period of higher maintenance costs (and lower profitability) as the facility ages.

• To have the funds necessary to ruthlessly replace equipment at the economically optimal time, and eliminate incentives to defer expensive replacement of equipment in order to enhance short-term profitability.

• ISCs can have very long-tailed payout patterns because of the longevity of capital equipment. They may present an opportunity to earn investment income, and benefit from deferral accounting and tax treatment.

As we have mentioned, insurers are not involved in underwriting these risks. Nor have we found non-insurance entities willing to cover these long-duration repair and replacement obligations under a stand-alone commercially available product. There are two market failures, which may explain why this is so:

• Information asymmetry—For an old facility, the owner of the physical assets knows far more about the age, condition, and maintenance history of capital equipment than an outside provider of an extended service contract, thus inviting adverse selection.

• Routine maintenance monitoring—For both new and old facilities, the inability of an extended service contract provider to monitor an owner’s compliance with OEM recommended routine maintenance requirements, thus encouraging moral hazard manifested by lapses in costly preventive maintenance.

The second of these problems is probably the most substantial one. It is due to a highly heterogeneous mix of equipment typical at an industrial facility. Each type of equipment will have different OEM instructions regarding scheduled, routine, preventive maintenance to minimize future unscheduled repairs. Non-compliance with such maintenance instructions cannot always be detected after the fact. Routine maintenance involves many factors such as lubrication, testing, changing of wearable components. These activities would be difficult to monitor and verify by a third party extended service contract provider, unless the service provider is also providing the routine maintenance services.

Although this coverage is not commercially available outside of the total suite of services described in section 2, the ISC could theoretically have vitality in a self-insurance model, which might be unaffected by these market failures. For example, an ISC, if administered through a captive entity, could insure the availability of funds and provide the contractual trigger for timely replacement of assets in order to gain the efficiencies predicted by the economic theory.

A self-insurance model may also provide an organization with a different accounting and legal treatment of cash flows associated with unscheduled physical asset expenditures. Service fees might be a tax-deductible business expense in certain situations, such that a company’s pre-tax earnings would be invested to pay for (uncertain) future capital expenditures through the instrument of an ISC. To gain such possible tax benefits in the absence of a commercial service contract, companies might form shared service provider subsidiaries to cover their parents’ exposures.

9. Potential impact on tax deductibility

Our discussion so far has focused on an enterprise policy to increase operational efficiency, but has inadvertently led to an understanding that efficient physical asset replacement costs depend on the occurrence of specified, uncertain, future events. Efficient asset mortality results in volatile future cash flows, so there is an interaction between efficiency and fortuity. Efficient replacement costs are fortuitous in a sense similar to death benefits. Although the tax deductibility of prepayments for future capital outlays, particularly in the aforementioned captive arrangement, is untested, when fortuity is truly present and when there is a valid business purpose (efficiency and risk transfer) for such prepayments, it influences the discussion of tax deductibility, at least theoretically.

According to Section 162(a) of the Internal Revenue Code (26 U.S.C. § 162(a)), an expense must first be deemed necessary and ordinary, among other requirements, in order to be considered deductible for federal income tax purposes. One can argue that an extended service fee based on the contractual trigger described in equation (4.7.8) is necessary, both from the standpoint of transferring risky (volatile) cash flows and for creating efficiency. In other words, there are two legitimate reasons for such an expense. These fees might also be considered ordinary, since extended service contracts already exist to repair and replace physical assets at different levels of aggregation. The only thing which sets the ISC apart from a conventional service contract is that it may replace physical assets up to the highest level of aggregation for the entire plant, and over much longer periods of time than most other types of extended service contracts. To the extent that such contracts already exist, their fees are ordinary.

In the Internal Revenue Service (IRS) revenue ruling 2007-47, the IRS does not allow deductibility for arrangements that are little more than prefunding of future known costs. It is evident that the subject of fortuity has a bearing on whether or not a payment for future services is tax deductible. This revenue ruling also goes on to describe the required aleatory nature of future costs as a condition for deductibility. In other words, there must be uncertainty as to whether or not future costs will be incurred. A service contract based on the contractual trigger described in equation 4.7.8 would meet both of these requirements. This IRS revenue ruling is a conclusion on the application of the law to a specific case that is quite different from the circumstances that we are describing. Nevertheless, revenue rulings can influence decisions made in other rulings.

10. Conclusion

We have applied simple financial mathematics to assumptions about the nature of a function called M(t), which describes the time-dependent nature of actual expenses and opportunity costs associated with individual physical assets. This has led to an understanding that there is an efficient time to replace a physical asset that is random and observable. Under a policy of efficiency, the future cost of replacing a physical asset is both fortuitous and aleatory.

Firms which use traditional capital budgeting methods to plan physical asset renewal may be experiencing a source of operational inefficiency. The magnitude of this inefficiency may be substantial, and comprises not only repair and replacement costs, but also any operational costs attributable to physical assets that are susceptible to replacement. It is not possible to measure this inefficiency under currently configured accounting systems.

Extended service contracts to repair and replace physical assets for large facilities exist, and can be made to include broader replacement obligations such as technological obsolescence. They may provide a means to implement an enterprise policy to coordinate efficient timing of replacements. Such extended service contracts are extreme both in the size of the risks they cover and in their unusually long durations. Because they span multiple decades, they challenge the accounting concept of fixed and deterministic useful lives of physical assets, and suggest that a good portion of capital budgeting, if operational efficiency is a goal, may be a risk management discipline. The service contract mechanism can ensure recognition of optimal replacement timing and the availability of funds at the economically efficient replacement time. If a stand-alone commercial product to achieve this purpose is not available, then there may be alternative risk structures that allow an owner of physical assets to benefit from the features of this unique class of extended service contract.