Loading [Contrib]/a11y/accessibility-menu.js
Variance
Adler, Avraham. 2015. “Estimating the Parameter Risk of a Loss Ratio Distribution—Revisited.” Variance 9 (1): 114–39.
Download all (8)
  • Figure 1. Contour plots of bootstrap parameters
    Download
  • Figure 2. Representative likelihood surfaces
    Download
  • Figure 3. Lognormal contour comparisons
    Download
  • Figure 4. Lognormal contour comparisons showing presence or absence of skew
    Download
  • Figure 5. Simple vs. hierarchical contour plot comparison
    Download
  • Figure 6. Superimposed lognormal contour plots
    Download
  • Figure 7. Contour plots comparison
    Download
  • Figure 8. Parameter cloud comparison
    Download

View more stats

Abstract

When building statistical models to help estimate future results, actuaries need to be aware that not only is there uncertainty inherent in random events (process risk), there is also uncertainty inherent in using a finite sample to parameterize the models (parameter risk). This paper revisits [@R24] in replicating its bootstrap method and compares it with measures of parameter uncertainty developed using maximum likelihood estimation and Bayesian MCMC analysis.

1. Introduction

Actuaries constantly build models. One of the beauties of mathematics is that it allows us to take random real-world phenomena, build a representation in the language of mathematics, and apply various tools allowing reasonable, and often surprisingly accurate, predictions about future phenomena. Of course, these models are just that—models, estimates of event behavior. If all real phenomena were perfectly predictable the universe would be a rather dull place.

Actuarially speaking, “risk” has a specific definition: it is the potential for future events to deviate from their expectation (Actuarial Standards Board 2012). There are many reasons why this could occur. The most basic reason is simply that such events are random events. The very process which generates the event has inherent uncertainty. Even if the model were perfectly specified, the stochastic nature of the process prevents absolute foreknowledge. In actuarial terminology this is called process risk. Another reason why events may differ from their expectation is that the expectation itself is somehow imperfect. The error arising from an incorrect framework specification, e.g., a lognormal distribution instead of a gamma, is called model risk. A third reason for deviation from expectation is that since the data used to select parameters for the model is inherently finite, the parameter estimators based on this sample may not be the perfect point estimates for the true underlying parameters. This source of risk is what is usually referred to as parameter risk. Sometimes, the more precise term finite-sample parameter risk is used to distinguish it from a separate cause of parameter risk: the possibility that parameters may change over time. This paper will focus on finite-sample parameter risk, and, for convenience, will use the term “parameter risk.” An introduction to these and other examples of potential bias and distortion can be found in Venter and Sahasrabuddhe (2012).

In the remainder of this paper, Section 2 will introduce Van Kampen’s data and bootstrapping method, Section 3 will discuss parameter risk estimation using maximum likelihood, Section 4 will use Bayesian Markov Chain Monte Carlo (MCMC) to estimate the parameter risk, and Section 5 will compare the methods and results. The appendix will bring much of the source code used to fit the models and generate this paper, which is predominantly performed using R (R Core Team 2014).[1] Bringing actual code, instead of only results, is intended to enhance transparency and reproducibility. While basic knowledge of R and MCMC techniques is not required, it would help the reader interested in reproducing or extending the results.

2. Bootstrapping

Van Kampen discusses estimating both a ground up loss ratio and the expected loss for an aggregate stop loss reinsurance contract. Table 1 reproduces the data, a sequence of historical ground-up loss ratios and the corresponding experience to an aggregate stop loss cover of 2.5% excess of 72.5%.

Table 1.Loss ratio distribution
Year Loss Ratio LN(Loss Ratio)a Agg Stop LR
1 0.5841 −0.5376 0.0000
2 0.6448 −0.4388 0.0000
3 0.6735 −0.3953 0.0000
4 0.5265 −0.6415 0.0000
5 0.5841 −0.5376 0.0000
6 0.6448 −0.4388 0.0000
7 0.7835 −0.2440 0.0250
8 0.7055 −0.3488 0.0000
9 0.6197 −0.4786 0.0000
10 0.6448 −0.4388 0.0000
Empirical Mean 0.6411 −0.4500 (μ) 0.0025
Empirical StDev 0.0712 0.1100 (σ) 0.00791
Empirical Skew 0.5003
Fitted LRb 0.6415 0.00235
Empirical Loss on Line 0.1000
Fitted Loss on Line 0.0939

aFor this table, the logged values in Van Kampen’s Exhibit 1 were taken as accurate and the loss ratios displayed in that table are assumed to be rounded.
bThe expected loss ratios are based on the empirical μ and σ parameters.

The approach taken by Van Kampen is to make an initial estimate and then create random variates on a grid of parameters near that estimate. All parameters sets which are deemed “close” are marked and used to create a new weighted average expectation. The theory is that the observed data leading to the best estimate of the parameters may have actually come from a different set of parameters. Allowing for the use of many sets of parameters and weighting them by some measure of probability that they were the “true” source will reflect parameter uncertainty. The bootstrap algorithm itself is:

  1. Generate a possible μ and σ for the lognormal.

  2. Generate 10,000 observations of 10-year blocks.

  3. Compare the simulated mean, standard deviation, and skew of each of the simulated blocks with those of the original data. If any 10-year block has all three check values sufficiently close to the best estimate, the parameter set is marked as viable.

  4. Assign a weight to each viable parameter set based on the number of its blocks found to be close.

  5. Calculate a weighted average expected ground up and aggregate stop loss ratio using all the viable parameter sets to arrive at a final point estimate which now includes the impact of parameter uncertainty.

Based on Van Kampen’s description, the search grids was set as the intersections of 51 data points for µ in the range −1.549–0.226 (50 equispaced points and the addition of −0.45) and 79 equispaced data points for σ in the range 0.0055–0.4345 for a total of 4,029 parameter sets. For each of these sets, 100,000 lognormal variates were generated and placed into a 10,000 by 10 matrix. A viable parameter set was selected based on the same measure of “closeness” used in the original paper (pp. 187–188). For each viable set, the expected ground-up and expected aggregate loss ratios were calculated, and the overall estimate is a frequency-weighted average of the viable results.

In 2003, this procedure took around 8 hours; in 2014, after some optimization described in Section 7.1.2, it took a little under two minutes. Hardware and software advances in the intervening years have created an over 270 times increase in speed! Taking advantage, a more finely-grained grid was investigated. Using the results of the original bootstrap to focus a new grid, a second procedure was run with µ ranging from −0.8 to −0.2 and σ from 0.05 to 0.45, each moving in steps of 0.0025. Bootstrapping these 38,801 pairs took about 17 minutes on the same machine.

Unsurprisingly, the results shown in Table 2 are similar to those in the original paper. While recognizing parameter risk is always important, it is more so when dealing with rare events. Even a small thickening of the tail of a distribution may make a significant difference in the expected results excess of a threshold. When parameter risk is contemplated with this data, there is almost no increase in the ground-up expected loss but a significant increase to the highly tail-sensitive excess layer. Note how the more fine-grained algorithm’s ground-up estimate is only slightly different from that of the original algorithm, but the aggregate stop loss ratio estimate is noticeably larger.

Table 2.Bootstrap parameter risk results
Statistic Original Adjusted Change
Original Algorithm
Ground Up LR 0.6415 0.6436 0.00328
Agg. Stop LR 0.00235 0.00318 0.3554
Fine-grain Algorithm
Ground Up LR 0.6415 0.644 0.00395
Agg. Stop LR 0.00235 0.00336 0.4323

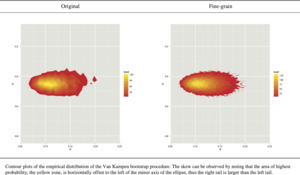
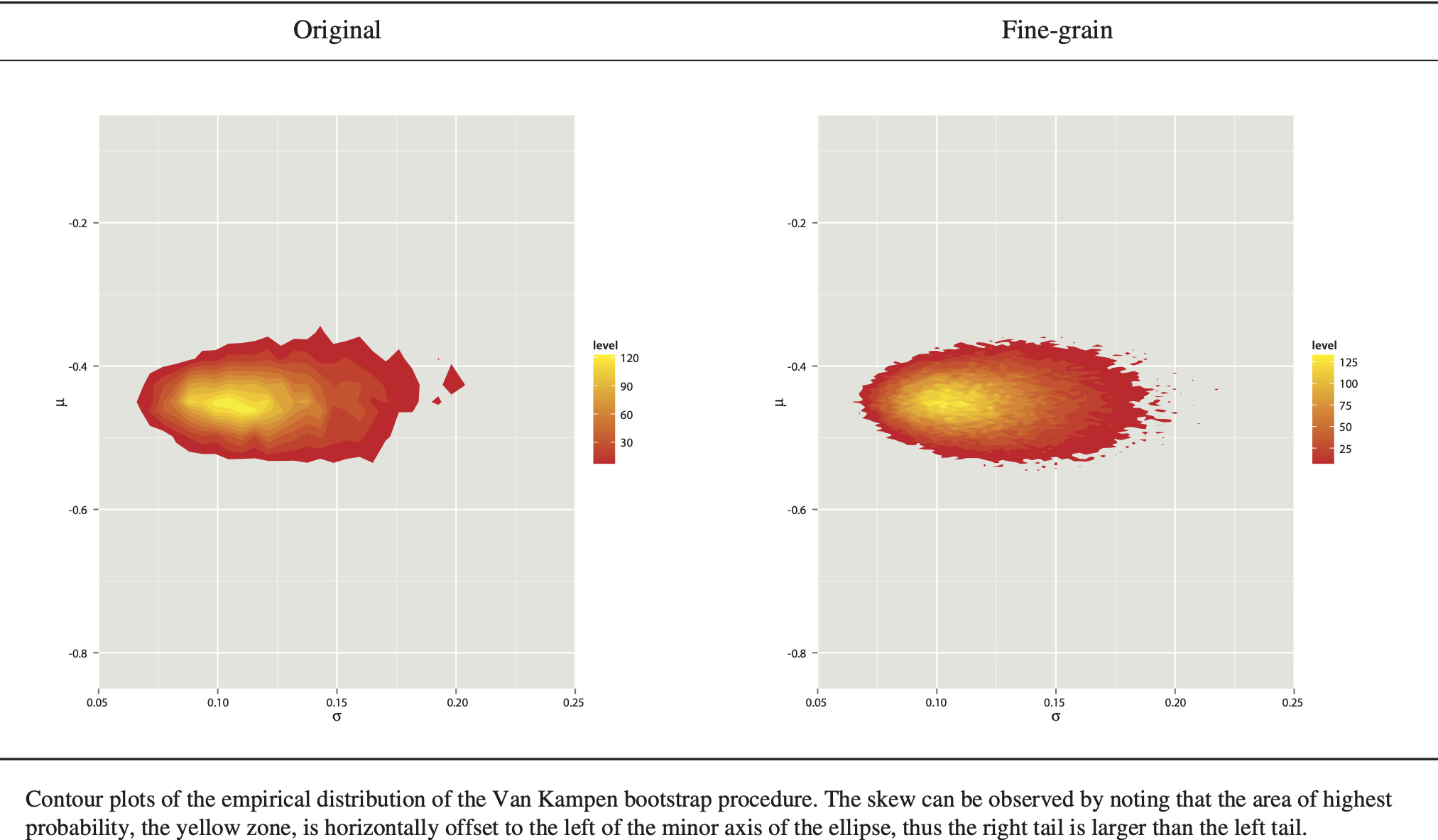
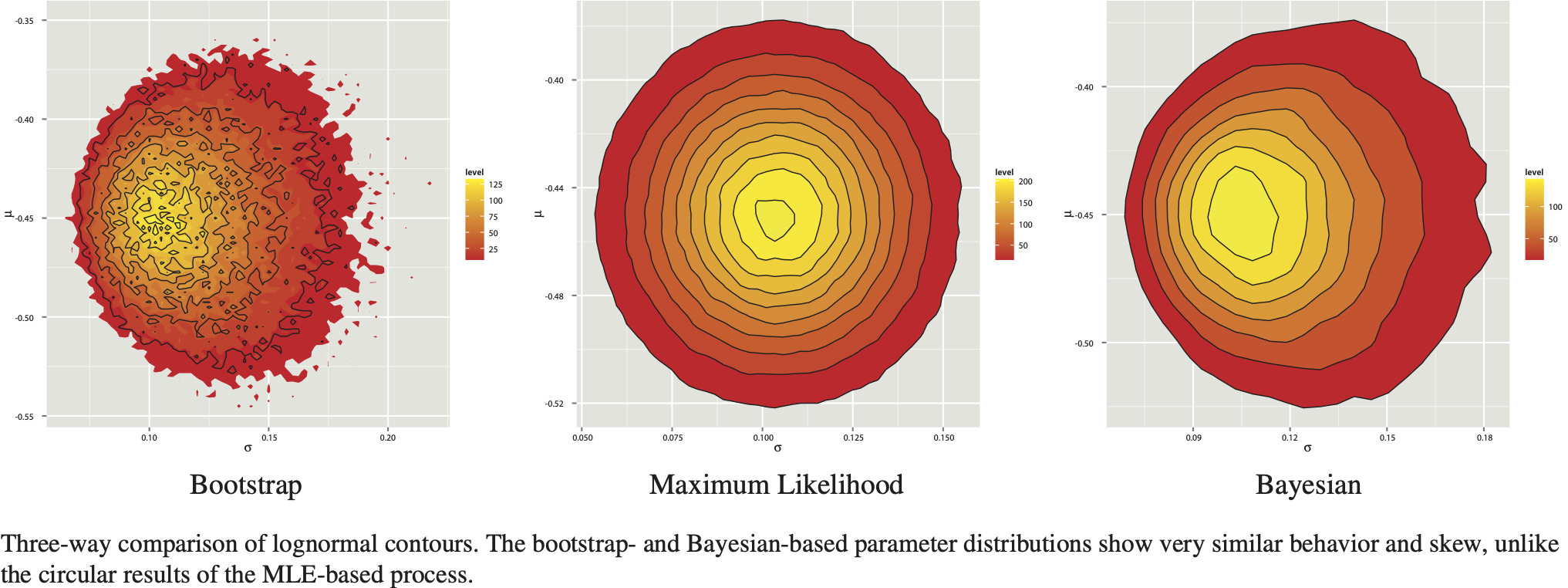
Visual inspection of data is always valuable (Anscombe 1973). When investigating parameter risk for two-parameter distributions, one useful tool is the contour plot—a two-dimensional projection of the three-dimensional surface of the joint distribution of the parameters. Contour images in this paper will reflect the increase in probability of a given set of parameters by a brightening of the color as it shades from red to yellow.

Contour plots of the joint empirical distribution of the close pairs of μ and σ for the original and fine-grained algorithms are plotted in Figure 1.[2] The skew of the distribution is clear.

Figure 1
Figure 1.Contour plots of bootstrap parameters

3. Maximum likelihood

3.1. Introduction

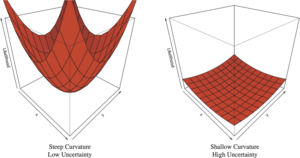
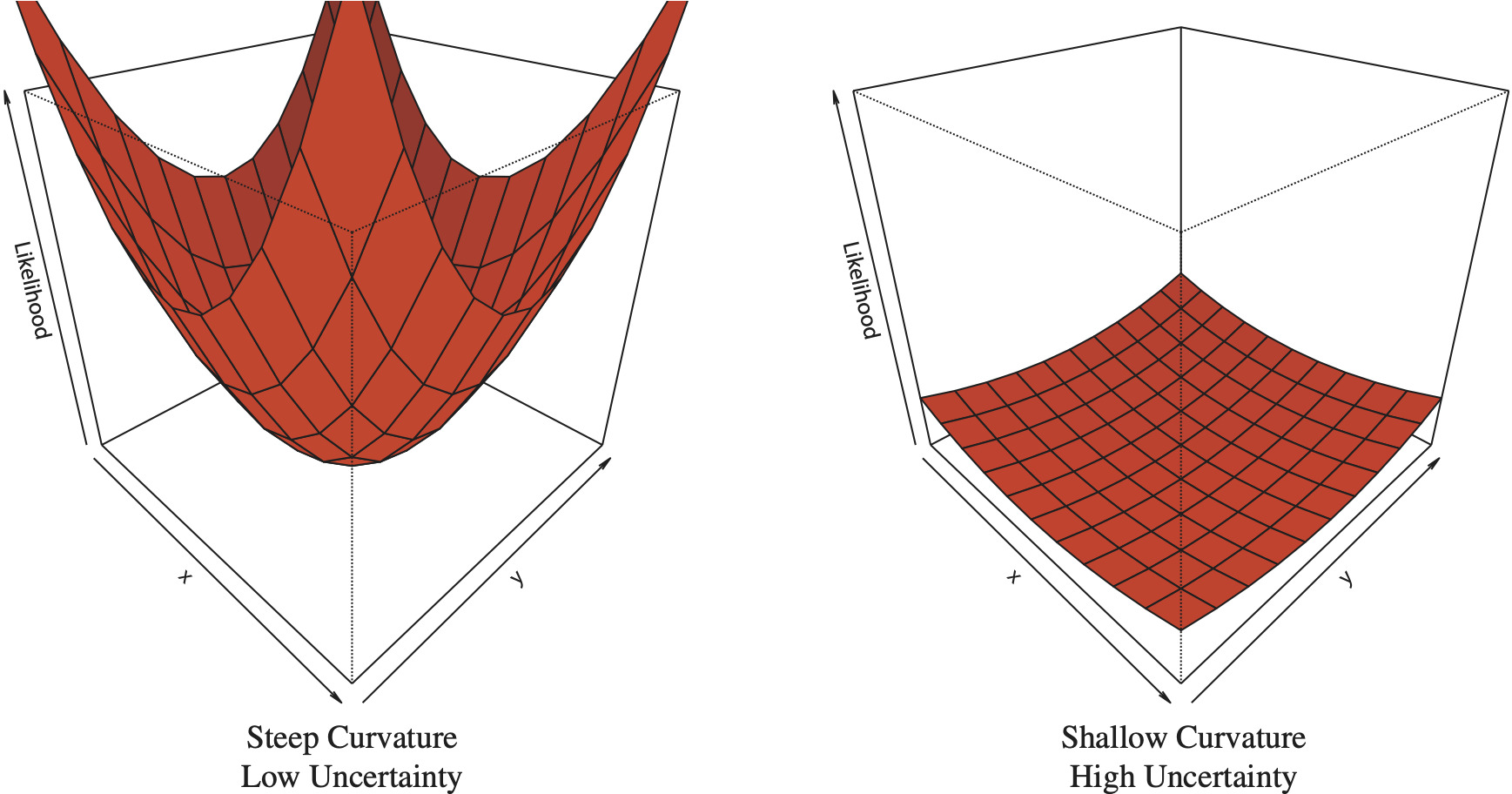
One of the most used tools in the actuarial toolbox is maximum likelihood estimation (MLE). Among the properties of MLE is that the estimated parameters have asymptotic normality—under general conditions, as the sample size increases, the distribution of the maximum likelihood estimate of the parameters tends to the multivariate normal with covariance matrix equal to the inverse of the Fisher information matrix (Klugman, Panjer, and Willmot 1998, §2.5.1). Assuming this normality, when performing MLE, the Hessian matrix at the point of convergence can be calculated and its inverse used to estimate parameter variances and covariances. An intuitive explanation for the relationship between the curvature of the log-likelihood and parameter uncertainty is as follows. The estimation process looks for a minimum for the negative log-likelihood by following the joint log-likelihood’s (hyper)surface. The Hessian matrix describes the curvature of a multivariate function, in this case, the log-likelihood. In a bivariate case, imagine the procedure as a marble rolling around on the log-likelihood surface. Compare the two surfaces in Figure 2. If the gradient at the found minimum is low, that would represent a shallow depression and it would be easy to “jostle” the marble to a different point nearby. This represents significant parameter uncertainty, as the true point could easily have been elsewhere. Conversely, if the gradient is high, the depression is deep and it would be difficult to move the marble. This implies the convergence to the found point is strong, and there is less parameter uncertainty.

Figure 2
Figure 2.Representative likelihood surfaces

3.2. Estimation and simulation

Given the assumption of normality, once a set of parameters is estimated by maximum likelihood, the Hessian can be used to generate the parameter variance-covariance matrix. Using these parameter means and covariances, sets of correlated parameters can be generated using a multivariate normal distribution—the asymptotic limiting distribution of maximum likelihood estimators. These correlated parameter sets are then used to draw one observation each from the distribution of interest. The collected observations now represent a sample with explicit recognition of parameter uncertainty, as the parameters generating the observations themselves were treated as random variables. Care needs to be taken, however, as the multivariate normal will sometimes generate parameters which themselves are illegal for the distribution in question. For example, the σ of a lognormal distribution must be greater than 0, yet a multivariate normal may generate a value less than 0. Similarly, a value very close to 0 may be generated when its reciprocal is needed, resulting in an astronomical value. There are a few ways to address this problem, the simplest being to ignore generated values which cause illegal results. It is also prudent, at times, to trim the mean to prevent edge cases from dominating the results. In all the MLE instances below, the mean is trimmed by 0.1%. As 1,000,000 samples are drawn for each of the MLE stochastic simulations, this means that the top and bottom 500 observations are removed and the statistics are calculated on the remaining 999,000 samples.

Continuing with the lognormal assumption, the results of solving for the parameters using MLE on the sample data are shown in Table 3.[3] A stochastic simulation was used to estimate the effects of parameter risk. Pairs of correlated μ and σ parameters were generated, each of which was then used for a stochastic lognormal draw of the observed ground-up loss ratio.[4] Given the drawn ground-up loss ratio, the resulting aggregate stop loss (ASL) ratio was simply the loss in a layer 2.5% excess of 72.5%. All means are trimmed as described above.

Table 3.Lognormal MLE parameters
Statistic Value SD Correlations μ σ
μ −0.4500 0.0330 μ 100.0000% 0.0000000000104%
σ 0.1043 0.0233 σ 0.0000000000104% 100.0000%
AICc −20.1072

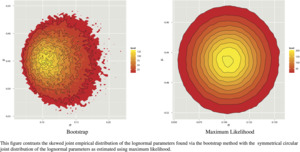
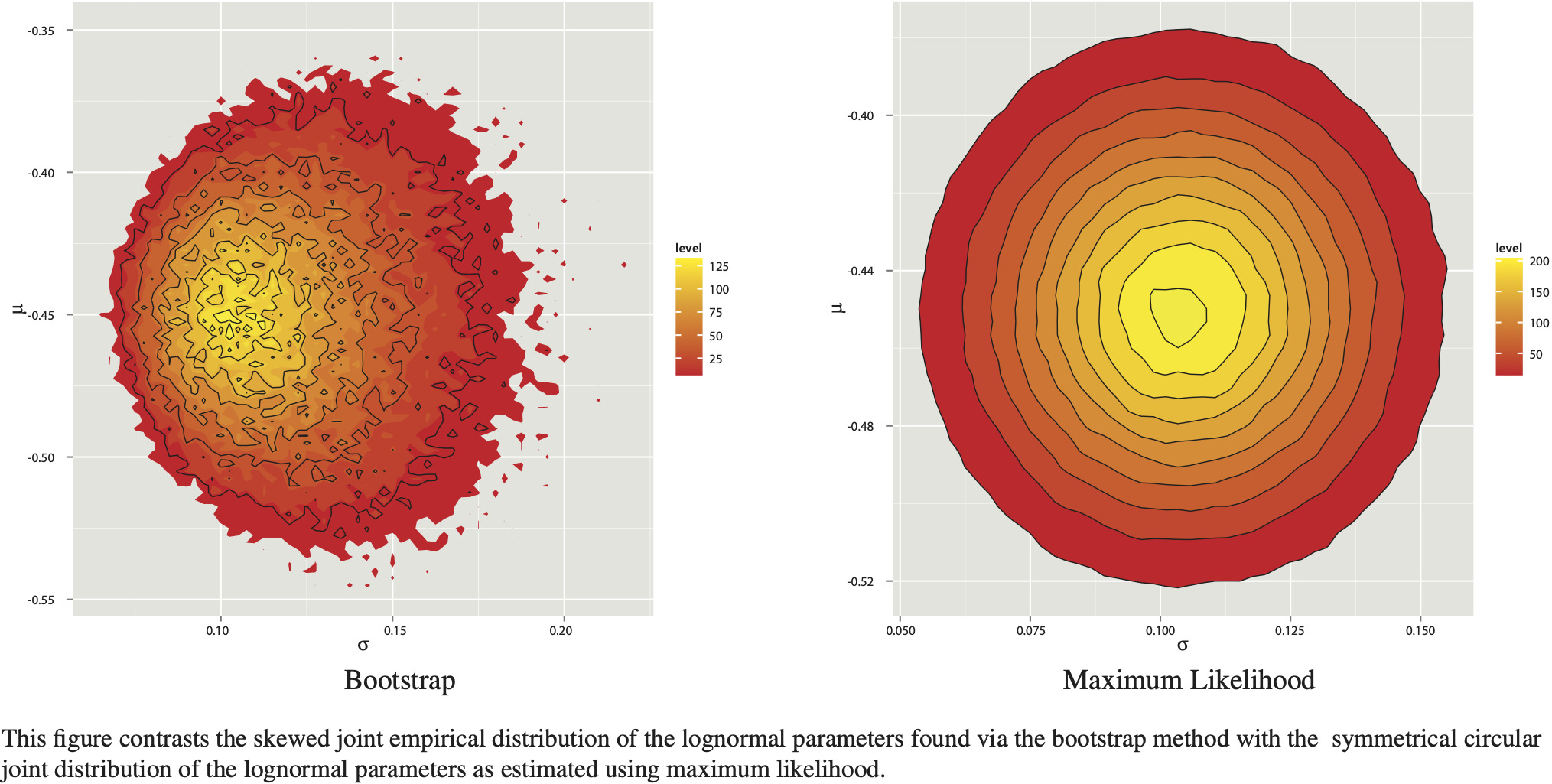
The simulated results, shown in Table 4, indicate almost no change from the original. This is more easily understood visually. Figure 3 compares re-scaled bootstrap and MLE-based contour plots, and also has explicitly plotted density isolines. When the plotted ranges are no longer restricted to the ranges in the original paper, the plot clearly contrasts the symmetrical uncorrelated nature of the MLE-based parameters with the skewed bootstrapped parameters. The isolines, along which each parameter set is equiprobable, further demonstrate the circular nature of the MLE-based results. This is predominantly due to the parameters being uncorrelated with each other.[5] When pairs of multivariate normal variables are uncorrelated (or ρ = 0 in the bivariate case), that is sufficient to imply their independence (Melnick and Tenenbein 1982). Therefore, under the lognormal assumption, since μ and σ are independent and uncorrelated, any pair of parameters which would result in a loss above the overall expectation is balanced by one equally probable which would cause an equally lower loss. When the parameters exhibit correlation, and possibly even more strongly in a skewed distribution, it is possible to obtain an observation which cannot be balanced by its equal and opposite “across the circle of probability.”

Table 4.Lognormal MLE stochastic results
Statistic Original Adjusted Change
Ground Up LR 0.6415 0.6415 −0.0000404
Agg. Stop LR 0.00235 0.0023 −0.0197
Figure 3
Figure 3.Lognormal contour comparisons

3.3. Other distributions

To investigate how correlation between the parameters may affect the results, the MLE fitting was done using other distributional families: the two parameter gamma and Weibull distributions and the three parameter Burr and inverse Burr distributions.[6] Information criteria, such as the Akaike Information Criteria (AICc)[7] are often used to compare models. When using information criteria, two points must be kept in mind. First, the criteria can only be compared between models based on the exact same data. Second, it is not the magnitude of the value, but the difference between the lowest value and all the others, which is important (Burnham and Anderson 2002, chap. 2). When used appropriately, accepted rules of thumb are that a difference of 0–2 implies model similarity, a difference of 4–7 shows that the model with the higher value has little support with respect to the model with the lower value, and larger differences imply that the higher-valued model should really not be considered at all (Burnham and Anderson 2002, 70–71; Spiegelhalter et al. 2002).

The best fits, as shown in Table 5, are the lognormal and the gamma, with the Weibull being acceptable. The Burr and inverse Burr are each more than 4 away from the minimum, showing little support. Nevertheless, it is instructive to see the difference between using a better model and a worse one. Don’t all the models arise from reasonable analyses and the same processes? The goodness-of-fit measures don’t really look that bad, do they? The AICc difference not even 5, right? What if the AICc’s were 18,204.3 and 18,208.9, wouldn’t that be “close enough”? These are questions the actuary may receive, if not ask of him or herself. Often, actuaries are exposed to “good” results and do not always have a yardstick for “bad” ones. Being able to recognize when processes fail and how that can affect analyses is an important part of actuarial analysis. Therefore, the stochastic parameter uncertainty process was applied to each of these models as well to provide a sense of poor performance.

Table 5.Comparison of MLE parameters for various distributions
Lognormal AICc −20.1072
Statistic Value SD Correlations α β
α −0.4500 0.033 α 100.0000% 0.0000000000104%
βa 0.1043 0.0233 β 0.0000000000104% 100.0000%
Gamma AICc −20.0431
Statistic Value SD Correlations α β
α 91.5874 40.8848 α 100.0000% 99.7272%
βa 142.8514 63.9436 β 99.7272% 100.0000%
Weibull AICc −18.2925
Statistic Value SD Correlations τ θ
τ 9.5425 2.1812 τ 100.0000% 33.6650%
θ 0.6723 0.0237 θ 33.6650% 100.0000%
Inverse Burr AICc −15.7649
Statistic Value SD Correlations τ γ θ
τ 1.196 1.5902 τ 100.0000% −85.3018% −96.7846%
γ 16.0524 8.1019 γ −85.3018% 100.0000% 83.4756%
θ 0.6266 0.0804 θ −96.7846% 83.4756% 100.0000%
Burr AICc −15.7579
Statistic Value SD Correlations α γ θ
α 0.8835 0.9462 α 100.0000% −83.2098% 94.1562%
γ 17.8443 8.6235 γ −83.2098% 100.0000% −77.489%
θ 0.6301 0.0599 θ 94.1562% −77.4890% 100.0000%

aAlthough in actuarial science the gamma is usually parameterized using the scale θ, in this case, as the data is very close to 0, the analysis was more numerically stable using the rate β where β = 1/θ.

Using the fitted parameter means and covariance matrix for each distribution, one million correlated observations were generated. Since using a multivariate normal to generate observations makes it possible to obtain negative values, the same filtering and trimming used for the lognormal were used for these distributions as well. Unfortunately, even with the trimming, the multivariate normal generated too many unacceptable parameter sets at times. This was due not only to “illegal” parameter sets but also to parameter sets which generated unreasonable results, such as ground-up loss ratios greater than 10196% for the inverse Burr. This further highlights the need for actuarial judgment, which should always temper raw algorithmic output, in any analysis. One of the largest contributions actuaries make is to understand, and provide the context for, the statistics which will be used. Yes, 10196% may be one observation out of one million that can mathematically arise from a random draw of underlying inverse Burr parameters, but it should it be considered a possible event? Certainly not! Therefore, not only were illegal parameters sets removed, but a judgment-based reasonability cap for the ground-up loss ratios of 300% was implemented as well. For the inverse Burr, there were 234,511 parameter sets which were removed from the analysis due to being invalid or in excess of the cap. For the Burr, there were 187,233 such observations.

Table 6 shows the results of the stochastic simulations for these distributions, and the inferences made using all, and then the 765,489 and 812,767 remaining reasonable, observations respectively. The “small” difference in the AICc of the parameters manifests as a very significant difference in the modeled results including parameter uncertainty. The results for the three-parameter distributions, even when trimmed, are just plain ridiculous. Even among the models which only reflect “realistic” observations, the results seem extreme when compared to the distributions with acceptable AICc measures.

Table 6.Comparison of MLE-based parameter uncertainty for various distribution
Statistic Original Adjusted Change
Lognormal
Ground Up Loss Ratio 0.6415 0.6415 −0.0000404
Agg. Stop Loss Ratio 0.00235 0.0023 −0.0197
Gamma
Ground Up Loss Ratio 0.6415 0.6430 0.00225
Agg. Stop Loss Ratio 0.00235 0.0027 0.1499
Weibull
Ground Up Loss Ratio 0.6415 0.6373 −0.00658
Agg. Stop Loss Ratio 0.00235 0.00274 0.1664
Inverse Burr
Ground Up Loss Ratio 0.6415 1068.5269 1664.6440
Agg. Stop Loss Ratio 0.00235 0.00374 0.5946
Inverse Burr—Valid Results
Ground Up Loss Ratio 0.6415 0.6356 −0.00923
Agg. Stop Loss Ratio 0.00235 0.00353 0.5030
Burr
Ground Up Loss Ratio 0.6415 3040903.5501 4740228.7458
Agg. Stop Loss Ratio 0.00235 0.00467 0.9908
Burr—Valid Results
Ground Up Loss Ratio 0.6415 0.6685 0.0421
Agg. Stop Loss Ratio 0.00235 0.00438 0.8651

3.4. Estimation and simulation on a log scale

Another common way to prevent negative parameters in a simulation is to reparameterize the distributions so that the optimization solves for an extremum of the log of the parameters, and this value is then exponentiated for use in simulation. This transformation also affects the shape of the joint distribution of the parameters in normal space, as parameters exhibiting symmetry on a log scale will not be symmetric on a normal scale. Table 7 displays the results of the simulations including the effects of parameter uncertainty using parameters fitted on a log scale. For the three distributions with acceptable goodness-of-fits, the lognormal continues to show little effect from parameter risk, the gamma now shows almost none as well, and the aggregate stop loss under the Weibull also demonstrates a smaller effect.

Table 7.Comparison of log scale MLE-based parameter uncertainty for various distribution
Statistic Original Adjusted Change
Lognormal
Ground Up Loss Ratio 0.6415 0.6417 0.000296
Agg. Stop Loss Ratio 0.00235 0.00241 0.0245
Gamma
Ground Up Loss Ratio 0.6415 0.6414 −0.000102
Agg. Stop Loss Ratio 0.00235 0.00236 0.00573
Weibull
Ground Up Loss Ratio 0.6415 0.6385 −0.00469
Agg. Stop Loss Ratio 0.00235 0.00267 0.1383
Inverse Burr
Ground Up Loss Ratio 0.6415 0.6625 0.0327
Agg. Stop Loss Ratio 0.00235 0.00428 0.8236
Inverse Burr—Valid Results
Ground Up Loss Ratio 0.6415 0.6630 0.0336
Agg. Stop Loss Ratio 0.00235 0.00429 0.8273
Burr
Ground Up Loss Ratio 0.6415 0.6370 −0.0071
Agg. Stop Loss Ratio 0.00235 0.0026 0.1073
Burr—Valid Results
Ground Up Loss Ratio 0.6415 0.6377 −0.00596
Agg. Stop Loss Ratio 0.00235 0.00261 0.1130

4. Bayesian analysis

4.1. Introduction

A third way to incorporate parameter risk is through a Bayesian model using Markov Chain Monte Carlo (MCMC) techniques. Roughly speaking, the Bayesian approach is that there exists an a priori estimate of the distribution of the parameters, which, when convoluted with the data, allows for the calculation of an a posteriori distribution of those parameters (Gelman et al. 2014, Chap. 1.3). The Bayesian model can be made even more sophisticated through explicit recognition of parameter dependency through hyperparameters. A model in which there exists a hierarchical structure of parameter dependency is called, understandably, a hierarchical model (Kruschke 2015, 221–223). Creating a model with such structure allows the joint probability model to reflect potential dependencies between the parameters (Gelman et al. 2014, 101). Both simple and hierarchical models explicitly recognize parameter risk by generating a posterior distribution around the parameters. Moreover, distributions of the statistics of interest, such as loss rations, can also be easily generated with explicit reflection of parameter risk.

While the Bayesian concept is relatively simple, for almost two centuries its application was difficult, as the convolution often required the calculation of integrals without nice analytic solutions. In the past few decades, advances in both algorithms and computer hardware have made these computations much simpler. The method used in this paper, MCMC, takes advantage of certain properties of Markov chains that allow it to converge to the posterior distribution without fully calculating some of the more difficult integrals. For more explanation, the interested reader is directed to Kruschke (2015, chap. 7) and Gelman et al. (2014, chap. 11).

4.2. Simple models

Initially, a simple model was used. This model placed a weakly informative prior on both μ and σ and allowed the data to “lead” the posterior. More specifically, using JAGS (Plummer 2003), not only were samples of μ and σ generated, but a stochastic ground-up loss observation based on the generated μ and σ was drawn as well.[8] The corresponding aggregate stop loss was calculated as a layer of 2.5% excess of 72.5%. For the lognormal distribution, the generated μ and σ parameters remain effectively uncorrelated—about −0.6672%. Nevertheless, the effect of parameter uncertainty on the aggregate stop loss, as shown in the first section of Table 8, is significant. Looking at a contour plot, the reason becomes clear. The skew that was seen using the bootstrap routine of Section 2 has returned, as shown in Figure 4.

Table 8.Bayesian analysis results—simple models
Statistic Original Adjusted Change
Lognormal WAIC −21.3219
Ground Up LR 0.6415 0.6444 0.0045
Agg. Stop LR 0.00235 0.00339 0.4440
Gamma WAIC −20.4365
Ground Up LR 0.6415 0.6409 −0.000879
Agg. Stop LR 0.00235 0.00188 −0.1980
Weibull WAIC −19.3850
Ground Up LR 0.6415 0.6415 0.0000451
Agg. Stop LR 0.00235 0.00316 0.3463
Inverse Burr WAIC −20.3855
Ground Up LR 0.6415 0.6476 0.00956
Agg. Stop LR 0.00235 0.00338 0.4402
Burr WAIC −19.5232
Ground Up LR 0.6415 0.6397 −0.00277
Agg. Stop LR 0.00235 0.00305 0.2978
Figure 4
Figure 4.Lognormal contour comparisons showing presence or absence of skew

For completeness, similar Bayesian analyses were done for the other distributions brought in Section 3.3.[9] As in the MLE case, comparing the models requires a goodness-of-fit measure. It remains an open question as to which measure to use to robustly compare Bayesian models. One of the more accepted measures is the deviance information criterion (DIC), a Bayesian analogue to the Akaike information criterion (Spiegelhalter et al. 2002). However, a more recently defined measure, the widely applicable information criterion (Watanabe 2013), also called the Watanabe-Akaike information criteria (sharing the acronym WAIC), has been gaining traction as being a more fully Bayesian measure than DIC (Gelman et al. 2014, 173–174). This paper will use WAIC as the goodness-of-fit measure. As shown in the remainder of Table 8, when using the simple model framework, the spread in both results and goodness-of-fit statistics for most families is smaller than when using maximum likelihood—all models are within the acceptable rule of thumb—but the lognormal distribution remains the model of choice. The most surprising result is the gamma model, which now shows the counterintuitive result of a reduced expected aggregate stop loss ratio! What is also clear is that the Burr and inverse Burr no longer result in unacceptable results.

4.3. Hierarchical models

Another benefit of the Bayesian procedure is the capability to express a hierarchical structure in the model. Instead of weakly informative priors directly on μ and σ, a multivariate normal distribution, itself with a weakly informed prior on the mean and the covariance matrix, was used to generate correlated pairs (μ, σ) which were then used to generate the lognormal draws. Unfortunately, when adding the multivariate normal structure into JAGS, which uses Gibbs sampling, the generated parameters were so auto-correlated that convergence was not achieved in reasonable time—even using thinning rates of over 1000. This is a property of Gibbs sampling in that it does not deal well with highly correlated posteriors (Stan Development Team 2014b, vi). Therefore, the model was rebuilt in Stan (Stan Development Team 2014a)—a Bayesian modeling language whose sampler is not Gibbs but Hamiltonian Monte Carlo (Gelman et al. 2014 p. 12.4–12.6).[10] The No-U-Turn-Sampler used by Stan is much more robust to highly autocorrelated parameters (Hoffman and Gelman 2014). To provide reassurance that the model was built correctly, the non-hierarchical lognormal model was also programmed in Stan to compare the fitted results with those of JAGS.

The ability to expressly consider a hierarchical structure becomes more valuable when contemplating the gamma distribution. The simple Bayesian gamma model showed the counter-intuitive reduced aggregate stop loss ratio. As the gamma parameters are extremely correlated with each other—99.7272% using maximum likelihood and 99.7251% in the simple Bayesian model—it makes sense to consider a hierarchical Bayesian model to directly generate correlated gamma parameters.

Table 9 shows that adding hierarchical hyperpriors to expressly model correlation between the lognormal μ and σ reduces the effect of parameter uncertainty in the aggregate stop loss for the lognormal distribution with almost no change to the goodness-of-fit as measured by WAIC. Expressly modeling the correlation in the gamma distribution had a much larger effect. Now, the effect of parameter risk much more in line with expectations—close to that of the hierarchical lognormal—and the goodness-of-fit measure is greatly improved and much closer to that of the lognormal. A comparison of the contour plots of the joint distributions of the parameter pairs between the simple and hierarchical models is shown in Figure 5.

Table 9.Bayesian analysis results—hierarchical models
Statistic Original Adjusted Change
Lognormal Simple—JAGS WAIC −21.3219
Ground Up LR 0.6415 0.6444 0.0045
Agg. Stop LR 0.00235 0.00339 0.4440
Lognormal Simple—Stan WAIC −21.3237
Ground Up LR 0.6415 0.6443 0.00436
Agg. Stop LR 0.00235 0.00338 0.4379
Lognormal Hierarchical—Stan WAIC −21.4386
Ground Up LR 0.6415 0.6425 0.00156
Agg. Stop LR 0.00235 0.00296 0.2609
Gamma Hierarchical—Stan WAIC −21.3235
Ground Up LR 0.6415 0.6421 0.000882
Agg. Stop LR 0.00235 0.00294 0.2525
Figure 5
Figure 5.Simple vs. hierarchical contour plot comparison

5. Comparison and conclusions

5.1. Comparisons

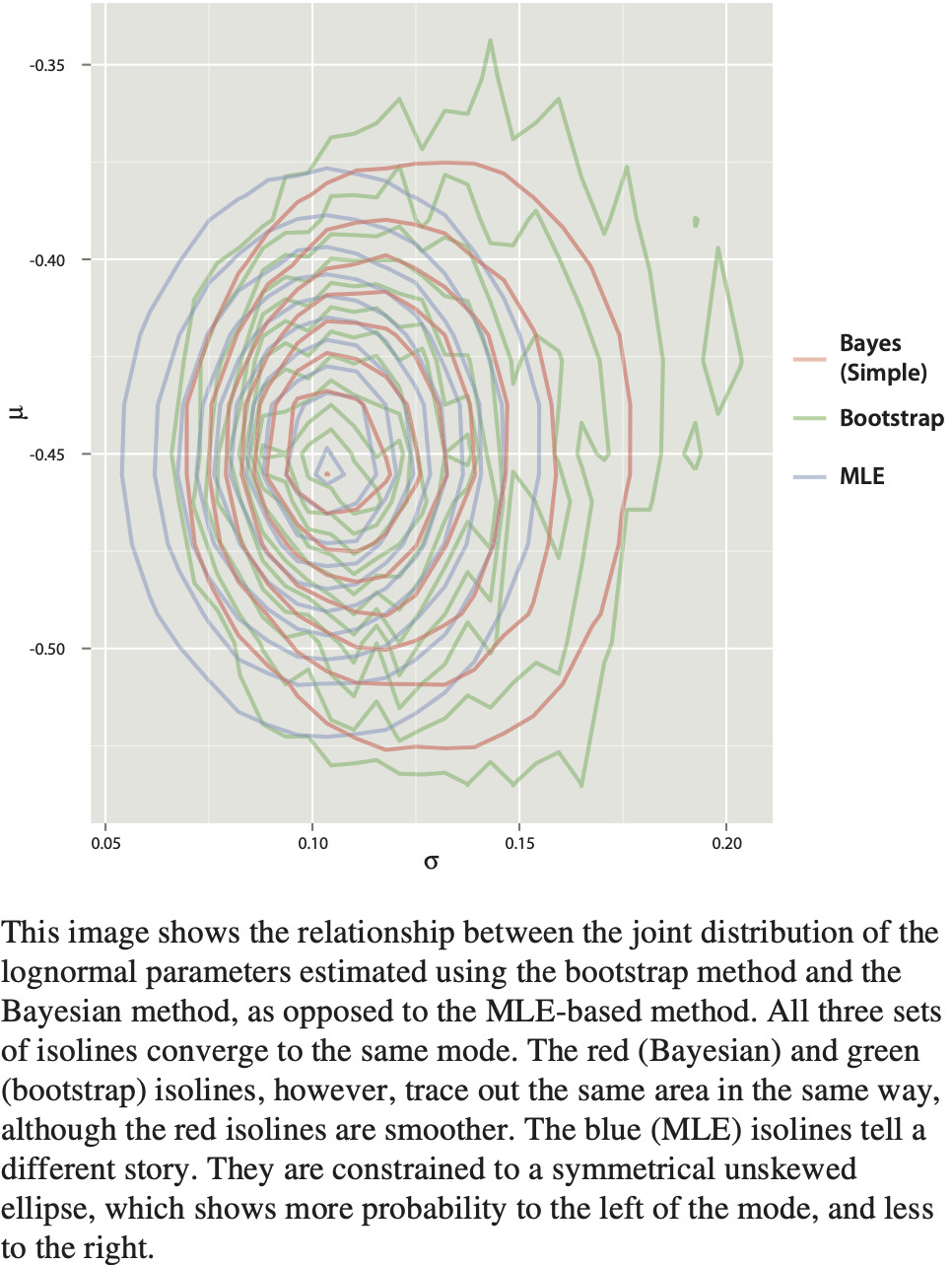
One of the first observations that can be made is that the bootstrap results appear very similar to the Bayesian results in both magnitude and distribution—especially with the simple model. Overlaying the contours of the distributed parameters, as shown in Figure 6, highlights the relationship between the methods. The area of highest density is shared by all three methods. However, while the Bayesian contours show the same skew and coverage as the bootstrap contours, the maximum likelihood contours are constrained to a symmetric ellipse centered on the area of highest density.

Figure 6
Figure 6.Superimposed lognormal contour plots

This near-identicality is not surprising. Van Kampen’s bootstrap is actually an example of Approximate Bayesian Computation (ABC). Described in theory by Rubin (1984), and named by Beaumont, Zhang, and Balding (2002), ABC comprises methods where approximations to Bayesian posteriors are calculated by simulating outcomes based on parameters selected from their prior distributions, rejecting parameter sets whose outcomes lie outside an accepted tolerance, and estimating the posterior distribution based on the remaining “accepted” samples.[11] This method circumvents the need to calculate any likelihood; all that is needed is the prior, summary statistics, and a tolerance. This is precisely what Van Kampen’s bootstrap does: sample from the uniform grid (prior on parameters), reject outcomes whose summary statistics are not close (rejection outside tolerance), and calculate results based on weighted averages of the remaining samples (posterior estimation).

Nevertheless, the truly Bayesian procedure has at least two benefits: 1) studies have shown that given data sets allowing for true MCMC, the MCMC results are more accurate than those of rejection-based methods (Beaumont, Zhang, and Balding 2002; Bornn et al. 2014); and 2) it allows for easier to expression and investigation of hierarchical relationships (Turner and Van Zandt 2014, 6–7). Therefore, where an analytic expression of the needed likelihood(s) are not that difficult to calculate, it makes sense to use the fully Bayesian technique.

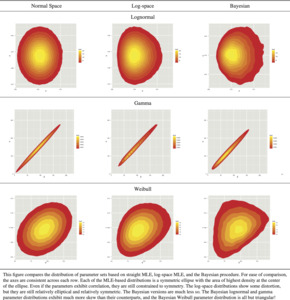
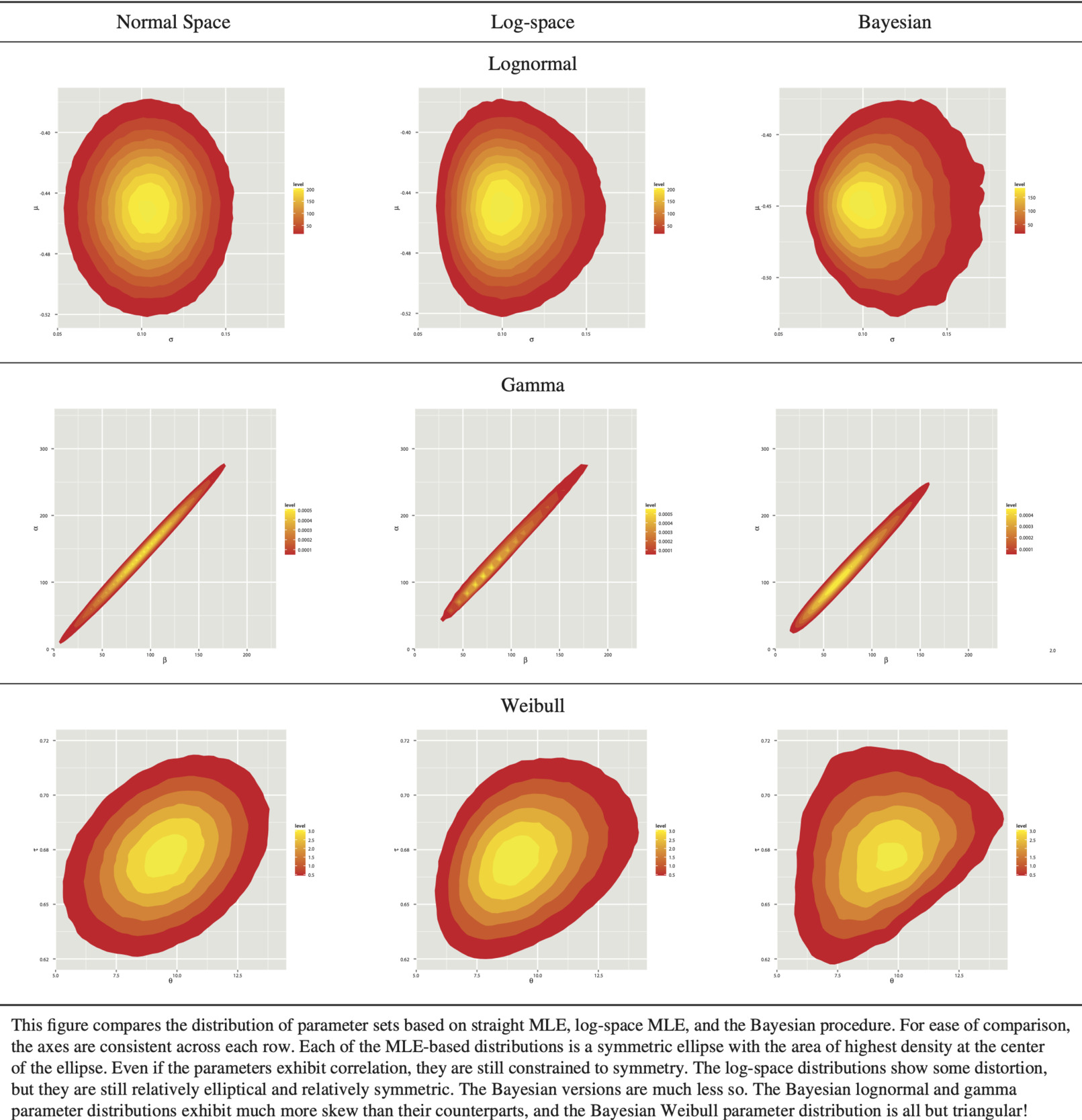
Figure 7 compares the joint distribution of the generated parameter sets under MLE, log-space MLE, and the Bayesian framework for the two-parameter distributions. The joint distribution of the parameters generated by maximum likelihood methods are constrained to a symmetric elliptical distribution. Even when solving for parameters in log-space, the resulting normal space parameters are still mainly elliptical with some distortion. The Bayesian models, however, are not constrained to symmetric ellipticity.

Figure 7
Figure 7.Contour plots comparison

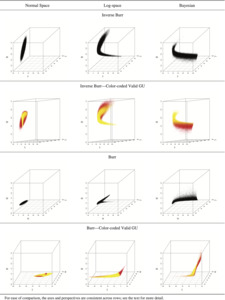
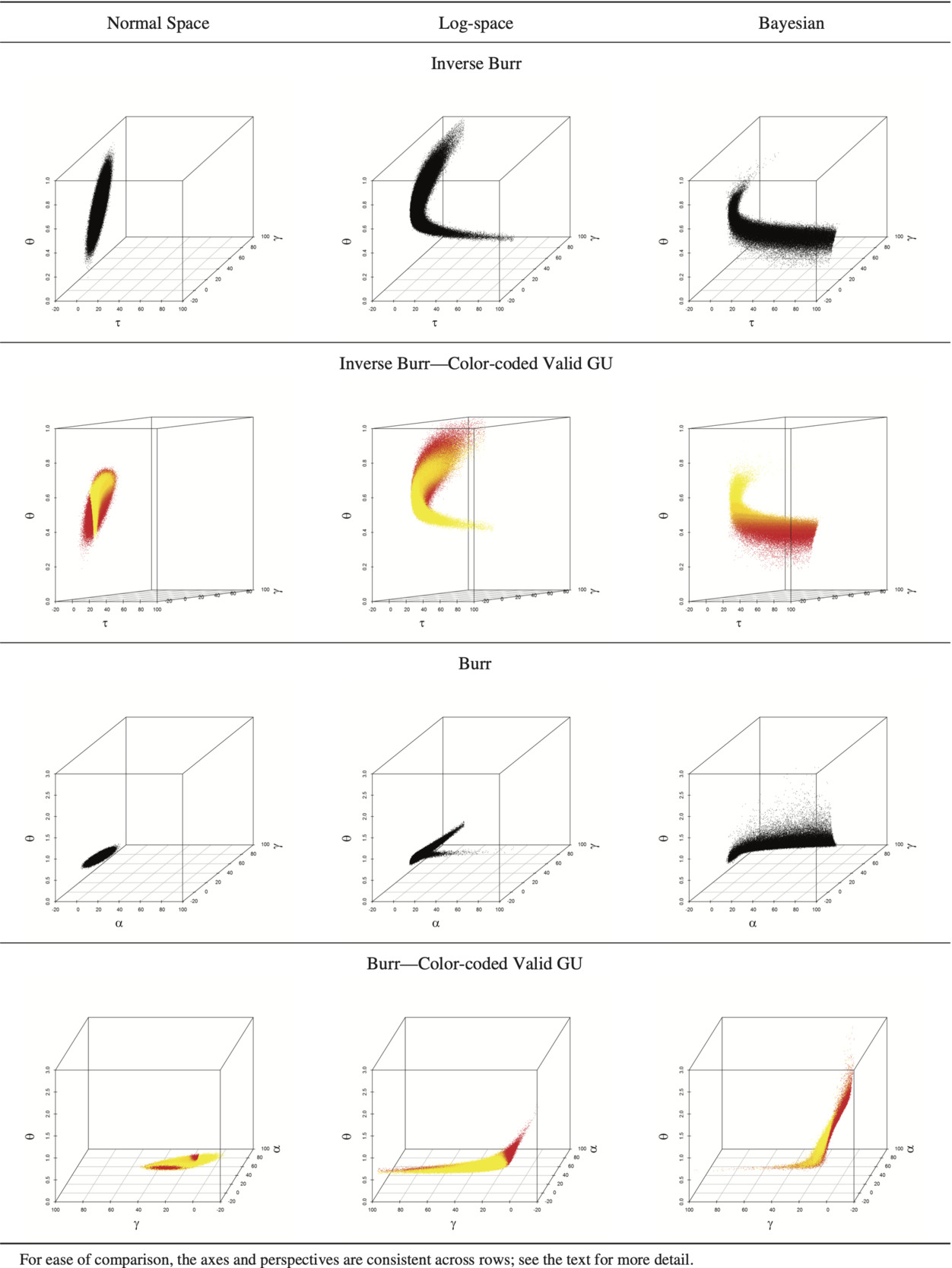
This is even clearer for the three-parameter distributions. Figure 8 compares the parameter clouds of the distributions; each point representing a parameter triplet. The colored version of the clouds have fewer points than the monochrome versions, as they are composed only of the points which led to valid values. For these plots, the brightness and color of the points reflect the magnitude of the resulting value; e.g., bright yellow triplets will have a correspondingly larger expected ground-up loss ratio than the dull red triplets.

Figure 8
Figure 8.Parameter cloud comparison

There are two important takeaways from Figure 8. The first regards the structure of the clouds. The normal space MLE clouds are clearly constrained to be ellipsoids. The log-space MLE clouds break from that constraint but seem to be more “stretched” and “bent” ellipsoids than entirely different shapes. The Bayesian process, however, allows the data to determine the shape of the posterior distribution and results in strangely-shaped surfaces which expand to fill the parameter space. The inverse Burr traces a sheet that inhabits different sections of θ and γ space than the other two inverse Burr clouds. The Burr cloud is more a sheet with a small tail that extends down γ space. The second takeaway is the relationship between parameter and value. In the normal ellipsoid it is difficult to see. In the log-space versions it is somewhat clearer to see a relationship between the parameter triplet’s position and resulting mean value. However, the relationship between structure and value appear clearest in the Bayesian clouds. The inverse Burr’s expectation’s relationship with θ is clearly seen. For the Burr, most of the parameter cloud is a thin sheet, yellow on one side and red on the other.

Looking at a summary of results, shown in Table 10, the Bayesian process allows the fit for each family to affect the ground-up loss ratio minimally yet show similar leveraged effects on the aggregate stop loss. Also, even the families with worse fits were not as unreasonable as they were using maximum likelihood. Another key difference is in identifying the “best” family to use. Using maximum likelihood estimation, it was difficult to choose between the lognormal and the gamma distributions based on the goodness-of-fit. This was especially troubling as the effect of parameter risk was markedly different between the two. Using the Bayesian process the decision is clearer. While the WAIC metrics for both the hierarchical lognormal and hierarchical gamma are very close, so too are their effects on both the ground-up and aggregate losses. In hindsight, for the maximum likelihood method, it is almost as if the distortion caused by symmetry of the lognormal was balanced by the distortion caused by the extreme correlation of the gamma, leading to the similar AICc values. This is less of an issue with the Bayesian process, as the area of interest could be more fully investigated without being subject to the elliptical constraints.

Table 10.Goodness-of-fit effects
Family Maximum Likelihood Bayesian
AICc GU Effect ASL Effect WAIC GU Effect ASL Effect
Lognormal −20.11 −0.004% −1.97% −21.44 0.16% 26.09%
Gamma −20.04 0.23% 14.99% −21.32 0.088% 25.25%
Weibull −18.29 −0.66% 16.64% −19.38 0.0045% 34.63%
Inverse Burr −15.76 166,464.00% 59.46% −20.39 0.96% 44.02%
Burr −15.76 474,023,000.00% 99.08% −19.52 −0.28% 29.78%

5.2. Conclusions

Reviewing the three methods discussed, the bootstrap is an example of approximate Bayesian computation. Comparing the maximum likelihood and Bayesian techniques, while basic MLE may be simpler to explain, it cannot escape the “prison of ellipticity,” even when using log scale transformations of the parameters. With the distribution of the parameters being only asymptotically normal, and especially when dealing with small ratios of observations to parameters, MLE’s ellipticity prevents it from fully investigating potential parameter sets and causes it to generate illegal values if it is too close to a boundary condition. The Bayesian method’s ability to “trace out” a proper posterior based on the supplied data, and for the true Bayesian procedure to easily expressly consider dependence structures within the data and parameters, makes a strong case for actuaries to increase their use of Bayesian techniques when analyzing risk. In cases where the likelihood is difficult to construct, using an approximate Bayesian computation would seem a worthwhile endeavor.

For the specific data in this paper, the results of the MLE method are inferior to the Bayesian method. The lognormal and gamma models with similar goodness-of-fit metrics provide different outcomes, and the other families do not supply an acceptable fit. The Bayesian methods, especially the hierarchical models, provide clearer and more consistent indications as to the presence and magnitude of parameter risk. It seems clear that for this data set parameter risk plays a significant role, and estimates which do not contemplate it will understate the risk in the aggregate stop loss contract.

One area of future research would be in enhancing the MLE method. As discussed in Venter and Sahasrabuddhe (2012, §3.2.3), with few data points, the asymptotic properties of maximum likelihood estimation do not manifest. Their suggestion is to generate the parameters via a gamma distributions with the correlation structure of the multivariate normal. Using a normal copula with gamma marginals is one way to achieve this. Other research opportunities include comparing data sets with different properties and explicitly modeling a temporal component to reflect parameter risk resulting from changes over time.

Acknowledgments

The author wishes to thank Glenn Meyers, Andrew Gelman, Bob Carpenter, Ben Goodrich, Michael Betancourt, and the anonymous reviewers for their helpful comments and suggestions. Any errors in the paper are solely the author’s own.

References

Actuarial Standards Board. 2012. “Risk Evaluation in Enterprise Risk Management.” Technical Report 46. Actuarial Standards Board. http:/​/​www.actuarialstandardsboard.org/​pdf/​asop046_165.pdf.
Anscombe, F. J. 1973. “Graphs in Statistical Analysis.” The American Statistician 270 (1): 17–21. https:/​/​doi.org/​10.1080/​00031305.1973.10478966.
Google Scholar
Bååth, R. 2014. “Tiny Data, Approximate Bayesian Computation and the Socks of Karl Broman.” Publishable Stuff: Rasmus Bååth’s Research Blog. October 2014. http:/​/​www.sumsar.net/​blog/​2014/​10/​tiny-data-and-the-socks-of-karl-broman/​.
Beaumont, M. A., W. Zhang, and D. J. Balding. 2002. “Approximate Bayesian Computation in Population Genetics.” Genetics 1620 (4): 2025–35. https:/​/​doi.org/​10.1093/​genetics/​162.4.2025.
Google ScholarPubMed CentralPubMed
Burnham, K. P., and D. R. Anderson. 2002. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. 2nd ed. Springer Science+Business Media.
Google Scholar
Denwood, M. J. In press. “Runjags: An R Package Providing Interface Utilities, Model Templates, Parallel Computing Methods and Additional Distributions for MCMC Models in JAGS.” Journal of Statistical Software. http:/​/​runjags.sourceforge.net.
Google Scholar
Eddelbuettel, D., and R. François. 2011. “Rcpp: Seamless R and C++ Integration.” Journal of Statistical Software 400 (8): 1–18. https:/​/​doi.org/​10.18637/​jss.v040.i08.
Google Scholar
Geary, R. C. 1936. “The Distribution of ‘Student’s’ Ratio for Non-Normal Samples.” Supplement to the Journal of the Royal Statistical Society 30 (2): 178–84. https:/​/​doi.org/​10.2307/​2983669.
Google Scholar
Gelman, A., J. B. Carlin, H. S. Stern, D. B. Dunson, A. Vehtari, and D. B. Rubin. 2014. Bayesian Data Analysis. 3rd ed. Boca Raton, FL: CRC. https:/​/​doi.org/​10.1201/​b16018.
Google Scholar
Genz, A., F. Bretz, T. Miwa, X. Mi, F. Leisch, F. Scheipl, and T. Hothorn. 2014. Mvtnorm: Multivariate Normal and t Distributions. R package version 1.0-2. http:/​/​CRAN.R-project.org/​package=mvtnorm.
Google Scholar
Hoffman, M. D., and A. Gelman. 2014. “The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo.” Journal of Machine Learning Research 15:1593–1623. http:/​/​jmlr.org/​papers/​v15/​hoffman14a.html.
Google Scholar
Johnson, S. G. 2010. The NLopt Nonlinear-Optimization Package. http:/​/​ab-initio.mit.edu/​nlopt.
Google Scholar
Klugman, S. A., H. H. Panjer, and G. E. Willmot. 1998. Loss Models: From Data to Decisions. Wiley.
Google Scholar
Kruschke, J. K. 2015. Doing Bayesian Data Analysis: A Tutorial with R, JAGS, and Stan. 2nd ed. Boston: Academic Press.
Google Scholar
Melnick, E. L., and A. Tenenbein. 1982. “Misspecifications of the Normal Distribution.” American Statistician 360 (4): 372–73. https:/​/​doi.org/​10.1080/​00031305.1982.10483052.
Google Scholar
Plummer, M. 2003. “JAGS: A Program forAnalysis of Bayesian Graphical Models Using Gibbs Sampling.” In Proceedings of the Third International Workshop on Distributed Statistical Computing (DSC 2003), edited by K. Hornik, F. Leisch, and A. Zeileis. http:/​/​www.ci.tuwien.ac.at/​Conferences/​DSC-2003/​Proceedings/​Plummer.pdf.
Google Scholar
R Core Team. 2014. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. http:/​/​www.R-project.org/​.
Google Scholar
Rubin, D. B. 1984. “Bayesianly Justifiable and Relevant Frequency Calculations for the Applies Statistician.” Annals of Statistics 120 (4): 1151–72. http:/​/​projecteuclid.org/​euclid.aos/​1176346785.
Google Scholar
Spiegelhalter, D. J., N. G. Best, B. P. Carlin, and A. Van Der Linde. 2002. “Bayesian Measures of Model Complexity and Fit.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 640 (4): 583–639. https:/​/​doi.org/​10.1111/​1467-9868.00353.
Google Scholar
Stan Development Team. 2014a. Stan: A C++ Library for Probability and Sampling. Version 2.5. http:/​/​mc-stan.org/​.
Google Scholar
———. 2014b. Stan Modeling Language Users Guide and Reference Manual. Version 2.5. http:/​/​mc-stan.org/​.
Google Scholar
Turner, B. M., and T. Van Zandt. 2014. “Hierarchical Approximate Bayesian Computation.” Psychometrika 790 (2): 185–209. https:/​/​doi.org/​10.1007/​s11336-013-9381-x.
Google ScholarPubMed CentralPubMed
Venter, G. G., and R. V. Sahasrabuddhe. 2012. “A Note on Parameter Risk.” Casualty Actuarial Society E-Forum, no. 2 (Summer), 1–16. http:/​/​www.casact.org/​research/​dare/​index.cfm?fa=view%20abstrID=6879.
Google Scholar
Watanabe, S. 2013. “A Widely Applicable Bayesian Information Criterion.” Journal of Machine Learning Research 140 (1): 867–97. http:/​/​jmlr.org/​papers/​v14/​watanabe13a.html.
Google Scholar
Wickham, H. 2009. Ggplot2: Elegant Graphics for Data Analysis. New York: Springer. https:/​/​doi.org/​10.1007/​978-0-387-98141-3.
Google Scholar
Xie, Y. 2013. Dynamic Documents with R and Knitr. Boca Raton, FL: Chapman and Hall/CRC.
Google Scholar
Ypma, J. 2014. Nloptr: R Interface to NLopt. R package version 1.0.4. http:/​/​cran.r-project.org/​web/​packages/​nloptr/​index.html.
Google Scholar

Appendix A. Code

There are a number of cases where code was reused, differing only in the distribution being analyzed. In these cases, only one example will be brought. Where there is a fundamental difference, such as a different kind of graph or a different structure for the negative log-likelihood function, the individual code chunks will be shown.

A.1.1. Set-up

set.seed(63854)
library(ggplot2)
library(reshape2)
library(Rcpp)
library(nloptr)
library(mvtnorm)
library(scatterplot3d)

LogLR - c(0.5376, 0.4388, 0.3953, 0.6415, 0.5376, 0.4388, 0.244, 0.3488, 0.4786, 0.4388)
LR - exp(LogLR)
ASL - pmin(pmax(LR  0.725, 0), 0.025)
BayesData - list(LR  LR, N  length(LR))

sourceCpp("BootC4.cpp")

AICC - function(NLL, k, n) {
    k2 - k * 2
    return(2 * NLL  k2  k2 * (k  1)/(n  k  1))
}

WAIC - function(pointMatrix) {
    colVars - function(Matrix) {
        vars - Matrix[1, ]
        for (n in seq_along(vars)) vars[n] - var(Matrix[, n])
        return(vars)
    }
    lppd - sum(log(colMeans(pointMatrix)))
    pWAIC2 - sum(colVars(log(pointMatrix)))
    return(2 * (lppd  pWAIC2))
}

A.1.2. Bootstrap algorithm and analysis

Originally, the bootstrap code was written completely in R and took 36 minutes on an Intel i7-3740QM at 2.7Ghz running Windows 7 64bit with 8GB RAM. This is orders of magnitude faster than the VBA code of the original paper, which took about 8 hours. However, the R implementation itself was sped up by profiling the code and identifying which elements were taking the most time—the sample skew and overall row statistic calculations. These were rewritten in C using the Rcpp package (Eddelbuettel and François 2011), bringing the elapsed time to under two minutes! Rcpp does require that the user is able to compile C code; in the Windows environment, this usually requires Rtools. In the following sections, the R code actually used will be brought first, followed by the original ‘R’ code for the two time-consuming functions, followed by the substitute Rcpp-based C code used instead.

Used R Code
MuRange - sort(c(seq(1.549, 0.226, length.out  50), 0.45))
SigRange - seq(0.0055, 0.4345, length.out  79)
CloseCount - function(X, lower, upper) {
    return(sum(X[, 1]  upper[[1]]  X[, 1]  lower[[1]]  X[, 2]  upper[[2]]   X[, 2]  lower[[2]]  X[, 3]  upper[[3]]  X[, 3]  lower[[3]]))
}
VKBS - function(muR, sigR, perms  c(length(muR), length(sigR))) {
    numBlocks - perms[[1]] * perms[[2]]
    Counts - matrix(nrow  numBlocks, ncol  3)
    colnames(Counts) - c("mu", "sigma", "CloseCount")
    idx - 1
    for (i in seq_len(perms[[1]])) {
        MU - muR[i]
        for (j in seq_len(perms[[2]])) {
            Counts[idx, 1] - MU
            SIGM - Counts[idx, 2] - sigR[j]
            Variate - matrix(rlnorm(100000, MU, SIGM), ncol  10)
            Stats - RowStats_C2(Variate)
            Counts[idx, 3] - CloseCount(Stats, lower  c(0.6352, 0.0662, 0.29), upper            c(0.6477, 0.0762, 0.71))
            idx - idx  1
        }
    }
    return(Counts)
}

BST - system.time(BootResult - VKBS(muR  MuRange, sigR  SigRange))
BootStrapMinutes - round(BST[3]%/%60, digits  0)
BootStrapSeconds - round(BST[3]%%60, digits  0)
BRDF - data.frame(BootResult)
BRDFPos - subset(BRDF, CloseCount  0)
ValidPairs - dim(BRDFPos)[1]
MostLikely - BRDFPos[which.max(BRDFPos$CloseCount), ]
BSResults - cbind(BRDFPos$mu, BRDFPos$sigma, exp(BRDFPos$mu  BRDFPos$sigma^2/2), (LEV_LN(0.75, BRDFPos$mu, BRDFPos$sigma)  LEV_LN(0.725, BRDFPos$mu, BRDFPos$sigma)))
GU_O - exp(mean(LogLR)  var(LogLR)/2)
ASL_O - LEV_LN(0.75, mean(LogLR), sd(LogLR))  LEV_LN(0.725, mean(LogLR), sd(LogLR))
GU_BS_PR - drop(crossprod(BSResults[, 3], BRDFPos$CloseCount) / sum(BRDFPos$CloseCount))
ASL_BS_PR - drop(crossprod(BSResults[, 4], BRDFPos$CloseCount) / sum(BRDFPos$CloseCount))
BRGG - ggplot(BRDF)
Original R Code
SampSkew - function(x) {
    n - length(x)
    mu - mean(x)
    num - sum((x  mu)^3)/n
    den - (sum((x  mu)^2)/n)^1.5
    return(sqrt(n * (n  1))/(n  2) * num/den)
}
RowStats - function(X) {
    Means - rowMeans(X)
    SDs - apply(X, 1, sd)
    Skews - apply(X, 1, SampSkew)
    return(cbind(Means, SDs, Skews))
}
Replacement C Code
# include Rcpp .h
# include math .h
using namespace Rcpp ;

// [[ Rcpp :: export ]]
double SampSkew_C ( NumericVector X) {
    int n  X. size ();
    double Mu  mean (X);
    NumericVector XM  X  Mu;
    NumericVector D1  XM * XM;
    NumericVector N1  D1 * XM;
    double N2  sum (N1) / n;
    double D1a  sum (D1) / n;
    double D2  sqrt (D1a * D1a * D1a );
    double P  sqrt (n * (n  1)) / (n  2);
    return P * N2 / D2;
}

// [[ Rcpp :: export ]]
NumericMatrix RowStats_C2 ( NumericMatrix X) {
    int nrow  X. nrow ();
    int ncol  X. ncol ();
    double n1  ncol  1.0;
    double P  ncol * sqrt (n1) / ( ncol  2.0);
    NumericMatrix Results (nrow , 3);
    for (int i  0; i  nrow ; i) {
        double M1  0.0;
        double M2  0.0;
        double M3  0.0;
        for (int j  0; j  ncol ; j) {
            double delta  X(i, j)  M1;
            double delta_j  delta / (j  1);
            double T1  delta * delta_j * j;
            M1  delta_j ;
            M3  (T1 * delta_j * (j  1)  3 * delta_j * M2 );
            M2  T1;
        }
        Results (i, 0)  M1;
        Results (i, 1)  sqrt (M2 / n1 );
        Results (i, 2)  P * M3 / sqrt (M2 * M2 * M2 );
    }
    return Results ;
}

A.1.3. Bootstrap graphs

Contour graph
BRGG  stat_contour(aes(x  sigma, y  mu, z  CloseCount, fill  . . level. .), geom  "polygon")  scale_fill_gradient(low  "red", high  "yellow")  coord_cartesian(xlim  c(0.05, 0.25), ylim  c(0.85, 0.05))  scale_y_continuous(expression(mu))  scale_x_continuous(expression(sigma))

A.2.1. First example likelihood surface

x - y - seq(1, 2, 0.1)
f1 - function(x, y) {
    4 * (x  1.5)^2  4 * (y  1.5)^2
}
f2 - function(x, y) {
    0.5 * (x  1.5)^2  0.5 * (y  1.5)^2
}
zf1 - outer(x, y, f1)
zf2 - outer(x, y, f2)
persp(x, y, zf1, theta  45, phi  30, shade  0.1, col  "orangered", xlim  c(1, 2), ylim  c(1, 2), zlim  c(0, 1.5), zlab  "Likelihood")

A.2.2. Maximum likelihood functions

Lognormal

Two parameter representative example:

NLL_LN - function(pars, X) {
    m - pars[[1]]
    s - pars[[2]]
    return(sum(log(X)  log(s)  0.5 * log(2 * pi)  0.5 * ((log(X)  m)/s)^2))
}
GH_LN - deriv3((log(X)  log(s)  0.5 * log(2 * pi)  0.5 * ((log(X)  m)/s)^2), c("m", "s"), function(m, s, X) NULL)
NLLG_LN - function(pars, X) {
    m - pars[[1]]
    s - pars[[2]]
    colSums(attr(GH_LN(m, s, X), "gradient"))
}
NLLH_LN - function(pars, X) {
    m - pars[[1]]
    s - pars[[2]]
    colSums(attr(GH_LN(m, s, X), "hessian"))
}
ULEV_LN - function(mu, sigma) {
    return(exp(mu  sigma^2/2))
}
LEV_LN - function(x, mu, sigma) {
    Z1 - (log(x)  mu  sigma^2)/sigma
    Z2 - (log(x)  mu)/sigma
    return(ULEV_LN(mu, sigma) * pnorm(Z1)  x * pnorm(Z2, lower.tail  FALSE))
}
Inverse Burr

Three parameter representative example:

NLL_IB - function(pars, X) {
    t - pars[[1]]
    g - pars[[2]]
    q - pars[[3]]
    return(sum(log(t)  log(g)  g * t * log(X/q)  log(X)  (t  1) * log1p((X/q)^g)))
}
GH_IB - deriv3((log(t)  log(g)  g * t * log(X/q)  log(X)  (t  1) * log((1  (X/q)^g))), c("t", "g", "q"), function(t, g, q, X) NULL)
NLLG_IB - function(pars, X) {
    t - pars[[1]]
    g - pars[[2]]
    q - pars[[3]]
    colSums(attr(GH_IB(t, g, q, X), "gradient"))
}
NLLH_IB - function(pars, X) {
    t - pars[[1]]
    g - pars[[2]]
    q - pars[[3]]
    colSums(attr(GH_IB(t, g, q, X), "hessian"))
}
ULEV_IB - function(t, g, q) {
    return(exp(log(q)  lgamma(t  1/g)  lgamma(1  1/g)  lgamma(t)))
}
LEV_IB - function(X, t, g, q) {
    u - ((X/q)^g)/(1  ((X/q)^g))
    First - pbeta(u, t  1/g, 1  1/g)
    Second - 1  u^t
    return(ULEV_IB(t, g, q) * First  X * Second)
}
GenIB - function(quantile, t, g, q) {
    P1 - quantile^(1/t)
    return(((P1/(1  P1))^(1/g)) * q)
}

A.2.3. Maximum likelihood evaluation

Lognormal

Two parameter representative example:

MLEfit_LN - nloptr(c(1, 1), eval_f  NLL_LN, eval_grad_f  NLLG_LN, X  LR, lb  c(Inf, 0), ub  c(Inf, Inf), opts  list(algorithm  "NLOPT_LD_LBFGS", maxeval  10000, xtol_rel  1e-12, ftol_rel  1e-12))
VCoV_LN - chol2inv(chol(NLLH_LN(MLEfit_LN$solution, LR)))
SDs_LN - sqrt(diag(VCoV_LN))
ParCor_LN - cov2cor(VCoV_LN)
AICC_LN - AICC(MLEfit_LN$objective, 2, length(LR))
Inverse Burr

Three parameter representative example:

MLEfit_IB - nloptr(c(1, 5, 2), eval_f  NLL_IB, eval_grad_f  NLLG_IB, X  LR, lb  c(0, 0, 0), ub  c(Inf, Inf, Inf), opts  list(algorithm  "NLOPT_LD_LBFGS", maxeval  10000, xtol_rel  1e-12, ftol_rel  1e-12))
VCoV_IB - chol2inv(chol(NLLH_IB(MLEfit_IB$solution, LR)))
SDs_IB - sqrt(diag(VCoV_IB))
ParCor_IB - cov2cor(VCoV_IB)
AICC_IB - AICC(MLEfit_IB$objective, 3, length(LR))

A.2.4. Stochastic simulation with MLE-based parameter risk

MLE_PR_Simulate - function(n, pars, sigma) {
    Simulation - matrix(nrow  n, ncol  length(pars))
    Simulation - rmvnorm(n, mean  pars, sigma  sigma)
    return(Simulation)
}
Lognormal simulation

Two parameter representative example:

MLESimulation_LN - MLE_PR_Simulate(n  1000000, pars  MLEfit_LN$solution, sigma  VCoV_LN)
LN_GU_Sim - rlnorm(length(MLESimulation_LN[, 1]), meanlog  MLESimulation_LN[, 1], sdlog  MLESimulation_LN[, 2])
LN_AGG_Sim - pmin(0.025, pmax(LN_GU_Sim  0.725, 0))
GU_MLE_PR_LN - mean(LN_GU_Sim, na.rm  TRUE, trim  0.001)
ASL_MLE_PR_LN - mean(LN_AGG_Sim, na.rm  TRUE, trim  0.001)
MLE_LN_DF - data.frame(MLESimulation_LN)
names(MLE_LN_DF) - c("mu", "sigma")
Inverse Burr simulation

Three parameter representative example:

MLESimulation_IB - MLE_PR_Simulate(n  1000000, pars  MLEfit_IB$solution, sigma  VCoV_IB)
IB_GU_Sim_Raw - runif(1000000, 0, 1)
IB_GU_Sim - GenIB(IB_GU_Sim_Raw, MLESimulation_IB[, 1], MLESimulation_IB[, 2], MLESimulation_IB[, 3])
IB_AGG_Sim - pmin(0.025, pmax(IB_GU_Sim  0.725, 0))
GU_MLE_PR_IB - mean(IB_GU_Sim, na.rm  TRUE, trim  0.001)
ASL_MLE_PR_IB - mean(IB_AGG_Sim, na.rm  TRUE, trim  0.001)

A.2.5. MLE graphs

MLE Lognormal Contour
MLE_LN_G - ggplot(MLE_LN_DF)
MLE_LN_G  stat_density2d(aes(x  sigma, y  mu, fill  . .level. .), geom  "polygon")  scale_fill_gradient(low  "red", high  "yellow")  scale_y_continuous(expression(mu))  scale_x_continuous(expression(sigma))  stat_density2d(aes(x  sigma, y  mu), colour  "black")

A.3. Bayesian Analysis

A.3.1. JAGS

Simple Lognormal Model
var N, LR[N], mu.post, sigma.post, tau.post, LR.post, ASL.post, PointPosteriors [N];
model {
    for (year in 1:N) {
        LR[ year ]  dlnorm (mu.post, tau.post)
    }
    mu.post  dnorm (0, 0.25)
    sigma.post  dunif (0, 1)
    tau.post - pow( sigma.post, 2)
    LR.post  dlnorm (mu.post, tau.post)
    ASL.post - min (0.025, max(LR. post  .725 , 0))
    for (i in 1:N) {
        PointPosteriors [i] - dlnorm (LR[i], mu.post, tau.post)
    }
}
Simple Lognormal Analysis
initsLN - function(chain) {
    list(mu.post  rnorm(1, 0, 2), sigma.post  runif(1, 0, 1), .RNG.seed  chain^2  1, .RNG.name  "base::Mersenne-Twister")
}
LN_Model - run.jags(model  "Bayes_LN.bug", monitor  c("mu.post", "sigma.post", "LR.post", "ASL.post", "PointPosteriors"), data  BayesData, n.chains  5, plots  TRUE, psrf.target  1.01, check.stochastic  TRUE, modules  c("bugs", "glm"), method  "interruptible", adapt  25000, burnin  25000, sample  10000, thin  25, inits  initsLN)
Comb_LN - combine.mcmc(LN_Model)
BayesGU_LN - LN_Model$summary$statistics[2, 1]
BayesASL_LN - LN_Model$summary$statistics[1, 1]
BayesWAIC_LN - WAIC(Comb_LN[, 4:13])
BayesParCor_LN - LN_Model$crosscorr[3, 14]
BayesDF_LN - data.frame(Comb_LN[, 3], Comb_LN[, 14])
names(BayesDF_LN) - c("mu", "sigma")

A.3.2. Stan

Simple Lognormal Model
data {
    int  lower  0 N; // number of years
    vector  lower  0.0 [N] LR; // loss ratios
}
parameters {
    real mu; // prior for mu
    real  lower  0.0  sigma ; // non - negative prior for sigma
}
model {
    mu  normal (0.0 , 2.0);
    sigma  uniform (0.0 , 1.0);
    LR  lognormal (mu , sigma );
}
generated quantities {
    real LR_post ; // distribution of LR based on posterior parameters
    real ASL_post ; // corresponding ASL
    vector [N] PointPosteriors ; // log pointwise predictive density
    for (i in 1:N) {
        PointPosteriors [i] - exp( lognormal_log (LR[i], mu , sigma ));
    }
    LR_post - lognormal_rng (mu , sigma ); // stochastic observation of LR
    ASL_post - fmin (0.025 , fmax ( LR_post  0.725 , 0.0));
}
Hierarchical Lognormal Model
data {
    int  lower  0 N; // number of years
    vector  lower  0.0 [N] LR; // loss ratios
}
parameters {
    vector [2] mu; // multivariate normal (MVN ) prior mean : implied (0 ,0)
    corr_matrix [2] Sigma_corr ; // MVN prior correlation ( implied uniform )
    vector  lower  0.0 [2] Sigma_scale ; // prior scale for cov: implied (0 ,0)
    vector [2] Pars ; // correlated lognormal parameter vector
}
transformed parameters {
    real mu_post ;
    real  lower  0.0  sigma_post ;
    mu_post - Pars [1];
    sigma_post - exp( Pars [2]); // ensure non - negativity
}
model {
    matrix [2, 2] Sigma ; // will become MVN prior covariance
    Sigma - diag_matrix ( Sigma_scale ) * cholesky_decompose ( Sigma_corr );
    Pars  multi_normal_cholesky (mu , Sigma ); // faster to use cholesky
    LR  lognormal ( mu_post , sigma_post );
}
generated quantities {
    real LR_post ; // distribution of LR based on posterior parameters
    real ASL_post ; // corresponding ASL
    vector [N] PointPosteriors ; // log pointwise predictive density
    for (i in 1:N) {
        PointPosteriors [i] - exp( lognormal_log (LR[i], mu_post , sigma_post ));
    }
    LR_post - lognormal_rng ( mu_post , sigma_post ); // stochastic observation of LR
    ASL_post - fmin (0.025 , fmax ( LR_post  0.725 , 0.0));
}
Lognormal Analysis
LNP_S - stan(file  "Bayes_LN_Plus2.stan", data  BayesData, pars  c("mu_post", "sigma_post", "LR_post", "ASL_post", "PointPosteriors"), iter  20200, warmup  200, thin  1, chains  5, seed  82, refresh  1, verbose  FALSE)
LNP_S_E - extract(LNP_S)
StanGU_LNP - mean(LNP_S_E$LR_post)
38
StanASL_LNP - mean(LNP_S_E$ASL_post)
StanWAIC_LNP - WAIC(LNP_S_E$PointPosteriors)
StanDF_LNP - data.frame(LNP_S_E$mu_post, LNP_S_E$sigma_post)
names(StanDF_LNP) - c("mu", "sigma")
StanCor_LNP - cor(StanDF_LNP)["mu", "sigma"]
Inverse Burr Model

Example of manually creating distribution functions

data {
    int  lower  0 N; // number of years
    vector  lower  0.0 [N] LR; // loss ratio
}
parameters {
    real  lower  0.0  tau ;
    real  lower  0.0  gamma ;
    real  lower  0.0  theta ;
}
transformed parameters {
    vector  lower  0.0 [N] U;
    U - LR / theta ;
}
model {
    tau  uniform (0.0 , 100.0);
    gamma  uniform (0.0 , 100.0);
    theta  uniform (0.0 , 1.0);
    for (i in 1:N) {
        increment_log_prob (log( gamma * tau)  multiply_log (( gamma * tau), U[i])  fma     (( tau  1), log1p (pow (U[i], gamma )), log (LR[i ])));
    }
}
generated quantities {
    real LR_post ;
    real ASL_post ;
    real  lower  0.0 , upper  1.0  Q; // quantile for inversion
    real  lower  0.0  P1; // Reused value
    vector [N] PointPosteriors ;
    for (i in 1:N) {
        PointPosteriors [i] - exp(log(tau)  log( gamma )  multiply_log (( gamma * tau ), U[i])  fma (( tau  1), log1p (pow(U[i], gamma )), log(LR[i ])));
    }
    P1 - pow( uniform_rng (0.0 , 1.0) , inv (tau )); // using inversion
    LR_post - pow (( P1 / (1  P1 )), inv ( gamma )) * theta ;
    ASL_post - fmin (0.025 , fmax ( LR_post  0.725 , 0.0));
}

A.4. Conclusion and findings

A.4.1. Superimposed contour plot

BRGG  stat_contour(aes(x  sigma, y  mu, z  CloseCount, colour  "Bootstrap"), alpha  0.4, size  1)  scale_y_continuous(expression(mu))  scale_x_continuous(expression(sigma))  stat_density2d(aes(x  sigma, y  mu, colour  "MLE"), alpha  0.4, size  1, data  MLE_LN_DF)  stat_density2d(aes(x  sigma, y  mu, colour  "Bayes (Simple)"), alpha  0.6, size  1, data  StanDF_LN)  theme(legend.title  element_blank())

A.4.2. Inverse Burr scatter plot (MLE)

scatterplot3d(MLESimulation_IB, pch  ".", xlab  expression(tau), ylab  expression(gamma), zlab  expression(theta), highlight.3d  FALSE, cex.lab  2, xlim  c(10, 100), ylim  c(20, 100), zlim  c(0, 1))

A.4.3. Color-coded inverse Burr scatter plot (Bayesian)

scatterplot3d(StanDF_IB, pch  ".", xlab  expression(tau), ylab  expression(gamma), zlab  expression(theta), highlight.3d  FALSE, cex.lab  2, xlim  c(10, 100), ylim  c(20, 100), zlim  c(0, 1), color  GUColorPalette_S_IB, angle  5)

A.5. Session info

## R version 3.2.3 Patched (2015-12-13 r69768)
## Platform: x86_64-w64-mingw32/x64 (64-bit)
## Running under: Windows 7 x64 (build 7601) Service Pack 1
##
## locale:
## [1] LC_COLLATEEnglish_United States.1252
## [2] LC_CTYPEEnglish_United States.1252
## [3] LC_MONETARYEnglish_United States.1252
## [4] LC_NUMERICC
## [5] LC_TIMEEnglish_United States.1252
##
## attached base packages:
## [1] stats    graphics    grDevices   utils   datasets    methods base
40
##
## other attached packages:
## [1] rstan_2.8.2  inline_0.3.14   runjags_2.0.3-1
## [4] rjags_4-4    coda_0.18-1 lattice_0.20-33
## [7] scatterplot3d_0.3-36 mvtnorm_1.0-3   nloptr_1.0.4
## [10] Rcpp_0.12.2 reshape2_1.4.1  ggplot2_2.0.0
## [13] knitr_1.11
##
## loaded via a namespace (and not attached):
## [1] magrittr_1.5 munsell_0.4.2   colorspace_1.2-6    highr_0.5.1
## [5] stringr_1.0.0    plyr_1.8.3  tools_3.2.3 parallel_3.2.3
## [9] grid_3.2.3   gtable_0.1.2    digest_0.6.8    gridExtra_2.0.0
## [13] formatR_1.2.1   codetools_0.2-14    evaluate_0.8    stringi_1.0-1
## [17] scales_0.3.0    stats4_3.2.3

  1. The paper, formulæ, R output, and images have been generated using knitr (Xie 2013).

  2. Contour plots generated using ggplot2 (Wickham 2009).

  3. Optimization performed using the nloptr (Ypma 2014) interface to the NLOPT library (Johnson 2010).

  4. Multivariate normal simulation performed using the mvtnorm package for R (Genz et al. 2014).

  5. This is actually a consequence of a known property of the normal distribution in that its sample mean and sample variance are independent (Geary 1936).

  6. Unless otherwise noted, all distributions follow the parameterization in Appendix A of Klugman, Panjer, and Willmot (1998).

  7. The actual criterion being used is the Akaike Information Criteria with small-sample bias correction, thus the second “c” (Burnham and Anderson 2002, 66).

  8. The runjags package (Denwood, in press) was used to interface between R and JAGS.

  9. These models were run in Stan instead of JAGS, for reasons which will be explained in Section 4.3.

  10. The hierarchical structure of the lognormal model was investigated prior to the simple models of the other distributions, which explains why the remaining simple models in Section 4.2 were built in Stan instead of JAGS. The original lognormal JAGS model remains to demonstrate that both types of sampling converge to very similar results.

  11. For a very clear, if informal, explanation and description of basic ABC, the interested reader is directed to Bååth (2014).