PEBELS: Policy Exposure Based Excess Loss Smoothing

undefined

1. Introduction

Anyone who has been responsible for property pricing has faced the issue of how to incorporate experience from very infrequent but very large claims into their analysis. This is particularly an issue for non-weather losses for which modeled average annual losses are not available. While it is relatively easy to determine an aggregate provision for non-catastrophe large losses (NCLL) for a large credible property book (Werner and Modlin 2010), it is far less obvious how to determine an appropriate provision for a smaller, less credible, subset of such a book, e.g. a specific program in a specific state.

The actuarial literature is silent on how to produce such a provision even though very infrequent but very large NCLLs drive a disproportionate amount of total loss in property lines (Hurley 1954). Determining appropriate NCLL provisions for smaller subsets of a larger book is an important step when developing rate level indications specifically for these subsets. PEBELS was developed as a method for producing such provisions by leveraging insured value data (which, thanks to the prevalence of catastrophe modeling, continues to become increasingly accurate and available), exposure curve theory (which was developed for pricing property per risk reinsurance treaties), and the aggregate NCLL provision for the more credible aggregate book (which is routinely determined using published methods).

The method given in this paper was designed for use in producing property rate level indications for primary insurers (personal or commercial). It will be demonstrated that PEBELS is actually a generalization of per-risk reinsurance exposure rating techniques in the published actuarial literature, which allows further refinement of existing reinsurance pricing techniques and facilitates the development of additional exposure-based ratemaking applications for both primary insurers and reinsurers. Furthermore, despite the method being developed specifically for use with non-catastrophe large loss experience, it will be shown that the method is equally applicable for catastrophe ratemaking applications given appropriate exposure curve assumptions.

1.1. Research context

PEBELS was born of the practical problem described above. Although the aggregate NCLL provision for an entire property book was available with full credibility, similar provisions for subsets of the book by program and state had very low credibility. Furthermore, it was clear by inspection of the underlying exposures in some of these smaller, non-credible subsets that their fundamental exposure to NCLL varied dramatically. Since the business imperative was to develop reliable indications at the program and state level, it became necessary to determine reliable NCLL provisions at this level.

The first step undertaken was a literature review, with the intention of adopting a previously published method for determining the NCLL provision. However, none was found. Hurley (1954) and Werner and Modlin (2010) provide methods for determining the overall NCLL provision for an entire book, either explicitly or implicitly, but that issue had already been resolved in this application. A two-sided percentile approach to excess loss loading was also identified in Dean et al. (1998), but it was also designed to smooth experience for an aggregate book. What was needed was a way to determine appropriate NCLL provisions by program and state even when such segments had extremely low credibility.

A second step was to expand the literature review beyond that available for primary property ratemaking. The literature for developing excess loss provisions in liability lines was much more developed than that for property lines. However, this was also of little help in solving the problem since the ground-up severity distribution of liability risks was generally assumed similar regardless of whether the insured selects a $1M limit or a $10M limit (Miccolis 1977), while this is far from the case with property insurance. In property insurance the insured value (loosely analogous to the “limit” of a liability policy) is strongly correlated with the size and value of the exposure. Thus the underlying severity distribution of the $1M policy is likely to be much different than that of the $10M policy. This distributional dependence on insured values will be formulated in terms of exposure curves in Section 3.

Continuing to expand the literature review to applications in reinsurance pricing led to the most relevant methods and theory, though these were not directly applicable to the problem at hand. Clark (1996) and Ludwig (1991) were the most significant, as they laid out the state of the art for exposure rating for property per risk reinsurance which became the basis for deriving PEBELS. Bernegger (1997) afforded valuable insight into options available to easily generate plausible exposure curves and how to vary these curves between heterogeneous risks. Most notably, Bernegger provided specific analytical curves that are sufficient for a very simple implementation of PEBELS.

Finally, a survey of current methods was conducted to determine whether any unpublished methods in common practice could be adapted to solve this problem. Commonly used methods fell into two broad categories: (1) empirical methods, and (2) allocation methods.

Empirical methods, which have been extensively used by ISO (Insurance Services Office), directly compute excess loss factors as total loss to loss below a specified threshold. The data are segmented as desired (in the example given above, this would be by program and state, while ISO’s commercial property filings have historically segmented by construction and protection classes). In addition, the data are further segmented by insured value interval. Segmenting the excess loss factor estimates by insured value improves estimates by partially controlling for bias in the empirical estimate from the distributional dependence on the insured value noted above. The main challenge with this method is process variance. Even with ISO’s massive volume of data, it had to make two adjustments to manage the extensive volatility in its commercial property analysis: (1) it used 10 years of experience in computing excess loss factor estimates (twice as much as it used in the experience period for rate level indications), and (2) it used the fitted values from curves fitted to the excess loss factor estimates rather than the estimates themselves as the large loss provisions in their rate level indications.

Large process variance in our data was apparent from the fact that the empirical excess loss factor estimates even at the state level (before subdividing by program or insured value interval) were extremely volatile. In fact, this was the reason a new method for determining excess loss provisions was needed. The fact that ISO with all of its industry data had to double its experience period and use fitted curves to stabilize their results only reinforced the conclusion to search for a more stable approach.

Another obstacle to using this method was the presence of mix shifts. ISO’s use of an extended experience period is reasonable only to the extent the implicit assumption that the industry portfolio is relatively stable over the ten year large loss experience period is reasonable. While it is plausible to assume this is true for bureau data which roughly correspond to the industry’s total data, it is far less reasonable to assume that any single carrier’s mix of business is stable for such a long period of time. Furthermore, it was well known that the book under consideration had experienced significant mix shifts over the last several years.

Although it is tempting to add experience from additional years to increase data volume, we must be cognizant that adding older years of historical data will not improve our loss projection when the historical book of business which produced that experience is not representative of the prospective book of business being rated. This phenomenon is demonstrated by Mahler (1990) in his study which concluded that using additional years of data when exposure risk characteristics are known to be shifting can actually decrease the predictive accuracy of the resulting projections.

Finally, allocation methods were considered where the goal was to allocate the NCLL provision for a large credible property book down to the level of program and state using a “reasonable” allocation base. This approach was intuitively appealing because it was simple to explain, easy to implement, and it tied directly to the credible overall NCLL provision of the total book of business under consideration. Furthermore, it was believed that an appropriate exposure base would yield stable results and control for mix shifts. Thus it was decided to use the allocation approach.

However, even though we had decided to pursue this approach, it was not clear what a “reasonable” allocation base would be. Given the intention to allocate this provision down to a level where there was little credibility and large heterogeneity in underlying exposure to NCLL, it was critical to develop a reliably predictive allocation base.

Taking the survey one step further, practitioners were interviewed as to the allocation bases in current use and their satisfaction with each. Allocation bases in common usage were: (1) loss (either total or capped below a specified threshold) and (2) earned premium. Practitioners surveyed were generally aware that neither of these bases were particularly satisfactory, the reasons for which will be elaborated on in Section 2.1.

Section 2 continues where Section 1.1 ends by demonstrating problems with the allocation bases in common usage. It goes on to describe issues with insured value which was the first unique allocation base explored, and defines PEBELS. Section 3 provides critical background on exposure curves which are the backbone of any practical PEBELS implementation. Section 4 explains the theory behind the many generalizations to traditional per risk reinsurance pricing theory that PEBELS relies on to make accurate estimates of excess loss exposure. Section 5 focuses on applications of PEBELS in catastrophe modeling, predictive modeling, and per risk reinsurance pricing, and ends with a discussion of practical issues that must be grappled with to successfully implement a PEBELS analysis.

2. Survey of methods

2.1. Allocation bases in common usage

The exhibits below were created based on simulated data from 10,000 hypothetical homeowners insurance exposures for a hypothetical insurer who writes homeowners business in three states (X, Y and Z) and in three programs: one for each of Barns, Houses and Estates. NCLL exposure is assumed identical by state, but is assumed to vary by program.

State X and Y are not catastrophe exposed and are assumed to have identically distributed rates; State Z is catastrophe exposed and is assumed to have 50% higher rates than States X and Y on average to compensate for this exposure. Barns are assumed to be small structures with insured values not exceeding $25,000, Houses are assumed to be single-family dwellings with insured values not exceeding $500,000, and Estates are considered to be large luxury dwellings with insured values not exceeding $10,000,000. The total exposures are equally distributed among States X, Y and Z. Houses comprise 90% of the exposures while Barns and Estates each comprise 5%. Ultimate losses at prospective levels for these exposures were simulated for these risks using loss distributions inferred from exposure curves assumed for each program. In each of the exhibits below, loss amounts in excess of $100,000 are considered “excess” and the overall NCLL provision for the entire book is defined as the total excess loss during the experience period, which is $16,920,439 (out of $23,172,176 in total loss) based on the simulation described above.

The actual simulated excess loss experience for this book by state and program is summarized in Table 1 below.

It can be immediately inferred from the data that not every cell can be fully credible. There are large differences between House and Estate NCLL experience by state, which we would not expect a priori since our assumptions imply that we have the same expected NCLL in each state and in each program. This is the motivation for allocating or “smoothing” the total experience as opposed to relying solely on historical results. Our first attempt at the allocation method uses losses capped at $100,000 as a proxy for NCLL exposure. The results are summarized in Table 2.

This first attempt suffers from many problems. The first problem is that it allocates NCLL to the Barns Program (because Barns generate losses below $100,000). However, since no Barns have insured values over $25,000, these exposures are not able to produce losses in excess of the $100,000 threshold and thus should have $0 allocated to them. This is the first red flag that capped loss is not an appropriate proxy for NCLL exposure. Another issue is that the allocated provision for Houses varies quite a bit, which is unexpected given that we are assuming that each state has the same expected NCLL exposure on average. Finally, Estates seem to be allocated much less than Houses, which seems wrong since Estates generated most of the actual excess losses. In short, this allocation base does not appear to be appropriately correlated with NCLL exposure.

A second closely related attempt is to allocate NCLL based on losses in excess of the $100,000 threshold. The results of this approach are summarized in Table 3.

The problem with the results of this allocation base is that it is numerically equal to the actual NCLL in Table 1, which we already decided had insufficient credibility. This implies that the use of total losses which is the sum of capped and excess losses will yield a result between that of the actual NCLL and the NCLL allocated using capped losses, both of which we have identified as undesirable options.

Searching for a more stable base leads us to earned premium. Table 4 summarizes the NCLL allocation based on earned premium.

As expected, these NCLL allocations are much more stable. However, we are back to allocating NCLL to the Barn program. An even more ominous problem is that we are systematically biased towards allocating more NCLL exposure to State Z. Recall that rates in State Z are assumed to be 50% higher than States X and Y to compensate for catastrophe exposure, even though all three states have the same expected NCLL exposure.

While we could achieve a satisfactory result in the example above by adjusting the premiums from State Z, that is only possible due to our simplistic 50% assumption. In practice, it is much harder to identify, quantify and adjust for the many considerations that would bias earned premium as a measure of NCLL exposure. Frequency of low severity claims and rate adequacy are prominent examples of such potential biases.

2.2. Insured value

Having exhausted the traditionally used allocation bases, insured value was considered as a potential allocation base. Historically, insured value data tended to be poorly captured or otherwise unavailable because it is not reported on financial statements. However, given the increasing reliance of insurers on catastrophe modeling, both the availability and quality of insured value data has dramatically increased in recent years. Interestingly, while it was commonly understood that insured value is highly predictive of catastrophic loss potential, the fact that it was also highly predictive of non-catastrophe large loss potential has gone largely unnoticed. This observation is fundamental to the formulation of PEBELS given in Section 2.3. Table 5 below summarizes the NCLL allocation based on insured value.

Aside from the fact that we are again allocating NCLL to Barns, this base seems to be a marked improvement in terms of stability and the proportion of NCLL allocated to Estates versus Houses.

A small modification that would alleviate the non-zero allocation to Barns would be to allocate based on layer insured value defined as the amount of insured value in the exposed layer. For example, in the tables above, the layer of interest is from $100,000 to infinity, so a barn with insured value of $25,000 would have a layer insured value of $0, while a $300,000 house would have a layer insured value of $300,000 − $100,000 = $200,000. Similarly a $5,000,0000 estate will have a layer insured value of $4,900,000. Table 6 summarizes the NCLL allocation based on layer insured value.

At this point it seems that all obvious allocation issues have been resolved. Furthermore, there is no doubt that NCLL exposure is strongly dependent on layer insured value. However, there remains a subtle issue as to whether the allocation between Houses and Estates is appropriate. Using layer insured value as the allocation base implies that the potential for loss in the layer from $100,000 to $200,000 on a $500,000 house contributes the same amount of NCLL exposure as the layer from $9,900,000 to $10,000,000 on a $10,000,000 estate. Is that “reasonable” to assume?

Intuitively, it seems far more likely that a $500,000 single-family dwelling will experience a partial loss of 40% ($200,000 / $500,000) or more than that a $10,000,000 estate will suffer a total loss. This is because:

• Total losses are less common than smaller, partial losses.

• Larger losses, as measured by the ratio of insured loss over insured value, become less likely as the insured value of the property increases.

The first bullet follows from the observation that people tend to put out the fire, or otherwise stop whatever damage is being incurred. The second bullet is a bit more subtle, but can be conceptualized in terms of how “spread-out” the property exposure is.

Barns are not very “spread-out” at all. The chances of a total loss to a barn given a fire is almost 100% (the barn would likely be engulfed in the time that it would take to detect the fire). At the other extreme, college campuses are highly “spread-out.” A fire is unlikely to cause damage to a large proportion of the campus since it will almost certainly be localized to a single building, or in extreme cases it may spread to a few nearby buildings before the fire is contained. Even extreme catastrophes are unlikely to totally destroy all the buildings on a campus. Thus, given a loss to a college campus the loss is very likely to be a small percentage of the total insured value.

2.3. The formulation of PEBELS

PEBELS, or policy exposure based excess loss smoothing, is based on the notion that exposure to excess loss should be directly computed based on the characteristics of the policy itself. A technique was devised based on a generalization of the traditional per risk reinsurance exposure rating algorithm to directly quantify the exposure to excess loss for a given policy which is defined as the policy exposure based excess loss (PEBEL) for that policy. When PEBEL is taken as the base for allocating or “smoothing” aggregate NCLL we call that the PEBELS method of allocating excess loss.

For ease of illustration, the general formulation of PEBEL for the i^th policy is copied below from Section 4.1 where it is derived,

$$P_{E B E L_{i}}=P_{i} * E L R_{i} * E F_{i} \text {, where } \tag{4.1}$$

1. P_i is the premium of the i^th policy,

2. ELR_i is the expected loss ratio, which is assumed to be constant for all policies (for now),

3. EF_i = the proportion of total loss cost expected in the excess layer.

Note that there is no theoretical reason why PEBEL_i could not be used as a direct estimate of NCLL for a given policy. However, in practice it is preferable to use it as an allocation base because (1) we are assuming that actual NCLL is fully credible at the aggregate level, which makes it desirable for the sum of the NCLL estimates for all segments to equal the aggregate NCLL, and (2) using $\text{PEBEL}_i$ directly as our estimate of NCLL implies we have full confidence in the estimate from Equation (4.1), which would require a great deal of precision in specifying inputs as will be demonstrated in the following sections.

The balance of this paper will develop the theory and intuition behind Equation (4.1), as well as the practical considerations that must be addressed to ensure a reasonable NCLL allocation using PEBELS. The emphasis will be on understanding the many complex dynamics of the property excess loss distributions by policy, and how PEBELS can be leveraged to reflect these dynamics leading to refined policy level NCLL estimates.

2.4. Property per risk reinsurance exposure rating

Exposure rating for high property loss layers has been common in reinsurance pricing since 1963 when Ruth Salzmann published a study (1963) using building losses from fire claims on a book of homeowners policies to quantify the relationship between size of loss and insured value. This study was widely utilized in reinsurance pricing despite its deliberately narrow scope. Among the results of Salzmann’s work were the first exposure curves. Ludwig (1991) greatly expanded on Salzmann’s work by considering perils other than just fire, first party coverages other than just building, and commercial property exposures.

Clark (1996) states in his study note on reinsurance pricing that “the exposure rating model is fairly simple, but at first appears strange as nothing similar is found on the primary insurance side,” although no implication is made that something similar could not exist on the primary insurance side. He then goes on to produce an example of how a reinsurer might use exposure rating in practice which is reproduced in Table 7 for background on this pricing technique.

Clark provided an illustrative exposure curve for the purpose of the example. Note that column (5) develops the exposure factor using that exposure curve. The next section is an introduction to practical considerations for selecting and using exposure curves.

3. Exposure curve background

3.1. Analytical treatment

An exposure curve, G(x), gives the proportion of the total loss cost at or below a specified threshold, x, as a function of the threshold itself. When using exposure curves the threshold is stated as a percent of a total measure of exposure. Most authors have used insured value as the denominator, though Bernegger (1997) varied his formulation by specifying maximum possible loss to be the denominator in order to facilitate his analytical distributional analysis by ensuring that the range of possible threshold values is always less than or equal to 100%. Mathematically this is a nice property; however, in practice it is rarely achieved since insured value is commonly used as the denominator. This paper uses insured value as the denominator since its focus is on practical applications.

Given a retention of interest, an exposure curve can help answer the question of what percent of total loss cost will be eliminated by the retention. The threshold can be expressed mathematically as

$$\mathrm{x}=(\text {Gross Loss Amount in Dollars}) /(\text {Insured Value}) . \tag{3.1}$$

In this formulation the exposure curve, G(x) is given by

$$G(x)=\frac{\int_{0}^{x}[1-F(y)] d y}{\int_{0}^{1}[1-F(y)] d y},\\ \quad \text{where } F(x)= \text{the cumulative distribution function of } x. \tag{3.2}$$

Because these curves describe the relationship between the proportion of loss under the retention relative to the total, they are equivalent to the loss distribution function conditional on having a loss. In fact, Bernegger (1997) demonstrates that the cumulative distribution function of the loss distribution, F(x), can be stated mathematically as a function of the exposure curve using the following relationship:

$$F(x)=1-\frac{G^{\prime}(x)}{G^{\prime}(0)} \text{ when x is in } [0,1)\\ \quad \text{or } F(x)=1 \text{ when } x=1. \tag{3.3}$$

This observation is important because it implies that determining the appropriate exposure curves for a given risk is indirectly equivalent to specifying a property loss distribution for that risk in a manner analogous to the way that making ILF selections is indirectly equivalent to specifying a liability loss distribution (Miccolis 1977).

Consequently, for the same reasons that it may be appropriate to select different ILFs between different classes of liability risks based on their underlying loss distributions, it is also appropriate to vary selected exposure curves by risk class to appropriately reflect the underlying loss distribution. For example, it will almost certainly be appropriate to vary the selected exposure curve by insured values due to significant differences that arise for the reasons outlined in Section 2.2.

3.2. Graphical treatment

In practice, a qualitative intuition of exposure curves is often more useful than the analytical formulation because curves appropriate for practical use are generally created from empirical data instead of theoretical probability distributions. A series of descriptive graphical examples along with explanatory narrative is provided below to help the practitioner develop this qualitative intuition.

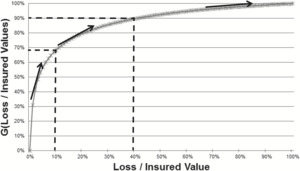
There are a number of visual observations that can be made from the single curve given in the graph of Figure 1.

1. Interpretation of the curve: At the most basic level it is important to be able to read and interpret the exposure curve. For Figure 1, assume that the insured value is $1M. In that case a loss of $100,000 corresponds to Loss / Insured Value of 10% and the graph implies that we expect just under 70% of total loss cost to occur at or below this level (or equivalently just over 30% of total loss cost occurs in the layer above $100,000). Likewise a loss of $400,000 corresponds to Loss / Insured Value of 40% and the graph implies that we expect approximately 90% of total loss cost to occur at or below this level (or equivalently 10% of total loss cost occurs in the layer above $400,000).

2. Shape: The distinct concave down shape of the curves implies that the marginal loss cost for increasingly higher loss layers is decreasing. This is consistent with the observation that the lower layer of exposure needs to be completely exhausted before the higher can be pierced. This is consistent with the intuition and common models for liability insurance.

3. Normalized Size of Loss: Normalizing the size of loss to be stated as a percent of total insured value is the key to the exposure curve formulation. Without this transformation, any large loss exposure analysis we complete will be biased by the fact that a set dollar amount of loss is more or less extreme depending on the overall exposure. For example a $100,000 loss might be fairly a modest loss for a $2M estate (5% of IV), but it is an extreme total loss event for a $100,000 home (100% of IV). This normalization step is a deviation from common modeling in liability insurance which typically assumes that dollar severity distributions are invariant to the underlying exposure.

4. Limiting Behavior: In order to meaningfully compare and contrast exposure curves, it is important to understand how exposure curves are expected to behave in the mathematical limits. Exposure curves provide insight into the underlying loss distributions by quantitatively relating the proportion of loss cost in lower layers to loss cost higher layers, which tends to be a complex relationship in practice. However, in the extremes this relationship is simple and takes on one of two forms, both of which are depicted in Figure 2. These extreme curves superimpose to form a right triangle within which we would expect any real exposure curve to be contained. The analytical assumptions between these two limiting curves is described in detail below.

   a. Losses in all layers are perfectly correlated: Intuitively, this corresponds to a perfectly concentrated risk such as a tiny shed for which any loss event results in a total loss. In this extreme there is no loss cost savings for a higher layer of loss versus a lower layer since all layers are equally exhausted given any loss. Graphically this corresponds to an exposure curve that is a straight line originating from the origin at a 45 degree angle.

   b. Losses in all layers are perfectly diversified: Intuitively, this corresponds to a perfectly “spread-out” risk such as an immense and sprawling university for which any type of loss is an infinitesimally small fraction of the total insured value. Graphically this corresponds to an exposure curve that is an “L-shape” with a vertical line from (0, 0) to (0,1), and then a horizontal line from (0,1) to (0, ∞).

5. Families of Exposure Curves: Now armed with an understanding of the basic elements and limiting behavior of exposure curves we are ready to evaluate an illustrative family of exposure curves taken from Bernegger’s formulations (Figure 3). Bernegger’s analytical formulations are explained and critiqued in more detail below. For now it is sufficient to observe that the curves corresponding to more dispersed risks mimic the limiting curve of the perfectly diversified risks more, while the exposure curves corresponding to more concentrated risks more closely mimic the limiting curve of the perfectly correlated risks.

3.3. Notes on the illustrative curves used in this paper

For the sake of the illustrative examples given in the sections below we will use Bernegger’s analytical exposure curve formulation (1997) derived from the Maxwell-Boltzmann, Bose-Einstein, Fermi-Dirac, and Planck, or MBBEFD distribution from statistical mechanics, which he found to be “very appropriate for the modeling of empirical loss distributions on the interval [0, 1].” While Bernegger’s conclusion that these curves are appropriate for practical use is questionable for the reasons outlined in Section 5.4, their closed form makes them ideal for illustration, which is why they were used to create the simulation used to populate the tables in this paper.

Bernegger’s parameterization of the MBBEFD exposure curve with the maximum loss limited to a maximum possible loss, which we have assumed to be insured value in Equation (3.1) is given in Equation (3.4):

$$G(x)=\frac{\ln \left[\frac{(g-1) b+(1-g b) b^{x}}{1-b}\right]}{\ln (g b)}\\ \quad \text{where } g \text{ and } b \text{ are the parameters} \tag{3.4}$$

In Bernegger’s paper this form is only one of four possible piecewise expressions given for G(x). However, the other three specify endpoint conditions or mathematical extremes, so we need only focus on this form to use the curve in practical applications.

Bernegger went on to fit this parameterization of the MBBEFD distribution he formulated to well-known exposure curves that were the result of a study conducted by Swiss Re, a well-known reinsurer. Four such exposure curves were fit to Equation (3.4), each curve loosely corresponding to risks of increasing size or how “spread-out” the exposure is, as discussed in Section 2.2. In addition, a fifth curve was fit based on data from Lloyd’s of London, the well-known insurance exchange. The curve resulting from these data is considered to correspond to larger and more spread out risks than are contemplated in any of the Swiss Re curves.

Having computed the pairs of (b, g) parameters from fits to each of the five exposure curves described above, Bernegger devised a parametric mapping of the pairs that transformed them from two dimensions to a single dimension which allowed linear interpolation between the well-known exposure curves. This interpolation scheme is given below:

$$g_{c}=e^{(0.78+0.12 c) c} \tag{3.5}$$

and

$$b_{c}=e^{3.1-0.15(1+c) c} \tag{3.6}$$

Bernegger concluded that the five fitted curves were adequately modeled using values of the parameter c = 1.5, 2.0, 3.0, 4.0, or 5.0, with 1.5 corresponding to the Swiss Re curve appropriate for the smallest properties and 5.0 corresponding to the Lloyd’s of London curve.

The example given in Table 7 assumed an illustrative exposure curve provided by Clark to facilitate his example. Unless specified otherwise, the numerical examples provided in the tables below use exposure factors derived from the continuous Bernegger exposure curve given in Equation (3.4) with parameters g = 4.221 and b = 12.648, which were derived using Bernegger’s fitted interpolation of the “well known” Swiss Re and Lloyd’s of London exposure with c = 1.5, which most closely corresponds to the first Swiss Re curve in Bernegger’s formulation. This c value was selected for convenience and ease of illustration.

4. Implementing PEBELS

4.1. The PEBELS exposure base: PEBEL and NLE

As stated in Section 2.3, PEBELS maintains that exposure to excess loss should be directly computed based on the characteristics of the policy itself. Up to this point, only indirect measures of excess loss exposure have been tested. However, the non-proportional per risk reinsurance pricing background developed in Section 2.4 can be used to develop the direct measure of excess loss exposure given in Section 2.3, in Equation (4.1).

To get the allocation base, we simply compute the expected excess loss implied by the exposure rating methodology developed in Section 2.4, for each policy individually. The result of this computation for each policy is defined to be the PEBEL for each policy, which is taken as the PEBELS base for allocating aggregate NCLL. Table 8 demonstrates this computation using four representative example risks from our simulation.

Notice that this calculation mimics the computation shown in Table 7 in every respect except that the calculation is done per policy; just as in Section 2.4, all policies are assumed to have the same expected loss ratio, and the same exposure curve was used for each exposure. The reasonableness of these assumptions will be explored in the sections below.

The NCLL allocation implied by using this basis is summarized in Table 9 below.

Now this allocation is starting to become refined in that it is not only capturing where there is exposure to excess loss, but it is also contemplating the likelihood of excess loss from the exposure by contemplating exposure factors derived from the exposure curve.

Unfortunately, this allocation still has at least one problem. Notice how the allocations to State Z are biased high relative to States X and Y. This is because premiums in State Z are higher than X and Y due to catastrophe exposure which is skewing this allocation high relative to its true non-catastrophe excess loss potential which is the same as the other states. The generalizations given in the balance of Section 4 will provide the flexibility necessary to correct for this and another more subtle distortion. However, before diving into techniques to refine the allocation we will decompose the PEBEL analytically to derive a simplified formulation which will allow this method to be used when exposure profiles used for catastrophe modeling are available but the data detail required to reliably attach policy premiums is not available.

We begin by abstracting the tabular computation illustrated in Table 8 as

$$P_{E B E L_{i}}=P_{i} * E L R_{i} * E F_{i} \text {, where } \tag{4.1}$$

1. P_i is the premium of the i^th policy

2. ELR_i is the expected loss ratio, which is assumed to be constant for all policies (for now)

3. EF_i = G(x_{Upper Bound}) − G(x_{Lower Bound}), is the exposure factor of the i^th policy.

Equation (4.1) can be expanded into

$$\operatorname{PEBEL}_{i}=\left(E_{i} * r\right) * E L R_{i} * E F_{i} \text {, where } \tag{4.2}$$

1. E_i is the insured value of the i^th policy

2. r is the base rate such that E_i * r = P_i, which is assumed to be the same for all policies in the absence of policy-specific premium information. (This is the key assumption for deriving the simplified formulation.)

Since the intended application is to use PEBEL_i as an allocation base, the implied excess loss potential attributable to the i^th policy will be:

$$\frac{P E B E L_{i}}{P E B E L_{\text {total }}}=\frac{E_{i} * r * E L R_{i} * E F_{i}}{\sum_{i} E_{i} * r * E L R_{i} * E F_{i}}=\frac{E_{i} * E F_{i}}{\sum_{i} E_{i} * E F_{i}} \tag{4.3}$$

Thus the simplified formulation is a reduced form allocation base equal to

$$N L E_{i}=E_{i} * E F_{i} \text {, where } \tag{4.4}$$

NLE_i is defined to be the net layer exposure for a given policy.

The allocation based on NLE will be numerically equal to the allocation based on PEBEL whenever the ELR and r are constant for each risk. The ELR assumption is common, but the rate assumption is less so and suffers from the obvious problem that it is not true. However, it is a fair a priori assumption in the absence of premium detail. If we had rate detail such as average premium modification we could incorporate such information into this allocation base improving its accuracy, but the chances that we would have such specific modifier detail without having policy premiums is exceedingly unlikely.

4.2. Per policy generalization

The first generalization to the exposure rating algorithm has already been introduced. It is simple and subtle, but should be pointed out since it is one of the cornerstones of the PEBELS approach. The per policy generalization is simply the insistence that excess loss exposure be quantified at the policy level.

Note that computing PEBEL at the policy level is a break from computing it for groups of policies with similar insured values, which is how it is computed in the published reinsurance approach reproduced in Section 2.4. While the use of grouped insured value bands was, no doubt, an artifact of some data or operational limitation, it is suboptimal in at least three ways.

Most obviously, it is approximate. The exposure factors are computed using the midpoints of the insured value bands which will be incorrect for most if not all risks in the band. As we become increasingly reliant on the distributional information in the exposure curves to set differences in excess loss exposure between risks, this inaccuracy becomes decreasingly acceptable. Luckily it is easily overcome by computing PEBEL per policy.

Second, it would be insufficient for our application. We are trying to allocate excess loss exposure down to the granular level of state and program. Attempting to use PEBEL implied by the broad grouping approach for this purpose would only compound the inaccuracy described directly above.

The third problem with a grouped approach is that it requires an assumption of homogeneity of all risks within the band, which, as Section 4.1 pointed out, might not be reasonable. In the example from Section 4.1, one band may include risks in both States X and Z which vary in their exposure to catastrophes and thus overall premium levels, even though their exposure to non-catastrophe excess loss potential is identical. In that example, assuming homogeneity is too restrictive.

4.3. Heterogeneity generalization

Up to this point no effort has been made to tailor the PEBEL assumptions by policy to reflect policy-specific characteristics even though failing to do so has introduced distortions in our NCLL allocation. This section will provide the tools to refine the allocation base for heterogeneity between policies.

The preferred method to correct for differing rate levels not driven by non-catastrophe loss exposure is to vary the ELR by policy. Specifically, we want to use an ELR representative of the true non-catastrophe expected loss (note: by varying the ELR by policy we are segmenting policies by expected total loss as measured by the ELR). If we assume that the 65.0% ELR assumed so far is appropriate for States X and Y, then the appropriate non-catastrophe ELR for State Z is 65% / 1.5 = 43.3% which follows from our assumption that Z has the same ex-catastrophe exposure as X and Y but has rates that are 50% higher due to its catastrophe exposure. In practice you would not know a priori how much rates varied so the ex-catastrophe ELR may be estimated as the total ELR minus the catastrophe LR implied by modeled AALs or whatever measure is deemed appropriate. The NCLL allocation derived by varying the ELR for cat exposure is summarized in Table 10.

Now this allocation looks very smooth, perhaps too smooth. If State Z really is catastrophe exposed, it probably requires a higher profit margin than States X and Y to support the additional capital required to write in that state. Suppose the additional profit margin required was 5%, then the true ex-catastrophe ELR for state Z is actually (65.0% − 5.0%) / 1.5 = 40.0%.

But we cannot stop there. Once we have opened the Pandora’s box of rate adequacy adjustments we have to consider other possible rate differentials. For example, we may require an additional profit margin, say another 5%, for Estates based on the additional capital required to write such large exposures. We could go even farther down this path specifying ELR differentials between different states, but at a certain point this gets impractical since we would need exactly the type of rate level indications we plan to use this analysis to produce. However, that does not keep us from reflecting significant deviations in ELR that we can reflect with confidence based on broad characteristics such as catastrophe-exposure, program, or pronounced rate inadequacy. In all other situations broad ELR assumptions are used. Table 11 gives the ELR assumptions for each segment used in the final allocation.

The NCLL allocation using these final ELR assumptions is summarized in Table 12.

The magnitude of the impact of adjusting for differing expected profit loads is much less than the magnitude of the impact of reflecting differences in cat exposures which reinforces the decision to only reflect significant differences in broad groups of policies.

The last significant source of heterogeneity we will discuss is that stemming from differences in underlying loss distributions by policy. By using the same exposure curve for all risks we are implicitly assuming that all risks are homogeneous with respect to their underlying loss distributions.

In particular, Clark (1996) identified this issue in his study note on reinsurance pricing, cautioning that “an implicit assumption in the exposure rating approach outlined above is that the same exposure curve applies regardless of the size of the insured value. This assumption of scale independence may be appropriate for homeowner’s business, for which this technique was first developed but may be a serious problem when applied to large commercial risks.”

Each of the three programs referenced throughout this paper can be expected to have dramatically differing distributions of insured values. Thus it is not reasonable to expect that they would have the same loss distributions and thus the same exposure curves.

In the simulation examples above, the exposure factors have been derived using the continuous Bernegger exposure curve given in Equation (3.4) with parameters g = 4.221 and b = 12.648, which were derived using Bernegger’s fitted interpolation of the “well known” Swiss Re and Lloyd’s of London exposure with c = 1.5, which was chosen because it most closely corresponds to the first Swiss Re curve in Bernegger’s formulation.

Recall from Section 3.3 that according to Bernegger’s formulation we can reflect an increase in the size or how “spread out” a risk is by selecting larger values of c. Reflecting this fact in the characterization of which curve is appropriate for a given risk will have the effect of producing thinner tails in the exposure curves of larger properties. This can produce the counterintuitive, yet empirically observable, phenomenon that larger properties can have less excess loss potential than smaller properties in a given loss layer.

For our purposes it is necessary to appropriately vary exposure curves by risk to reflect distributional differences in underlying policy exposure to excess loss. For the purpose of the illustration we will assume that the Bernegger interpolation with c = 1.5 is appropriate for Houses, but not for Barns or Estates. For Barns we will assume that given a loss, a barn will suffer a total loss which is consistent with the very concentrated nature of such a small exposure; for Estates we will assume that the Bernegger interpolation with c = 4.0 (loosely corresponding to the fourth Swiss Re curve according to Bernegger) is appropriate. The results of the NCLL allocation reflecting these refined exposure curve selections are summarized in Table 13.

The results of this allocation are interesting in that NCLL exposure has shifted modestly from Estates to Houses. The larger the difference in underlying loss distribution, and thus exposure curve, the more dramatic this NCLL shift will be, and in practice it can be quite dramatic. Note that Section 2.2 discussed the phenomenon whereby larger exposures have a lower likelihood of having larger losses as a percentage of insured value, so this shift is consistent with our intuition of the underlying loss process. By reflecting the differences in loss distributional characteristic via selection of an appropriate exposure curve, we can quantify how much exposure a nominal amount of high layer of exposure incurs for a small property versus a larger property, a quantity we were not previously able to measure.

It is worth noting that determining an appropriate exposure curve requires care and judgment. Furthermore, the universe of available exposure curves is less expansive than one would hope for. That being said, there are reasonable curves available for these applications that at least allow the practitioner to reflect major loss distributional differences for significantly different classes of risks. While a comprehensive discussion of exposure curves is beyond the scope of this paper, it is also worth noting that there exists significant opportunity to expand the library and understanding of exposure curves. Currently available exposure curve options are discussed in Section 5.4.

4.4. Historical versus prospective exposure distribution generalization

To this point we have made no effort to specify when the exposure distribution to be used in computing the PEBEL or NLE should be evaluated. For common analyses requiring an exposure distribution such as catastrophe modeling or reinsurance quoting, the latest available exposure distribution is desired, which is reasonable given the prospective nature of those tasks. Therefore we will define the latest available exposure distribution to be the prospective exposure distribution.

For loss ratio ratemaking we are uniquely interested in allocating the historical losses stated at their prospective level. By virtue of producing loss ratio based rate level indications, we are using historical experience we have determined to be relevant as the basis for our loss ratio projection. The exercise now is to allocate that experience to where exposure was earned. This is a fundamentally different task than catastrophe modeling where simulations are used as the basis for the projection instead of historical experience.

The losses used in the examples throughout this paper are stated at their prospective level by virtue of the assumption that they have been developed and trended as specified in Section 2.1. This is a fair assumption because developing and trending property losses are both routine tasks in practice. The challenge this paper was written to address is how to allocate the historical NCLL to the historical exposures whose experience forms the basis for our loss ratio based rate level indications. Using the prospective exposure distribution to allocate historical NCLL can lead to significantly skewed and in some cases nonsensical loss ratio based rate level indications.

For example, consider a situation where the company has decided to non-renew all policies in State Z over the last year in order to curtail catastrophe risk. If that were the case then the prospective exposure distribution would reflect the fact that there is no longer any business in force in State Z and thus all historical NCLL experience would be allocated between states X and Y, dramatically overstating their rate level indications. This example was deliberately dramatic (though not unrealistic) in order to demonstrate the phenomenon. In practice even small shifts will distort the NCLL allocation if the prospective exposure distribution is used in place of historical.

Another example is an insurer entering a new state. Suppose the company has decided to expand its writings into State N this last year. The company’s new product has proven to be competitive in State N and the insurer now has a comparable number of policies in State N as it does in X, Y and Z. Using the prospective exposure distribution will cause roughly a fourth of the NCLL experience from the entire experience period to be allocated to state N even though it has not yet earned even a full year’s exposure. This will cause the rate level indications for states X, Y and Z to be understated.

Thus we need a meaningful definition of historical exposures which can be used to develop the NCLL allocations needed for our rate level indications. To accomplish this we define the historical exposures to be the sum of the “earned” exposures for each accounting period in the experience period. For example, if the experience period is five years and the accounting period is a calendar year, then there will be five historical exposure distributions to reflect in the computation of the historical PEBEL. The historical PEBEL for the experience period will then be the annualized sum of the five historical PEBEL associated with each of the five accounting periods in the experience period. Similarly, if the experience period is five years, and the accounting period is calendar quarter, then there will be 20 historical exposure distributions used to compute the historical PEBEL for the experience period.

It is of practical importance to note that since earned exposures will never be available in our data sources, we will have to determine a reliable proxy for it. To do this we can use an accountant’s trick. We observe that exposures (and written premiums) of in force policies are stated as of a specified date in the same way that assets on a balance sheet are stated as of a specified date. For accounting purposes the average value of assets during the year is often taken as the average of the asset values at the beginning and end of a year. Extrapolating this rationale, we can estimate earned exposures of a specific segment during a given accounting period as the average of the historical exposures at the beginning and end of the calendar period.

Of course this is not to say that there is no value to computing PEBEL using the prospective exposure distribution. Such an analysis could be quite useful for NCLL exposure monitoring, analogous to the catastrophe exposure modeling frequently performed by insurance companies. It is just not the right exposure distribution for loss ratio ratemaking.

4.5. Low credibility generalization

Keep in mind that all of the analysis above assumes that historical NCLL experience is fully credible in total. If this is not the case, then credibility methods must be applied in order to develop a reliable total expected historical NCLL provision that can be allocated.

The first thing to note is that we can and should band historical NCLL experience in layers to get more credibility out of our data. In the examples derived above we have considered only two bands: the primary layer and the excess layer from $100,000 to infinity which was selected to keep the examples simple. However, in practice we will want to band to maximize credibility in lower bands and give ourselves an opportunity to use reasonable complements in less credible bands.

Consider the following simple banding scheme that can be used to illustrate the method:

• $0 to $100,000—the primary layer

• $100,001 to $500,000—the first excess layer which we will assume fully credible

• $500,001 to infinity—the high excess layer assumed to be only 30% credible.

The PEBEL per policy will now have to be computed by layer. The only difference in the computation will be that the argument of the exposure curve, G(x) must be limited to the upper and lower bounds the layer when determining the exposure factor EF_i for the given layer (the example reproduced in Table 7 provides a numerical example of this). A separate allocation will then be performed for each layer using the techniques developed in this paper.

The only new complication in this scenario is that the NCLL experience in the $500,001 to infinity layer is only 30% credible. Thus it must be credibility weighted with an appropriate complement before the allocation can be completed.

The task then is to identify a meaningful complement of credibility. One method suggested by Clark (1996) for pricing non-credible per risk reinsurance layers was to use the actual experience in a credible lower loss layer to approximate the expected experience in a non-credible higher loss layer by applying the relationship implied by the PEBEL in each layer. We can apply this approach in our problem to derive reasonable complements of credibility from the $100,001 to $500,000 layer as follows:

$$N C L L_{\$ 0.1 M \text { to } \$ 0.5 M}^{\text {Historical }} * \frac{P E B E L_{\$ 0.5 M \text{ to infinity}}^{\text {Historical }}}{P E B E L_{\$ 0.1 M \text { to } \$ 0.5 M}^{\text {Historical }}} . \tag{4.5}$$

Or alternately using the primary layer as follows:

$$N C L L_{\$ 0 \text { to } \$ 0.1 M}^{\text {Historical }} * \frac{P E B E L_{\$ 0.5 M \text{ to infinity}}^{\text {Historical }}}{P E B E L_{\$ 0 \text { to } \$ 0.1 M}^{\text {Historical }}} . \tag{4.6}$$

An alternate complement can be inferred from the quoted cost of per risk excess of loss reinsurance rates using the formulation below:

$$\begin{array}{l} \text { (Direct Earned Premium) * (Reinsurance Rate) } \\ \quad * \text { (Reinsurer's Permissible LR). } \end{array} \tag{4.7}$$

The reinsurance rate in this context would be specific to the company’s property per risk excess of loss treaty which would probably be quoted by layer. This complement is messy for several reasons, including:

• It will likely cover multiple property lines as opposed to just the line under review

• The rate will likely cover catastrophic excess loss in addition to non-catastrophic

• The quoted layers may not align with those being used for PEBELS analysis

• The reinsurer’s permissible loss ratio will not be obvious.

However, despite all these complications this complement has the very desirable property that it reflects the actual cost to the insurer for the reinsured layer of loss because this is what the insurer actually pays to insure those layers. This gives it a very concrete interpretation and makes it easy to explain and easy to defend. In fact, the smaller an insurer’s property portfolio is, and thus the lower the credibility implicit in the insurer’s actual experience, the more attractive this complement becomes relative to the alternative.

4.6. The scope of PEBELS

Property actuaries do not currently have a systematic framework to quantify the non-linear relationship between expected losses in primary and excess loss layers. For liability insurance, increased loss factors (ILFs) have long been the framework for quantifying this relationship. In practice ILFs are often developed based on a broad group of risks and then imposed on similar risks in a straightforward manner which makes them easy to use and explain. A key reason for the crispness of this formulation is due to the large degree of independence between the loss process and the limit purchased by the insured which simplifies the formulation greatly (Miccolis 1977).

Property is not afforded any such simplifying assumptions. On the contrary, property lines are plagued by a high level of dependence between insured value and the underlying loss process. Furthermore, property lines are also beset by complications such as catastrophic exposure, diverse capital requirements, etc. PEBELS provides a framework from which to reflect and quantify all of these moving parts simultaneously in determining the relationship between the expected primary and excess loss.

Even though PEBELS was created to solve a very specific allocation problem, it evolved into the theory of property excess loss rating described above. The theoretical framework of inputs and levers for allocating property losses between primary and excess layers given in the sections above is general enough that it can be tailored for use in any application that requires segmentation between primary and excess property loss layers, given appropriate actuarial input assumptions.

The sections below provide some examples of applications which could benefit from the segmentation between property loss layers that PEBELS affords.

5. Applications and practical considerations

5.1. PEBELS and adjusting modeled catastrophe AALs

Traditionally, catastrophe models have assumed that average annual losses (AALs) are linearly proportional to exposure. However, we know both from practice and from the theory presented in this paper that this is not a valid assumption. All of our discussion about the theory of exposure curves and the property loss distributions that underlie them suggest that property loss costs are non-linear. This a priori reasoning was empirically validated for catastrophe loss costs by the hurricane exposure curve study completed by Ludwig using Hurricane Hugo (1991).

As such, we would expect, given that total AAL results are calibrated to total industry catastrophes, that the catastrophe loss ratios implied by modeled AALs should be understated for property books with smaller insured values (such as personal lines) and overstated for property books with larger insured values (such as commercial lines). This reasoning is consistent with anecdotal observations.

As discussed in Section 4.6, the methods developed from PEBELS provide the framework from which to quantify an appropriate measure of the amount by which modeled AALs should increase with a linear increase in exposure. Adjusting modeled AALs for this PEBELS effect would eliminate the systematic bias from the implicit modeling assumption that AALs increase linearly with exposure.

To implement this type of refinement the practitioner would need to identify appropriate exposure curves to be used for the given catastrophe exposure under consideration. This would require care and judgment, but no more so than any of the myriad of other assumptions that comprise a typical catastrophe model.

Of course there exists an opportunity for catastrophe modelers to directly enhance their models to reflect the non-linearity of expected catastrophe loss cost with insured value in their models. However, until such a refinement is implemented within the models, insurers can directly adjust their own AALs estimates using a post-modeling PEBELS adjustment.

5.2. PEBELS and predictive models

It is common practice when creating predictive models such as generalized linear models (GLMs) to use separate models to predict the frequency and severity components of the reviewed line of business’s expected loss. Not surprisingly, the severity model tends to be tremendously less stable than the frequency model for lines and coverages with significant exposure to very infrequent but very large losses, such as the property exposures this paper has focused on. This phenomenon is amplified when property coverage is modeled by peril, because total loss for perils such as fire and lightning are disproportionately driven by very infrequent but very large losses relative to other perils.

My hypothesis is that modeling on PEBELS for representative layers in the models would be more predictive than modeling on insured value alone for the reasons explored in the this paper. This is plausible because PEBELS was developed to contemplate actual expected exposure within a layer of insured value and thus contains more information about layer exposure than raw insured value does, assuming that reasonable exposure curves and heterogeneity assumptions are applied.

While PEBELS estimates do contain frequency information from the exposure curve assumptions, the biggest benefit from using PEBELS in predictive modeling would likely be from refining the severity model where large loss observations are so sparse. This is true whether a single uncapped severity model is used, or if uncapped severity is modeled using a combination of (1) a capped severity model (say the cap is $100,000 to be consistent with our preceding examples), (2) a propensity model (the probability that the claim amount will exceed $100,000 given that there is a claim), and (3) an excess model (the severity of the excess portion of the claim given that the claim amount exceeds $100,000). When the combination model is used I would hypothesize that PEBELS would be most predictive in the excess model.

5.3. PEBELS and revised property per risk reinsurance exposure rating

Besides moving to a per policy computation and reflecting heterogeneity by policy which are discussed in Sections 4.2 and 4.3, a major point in the PEBELS formulation discussed in Section 4.4 is the importance of distinguishing between the historical exposure distribution and prospective exposure distribution, and applying the appropriate distribution for the appropriate application.

Clark (1996) states that property per risk exposure rates are generally used to determine the exposure relativities between a credible and non-credible layer. This relativity is then multiplied by the ratio to historical losses in the credible layer to develop the indicated exposure base rate

$$\begin{array}{l} N C L L_{\text {Non-Credible Higher Layer }}^{\text {Expected Prospective }}=N C L L_{\text {Credible Lower Layer }}^{\text {Historical }} \\ \quad * \frac{P E B E L_{\text {Non-Crededible Higher Layer }}^{\text {Prospective }}}{P E B E L_{\text {Credibile Lower Layer }}^{\text {Prospective }}} . \\ \end{array} \tag{5.1}$$

Based on the reasoning presented in Section 4.4 there are two problems with this approach. First, there is no reason that the ratio of PEBEL between the higher and lower layers based on the prospective exposure distribution is representative to the relationship based on the historical exposure distribution (which is the relationship we need to establish). Second, there is no adjustment to reflect the relative change in exposure between prospective and historical exposure distributions for the layer being rated.

An alternate formulation that would reconcile both issues is

$$\begin{array}{l} NCLL^{\text{Expected Prospective}}_{\text{Non-Credible Higher Layer}} = (NCLL^{\text{Historical}}_{\text{Credible Lower Layer}})\\ \quad * \left(\frac{PEBEL^{\text{Historical}}_{\text{Non-Credible Higher Layer}}}{PEBEL^{\text{Historical}}_{\text{Credible Lower Layer}}}\right)\\ \quad * \left(\frac{PEBEL^{\text{Prospective}}_{\text{Non-Credible Higher Layer}}}{PEBEL^{\text{Historical.Annualized}}_{\text{Non-Credible Higher Layer}}}\right). \end{array}\tag{5.2}$$

The first ratio adjusts for the historical ratio of the high layer exposure relative to low layer exposure, while the second ratio allows us to quantify the prospective layer exposure relative to the historical, which for all the reasons outlined in Section 4.4 is more accurate than the traditional approach. The historical PEBEL can be annualized by simply dividing by the total number of years in the experience period.

Note that for reinsurance pricing we are using historical experience to project a prospective loss cost so there is an additional layer of computation to bring the estimate to the level of the prospective exposure distribution, which is not done in loss ratio ratemaking as described in Section 4.4.

My anticipation is that the most difficult part of implementing this more refined exposure rating algorithm will be obtaining the historical exposure profiles from the reinsured. However, in many cases the reinsurer should have a history of exposure profiles from past quotes if the insured has renewed multiple times. Furthermore, given the prevalence of catastrophe modeling, it is becoming increasingly likely that the primary insurer may have a history of historical exposure profiles readily available.

5.4. A final word on exposure curves

In practice, specifying appropriate exposure curves is the key step in determining the accuracy of a PEBELS analysis. The more homogeneous the book of business being analyzed, the more likely it is that using a single exposure curve in the analysis is a reasonable approach. However, regardless of how many curves are required, a decision must ultimately be made as to what curve to use for each given policy. Ideally we would select curves that are particularly appropriate for the risks under consideration, but the universe of available curves is limited so we must operate within our available choices.

There are a few publically available curves published in the actuarial literature, but only the fitted Bernegger curves offer more than a few points, which is why I used them for the illustrations in this paper. While the Bernegger curves are useful for illustration, I would caution against using them for practical applications due to the flatness of their tails relative to exposure curves developed using empirical data. Tail behavior is critical in a PEBELS application since we are predominantly interested in loss exposure from extreme losses which is modeled by the tail of the curve.

There are also some well-known curves such as the Swiss Re or Lloyd’s of London curves which may be more appropriate for practical use in the absence of more refined curves. Additionally, commercially produced curves such as ISO’s PSOLD curves may be available for purchase. A motivated insurer may also choose to create proprietary curves, which, given sufficient data and resource, is the ideal approach.

Furthermore, the practitioner should be aware that the more complex the underlying policy is, the more judgment is required. An example of an area where judgment must be applied is in defining “insured value” for large commercial risks with a stand-alone contents limit. A reasonable approach is to add this value to the stand-alone building limit in determining the total insured value since they are both exposed to a total loss; however, this is not necessarily the optimal choice since the building and contents may not share the same underlying loss distribution, thus the need for actuarial judgment. Another wrinkle is the question of how to incorporate the limit for business interruption coverage, especially when coverage is provided on an “actual loss sustained” basis, in which case the exposure is essentially unlimited.

Despite the additional judgment required for more complex risks, analyses involving these more complex risks tend to benefit most strongly from a PEBELS approach because it is with these risks that data are least credible and heterogeneity among policies is greatest, affording them the most utility from PEBELS’s ability to segment excess loss exposure based on policy characteristics.

Last, an interesting property of exposure curves that was highlighted in Ludwig’s study (1991) is that exposure curves vary by peril. While this conclusion may seem somewhat obvious, it is significant in that most of the available exposure curves are given on a combined peril basis. In most cases they are not segmented by many attributes at all, even ones that might obviously seem predictive of the underlying loss distribution such as class, occupancy or protection.

6. Summary

The original intention of the project that led to the development of PEBELS was to identify a method from the existing literature via literature review. The expectation was to find a method or theory analogous that of ILFs used in liability insurance or ELFs used in workers compensation insurance, but no comparable method or theory for property insurance was identified. However, theory on property exposure curves and methods for pricing property per risk treaties in the property reinsurance literature was identified, and came to form the theoretical foundation upon which PEBELS was built.

The key result of this work was the development of PEBELS, which was designed to be an accurate and practical theory of property non-catastrophe excess loss exposure. Although the scope of the original problem was quite narrow, the numerous challenges worked through to develop an allocation basis that passed the necessary reasonability tests led to the development of an increasingly sophisticated model in order to quantify the non-linearity between the expected loss costs in different loss layers for a given property risk. PEBELS provides a framework that is general enough to apply in a variety of situations.

Because PEBELS is a theory of expected property excess loss by layer, it can be used in any application where such a tool would be of value. Some applications explored in this paper were

• Catastrophe Modeling—to correct for implicit assumption that AAL is linearly proportional to insured value

• Predictive Modeling—to use PEBELS to improve predictiveness of severity models

• Property Per Risk Reinsurance Pricing—to use findings to refine the existing model.

PEBELS requires far more care and judgment to use than ILFs do, mainly due to the presence of many more sources of heterogeneity between policies and the interactions between those sources of heterogeneity present in property insurance relative to liability. The PEBELS formulation in this paper provides the framework of theory and practical levers required to utilize this theory in practical applications.

---

Abbreviations and notations

NCLL, Non-Catastrophe Large Loss
PEBEL, Policy Exposure Based Excess Loss
PEBELS, Policy Exposure Based Excess Loss Smoothing