On Developing a Solvency Framework for Bookmakers

1. Introduction

Actuaries are leading professionals in managing risk (BeAnActuary.org 2015) and consequently have ventured into nontraditional research sometimes with impressive outcomes. Two such cases are Tilley’s (1993) seminal paper showing the first Monte Carlo method to price a derivative option with early exercise features and Redington’s development of immunization theory (Redington 1952).

Gambling is at times considered in a bad light, a vice not to be discussed in an academic or research setting except for evaluating its negative social implications. Yet gambling has been instrumental to the development of probability (David 1962). Gerolamo Cardano (1501–1576) was an astrologer, physician, mathematician and gambler who, in an attempt to understand games of chance, first coined the classical definition of probability: Given a total number n of equally possible outcomes of which m result in the occurrence of a given event, then the probability of that event occurring is $\frac{m}{n}$.

However, many recognize Chevalier de Mere’s (1607–1684) questions on gambling games (specifically his continuous losses and the problem of points) along with Blaise Pascal (1623–1662) as the initial foundations to probability theory. Pascal famously discussed the problem of points in his correspondence with Pierre de Fermat and, through their discussions, these two mathematicians developed the initial stages for probability. Pascal was also instrumental in encouraging Christiaan Huygens (1629–1695) to write the first book on probability theory, De Ratiociniis in Ludo Aleae (On Reasoning in Games of Chance), in 1657 (Bernstein 1998).

Pierre-Simon Laplace (1749–1827) introduced the application of probability theory to scientific and practical problems in the early nineteenth century and this spurred the developments of the theory of errors, Bayes’ theory, statistics and actuarial mathematics during the same century. Subsequently Markov chains, which are extensively used in stochastic processes, were introduced in 1906 (Markov 1906, 1971). Modern theory of probability is based on Andrey Kolmogorov’s (1903–1987) work on measure theory. Other significant theories within probability theory during the last century include Markowitz theory of portfolio selection (Markowitz 1952), Monte-Carlo simulation, game theory and chaos theory.

More recently betting markets have been of great interest to economists and other researchers mainly because they can be interpreted to be a simple alternative to financial markets (Lessmann, Sung, and Johnson 2009; Sauer 1998; Shin 1993; Tirole 1982). Participants in both markets have large money at stake that is used to make a profit based on different beliefs and information at hand, making this a zero-sum game (Levitt 2004). Lessmann, Sung, and Johnson (2009) and Sauer (1998) extend this further by implying that gambling markets act as simple financial markets since they provided a clearer view of pricing issues. Cases of investigations in betting markets include inquiries in insider trading (Schnyzter and Shilony 1995; Shin 1993; Vaughan Williams and Paton 1997), herding behavior (Buhagiar, Cortis, and Newall 2018; Law and Peel 2002), a comparison of group to individual decision making (Adams and Ferreira 2009) and market efficiency (Cortis, Hales, and Bezzina 2013; Terrell and Farmer 1996; Woodland and Woodland 2001).

A further motivation is the actual size of the industry itself (Levitt 2004). In particular the gambling industry is a key contributor to the gross domestic product (GDP) of some jurisdictions. For instance, it contributes to over 10% of the Maltese GDP (Agius 2014). On a smaller relative scale, betting on outcomes, also referred to as sports betting, is a subcategory of gambling that contributed £2.3 billion (circa 0.16%) to the United Kingdom GDP in 2011 (Deloitte 2013).

During 2014 the sports betting industry is estimated to have made gross gambling revenue (GGR), evaluated as wagers less winning pay outs, of around forty five billion euro (H2 Gambling Capital, November 20, 2014). Interactive betting, which includes internet and mobile betting, has been a key driver together with deregulation to the increase in sports betting (European Gaming and Betting Association 2014; Fawcett 2014; Griffiths 2004). Indeed, there has been an increase of over 200% in GGR of interactive sports betting over the past ten years, as shown in Figure 1. There are no signs of a change in the trend of a growing sports betting market as mobile and social gaming become more popular (Torres and Goggin 2014) and governments are viewing the regulation of the industry as possible economic and taxation gain rather than controlling a vice (Atkinson, Nichols, and Oleson 2000). Such a development could happen in the USA, where sports betting is illegal in most states by federal law. Although this has been challenged unsuccessfully by a New Jersey law that lost the case up to appeals court (Reuters 2015), more movements are expected to focus on liberating the market in lieu of the significant amount wagered illegally in the USA.

Figure 1.Estimated Yearly Gross Gambling Revenues (H2 Gambling Capital, November 20, 2014)

Due to the size of the market, the solvency of bookmakers is an issue to be addressed with a similar rigour to that of financial institutions. Bookmakers are not immune to making losses (e.g., iGaming Business 2013, 2014), and bookmakers cannot be expected to keep a reserve equivalent to all outcomes. In a similar vein, banks reserve a proportion of their depositors’ funds as they assume that not all depositors will withdraw their investments at the same instant; in another example, insurers do not reserve the sum insured of all policies since not all extreme adverse events are likely to occur at the same time. In this respect, this paper introduces a method to evaluate risk metrics that can be extended to limit, grant or insure a bookmaker.

Managing a bookmaker has many similarities to running an insurer. A bet can interpreted as an insurance cover that pays out contingent on an outcome occurring. Therefore, betting and insurance share the same common theme with only a few differences. First, there must be insurable interest for one to open up an insurance policy while one must be independent of an outcome to bet on it. A contract that pays the author $1,000 on Queen Elizabeth II’s death is a bet, not an insurance policy, given that the author has no insurable interest in the queen’s survival. Second, the value of a pay out on an insurance claim can fluctuate, especially in a general business scenario, while that of a bet tends to be fixed. For example, a car accident may be a few dollars in the case of a scratch to millions if it results in deaths. There are alternative situations, such as the fluctuating pay out on a spread-bet^[1] or the fixed predetermined amount paid on an injury at work covered by a workers’ compensation scheme. A third difference is that the timing of a bet is usually known because it is paid at the end of an event, while the trigger for an insurance pay out may fluctuate. The model presented here can be considered as the equivalent of an insurer’s underwriting risk under a Solvency II framework for a bookmaker.

The next section introduces the key relevant findings from other publications. These lead to the core of the paper: a method to evaluate the distribution of a portfolio of bets placed with a bookmaker and subsequently the determination of bookmaker solvency. Finally, the conclusion is preceded by a discussion of challenges in applying this method as well as its possible extensions.

2. Distribution of odds

Bookmakers set odds on outcomes of different events on which customers can place wagers. Typically these are set in different markets since there are various outcomes from one event. For example the 1X2 market in a soccer match (the event) might result into three outcomes (home team win, draw, away team win). The same event could be used to determine the half-time 1X2 market. Furthermore, odds can be displayed in a variety of manners.^[2] One such method is European (or decimal) odds whereby the odd is the reciprocal of the probability. For example, an odd of two represents an implied probability of one half. Another method is American Money-Line Odds that display the amount to be wagered to win 100 units for likely events and the amount to be won on a 100-unit wager on unlikely events.

In order for bookmakers to be able to make profits, the sum of implied probabilities of all mutually exclusive outcomes for any market adds up to more than 100% (Cain, Law, and Peel 2003; Cortis, Hales, and Bezzina 2013; Peel and Thomas 1992; Štrumbelj 2014; Zafiris 2014). The excess of this sum over 100% is called the bookmaker margin, the over-round or the vig. Typically the bookmaker margin is considered to be a constant factor that grosses up real-to-implied probability for all outcomes (e.g., Archontakis and Osborne 2007; Cortis, Hales, and Bezzina 2013; Goddard and Asimakopoulos 2004; Zafiris 2014), but other approaches, such as using a finite list of odds (Koch and Shing 2008) or conversions minimizing the effects of insider trading (Shin 1993; Štrumbelj 2014), are also possible.

Cortis (2015) shows that for a market with $n$ outcomes each denoted $i$ with real probability of occurring $\pi_i$ such that $\sum_{i=1}^n \pi_i=1$ and a wager $w_i$ made on each outcome $i$; the profitability for the bookmaker has a mean and variance as shown in Equation 1, if a constant bookmaker margin of $k$ is assumed,

$$P \sim N\left(\frac{k}{1+k} \sum_{i=1}^n w_i, \sum_{i=1}^n \frac{w_i^2}{(1+k) \pi_i}-\left(\frac{\sum_{i=1}^n w_i}{1+k}\right)^2\right) . \tag{1}$$

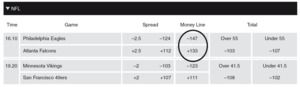
This has been further expanded such that the real probability is not required to be known by a bookmaker to have positive expected profits. For example, the odds on the match outcome for Philadelphia Eagles - Atlanta Falcons NFL match as circled in Figure 2 indicate implied probabilities of $\frac{147}{147+100}=59.51 \%$ and $\frac{100}{100+133}=42.92 \%$ for each team to win, respectively. The total implied probabilities add up to $102.43 \%$, where the excess of $2.43 \%$ is the bookmaker margin denoted as $k$ in Equation 1. Therefore using this equation, Pinnacle Sports expects to make a profit of $\frac{2.43}{102.43}=2.37 \%$ of the total wagers made on match outcome for this case.

Figure 2.Odds on National Football League as at 03:20CDT on September 14, 2014 as shown on Pinnacle Sports

The findings can be extended to multiples or accumulators, which are a series of bets made on $m$ independent events, by Equation 2. This is equivalent to Equation 1, assuming an overall bookmaker margin of $\left(1+k_m\right)^m-1$. In an applied scenario this means that wagers on high odds are likely to be multiples and therefore placed at higher overall bookmaker margin. Indeed, the bookmaker profits on multiples are much higher than those on normal bets^[3] (Cain, Law, and Peel 2003; Cortis 2015; Zafiris 2014).

$$P^{(m)} \sim N\binom{\frac{\left(1+k_m\right)^m-1}{\left(1+k_m\right)^m} \sum W,}{\frac{1}{\left(1+k_m\right)^m} \sum \frac{W^2}{\pi^{(m)}}-\left(\frac{\sum W}{\left(1+k_m\right)^m}\right)^2}, \tag{2}$$

where

• k_m is the geometric mean of bookmaker margin per market.

• $\sum W=\sum_{i_1=1}^{n_1}\left(\sum_{i_2=1}^{n_2}\left(\cdots\left(\sum_{i_m=1}^{n_m} w_{1_{i_1} i_i \cdots m_{i_m}}\right)\right)\right)$.

• $\sum \frac{w^2}{\pi^{(m)}}=\sum_{i_1=1}^{n_1}\left(\sum_{i_2=1}^{n_2}\left(\cdots\left(\sum_{i_{m=1}}^{n_m} \frac{w_{1_{i_1} 2_{i 2} \cdots m_{i_m}}^2}{\pi_{1_{i_1}}^\alpha \pi_{2_{i_2}}^\alpha \cdots \pi_{m_{i_m}}^\alpha}\right)\right)\right)$.

• $w_{1_{1_1 2_1 i_2} \cdots m_{i_m}}$ represents the total amount wagered on a multiple bet that pays out if all outcomes $i_1, i_2$ to $i_m$ within independent events $1,2,3, \ldots, m$ respectively occur.

3. Bookmaker’s portfolio

In calculating the variance of company profits for multiples placed over the same set of m events, multiple outcomes are mutually exclusive and complete the probability space of all outcomes. However, a company typically offers a significantly large number of events to place wagers on, such that little to no multiples refer to the same events. Consider the following multiple/accumulator bets made on the 2014 International Basketball Federation (FIBA) World Cup as shown in Figure 3.

• Bet α: Bet on Iran to win their match versus France @ 6.880 and Bet on Croatia to win their match versus Puerto Rico @ 1.309 for total odd 9.006.

• Bet β: Bet on Puerto Rico to win versus Croatia @ 3.830 and Argentina to win versus Greece @ 3.160 for total odd 12.103.

• Bet γ: Bet on Argentina to win versus Greece and Turkey to win versus Dominican Republic @ 3.16 and 1.595, respectively, for total odd 5.040.

• Bet δ: Bet on Lithuania to win versus Slovenia @2.030.

Figure 3.Odds available on Pinnacle as at 10:49 CDT on September 4, 2014

In this case, bets α and β are mutually exclusive since Croatia are playing Puerto Rico, while bets β and γ have a positive correlation as they both depend on Argentina winning. Bet δ is independent of other bets. Assuming that these bets were made in the given order, bet β reduces the total variance in company profits since it acts as a hedge to bet α. On the other hand, bet γ increases risk by a larger factor than bet δ.

The portfolio of bets placed with a bookmaker is constantly changing, especially with the popularity of live in-play betting (Hogg 2013; Keogh and Rose 2013; Newall, n.d.; Robinson 2012) which is the possibility of placing wagers of outcomes while a match is being played (Brown 2012; Croxton and Reade 2014). Therefore a simple estimate is required.

My proposition is to subdivide the portfolio of bets wagered with a bookmaker in bundles according to odds, evaluate the distribution of each bundle separately, and then calculate the distribution of the portfolio. These bundles can be set according to the odd grids set up by the bookmaker, but the odds offered to customers will increase significantly if multiples are used. Therefore, a range of odds within each bundle would be preferable.

3.1. Variance per bundle

For each bundle $q$, evaluate the distribution of wagers $W \sim N\left(\bar{W}_q, \sigma_{w_q}^2\right)$; the number of different wagers, ^[4] denoted $n_q$; the geometric mean of the market spread $k_q$ (weighted by $n_q$ ) over these bets ^[5]; and the arithmetic mean of odds offered $\pi_q$. The average variance per bet, denoted $\overline{V a r}$, can be therefore estimated as shown in Equation 3. This is a straightforward application of Equation 1.

$$\begin{aligned} \overline{\operatorname{Var}}_q & =\bar{W}_q^2\left(\frac{1}{\left(1+k_q\right) \pi_q}-\frac{1}{\left(1+k_q\right)^2}\right) \\ & =\frac{\bar{W}_q^2}{1+k_q}\left[\frac{1}{\pi_q}+\frac{1}{1+k_q}\right] . \end{aligned} \tag{3}$$

Since each bundle contains n bets, we can evaluate the total bundle variance Var_q (Equation 4) as the addition of all variances per bet (Var_q). This takes into consideration the average correlation for all pairs of bets within a particular bundle, denoted as r.

$$\begin{aligned} & \operatorname{Var}_{q}={n} \overline{\operatorname{Var}}_{q}+{2} \sum\left({r} \sqrt{\overline{\operatorname{Var}}_{q}} \sqrt{\overline{\operatorname{Var}}_{q}}\right) \\ & ={n} \overline{Var}_{q}+{2} \bigl( ^{n} {C}_{2}\bigr) {r} \overline{V a r}_{q} . \end{aligned}\tag{4}$$

The variance of a bundle can fluctuate to anyapplicative scenario, it would be recommended to back-test the correlation between all bets made within a particular bundle. The value of $\sigma_{w_1}^2$ furthermore helps in controlling the dispersion in the amount of odds as a possible consideration for bundling could be the size of the wager. Assuming an infinite number of possibilities and a finite number of bets, the example of no correlation is used, whereby $\operatorname{Var}_q=n \overline{\operatorname{Var}}_q$, leading to the profitability of a bundle $q$, denoted $B_q$ following the distribution shown in Equation 5. One can clearly notice the similarities of the per-bundle distribution, with the distribution per event shown in Equation 1.

$$B_q \sim N\left(\frac{k_q}{1+k_q} n_q \bar{W}_q, n_q \bar{W}_q^2\left(\frac{1}{(1+k) \pi_q}-\frac{1}{(1+k)^2}\right)\right) . \tag{5}$$

For instance, consider that a company has 300 bets of odds averaging at an odd of 1.07. The wagers have an average of 10 units and a bookmaker margin of 5%. The profits in this bundle follow the distribution B_q ∼ N(142.86,3360.55) and have a probability of a loss of less than 0.7%.^[6] This result is highly sensitive to the correlation coefficient. If this was considered to be 0.5, then the variance of this bundle would be 502401.36 and the probability of loss as high as 42%.^[7]

3.2. Portfolio variance

Having calculated the parameters for each bundle, one can finally calculate the joint distribution for the company’s whole portfolio of bets. Assuming that $b$ bundles are created, the total portfolio variance is $\sum_s \operatorname{Var}_s+2 \sum_{s>1} r_{s, t} \sqrt{\operatorname{Var}_s \operatorname{Var}_t}$ for $s, t \in\{1,2, \ldots, b\}$ where $r_{s, t}$ is the correlation coefficient between bundles $s$ and $t$.

As an example, consider calculating the distribution of bookmaker profits for a portfolio of one hundred thousand bets uniformly subdivided over 20 bundles as shown in Table 1. It is further assumed that the bookmaker margin per bundle increases for low-likelihood outlooks in line with the longshot bias, which states that the gap between real and implied probabilities is higher for less likely outcomes (Vaughan Williams and Paton 1997; Štrumbelj 2014). This assumption is also consistent with the expectancies of a higher proportion of multiple/accumulator bets at higher odds. For example an odd with a likelihood of 0.01% is more likely to be a bet on a combination of outcomes from different events, such as guessing the series of winners on 10 matches, rather than one outcome from a particular event. Equation 2 shows that these bets will result in a higher betting margin per bet placed.

A presumption that one can make is that closer bundles are more likely to be related than distant ones. The reasoning behind this is that, since low odds imply high likelihood while high odds imply low likelihood, these are more likely to belong to a set of mutually exclusive outcomes. Although this might not be always true. For example, a market with many possible outcomes is likely to produce many high mutually exclusive odds. Notwithstanding, the correlation between different bundles can again range between −1 and 1, but as a further specimen example, it can be set as shown in Equation 6.

$$r_{s, t}\left\{\begin{array}{r} 0.75 \text {; if }|s-t|=1,2 \\ 0.50 \text {; if }|s-t|=3,4 \\ 0.25 \text {; if }|s-t|=5,6 \\ 0 \text {; if } 6<|s-t|<14 \\ -0.25 \text {; if }|s-t|=14,15 \\ -0.50 \text {; if }|s-t|=16,17 \\ -0.75 \text {; if }|s-t|=18,19 . \end{array}\right. \tag{6}$$

The total variance is calculated as Vector ${\sqrt{\text { Var }}} \times$ Correlation Matrix $\times \operatorname{Vector}_{\sqrt{\operatorname{Var}_q}}^T$ where the correlation matrix is a $20 \times 20$ matrix showing the correlations between different bundles and

$$\text { Vector }_{\sqrt{\operatorname{Varq}_9}}=\left(\begin{array}{c} 654 \\ 879 \\ 613 \\ 537 \\ 408 \\ 457 \\ 507 \\ 569 \\ 569 \\ 614 \\ 405 \\ 446 \\ 494 \\ 553 \\ 629 \\ 731 \\ 354 \\ 467 \\ 827 \end{array}\right) \tag{7}$$

The distribution of the portfolio of bets placed with the bookmaker, denoted Port can therefore be evaluated as following the distribution:

$$\text { Port } \sim N(72261,30026410) . \tag{8}$$

4. Determining solvency

The estimation of the expected profit and variance of a portfolio of bets for a bookmaker can lead to further tools for regulators and bookmakers to manage their own risk, here described as the deviation from the expected. One application could be an extension of the six sigma method (Kwak and Anbari 2006; Schroeder et al. 2008), whereby the expected profit of the portfolio needs to be at least four and a half times the standard deviation for the bookmaker to be able to operate.

Many financial regulatory regimes require a minimum of capital funds to be held by the financial institution to operate. Such regimes tend to determine this amount as a percentile measure, typically the value-at-risk (VaR) measure at some level of confidence. A clear example is the Solvency II insurance regime that is being introduced for the European insurance industry (Barbara et al. 2017; Doff 2008). The VaR evaluates the amount of capital required for the financial institution to be able to withstand extreme events. In layman terms, the VaR answers the question: What amount of capital is required for the company not to go bankrupt by x% probability?

This measure has been widely criticized from a theoretical perspective as it seems to suggest that a small level [(1 − x)%] of failures are tolerated (Doff 2008), and it does not have adequate mathematical properties such as subadditivity (Acerbi and Tasche 2002; Artzner et al. 1999; Dhaene et al. 2006).

Furthermore, VaR does not consider the magnitude of the losses beyond its value. In this respect, many recommend the use of the expected shortfall (ES), also referred to as the tail-value-at-risk (Acerbi and Tasche 2002; Tasche 2002; Yamai and Yoshiba 2005). ES can be described as the expected loss in the extreme percentile beyond the VaR.

5. Challenges and extensions

One key challenge in applying this method relates to which timeframe of bets to use: Should a bookmaker apply risk measurement for all bets placed within a particular time-frame, open at a particular moment or closing at a particular time-frame? The per-bundle parameters for each bookmaker can be calculated at different times and used to project future capital requirements. Furthermore, the use of different correlation parameters may result in evaluating best-estimate, pessimistic and optimistic measures, which are then utilized to rate the riskiness of each bookmaker.

On the plus side, the method presented here is modular and can be easily enriched. In the example shown here, each bundle has an equivalent range of implied probability (5%) even if realistically one would not expect many outcomes with a 95%–100% likelihood. Indeed, the ideal number of bundles and the subdivision of these would depend on the scenario at hand.^[8] The bundling technique may provide more accurate best-estimates if subdivided in more dimensions such as the bookmaker margin, size of wagers, type of event, type of market, and timeframe.

The application of any model to measure risk is bound to be imperfect (Greenspan 2008) and therefore should not be an end-all. Following a number of model failures, many point out that risk models act more as a false sense of security rather than a proven system for insolvency prevention (Colander 2009; Danielsson 2002). On a similar tone, many have investigated inadequacies in the models used to measure risk in the financial sector (e.g., Berkowitz and O’Brien 2002) or discussed methods on how to asses these (Kupiec 1995). Fundamentally financial institutions operate in a market in which their actions affect the value of market securities (Colander 2009) and financial models depend on the solvency of counter-parties since they operate in a highly leveraged environment with significant trade between the institutions.

In contrast to financial markets, the outcome of an event is not and should not be affected by a bookmaker since trade between bookmakers is currently minimal and bookmakers are not highly leveraged. The failures in application of mathematical developments in finance, such as risk models and derivatives, can also be blamed on misuse rather than simply design limitations (Bezzina and Grima 2012; Salmon 2012). Moreover, mathematical models add insight (Geoffrion 1976) and provide a deeper understanding of the sensitivities of output to changes (Thiele, Kurth, and Grimm 2014). A model cannot be assumed to describe perfectly the behavior of the underlying system but it gives us a chance to see how to react in the extreme case.

Another justification for imposed reserves on banks and insurances is that they provide services that are at times compulsory (such as car insurance) and act as a public good (Born 2001). The consideration of the betting industry as a vice may limit developments in determining solvency regimes. There is a greater natural social desire to have banks, insurances and other financial institutions protect consumers who are saving their income or protecting their wealth and loved ones; the desire to protect individuals who gamble is less so. As an example, one would feel more empathy towards an individual whose insurance is unable to settle claims for earthquake damage to her property due to the insurer’s insolvency rather than a bettor who did not receive his prize winnings due to the bookmaker’s insolvency.

Notwithstanding, both deserve their compensation. Another factor is that betting markets can serve as a public good, for example, by providing farmers with a likelihood of bad weather as evidence by odds on betting markets in order to hedge against the risk of low or no harvest (Hahn and Tetlock 2006). It is also unclear whether onerous regulatory regimes would result in entry barriers that would distort the market in the current betting industry environment of mergers and take-overs (e.g., Farrell 2015).

While one can argue that any formal quantitative requirements would increase regulatory and enforcement costs, bookmakers and regulators are already significantly data-intensive enterprises and should be able to cope with new quantitative improvements. Nevertheless implementation of quantitative requirements may not be as straightforward as the experience of implementing Solvency II for insurance solvency regimes in Europe has shown.

Some regulators, such as the ones based in Malta and Gibraltar, would benefit greatly from a reputational perspective by ensuring that one of their largest industries are solvent. Likewise countries were a significant number of wagers are placed, such as the United Kingdom, would also benefit by adding more rigorous measures that protect customers. Yet the greatest benefactors would most likely be bookmakers themselves. Currently, the solvency is a one-by-one scenario; usually being covered by a bank guarantee may be an inefficient allocation of capital. Runs of this model held on different assumptions show that a bookmaker would be solvent if well diversified. That is, unless the operator has some concentration of risk — say a Greek bookmaker is more at a risk of default if Greece wins the European Soccer tournament another time since it would have many local sentimental bets.

The gambling industry is currently a revenue source for states and governments, but the introduction of quantitative requirements may increase regulation costs. The additional cost is likely to be financed by increased fees and penalties, rather than public financing, which costs may be ultimately borne by gamblers. Lessons learned from the implementation of the insurance regime would entice any implementation of a bookmakers’ solvency regime to be simpler in order to minimize costs and time to enactment.

6. Conclusion

The setting of reserves of a portfolio of bets wagered with a bookmaker is therefore a gap that needs to be addressed. Financial regulation has focused significantly on risk measurement, management and culture over the past few years (Ring et al. 2014). Similarly as the gambling sector continues to grow; a consolidated regulatory and internal approach to risk would promote active management of own risks, increase customer protection, enhance investors’ ability to analyze bookmakers, and reduce regulatory arbitrage.

This paper introduces a method that measures the betting risk of a bookmaker by subdividing bets in different bundles. The model presented here is based on a number of assumptions such as distributions being mainly normal distributed, bundle sizes being equal, and internal correlation for each bundle being zero. This leads to significant scope for further research that would focus on ideal bundling regime, actual experienced per-bundle correlations, and challenges in setting up a risk-management framework that adapts this risk measurement technique.

Acknowledgments

I thank Prof. Frank Bezzina (University of Malta), Mr. Ian Borg (Betsson), Mr. Sandro Borg (Kyte Consultants Ltd.), Mr. Nick Foster, FIA (University of Leicester), Mr. Christian Grima (University of Malta), Dr. Simon Grima (University of Malta), Prof. Jeremy Levesley (University of Leicester), Mr. Thomas Saliba, FIA (Direct Line Group), and two anonymous referees for their valuable comments and recommendations.