A Family of Chain-Ladder Factor Models for Selected Link Ratios

undefined

1. Introduction

The chain-ladder variance formulas first proposed by Dr. Thomas Mack (1993) are based upon all-year volume-weighted average report-to-report factors (“link ratios” or “factors”) and an assumed variance structure that is proportional to the development period’s initial loss. Under the regression approach of Daniel Murphy (1994) it was shown that the proportional variance structure assumption is sufficient for the weighted average link ratio to be considered the best linear unbiased estimate (BLUE) of such a chain-ladder model.^[1]

In practice, however, the actuary selects factors. Factor selection is an important component of actuarial analysis^[2] that utilizes actuarial judgment in its consideration of those—and other—averages as well as additional information gleaned from benchmark link ratios, industry trends, discussions with company management, etc. Although much research has been dedicated to framing the chain-ladder method within a statistical structure,^[3] little ground is devoted to the treatment of the uncertainty of the unpaid claim estimates when the selected factors differ from some prescribed formula. The few treatments on the subject tend to adopt a bifurcated approach, that is, one which supplements the expected value estimates from one model with variability estimates from a different model.

A Bayesian perspective can be exploited to combine point and uncertainty estimates derived from bifurcated models. For example, Verrall (2007) assumes the actuary selects volume-weighted average link ratios from the most recent five years but derives variation estimates that reflect information from all years, not just the most recent five. Verrall’s approach holds promise as actuaries become more comfortable with the Bayesian perspective, which can be useful for combining statistics and judgment but which requires “prior” distributions and sophisticated statistical software.

An approach with which actuaries do appear comfortable is based on scaling. Panning (2006) argues that loss reserve uncertainty under his method is “scalable.” By that he means that his method’s coefficient of variation (CV) “is applicable to reserves that have been estimated in different ways” (Panning 2006). Scaling is an actuarial technique utilized in a wide variety of applications. In stochastic analysis the authors are aware that it is common practice to apply a CV based on the Mack method to a chain-ladder point estimate that is based on selected factors other than the all-year volume-weighted average. The authors are concerned that bifurcated point and variability estimates may underestimate the volatility of the underlying claims process.

This paper takes a more direct approach. We show how, under certain restrictions on the selected link ratio, a chain-ladder model can be formulated such that the actuary’s selection can be considered a “consistent unbiased estimate” of the model. Our chain-ladder models are similar to those of Mack and Murphy, but allow for a broader set of “weights” by expanding the domain of the exponent of the beginning value of loss to the entire real line. Using classical regression analysis, variability estimates fall out of the same model. This overcomes the scaling disconnect alluded to above. We also believe our approach is more accessible to practicing actuaries than Verrall’s Bayesian approach. Although a drawback of our approach is that our mean square error formulas are more complicated than those of Mack and Murphy, this should not be unexpected for models that allow for a continuum of selected factors rather than just the standard averages. Despite the higher degree of difficulty, our formulas can be calculated in a spreadsheet.

To the authors’ knowledge, this is the first paper to posit models that reflect the chain-ladder method in practice, i.e., when selected factors are other than the volume-weighted or simple averages. The authors believe that by associating the actuary’s choice with a model, the selected link ratio can better be back-tested against the observable data, which can add more insight into the reserving exercise. We caution, however, that it is not necessarily possible to identify a chain-ladder model in our framework that is consistent with every potential selected factor. Restrictions are defined in the paper. Of course, the results of our chain-ladder model are subject to model error. As with all stochastic models, the actuary must assess the applicability of the indications relative to his or her understanding of the model’s assumptions, familiarity with the triangle and other data, and the judgment underlying the factor selections.

The remainder of this paper is organized as follows. In Section 2 we present a family of models that generalizes those in Mack (1993, 1999) and Murphy (1994) and is consistent with the practical implementation of the chain-ladder method, because it allows for conformance with a broad set of judgmentally selected factors. In Section 3 we give formulas for the expected value and mean square error of chain-ladder projections from selected factors. In Section 4 we demonstrate the concepts and calculations in a worked-through, spreadsheet-based example. Section 5 is a summary. Appendix A includes proofs of our results. Appendix B compares our model’s recursive formulas with those of Mack (1999).

2. A chain-ladder model for judgmentally selected link ratios

Adopting notation commonly found in the literature, we denote the observed triangle of positive cumulative losses^[4] by D = {C_i,j|1 ≤ i ≤ I, 1 ≤ j ≤ I}. A model equivalent to the chain-ladder method is

$$\begin{align} &C_{i, j+1}=f_{j} C_{i, j}+C_{i, j}^{\alpha_{j} / 2} \sigma_{j} \varepsilon_{i, j} \\ &\text{independent random variables} \ \varepsilon_{i, j} \ \text{have mean 0 and variance 1} \tag{1} \end{align}$$

for 1 ≤ i ≤ I and 1 ≤ j ≤ I. Under these assumptions it is well known (first shown by Aitken 1935) that the BLUE of the link ratio f_j from age j to age j + 1 given triangle D, denoted f̂_j, is a weighted average of the observed link ratios:

$$\hat{f}_{j}:=\hat{f}_{j}\left(\alpha_{j}\right):=\sum_{i=1}^{I-j} w_{i, j}^{\left(\alpha_{j}\right)} F_{i, j} \tag{2}$$

where the weights

$$w_{i, j}^{\left(\alpha_{j}\right)}=\frac{C_{i, j}^{2-\alpha_{j}}}{\sum_{k=1}^{I-j} C_{k, j}^{2-\alpha_{j}}} \tag{3}$$

are functions of the $\alpha_j$ and

$$F_{i, j}=\frac{C_{i, j+1}}{C_{i, j}} \tag{4}$$

are the observed link ratios based on the triangle.

Model (1) describes a family of models indexed by a continuous parameter $\alpha_j$ ∈ ℝ. This family contains the models given in Mack (1993, 1999) and Murphy (1994) as special cases, where those authors propose that the $\alpha_j$ indices assume the values 0, 1, and 2, at most.^[5] Murphy (1994) demonstrated that for the member indexed by $\alpha_j$ = 1 the weighted average link ratio is the BLUE consistent with the model’s parameter f; for the $\alpha_j$ = 2 member, the simple average link ratio is a consistent estimator; for $\alpha_j$ = 0, a consistent link ratio is the slope of a simple regression line through the origin. Model (1) allows the domain of possible values for α to encompass the entire real line rather than just the values 0, 1, and 2. As a result, a continuum of selected factors has the potential to be consistent with Model (1). Put another way, Model (1) allows for an actuary’s selected link ratio that is different from the simple or volume-weighted average to be, nevertheless, a linear unbiased estimate of a statistical model consistent with the chain-ladder method.

We refer to Model (1) as the chain-ladder factor model (CLFM). With that as background, there remain the following questions:

• When a selected link ratio is not one of the usual averages, how does one find a member of the CLFM family for which it could be considered consistent?

• How does one calculate the value and the risk of a point estimate under the CLFM framework, and what additional assumptions are needed?

To help answer these questions we introduce the link ratio function, a concept fundamental to CLFM theory and results.

2.1. The link ratio function

Definition:

Given observations of loss at the beginning and end of development period j, the link ratio function LR_j(α) is a mapping on the real line given by

$$\mathrm{LR}_{\mathrm{j}}(\alpha):=\sum_{i=1}^{I-j} w_{i j}^{(\alpha)} F_{i j},(\alpha \in \mathrm{R}) \tag{5}$$

where w_i,j^(α) and F_i,j are defined in (3) and (4) above.^[6] The link ratio function calculates weighted averages of the observed link ratios, where the weights depend on the exponent of loss at the beginning of the period. We begin our investigation of the link ratio function by considering its asymptotic properties as α→±∞.

Lemma 1: Asymptotic properties of the link ratio function

Consider for a given triangle D and development period j the set of all possible values of linear estimates (2) as a function of a real valued parameter α ∈ ℝ. Let aymin_j and aymax_j denote the accident years with the smallest and largest values of loss, respectively, as of the beginning of development period j:

$$\begin{aligned} \text { aymin }_{j} & =\min _{i}\left\{C_{i j}\right\} \text { and } \\ \operatorname{aymax}_{j} & =\max _{i}\left\{C_{i, j}\right\}(1 \leq i \leq I-j) . \end{aligned}$$

Then lim_α→∞ LR_j(α) = F_ayminj_,j and lim_α→−∞ LR_j(α) = F_aymaxj_,j. In the case of “ties” for accident years having the smallest or largest beginning value C_i,j, lim_α→∞ LR_j(α) = mean{F_i,j|i ∈ aymin_j} and limα→−∞ LR_j(α) = mean{F_i,j|i ∈aymax_j}.

The proof can be found in the appendix.

Lemma 1 says that the BLUE of a link ratio for a given development period approaches the link ratio experienced by the accident year with the smallest/largest value of loss at the beginning of the development period as index α approaches +∞/−∞.

To illustrate, suppose losses as of the beginning and end of development period 1 for five accident years are as shown in Table 1. The largest and smallest values of loss as of the beginning of the period are highlighted in yellow.

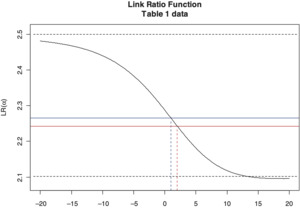
The link ratio function corresponding to these losses is graphed in Figure 1.

As predicted by Lemma 1, the graph is asymptotic to the line y = 2.500, the link ratio corresponding to accident year 3, and to the line y = 2.101, the link ratio corresponding to accident year 5. The blue line corresponds to the volume-weighted average link ratio (α = 1) and the red line to the simple average (α = 2).

The link ratio function need not be monotonic. Indeed, change the ending value of accident year 5 to 500. Year 5 would still have the smallest beginning value so its link ratio, now 2.415, would still be the asymptote. The new non-monotonic link ratio function, graphed in Figure 2, has a minimum somewhere in the vicinity of α = 6.

From Figures 1 and 2 it should be clear that not all possible link ratios (abscissa) are achievable from a given triangle. In fact, the maximum or minimum empirical link ratio may not even be achievable (the 1.983 link ratio for accident year 4 is literally “off the chart” in Figure 2). Mathematically stated, the image of the link ratio function is not the entire real line. In other words, many link ratio selections would be inconsistent for any member of the CLFM family relative to a given triangle D.^[7] This brings us to our next definition, that of a reasonable link ratio.

Definition:

A link ratio lr is reasonable with respect to a given triangle D if there exists a member of the α-indexed CLFM family for which lr can be calculated as in (5). We denote the set of all reasonable development period j link ratios by LR_j(D):

$$\mathrm{LR}_{\mathrm{j}}(D)=\left\{\begin{array}{l} l r \mid l r=\mathrm{LR}_{\mathrm{j}}(\alpha) \text { for some } \alpha \in \mathbb{R}, \\ \text { given triangle } D \end{array}\right\}$$

Noting that large values of α may lead to impractically large factors C^α/2 in the error term of (1), we recommend limiting α to a prudently bounded interval; we selected [−8, 8] judgmentally.

A selected link ratio may be associated with more than one value of α (e.g., in Figure 2 the blue, volume-weighted line crosses the graph at more than one point). That is to say, there may be more than one member of the CLFM family whose BLUE is the selected factor. We suggest the following procedure for selecting the selection-consistent alpha value.

Definition:

The selection-consistent alpha of a reasonable link ratio lr_j is the smallest positive solution α ∈ [−8, 8] of the equation lr_j = LR_j(α), or, if no positive solution exists, the smallest solution in absolute value. Mathematically this is expressed as

$$\hat{\alpha}_{j} \equiv \max \binom{\min \left(\alpha>0 \mid l r_{j}=\mathrm{LR}_{\mathrm{j}}(\alpha)\right),}{\max \left(\alpha \leq 0 \mid l r_{j}=\mathrm{LR}_{\mathrm{j}}(\alpha)\right)} .$$

By convention, if the selected link ratio $l r_j$ is the volume-weighted average we set $\hat{\alpha}_j=1$; for the simple average we set $\hat{\alpha}_j=2$.

Given a selected link ratio lr_j, the selection-consistent member of the CLFM family can be determined by finding positive and negative solutions α of the equation

$$l r_{j}=l r_{j} \cdot \sum_{i=1}^{I-i} C_{i, j}^{2-\alpha}-\sum_{i=1}^{L-j} C_{i, j}^{1-\alpha} C_{i, j+1} \tag{6}$$

and selecting the smallest positive value if one exists or the negative value closest to the origin.

According to traditional actuarial thinking, the variability of projected loss increases as the beginning value of loss increases, i.e., the value of α in the exponent of C_ij in model (1) should be positive. A negative value of α would say that the variability of projected losses is inversely proportional to the beginning value, a seemingly counterintuitive result. However, we have found contexts in which such a counterintuitive result is not unreasonable. For example, given a book of first party business with low policy limits, case reserves for “obvious limits losses” would tend to be more certain than reserves on smaller claims. For that situation it would not be unreasonable to find the variability of losses at the end of a calendar period to be inversely proportional to the beginning value of loss. We only suggest that actuaries stay open to the story that data have to tell.

3. CLFM chain-ladder projection formulas

CLFM formulas are recursive because that allows for maximum flexibility in selecting different family members from one period to the next.

3.1. Expected value formulas

We adopt the usual chain-ladder convention of developing the current diagonal. For accident year $i$ with current diagonal value $C_{i, j}$ and a selected link ratio $\hat{f}_j$, the expected value at the end of the first future development period is $\hat{C}_{i, j+1}=\hat{C}_{i j} \hat{f}_j$. This estimate is clearly unbiased if $\hat{f}_j$ is unbiased because $C_{i j}$ is a scalar. The expected value at the end of the next development period is $\hat{C}_{i j+2}=\hat{C}_{i j+1} \hat{f}_{j+1}$. Expected value estimates for subsequent development periods are iterated in a similar fashion.

The estimate $\hat{C}_{i j+2}$ will be unbiased if we assume that the product of the two estimates $\hat{f}_j$ and $\hat{f}_{j+1}$ equals the product of the two underlying parameters $f_j$ and $f_{j+1^*}$. Note that this assumption is implicit in chain-ladder calculations where, say, a higher than average link ratio on the current diagonal has no bearing on the factors selected to develop that year going
forward.^[8]

The expected value of the sum of all accident years combined at development age j is the sum of the estimates of the individual accident years at the same age.

3.2. Standard error formulas

The first step in working with loss variation over a given development period is estimating the scale parameters $\sigma{j}$, which can easily be found using weighted least squares available in virtually all popular statistical packages. Equivalently, for each development period the data can be transformed into ordinary least squares (OLS) form by dividing the beginning and ending values of loss by the beginning value raised to the power α/2. As transformed, model (1) is

$$C_{i, j+1} / C_{i, j}^{\alpha_{j} / 2}=f_{j} C_{i, j} / C_{i, j}^{\alpha_{j} / 2}+\sigma_{j} \varepsilon_{i, j} . \tag{7}$$

The formula for calculating an estimate σ̂²_j of σ²_j can be found in any good statistical text. In the example we illustrate this approach using the LINEST function in Excel.

The next step is to estimate the variability of the selected factors f̂_j. The estimate of the conditional variance of those factors, which we denote by Δ,^[9] is by definition the quantity $\Delta^{2}\left(f_{j}\right):=\mathrm{E}\left(\left(\hat{f}_{j}-\mathrm{E}\left(\hat{f}_{j} \mid D\right)\right)^{2} \mid D\right)$. As with the estimates of σ²_j, these estimates are also standard outputs of regression software.^[10]

3.2.1. Standard error formulas for an individual accident year

Consider an individual accident year i and its estimate Ĉ_i,j at age j. The mean square error of the estimate Ĉ_i,j is the sum of parameter risk and process risk:

$$\begin{aligned} \operatorname{mse}\left(\hat{C}_{i, j}\right)= & \mathrm{E}\left(\left(\hat{C}_{i, j}-C_{i, j}\right)^{2} \mid D\right) \\ = & \mathrm{E}\left(\left(\hat{C}_{i, J}-C_{i, J}\right)^{2} \mid D\right) \\ = & \mathrm{E}\left(\left(\hat{C}_{i, J}-\mathrm{E}\left(C_{i, J} \mid D\right)\right)^{2} \mid D\right) \\ & +\mathrm{E}\left(\left(C_{i, J}-\mathrm{E}\left(C_{i, I} \mid D\right)\right)^{2} \mid D\right) \\ := & \Delta^{2}\left(C_{i, J}\right)+\Gamma^{2}\left(C_{i, J}\right) \end{aligned}$$

Parameter risk (denoted Δ²) and process risk (denoted Γ²), notation borrowed from the literature, can be calculated recursively according to the formulas shown next.^[11]

3.2.1.1. Parameter risk: Variance of the estimate of the mean future value of loss

For the first period after the current diagonal (s = 1),

$$\Delta^{2}\left(C_{i, j+1}\right)=C_{i, j}^{2} \Delta^{2}\left(f_{j}\right) \tag{8}$$

because C_i,j² is a constant. For s = 2, 3, . . .

$$\begin{aligned} \Delta^{2}\left(C_{i, j+s}\right)= & \mu_{i, j s-1}^{2} \Delta^{2}\left(f_{j+s-1}\right)+\hat{f}_{j+s-1}^{2} \Delta^{2}\left(C_{i, j s-1}\right) \\ & +\Delta^{2}\left(f_{j+s-1}\right) \Delta^{2}\left(C_{i, j s-1}\right) \end{aligned} \tag{9}$$

where $\mu_{i, j+s-1}^{2}:=\mathrm{E}\left(C_{i, j s-1} \mid D\right)$. Formula (9) is consistent with the formula in Mack (1999) for α = 1, 2 except for the third term, which Mack excludes.^[12]

3.2.1.2. Process risk: Variance of the deviation of future value of loss from its mean

For the first period after the current diagonal

$$\Gamma^{2}\left(C_{i, j+1}\right)=C_{i, j}^{a_{j}} \hat{\sigma}_{j}^{2} . \tag{10}$$

For subsequent periods

$$\begin{aligned} \Gamma^{2}\left(C_{i, j s s}\right)= & \mathrm{E}\left(C_{i, j s-1} \mid D\right)^{\alpha_{j+s-1}} \cdot \Psi\left(\alpha_{j+s-1}, \frac{\Gamma\left(C_{i, j s-1}\right)}{\mathrm{E}\left(C_{i, j s-1}\right)}\right) \\ & \cdot \sigma_{j, s-1}^{2}+f_{j, s-1}^{2} \Gamma^{2}\left(C_{i, j s-1}\right) . \end{aligned} \tag{11}$$

As noted in the proof in Appendix A, the process risk calculation, drawing upon the Law of Total Variation, involves the expectation E(C^α) which is not the same as E(C)^α. Since E(C) is a readily available quantity, Ψ is our “helper” function which, when multiplied by E(C)^α, yields E(C^α). For example, since E(X²) = E²(X) + Var(X), E(X²)/E²(X) = 1 + cv²(X), so Ψ(2, κ) = 1 + κ². Clearly Ψ(1, κ) = 1, and Ψ(0, κ) = 1 as well. For higher raw moments, the ratio of E(C^α) to E(C)^α depends on the distribution; for the normal distributions it is a polynomial in κ. We adopt that simplification for our purposes. Therefore, for non-negative integer values n of alpha we define Ψ as

$$\Psi(\alpha, \kappa)=\sum_{\substack{j=0 \\ j \text { even }}}^{n} \frac{1 \cdot n \cdot(n-1) \cdots(n-(j-1))}{2^{j / 2\left(\frac{j}{2}\right)!}} \kappa^{j} .$$

For α > 0 but not an integer, we define Ψ(α,κ) to be the linear interpolation between Ψ([α],κ) and Ψ([α] + 1,κ) where [x] denotes the greatest integer function. For negative values of α we recommend approximating Ψ using simulation.^[13]

3.2.2. Standard error formulas for all accident years combined

Recursive variance formulas for all accident years combined become slightly more complicated because at each new age an additional accident year is included.

For ages j = 2, 3, . . . , let $X_{j}=\sum_{i=I-j+2}^{I} C_{i, j}$ be the sum of the future losses for accident years that have not yet matured to age j. Let $M_{j}:=\sum_{i=I-j+2}^{I} \mu_{i, j}$ denote the expected value of X_j and let $\hat{X}_{j}=\sum_{i=I-j+2}^{I} \hat{C}_{i, j}$ be its chain-ladder estimate.

3.2.2.1. Parameter risk: Variance of the estimate of the mean future value of total loss

For $j=2$, only the most recent accident year is included in the total, so the parameter risk of the total is equal to the parameter risk of the most recent year: $\Delta^2\left(X_2\right)=\Delta^2\left(f_1\right) \cdot C_{l, 1}^2$. For $j=3,4, \ldots$,

$$\begin{aligned} \Delta^{2}\left(X_{j}\right)= & \left(M_{j-1}+C_{I-j+2, j-1}\right)^{2} \Delta^{2}\left(f_{j-1}\right)+f_{j-1}^{2} \Delta^{2}\left(X_{j-1}\right) \\ & +\Delta^{2}\left(f_{j-1}\right) \Delta^{2}\left(X_{j-1}\right) . \end{aligned} \tag{12}$$

3.2.2.2. Process risk: Variance of X_j

Model (1) assumes all accident years are independent. Therefore the process variance of the sum of the future values as of a given age is the sum of the process variances:

$$\Gamma^{2}\left(X_{j}\right)=\sum_{i=1 j+j+}^{I} \Gamma^{2}\left(C_{i, j}\right) . \tag{13}$$

4. An example

We consider the triangle of RAA data analyzed in Mack (1993), Barnett and Zehnwirth (2000), and elsewhere in the literature and illustrate spreadsheet calculations of process risk and parameter risk within the CLFM framework. We selected simple and volume-weighted average link ratios for a few ages and “judgmental” selections for other periods to demonstrate the concepts. Losses, link ratios, simple and volume-weighted averages and the selections are shown in Table 2.

The mean and standard error estimates based on this triangle D, the selected factors, and the CLFM formulas are summarized in Table 3. We will illustrate the CLFM calculations for a few representative entries.

4.1. Expected value calculations

Table 4 shows the projected chain-ladder values based on the latest diagonal and the selected factors. For example, for accident year 10 the projected value in the first future diagonal is the product of the diagonal value and the 1-2 selected factor (2,063 ⋅ 8.206 = 16,929). For the next diagonal the projected value is the product of the age 2 projection and the 2-3 selected factor (16,929 ⋅ 1.624 = 27,485). The values in the bottom row (“All”) are the sums of the values in their respective columns.

4.2. Variability calculations

4.2.1. Selection-consistent alphas

The simple average was selected for development period 1-2 and the volume-weighted average for periods 2-3 and 6-7. Accordingly, the respective selection-consistent alphas are 2 and 1 by convention. For the remaining selections the selection-consistent alphas are the solutions of Equation (6), which we solved in Excel with a Newton-Raphson technique.^[14] The values of α shown in Table 5 thus identify selection-consistent members of the CLFM family.

4.2.2. σ²

We chose the OLS approach to illustrate how to carry out the CLFM calculations in Excel. For example, for period 3-4, α = 1.158 (Table 5), the data for the transformed model (7) are given in Table 6, and the LINEST estimate for σ is 13.03.

The 9 to 10 development period has only one observation, insufficient for regression; we used Mack’s suggested heuristic [10, p. 363] $\sigma_{n-1}^2=\min \left(\sigma_{n-2}^4 / \sigma_{n-3}^2\right.$, $\min \left(\sigma_{n-3}^2, \sigma_{n-2}^2\right)$ ). Table 7 summarizes the $\sigma^2$ estimates for all development periods.

4.2.3. Δ²(f_j)

For the standard error of the selected link ratio, denoted in our paper as Δ²(f_j), either refer to the output of the software employed—LINEST^[15] in our case—or use the formula [(Mack 1999, 363); see footnote ^[16]] $\Delta^{2}\left(f_{j}\right)=\frac{\hat{\sigma}_{j}^{2}}{\sum_{i=1}^{n-j} c_{i, j}^{\alpha_{j}}}$ which we did for the problematic 9-10 development period. Table 8 summarizes these estimates.

4.2.4. Parameter risk (Δ) for projected loss

Parameter risk is estimated recursively in an analogous fashion to the expected value. Table 9 displays the parameter risk estimates by accident year as of each future evaluation and for all accident years combined.

4.2.4.1. Δ²(C) for an individual accident year

To illustrate how we calculate these parameter risk estimates for an individual accident year, let’s work with accident year 10. For the first period after the current diagonal (i = 10 and j = 2) we use Formula (8), the actual loss in Table 2, and the link ratio uncertainty estimate from Table 8:

$$\begin{aligned} \Delta^{2}\left(C_{10,2}\right) & =C_{10,1}^{2} \cdot \Delta^{2}\left(f_{1}\right)=2,063^{2} \cdot 16.921 \\ & =72,014,303 \end{aligned}$$

For the next development period we use Formula (9), the estimated projected loss µ_10,2 from Table 4, the selected link ratio in Table 2, Table 8 and the result of the previous calculation:

$$\begin{aligned} \Delta^{2}\left(C_{10,3}\right)= & \mu_{10,2}^{2} \Delta^{2}\left(f_{2}\right)+f_{2}^{2} \Delta^{2}\left(C_{10,2}\right)+\Delta^{2}\left(f_{2}\right) \Delta^{2}\left(C_{10,2}\right) \\ = & 16,929^{2} \cdot 0.018+1.624^{2} \cdot 72,014,303 \\ & +0.018 \cdot 72,014,303 \\ = & 196,434,086 . \end{aligned}$$

Estimates for the remaining ages are iterated in a similar fashion.

4.2.4.2. Parameter risk: Δ²(X) for all accident years combined

For all accident years combined, the parameter risk for age 2 is identical with the parameter risk for accident year 10 alone: Δ²(X₂) = 72,014,303. For age 3, we use Formula (12):

$$\begin{aligned} \Delta^{2}\left(X_{3}\right)= & \left(M_{2}+C_{9,2}\right)^{2} \Delta^{2}\left(f_{2}\right) \\ & +\hat{f}_{2}^{2} \Delta^{2}\left(X_{2}\right)+\Delta^{2}\left(f_{2}\right) \Delta^{2}\left(X_{2}\right) \\ = & (16,929+5,395)^{2} \cdot 0.018 \\ & +1.624^{2} \cdot 72,014,303+0.018 \cdot 72,014,303 \\ = & 200,341,585 . \end{aligned}$$

The value for M₂ = E(X₂) comes from Table 4, the actual diagonal value C_9,2 from Table 3 and the value of Δ²(X₂) from the previous recursion step. Estimates for the remaining ages are iterated in a similar fashion.

4.2.5. Process risk (Γ) for projected loss

Table 10 summarizes the process risk estimates by accident year and for all accident years combined. The process risk estimates for all accident years combined is the sum of the process risk estimates for the individual accident years. The process risk estimates for individual accident years are calculated recursively. We illustrate with accident year 10.

For the first period after the current diagonal (i = 10 and j = 2), we use Formula (10), the actual loss in Table 2, and the scale parameter estimate from Table 7:

$$\Gamma^{2}\left(C_{10,2}\right)=C_{10,1}^{\alpha_{1}} \hat{\sigma}_{1}^{2}=2,063^{2} \cdot 152.287=648,128,730 .$$

For the next development period (j = 3) we use Formula (11):

$$\begin{aligned} \Gamma^{2}\left(C_{10,3}\right)= & \mathrm{E}\left(C_{10,2} \mid D\right)^{\alpha_{2}} \cdot \Psi\left(\alpha_{2}, \frac{\Gamma\left(C_{10,2}\right)}{\mathrm{E}\left(C_{10,2}\right)}\right) \cdot \hat{\sigma}_{2}^{2} \\ & +\hat{f}_{2}^{2} \Gamma^{2}\left(C_{10,2}\right) \\ = & 16,929^{1.000} \cdot 1 \cdot 1,108.526 \\ & +1.624^{2} \cdot 648,128,730 \\ = & 1,727,121,088 . \end{aligned}$$

because Ψ(α, κ) ≡ 1 when α = 1. For the process risk at age j = 4 where α₃ = 1.158 we linearly interpolate between Ψ(1, κ) = 1 and Ψ(2, κ) = 1 + κ² where $\kappa=\sqrt{1,727,121,088} / 27,485=1.512$ and get Ψ(1.158, 1.51) = 1 + (1.158 − 1)(1.512)² = 1.362. So

$$\begin{aligned} \Gamma^{2}\left(C_{10,4}\right)= & \mathrm{E}\left(C_{10,3} \mid D\right)^{\alpha_{3}} \cdot \Psi\left(\alpha_{3}, \frac{\Gamma\left(C_{10,3}\right)}{\mathrm{E}\left(C_{10,3}\right)}\right) \cdot \hat{\sigma}_{3}^{2} \\ & +f_{3}^{2} \Gamma^{2}\left(C_{10,3}\right) \\ = & 27,485^{1.158} \cdot 1.362 \cdot 169.856 \\ & +1.275^{2} \cdot 1,727,121,088 \\ = & 2,839,654,629 . \end{aligned}$$

Estimates for the remaining ages are iterated in a similar fashion.

4.3. Comparison of the CLFM vs. the Mack method

The question of how the CLFM and Mack results compare often arises.^[17] As we understand the popular practice of the method of Mack (1993), the Mack method CV assuming weighted average link ratios and all years in the triangle would be applied to the point estimate based on a different set of factors. The Mack method CV from the RAA data is 51.6%.^[18] This is about half the CLFM CV in Table 3. Thus, the CLFM risk estimate would be about twice the value of the risk estimate from the Mack method as we understand its common implementation in practice.

5. Summary

This paper presents a family of models that is consistent with the implementation of the chain-ladder method as used in practice. Our approach is different from the methods of Mack (1993, 1999) and Murphy (1994) because, whereas their models assume that the selected chain-ladder link ratio is a volume-weighted or simple average, our model accepts an actuary’s judgmentally selected factor as a fundamental input. By enlarging the domain of the exponent of the chain-ladder method’s “explanatory variable” (the value of loss at the beginning of the development period) in its influence on modeling loss development variability, our approach allows for many more selected link ratios than just the usual averages to be considered BLUEs within a chain-ladder-consistent stochastic model. As a result, point estimates and risk estimates of unpaid claim liabilities can be calculated simultaneously. This avoids the need to scale chain-ladder point estimates based on one model (selected factors) with CVs based on a different model (e.g., volume-weighted or simple averages) or with CVs based on a different methodology entirely (e.g., bootstrapping). Our approach can be implemented in a spreadsheet, thus avoiding the need for more sophisticated statistical software.

The theory of our approach and illustrated in the example suggests that scaling a chain-ladder point estimate with a Mack method CV based on the all-year volume-weighted average will understate the standard error of the projections; the greater the difference between the actuary’s selections and the volume-weighted averages, the greater the understatement.

It goes without saying that to model loss development within the CLFM family does not eliminate model risk, an inescapable side effect of any statistical model by definition. The authors also caution that it is not necessarily possible to identify a CLFM family member that is consistent with every potential link ratio selection. Refer to the constraints outlined in the paper.

Various reviewers have suggested that the alpha index that identifies a member of a CLFM family can be considered a “parameter” rather than an “index” and therefore some component of the model risk might possibly be quantified by an estimate of that parameter’s estimation risk. The authors had indeed investigated that work stream within a maximum likelihood context. Although the mathematics was interesting, that research thread was abandoned because there was no guarantee that the likelihood maximizing value of alpha would index the CLFM member consistent with the actuary’s selection. Others may find this work stream more fruitful, but our primary goal was to identify selection-consistent models that cater to the needs of practitioners who select development factors based on judgment on a daily basis.

For diagnostics regarding the selections relative to potential trends in the triangle, we refer the reader to our first paper (Bardis, Majidi, and Murphy 2008).

The authors also wish to point out the CLFM framework assumes that the only available data that might shed light on link ratio uncertainty is the triangle alone. When exogenous data help determine factor selection, unpaid claim estimate uncertainty will undoubtedly be improved by incorporating additional sources of pertinent quantifiable information within a broader model that is not limited to the triangle alone. We anticipate much research in that area in the future.

The authors want to thank Tom Ghezzi and the many reviewers for their helpful comments and suggestions.