1. Introduction
“Past performance does not necessarily indicate future results” is a ubiquitous phrase, whether in radio ads or the fine print of a prospectus. Actuaries, however, do base a large portion of their analyses on the assumption that, when properly restated, past performance can be indicative of future results. Of course, this is not always the case. Sometimes, performance may have radically changed in the recent past, and the long-term history should not be used to predict the future. When is the past sufficiently different from the future?
This question is referred to as a “changepoint” problem, a problem wherein historical data can be analyzed, including what may seem to be drastic shifts, and then used to identify both the timing and magnitude of said shifts. More formally, a sample of independent observations (x1, x2, …, xn) is said to have a changepoint at m, if the null hypothesis—that all the observations come from the same distribution F(x|θ)—is rejected in favor of the alternative hypothesis—that there exists an m, m < n, such that (x1, x2, . . . , xm−1) comes from F(x|θ) and (xm, xm+1, …, xn) comes from F(x|θ′), where θ ≠ θ′ (Page 1955). The condition of independence is not necessary, but tends to simplify much of the underlying derivations (Carlin, Gelfand, and Smith 1992; Smith 1975). Although the changepoint problem covers the potential for multiple shifts, this paper will focus on the case with “at most one change” (AMOC). While there is extensive general statistical literature about changepoint problems from both classical and Bayesian perspectives, there appears to be less focus in the actuarial literature (for one example in a life and health actuarial context, see Gandy, Jensen, and Lütkebohmert 2005).
The dataset that will be analyzed can be found in Table A1. This is a list of 29 artificial annual average loss severities in chronological order, together with their respective ranks. Figure 1 is a line plot of the data.

Figure 1.Average loss severity over the 29-year dataset.
A first glance at the data shows that severities in the last few years, the last four in particular, are larger than usual. A basic response to a dataset of this nature is to find a changepoint, evaluate the data on either side of it, decide whether or not it truly is different, and, based on that decision, use either all or a subset of the data to make a prediction.
In the remainder of the paper, Section 2 will pre-sent some classical analyses, Section 3 will present a Bayesian approach and models, and Section 4 will demonstrate some sensitivity testing using the Bayesian framework. Appendix A contains tables not included in the text of the paper itself, and Appendix B contains most of the code used to generate the results in this paper, with the idea that it can serve as a building block for others interested in this kind of analysis. Experience with R (2014) and JAGS (Plummer 2003), while not necessary, will enhance understanding and repeatability of the analysis.
2. Classical analysis
2.1. Finding the changepoint
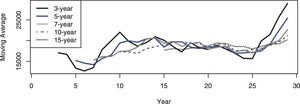
One of the more basic tools for identifying the existence and timing of any change is the moving average (Page 1954). Figure 2 shows the plots of moving averages of various durations. The plots all show a distinct increase in the moving average around year 26. Although Page focuses on quality inspection in that paper, he does describe a more general changepoint test, which he expands in a subsequent paper (Page 1955). Assuming that the overall mean of the original distribution, θ, is known, Page suggests calculating the cumulative sums Sr=∑ri−1(xi−θ),S0=0, and “acting” when Sr−min0≤i<rSi≥h for some threshold h. A reasonable procedure to keep track of changepoints using Page’s process would be to take a long-term average after the data has stabilized, consider that value to be the known mean, and then use it as the θ to track future Sr sums. The data and Figure 1 indicate that the values do not seem to settle down until year 8. Taking the 10-year average between years 8 and 17 as the long-term average gives a θ of 19,666.20. The process inspection Sr sums from years 18 through 29 using this value are plotted in Figure 3.

Figure 2.Moving averages over the 29 year dataset.

Figure 3.Process inspection scheme—mean based on the 10-year average loss between years 8 and 17.
The plot shows that the long-term average is reasonable until year 26. While the difference in year 26 itself may not have been enough to flag a review, subsequent years would almost certainly indicate a change. Moreover, in hindsight, year 26 began the upward trend, which is consistent with the moving average indications. Therefore, a preliminary approach to this problem would be to determine if there is a statistically significant difference between the first 25 and the last 4 years of the data.
2.2. Comparing distributions across the changepoint
2.2.1. Normal assumption
Although property and casualty actuaries are conditioned to consider data coming from non-normal distributions, it is educational to start the analysis from a perspective of total ignorance. The most important summary statistics for the data are the sample mean and sample standard deviations for the two blocks of years. These are shown in Table 1.
Table 1.Sample means and standard deviations for test data
| First 25 Years |
17,728.34 |
4,038.93 |
| Last 4 Years |
27,977.08 |
4,845.92 |
| All Years |
19,141.96 |
5,425.33 |
One of the first investigations that can be done is a test for normality using the empirical mean and standard deviation as estimates for the underlying population. One of the most common tests for normality is Pearson’s χ2 test, although now the G test, of which Pearson’s χ2 test is an estimate, is often suggested (Sokal and Rohlf 1995). An issue with these tests, however, is that as they require placing the data into bins, the results may be subject to how the underlying bins are created (D’Agostino and Stephens 1986, chap. 3.2).
Table 2 shows the results of the tests using bins that generate at least 5 observations in each, and Table 3 shows the results of the tests using equiprobable bins selected per chapter 3.2.4 of D’Agostino and Stephens (1986). In both, at the 0.05 level of significance, neither the χ2 nor the G tests support the rejection of the null hypothesis that the first 25 data elements come from a normal distribution with the sample mean and standard deviation as shown.
Table 2.χ2 and G tests—Equal observation bins
| 0–15,000 |
5 |
6.242 |
0.247 |
−1.109 |
| 15,000–16,000 |
5 |
2.117 |
3.926 |
4.297 |
| 16,000–19,000 |
5 |
7.230 |
0.688 |
−1.844 |
| 19,000–22,000 |
5 |
5.783 |
0.106 |
−0.727 |
| 22,000–∞ |
5 |
3.628 |
0.519 |
1.604 |
| Total |
25 |
25.000 |
5.486 |
4.441 |
|
|
p-valueb
|
0.064 |
0.109 |
ax̅25 = 17,728.337, s25 = 4,038.935
bn = 5 and p = 3 so 2 degrees of freedom
Table 3.χ2 and G tests—Equiprobable bins
| 0–13,082.151 |
2 |
3.125 |
0.405 |
−0.892 |
| 13,082.151–15,004.117 |
3 |
3.125 |
0.005 |
−0.122 |
| 15,004.117–16,441.374 |
7 |
3.125 |
4.805 |
5.645 |
| 16,441.374–17,728.337 |
1 |
3.125 |
1.445 |
−1.139 |
| 17,728.337–19,015.301 |
2 |
3.125 |
0.405 |
−0.893 |
| 19,015.301–20,452.557 |
5 |
3.125 |
1.125 |
2.350 |
| 20,452.557–22,374.523 |
1 |
3.125 |
1.445 |
−1.139 |
| 22,374.523–∞ |
4 |
3.125 |
0.245 |
0.987 |
| Total |
25 |
25.000 |
9.880 |
9.593 |
| (l)3-5 |
|
p-valueb
|
0.079 |
0.088 |
ax̅25 = 17,728.337, s25 = 4,038.935
bn = 8 and p = 3 so 5 degrees of freedom
There are other tests for normality which are not subject to potential bias due to binning, often based on testing the goodness-of-fit against the empirical CDF. These tests, such as the Cramér–von Mises and Anderson–Darling tests for normality, also do not allow the rejection of the null hypothesis at the 0.05 level of significance, as seen in Table 4.
Table 4.Various tests for normality of the first 25 yearsa
| Cramér–von Mises |
0.058 |
0.391 |
| Anderson–Darling |
0.302 |
0.551 |
| Shapiro–Francia |
0.978 |
0.767 |
| Lilliefors (Kolmogorov-Smirnov) |
0.137 |
0.263 |
Given the assumption that the first 25 years come from a normal distribution, the data would indicate that there is no greater than about a 5.5% chance of any one of the last four years coming as independent draws from the distribution defined above. Furthermore, as the sum of n normally-distributed random variables is itself normally distributed with mean and variance equal to the sum of the means and variances of the n components (DeGroot 1986, 270), the probability of the block of the last four years coming from the distribution defined by the first 25 can be shown to be very improbable—approximately 0.00000019. This is orders of magnitude smaller than any contiguous set of four years in the first 25 years.
To test for the difference between the two distributions, as the means and standard deviations used are themselves estimates and not known values, and the variances of both groups are not necessarily—or likely—to be equal, Welch’s t-test (Welch 1947) should be used. This test returns a one-sided p-value of approximately 0.0093, indicating that it is significant that the second group comes from a distribution with a greater mean than the first. This further confirms that nearly all of the past history may not be helpful in predicting future results, and that from year 26 and on, the loss process is different.
2.2.2. Beyond the normal
The normal distribution, however, is not one commonly seen in property/casualty insurance work. To test whether or not another distributional family may be more appropriate, the method of maximum likelihood estimation (MLE) can be used to find the “best-fitting” parameters for various families of distributions. Those distributions can then be compared with each other using one of various information criteria. Using the Akaike information criterion with small sample correction (AICc), the three best resulting families for the first 25 years from a set of about 15 distributions are the gamma, normal, and lognormal distributions. Their AICc values, together with those of the poorly fitting Pareto distribution for comparison, are shown in Table 5.
Table 5.MLE results for first 25 years
| Shape or Mean |
19.52 |
17,728.34 |
9.76 |
2,222,899.62 |
| Scale or SD |
907.99 |
3,957.33a
|
0.23a
|
39,574,910,823.53 |
| AICc |
489.48 |
489.66 |
490.02 |
543.69 |
aThe MLE estimate for the standard deviation of the normal and lognormal distribution is the population estimate, not the sample estimate.
Interestingly, the initial assumption of a normal distribution was not so bad in hindsight. With the assumption that the first 25 years come from a gamma distribution, there is no greater than about a 6.4% chance of any one of the last four years coming from the gamma distribution defined by the first 25 years. The gamma distribution also has the property that a sum of n independent gamma variables, each with shape αi and identical scale θ, is itself gamma distributed with shape equal to ∑ni=1αi and the original scale θ (DeGroot 1986, 289). In this case, the probability of the last four years coming from the historical distribution is about 0.0000054. While this is almost 28 times more likely than under the normal assumption, it is still orders of magnitude smaller than any contiguous set of four years in the first 25 years.
The tests performed until now all depended on an assumption of distributional form. However, there are tests that can be used to determine whether or not the mean of one group of data is significantly different than that of another group without any assumptions about the underlying distributions. One of the more popular of these non-parametric tests is the Mann–Whitney–Wilcoxon (MWW) test (Thas 2010, 225–230). Given two sets of samples, not necessarily of equal size, the MWW test compares the null hypothesis that both sets of samples come from the same distribution against the alternative hypothesis that they do not. It does so through the assumption that if the two samples come from the same distribution, the probability of a randomly selected value from the first sample exceeding a randomly selected value from the second sample is equal to the reverse. More precisely, it tests the null hypothesis H0 : F1(x) = F2(x) ∀x ∈ S against the alternative hypothesis H1: P{X1 ≤ X2} ≠ 12 for the two-sided version, and {≤, ≥12} for the one-sided version. With the data under analysis, the alternative hypothesis is that the last four years are not only different from the first 25, but that they are larger, so the one-sided test is appropriate. Thus, the null hypothesis will be that the two sets of data tend to have similar magnitudes, and the alternative hypothesis will be that the first 25 years of data tend to have lower magnitudes than the last 4 years. Using the MWW’s asymptotic normal approximation, the test returns a (one-sided) p-value of 0.0012. Using the more precise calculation based on actual enumeration or Monte Carlo estimates of the distribution of the null hypothesis, as programmed by the coin package (Hothorn et al. 2008) for R, the “exact” p-value is calculated to be 0.00017. Once again, this demonstrates that from a classical perspective, the last four years’ results are generated from a different process than those of the first 25 years.
2.3. Prediction based on known changepoint
Now that the existence of a change in the loss process is recognized, how can the timing and magnitude of that change best be estimated? At this point, having shown that the last four years are statistically significantly different than the previous twenty-five, the simplest procedure is to parameterize a model using only those last four years.
The best-fitting option, according to the information criteria shown in Table 6, is the lognormal distribution, and the prediction for next year would be an expected loss of 27,968.53 with a standard deviation of 4,038.21. Unfortunately, this estimate is based on a small sample of the experience—possibly too small to give significant credibility to an estimate based solely on those four data elements. An actuary would certainly want to look for a complement of credibility and weight that against the four years’ experience, but what the complement of credibility should be, and how much weight to give it, remains an open question.
Table 6.MLE results for last 4 years
| Scale or Mean |
47.24 |
27,977.08 |
10.23 |
14,667,166.44 |
| Shape or SD |
592.25 |
4,196.69a
|
0.14a
|
412,183,303,322.15 |
| AICc |
93.79 |
94.09 |
93.66 |
105.91 |
aThe MLE estimate for the standard deviation of the normal and lognormal distribution is the population estimate, not the sample estimate.
2.4. Combined changepoint and distribution model
Another approach to the changepoint problem is to consider the distribution on both sides of the changepoint as one, with the changepoint itself being one of the parameters of the distribution. Under the assumption that there exists at most a single changepoint, m, at which the random variables switch from one distribution, F(x), to a different one, G(x), where m ∈ 1, 2, . . . , n, the likelihood of the entire problem can be written as:
L(X;m)=m−1∏i=1f(Xi)n∏i=mg(Xi)
Unlike prior approaches, such as Hinkley (1970), the advances in modern computing power and non-linear optimizers allow for investigating this problem with just the choice of distributional families to be made, and not presupposing the parameters of the distributions. Using the four distributional families from the previous section, and assuming that the family does not change across the changepoint—solely the parameters, Table 7 shows a reassuring finding in that for each family, the optimal changepoint is at year 26 as was presumed above. The full results are shown in Tables A2–A5.
Table 7.MLE results for combined changepoint analysis
| Changepoint |
26 |
26 |
26 |
26 |
| NLL |
281.36 |
281.60 |
281.57 |
314.53 |
| AICc |
575.33 |
575.81 |
575.74 |
641.67 |
3. A Bayesian approach
One shortcoming of the changepoint analysis methods based on classical statistical theory is that while they give an indication of when the change may have occurred, they cannot provide any measure of how likely the change is at that, or at any other, point. At best, an estimate of how likely or unlikely the result of the test is under the null hypothesis can be calculated, but that is not the same as calculating the actual probability of the results of the test. This is one of the fundamental differences between the classical approach to statistics and the Bayesian approach. A non-rigorous, but helpful, synopsis of the difference between the two is that the classical approach to probability believes that there are true, fixed parameters, and that an infinite set of trials would uncover those parameters. It is the finite sample size of the data that prevents us from uncovering those “true” parameters. The Bayesian approach believes that all unknowns are random variables and that the sample data is used to adjust the estimates about the parameters of the distribution—which are not fixed. However, this approach requires the recognition of a preconception about the universe, called an a priori, or prior, estimate, and then an analysis as to how the data changes that preconception to create an a posteriori, or posterior, estimate. For a good, and more comprehensive, introduction to Bayesian analysis, the interested reader is directed to Lynch (2007).
3.1. Finding the changepoint
An early Bayesian approach to changepoint analysis which focuses on finding the changepoint is discussed by Chernoff and Zacks (1964). Their framework assumes n independently and normally distributed random variables X1, X2, . . . , Xn with means μ1, μ2, . . . , μn and variances all equal to 1. Each μi is equal to μi−1 except at changepoints, where the mean shifts. The timing of the shifts follows an arbitrary, but specified, a priori distribution and the shifts themselves are normally distributed random variables with mean 0 and variance σ2. They then build a Bayesian framework in which to obtain the a posteriori distribution for μn—the current mean. They also construct a simpler “at most one change” (AMOC) test which is easier and more efficient to calculate. However, it suffers when there are multiple changes with one large earlier change, as that can “hide” other subsequent smaller one. To overcome this issue, and yet have a reasonable algorithm, they suggest an ad hoc method for estimating the a posteriori of the single changepoint, which uses the simpler AMOC test, on a growing sequence, starting from the penultimate observation back to the first. This way, in the shorter sequences, a later changepoint can be seen without being hidden by an earlier, larger one.
Adjusting the data to have σ2 = 1, which preserves the rank order, and then applying their procedure indicates clearly that the most likely time for a change was immediately after year 25, namely year 26. Tables A6 and A7 show the results of applying their process. Moving down the rows of the each table reflects checking for the “at most one change” starting at an earlier year, the values in the table are the a posteriori probability of the changepoint occurring after that point, and each row sums to 100%. When the a priori probability for a change to occur in any given year is 50%, Table A6 shows that the a posteriori of the change after year 25 is between 30% and 36%—significantly higher than any other year. Even when the a priori probability for a change to occur in any given year is only 5%, Table A7 shows that the a posteriori probability of the change being after year 25 remains consistently between 20% and 30%—still significantly higher than any other year. Unlike the classical methods above, this process can answer the question of what is the probability of the changepoint being a given year.
3.2. Hierarchical model
As with the classical approach, a combined changepoint and distributional model can be analyzed. The key difference is that in the classical approach, the analysis was restricted to the likelihood. The Bayesian approach requires an a priori estimate of the distribution, which allows for the calculation of an a posteriori distribution of the parameters as well (Carlin, Gelfand, and Smith 1992). Moreover, there can be explicit recognition that some parameters may jointly depend with other parameters on a set of hyperparameters. In Bayesian analysis, this is called a hierarchical model—a model where there is some sort of hierarchical structure to the parameters (Lynch 2007, 232). Creating a model with such structure allows the joint probability model to reflect potential dependencies between the parameters (Gelman et al. 2014, 101).
Assuming a parametric family based on θ and η for the pre- and post-changepoint distributions respectively, θ and η possibly being vector-valued, and a joint prior π(θ, η, m) on the parameters, the likelihood becomes:
L(X;m,θ,η)=m−1∏i=1f(Xi∣θ)n∏i=mg(Xi∣η)
and the joint distribution can be represented as:
L(X;m,θ,η)π(θ,η,m)
Analysis of hierarchical models is most often focused on developing a posterior distribution for m, the loss processes based on θ and η, and possibly their components. Models such as the one above can also be extended to a generalized hierarchical Bayesian framework with hyperparameters on θ and η as well (Carlin, Gelfand, and Smith 1992).
3.2.1. Basic hierarchical model
A basic hierarchical model would assume the same distributional form on either side of the changepoint and only allow the parameters of the distribution a one-time adjustment at the time of the changepoint. There are a number of tools which can be used to create the hierarchical model and relationships instead of having to build the Markov chain Monte Carlo (MCMC) code directly. This paper uses JAGS—Just Another Gibbs Sampler—(Plummer 2003), together with the runjags package (Denwood, in press), to create, run, and summarize the models.
In order to run JAGS using runjags, one needs to load both the data and a model. The data needs to be a named R list, while the model can either be a list or an external file. In this paper, the data is shown in Appendix B.14.1. The model files, some of which are replicated in Appendix B.14.2–B.14.4, describe the desired parameters—including hyperparameters if necessary, functions of those parameters, and any potential relationship between the parameters which should be modeled.
At this point, the a priori distribution of the model parameters needs to be formulated. Based on the classical analysis above, a reasonable assumption would be that the losses follow a gamma distribution with parameters α and θ, which themselves are allowed to “switch” on either side of the changepoint m. Both α and θ themselves need prior distributions. For that, the assumption will be made that the first 25 years are more authoritative, so αi : Γ(0.5,40); i ∈ {1,2} and θi: Γ(0.5,2000); i ∈ {1,2}. Thus, all α have an expected mean of 20 and all θ have an expected mean of 1,000, roughly based on Table 5, but the distributions have a wide enough CV to allow for values significantly different than the mean. The changepoint m itself is discretely uniformly distributed between 1 and 29. If the posterior distribution for the changepoint shows that the most likely value is at the endpoints, or equally likely throughout the span of time, that would imply the data does not indicate a change.
Some MCMC-specific selections also need to be made. In this paper, unless otherwise stated, all models will be run with 5 simultaneous chains, a thinning value of 3, and for 65,000 total iterations of which the first 20,000 are adaptation and burn-in. With each chain collecting 15,000 observations, the model distributions are based on a pooled 75,000 observations. One last important element is to select the starting point from which the MCMC chains will run. A poorly chosen start value can prevent convergence in reasonable time, especially for highly correlated parameters, as these are. The initial starting point for the parameters of the gamma distribution will be based on the expected values of their a priori distributions with some small random perturbations for each chain. The changepoint will start at either 1, 2, or 3 with probability 80%, 15%, and 5% respectively.
Table 8 summarizes some of the results of the Bayesian model. Most importantly, the model indicates that a changepoint exists, and that the distribution for the last 4 years is more severe than that of the first 25—as was expected. The mean of the posterior distribution for the changepoint is 25.08 and the mode of the posterior distribution for the changepoint is 25.99. The graph of the posterior distribution for m, shown in Figure 4, shows that the preponderance of the probability for the changepoint is around year 26, but that there is some small probability earlier, around years 6 and 7, which affects the mean. The mean of the posterior distribution for the pre-changepoint loss process, generated from the simulations of αprior and θprior, is approximately 17,768.43, and the best estimate of the mean of the post-changepoint loss process, generated from simulations of αpost and θpost, is 28,365.61. The R̂ value is the potential scale reduction factor (Gelman and Shirley 2011, 170), which is a diagnostic for checking convergence of the MCMC chains. When its value is near 1, below 1.1 is usually accepted as “near enough,” the chains are considered to have converged.
Table 8.Split gamma model—29 years
| Loss (year < m) |
17,768.43 |
16,800.77 |
1.02 |
| Loss (year ≥ m) |
28,365.61 |
27,314.80 |
1.00 |
| m |
25.08 |
25.99 |
1.00 |
| αprior |
18.44 |
17.22 |
1.02 |
| αpost |
30.86 |
14.56 |
1.00 |
| θprior |
1,051.69 |
900.11 |
1.00 |
| θpost |
1,404.32 |
693.19 |
1.00 |
| DIC |
576.46 |
pD |
7.51 |
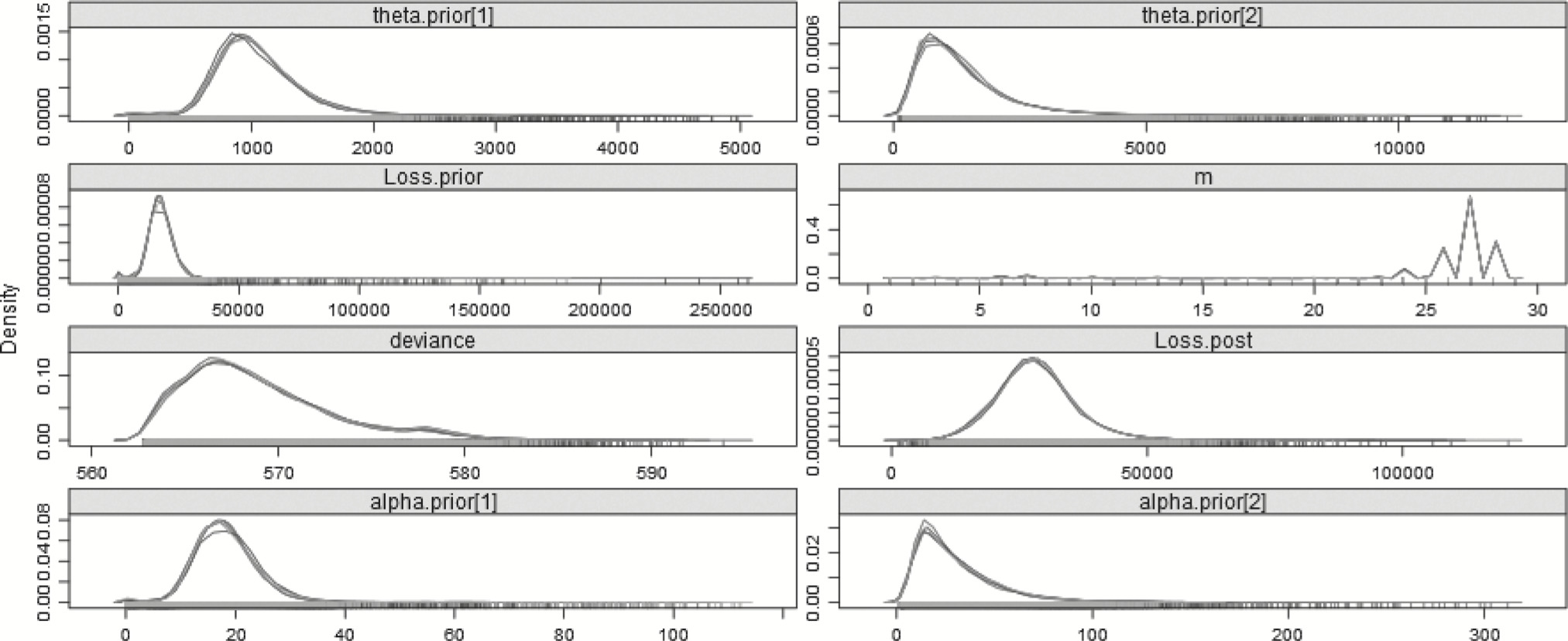
Figure 4.Posterior distributions of the parameters—29 years—Split model.
Another key difference between the classical and Bayesian approaches to analysis relates to error bounds. In classical analysis, one does not have a distribution of the parameters in question. When using p-values, it is not the uncertainty around the parameter that is being measured, but the likelihood of achieving the observed result given that the null hypothesis is true. For example, when rolling two fair six-sided dice, the probability of getting “snake-eyes”—a pair of ones—is 136, or 0.028. Using a p-value of 0.05 one would reject the null hypothesis that the dice are fair. Of course, a sample size of one should not be considered conclusive, but the p-value does not give us information about the distribution of the parameters. Similarly, α, the type-1 error, also does not give us information about the probability of the observed parameters but about the probability of improperly rejecting a true null hypothesis.
The Bayesian approach, however, is one that generates a probability distribution about parameters and other metrics of interest. In the case above, there is a posterior distribution not only around the shape and scale of the gamma, but around the expected loss as well. Therefore, instead of a 95% confidence interval around rejecting the null hypothesis, a 95% credible interval around the expected loss itself can be given. The interval suggested is usually the highest density interval (HDI), which is not the interval which trims the lowest and highest 2.5% (equal-tailed credible interval), but the smallest interval which comprises 95% of the probability (Kruschke 2014). For comparison, from Table 6, the MLE estimate for the gamma shape and scale post-changepoint were 47.24 and 592.25 respectively. Using the normal approximation to the gamma described in Krishnamoorthy, Mathew, and Mukherjee (2008), the 95% confidence interval would be (14,234.00–47,973.65). This is the interval in which rejecting the null hypothesis would be incorrect 95% of the time. From the analysis above, the 95% HDI for the post-changepoint loss is (12,761.10–44,057.50)—a slightly narrower range of smaller values. We can now talk about the distribution of the quantity of interest, not how often we may be incorrectly rejecting null hypotheses.
The last two entries in the table are measures of model fit and complexity. Information criteria, such as AICc, are used as model goodness-of-fit measures. To measure model effectiveness in the Bayesian context, Spiegelhalter et al. (2002) introduced DIC—the deviance information criterion. Just as AICc can be decomposed into likelihood and parameter components, DIC is a goodness-of-fit measure which reflects the loglikelihood of the model when using the posterior mean of the parameters subject to a penalty based on the number of “effective” parameters—pD. Twice the negative loglikelihood of the model when using the posterior mean of the parameters, together with some standardizing factor that often cancels out of any calculations, is called the deviance of the model, thus the name. When dealing with a hierarchical model, the structure of the model, together with the data upon which it is based, often results in having a lower value for effective parameters than their actual count. For example, if the hyperpriors affect lower-level parameters similarly, those lower-level parameters are not independent, and may not contribute “full-value” to the penalty.
Using DIC is one way different models can be compared, as long as they are based on the exact same data, of course. It is educational, therefore, to compare this model with one which has no split—there is only one α and one θ, both of whose posterior distributions are based on all 29 years. This model can be found in Appendix B.14.3, and plots of the posterior distributions can be found in Figure 5.

Figure 5.Posterior distributions of the parameters—29 years—No-split model.
Table 9 shows a difference in the DIC between the models. When comparing information criteria across models, regardless of the type of criterion, it is not the magnitude of the value, but the difference between the lowest value and all the others, which is important (Burnham and Anderson 2002, 63). Rules of thumb for AICc and DIC are that a difference of 0–2 implies model similarity, a difference of 4–7 shows that the model with the higher value has little support with respect to the model with the lower value, and larger differences imply that the higher-valued model should really not be considered at all (Burnham and Anderson 2002, 70–71; Spiegelhalter et al. 2002). Often, however, there is no one model that dominates all the others, but a group of models that each performs relatively well. In these cases, multimodel inference may be a better approach than selecting one model over all others (Burnham and Anderson 2002). Here, the split model has a DIC of about 4.79 less than that of the non-split model. Thus, it is reasonable to say that the split model does a significantly better job than the non-split model in explaining the full 29 years of data.
Table 9.No-split gamma model—29 years
| Loss |
19,171.06 |
17,638.49 |
1.00 |
| α |
13.29 |
12.11 |
1.00 |
| θ |
1,541.60 |
1,348.39 |
1.00 |
| DIC |
581.25 |
pD |
2.05 |
3.2.2. Step-change model
The model in section 3.2.1 assumed a new set of parameters on either side of the changepoint. The flexibility of the Bayesian framework allows a different model to be investigated—one which assumes a long-term set of parameters to which a change may be added or subtracted at a point in time. This differs from the previous philosophy in that the parameters “gleaned” from the data prior to the changepoint are still used when fitting the data beyond the changepoint. This type of model is often referred to as a “step-change” model. There is a much-analyzed dataset in changepoint statistical literature (Jarett 1979) for which the step-change model described in Albert (2009, 268–272) can be adapted to the data in this paper. The step-change model used is replicated in section B.14.4.
The same a priori assumptions made for the prior hyperparameters in section 3.2.1 will apply to this model. What is different now is that instead of having pre- and post-changepoint parameters, there will be one long-term prior α and long-term prior θ to which “step” parameters, either positive or negative, will be added. These parameters will be both set as N : (μ = 0, σ2 = 104), to represent uninformed priors and the “changed” α and θ will be constrained to be positive to ensure the distribution is valid. Table 10 summarizes the result of using this model to explain the full 29 years of data, with the posterior distribution plotted in Figure 6.
Table 10.Step-change gamma model—29 years
| Loss (year < m) |
17,832.83 |
17,342.10 |
1.00 |
| Loss (year ≥ m) |
29,055.73 |
27,001.05 |
1.00 |
| m |
26.09 |
25.99 |
1.03 |
| αprior |
19.36 |
17.44 |
1.05 |
| αstep |
13.03 |
10.62 |
1.00 |
| θprior |
988.76 |
863.08 |
1.00 |
| θstep |
−9.14 |
−13.01 |
1.00 |
| DIC |
573.96 |
pD |
6.20 |
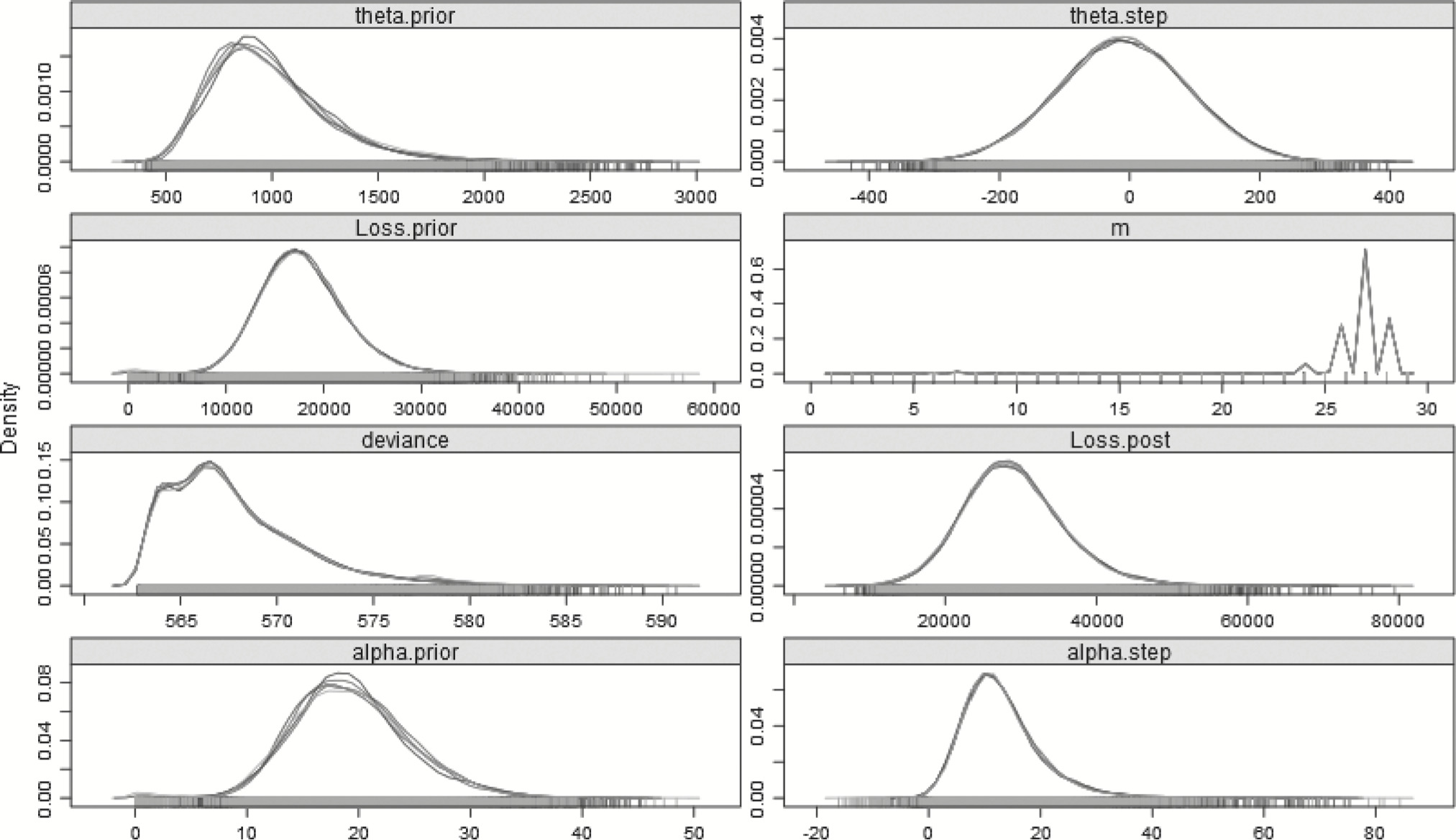
Figure 6.Posterior distributions of the parameters—29 years—Step-change model.
The step-change model’s DIC is about 2.50 lower than that of the split model, and 7.29 less than the no-split model, which implies that the step-change model is somewhat better than the split model, and far better than the no-split model, in explaining the full 29 years of data. The step-change idea is not dissimilar to having a form of credibility-weighting, where weight is given to both the pre- and post-change year experience. Using the step-change model, the 95% HDI is (16,375.40–42,661.50), noticeably narrower than that of the split model.
4. Sensitivity testing
One of the key differences between classical and Bayesian analysis, the necessity to have an a priori distribution, is itself one of its key strengths. Requiring each analysis to have an explicit preconception about the data allows analyses based on different preconceptions. Another important question would be how sensitive is the finding of a changepoint to the last few years? What would the results have been if this analysis was done last year, or the year before, or the year before that? In the Bayesian framework, both of these questions can be addressed.
In the basic hierarchical model described in section 3.2.1, a discrete uniform prior (MPrior in the model) was used for the changepoint. Instead, an “informed” prior can be substituted. If, for example, there was reason to believe that a change has not occurred, one could put more weight on the probability that the first year is the changepoint. Adjusting the model so that there is a 50% probability that the first year is the changepoint, with the rest of the probability split evenly across the remaining 28 years, can be easily implemented by changing the MPrior vector in the data file to have the first entry be 28 instead of 1. Now a full 50% weight is given to the first year, which is 28 times as likely to have the changepoint as any one other year, or equally likely to have the changepoint as opposed to all the rest of them combined. Table 11 summarizes the key parameters and the plots of the posterior distributions are in Figure 7.
Table 11.Split gamma model—29 years—50% weight given to m 1
| Loss (year < m) |
18,026.98 |
677.80 |
1.01 |
| Loss (year ≥ m) |
24,954.49 |
23,559.39 |
1.00 |
| m |
16.14 |
26.44 |
1.00 |
| αprior |
18.98 |
15.77 |
1.02 |
| αpost |
24.78 |
12.88 |
1.01 |
| θprior |
1,019.15 |
924.62 |
1.01 |
| θpost |
1,450.41 |
1,292.84 |
1.01 |
| DIC |
580.91 |
pD |
8.12 |

Figure 7.Posterior distributions of the parameters—29 years—Split model—50% prior for m 1.
Despite the fact that so much weight is given to the first year, the most probable changepoint, the mode of the posterior distribution for m, remains year 26. However, as the plots show, the unbalanced prior of no changepoint is almost as likely. This explains why the mean of the posterior distribution for loss subsequent to the changepoint is lower than the mode, as almost as often as not, the changepoint is year 1, and all the losses must come from one gamma distribution. This model’s DIC, however, indicates that it is an inferior model to the step and split models, and not significantly better than the no-split model, and so should be ignored in favor of the split, or more accurately, the step model. This model is valuable in demonstrating that an a priori assumption of a full 50% weight given to no change still results in the most likely changepoint being year 26.
4.2. Looking back
From both the classical and Bayesian perspective, there is strong reason to believe that there has been a change in the underlying severity distribution. Of course, this is supported by three out of the last four years being significantly different than the previous twenty-some-odd years. A question that can be considered is were this model to have been run last year, would the results be different? This is easily considered by realizing that the only difference would be that there would have been 28 data points instead of 29. The data file can be adjusted so that N is defined as 28, the value 34,737.79201 is removed from the loss list, and that there are only 28 entries in the changepoint prior likelihood list. Table 12 reflects the application of the split model to the first 28 years.
Table 12.Split gamma model—28 years
| Loss (year < m) |
18,237.98 |
16,487.88 |
1.01 |
| Loss (year ≥ m) |
23,301.63 |
23,632.81 |
1.00 |
| m |
18.36 |
26.19 |
1.00 |
| αprior |
18.97 |
16.45 |
1.01 |
| αpost |
29.55 |
15.79 |
1.01 |
| θprior |
1,087.07 |
878.86 |
1.00 |
| θpost |
1,254.64 |
1,004.22 |
1.01 |
| DIC |
555.17 |
pD |
7.11 |
From the plot of the change year, shown in Figure 8, it can be seen that similarly to section 4.1, the mean changepoint is more truly an average of a bimodal distribution. While year 26 is still the most likely time for a change to have happened, the first 10 years indicate some possibility of being the changepoint as well. With the changepoint having more possibility of being earlier, the posterior estimate of the mean of the losses post-changepoint is lower, similar to section 4.1. More years of loss would be attributed to the post-changepoint regime, most of which are lower than the last four years. As the data has changed—only 28 years are used—the DIC cannot be compared with previous models.

Figure 8.Posterior distributions of the parameters—28 years—Split model.
Using the step-change model instead of the split mode, the results in Table 13 and Figure 9 are obtained. Similar to the results on the full 29 years of data, the step model’s DIC is lower than the split model’s DIC by 0.89, indicating that the step model does perform better in explaining the data restricted to the first 28 years, although the convergence for the loss pre-changepoint is more strained.
Table 13.Gamma model—28 years
| Loss (year < m) |
17,389.28 |
16,707.15 |
1.05 |
| Loss (year ≥ m) |
24,197.88 |
23,266.71 |
1.00 |
| m |
20.72 |
26.14 |
1.01 |
| αprior |
19.44 |
18.28 |
1.02 |
| αstep |
8.83 |
4.98 |
1.02 |
| θprior |
963.36 |
819.33 |
1.00 |
| θstep |
−10.11 |
−2.25 |
1.00 |
| DIC |
553.35 |
pD |
6.23 |

Figure 9.Posterior distributions of the parameters—28 years—Step-change model.
Continuing the pattern, applying the split model to the first 27 years is summarized in Table 14 and plotted in Figure 10. Should this analysis have been run two years ago, the density plots indicate that a change any time in the first 10 years, especially around year 8, would have been just as, if not more, likely as one around year 26. Moreover, the shape and scale parameters are less different, and the means of the posterior distributions for loss are also relatively close. The 27-year step-change model is summarized in Table 15 and plotted in Figure 11.
Table 14.Split gamma model—27 years
| Loss (year < m) |
17,142.38 |
15,818.04 |
1.00 |
| Loss (year ≥ m) |
19,997.55 |
18,149.93 |
1.00 |
| m |
10.66 |
1.09 |
1.00 |
| αprior |
19.66 |
16.03 |
1.01 |
| αpost |
23.58 |
16.94 |
1.01 |
| θprior |
1,066.64 |
874.06 |
1.01 |
| θpost |
1,111.37 |
930.69 |
1.01 |
| DIC |
533.08 |
pD |
5.37 |

Figure 10.Posterior distributions of the parameters—27 years—Split model.
Table 15.Step-change gamma model—27 years
| Loss (year < m) |
16,520.26 |
15,312.43 |
1.09 |
| Loss (year ≥ m) |
20,585.93 |
18,827.06 |
1.00 |
| m |
13.18 |
7.26 |
1.00 |
| αprior |
18.60 |
16.67 |
1.03 |
| αstep |
5.05 |
3.24 |
1.06 |
| θprior |
946.99 |
834.44 |
1.00 |
| θstep |
1.14 |
−6.67 |
1.00 |
| DIC |
531.96 |
pD |
5.08 |
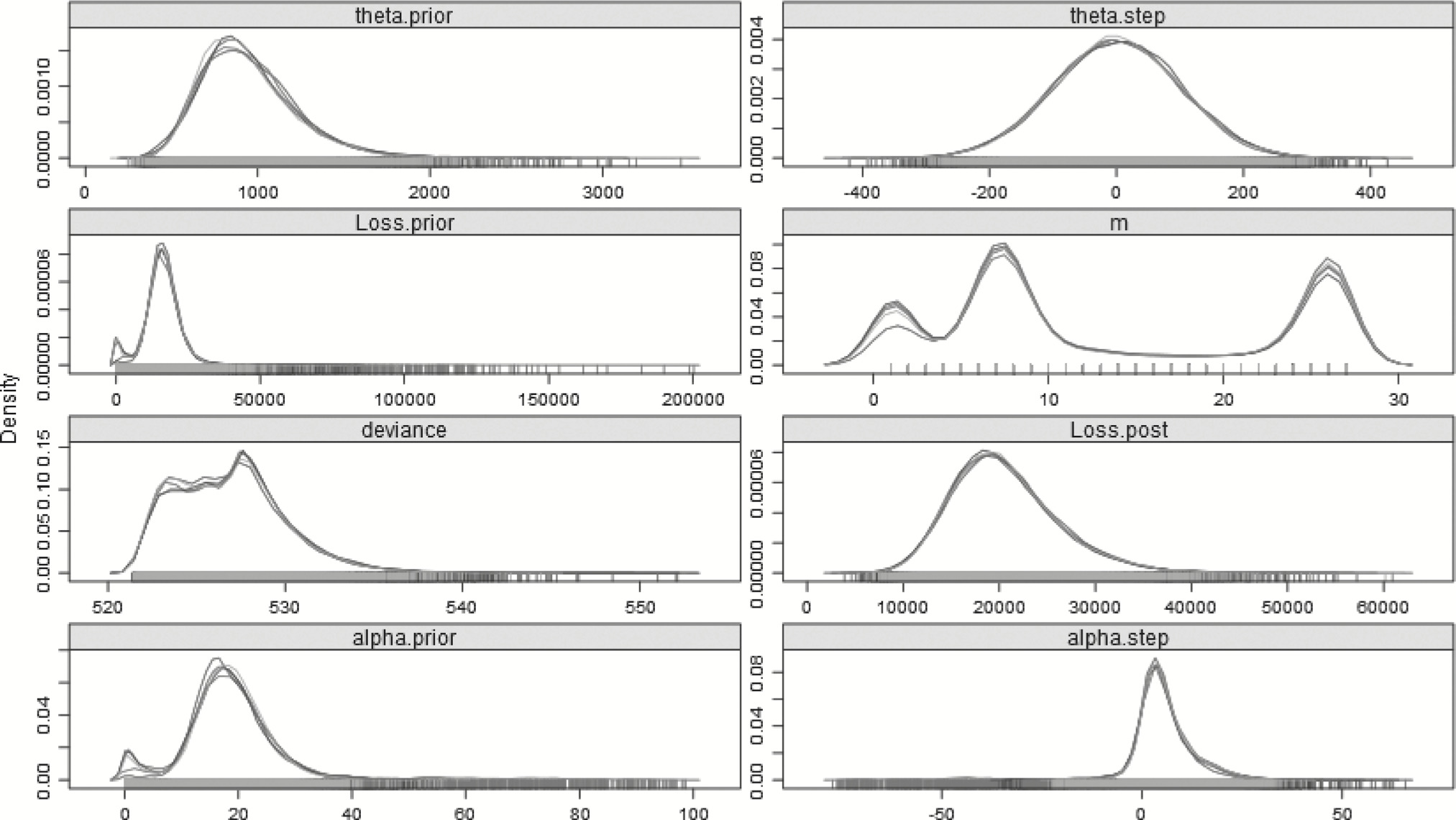
Figure 11.Posterior distributions of the parameters—27 years—Step-change model.
What can be seen from the tables is that as the number of years of available data decreases, for the step models, the R̂ convergence statistic rises, and at 27 years, it is near 1.10. Variables often have difficulty achieving convergence when their posterior distributions are highly correlated (Stan Development Team 2013, vi). In this case, where there are only two years post changepoint for the step to be active, and the post-changepoint loss depends on the highly correlated sets of prior and step parameters, standard MCMC often takes an inordinately long time, and may never properly converge.
Finally, Table 16 and Figure 12 show the results of running the no-split model against the 27 years of data. The no-split model’s DIC is 1.93 lower than the split model and 0.81 lower than the barely-converging step model, which indicates that while the models have similar explanatory powers as regards first 27 years, the no-split model would be preferred, or given more weight in a multimodel inference procedure.
Table 16.No-split gamma model—27 years
| Loss |
18,239.88 |
17,652.77 |
1.00 |
| α |
17.56 |
15.95 |
1.00 |
| θ |
1,116.63 |
954.94 |
1.00 |
| DIC |
531.15 |
pD |
2.02 |
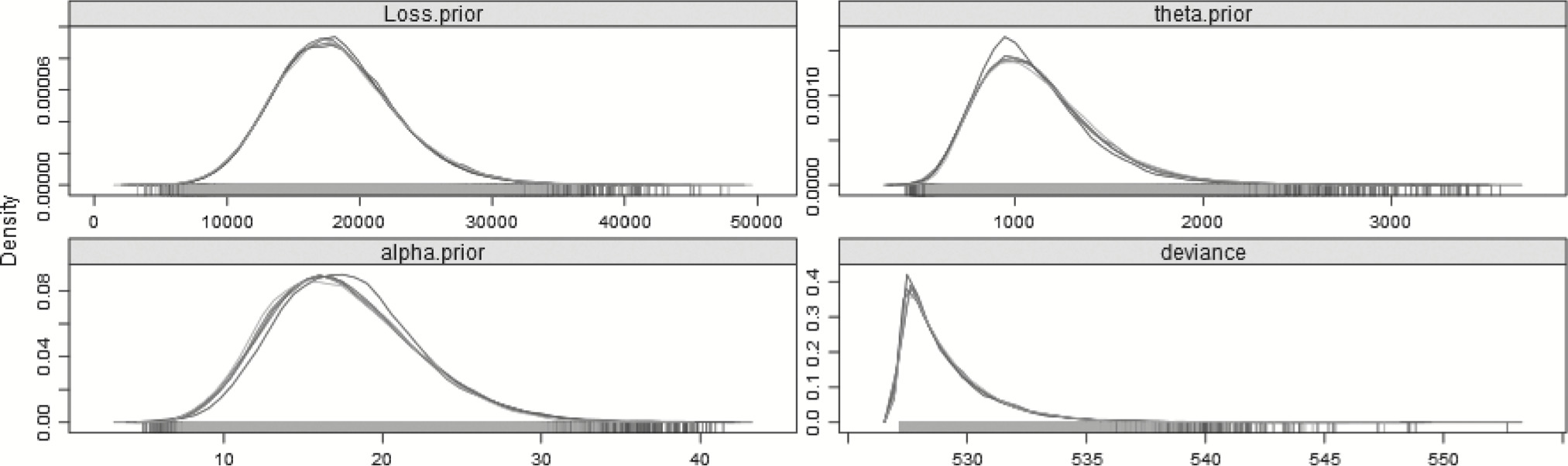
Figure 12.Posterior distributions of the parameters—27 years—No-split model.
Thus, the sensitivity testing supports that it is the recent run of three years that made the initial results so convincing, and that had this analysis been done previously, the decision may have been different. When compared to a prediction based on the classic 10-year rolling average, the Bayesian procedure appears to be more responsive, as seen in Figure 13, where using the 10-year rolling average as a prediction is plotted using the dotted lines, the split-model predictions using dashed lines, and the actual observations using solid lines.

Figure 13.Actual losses, 10-year moving averages, and Bayesian predictions for years 28–30.
5. Conclusion
This paper demonstrated both classical and Bayesian approaches to a changepoint problem. The issues of both changepoint identification and predictive value were addressed. All of the analyses can be performed using easily accessible free and open-source software. For the Bayesian approach, the ability to separate data and model files allow for sensitivity and “what-if” testing to be done efficiently and easily, and more complex questions can be addressed by starting with simpler models and building on them. It is hoped that the code provided in Appendix B will stimulate readers to apply this kind of analysis to their own problems, and serve as a building block for more complex analyses. Future investigations may include building more complex hierarchical models including multiple changepoints or allowing different distributional forms, using more sophisticated sampling and MCMC techniques to handle highly correlated cases, and extending this kind of analysis beyond a pricing exercise.
Acknowledgments
The author wishes to thank John A. Major and the anonymous reviewers for their helpful comments and suggestions. Any errors in the paper are solely the author’s own.
Appendix
Appendix A. Tables
Table A1.Data and ranks
| 1 |
16,527 |
13 |
| 2 |
19,424 |
17 |
| 3 |
15,261 |
6 |
| 4 |
15,379 |
7 |
| 5 |
9,460 |
1 |
| 6 |
13,203 |
3 |
| 7 |
17,753 |
14 |
| 8 |
22,563 |
22 |
| 9 |
19,433 |
18 |
| 10 |
24,110 |
24 |
| 11 |
15,932 |
10 |
| 12 |
16,009 |
11 |
| 13 |
26,602 |
27 |
| 14 |
20,217 |
20 |
| 15 |
13,437 |
4 |
| 16 |
22,168 |
21 |
| 17 |
16,189 |
12 |
| 18 |
20,140 |
19 |
| 19 |
18,517 |
15 |
| 20 |
14,943 |
5 |
| 21 |
23,189 |
23 |
| 22 |
15,747 |
9 |
| 23 |
11,999 |
2 |
| 24 |
19,407 |
16 |
| 25 |
15,597 |
8 |
| 26 |
24,750 |
26 |
| 27 |
24,200 |
25 |
| 28 |
28,221 |
28 |
| 29 |
34,738 |
29 |
Table A2.MLE results for combined loss and changepoint—gammaa
| 1 |
288.62 |
13.49 |
1,418.93 |
0.00 |
0.00 |
| 2 |
285.16 |
10,000.00 |
1.65 |
13.16 |
1,461.93 |
| 3 |
287.01 |
153.69 |
116.96 |
12.69 |
1,514.76 |
| 4 |
286.60 |
98.34 |
173.59 |
12.52 |
1,547.60 |
| 5 |
285.63 |
103.84 |
160.32 |
12.34 |
1,582.94 |
| 6 |
286.48 |
18.97 |
801.84 |
14.96 |
1,334.53 |
| 7 |
285.32 |
21.44 |
693.93 |
15.83 |
1,279.30 |
| 8 |
285.32 |
22.75 |
672.09 |
15.33 |
1,328.63 |
| 9 |
286.55 |
17.71 |
914.78 |
14.76 |
1,373.30 |
| 10 |
286.70 |
18.64 |
887.98 |
14.08 |
1,442.33 |
| 11 |
287.57 |
16.10 |
1,075.35 |
13.69 |
1,468.15 |
| 12 |
287.16 |
17.52 |
980.80 |
13.48 |
1,508.65 |
| 13 |
286.67 |
18.97 |
900.96 |
13.28 |
1,550.59 |
| 14 |
287.79 |
15.58 |
1,143.85 |
13.29 |
1,521.43 |
| 15 |
287.80 |
16.47 |
1,092.48 |
12.47 |
1,621.53 |
| 16 |
287.28 |
16.26 |
1,087.68 |
13.31 |
1,555.33 |
| 17 |
287.55 |
16.44 |
1,092.75 |
12.43 |
1,656.27 |
| 18 |
287.12 |
17.29 |
1,033.30 |
12.13 |
1,727.19 |
| 19 |
287.02 |
18.04 |
997.15 |
11.15 |
1,885.44 |
| 20 |
286.66 |
19.02 |
947.32 |
10.33 |
2,060.86 |
| 21 |
286.03 |
19.41 |
920.29 |
10.59 |
2,075.37 |
| 22 |
286.35 |
19.09 |
948.83 |
9.47 |
2,305.75 |
| 23 |
285.66 |
19.68 |
915.14 |
9.46 |
2,399.58 |
| 24 |
284.56 |
18.32 |
968.99 |
15.73 |
1,556.30 |
| 25 |
284.08 |
18.99 |
938.32 |
15.46 |
1,649.72 |
| 26 |
281.36 |
19.52 |
907.99 |
47.24 |
592.25 |
| 27 |
282.51 |
18.60 |
967.53 |
45.47 |
638.95 |
| 28 |
282.59 |
18.13 |
1,005.33 |
93.00 |
338.50 |
| 29 |
281.92 |
16.50 |
1,126.58 |
10,000.00 |
3.47 |
aValues for row 2 and 29 are not reliable as MLE does not necessarily converge properly when there is only one data point. Parameters were capped at unreasonable values to prevent even more unreasonable results.
Table A3.MLE results for combined loss and changepoint—normala
| 1 |
290.01 |
19,141.96 |
5,330.97 |
0.00 |
0.00 |
| 2 |
287.51 |
16,527.24 |
500.00 |
19,235.34 |
5,401.97 |
| 3 |
288.25 |
17,975.62 |
1,448.38 |
19,228.35 |
5,500.97 |
| 4 |
287.70 |
17,070.73 |
1,742.47 |
19,380.95 |
5,549.40 |
| 5 |
286.61 |
16,647.87 |
1,677.36 |
19,541.01 |
5,600.14 |
| 6 |
287.45 |
15,210.31 |
3,243.03 |
19,961.05 |
5,315.77 |
| 7 |
286.25 |
14,875.83 |
3,053.48 |
20,254.86 |
5,235.86 |
| 8 |
285.96 |
15,286.87 |
3,000.92 |
20,368.57 |
5,325.69 |
| 9 |
287.46 |
16,196.44 |
3,697.43 |
20,264.06 |
5,428.93 |
| 10 |
287.39 |
16,556.07 |
3,631.35 |
20,305.61 |
5,559.74 |
| 11 |
288.49 |
17,311.48 |
4,123.57 |
20,105.36 |
5,633.44 |
| 12 |
287.91 |
17,186.05 |
3,951.63 |
20,337.23 |
5,698.88 |
| 13 |
287.26 |
17,088.00 |
3,797.35 |
20,591.81 |
5,763.77 |
| 14 |
288.81 |
17,819.86 |
4,442.76 |
20,216.16 |
5,735.72 |
| 15 |
288.66 |
17,991.10 |
4,325.45 |
20,216.09 |
5,923.82 |
| 16 |
288.16 |
17,687.52 |
4,330.41 |
20,700.28 |
5,837.94 |
| 17 |
288.31 |
17,967.56 |
4,330.91 |
20,587.37 |
6,043.57 |
| 18 |
287.76 |
17,862.95 |
4,222.38 |
20,953.89 |
6,149.96 |
| 19 |
287.48 |
17,989.44 |
4,136.43 |
21,027.89 |
6,418.31 |
| 20 |
286.94 |
18,017.22 |
4,027.83 |
21,278.95 |
6,679.88 |
| 21 |
286.20 |
17,863.50 |
3,982.61 |
21,982.97 |
6,680.00 |
| 22 |
286.49 |
18,117.08 |
4,048.69 |
21,832.27 |
7,070.77 |
| 23 |
285.66 |
18,009.36 |
3,986.29 |
22,701.56 |
7,147.92 |
| 24 |
284.71 |
17,748.05 |
4,086.79 |
24,485.29 |
6,110.35 |
| 25 |
283.97 |
17,817.15 |
4,014.45 |
25,501.02 |
6,213.96 |
| 26 |
281.60 |
17,728.34 |
3,957.33 |
27,977.08 |
4,196.69 |
| 27 |
282.62 |
17,998.38 |
4,108.68 |
29,052.94 |
4,342.02 |
| 28 |
282.57 |
18,228.08 |
4,198.55 |
31,479.33 |
3,258.47 |
| 29 |
282.52 |
18,584.96 |
4,520.74 |
34,737.79 |
500.00 |
aValues for row 2 and 29 are not reliable as MLE does not necessarily converge properly when there is only one data point. Parameters were capped at unreasonable values to prevent even more unreasonable results.
Table A4.MLE results for combined loss and changepoint—lognormala
| 1 |
288.46 |
9.82 |
0.27 |
0.00 |
0.00 |
| 2 |
285.06 |
9.71 |
0.01 |
9.83 |
0.28 |
| 3 |
286.89 |
9.79 |
0.081 |
9.82 |
0.28 |
| 4 |
286.55 |
9.74 |
0.10 |
9.83 |
0.29 |
| 5 |
285.63 |
9.72 |
0.097 |
9.84 |
0.29 |
| 6 |
286.38 |
9.60 |
0.24 |
9.87 |
0.26 |
| 7 |
285.22 |
9.58 |
0.22 |
9.88 |
0.25 |
| 8 |
285.36 |
9.61 |
0.22 |
9.89 |
0.26 |
| 9 |
286.48 |
9.66 |
0.25 |
9.88 |
0.26 |
| 10 |
286.73 |
9.69 |
0.24 |
9.88 |
0.27 |
| 11 |
287.52 |
9.73 |
0.26 |
9.87 |
0.27 |
| 12 |
287.19 |
9.72 |
0.25 |
9.88 |
0.27 |
| 13 |
286.79 |
9.72 |
0.24 |
9.89 |
0.28 |
| 14 |
287.73 |
9.76 |
0.26 |
9.88 |
0.27 |
| 15 |
287.82 |
9.77 |
0.25 |
9.87 |
0.28 |
| 16 |
287.29 |
9.75 |
0.25 |
9.90 |
0.27 |
| 17 |
287.59 |
9.77 |
0.25 |
9.89 |
0.28 |
| 18 |
287.24 |
9.76 |
0.25 |
9.91 |
0.29 |
| 19 |
287.22 |
9.77 |
0.24 |
9.91 |
0.30 |
| 20 |
286.95 |
9.77 |
0.24 |
9.92 |
0.31 |
| 21 |
286.36 |
9.76 |
0.23 |
9.95 |
0.31 |
| 22 |
286.70 |
9.78 |
0.23 |
9.94 |
0.33 |
| 23 |
286.07 |
9.77 |
0.23 |
9.98 |
0.34 |
| 24 |
284.84 |
9.76 |
0.24 |
10.07 |
0.26 |
| 25 |
284.51 |
9.76 |
0.23 |
10.11 |
0.26 |
| 26 |
281.57 |
9.76 |
0.23 |
10.23 |
0.14 |
| 27 |
282.78 |
9.77 |
0.24 |
10.27 |
0.15 |
| 28 |
282.93 |
9.78 |
0.24 |
10.35 |
0.10 |
| 29 |
282.18 |
9.80 |
0.25 |
10.46 |
0.01 |
aValues for row 2 and 29 are not reliable as MLE does not necessarily converge properly when there is only one data point. Parameters were capped at unreasonable values to prevent even more unreasonable results.
Table A5.MLE results for combined loss and changepoint—Paretoa
| 1 |
314.93 |
4,046,223.25 |
77,774,516,626.88 |
0.00 |
0.00 |
| 2 |
316.41 |
0.23 |
209.62 |
11,283,084.59 |
217,010,623,797.69 |
| 3 |
314.93 |
11,754,517.26 |
212,243,020,458.65 |
21,630,174.57 |
417,769,438,224.60 |
| 4 |
314.91 |
11,818,702.42 |
202,659,258,666.88 |
7,967,909.34 |
154,421,619,973.69 |
| 5 |
314.89 |
21,726,760.23 |
363,324,415,575.75 |
13,534,438.18 |
265,660,278,575.22 |
| 6 |
314.79 |
1,428,416.19 |
21,745,404,704.90 |
9,746,105.91 |
194,540,524,750.42 |
| 7 |
314.72 |
4,046,644.53 |
60,197,483,451.95 |
4,046,213.41 |
81,956,473,256.65 |
| 8 |
314.72 |
674,614.82 |
10,312,424,171.49 |
21,506,651.48 |
440,019,348,785.54 |
| 9 |
314.79 |
9,807,891.64 |
159,563,627,282.92 |
20,096,176.08 |
409,051,462,334.91 |
| 10 |
314.80 |
2,222,878.21 |
36,802,949,953.89 |
155,510.45 |
3,157,679,260.96 |
| 11 |
314.86 |
44,263,694.49 |
769,696,137,860.09 |
16,812,772.01 |
339,541,564,002.52 |
| 12 |
314.83 |
24,142,337.18 |
416,757,851,832.29 |
28,028,782.79 |
572,593,331,539.20 |
| 13 |
314.81 |
4,061,151.14 |
69,429,197,580.31 |
4,063,953.20 |
83,665,320,908.97 |
| 14 |
314.87 |
9,085,553.03 |
161,892,445,389.15 |
15,331,984.14 |
309,943,740,977.08 |
| 15 |
314.88 |
24,725,915.46 |
446,845,775,847.67 |
24,703,975.26 |
501,662,345,580.49 |
| 16 |
314.84 |
8,195,815.50 |
144,969,177,021.88 |
8,711,674.07 |
180,321,267,099.25 |
| 17 |
314.86 |
12,663,810.66 |
227,557,899,887.73 |
15,673,518.08 |
322,694,335,744.16 |
| 18 |
314.84 |
16,541,946.87 |
296,825,695,133.74 |
675,436.01 |
14,155,449,927.80 |
| 19 |
314.85 |
4,046,241.75 |
73,091,855,189.21 |
15,389,349.06 |
323,634,871,362.93 |
| 20 |
314.84 |
4,046,232.16 |
72,900,184,441.45 |
177,839.94 |
3,784,201,190.10 |
| 21 |
314.79 |
673,097.17 |
12,023,799,320.98 |
1,658,693.03 |
36,462,800,857.88 |
| 22 |
314.83 |
28,970,769.73 |
527,210,331,049.49 |
14,855,219.87 |
324,351,675,507.97 |
| 23 |
314.78 |
4,063,079.15 |
73,172,505,179.95 |
1,443,019.76 |
32,758,897,325.45 |
| 24 |
314.67 |
4,046,242.47 |
72,110,995,225.37 |
27,883,334.39 |
685,795,311,106.64 |
| 25 |
314.64 |
4,046,232.16 |
72,089,606,864.56 |
673,097.08 |
17,164,553,964.32 |
| 26 |
314.53 |
2,222,436.85 |
39,406,144,233.44 |
14,668,587.95 |
411,957,598,899.48 |
| 27 |
314.58 |
4,046,232.40 |
72,825,896,800.90 |
22,410,960.21 |
653,856,701,803.49 |
| 28 |
314.60 |
7,330,713.30 |
133,625,884,112.08 |
19,887,018.35 |
628,829,953,858.90 |
| 29 |
314.71 |
12,607,465.11 |
234,192,258,008.28 |
62.97 |
2,170,218.12 |
aValues for row 2 and 29 are not reliable as MLE does not necessarily converge properly when there is only one data point. Parameters were capped at unreasonable values to prevent even more unreasonable results.
Table A6.ab. Chernoff–Zacks procedure on adjusted dataa, a priori probability of change in a given year—50%
|
m ↓ bk → |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
m |
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.479 |
0.521 |
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.322 |
0.352 |
0.327 |
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.205 |
0.262 |
0.288 |
0.245 |
| 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.229 |
0.198 |
0.248 |
0.203 |
0.122 |
| 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.081 |
0.234 |
0.195 |
0.235 |
0.169 |
0.086 |
| 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.071 |
0.085 |
0.332 |
0.199 |
0.187 |
0.093 |
0.034 |
| 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.021 |
0.073 |
0.089 |
0.366 |
0.196 |
0.165 |
0.069 |
0.021 |
| 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.020 |
0.020 |
0.057 |
0.078 |
0.318 |
0.203 |
0.189 |
0.087 |
0.028 |
| 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.019 |
0.013 |
0.018 |
0.062 |
0.084 |
0.352 |
0.201 |
0.169 |
0.066 |
0.018 |
| 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.012 |
0.016 |
0.011 |
0.017 |
0.060 |
0.083 |
0.351 |
0.202 |
0.168 |
0.063 |
0.016 |
| 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.012 |
0.011 |
0.015 |
0.011 |
0.016 |
0.057 |
0.080 |
0.340 |
0.204 |
0.173 |
0.065 |
0.017 |
| 13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.011 |
0.009 |
0.009 |
0.014 |
0.010 |
0.016 |
0.059 |
0.082 |
0.354 |
0.202 |
0.163 |
0.057 |
0.013 |
| 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.011 |
0.010 |
0.009 |
0.009 |
0.013 |
0.010 |
0.015 |
0.054 |
0.078 |
0.332 |
0.205 |
0.174 |
0.064 |
0.016 |
| 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.012 |
0.008 |
0.009 |
0.008 |
0.008 |
0.013 |
0.009 |
0.015 |
0.058 |
0.082 |
0.358 |
0.201 |
0.157 |
0.051 |
0.011 |
| 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.008 |
0.009 |
0.007 |
0.008 |
0.008 |
0.008 |
0.013 |
0.009 |
0.015 |
0.056 |
0.080 |
0.349 |
0.203 |
0.162 |
0.053 |
0.012 |
| 17 |
|
|
|
|
|
|
|
|
|
|
|
|
0.016 |
0.012 |
0.009 |
0.008 |
0.008 |
0.008 |
0.008 |
0.012 |
0.010 |
0.015 |
0.049 |
0.073 |
0.309 |
0.203 |
0.179 |
0.067 |
0.016 |
| 18 |
|
|
|
|
|
|
|
|
|
|
|
0.012 |
0.008 |
0.008 |
0.008 |
0.007 |
0.007 |
0.007 |
0.008 |
0.012 |
0.009 |
0.015 |
0.051 |
0.075 |
0.323 |
0.204 |
0.173 |
0.061 |
0.014 |
| 19 |
|
|
|
|
|
|
|
|
|
|
0.010 |
0.011 |
0.006 |
0.006 |
0.007 |
0.006 |
0.007 |
0.007 |
0.007 |
0.012 |
0.009 |
0.014 |
0.052 |
0.077 |
0.334 |
0.203 |
0.166 |
0.055 |
0.012 |
| 20 |
|
|
|
|
|
|
|
|
|
0.012 |
0.008 |
0.008 |
0.007 |
0.007 |
0.007 |
0.006 |
0.007 |
0.007 |
0.008 |
0.011 |
0.009 |
0.014 |
0.049 |
0.073 |
0.312 |
0.203 |
0.175 |
0.062 |
0.014 |
| 21 |
|
|
|
|
|
|
|
|
0.010 |
0.009 |
0.008 |
0.008 |
0.006 |
0.006 |
0.007 |
0.006 |
0.007 |
0.007 |
0.007 |
0.011 |
0.009 |
0.014 |
0.048 |
0.072 |
0.310 |
0.203 |
0.176 |
0.062 |
0.014 |
| 22 |
|
|
|
|
|
|
|
0.011 |
0.009 |
0.009 |
0.007 |
0.007 |
0.007 |
0.007 |
0.007 |
0.006 |
0.007 |
0.007 |
0.008 |
0.011 |
0.009 |
0.014 |
0.046 |
0.070 |
0.296 |
0.201 |
0.180 |
0.066 |
0.015 |
| 23 |
|
|
|
|
|
|
0.011 |
0.009 |
0.008 |
0.007 |
0.007 |
0.007 |
0.006 |
0.006 |
0.006 |
0.006 |
0.007 |
0.007 |
0.007 |
0.011 |
0.009 |
0.014 |
0.046 |
0.070 |
0.300 |
0.202 |
0.177 |
0.064 |
0.014 |
| 24 |
|
|
|
|
|
0.012 |
0.011 |
0.007 |
0.007 |
0.005 |
0.006 |
0.007 |
0.005 |
0.005 |
0.006 |
0.005 |
0.006 |
0.006 |
0.007 |
0.011 |
0.008 |
0.014 |
0.048 |
0.073 |
0.316 |
0.200 |
0.167 |
0.055 |
0.012 |
| 25 |
|
|
|
|
0.014 |
0.024 |
0.020 |
0.010 |
0.008 |
0.005 |
0.006 |
0.007 |
0.004 |
0.004 |
0.006 |
0.005 |
0.006 |
0.006 |
0.006 |
0.010 |
0.008 |
0.013 |
0.051 |
0.074 |
0.328 |
0.190 |
0.145 |
0.043 |
0.008 |
| 26 |
|
|
|
0.006 |
0.013 |
0.024 |
0.021 |
0.010 |
0.008 |
0.005 |
0.006 |
0.008 |
0.004 |
0.004 |
0.006 |
0.005 |
0.006 |
0.006 |
0.006 |
0.011 |
0.008 |
0.013 |
0.051 |
0.075 |
0.332 |
0.187 |
0.139 |
0.039 |
0.006 |
| 27 |
|
|
0.005 |
0.005 |
0.014 |
0.026 |
0.023 |
0.011 |
0.009 |
0.005 |
0.006 |
0.008 |
0.004 |
0.004 |
0.006 |
0.004 |
0.006 |
0.006 |
0.006 |
0.011 |
0.007 |
0.013 |
0.052 |
0.075 |
0.336 |
0.184 |
0.133 |
0.036 |
0.006 |
| 28 |
|
0.005 |
0.004 |
0.004 |
0.010 |
0.018 |
0.017 |
0.009 |
0.008 |
0.005 |
0.006 |
0.008 |
0.004 |
0.004 |
0.006 |
0.005 |
0.006 |
0.006 |
0.006 |
0.011 |
0.008 |
0.013 |
0.053 |
0.076 |
0.340 |
0.188 |
0.137 |
0.037 |
0.007 |
| 29 |
0.005 |
0.004 |
0.004 |
0.004 |
0.010 |
0.018 |
0.017 |
0.009 |
0.008 |
0.005 |
0.006 |
0.008 |
0.004 |
0.004 |
0.006 |
0.004 |
0.006 |
0.006 |
0.006 |
0.011 |
0.007 |
0.013 |
0.053 |
0.077 |
0.343 |
0.187 |
0.135 |
0.036 |
0.006 |
aData is adjusted to have standard deviation of 1.
bFirst column is m—the number of years from the end selected as data, the remaining columns are k—how far along the subset of years, data in table is B(m, m − k)—the posterior probability of the change occurring in that year.
Table A7.Chernoff–Zacks procedure on adjusted dataa, a priori probability of change in a given year—5%
|
m ↓ bk → |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
m |
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.046 |
0.954 |
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.047 |
0.051 |
0.902 |
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.038 |
0.049 |
0.053 |
0.860 |
| 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.072 |
0.062 |
0.078 |
0.064 |
0.725 |
| 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.032 |
0.092 |
0.077 |
0.092 |
0.066 |
0.642 |
| 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.044 |
0.053 |
0.207 |
0.124 |
0.116 |
0.058 |
0.399 |
| 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.015 |
0.053 |
0.065 |
0.267 |
0.143 |
0.120 |
0.050 |
0.287 |
| 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.014 |
0.014 |
0.038 |
0.052 |
0.212 |
0.136 |
0.127 |
0.058 |
0.350 |
| 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.014 |
0.010 |
0.013 |
0.047 |
0.063 |
0.266 |
0.152 |
0.128 |
0.050 |
0.258 |
| 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.010 |
0.013 |
0.009 |
0.013 |
0.046 |
0.064 |
0.272 |
0.156 |
0.130 |
0.049 |
0.240 |
| 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.009 |
0.008 |
0.011 |
0.008 |
0.012 |
0.043 |
0.061 |
0.261 |
0.157 |
0.133 |
0.050 |
0.245 |
| 13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.009 |
0.008 |
0.008 |
0.011 |
0.008 |
0.013 |
0.047 |
0.066 |
0.285 |
0.163 |
0.131 |
0.046 |
0.205 |
| 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.009 |
0.008 |
0.007 |
0.007 |
0.010 |
0.008 |
0.012 |
0.042 |
0.061 |
0.259 |
0.160 |
0.136 |
0.050 |
0.232 |
| 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.010 |
0.006 |
0.007 |
0.007 |
0.007 |
0.011 |
0.008 |
0.013 |
0.049 |
0.068 |
0.299 |
0.168 |
0.131 |
0.042 |
0.175 |
| 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.007 |
0.008 |
0.006 |
0.007 |
0.006 |
0.007 |
0.010 |
0.008 |
0.012 |
0.046 |
0.066 |
0.289 |
0.168 |
0.134 |
0.044 |
0.183 |
| 17 |
|
|
|
|
|
|
|
|
|
|
|
|
0.012 |
0.009 |
0.007 |
0.006 |
0.006 |
0.006 |
0.006 |
0.009 |
0.008 |
0.011 |
0.038 |
0.056 |
0.239 |
0.157 |
0.139 |
0.052 |
0.238 |
| 18 |
|
|
|
|
|
|
|
|
|
|
|
0.009 |
0.007 |
0.006 |
0.006 |
0.005 |
0.006 |
0.006 |
0.006 |
0.009 |
0.007 |
0.012 |
0.041 |
0.060 |
0.259 |
0.163 |
0.138 |
0.049 |
0.210 |
| 19 |
|
|
|
|
|
|
|
|
|
|
0.008 |
0.009 |
0.005 |
0.005 |
0.006 |
0.005 |
0.006 |
0.006 |
0.006 |
0.009 |
0.007 |
0.012 |
0.043 |
0.063 |
0.275 |
0.167 |
0.137 |
0.045 |
0.186 |
| 20 |
|
|
|
|
|
|
|
|
|
0.009 |
0.007 |
0.007 |
0.006 |
0.005 |
0.005 |
0.005 |
0.006 |
0.006 |
0.006 |
0.009 |
0.007 |
0.011 |
0.039 |
0.058 |
0.249 |
0.162 |
0.140 |
0.050 |
0.215 |
| 21 |
|
|
|
|
|
|
|
|
0.008 |
0.007 |
0.006 |
0.006 |
0.005 |
0.005 |
0.005 |
0.005 |
0.005 |
0.005 |
0.006 |
0.009 |
0.007 |
0.011 |
0.038 |
0.058 |
0.247 |
0.162 |
0.140 |
0.050 |
0.213 |
| 22 |
|
|
|
|
|
|
|
0.009 |
0.007 |
0.007 |
0.006 |
0.006 |
0.005 |
0.005 |
0.005 |
0.005 |
0.005 |
0.005 |
0.006 |
0.008 |
0.007 |
0.011 |
0.036 |
0.054 |
0.232 |
0.158 |
0.141 |
0.052 |
0.229 |
| 23 |
|
|
|
|
|
|
0.009 |
0.007 |
0.006 |
0.006 |
0.005 |
0.005 |
0.005 |
0.005 |
0.005 |
0.005 |
0.005 |
0.005 |
0.006 |
0.008 |
0.007 |
0.011 |
0.037 |
0.056 |
0.238 |
0.160 |
0.141 |
0.051 |
0.218 |
| 24 |
|
|
|
|
|
0.010 |
0.009 |
0.006 |
0.006 |
0.004 |
0.005 |
0.005 |
0.004 |
0.004 |
0.005 |
0.004 |
0.005 |
0.005 |
0.006 |
0.009 |
0.007 |
0.011 |
0.040 |
0.060 |
0.261 |
0.166 |
0.138 |
0.046 |
0.183 |
| 25 |
|
|
|
|
0.012 |
0.021 |
0.017 |
0.008 |
0.007 |
0.004 |
0.005 |
0.006 |
0.004 |
0.003 |
0.005 |
0.004 |
0.005 |
0.005 |
0.006 |
0.009 |
0.007 |
0.011 |
0.044 |
0.065 |
0.286 |
0.166 |
0.127 |
0.037 |
0.134 |
| 26 |
|
|
|
0.005 |
0.012 |
0.022 |
0.019 |
0.009 |
0.008 |
0.004 |
0.005 |
0.007 |
0.004 |
0.003 |
0.005 |
0.004 |
0.005 |
0.005 |
0.006 |
0.009 |
0.007 |
0.011 |
0.046 |
0.066 |
0.295 |
0.166 |
0.123 |
0.035 |
0.107 |
| 27 |
|
|
0.005 |
0.005 |
0.012 |
0.023 |
0.021 |
0.010 |
0.008 |
0.004 |
0.006 |
0.007 |
0.004 |
0.003 |
0.005 |
0.004 |
0.005 |
0.005 |
0.006 |
0.009 |
0.007 |
0.012 |
0.047 |
0.067 |
0.302 |
0.165 |
0.119 |
0.032 |
0.107 |
| 28 |
|
0.004 |
0.004 |
0.004 |
0.009 |
0.016 |
0.016 |
0.008 |
0.007 |
0.004 |
0.005 |
0.007 |
0.004 |
0.003 |
0.005 |
0.004 |
0.005 |
0.005 |
0.006 |
0.010 |
0.007 |
0.012 |
0.047 |
0.068 |
0.304 |
0.168 |
0.123 |
0.034 |
0.112 |
| 29 |
0.004 |
0.003 |
0.003 |
0.004 |
0.009 |
0.016 |
0.016 |
0.008 |
0.007 |
0.004 |
0.005 |
0.007 |
0.004 |
0.003 |
0.005 |
0.004 |
0.005 |
0.005 |
0.006 |
0.010 |
0.007 |
0.012 |
0.048 |
0.069 |
0.309 |
0.168 |
0.121 |
0.032 |
0.105 |
aData is adjusted to have standard deviation of 1.
bFirst column is m—the number of years from the end selected as data, the remaining columns are k—how far along the subset of years, data in table is B(m, m – k)—the posterior probability of the change occurring in that year.
Appendix B. R code
B.1. Load data
Data <- data.frame(loss = c(16527.23818, 19423.99527, 15260.94623, 15379.31657, 9460.044429, 13203.41339, 17753.16426, 22563.39599, 19433.13233, 24110.19247, 15931.73295, 16009.41087, 26602.24242, 20217.20507, 13437.38657, 22168.16504, 16189.10347, 20139.90678, 18517.22265, 14942.85989, 23188.54532, 15747.2464, 11999.18351, 19406.61283, 15596.77033, 24749.51564, 24200.16346, 28220.85832, 34737.79201), group = factor(c(rep(“A”, 25), rep(“B”, 4))))
B.2. Data plot
plot(Data$loss, xlab = “Year”, ylab = “Value”, col = “black”, lwd = 2, type = “o”, pch = 20)
B.3. Group means and standard deviations
Means <- c(mean(Data$loss), tapply(Data$loss, Data$group, mean))
SD <- c(sd(Data$loss), tapply(Data$loss, Data$group, sd))
B.4. Moving average plot code
MovingAverage <- function(data, n) {
filter(data, rep(1/n, n), sides = 1)
}
plot(MovingAverage(Data$loss, 3), xlab = “Year”, ylab = “Moving Average”, col = “black”, lwd = 2)
lines(MovingAverage(Data$loss, 5), col = “blue”, lwd = 2)
lines(MovingAverage(Data$loss, 7), col = “red2”, lwd = 2)
lines(MovingAverage(Data$loss, 10), col = “green3”, lwd = 2)
lines(MovingAverage(Data$loss, 15), col = “yellow3”, lwd = 2)
legend(x = “topleft”, legend = c(“3-year”, “5-year”, “7-year”, “10-year”, “15-year”), col = c(“black”, “blue”, “red2”, “green3”, “yellow3”), lwd = 2)
B.5. Process inspection scheme code
runningmin <- function(x) {
v <- rep(0, length(x))
v[1] <- x[1]
for (i in 2:length(x)) {
if (x[i] <= v[i - 1]) {
v[i] <- x[i]
} else {
v[i] <- v[i - 1]
}
}
return(v)
}
LongTermMean <- mean(Data$loss[8:17])
S0 <- Data$loss - LongTermMean
Si <- cumsum(S0)
Sr <- Si - runningmin(Si)
plot(Sr[18:29], xaxt = “n”, pch = 16, type = “o”, xlab = “Year”, ylab = “Difference”)
axis(1, at = 1:12, labels = seq(18, 29))
B.6. χ2 equal observations bin code
Bin boundaries were selected judgmentally to have 5 observations in each.
C5_1 <- sum(Data$loss[1:25] < 15000)
C5_2 <- sum(Data$loss[1:25] < 16000 & Data$loss[1:25] >=15000)
C5_3 <- sum(Data$loss[1:25] < 19000 & Data$loss[1:25] >=16000)
C5_4 <- sum(Data$loss[1:25] < 22000 & Data$loss[1:25] >=19000)
C5_5 <- sum(Data$loss[1:25] >= 22000)
C5 <- C5_1 + C5_2 + C5_3 + C5_4 + C5_5
E5_1 <- (pnorm(15000, mean = Means[[2]], sd = SD[[2]]) - pnorm(0, mean = Means[[2]], sd = SD[[2]])) * 25
E5_2 <- (pnorm(16000, mean = Means[[2]], sd = SD[[2]]) - pnorm(15000, mean = Means[[2]], sd = SD[[2]])) * 25
E5_3 <- (pnorm(19000, mean = Means[[2]], sd = SD[[2]]) - pnorm(16000, mean = Means[[2]], sd = SD[[2]])) * 25
E5_4 <- (pnorm(22000, mean = Means[[2]], sd = SD[[2]]) - pnorm(19000, mean = Means[[2]], sd = SD[[2]])) * 25
E5_5 <- (pnorm(Inf, mean = Means[[2]], sd = SD[[2]]) - pnorm(22000, mean = Means[[2]], sd = SD[[2]])) * 25
E5 <- E5_1 + E5_2 + E5_3 + E5_4 + E5_5
X5_1 <- (C5_1 - E5_1)^2/E5_1
X5_2 <- (C5_2 - E5_2)^2/E5_2
X5_3 <- (C5_3 - E5_3)^2/E5_3
X5_4 <- (C5_4 - E5_4)^2/E5_4
X5_5 <- (C5_5 - E5_5)^2/E5_5
X5 <- X5_1 + X5_2 + X5_3 + X5_4 + X5_5
G5_1 <- log(C5_1/E5_1) * C5_1
G5_2 <- log(C5_2/E5_2) * C5_2
G5_3 <- log(C5_3/E5_3) * C5_3
G5_4 <- log(C5_4/E5_4) * C5_4
G5_5 <- log(C5_5/E5_5) * C5_5
G5 <- G5_1 + G5_2 + G5_3 + G5_4 + G5_5
B.7. χ2 equiprobable bin code
B <- qnorm(seq_len(8)/8, 0, 1)
Bounds <- Means[[2]] + SD[[2]] * B
C8_1 <- sum(Data$loss[1:25] < Bounds[[1]])
C8_2 <- sum(Data$loss[1:25] < Bounds[[2]] & Data$loss[1:25] >= Bounds[[1]])
C8_3 <- sum(Data$loss[1:25] < Bounds[[3]] & Data$loss[1:25] >= Bounds[[2]])
C8_4 <- sum(Data$loss[1:25] < Bounds[[4]] & Data$loss[1:25] >= Bounds[[3]])
C8_5 <- sum(Data$loss[1:25] < Bounds[[5]] & Data$loss[1:25] >= Bounds[[4]])
C8_6 <- sum(Data$loss[1:25] < Bounds[[6]] & Data$loss[1:25] >= Bounds[[5]])
C8_7 <- sum(Data$loss[1:25] < Bounds[[7]] & Data$loss[1:25] >= Bounds[[6]])
C8_8 <- sum(Data$loss[1:25] >= Bounds[[7]])
C8 <- C8_1 + C8_2 + C8_3 + C8_4 + C8_5 + C8_6 + C8_7 + C8_8
E8_1 <- (pnorm(Bounds[[1]], mean = Means[[2]], sd = SD[[2]]) - pnorm(0, mean = Means[[2]], sd = SD[[2]])) * 25
E8_2 <- (pnorm(Bounds[[2]], mean = Means[[2]], sd = SD[[2]]) - pnorm(Bounds[[1]], mean = Means[[2]], sd = SD[[2]])) * 25
E8_3 <- (pnorm(Bounds[[3]], mean = Means[[2]], sd = SD[[2]]) - pnorm(Bounds[[2]], mean = Means[[2]], sd = SD[[2]])) * 25
E8_4 <- (pnorm(Bounds[[4]], mean = Means[[2]], sd = SD[[2]]) - pnorm(Bounds[[3]], mean = Means[[2]], sd = SD[[2]])) * 25
E8_5 <- (pnorm(Bounds[[5]], mean = Means[[2]], sd = SD[[2]]) - pnorm(Bounds[[4]], mean = Means[[2]], sd = SD[[2]])) * 25
E8_6 <- (pnorm(Bounds[[6]], mean = Means[[2]], sd = SD[[2]]) - pnorm(Bounds[[5]], mean = Means[[2]], sd = SD[[2]])) * 25
E8_7 <- (pnorm(Bounds[[7]], mean = Means[[2]], sd = SD[[2]]) - pnorm(Bounds[[6]], mean = Means[[2]], sd = SD[[2]])) * 25
E8_8 <- (pnorm(Inf, mean = Means[[2]], sd = SD[[2]]) - pnorm(Bounds[[7]], mean = Means[[2]], sd = SD[[2]])) * 25
E8 <- E8_1 + E8_2 + E8_3 + E8_4 + E8_5 + E8_6 + E8_7 + E8_8
X8_1 <- (C8_1 - E8_1)^2/E8_1
X8_2 <- (C8_2 - E8_2)^2/E8_2
X8_3 <- (C8_3 - E8_3)^2/E8_3
X8_4 <- (C8_4 - E8_4)^2/E8_4
X8_5 <- (C8_5 - E8_5)^2/E8_5
X8_6 <- (C8_6 - E8_6)^2/E8_6
X8_7 <- (C8_7 - E8_7)^2/E8_7
X8_8 <- (C8_8 - E8_8)^2/E8_8
X8 <- X8_1 + X8_2 + X8_3 + X8_4 + X8_5 + X8_6 + X8_7 + X8_8
G8_1 <- log(C8_1/E8_1) * C8_1
G8_2 <- log(C8_2/E8_2) * C8_2
G8_3 <- log(C8_3/E8_3) * C8_3
G8_4 <- log(C8_4/E8_4) * C8_4
G8_5 <- log(C8_5/E8_5) * C8_5
G8_6 <- log(C8_6/E8_6) * C8_6
G8_7 <- log(C8_7/E8_7) * C8_7
G8_8 <- log(C8_8/E8_8) * C8_8
G8 <- G8_1 + G8_2 + G8_3 + G8_4 + G8_5 + G8_6 + G8_7 + G8_8
B.8. Tests for normality code
library(nortest)
AD <- ad.test(Data$loss[1:25])
CVM <- cvm.test(Data$loss[1:25])
SW <- sf.test(Data$loss[1:25])
LF <- lillie.test(Data$loss[1:25])
B.9. Welch’s t-test
WT <- t.test(x = Data$loss[1:25], y = Data$loss[26:29], alternative = “l”, var.equal = FALSE, paired = FALSE)
B.10. Mann-Whitney-Wilcoxon code and results
library(coin)
wilcox_test(loss ∼ group, data = Data, alternative = “less”, distribution = “asymptotic”)
##
## Asymptotic Wilcoxon Mann-Whitney Rank Sum Test
##
## data: loss by group (A, B)
## Z = -3, p-value = 0.0012
## alternative hypothesis: true mu is less than 0
wilcox_test(loss ∼ group, data = Data, alternative = “less”, distribution = “exact”)
##
## Exact Wilcoxon Mann-Whitney Rank Sum Test
##
## data: loss by group (A, B)
## Z = -3, p-value = 0.0001684
## alternative hypothesis: true mu is less than 0
B.11. Maximum likelihood estimation
library(nloptr)
AICC <- function(NLL, k, n) {return(2 * NLL + 2 * k + 2 * k * (k + 1)/(n - k - 1))}
InitGamma <- function(X) {return(c(mean(X)^2/var(X), var(X)/mean(X)))}
GammaNLL <- function(pars, X) f
a <- pars[[1]]
q <- pars[[2]]
return(sum(-(a * (log(X) - log(q)) - (X/q) - log(X) - lgamma(a))))
}
InitN <- function(X) {return(c(mean(X), sd(X)))}
NNLL <- function(pars, X) {
m <- pars[[1]]
s <- pars[[2]]
return(sum(log(s) + 0.5 * log(2 * pi) + (X - m)^2/(2 * s^2)))
}
InitLN <- function(X) {return(c(mean(log(X)), sd(log(X))))}
LNNLL <- function(pars, X) {
m <- pars[[1]]
s <- pars[[2]]
return(sum(log(X) + log(s) + 0.5 * log(2 * pi) + (log(X) - m)^2/(2 * s^2)))
}
InitP <- function(X) {
m <- mean(X)
t <- sum(X^2)/length(X)
a <- max(2 * (t - m^2)/(t - 2 * m^2), 2.5)
q <- m * (a - 1)
return(c(a, q))
}
PNLL <- function(pars, X) {
a <- pars[[1]]
q <- pars[[2]]
return(sum(((a + 1) * log(X + q)) - log(a) - a * log(q)))
}
G25 <- nloptr(x0 = InitGamma(Data$loss[1:25]), eval_f = GammaNLL, lb = c(0, 0), ub = c(Inf, Inf), X = Data$loss[1:25], opts = list(maxeval = 30000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
LN25 <- nloptr(x0 = InitLN(Data$loss[1:25), eval_f = LNNLL, lb = c(-Inf, 0), ub = c(Inf, Inf), X = Data$loss[1:25], opts = list(maxeval = 30000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
N25 <- nloptr(x0 = InitN(Data$loss[1:25]), eval_f = NNLL, lb = c(0, 0), ub = c(Inf, Inf), X = Data$loss[1:25], opts = list(maxeval = 30000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
P25 <- nloptr(x0 = InitP(Data$loss[1:25]), eval_f = PNLL, eval_grad_f = NULL, lb = c(0, 0), ub = c(Inf, Inf),
X = Data$loss[1:25], opts = list(maxeval = 30000, xtol_rel = 1e-14, algorithm = “NLOPT_LN_SBPLX”))
G4 <- nloptr(x0 = InitGamma(Data$loss[26:29]), eval_f = GammaNLL, lb = c(0, 0), ub = c(Inf, Inf), X = Data$loss[26:29], opts = list(maxeval = 30000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
LN4 <- nloptr(x0 = InitLN(Data$loss[26:29]), eval_f = LNNLL, lb = c(-Inf, 0), ub = c(Inf, Inf), X = Data$loss[26:29], opts = list(maxeval = 30000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
N4 <- nloptr(x0 = InitN(Data$loss[26:29]), eval_f = NNLL, lb = c(0, 0), ub = c(Inf, Inf), X = Data$loss[26:29], opts = list(maxeval = 30000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
P4 <- nloptr(x0 = InitP(Data$loss[26:29]), eval_f = PNLL, eval_grad_f = NULL, lb = c(0, 0), ub = c(Inf, Inf), X = Data$loss[26:29], opts = list(maxeval = 30000, xtol_rel = 1e-14, algorithm = “NLOPT_LN_SBPLX”))
B.12. Combined changepoint and data maximum likelihood estimation
The constraints on the parameters and non-ideal initial selections for some of the distributions is a result of MLE “misbehaving” when being fit to one data point, as is the case if m ∈ {2,29}.
TT <- function(X) {return(sum(X^2)/length(X))}
InitGC <- function(X, m) {
n <- length(X)
X1 <- X[1:(m - 1)]
X2 <- X[m:n]
if (length(X1) == 1) {
a1 <- 10
} else {
a1 <- mean(X1)^2/(TT(X1) - mean(X1)^2)
}
if (a1 == 10) {
q1 <- sum(X1)/10
} else {
q1 <- (TT(X1) - mean(X1)^2)/mean(X1)
}
if (length(X2) == 1) {
a2 <- 10
} else {
a2 <- mean(X2)^2/(TT(X2) - mean(X2)^2)
}
if (a2 == 10) {
q2 <- sum(X2)/10
} else {
q2 <- (TT(X2) - mean(X2)^2)/mean(X2)
}
return(c(a1, q1, a2, q2))
}
GCNLL <- function(pars, X, m) {
n <- length(X)
a1 <- pars[[1]]
q1 <- pars[[2]]
a2 <- pars[[3]]
q2 <- pars[[4]]
X1 <- X[1:(m - 1)]
X2 <- X[m:n]
LX1 <- a1 * (log(X1) - log(q1)) - (X1/q1) - log(X1) - lgamma(a1)
LX2 <- a2 * (log(X2) - log(q2)) - (X2/q2) - log(X2) - lgamma(a2)
return(-(sum(LX1) + sum(LX2)))
}
FitGCC <- function(X) {
n <- length(X)
Results <- matrix(ncol = 6, nrow = (n))
NC <- nloptr(x0 = InitGamma(Data$loss), eval_f = GammaNLL, lb = c(0, 0), ub = c(Inf, Inf), X = Data$loss, opts = list(maxeval = 50000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
Results[1, 1] <- 1
Results[1, 2] <- NC$objective
Results[1, 3] <- NC$solution[[1]]
Results[1, 4] <- NC$solution[[2]]
Results[1, 5] <- 0
Results[1, 6] <- 0
for (i in 2:29) {
Results[i, 1] <- i
GC <- nloptr(x0 = InitGC(Data$loss, i), eval_f = GCNLL, lb = c(0, 0, 0, 0), ub = c(10000, Inf, 10000, Inf), X = Data$loss, m = i, opts = list(maxeval = 100000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
Results[i, 2] <- GC$objective
Results[i, 3] <- GC$solution[[1]]
Results[i, 4] <- GC$solution[[2]]
Results[i, 5] <- GC$solution[[3]]
Results[i, 6] <- GC$solution[[4]]
}
return(Results)
}
NCNLL <- function(pars, X, m) {
n <- length(X)
mu1 <- pars[[1]]
sig1 <- pars[[2]]
mu2 <- pars[[3]]
sig2 <- pars[[4]]
X1 <- X[1:(m - 1)]
X2 <- X[m:n]
LX1 <- log(sig1) + 0.5 * log(2 * pi) + (X1 - mu1)^2/(2 * sig1^2)
LX2 <- log(sig2) + 0.5 * log(2 * pi) + (X2 - mu2)^2/(2 * sig2^2)
return(sum(LX1) + sum(LX2))
}
FitNCC <- function(X) {
sdp <- function(z) {
m <- mean(z)
u <- (z - m)^2
return(sqrt(sum(u)/length(u)))
}
n <- length(X)
Results <- matrix(ncol = 6, nrow = n)
NC <- nloptr(x0 = InitN(Data$loss), eval_f = NNLL, lb = c(0, 0), ub = c(Inf, Inf), X = Data$loss, opts = list(maxeval = 30000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
Results[1, 1] <- 1
Results[1, 2] <- NC$objective
Results[1, 3] <- NC$solution[[1]]
Results[1, 4] <- NC$solution[[2]]
Results[1, 5] <- 0
Results[1, 6] <- 0
for (i in 2:29) {
Results[i, 1] <- i
NC <- nloptr(x0 = c(1000, 1000, 1000, 1000), eval_f = NCNLL, lb = c(0, 500, 0, 500), ub = c(Inf, Inf, Inf, Inf), X = Data$loss, m = i, opts = list(maxeval = 50000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
Results[i, 2] <- NC$objective
Results[i, 3] <- NC$solution[[1]]
Results[i, 4] <- NC$solution[[2]]
Results[i, 5] <- NC$solution[[3]]
Results[i, 6] <- NC$solution[[4]]
}
return(Results)
}
InitLNC <- function(X, m) {
n <- length(X)
X1 <- X[1:(m - 1)]
X2 <- X[m:n]
s1 <- sqrt(log(TT(X1)) - 2 * log(mean(X1)))
m1 <- log(mean(X1)) - s1^2/2
s2 <- sqrt(log(TT(X2)) - 2 * log(mean(X2)))
m2 <- log(mean(X2)) - s2^2/2
return(c(m1, s1, m2, s2))
}
LNCNLL <- function(pars, X, m) {
n <- length(X)
mu1 <- pars[[1]]
sig1 <- pars[[2]]
mu2 <- pars[[3]]
sig2 <- pars[[4]]
X1 <- X[1:(m - 1)]
X2 <- X[m:n]
LX1 <- log(X1) + log(sig1) + 0.5 * log(2 * pi) + (log(X1) - mu1)^2/(2 * sig1^2)
LX2 <- log(X2) + log(sig2) + 0.5 * log(2 * pi) + (log(X2) - mu2)^2/(2 * sig2^2)
return(sum(LX1) + sum(LX2))
}
FitLNCC <- function(X) {
n <- length(X)
Results <- matrix(ncol = 6, nrow = n)
LNC <- nloptr(x0 = InitLN(Data$loss), eval_f = LNNLL, lb = c(-Inf, 0), ub = c(Inf, Inf), X = Data$loss, opts = list(maxeval = 30000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
Results[1, 1] <- 1
Results[1, 2] <- LNC$objective
Results[1, 3] <- LNC$solution[[1]]
Results[1, 4] <- LNC$solution[[2]]
Results[1, 5] <- 0
Results[1, 6] <- 0
for (i in 2:29) {
Results[i, 1] <- i
LNC <- nloptr(x0 = c(10, 0.1, 10, 0.1), eval_f = LNCNLL, lb = c(-Inf, 0.01, -Inf, 0.01), ub = c(Inf, Inf, Inf, Inf), X = Data$loss, m = i, opts = list(maxeval = 100000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
Results[i, 2] <- LNC$objective
Results[i, 3] <- LNC$solution[[1]]
Results[i, 4] <- LNC$solution[[2]]
Results[i, 5] <- LNC$solution[[3]]
Results[i, 6] <- LNC$solution[[4]]
}
return(Results)
}
InitPC <- function(X, m) {
n <- length(X)
X1 <- X[1:(m - 1)]
X2 <- X[m:n]
if (length(X1) == 1) {
a1 <- 1000
} else {
a1 <- max((2 * (TT(X1) - mean(X1)^2)/(TT(X1) - 2 * mean(X1)^2)), 2.5)
}
if (a1 == 1000) {
q1 <- sum(X1)/1000
} else {
q1 <- mean(X1) * (a1 - 1)
}
if (length(X2) == 1) {
a2 <- 1000
} else {
a2 <- max((2 * (TT(X2) - mean(X2)^2)/(TT(X2) - 2 * mean(X2)^2)), 2.5)
}
if (a2 == 1000) {
q2 <- sum(X2)/1000
} else {
q2 <- mean(X2) * (a2 - 1)
}
return(c(a1, q1, a2, q2))
}
PCNLL <- function(pars, X, m) {
n <- length(X)
a1 <- pars[[1]]
q1 <- pars[[2]]
a2 <- pars[[3]]
q2 <- pars[[4]]
X1 <- X[1:(m - 1)]
X2 <- X[m:n]
LX1 <- ((a1 + 1) * log(X1 + q1)) - log(a1) - a1 * log(q1)
LX2 <- ((a2 + 1) * log(X2 + q2)) - log(a2) - a2 * log(q2)
return(sum(LX1) + sum(LX2))
}
FitPCC <- function(X) {
n <- length(X)
Results <- matrix(ncol = 6, nrow = n)
PC <- nloptr(x0 = InitP(Data$loss), eval_f = PNLL, eval_grad_f = NULL, lb = c(0, 0), ub = c(Inf, Inf), X = Data$loss, opts = list(maxeval = 30000, xtol_rel = 1e-14, algorithm = “NLOPT_LN_SBPLX”))
Results[1, 1] <- 1
Results[1, 2] <- PC$objective
Results[1, 3] <- PC$solution[[1]]
Results[1, 4] <- PC$solution[[2]]
Results[1, 5] <- 0
Results[1, 6] <- 0
for (i in 2:29) {
Results[i, 1] <- i
LNC <- nloptr(x0 = InitPC(Data$loss, i), eval_f = PCNLL, lb = c(0, 0, 0, 0), ub = c(Inf, Inf, Inf, Inf), X = Data$loss, m = i, opts = list(maxeval = 100000, xtol_rel = 1e-12, algorithm = “NLOPT_LN_SBPLX”))
Results[i, 2] <- LNC$objective
Results[i, 3] <- LNC$solution[[1]]
Results[i, 4] <- LNC$solution[[2]]
Results[i, 5] <- LNC$solution[[3]]
Results[i, 6] <- LNC$solution[[4]]
}
return(Results)
}
CombinedGamma <- FitGCC(Data$loss)
CombinedNormal <- FitNCC(Data$loss)
CombinedLogNormal <- FitLNCC(Data$loss)
CombinedPareto <- FitPCC(Data$loss)
B.13. Chernoff–Zacks changepoint procedure
Phi <- function(k, X, m, sigma) {
n <- length(X)
s2 <- sigma * sigma
mk <- m - k
front <- 1/sqrt(s2 * k * mk + m)
part1 <- (k^2 * mk^2 * s2)/((m^2 + (s2 * m * k * mk)) * 2)
Xbar_km <- if (k == 0) {
0
} else {
sum(X[(n - m + 1):(n - m + k)])/k
}
Xbarstar_km <- sum(X[(n - m + k + 1):n])/(m - k)
inner <- (Xbar_km - Xbarstar_km)^2
return(front * exp(part1 * inner))
}
Dstar_m <- function(X, m, sigma, p) {
D <- (1 - p)^(m - 1) * Phi(0, X, m, sigma)
ps <- p * (1 - p)^(m - 2)
for (k in 1:(m - 1)) {
D <- D + ps * Phi(k, X, m, sigma)
}
return(D)
}
B <- function(X, m, k, sigma, p) {
p_km <- (1 - p)^(m - 2)
PKM <- if (k == 0) {
p_km * (1 - p)
} else {
p_km * p
}
Q <- PKM * Phi(k, X, m, sigma)
return(Q/Dstar_m(X, m, sigma, p))
}
B.14. JAGS files
B.14.1. Data for JAGS
DL29 <- list(Loss = c(16527.23818, 19423.99527, 15260.94623, 15379.31657, 9460.044429, 13203.41339, 17753.16426, 22563.39599, 19433.13233, 24110.19247, 15931.73295, 16009.41087, 26602.24242, 20217.20507, 13437.38657, 22168.16504, 16189.10347, 20139.90678, 18517.22265, 14942.85989, 23188.54532, 15747.2464, 11999.18351, 19406.61283, 15596.77033, 24749.51564, 24200.16346, 28220.85832, 34737.79201), N = 29, MPrior = c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1))
DL2950 <- list(Loss = c(16527.23818, 19423.99527, 15260.94623, 15379.31657, 9460.044429, 13203.41339, 17753.16426, 22563.39599, 19433.13233, 24110.19247, 15931.73295, 16009.41087, 26602.24242, 20217.20507, 13437.38657, 22168.16504, 16189.10347, 20139.90678, 18517.22265, 14942.85989, 23188.54532, 15747.2464, 11999.18351, 19406.61283, 15596.77033, 24749.51564, 24200.16346, 28220.85832, 34737.79201), N = 29, MPrior = c(28, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1))
DL28 <- list(Loss = c(16527.23818, 19423.99527, 15260.94623, 15379.31657, 9460.044429, 13203.41339, 17753.16426, 22563.39599, 19433.13233, 24110.19247, 15931.73295, 16009.41087, 26602.24242, 20217.20507, 13437.38657, 22168.16504, 16189.10347, 20139.90678, 18517.22265, 14942.85989, 23188.54532, 15747.2464, 11999.18351, 19406.61283, 15596.77033, 24749.51564, 24200.16346, 28220.85832), N = 28, MPrior = c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1))
DL27 <- list(Loss = c(16527.23818, 19423.99527, 15260.94623, 15379.31657, 9460.044429, 13203.41339, 17753.16426, 22563.39599, 19433.13233, 24110.19247, 15931.73295, 16009.41087, 26602.24242, 20217.20507, 13437.38657, 22168.16504, 16189.10347, 20139.90678, 18517.22265, 14942.85989, 23188.54532, 15747.2464, 11999.18351, 19406.61283, 15596.77033, 24749.51564, 24200.16346), N = 27, MPrior = c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1))
B.14.2. Gamma split model file
var N, Loss[N], MPrior[N];
model {
for (year in 1:N) {
alpha[year] <- ifelse(year < m, alpha.prior[1], alpha.prior[2])
lambda[year] <- ifelse(year < m, lambda.prior[1], lambda.prior[2])
Loss[year] ∼ dgamma(alpha[year], lambda[year])
}
for (i in 1:2) {
alpha.prior[i] ∼ dgamma (0.5, 0.025)
lambda.prior[i] <- pow(theta.prior[i], -1)
theta.prior[i] ∼ dgamma (0.5, 5.0E-4)
}
Loss.prior ∼ dgamma(alpha.prior[1], lambda.prior[1])
Loss.post ∼ dgamma(alpha.prior[2], lambda.prior[2])
m ∼ dcat(MPrior)
}
B.14.3. Gamma no-split model file
var N, Loss[N], MPrior[N];
model {
for (year in 1:N) {
alpha[year] <- alpha.prior
lambda[year] <- pow(theta.prior, -1)
Loss[year] ∼ dgamma(alpha[year], lambda[year])
}
alpha.prior ∼ dgamma (0.5, 0.025)
theta.prior ∼ dgamma (0.5, 5.0E-4)
Loss.prior ∼ dgamma(alpha.prior, pow(theta.prior, -1))
m ∼ dcat(MPrior)
}
B.14.4. Gamma step model file
var N, Loss[N], MPrior[N];
model {
for (year in 1:N) {
alpha[year] <- ifelse(year < m, alpha.prior, max(alpha.prior + alpha.step, 1.0E-4))
theta[year] <- ifelse(year < m, theta.prior, max(theta.prior + theta.step, 1.0E-4))
lambda[year] <- pow(theta[year], -1)
Loss[year] ∼ dgamma(alpha[year], lambda[year])
}
alpha.prior ∼ dgamma (0.5, 0.025)
alpha.step ∼ dnorm(0.0, 1.0E-4)
theta.prior ∼ dgamma (0.5, 5.0E-4)
theta.step ∼ dnorm(0.0, 1.0E-4)
Loss.prior ∼ dgamma(alpha.prior, 1/theta.prior)
Loss.post ∼ dgamma(max(alpha.prior + alpha.step, 1.0E-4), 1/max(theta.prior + theta.step, 1.0E-4))
m∼ dcat(MPrior)
}
B.14.5. R code to call JAGS
Note that while specific seeds have been set for repeatability, in practice, random or changing seeds should be used to test the sensitivity of the parameter fits. Calls for adjusted files are the same with only the file names changing as appropriate.
library(rjags)
library(runjags)
set.seed(187)
inits <- function(chain) {
list(alpha.prior = 20 + rnorm(2, 0, 1), theta.prior = 1000 + rnorm(2, 0, 10), m = sample(c(1, 2, 3), size = 1, prob = c(0.8, 0.15, 0.05)), .RNG.seed = chain^2 + 1, .RNG.name = “base::Mersenne-Twister”)
}
Fit29 <- run.jags(model = “GammaModelSplit.bug”, monitor = c(“alpha.prior”, “theta.prior”, “m”, “Loss.prior”, “Loss.post”, “pd”, “dic”, “deviance”), data = DL29, inits = inits, n.chains = 5, sample = 15000, burnin = 10000, adapt = 10000, psrf.target = 1.05, thin = 3, method = “interruptible”, silent.jags = TRUE)
FM29 <- as.matrix(Fit29$mcmc)
B.14.6. R code to calculate statistics
There are two accepted ways to calculate pD, either the difference between the average deviance and the deviance at the posterior parameter means, or one-half the posterior variance of the deviance (Gelman et al. 2014, 172–173). This paper is using the former, as programmed into JAGS.
mSpot29 <- which(rownames(Fit29$summary$statistics) == “m”)
FLSpot29 <- which(rownames(Fit29$summary$statistics) == “Loss.post”)
CLSpot29 <- which(rownames(Fit29$summary$statistics) == “Loss.prior”)
a1Spot29 <- which(rownames(Fit29$summary$statistics) == “alpha.prior[1]”)
a2Spot29 <- which(rownames(Fit29$summary$statistics) == “alpha.prior[2]”)
t1Spot29 <- which(rownames(Fit29$summary$statistics) == “theta.prior[1]”)
t2Spot29 <- which(rownames(Fit29$summary$statistics) == “theta.prior[2]”)
devSpot29 <- which(rownames(Fit29$summary$statistics) == “deviance”)
Pmode29 <- apply(FM29, 2, post.mode)
Pmean29 <- Fit29$summary$statistics[, 1]
Pquant29 <- Fit29$summary$quantiles
Rhat29 <- Fit29$psrf$psrf
pD29 <- Fit29$dic$meanpd
DIC29 <- Fit29$dic$dic
HDI29 <- HDI(FM29[, 4], 0.95)
B.14.7. Posterior mode function
post.mode <- function(x, . . .) {
return(density(x, . . .)$x[which.max(density(x, . . .)$y)])
}
B.14.8. Highest density interval
HDI <- function(SampVec, prob = 0.95) {
# Returns Highest Density Interval Based on Kruschke
# 2014, pp. 727–728 Finds shortest interval containing
# prob% of sample Assumes unimodal distribution
n <- length(SampVec)
SortSamp <- sort(SampVec)
ProbWidth <- ceiling(prob * n) #Length of interval containing prob% of sample
TestIntervals <- n - ProbWidth #Number of intervals of this length in sample
StartIndices <- seq_len(TestIntervals)
IntervalWidths <- SortSamp[StartIndices + ProbWidth] - SortSamp[StartIndices]
HDIStart <- SortSamp[which.min(IntervalWidths)]
HDIStop <- SortSamp[which.min(IntervalWidths) + ProbWidth]
return(c(HDIStart, HDIStop))
}
B.15. Session info
## R version 3.1.2 (2014-10-31)
## Platform: x86_64-w64-mingw32/x64 (64-bit)
##
## locale:
## [1] LC_COLLATE=English_United States.1252
## [2] LC_CTYPE=English_United States.1252
## [3] LC_MONETARY=English_United States.1252
## [4] LC_NUMERIC=C
## [5] LC_TIME=English_United States.1252
##
## attached base packages:
## [1] splines stats graphics grDevices utils datasets methods
## [8] base
##
## other attached packages:
## [1] runjags_1.2.1-0 rjags_3-14 coda_0.16-1 lattice_0.20-29
## [5] coin_1.0-24 survival_2.37-7 nloptr_1.0.4 nortest_1.0-2
## [9] knitr_1.9
##
## loaded via a namespace (and not attached):
## [1] codetools_0.2-10 digest_0.6.8 evaluate_0.5.5
## [4] formatR_1.0 grid_3.1.2 highr_0.4
## [7] modeltools_0.2-21 mvtnorm_1.0-2 parallel_3.1.2
## [10] stats4_3.1.2 stringr_0.6.2 tools_3.1.2