Combining Chain-Ladder and Additive Loss Reserving Methods for Dependent Lines of Business

undefined

1. Introduction and motivation

1.1. Claims reserving for several correlated run-off subportfolios

Often, claim reserves are the largest position on the liability side of the balance sheet of a non-life insurance company. Therefore, given the available information about the past development, the prediction of adequate claim reserves as well as the quantification of the uncertainties in these reserves is a major task in actuarial practice and science (e.g., Wüthrich and Merz (2008), Casualty Actuarial Society (2001), or Teugels and Sundt (2004)).

In this paper we consider the claim reserving problem in a multivariate context. More precisely, we consider a portfolio consisting of several correlated run-off subportfolios. On some subportfolios we use the chain-ladder (CL) method and on the other subportfolios we use the additive loss reserving (ALR) method to estimate the claim reserves. Since in actuarial practice the conditional mean square error of prediction (MSEP) is the most popular measure to quantify the uncertainties, we provide an MSEP estimator for the overall reserves. This means that we provide a first step towards an estimate of the overall MSEP for the predictor of the ultimate claims for aggregated subportfolios using different claims reserving methods for different subportfolios. These studies of uncertainties are crucial in the development of new solvency guidelines where one exactly quantifies the risk profiles of the different insurance companies.

1.2. Multivariate claims reserving methods

The simultaneous study of several correlated run-off subportfolios is motivated by the fact that:

1. In practice it is quite natural to subdivide a non-life run-off portfolio into several correlated subportfolios, such that each subportfolio satisfies certain homogeneity properties (e.g., the CL assumptions or the assumptions of the ALR method).

2. It addresses the problem of dependence between run-off portfolios of different lines of business (e.g., bodily injury claims in auto liability and in general liability business).

3. The multivariate approach has the advantage that by observing one run-off subportfolio we learn about the behavior of the other run-off subportfolios (e.g., subportfolios of small and large claims).

4. It resolves the problem of additivity (i.e., the estimators of the ultimate claims for the whole portfolio are obtained by summation over the estimators of the ultimate claims for the individual run-off subportfolios).

Holmberg (1994) was probably one of the first to investigate the problem of dependence between run-off portfolios of different lines of business. Braun (2004) and Merz and Wüthrich (2007, 2008) generalized the univariate CL model of Mack (1993) to the multivariate CL case by incorporating correlations between several run-off subportfolios. Another feasible multivariate claims reserving method is given by the multivariate ALR method proposed by Hess, Schmidt, and Zocher (2006) and Schmidt (2006b) which is based on a multivariate linear model. Under the assumptions of their multivariate ALR model Hess, Schmidt, and Zocher (2006) and Schmidt (2006b) derived a formula for the Gauss-Markov predictor for the nonobservable incremental claims which is optimal in terms of the classical optimality criterion of minimal expected squared loss. Merz and Wüthrich (2009) derived an estimator for the conditional MSEP in the multivariate ALR method using the Gauss-Markov predictor proposed by Hess, Schmidt, and Zocher (2006) and Schmidt (2006b).

1.3. Combination of the multivariate CL and ALR methods

In the sequel we provide a framework in which we combine the multivariate CL model and the multivariate ALR model into one multivariate model. The use of different reserving methods for different subportfolios is motivated by the fact that

1. in general not all subportfolios satisfy the same homogeneity assumptions; and/or

2. sometimes we have a priori information (e.g., premium, number of contracts, external knowledge from experts, data from similar portfolios, market statistics) for some selected subportfolios which we want to incorporate into our claims reserving analysis.

That is, we use the CL method for a subset of subportfolios on the one hand and we use the ALR method for the complementary subset of subportfolios on the other hand. From this point of view it is interesting to note that the CL method and the ALR method are very different in some aspects and therefore exploit differing features of the data belonging to the individual subportfolios:

1. The CL method is based on cumulative claims whereas the ALR method is applied to incremental claims.

2. Unlike the CL method, the ALR method combines past observations in the upper triangle with external knowledge from experts or with a priori information.

3. The ALR method is more robust to outliers in the observations than the CL method.

Organization of this paper. In Section 2 we provide the notation and data structure for our multivariate framework. In Section 3 we define the combined model and derive the properties of the estimators for the ultimate claims within the framework of the combined method. In Section 4 we give an estimation procedure for the conditional MSEP in the combined method and our main results are presented in Estimator 4.7 and Estimator 4.8. Section 5 is dedicated to the estimation of the model parameters, and, finally, in Section 6 we give an example. An interested reader will find proofs of the results in Section 7.

2. Notation and multivariate framework

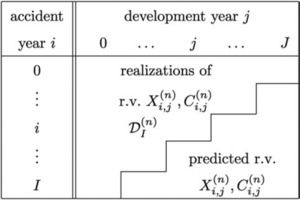
We assume that the subportfolios consist of N ≥ 1 run-off triangles of observations of the same size. However, the multivariate CL method and the multivariate ALR method can also be applied to other shapes of data (e.g., run-off trapezoids). In these N triangles the indices

1. n, 1 ≤ n ≤ N, refer to subportfolios (triangles),

2. i, 0 ≤ i ≤ I, refer to accident years (rows),

3. j, 0 ≤ j ≤ J = I, refer to development years (columns).

The incremental claims (i.e., incremental payments, change of reported claim amounts or number of newly reported claims) of run-off triangle \(n\) for accident year \(i\) and development year \(j\) are denoted by \(X_{i, j}^{(n)}\) and cumulative claims (i.e., cumulative payments, claims incurred or total number of reported claims) are given by

\[ C_{i, j}^{(n)}=\sum_{k=0}^{j} X_{i, k}^{(n)} . \tag{1} \]

Figure 1 shows the claims data structure for N individual claims development triangles described above.

Usually, at time I, we have observations

\[ \mathcal{D}_{I}^{(n)}=\left\{C_{i, j}^{(n)} ; i+j \leq I\right\}, \tag{2} \]

for all run-off subportfolios n ∈ {1, . . . , N}. This means that at time I (calendar year I) we have a total of observations over all subportfolios given by

\[ \mathcal{D}_{I}^{N}=\bigcup_{n=1}^{N} \mathcal{D}_{I}^{(n)}, \tag{3} \]

and we need to predict the random variables in its complement

\[ \mathcal{D}_{I}^{N, c}=\left\{C_{i, j}^{(n)} ; i \leq I, i+j>I, 1 \leq n \leq N\right\} . \tag{4} \]

In the sequel we assume without loss of generality that we use the multivariate CL method for the first K (i.e., K ≤ N) run-off triangles n = 1, . . . , K and the multivariate ALR method for the remaining n = K + 1, . . . , N triangles. Therefore, we introduce the following vector notation

\[ \begin{array}{l} \mathbf{C}_{i, j}^{\mathrm{CL}}=\left(\begin{array}{c} C_{i, j}^{(1)} \\ \vdots \\ C_{i, j}^{(K)} \end{array}\right), \quad \mathbf{X}_{i, j}^{\mathrm{CL}}=\left(\begin{array}{c} X_{i, j}^{(1)} \\ \vdots \\ X_{i, j}^{(K)} \end{array}\right), \\ \mathbf{C}_{i, j}^{\mathrm{AD}}=\left(\begin{array}{c} C_{i, j}^{(K+1)} \\ \vdots \\ C_{i, j}^{(N)} \end{array}\right) \quad \text { and } \quad \mathbf{X}_{i, j}^{\mathrm{AD}}=\left(\begin{array}{c} X_{i, j}^{(K+1)} \\ \vdots \\ X_{i, j}^{(N)} \end{array}\right) \end{array} \tag{5} \]

for all i ∈ {0, . . . , I} and j ∈ {0, . . . , J}. In particular, this means that the cumulative/incremental claims of the whole portfolio are given by the vectors

\[ \mathbf{C}_{i, j}=\binom{\mathbf{C}_{i, j}^{\mathrm{CL}}}{\mathbf{C}_{i, j}^{\mathrm{AD}}} \quad \text { and } \quad \mathbf{X}_{i, j}=\binom{\mathbf{X}_{i, j}^{\mathrm{CL}}}{\mathbf{X}_{i, j}^{\mathrm{AD}}} . \tag{6} \]

We define the first k + 1 columns of CL observations by

\[ \mathcal{B}_{k}^{K}=\left\{\mathbf{C}_{i, j}^{\mathrm{CL}} ; i+j \leq I \text { and } 0 \leq j \leq k\right\} \tag{7} \]

for \(k \in\{0, \ldots, J\}\). Finally, we define \(L\)-dimensional column vectors for \(L=N, K, N-K\) consisting of ones by \(\mathbf{1}_L=(1, \ldots, 1)^{\prime} \in \mathbb{R}^L\), and denote by

\[ \begin{aligned} \mathrm{D}(\mathbf{a}) & =\left(\begin{array}{lll} a_{1} & & 0 \\ & \ddots & \\ 0 & & a_{L} \end{array}\right) \quad \text { and } \\ \mathrm{D}(\mathbf{c})^{b} & =\left(\begin{array}{lll} c_{1}^{b} & & 0 \\ & \ddots & \\ 0 & & c_{L}^{b} \end{array}\right) \end{aligned} \tag{8} \]

the \(L \times L\)-diagonal matrices of the \(L\)-dimensional vectors \(\mathbf{a}=\left(a_1, \ldots, a_L\right)^{\prime} \in \mathbb{R}^L\) and \(\left(c_1^b, \ldots, c_L^b\right)^{\prime} \in \mathbb{R}_{+}^L\), where \(b \in \mathbb{R}\) and \(\mathbf{c}=\left(c_1, \ldots, c_L\right)^{\prime} \in \mathbb{R}_{+}^L\).

3. Combined multivariate CL and ALR method

The following model is a combination of the multivariate CL model and the multivariate ALR model presented in Merz and Wüthrich (2008) and Merz and Wüthrich (2009), respectively.

(CombinedCLandALRmodel)

• Incremental claims \(\mathbf{X}_{i, j}\) of different accident years \(i\) are independent.

• There exist \(K\)-dimensional constants

  \[ \begin{aligned} \mathbf{f}_{j} & =\left(f_{j}^{(1)}, \ldots, f_{j}^{(K)}\right)^{\prime} \quad \text { and } \\ \boldsymbol{\sigma}_{j}^{\mathrm{CL}} & =\left(\sigma_{j}^{(1)}, \ldots, \sigma_{j}^{(K)}\right)^{\prime} \end{aligned} \tag{9} \]

  with \(f_j^{(k)}>0, \sigma_j^{(k)}>0\) and \(K\)-dimensional random variables

  \[ \varepsilon_{i, j+1}^{\mathrm{CL}}=\left(\varepsilon_{i, j+1}^{(1)}, \ldots, \varepsilon_{i, j+1}^{(K)}\right)^{\prime}, \tag{10} \]

  such that for all i ∈ {0, . . . , I} and j ∈ {0, . . . , J − 1} we have

  \[ \mathbf{C}_{i, j+1}^{\mathrm{CL}}=\mathrm{D}\left(\mathbf{f}_{j}\right) \cdot \mathbf{C}_{i, j}^{\mathrm{CL}}+\mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)^{1 / 2} \cdot \mathrm{D}\left(\varepsilon_{i, j+1}^{\mathrm{CL}}\right) \cdot \sigma_{j}^{\mathrm{CL}} . \tag{11} \]

• There exist (N − K)-dimensional constants

  \[ \begin{aligned} \mathbf{m}_{j} & =\left(m_{j}^{(1)}, \ldots, m_{j}^{(N-K)}\right)^{\prime} \\ \sigma_{j-1}^{\mathrm{AD}} & =\left(\sigma_{j-1}^{(K+1)}, \ldots, \sigma_{j-1}^{(N)}\right)^{\prime}, \end{aligned} \tag{12} \]

  with \(\sigma_{j-1}^{(n)}>0\) and \((N-K)\)-dimensional random variables

  \[ \varepsilon_{i, j}^{\mathrm{AD}}=\left(\varepsilon_{i, j}^{(K+1)}, \ldots, \varepsilon_{i, j}^{(N)}\right)^{\prime}, \tag{13} \]

  such that for all i ∈ {0, . . . , I} and j ∈ {1, . . . , J} we have

  \[ \mathbf{X}_{i, j}^{\mathrm{AD}}=\mathrm{V}_{i} \cdot \mathbf{m}_{j}+\mathrm{V}_{i}^{1 / 2} \cdot \mathrm{D}\left(\varepsilon_{i, j}^{\mathrm{AD}}\right) \cdot \boldsymbol{\sigma}_{j-1}^{\mathrm{AD}}, \tag{14} \]

  where \(\mathrm{V}_i \in \mathbb{R}^{(N-K) \times(N-K)}\) are deterministic positive definite symmetric matrices.

• The N-dimensional random variables

  \[ \varepsilon_{i, j+1}=\binom{\varepsilon_{i, j+1}^{\mathrm{CL}}}{\varepsilon_{i, j+1}^{\mathrm{AD}}} \quad \text { and } \quad \varepsilon_{k, l+1}=\binom{\varepsilon_{k, l+1}^{\mathrm{CL}}}{\varepsilon_{k, l+1}^{\mathrm{AD}}} \]

  are independent for \(i \neq k\) or \(j \neq l\), with \(E\left[\varepsilon_{i, j+1}\right] =\mathbf{0}\) and

  \[ \begin{aligned} \operatorname{Cov} & \left(\varepsilon_{i, j+1}, \varepsilon_{i, j+1}\right) \\ & =E\left[\varepsilon_{i, j+1} \cdot \varepsilon_{i, j+1}^{\prime}\right] \\ & =\left(\begin{array}{ccccc} 1 & \rho_{j}^{(1,2)} & \cdots & \cdots & \rho_{j}^{(1, N)} \\ \rho_{j}^{(2,1)} & 1 & \cdots & \cdots & \rho_{j}^{(2, N)} \\ \vdots & \vdots & \ddots & & \vdots \\ \vdots & \vdots & & \ddots & \vdots \\ \rho_{j}^{(N, 1)} & \rho_{j}^{(N, 2)} & \cdots & \cdots & 1 \end{array}\right), \end{aligned} \tag{15} \]

  for fixed \(\rho_j^{(n, m)} \in(-1,1)\) for \(n \neq m\).

We introduce the notation

\[ \begin{aligned} \sigma_{j} & =\left(\sigma_{j}^{\mathrm{CL}}, \sigma_{j}^{\mathrm{AD}}\right)^{\prime}, \\ \Sigma_{j} & =E\left[\mathrm{D}\left(\varepsilon_{i, j+1}\right) \cdot \sigma_{j} \cdot \sigma_{j}^{\prime} \cdot \mathrm{D}\left(\varepsilon_{i, j+1}\right)\right], \\ \Sigma_{j}^{(C)} & =E\left[\mathrm{D}\left(\varepsilon_{i, j+1}^{\mathrm{CL}}\right) \cdot \sigma_{j}^{\mathrm{CL}} \cdot\left(\sigma_{j}^{\mathrm{CL}}\right)^{\prime} \cdot \mathrm{D}\left(\varepsilon_{i, j+1}^{\mathrm{CL}}\right)\right], \\ \Sigma_{j}^{(A)} & =E\left[\mathrm{D}\left(\varepsilon_{i, j+1}^{\mathrm{AD}}\right) \cdot \sigma_{j}^{\mathrm{AD}} \cdot\left(\sigma_{j}^{\mathrm{AD}}\right)^{\prime} \cdot \mathrm{D}\left(\varepsilon_{i, j+1}^{\mathrm{AD}}\right)\right], \end{aligned} \tag{16} \]

\[ \begin{aligned} \Sigma_{j}^{(C, A)} & =E\left[\mathrm{D}\left(\varepsilon_{i, j+1}^{\mathrm{CL}}\right) \cdot \sigma_{j}^{\mathrm{CL}} \cdot\left(\sigma_{j}^{\mathrm{AD}}\right)^{\prime} \cdot \mathrm{D}\left(\varepsilon_{i, j+1}^{\mathrm{AD}}\right)\right], \\ \Sigma_{j}^{(A, C)} & =E\left[\mathrm{D}\left(\varepsilon_{i, j+1}^{\mathrm{AD}}\right) \cdot \sigma_{j}^{\mathrm{AD}} \cdot\left(\sigma_{j}^{\mathrm{CL}}\right)^{\prime} \cdot \mathrm{D}\left(\varepsilon_{i, j+1}^{\mathrm{CL}}\right)\right] \\ & =\left(\Sigma_{j}^{(C, A)}\right)^{\prime} . \end{aligned} \tag{17} \]

Thus, we have

\[\small{ \Sigma_{j}=\left(\begin{array}{ccccc} \left(\sigma_{j}^{(1)}\right)^{2} & \sigma_{j}^{(1)} \sigma_{j}^{(2)} \rho_{j}^{(1,2)} & \cdots & \cdots & \sigma_{j}^{(1)} \sigma_{j}^{(N)} \rho_{j}^{(1, N)} \\ \sigma_{j}^{(2)} \sigma_{j}^{(1)} \rho_{j}^{(2,1)} & \left(\sigma_{j}^{(2)}\right)^{2} & \cdots & \cdots & \sigma_{j}^{(2)} \sigma_{j}^{(N)} \rho_{j}^{(2, N)} \\ \vdots & \vdots & \ddots & & \vdots \\ \vdots & \vdots & & \ddots & \vdots \\ \sigma_{j}^{(N)} \sigma_{j}^{(1)} \rho_{j}^{(N, 1)} & \sigma_{j}^{(N)} \sigma_{j}^{(2)} \rho_{j}^{(N, 2)} & \cdots & \cdots & \left(\sigma_{j}^{(N)}\right)^{2} \end{array}\right)=\left(\begin{array}{cc} \Sigma_{j}^{(C)} & \Sigma_{j}^{(C, A)} \\ \Sigma_{j}^{(A, C)} & \Sigma_{j}^{(A)} \end{array}\right) . \tag{18}} \]

The Multivariate Model 3.1 is suitable for portfolios of \(N\) correlated subportfolios in which the first \(K\) subportfolios satisfy the homogeneity assumptions of the CL method, and the other \(N- K\) subportfolios satisfy the homogeneity assumptions of the ALR method. Under Model Assumptions 3.1, the properties of the cumulative claims \(\mathbf{C}_{i, j}^{\text {CL }}\) and the incremental claims \(\mathbf{X}_{i, j}^{\text {AD }}\) are consistent with the assumptions of the multivariate CL time series model (see Merz and Wüthrich (2008)) and the multivariate ALR model (see Merz and Wüthrich (2009)). In particular for \(K= N\) and \(K=0\) Model Assumptions 3.1 reduce to the model assumptions of the multivariate CL time series model and the multivariate ALR model, respectively.

Remark 3.2

• The factors \(\mathbf{f}_j\) are called \(K\)-dimensional development factors, CL factors, age-to-age factors or link-ratios. The \(N-K\)-dimensional constants \(\mathbf{m}_j\) are called incremental loss ratios and can be interpreted as a multivariate scaled expected reporting/cashflow pattern over the different development years.

• In most practical applications, \(\mathrm{V}_i\) is chosen to be diagonal so as to represent a volume measure of accident year \(i\), a priori known (e.g., premium, number of contracts, expected number of claims, etc.) or external knowledge from experts, similar portfolios or market statistics. Since we assume that \(\mathrm{V}_i\) is a positive definite symmetric matrix, there is a well-defined positive definite symmetric matrix \(\mathrm{V}_i^{1 / 2}\) (called square root of \(\mathrm{V}_i\) ) satisfying \(\mathrm{V}_i=\mathrm{V}_i^{1 / 2} \cdot \mathrm{~V}_i^{1 / 2}\).

• Within the CL and ALR framework, Braun (2004) and Merz and Wüthrich (2007, 2008, 2009) proposed the development year-based correlations given by (15). Often correlations between different run-off triangles are attributed to claims inflation. Under this point of view it may seem more reasonable to allow for correlation between the cumulative or incremental claims of the same calender year (diagonals of the claims development triangles). This would introduce dependencies between accident years. However, at the moment it is not mathematically tractable to treat such year-based correlations within the CL and ALR framework. That is, all calender year-based dependencies should be removed from the data before calculating the reserves with the CL or ALR method. However, after correcting the data for the calender year-based correlations, further direct and indirect sources for correlations between different run-off triangles of a portfolio exist and should be taken into account (cf. Houltram (2003)). This is exactly what our model does.

• Matrix \(\Sigma_{j-1}^{(c)}\) reflects the correlation structure between the cumulative claims of development year \(j\) within the first \(K\) subportfolios and matrix \(\Sigma_{j-1}^{(A)}\) the correlation structure between the incremental claims of development year \(j\) within the last \(N-K\) subportfolios. The matrices \(\Sigma_{j-1}^{(C, A)}\) and \(\Sigma_{j-1}^{(A, C)}\) reflect the correlation structure between the cumulative claims of development year \(j\) in the first \(K\) subportfolios and the incremental claims of development year \(j\) in the last \(N-K\) subportfolios.

• There may occur difficulties about positivity in the time-series definition (11), which can be solved in a mathematically correct way. We omit these derivations since they do not lead to a deeper understanding of the model. Refer to Wüthrich, Merz, and Bühlmann (2008) for more details.

• The indices for σ and ε differ by 1, since it simplifies the comparability with the derivations and results in Merz and Wüthrich (2008, 2009).

We obtain for the conditionally expected ultimate claim \(E\left[\mathbf{C}_{i, J} \mid \mathcal{D}_I^N\right]\) :

Lemma 3.3 Under Model Assumptions 3.1 we have for all \(1 \leq i \leq I\) :

a)

\[ \begin{aligned} E\left[\mathbf{C}_{i, J}^{\mathrm{CL}} \mid \mathcal{D}_{I}^{N}\right] & =E\left[\mathbf{C}_{i, J}^{\mathrm{CL}} \mid \mathbf{C}_{i, I-i}\right]=E\left[\mathbf{C}_{i, J}^{\mathrm{CL}} \mid \mathbf{C}_{i, I-i}^{\mathrm{CL}}\right] \\ & =\prod_{j=I-i}^{J-1} \mathrm{D}\left(\mathbf{f}_{j}\right) \cdot \mathbf{C}_{i, I-i}^{\mathrm{CL}}, \end{aligned} \]

b)

\[ \begin{aligned} E\left[\mathbf{C}_{i, J}^{\mathrm{AD}} \mid \mathcal{D}_{I}^{N}\right] & =E\left[\mathbf{C}_{i, J}^{\mathrm{AD}} \mid \mathbf{C}_{i, I-i}\right]=E\left[\mathbf{C}_{i, J}^{\mathrm{AD}} \mid \mathbf{C}_{i, I-i}^{\mathrm{AD}}\right] \\ & =\mathbf{C}_{i, I-i}^{\mathrm{AD}}+\mathrm{V}_{i} \cdot \sum_{j=I-i+1}^{J} \mathbf{m}_{j} . \end{aligned} \]

ProofThis immediately follows from Model Assumptions 3.1.

This result motivates an algorithm for estimating the outstanding claims liabilities, given the observations \(\mathcal{D}_I^N\). If the \(K\)-dimensional CL factors \(\mathbf{f}_j\) and the ( \(N-K\) )-dimensional incremental loss ratios \(\mathbf{m}_j\) are known, the outstanding claims liabilities of accident year \(i\) for the first \(K\) and the last \(N-K\) correlated run-off triangles are predicted by

\[ E\left[\mathbf{C}_{i, J}^{\mathrm{CL}} \mid \mathcal{D}_{I}^{N}\right]-\mathbf{C}_{i, I-i}^{\mathrm{CL}}=\prod_{j=I-i}^{J-1} \mathrm{D}\left(\mathbf{f}_{j}\right) \cdot \mathbf{C}_{i, I-i}^{\mathrm{CL}}-\mathbf{C}_{i, I-i}^{\mathrm{CL}} \tag{19} \]

and

\[ E\left[\mathbf{C}_{i, J}^{\mathrm{AD}} \mid \mathcal{D}_{I}^{N}\right]-\mathbf{C}_{i, I-i}^{\mathrm{AD}}=\mathrm{V}_{i} \cdot \sum_{j=I-i+1}^{J} \mathbf{m}_{j}, \tag{20} \]

respectively. However, in practical applications we have to estimate the parameters \(\mathbf{f}_j\) and \(\mathbf{m}_j\) from the data in the \(N\) upper triangles. Pröhl and Schmidt (2005) and Schmidt (2006b) proposed the multivariate CL factor estimates for \(\mathbf{f}_j(j= 0, \ldots, J-1)\)

\[ \begin{aligned} \hat{\mathbf{f}}_{j}= & \left(\hat{f}_{j}^{(1)}, \ldots, \hat{f}_{j}^{(K)}\right)^{\prime} \\ = & \left(\sum_{i=0}^{I-j-1} \mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)^{1 / 2}\left(\Sigma_{j}^{(C)}\right)^{-1} \mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)^{1 / 2}\right)^{-1} \\ & \cdot \sum_{i=0}^{I-j-1} \mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)^{1 / 2}\left(\Sigma_{j}^{(C)}\right)^{-1} \mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)^{-1 / 2} \cdot \mathbf{C}_{i, j+1}^{\mathrm{CL}} . \end{aligned} \tag{21} \]

In the framework of the multivariate ALR method Hess, Schmidt, and Zocher (2006) and Schmidt (2006b) proposed the multivariate estimates for the incremental loss ratios \(\mathbf{m}_j(j= 1, \ldots, J)\)

\[ \begin{aligned} \hat{\mathbf{m}}_{j}= & \left(\hat{m}_{j}^{(1)}, \ldots, \hat{m}_{j}^{(N-K)}\right)^{\prime} \\ = & \left(\sum_{i=0}^{I-j} \mathrm{~V}_{i}^{1 / 2} \cdot\left(\Sigma_{j-1}^{(A)}\right)^{-1} \cdot \mathrm{~V}_{i}^{1 / 2}\right)^{-1} \\ & \cdot \sum_{i=0}^{I-j} \mathrm{~V}_{i}^{1 / 2} \cdot\left(\Sigma_{j-1}^{(A)}\right)^{-1} \cdot \mathrm{~V}_{i}^{-1 / 2} \cdot \mathbf{X}_{i, j}^{\mathrm{AD}} . \end{aligned} \tag{22} \]

• In the case K = 1 (i.e., only one CL run-off subportfolio) the estimator (21) coincides with the classical univariate CL estimator of Mack (1993). Analogously, in the case N − K =1 (i.e., only one additive run-off subportfolio) the estimator (22) coincides with the univariate incremental loss ratio estimates \[\hat{m}_{j}=\sum_{i=0}^{I-j} \frac{X_{i, j}}{\sum_{k=0}^{I-j} V_{k}} \tag{23}\] with deterministic one-dimensional weights V_i (see, e.g., Schmidt (2006b, 2006a)).

• With respect to the criterion of minimal expected squared loss the multivariate CL factor estimates (21) are optimal unbiased linear estimators for \(\mathbf{f}_j\) (cf. Pröhl and Schmidt (2005) and Schmidt (2006b)) and the multivariate incremental loss ratio estimates (22) are optimal unbiased linear estimators for \(\mathbf{m}_j\) (cf. Hess, Schmidt, and Zocher (2006) and Schmidt (2006b)).

• For uncorrelated cumulative and incremental claims in the different run-off subportfolios (i.e., we set \(\Sigma=\mathbf{I}\), where \(\mathbf{I}\) denotes the identity matrix) we obtain the (unbiased) estimators for \(\mathbf{f}_j\) and \(\mathbf{m}_j\)

  \[ \hat{\mathbf{f}}_{j}^{(0)}=\left(\sum_{i=0}^{I-j-1} \mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)\right)^{-1} \cdot \sum_{i=0}^{I-j-1} \mathbf{C}_{i, j+1}^{\mathrm{CL}} \tag{24} \]

  and

  \[ \hat{\mathbf{m}}_{j}^{(0)}=\left(\sum_{i=0}^{I-j} \mathrm{~V}_{i}\right)^{-1} \cdot \sum_{i=0}^{I-j} \mathbf{X}_{i, j}^{\mathrm{AD}} . \tag{25} \]

  For a given \(\Sigma\), both \(\hat{\mathbf{f}}_j\) and \(\hat{\mathbf{f}}_j^{(0)}\) as well as \(\hat{\mathbf{m}}_j\) and \(\hat{\mathbf{m}}_j^{(0)}\) are unbiased estimators for the multivariate CL factor \(\mathbf{f}_j\) and multivariate incremental loss ratio \(\mathbf{m}_j\), respectively (see Lemma 3.6 below). However, only \(\hat{\mathbf{f}}_j\) and \(\hat{\mathbf{m}}_j\) are optimal in the sense that they have minimal expected squared loss; see the second bullet of these remarks.

In the sequel we predict the cumulative claims \(\mathbf{C}_{i, j}^{C L}\) of the first \(K\) run-off triangles and the cumulative claims \(\mathbf{C}_{i, j}^{\mathrm{AD}}\) of the last \(N-K\) run-off triangles for \(i+j>I\) by the multivariate CL predictors

\[ \begin{aligned} \widehat{\mathbf{C}_{i, j}} \mathrm{CL} & \left.=\widehat{\left(\widehat{C}_{i, j}^{(1)}\right.} \mathrm{CL}, \ldots, \widehat{C_{i, j}^{(K)}}\right)^{\mathrm{CL}}=\hat{E}\left[\mathbf{C}_{i, j}^{\mathrm{CL}} \mid \mathcal{D}_{I}^{N}\right] \\ & =\prod_{l=I-i}^{j-1} \mathrm{D}\left(\hat{\mathbf{f}}_{l}\right) \cdot \mathbf{C}_{i, I-i}^{\mathrm{CL}} \end{aligned} \tag{26} \]

and the multivariate ALR predictors

\[ \begin{aligned} \widehat{\mathbf{C}_{i, j}} \mathrm{AD} & =\left(\widehat{C}_{i, j}^{(\widehat{K+1})} \mathrm{AD}, \ldots,{\widehat{C_{i, j}^{(N)}}}^{\mathrm{AD}}\right)^{\prime}=\hat{E}\left[\mathbf{C}_{i, j}^{\mathrm{AD}} \mid \mathcal{D}_{I}^{N}\right] \\ & =\mathbf{C}_{i, I-i}^{\mathrm{AD}}+\mathrm{V}_{i} \cdot \sum_{l=I-i+1}^{j} \hat{\mathbf{m}}_{l}. \end{aligned} \tag{27} \]

This means that we predict the \(N\)-dimensional ultimate claims \(\mathbf{C}_{i, J}\) by

\[ \widehat{\mathbf{C}_{i, J}}=\binom{{\widehat{\mathbf{C}_{i, J}}}^{\mathrm{CL}}}{\widehat{\mathbf{C}_{i, J}} \mathrm{AD}}. \tag{28} \]

Estimator 3.5 (Combined CL and ALR estimator) The combined \(C L\) and \(A L R\) estimator for \(E\left[\mathbf{C}_{i, j} \mid \mathcal{D}_I^N\right]\) is for \(i+j>I\) given by

\[ \widehat{\mathbf{C}_{i, j}}=\hat{E}\left[\mathbf{C}_{i, j} \mid \mathcal{D}_{I}^{N}\right]=\binom{{\widehat{\mathbf{C}_{i, j}}}^{\mathrm{CL}}}{{\widehat{\mathbf{C}_{i, j}}}^{\mathrm{AD}}}. \]

The following lemma collects results from Lemma 3.5 in Merz and Wüthrich (2008) as well as from Property 3.4 and Property 3.7 in Merz and Wüthrich (2009).

Lemma 3.6 Under Model Assumptions 3.1 we have:
a) \(\hat{\mathbf{f}}_j\) is, given \(\mathcal{B}_j^K\), an unbiased estimator for \(\mathbf{f}_j\), i.e., \(\mathrm{E}\left[\hat{\mathbf{f}}_j \mid \mathcal{B}_j^K\right]=\mathbf{f}_j\);
b) \(\hat{\mathbf{f}}_j\) and \(\hat{\mathbf{f}}_k\) are uncorrelated for \(j \neq k\), i.e., \(\mathrm{E}\left[\hat{\mathbf{f}}_j \cdot \hat{\mathbf{f}}_k^{\prime}\right]=\mathbf{f}_j \cdot \mathbf{f}_k^{\prime}=\mathrm{E}\left[\hat{\mathbf{f}}_j\right] \cdot \mathrm{E}\left[\hat{\mathbf{f}}_k\right]^{\prime} ;\)
c) \(\hat{\mathbf{m}}_j\) is an unbiased estimator for \(\mathbf{m}_j\), i.e., \(\mathrm{E}\left[\hat{\mathbf{m}}_j\right]=\mathbf{m}_j\);
d) \(\hat{\mathbf{m}}_j\) and \(\hat{\mathbf{m}}_k\) are independent for \(j \neq k\);
e) \(\operatorname{Var}\left(\hat{\mathbf{m}}_j\right)=\left(\sum_{l=0}^{I-j} \mathrm{~V}_l^{1 / 2} \cdot\left(\Sigma_{j-1}^{(A)}\right)^{-1} \cdot \mathrm{~V}_l^{1 / 2}\right)^{-1}\);
f) \(\widehat{\mathbf{C}_{i, J}}\) is, given \(\mathbf{C}_{i, I-i}\), an unbiased estimator for \(E\left[\mathbf{C}_{i, J} \mid \mathcal{D}_I^N\right]\), i.e., \(E\left[\widehat{\mathbf{C}_{i, J}} \mid \mathbf{C}_{i, I-i}\right]=E\left[\mathbf{C}_{i, J} \mid \mathcal{D}_I^N\right] =E\left[\mathbf{C}_{i, J} \mid \mathbf{C}_{i, I-i}\right]\).

Remark 3.7

• Note that Lemma 3.6 f) shows that we have unbiased estimators of the conditionally expected ultimate claim \(E\left[\mathbf{C}_{i, J} \mid \mathcal{D}_I^N\right]\). Moreover, it implies that the estimator of the aggregated ultimate claims for accident year \(i\) \[\begin{aligned}& \sum_{n=1}^K{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}+\sum_{n=K+1}^N{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}} \\& \quad=\mathbf{1}^{\prime} \cdot{\widehat{\mathbf{C}_{i, J}}}^{\prime}=\mathbf{1}_K^{\prime} \cdot{\widehat{\mathbf{C}_{i, J}}}^{\mathrm{CL}}+\mathbf{1}_{N-K}^{\prime} \cdot{\widehat{\mathbf{C}_{i, J}}}^{\mathrm{AD}}\end{aligned}\]

  is, given \(\mathbf{C}_{i, I-i}\), an unbiased estimator for \(\sum_{n=1}^N E\left[C_{i, J}^{(n)} \mid \mathbf{C}_{i, I-i}\right]\).

• Note that the parameters for the CL method are estimated independently from the observations belonging to the ALR method and vice versa. That is, here we could even go one step beyond and learn from ALR method observations when estimating CL parameters and vice versa. We omit these derivations since formulas get more involved and neglect the fact that one may even improve estimators. Our goal here is to give an estimate for the overall MSEP for the parameter estimators (21) and (22).

4. Conditional MSEP

In this section we consider the prediction uncertainty of the predictors

\[ \begin{array}{l} \sum_{n=1}^{K} \widehat{C_{i, J}^{(n)}} \mathrm{CL}+\sum_{n=K+1}^{N} \widehat{C_{i, J}^{(n)}} \mathrm{AD} \qquad \text{and}\\ \sum_{i=1}^{I}\left(\sum_{n=1}^{K}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}+\sum_{n=K+1}^{N}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}\right), \end{array} \]

given the observations 𝒟_I^N, for the ultimate claims. This means our goal is to derive an estimate of the conditional MSEP for single accident years i ∈ {1, . . . , I} which is defined as

\[ \begin{array}{l} \operatorname{msep}_{\sum_{n=1}^{N} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=1}^{K} \widehat{C_{i, J}^{(n)}}+\sum_{n=K+1}^{N} \widehat{C_{i, J}^{(n)}} \mathrm{AD}\right) \\ \quad=E\left[\left(\sum_{n=1}^{K} \widehat{C_{i, J}^{(n)}}+\sum_{n=K+1}^{N}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=1}^{N} C_{i, J}^{(n)}\right)^{2} \mid \mathcal{D}_{I}^{N}\right], \end{array} \tag{29} \]

as well as an estimate of the conditional MSEP for aggregated accident years given by

\[ \begin{array}{c} \operatorname{msep}_{\Sigma_{i, n} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{i=1}^{I} \sum_{n=1}^{K}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}+\sum_{i=1}^{I} \sum_{n=K+1}^{N}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}\right) \\ =E\left[\left(\sum_{i=1}^{I} \sum_{n=1}^{K}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}+\sum_{i=1}^{I} \sum_{n=K+1}^{N}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}\right.\right. \\ \left.\left.-\sum_{i=1}^{I} \sum_{n=1}^{N} C_{i, J}^{(n)}\right)^{2} \mid \mathcal{D}_{I}^{N}\right] . \end{array} \tag{30} \]

4.1. Conditional MSEP for single accident years

We choose i ∈ {1, . . . , I}. The conditional MSEP (29) for a single accident year i decomposes as

\[ \begin{array}{l} \operatorname{msep}_{\Sigma_{n=1}^{N} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=1}^{K}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}+\sum_{n=K+1}^{N}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}\right) \\ \quad= \operatorname{msep}_{\Sigma_{n=1}^{K} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=1}^{K}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}\right) \\ \quad+\operatorname{msep}_{\Sigma_{n=K+1}^{N} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=K+1}^{N}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}\right) \\ +2 \cdot E\left[\left(\sum_{n=1}^{K}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}-\sum_{n=1}^{K} C_{i, J}^{(n)}\right)\right. \\ \left.\cdot\left(\sum_{n=K+1}^{N}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=K+1}^{N} C_{i, J}^{(n)}\right) \mid \mathcal{D}_{I}^{N}\right] . \end{array} \tag{31} \]

The first two terms on the right-hand side of (31) are the conditional MSEP for single accident years i if we use the multivariate CL method for the first K run-off triangles (numbered by n = 1, . . . , K) and the multivariate ALR method for the last N − K run-off triangles (numbered by n = K + 1, . . . , N), respectively. Estimators for these two conditional MSEPs are derived in Merz and Wüthrich (2008, 2009) and are given by Estimator 4.1 and Estimator 4.2, below.

Estimator 4.1 (MSEP for single accident years, CL method, cf. Merz and Wüthrich (2008)) Under Model Assumptions 3.1 we have the estimator for the conditional MSEP of the ultimate claims in the first K run-off triangles for a single accident year i ∈ {1, . . . , I}

\[ \begin{array}{l} \widehat{\operatorname{msep}}_{\Sigma_{n=1}^{K} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=1}^{K} \widehat{C_{i, J}^{(n)}} \mathrm{CL}\right) \\ = \mathbf{1}_{K}^{\prime} \cdot\left(\sum_{l=I-i+1}^{J} \prod_{k=l}^{J-1} \mathrm{D}\left(\hat{\mathbf{f}}_{k}\right) \cdot \hat{\Sigma}_{i, l-1}^{\mathbf{C}} \cdot \prod_{k=l}^{J-1} \mathrm{D}\left(\hat{\mathbf{f}}_{k}\right)\right) \cdot \mathbf{1}_{K} \\ +\mathbf{1}_{K}^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot\left(\hat{\Delta}_{i, J}^{(n, m)}\right)_{1 \leq n, m \leq K} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot \mathbf{1}_{K}, \end{array} \tag{32} \]

with

\[ \hat{\Sigma}_{i, l-1}^{\mathrm{C}}=\mathrm{D}\left({\widehat{\mathbf{C}_{i, l-1}}}^{\mathrm{CL}}\right)^{1 / 2} \cdot \hat{\Sigma}_{l-1}^{(C)} \cdot \mathrm{D}\left({\widehat{\mathbf{C}_{i, l-1}}}^{\mathrm{CL}}\right)^{1 / 2}, \tag{33} \]

\[ \begin{aligned} \hat{\Delta}_{i, J}^{(n, m)}= & \prod_{l=I-i}^{J-1}\left(\hat{f}_{l}^{(n)} \cdot \hat{f}_{l}^{(m)}+\sum_{k=0}^{I-l-1} \hat{\mathbf{a}}_{n \mid l}^{k} \cdot \hat{\Sigma}_{l}^{(C)} \cdot\left(\hat{\mathbf{a}}_{m \mid l}^{k}\right)^{\prime}\right) \\ & -\prod_{l=I-i}^{J-1} \hat{f}_{l}^{(n)} \cdot \hat{f}_{l}^{(m)}, \end{aligned} \tag{34} \]

where \(\hat{\mathbf{a}}_{n \mid l}^k\) and \(\hat{\mathbf{a}}_{m \mid l}^k\) are the nth and mth row of

\[ \begin{aligned} \hat{\mathbf{A}}_{l}^{k}= & \left(\sum_{i=0}^{I-l-1} \mathrm{D}\left(\mathbf{C}_{i, l}^{\mathrm{CL}}\right)^{1 / 2} \cdot\left(\hat{\Sigma}_{l}^{(C)}\right)^{-1} \cdot \mathrm{D}\left(\mathbf{C}_{i, l}^{\mathrm{CL}}\right)^{1 / 2}\right)^{-1} \\ & \cdot \mathrm{D}\left({\widehat{\mathbf{C}_{k, l}}}^{\mathrm{CL}}\right)^{1 / 2} \cdot\left(\hat{\Sigma}_{l}^{(C)}\right)^{-1} \end{aligned} \tag{35} \]

and the parameter estimates \(\hat{\Sigma}_{l-1}^{(C)}\) are given in Section 5.

Estimator 4.2 (MSEP for single accident years, ALR method, cf. Merz and Wüthrich (2009)) Under Model Assumptions 3.1 we have the estimator for the conditional MSEP of the ultimate claims in the last N − K run-off triangles for a single accident year i ∈ {1, . . . , I}

\[ \begin{array}{l} \widehat{\operatorname{msep}_{\Sigma_{n=K+1}^{N}} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=K+1}^{N} \widehat{C_{i, J}^{(n)}} \mathrm{AD}\right) \\ = \mathbf{1}_{N-K}^{\prime} \cdot \mathrm{V}_{i}^{1 / 2} \cdot \sum_{j=I-i+1}^{J} \hat{\Sigma}_{j-1}^{(A)} \cdot \mathrm{V}_{i}^{1 / 2} \cdot \mathbf{1}_{N-K} \\ +\mathbf{1}_{N-K}^{\prime} \cdot \mathrm{V}_{i} \\ \cdot \sum_{j=I-i+1}^{J}\left(\sum_{l=0}^{I-j} \mathrm{~V}_{l}^{1 / 2} \cdot\left(\hat{\Sigma}_{j-1}^{(A)}\right)^{-1} \cdot \mathrm{~V}_{l}^{1 / 2}\right)^{-1} \\ \cdot \mathrm{~V}_{i} \cdot \mathbf{1}_{N-K}, \end{array} \tag{36} \]

where the parameter estimates \(\hat{\Sigma}_{j-1}^{(A)}\) are given in Section 5.

• The first terms on the right-hand side of (32) and (36) are the estimators of the conditional process variances and the second terms are the estimators of the conditional estimation errors, respectively.

• For K = 1 Estimator 4.1 reduces to the estimator of the conditional MSEP for a single run-off triangle in the univariate CL time series model of Buchwalder et al. (2006).

• For N − K = 1 Estimator 4.2 reduces to the estimator of the conditional MSEP for a single run-off triangle in the univariate ALR model (see Mack (2002)).

In addition to Estimators 4.1 and 4.2 we have to estimate the cross product terms between the CL estimators and the ALR method estimators, namely (see (31))

\[ \begin{array}{l} E\left[\left(\sum_{n=1}^{K} \widehat{C_{i, J}^{(n)}}-\sum_{n=1}^{K} C_{i, J}^{(n)}\right)\right. \\ \left.\quad \cdot\left(\sum_{n=K+1}^{N}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=K+1}^{N} C_{i, J}^{(n)}\right) \mid \mathcal{D}_{I}^{N}\right] \\ \quad=\mathbf{1}_{K}^{\prime} \cdot \operatorname{Cov}\left(\mathbf{C}_{i, J}^{\mathrm{CL}}, \mathbf{C}_{i, J}^{\mathrm{AD}} \mid \mathcal{D}_{I}^{N}\right) \cdot \mathbf{1}_{N-K} \\ \quad+\mathbf{1}_{K}^{\prime} \cdot\left({\widehat{\mathbf{C}_{i, J}}}^{\mathrm{CL}}-E\left[\mathbf{C}_{i, J}^{\mathrm{CL}} \mid \mathcal{D}_{I}^{N}\right]\right) \\ \quad \cdot\left({\widehat{\mathbf{C}_{i, J}}}^{\mathrm{AD}}-E\left[\mathbf{C}_{i, J}^{\mathrm{AD}} \mid \mathcal{D}_{I}^{N}\right]\right)^{\prime} \cdot \mathbf{1}_{N-K}. \end{array} \tag{37} \]

That is, this cross product term, again, decouples into a process error part and an estimation error part (first and second term on the right-hand side of (37)).

4.1.1. Conditional cross process variance

In this subsection we provide an estimate of the conditional cross process variance. The following result holds

Lemma 4.4 (Cross process variance for single accident years) Under Model Assumptions 3.1 the conditional cross process variance for the ultimate claims \(\mathbf{C}_{i, J}\) of accident year \(i \in\{1, \ldots, I\}\), given the observations \(\mathcal{D}_I^N\), is given by

\[ \begin{array}{l} \mathbf{1}_{K}^{\prime} \cdot \operatorname{Cov}\left(\mathbf{C}_{i, J}^{\mathrm{CL}}, \mathbf{C}_{i, J}^{\mathrm{AD}} \mid \mathcal{D}_{I}^{N}\right) \cdot \mathbf{1}_{N-K} \\ \quad=\mathbf{1}_{K}^{\prime} \cdot \sum_{j=I-i+1}^{J} \prod_{l=j}^{J-1} \mathrm{D}\left(\mathbf{f}_{l}\right) \cdot \Sigma_{i, j-1}^{\mathrm{CA}} \cdot \mathbf{1}_{N-K}, \end{array} \tag{38} \]

where

\[ \Sigma_{i, j-1}^{\mathrm{CA}}=E\left[\mathrm{D}\left(\mathbf{C}_{i, j-1}^{\mathrm{CL}}\right)^{1 / 2} \cdot \Sigma_{j-1}^{(C, A)} \mid \mathbf{C}_{i, I-i}\right] \cdot \mathrm{V}_{i}^{1 / 2}. \tag{39} \]

Proof See appendix, Section 7.1.

If we replace the parameters \(\mathbf{f}_l\) and \(\Sigma_{i, j-1}^{\mathbf{C A}}\) in (38) by their estimates (cf. Section 5), we obtain an estimator of the conditional cross process variance for a single accident year.

4.1.2. Conditional cross estimation error

In this subsection we deal with the second term on the right-hand side of (37). Using Lemma 3.3 as well as definitions (26) and (27), we obtain for the cross estimation error of accident year i ∈ {1, . . . , I} the representation

\[ \begin{aligned} \mathbf{1}_{K}^{\prime} \cdot & \left({\widehat{\mathbf{C}_{i, J}}}^{\mathrm{CL}}-E\left[\mathbf{C}_{i, J}^{\mathrm{CL}} \mid \mathcal{D}_{I}^{N}\right]\right) \cdot\left({\widehat{\mathbf{C}_{i, J}}}^{\mathrm{AD}}-E\left[\mathbf{C}_{i, J}^{\mathrm{AD}} \mid \mathcal{D}_{I}^{N}\right]\right)^{\prime} \\ \cdot \mathbf{1}_{N-K} & \\ = & \mathbf{1}_{K}^{\prime} \cdot\left(\prod_{j=I-i}^{J-1} \mathrm{D}\left(\hat{\mathbf{f}}_{j}\right)-\prod_{j=I-i}^{J-1} \mathrm{D}\left(\mathbf{f}_{j}\right)\right) \cdot \mathbf{C}_{i, I-i}^{\mathrm{CL}} \\ & \cdot\left(\sum_{j=I-i+1}^{J}\left({\widehat{\mathbf{X}_{i, j}}}^{\mathrm{AD}}-E\left[\mathbf{X}_{i, j}^{\mathrm{AD}}\right]\right)\right)^{\prime} \cdot \mathbf{1}_{N-K} \\ = & \mathbf{1}_{K}^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot\left(\hat{\mathbf{g}}_{i \mid J}-\mathbf{g}_{i \mid J}\right) \\ & \cdot\left(\sum_{j=I-i+1}^{J}\left(\hat{\mathbf{m}}_{j}-\mathbf{m}_{j}\right)\right)^{\prime} \cdot \mathrm{V}_{i} \cdot \mathbf{1}_{N-K}, \end{aligned} \tag{40} \]

where \(\hat{\mathbf{g}}_{i \mid J}\) and \(\mathbf{g}_{i \mid J}\) are defined by

\[ \begin{array}{l} \hat{\mathbf{g}}_{i \mid J}=\mathrm{D}\left(\hat{\mathbf{f}}_{I-i}\right) \cdot \ldots \cdot \mathrm{D}\left(\hat{\mathbf{f}}_{J-1}\right) \cdot \mathbf{1}_{K}, \\ \mathbf{g}_{i \mid J}=\mathrm{D}\left(\mathbf{f}_{I-i}\right) \cdot \ldots \cdot \mathrm{D}\left(\mathbf{f}_{J-1}\right) \cdot \mathbf{1}_{K} . \end{array} \tag{41} \]

In order to derive an estimator of the conditional cross estimation error we would like to calculate the right-hand side of (40). Observe that the realizations of the estimators \(\hat{\mathbf{f}}_{I-i}, \ldots, \hat{\mathbf{f}}_{J-1}\) and \(\hat{\mathbf{m}}_{I-i+1}, \ldots, \hat{\mathbf{m}}_J\) are known at time \(I\), but the “true” CL factors \(\mathbf{f}_{I-i}, \ldots, \mathbf{f}_{J-1}\) and the incremental loss ratios \(\mathbf{m}_{I-i+1}, \ldots, \mathbf{m}_J\) are unknown. Hence (40) cannot be calculated explicitly. In order to determine the conditional cross estimation error we analyze how much the “possible” CL factor estimators and the incremental loss ratio estimators fluctuate around their “true” mean values \(\mathbf{f}_j\) and \(\mathbf{m}_j\). In the following, analogously to Merz and Wüthrich (2008), we measure these volatilities of the estimators \(\hat{\mathbf{f}}_j\) and \(\hat{\mathbf{m}}_j\) by means of resampled observations for \(\hat{\mathbf{f}}_j\) and \(\hat{\mathbf{m}}_j\). For this purpose we use the conditional resampling approach presented in Buchwalder et al. (2006), Section 4.1.2, to get an estimate for the term (40). By conditionally resampling the observations for \(\hat{\mathbf{f}}_{I-i}, \ldots, \hat{\mathbf{f}}_{J-1}\) and \(\hat{\mathbf{m}}_{I-i+1}, \ldots, \hat{\mathbf{m}}_J\), given the upper triangles \(\mathcal{D}_I^N\), we take into account the possibility that the observations for \(\hat{\mathbf{f}}_j\) and \(\hat{\mathbf{m}}_j\) could have been different from the observed values. This means that, given \(\mathcal{D}_I^N\), we generate “new” observations \(\tilde{\mathbf{C}}_{i, j+1}^{C L}\) and \(\tilde{\mathbf{X}}_{i, j+1}^{\mathrm{AD}}\) for \(i \in\{0, \ldots, I\}\) and \(j \in\{0, \ldots, J-1\}\) using the formulas (conditional resampling)

\[ \tilde{\mathbf{C}}_{i, j+1}^{\mathrm{CL}}=\mathrm{D}\left(\mathbf{f}_{j}\right) \cdot \mathbf{C}_{i, j}^{\mathrm{CL}}+\mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)^{1 / 2} \cdot \mathrm{D}\left(\tilde{\varepsilon}_{i, j+1}^{\mathrm{CL}}\right) \cdot \sigma_{j}^{\mathrm{CL}} \tag{42} \]

and

\[ \tilde{\mathbf{X}}_{i, j+1}^{\mathrm{AD}}=\mathrm{V}_{i} \cdot \mathbf{m}_{j+1}+\mathrm{V}_{i}^{1 / 2} \cdot \mathrm{D}\left(\tilde{\varepsilon}_{i, j+1}^{\mathrm{AD}}\right) \cdot \sigma_{j}^{\mathrm{AD}}, \tag{43} \]

With

\[ \tilde{\varepsilon}_{i, j+1}=\binom{\tilde{\varepsilon}_{i, j+1}^{\mathrm{CL}}}{\tilde{\varepsilon}_{i, j+1}^{\mathrm{AD}}}, \quad \varepsilon_{i, j+1}=\binom{\varepsilon_{i, j+1}^{\mathrm{CL}}}{\varepsilon_{i, j+1}^{\mathrm{AD}}} \tag{44} \]

are independent and identically distributed copies.

We define

\[ \mathrm{W}_{j}=\left(\sum_{k=0}^{I-j-1} \mathrm{D}\left(\mathbf{C}_{k, j}^{\mathrm{CL}}\right)^{1 / 2}\left(\Sigma_{j}^{(C)}\right)^{-1} \mathrm{D}\left(\mathbf{C}_{k, j}^{\mathrm{CL}}\right)^{1 / 2}\right)^{-1} \]

and

\[ \mathrm{U}_{j}=\left(\sum_{k=0}^{I-j-1} \mathrm{~V}_{k}^{1 / 2}\left(\Sigma_{j}^{(A)}\right)^{-1} \mathrm{~V}_{k}^{1 / 2}\right)^{-1} . \]

The resampled representations for the estimates of the multivariate CL factors and the incremental loss ratios are then given by (see (21) and (22))

\[ \hat{\mathbf{f}}_{j}=\mathbf{f}_{j}+\mathrm{W}_{j} \sum_{i=0}^{I-j-1} \mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)^{1 / 2}\left(\Sigma_{j}^{(C)}\right)^{-1} \mathrm{D}\left(\tilde{\varepsilon}_{i, j+1}^{\mathrm{CL}}\right) \sigma_{j}^{\mathrm{CL}}, \tag{45} \]

and

\[ \hat{\mathbf{m}}_{j+1}=\mathbf{m}_{j+1}+\mathrm{U}_{j} \sum_{i=0}^{I-j-1} \mathrm{~V}_{i}^{1 / 2}\left(\Sigma_{j}^{(A)}\right)^{-1} \mathrm{D}\left(\tilde{\varepsilon}_{i, j+1}^{\mathrm{AD}}\right) \sigma_{j}^{\mathrm{AD}} . \tag{46} \]

Note, in (45) and (46) as well as in the following exposition, we use the previous notations \(\hat{\mathbf{f}}_j\) and \(\hat{\mathbf{m}}_{j+1}\) for the resampled estimates of the multivariate CL factors \(\mathbf{f}_j\) and the incremental loss ratios \(\mathbf{m}_{j+1}\), respectively, to avoid an overloaded notation. Furthermore, given the observations \(\mathcal{D}_I^N\), we denote the conditional probability measure of these resampled multivariate estimates by \(P_{\mathcal{D}_l^N}^*\). For a more detailed discussion of this conditional resampling approach we refer to Merz and Wüthrich (2008). We obtain the following lemma:

Lemma 4.5 Under Model Assumptions 3.1 and resampling assumptions (42)-(44) we have:

a) \(\hat{\mathbf{f}}_0, \ldots, \hat{\mathbf{f}}_{J-1}\) are independent under \(P_{D_I^N}^*, \hat{\mathbf{m}}_1\), \(\ldots, \hat{\mathbf{m}}_J\) are independent under \(P_{D_I^N}^*\), and \(\hat{\mathbf{f}}_j\) and \(\hat{\mathbf{m}}_k\) are independent under \(P_{\mathcal{D}_I^N}^*\) if \(k \neq j+1\),

b) \(E_{D_I^N}^*\left[\hat{\mathbf{f}}_j\right]=\mathbf{f}_j\) and \(E_{D_I^N}^*\left[\hat{\mathbf{m}}_{j+1}\right]=\mathbf{m}_{j+1}\) for \(0 \leq j \leq J-1\) and

c) \(E_{D_I^N}^*\left[\hat{f}_j^{(m)} \hat{m}_{j+1}^{(n)}\right]=f_j^{(m)} m_{j+1}^{(n)}+\mathrm{T}_j(m, n)\),
where \(\mathrm{T}_j(m, n)\) is the entry \((m, n)\) of the \(K \times\) ( \(N-K\) )-matrix

\[ \begin{aligned} \mathrm{T}_{j}= & \mathrm{W}_{j} \sum_{i=0}^{I-j-1} \mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)^{1 / 2}\left(\Sigma_{j}^{(C)}\right)^{-1} \Sigma_{j}^{(C, A)} \\ & \cdot\left(\Sigma_{j}^{(A)}\right)^{-1} \mathrm{~V}_{i}^{1 / 2} \mathrm{U}_{j}. \end{aligned} \tag{47} \]

Proof See appendix, Section 7.2.

Using Lemma 4.5 we choose for the conditional cross estimation error (40) the estimator

\[ \begin{array}{l} \mathbf{1}_{K}^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot E_{\mathcal{D}_{I}^{N}}^{*}\left[\left(\hat{\mathbf{g}}_{i \mid J}-\mathbf{g}_{i \mid J}\right) \cdot\left(\sum_{j=I-i+1}^{J}\left(\hat{\mathbf{m}}_{j}-\mathbf{m}_{j}\right)\right)^{\prime}\right] \\ \cdot \mathrm{V}_{i} \cdot \mathbf{1}_{N-K} \\ \quad=\mathbf{1}_{K}^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot \operatorname{Cov}_{\mathcal{D}_{I}^{N}}^{*}\left(\hat{\mathbf{g}}_{i \mid J}, \sum_{j=I-i+1}^{J} \hat{\mathbf{m}}_{j}\right) \\ \quad \cdot \mathrm{V}_{i} \cdot \mathbf{1}_{N-K}. \end{array} \tag{48} \]

We define the matrix

\[ \begin{aligned} \Psi_{k, i} & =\left(\Psi_{k, i}^{(m, n)}\right)_{m, n}=\operatorname{Cov}_{\mathcal{D}_{I}^{N}}^{*}\left(\hat{\mathbf{g}}_{k \mid J}, \sum_{j=I-i+1}^{J} \hat{\mathbf{m}}_{j}\right) \\ & =\sum_{j=I-i+1}^{J} \operatorname{Cov}_{\mathcal{D}_{I}^{N}}^{*}\left(\hat{\mathbf{g}}_{k \mid J}, \hat{\mathbf{m}}_{j}\right) \end{aligned} \tag{49} \]

for all \(k, i \in\{1, \ldots, I\}\). The following result holds for its components \(\Psi_{k, i}^{(m, n)}\):

Lemma 4.6 Under Model Assumptions 3.1 and resampling assumptions (42)–(44) we have for m = 1, . . . , K and n = 1, . . . , N − K

\[ \Psi_{k, i}^{(m, n)}=\sum_{j=(I-i+1) \vee(I-k+1)}^{J} \prod_{r=I-k}^{J-1} f_{r}^{(m)} \frac{1}{f_{j-1}^{(m)}} \mathrm{T}_{j-1}(m, n) . \]

Proof See appendix, Section 7.3.

Putting (31), (37), (38) and (48) together and replacing the parameters by their estimates we motivate the following estimator for the conditional MSEP of a single accident year in the multivariate combined method:

Estimator 4.7 (MSEP for single accident years, combined method) Under Model Assumptions 3.1 we have the estimator for the conditional MSEP of the ultimate claims for a single accident year \(i \in\{1, \ldots, I\}\)

\[ \begin{array}{l} \widehat{\operatorname{msep}}_{\Sigma_{n=1}^{N} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=1}^{K}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}+\sum_{n=K+1}^{N}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}\right) \\ =\widehat{\operatorname{msep}}_{\Sigma_{n=1}^{K} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=1}^{K}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}\right) \\ +\widehat{\operatorname{msep}}_{\Sigma_{n=K+1}^{N} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=K+1}^{N}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}\right) \\ +2 \cdot \mathbf{1}_{K}^{\prime} \cdot \sum_{j=I-i+1}^{J} \prod_{l=j}^{J-1} \mathrm{D}\left(\hat{\mathbf{f}}_{l}\right) \cdot \hat{\Sigma}_{i, j-1}^{\mathrm{CA}} \cdot \mathbf{1}_{N-K} \\ +2 \cdot \mathbf{1}_{K}^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot\left(\hat{\Psi}_{i, i}^{(m, n)}\right)_{m, n} \cdot \mathrm{~V}_{i} \cdot \mathbf{1}_{N-K}, \end{array} \tag{50} \]

with

\[ \hat{\Sigma}_{i, j-1}^{\mathbf{C A}}=\mathrm{D}\left(\widehat{\mathbf{C}_{i, j-1}}{ }^{\mathrm{CL}}\right)^{1 / 2} \cdot \hat{\Sigma}_{j-1}^{(C, A)} \cdot \mathrm{V}_{i}^{1 / 2}, \tag{51} \]

\[ \hat{\Psi}_{k, i}^{(m, n)}=\hat{g}_{k \mid J}^{(m)} \sum_{j=(I-i+1) \vee(I-k+1)}^{J} \frac{1}{\hat{f}_{j-1}^{(m)}} \hat{\mathrm{T}}_{j-1}(m, n) . \tag{52} \]

Thereby, the first two terms on the right-hand side of (50) are given by (32) and (36), \(\hat{g}_{k \mid J}^{(m)}\) denotes the mth coordinate of \(\hat{\mathbf{g}}_{k \mid J}\) (cf. (41)) and the parameter estimates \(\hat{\Sigma}_{j-1}^{(C, A)}\) as well as \(\hat{\mathrm{T}}_{j-1}(m, n)\) (entry \((m, n)\) of the estimate \(\hat{\mathrm{T}}_{j-1}\) for the \(K \times(N-K)\)-matrix \(\left.\mathrm{T}_{j-1}\right)\) are given in Section 5.

4.2. Conditional MSEP for aggregated accident years

Now, we derive an estimator of the conditional MSEP (30) for aggregated accident years. To this end we consider two different accident years \(1 \leq i<l \leq I\). We know that the ultimate claims \(\mathbf{C}_{i, J}\) and \(\mathbf{C}_{l, J}\) are independent but we also know that we have to take into account the dependence of the estimators \(\widehat{\mathbf{C}_{i, J}}\) and \(\widehat{\mathbf{C}_{l, J}}\). The conditional MSEP for two aggregated accident years \(i\) and \(l\) is given by

\[\small{ \begin{array}{l} \operatorname{msep}_{\Sigma_{n=1}^{N}\left(C_{i, J}^{(n)}+C_{l, J}^{(n)}\right) \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=1}^{K} \widehat{C_{i, J}^{(n)}}+\sum_{n=K+1}^{N} \widehat{C_{i, J}^{(n)}} \mathrm{AD}+\sum_{n=1}^{K}{\widehat{C_{l, J}^{(n)}}}^{\mathrm{CL}}+\sum_{n=K+1}^{N} \widehat{C_{l, J}^{(n)}} \mathrm{AD}\right) \\ \quad = \operatorname{msep}_{\Sigma_{n=1}^{N} C_{i, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=1}^{K}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}+\sum_{n=K+1}^{N} \widehat{C_{i, J}^{(n)}} \mathrm{AD}\right)\\ \qquad +\operatorname{msep}_{\Sigma_{n=1}^{N} C_{l, J}^{(n)} \mid \mathcal{D}_{I}^{N}}\left(\sum_{n=1}^{K} \widehat{C_{l, J}^{(n)}} \mathrm{CL}+\sum_{n=K+1}^{N} \widehat{C_{l, J}^{(n)}} \mathrm{AD}\right) \\ \qquad +2 \cdot E\left[\left(\sum_{n=1}^{K}{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}+{\widehat{\sum_{n=K+1}^{N}}}^{\mathrm{AD}}{\widehat{C_{i, J}^{(n)}}}^{N}-\sum_{n=1} C_{i, J}^{(n)}\right)\\ \qquad \cdot\left(\sum_{n=1}^{K}{\widehat{C_{l, J}^{(n)}}}^{\mathrm{CL}}+{\widehat{\sum_{n=K+1}^{N}}}^{\mathrm{AD}}-{\widehat{C_{l, J}^{(n)}}}^{N} C_{l, J}^{(n)}\right) \mid \mathcal{D}_{I}^{N}\right] . \end{array} \tag{53}} \]

The first two terms on the right-hand side of (53) are the conditional prediction errors for the two single accident years 1 ≤ I ≤ l ≤ I, respectively, which we estimate by Estimator 4.7. For the third term on the right-hand side of (53) we obtain the decomposition

\[ \begin{align} &E\left[\left(\sum_{n=1}^K{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}+\sum_{n=K+1}^N{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=1}^N C_{i, J}^{(n)}\right)\right. \\ &\quad\left.\cdot\left(\sum_{n=1}^K{\widehat{C_{l, J}^{(n)}}}^{\mathrm{CL}}+\sum_{n=K+1}^N{\widehat{C_{l, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=1}^N C_{l, J}^{(n)}\right) \mid \mathcal{D}_I^N\right] \\ &\qquad=E\left[\left(\sum_{n=1}^K{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}-\sum_{n=1}^K C_{i, J}^{(n)}\right)\right. \\ &\qquad\qquad\left.\cdot\left(\sum_{n=K+1}^N{\widehat{C_{l, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=K+1}^N C_{l, J}^{(n)}\right) \mid \mathcal{D}_I^N\right] \\ &\qquad\quad+E\left[\left(\sum_{n=K+1}^N{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=K+1}^N C_{i, J}^{(n)}\right)\right. \\ &\qquad\qquad\left.\cdot\left(\sum_{n=1}^K{\widehat{C_{l, J}^{(n)}}}^{\mathrm{CL}}-\sum_{n=1}^K C_{l, J}^{(n)}\right) \mid \mathcal{D}_I^N\right] \\ &\qquad\quad+E\left[\left(\sum_{n=1}^K{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}-\sum_{n=1}^K C_{i, J}^{(n)}\right)\right. \\ &\qquad\qquad\left.\cdot\left(\sum_{n=1}^K{\widehat{C_{l, J}^{(n)}}}^{\mathrm{CL}}-\sum_{n=1}^K C_{l, J}^{(n)}\right) \mid \mathcal{D}_I^N\right] \\ &\qquad\quad+E\left[\left(\sum_{n=K+1}^N{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=K+1}^N C_{i, J}^{(n)}\right)\right. \\ &\qquad\qquad\left.\cdot\left(\sum_{n=K+1}^N{\widehat{C_{l, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=K+1}^N C_{l, J}^{(n)}\right) \mid \mathcal{D}_I^N\right]. \end{align} \tag{54} \]

Using the independence of different accident years we obtain for the first two terms on the right-hand side of (54)

\[ \begin{aligned} & E\left[\left(\sum_{n=1}^K{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}-\sum_{n=1}^K C_{i, J}^{(n)}\right)\right. \\ & \left.\quad \cdot\left(\sum_{n=K+1}^N{\widehat{C_{l, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=K+1}^N C_{l, J}^{(n)}\right) \mid \mathcal{D}_I^N\right] \\ & \quad=\mathbf{1}_K^{\prime} \cdot\left(\widehat{\mathbf{C}}_{i, J}^{\mathrm{CL}}-E\left[\mathbf{C}_{i, J}^{\mathrm{CL}} \mid \mathcal{D}_I^N\right]\right) \\ & \qquad \cdot\left(\widehat{\mathbf{C}}_{l, J}^{\mathrm{AD}}-E\left[\mathbf{C}_{l, J}^{\mathrm{AD}} \mid \mathcal{D}_I^N\right]\right)^{\prime} \cdot \mathbf{1}_{N-K} \\ & \quad=\mathbf{1}_K^{\prime} \cdot\left(\prod_{j=I-i}^{J-1} \mathrm{D}\left(\hat{\mathbf{f}}_j\right)-\prod_{j=I-i}^{J-1} \mathrm{D}\left(\mathbf{f}_j\right)\right)^{\prime} \cdot \mathbf{C}_{i, I-i}^{\mathrm{CL}} \\ & \qquad \cdot\left(\sum_{j=I-l+1}^J\left(\widehat{\mathbf{X}}_{l, j}^{\mathrm{AD}}-E\left[\mathbf{X}_{l, j}^{\mathrm{AD}}\right]\right)\right)^{\prime} \cdot \mathbf{1}_{N-K} \\ & =\mathbf{1}_K^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot\left(\hat{\mathbf{g}}_{i \mid J}-\mathbf{g}_{i \mid J}\right) \\ & \qquad \cdot\left(\sum_{j=I-l+1}^J\left(\hat{\mathbf{m}}_j-\mathbf{m}_j\right)\right)^{\prime} \cdot \mathrm{V}_l \cdot \mathbf{1}_{N-K}, \end{aligned} \tag{55} \]

and analogously

\[ \begin{aligned} & E\left[\left(\sum_{n=K+1}^N{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=K+1}^N C_{i, J}^{(n)}\right)\right. \\ &\quad \left.\cdot\left(\sum_{n=1}^K{\widehat{C_{l, J}^{(n)}}}^{\mathrm{CL}}-\sum_{n=1}^K C_{l, J}^{(n)}\right) \mid \mathcal{D}_I^N\right] \\ &\qquad =\mathbf{1}_K^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{l, I-l}^{\mathrm{CL}}\right) \cdot\left(\hat{\mathbf{g}}_{l \mid J}-\mathbf{g}_{l \mid J}\right) \\ &\qquad \quad \cdot\left(\sum_{j=I-i+1}^J\left(\hat{\mathbf{m}}_j-\mathbf{m}_j\right)\right)^{\prime} \cdot \mathrm{V}_i \cdot \mathbf{1}_{N-K} \cdot \end{aligned} \tag{56} \]

Under the conditional resampling measure \(P_{\mathcal{D}_I^N}^*\) these two terms are estimated by (see also Lemma 4.6), \(s=i, l\) and \(t=l, i\),

\[ \begin{aligned} & \mathbf{1}_K^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{s, I-s}^{\mathrm{CL}}\right) \cdot E_{\mathcal{D}_I^N}^*\left[\left(\hat{\mathbf{g}}_{s \mid J}-\mathbf{g}_{s \mid J}\right) \cdot\left(\sum_{j=I-t+1}^J\left(\hat{\mathbf{m}}_j-\mathbf{m}_j\right)\right)^{\prime}\right] \\ & \cdot \mathrm{V}_t \cdot \mathbf{1}_{N-K} \\ & \quad=\mathbf{1}_K^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{s, I-s}^{\mathrm{CL}}\right) \cdot\left(\Psi_{s, t}^{(m, n)}\right)_{m, n} \cdot \mathrm{~V}_t \cdot \mathbf{1}_{N-K} \cdot \end{aligned} \]

Now we consider the third term on the right hand side of (54). Again, using the independence of different accident years we obtain

\[ \begin{aligned} & E\left[\left(\sum_{n=1}^K{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}-\sum_{n=1}^K C_{i, J}^{(n)}\right)\right. \\ &\quad \left.\cdot\left(\sum_{n=1}^K{\widehat{C_{l, J}^{(n)}}}^{\mathrm{CL}}-\sum_{n=1}^K C_{l, J}^{(n)}\right) \mid \mathcal{D}_I^N\right] \\ &\qquad =\mathbf{1}_K^{\prime} \cdot\left(\widehat{\mathbf{C}}_{i, J}^{\mathrm{CL}}-E\left[\mathbf{C}_{i, J}^{\mathrm{CL}} \mid \mathcal{D}_I^N\right]\right) \\ &\qquad \quad \cdot\left({\widehat{\mathbf{C}_{l, J}}}^{\mathrm{CL}}-E\left[\mathbf{C}_{l, J}^{\mathrm{CL}} \mid \mathcal{D}_I^N\right]\right)^{\prime} \cdot \mathbf{1}_K \\ &\qquad =\mathbf{1}_K^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot\left(\hat{\mathbf{g}}_{i \mid J}-\mathbf{g}_{i \mid J}\right) \\ &\qquad \quad \cdot\left(\hat{\mathbf{g}}_{l \mid J}-\mathbf{g}_{l \mid J}\right)^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{l, I-l}^{\mathrm{CL}}\right) \cdot \mathbf{1}_K . \end{aligned} \tag{57} \]

This term is estimated by

\[ \begin{aligned} & \mathbf{1}_K^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot E_{D_I^N}^*\left[\left(\hat{\mathbf{g}}_{i \mid J}-\mathbf{g}_{i \mid J}\right)\right. \\ & \left.\cdot\left(\hat{\mathbf{g}}_{l \mid J}-\mathbf{g}_{l \mid J}\right)^{\prime}\right] \cdot \mathrm{D}\left(\mathbf{C}_{l, I-l}^{\mathrm{CL}}\right) \cdot \mathbf{1}_K \\ &\quad =\mathbf{1}_K^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot\left(\Delta_{i, J}^{(n, m)}\right)_{1 \leq n, m \leq K} \\ & \qquad \cdot \mathrm{D}\left(\mathbf{C}_{l, I-l}^{\mathrm{CL}}\right) \cdot \prod_{k=I-l}^{I-i-1} \mathrm{D}\left(\mathbf{f}_k\right) \cdot \mathbf{1}_K, \end{aligned} \tag{58} \]

where \(\Delta_{i, J}^{(n, m)}\) is estimated by

\[ \begin{aligned} \hat{\Delta}_{i, J}^{(n, m)}= & \prod_{l=I-i}^{J-1}\left(\hat{f}_l^{(n)} \cdot \hat{f}_l^{(m)}+\sum_{k=0}^{I-l-1} \hat{\mathbf{a}}_{n \mid l}^k \cdot \hat{\Sigma}_l^{(C)} \cdot\left(\hat{\mathbf{a}}_{m \mid l}^k\right)^{\prime}\right) \\ & -\prod_{l=I-i}^{J-1} \hat{f}_l^{(n)} \cdot \hat{f}_l^{(m)}. \end{aligned} \tag{59} \]

The parameter estimates \(\hat{\mathbf{a}}_{n \mid l}^k\) and \(\hat{\mathbf{a}}_{m \mid l}^k\) are the \(n\)th and \(m\) th row of (35) and the parameter estimate \(\hat{\Sigma}_l^{(C)}\) is given in Section 5 (see also Merz and Wüthrich (2008)).

Finally, we obtain for the last term on the right-hand side of (54)

\[ \begin{aligned} E & {\left[\left(\sum_{n=K+1}^N{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=K+1}^N C_{i, J}^{(n)}\right)\right.} \\ &\quad \left.\cdot\left(\sum_{n=K+1}^N{\widehat{C_{l, J}^{(n)}}}^{\mathrm{AD}}-\sum_{n=K+1}^N C_{l, J}^{(n)}\right) \mid \mathcal{D}_I^N\right] \\ &\qquad =\mathbf{1}_{N-K}^{\prime} \cdot\left(\widehat{\mathbf{C}}_{i, J}^{\mathrm{AD}}-E\left[\mathbf{C}_{i, J}^{\mathrm{AD}} \mid \mathcal{D}_I^N\right]\right) \\ &\qquad \quad \cdot\left(\widehat{\mathbf{C}}_{l, J}^{\mathrm{AD}}-E\left[\mathbf{C}_{l, J}^{\mathrm{AD}} \mid \mathcal{D}_I^N\right]\right)^{\prime} \cdot \mathbf{1}_{N-K}, \end{aligned} \tag{60} \]

which is estimated by (see also Merz and Wüthrich (2009))

\[ \begin{aligned} & \mathbf{1}_{N-K}^{\prime} \cdot E\left[\left({\widehat{\mathbf{C}_{i, J}}}^{\mathrm{AD}}-E\left[\mathbf{C}_{i, J}^{\mathrm{AD}} \mid \mathcal{D}_I^N\right]\right)\right. \\ &\quad \left.\cdot\left({\widehat{\mathbf{C}_{l, J}}}^{\mathrm{AD}}-E\left[\mathbf{C}_{l, J}^{\mathrm{AD}} \mid \mathcal{D}_I^N\right]\right)^{\prime}\right] \cdot \mathbf{1}_{N-K} \\ &\qquad =\mathbf{1}_{N-K}^{\prime} \cdot \mathrm{V}_i \\ & \qquad \quad \cdot\left[\sum_{j=I-i+1}^J\left(\sum_{k=0}^{I-j} \mathrm{~V}_k^{1 / 2} \cdot\left(\Sigma_{j-1}^{(A)}\right)^{-1} \cdot \mathrm{~V}_k^{1 / 2}\right)^{-1}\right] \\ & \qquad \quad \cdot \mathrm{V}_l \cdot \mathbf{1}_{N-K}. \end{aligned} \tag{61} \]

Putting all the terms together and replacing the parameters by their estimates we obtain the following estimator for the conditional MSEP of aggregated accident years in the multivariate combined method:

Estimator 4.8 (MSEP for aggregated accident years, combined method) Under Model Assumptions 3.1 we have the estimator for the conditional MSEP of the ultimate claims for aggregated accident years

\[ \begin{aligned} &\widehat{\operatorname{msep}}_{\Sigma_i} \Sigma_n C_{i, J}^{(n)} \mid \mathcal{D}_I^N\left(\sum_{i=1}^I \sum_{n=1}^K{\widehat{C_{i, J}^{(n)}}}^{\mathrm{CL}}+\sum_{i=1}^I \sum_{n=K+1}^N{\widehat{C_{i, J}^{(n)}}}^{\mathrm{AD}}\right) & \\ &\quad= \sum_{i=1}^I \widehat{\operatorname{msep}}_{\Sigma_n} C_{i, J}^{(n)} \mid \mathcal{D}_I^N\left(\sum_{n=1}^K \widehat{C_{i, J}^{(n)}}+\sum_{n=K+1}^N \widehat{C_{i, J}^{(n)}} \mathrm{AD}\right) \\ &\qquad +2 \cdot \sum_{1 \leq i<l \leq I} \mathbf{1}_K^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot\left(\hat{\Psi}_{i, l}^{(m, n)}\right)_{m, n} \cdot \mathrm{~V}_l \cdot \mathbf{1}_{N-K} \\ &\qquad +2 \cdot \sum_{1 \leq i<l \leq I} \mathbf{1}_K^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{l, I-l}^{\mathrm{CL}}\right) \cdot\left(\hat{\Psi}_{l, i}^{(m, n)}\right)_{m, n} \cdot \mathrm{~V}_i \cdot \mathbf{1}_{N-K} \\ & \qquad+2 \cdot \sum_{1 \leq i<l \leq I} \mathbf{1}_K^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, I-i}^{\mathrm{CL}}\right) \cdot\left(\hat{\Delta}_{i, J}^{(m, n)}\right)_{m, n} \\ &\qquad \cdot \mathrm{D}\left(\mathbf{C}_{l, I-l}^{\mathrm{CL}}\right) \cdot \prod_{j=I-l}^{I-i-1} \mathrm{D}\left(\hat{\mathbf{f}}_j\right) \cdot \mathbf{1}_K \\ &\qquad +2 \cdot \sum_{1 \leq i<l \leq I} \mathbf{1}_{N-K}^{\prime} \cdot \mathrm{V}_i \\ &\qquad \cdot \sum_{j=I-i+1}^J\left(\sum_{k=0}^{I-j} \mathrm{~V}_k^{1 / 2} \cdot\left(\hat{\Sigma}_{j-1}^{(A)}\right)^{-1} \cdot \mathrm{~V}_k^{1 / 2}\right)^{-1} \\ &\qquad \cdot \mathrm{~V}_l \cdot \mathbf{1}_{N-K} \cdot \end{aligned} \tag{62}\]

4.3. Conditional MSEP with \(\hat{\mathbf{f}}_j^{(0)}\) and \(\hat{\mathbf{m}}_j^{(0)}\)

In some cases, it may be more convenient to use estimators (24) and (25) to estimate \(\mathbf{f}_j\) and \(\mathbf{m}_j\), respectively, instead of (21) and (22). Estimators (24) and (25) do not reflect the correlation among subportfolios and are thus simpler to calculate, but being less than optimal, will have greater MSEP than estimators (21) and (22).

The changes that occur when estimators (24) and (25) are used are noted here. In Estimator 4.1, (35) becomes

\[ \hat{\mathbf{A}}_l^k=\left(\sum_{i=0}^{I-l-1} \mathrm{D}\left(\mathbf{C}_{i, l}^{\mathrm{CL}}\right)\right)^{-1} \cdot \mathrm{D}\left({\widehat{\mathbf{C}_{k, l}}}^{\mathrm{CL}}\right)^{1 / 2}. \]

In Estimator 4.2, the last term of (36) becomes

\[ \begin{aligned} \mathbf{1}_{N-K}^{\prime} \cdot \mathrm{V}_i \cdot[ & \sum_{j=I-i+1}^J\left(\sum_{l=0}^{I-j} \mathrm{~V}_l\right)^{-1} \\ & \left.\cdot\left(\sum_{l=0}^{I-j} \mathrm{~V}_l^{1 / 2} \cdot \hat{\Sigma}_{j-1}^{(A)} \cdot \mathrm{V}_l^{1 / 2}\right) \cdot\left(\sum_{l=0}^{I-j} \mathrm{~V}_l\right)^{-1}\right] \\ & \cdot \mathrm{V}_i \cdot \mathbf{1}_{N-K}. \end{aligned} \]

\(\mathrm{W}_j\) becomes

\[ \left(\sum_{k=0}^{I-j-1} \mathrm{D}\left(\mathbf{C}_{k, j}^{\mathrm{CL}}\right)\right)^{-1}, \]

\(\mathrm{U}_j\) becomes

\[ \left(\sum_{k=0}^{I-j-1} \mathrm{~V}_{k}\right)^{-1}, \]

and \(T_j\) becomes

\[ \mathrm{W}_{j} \sum_{i=0}^{I-j-1} \mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)^{1 / 2} \Sigma_{j}^{(C, A)} \mathrm{V}_{i}^{1 / 2} \mathrm{U}_{j}, \]

with analogous changes to their estimators. The right-hand side of (61) and the expression to the right of the first summation sign in the last term of (62) become

\[ \begin{aligned} \mathbf{1}_{N-K}^{\prime} \cdot \mathrm{V}_{i} \cdot & {\left[\sum_{j=I-i+1}^{J}\left(\sum_{k=0}^{I-j} \mathrm{~V}_{k}\right)^{-1}\right.} \\ & \left.\cdot\left(\sum_{k=0}^{I-j} \mathrm{~V}_{k}^{1 / 2} \cdot \hat{\Sigma}_{j-1}^{(A)} \cdot \mathrm{V}_{k}^{1 / 2}\right) \cdot\left(\sum_{k=0}^{I-j} \mathrm{~V}_{k}\right)^{-1}\right] \\ & \cdot \mathrm{V}_{l} \cdot \mathbf{1}_{N-K} . \end{aligned} \]

5. Parameter estimation

Estimation of \(\mathbf{f}_j\) and \(\mathbf{m}_j\). As starting values for the iteration we use the unbiased estimators \(\hat{\mathbf{f}}_{j-1}^{(0)}\) and \(\hat{\mathbf{m}}_j^{(0)}\) defined by (24) and (25) for \(j= 1, \ldots, J\). From \(\hat{\mathbf{f}}_{j-1}^{(0)}\) and \(\hat{\mathbf{m}}_j^{(0)}\) we derive the estimates \(\hat{\Sigma}_{j-1}^{(C)(1)}\) and \(\hat{\Sigma}_{j-1}^{(A)(1)}\) of the covariance matrices \(\Sigma_{j-1}^{(C)}\) and \(\Sigma_{j-1}^{(A)}\) for \(j=1, \ldots, J\) (see estimators (64) and (67) below). Then these estimates \(\hat{\Sigma}_{j-1}^{(C)(1)}\) and \(\hat{\Sigma}_{j-1}^{(A)(1)}\) are used to determine \(\hat{\mathbf{f}}_{j-1}^{(1)}\) and \(\hat{\mathbf{m}}_j^{(1)} \operatorname{via}(s \geq 1)\)

\[ \begin{aligned} \hat{\mathbf{f}}_{j-1}^{(s)}= & \left(\sum_{i=0}^{I-j} \mathrm{D}\left(\mathbf{C}_{i, j-1}^{\mathrm{CL}}\right)^{1 / 2}\left(\hat{\Sigma}_{j-1}^{(C)(s)}\right)^{-1} \mathrm{D}\left(\mathbf{C}_{i, j-1}^{\mathrm{CL}}\right)^{1 / 2}\right)^{-1} \\ & \cdot \sum_{i=0}^{I-j} \mathrm{D}\left(\mathbf{C}_{i, j-1}^{\mathrm{CL}}\right)^{1 / 2}\left(\hat{\Sigma}_{j-1}^{(C)(s)}\right)^{-1} \mathrm{D}\left(\mathbf{C}_{i, j-1}^{\mathrm{CL}}\right)^{-1 / 2} \cdot \mathbf{C}_{i, j}^{\mathrm{CL}} \end{aligned} \tag{63} \]

and

\[ \begin{aligned} \hat{\mathbf{m}}_{j}^{(s)}= & \left(\sum_{i=0}^{I-j} \mathrm{~V}_{i}^{1 / 2} \cdot\left(\hat{\Sigma}_{j-1}^{(A)(s)}\right)^{-1} \cdot \mathrm{~V}_{i}^{1 / 2}\right)^{-1} \\ & \cdot \sum_{i=0}^{I-j} \mathrm{~V}_{i}^{1 / 2} \cdot\left(\hat{\Sigma}_{j-1}^{(A)(s)}\right)^{-1} \cdot \mathrm{~V}_{i}^{-1 / 2} \cdot \mathbf{X}_{i, j}^{\mathrm{AD}} . \end{aligned} \]

This algorithm is then iterated until it has sufficiently converged.

Estimation of \(\Sigma_{j-1}^{(C)}, \Sigma_{j-1}^{(A)}\) and \(\Sigma_{j-1}^{(C, A)}\). The covariance matrices \(\Sigma_{j-1}^{(C)}\) and \(\Sigma_{j-1}^{(A)}\) are estimated iteratively from the data for \(j=1, \ldots, J\). For the covariance matrices \(\Sigma_{j-1}^{(C)}\) we use the estimator proposed by Merz and Wüthrich (2008) \((s \geq 1)\)

\[ \begin{aligned} \hat{\Sigma}_{j-1}^{(C)(s)}= & Q_{j} \odot \sum_{i=0}^{I-j} \mathrm{D}\left(\mathbf{C}_{i, j-1}^{\mathrm{CL}}\right)^{1 / 2} \cdot\left(\mathbf{F}_{i, j}^{\mathrm{CL}}-\hat{\mathbf{f}}_{j-1}^{(s-1)}\right) \\ & \cdot\left(\mathbf{F}_{i, j}^{\mathrm{CL}}-\hat{\mathbf{f}}_{j-1}^{(s-1)}\right)^{\prime} \cdot \mathrm{D}\left(\mathbf{C}_{i, j-1}^{\mathrm{CL}}\right)^{1 / 2}, \end{aligned} \tag{64} \]

where ⊙ denotes the Hadamard product (entrywise product of two matrices),

\[ \begin{aligned} \mathbf{F}_{i, j}^{\mathrm{CL}} & =\mathrm{D}\left(\mathbf{C}_{i, j-1}^{\mathrm{CL}}\right)^{-1} \cdot \mathbf{C}_{i, j}^{\mathrm{CL}} \quad \text { and } \\ Q_{j} & =\left(\frac{1}{I-j-1+w_{j}^{(n, m)}}\right)_{1 \leq n, m \leq K} \end{aligned} \tag{65} \]

with

\[ w_{j}^{(n, m)}=\frac{\left(\sum_{l=0}^{I-j} \sqrt{C_{l, j-1}^{(n)}} \cdot \sqrt{C_{l, j-1}^{(m)}}\right)^{2}}{\sum_{l=0}^{I-j} C_{l, j-1}^{(n)} \cdot \sum_{l=0}^{I-j} C_{l, j-1}^{(m)}} . \tag{66} \]

For more details on this estimator see Merz and Wüthrich (2008), Section 5.

For the covariance matrices \(\Sigma_{j-1}^{(A)}\) we use the iterative estimation procedure suggested by Merz and Wüthrich (2009) ( \(s \geq 1\) )

\[ \begin{aligned} \hat{\Sigma}_{j-1}^{(A)(s)}= & \frac{1}{I-j} \cdot \sum_{i=0}^{I-j} \mathrm{~V}_{i}^{-1 / 2} \cdot\left(\mathbf{X}_{i, j}^{\mathrm{AD}}-\mathrm{V}_{i} \cdot \hat{\mathbf{m}}_{j}^{(s-1)}\right) \\ & \cdot\left(\mathbf{X}_{i, j}^{\mathrm{AD}}-\mathrm{V}_{i} \cdot \hat{\mathbf{m}}_{j}^{(s-1)}\right)^{\prime} \cdot \mathrm{V}_{i}^{-1 / 2}. \end{aligned} \tag{67} \]

For more details on this estimator see Merz and Wüthrich (2009), Section 5.

Motivated by estimators (64) and (67) for matrices \(\Sigma_{j-1}^{(C)}\) and \(\Sigma_{j-1}^{(A)}\), we propose for the covariance matrix \(\Sigma_{j-1}^{(C, A)}=\left(\Sigma_{j-1}^{(A, C)}\right)^{\prime}\) estimator

\[ \begin{aligned} \hat{\Sigma}_{j-1}^{(C, A)}= & \frac{1}{I-j} \cdot \sum_{i=0}^{I-j} \mathrm{D}\left(\mathbf{C}_{i, j-1}^{\mathrm{CL}}\right)^{1 / 2} \cdot\left(\mathbf{F}_{i, j}^{\mathrm{CL}}-\hat{\mathbf{f}}_{j-1}\right) \\ & \cdot\left(\mathbf{X}_{i, j}^{\mathrm{AD}}-\mathrm{V}_{i} \cdot \hat{\mathbf{m}}_{j}\right)^{\prime} \cdot \mathrm{V}_{i}^{-1 / 2}. \end{aligned} \tag{68} \]

Estimation of \(\Sigma_{i, j}^{\mathrm{CA}}\) and \(\mathrm{T}_j\). With these estimates we obtain as estimates of the matrices \(\Sigma_{i, j}^{\mathrm{CA}}\) and \(\mathrm{T}_j\)

\[ \begin{aligned} {\widehat{\Sigma_{i, j}}}^{\mathbf{C A}}= & \mathrm{D}\left({\widehat{\mathbf{C}_{i, j}}}^{\mathrm{CL}}\right)^{1 / 2} \hat{\Sigma}_{j}^{(C, A)} \mathrm{V}_{i}^{1 / 2}, \\ \hat{\mathrm{~T}}_{j}= & \hat{\mathrm{W}}_{j} \sum_{i=0}^{I-j-1} \mathrm{D}\left(\mathbf{C}_{i, j}^{\mathrm{CL}}\right)^{1 / 2} \\ & \cdot\left(\hat{\Sigma}_{j}^{(C)}\right)^{-1} \hat{\Sigma}_{j}^{(C, A)}\left(\hat{\Sigma}_{j}^{(A)}\right)^{-1} \mathrm{~V}_{i}^{1 / 2} \hat{\mathrm{U}}_{j}, \end{aligned} \]

where

\[ \hat{\mathrm{W}}_{j}=\left(\sum_{k=0}^{I-j-1} \mathrm{D}\left(\mathbf{C}_{k, j}^{\mathrm{CL}}\right)^{1 / 2}\left(\hat{\Sigma}_{j}^{(C)}\right)^{-1} \mathrm{D}\left(\mathbf{C}_{k, j}^{\mathrm{CL}}\right)^{1 / 2}\right)^{-1} \]

and

\[ \hat{\mathrm{U}}_{j}=\left(\sum_{k=0}^{I-j-1} \mathrm{~V}_{k}^{1 / 2}\left(\hat{\Sigma}_{j}^{(A)}\right)^{-1} \mathrm{~V}_{k}^{1 / 2}\right)^{-1} . \]

The matrices \(\hat{\Sigma}_j^{(C)}\) and \(\hat{\Sigma}_j^{(A)}\) are the resulting estimates in the iterative estimation procedure for the parameters \(\Sigma_j^{(C)}\) and \(\Sigma_j^{(A)}\) (cf. (64) and (67)).

Remark 5.1

• For a more detailed motivation of the estimates for the different covariance matrices see Merz and Wüthrich (2008, 2009) and Sections 8.2.5 and 8.3.5 in Wüthrich and Merz (2008).

• If we have enough data (i.e., \(I>J\) ), we are able to estimate the parameters \(\Sigma_{J-1}^{(C)}, \Sigma_{J-1}^{(A)}\) and \(\Sigma_{J-1}^{(C, A)}=\left(\Sigma_{J-1}^{(A, C)}\right)^{\prime}\) by (64), (67) and (68) respectively. Otherwise, if \(I=J\), we do not have enough data to estimate the last covariance matrices. In such cases we can use the estimates \(\hat{\varphi}_{j-1}^{(m, n)}\) of the elements \(\varphi_{j-1}^{(m, n)}\) of \(\Sigma_{j-1}^{(C)}\) for \(j \leq J-1\) (i.e., \(\hat{\varphi}_{j-1}^{(m, n)}\) is an estimate of \(\varphi_{j-1}^{(m, n)} =\sigma_{j-1}^{(m)} \cdot \sigma_{j-1}^{(n)} \cdot \rho_{j-1}^{(m, n)}\), cf. (16)) to derive estimates \(\hat{\varphi}_{J-1}^{(m, n)}\) of the elements \(\varphi_{J-1}^{(m, n)}\) of \(\Sigma_{J-1}^{(C)}\) for all \(1 \leq m, n \leq K\). For example, this can be done by extrapolating the usually decreasing series \[\left|\hat{\varphi}_{0}^{(m, n)}\right|, \ldots,\left|\hat{\varphi}_{J-2}^{(m, n)}\right| \tag{69}\] by one additional member \(\hat{\varphi}_{J-1}^{(m, n)}\) for \(1 \leq m, n \leq K\). Analogously, we can derive estimates for \(\Sigma_{J-1}^{(A)}, \Sigma_{J-1}^{(C, A)}\) and \(\Sigma_{J-1}^{(A, C)}=\left(\Sigma_{J-1}^{(C, A)}\right)^{\prime}\) (see Merz and Wüthrich (2008, 2009) and the example below). However, in all cases it is important to verify that the estimated covariance matrices are positive definite.

• Observe that the \(K \times K\)-dimensional estimate \(\hat{\Sigma}_{j-1}^{(C)(s)}\) is singular if \(j \geq I-K+2\) since in this case the dimension of the linear space generated by any realizations of the \((I-j+1) K\) dimensional random vectors \[ \mathrm{D}\left(\mathbf{C}_{i, j-1}^{\mathrm{CL}}\right)^{1 / 2} \cdot\left(\mathbf{F}_{i, j}^{\mathrm{CL}}-\hat{\mathbf{f}}_{j-1}^{(s-1)}\right) \quad \text { with } \quad i \in\{0, \ldots, I-j\} \tag{70}\] is at most \(I-j+1 \leq I-(I-K+2)+1=K\) -1 . Analogously, the \((N-K) \times(N-K)\) dimensional estimate \(\hat{\Sigma}_{j-1}^{(A)(s)}\) is singular when \(j \geq I-(N-K)+2\). Furthermore, the random matrix \(\hat{\Sigma}_{j-1}^{(C)(s)}\) and/or \(\hat{\Sigma}_{j-1}^{(A)(s)}\) may be ill-conditioned for some \(j<I-K+2\) and \(j<I- (N-K)+2\), respectively. Therefore, in practical application it is important to verify whether the estimates \(\hat{\Sigma}_{j-1}^{(C)(s)}\) and \(\hat{\Sigma}_{j-1}^{(A)(s)}\) are well-conditioned or not and to modify those estimates (e.g., by extrapolation as in the example below) which are ill-conditioned (see also Merz and Wüthrich (2008, 2009)).

6. Example

To illustrate the methodology, we consider two correlated run-off portfolios A and B (i.e., N = 2) which contain data of general and auto liability business, respectively. The data is given in Tables 1 and 2 in incremental and cumulative form, respectively. This is the data used in Braun (2004) and Merz and Wüthrich (2007, 2008, 2009). The assumption that there is a positive correlation between these two lines of business is justified by the fact that both run-off portfolios contain liability business; that is, certain events (e.g., bodily injury claims) may influence both run-off portfolios, and we are able to learn from the observations from one portfolio about the behavior of the other portfolio.

In contrast to Merz and Wüthrich (2008) (multivariate CL method for both portfolios) and Merz and Wüthrich (2009) (multivariate ALR method for both portfolios) we use different claims reserving methods for the two portfolios A and B. We now assume that we only have estimates \(V_i\) of the ultimate claims for portfolio \(A\) and use the ALR method for portfolio A . The CL method is applied for portfolio \(B\). This means we have \(K=N-K=1\), and the parameters \(\mathbf{f}_j, \mathbf{m}_j\), \(\Sigma_j^{(C)}, \Sigma_j^{(A)}, \Sigma_j^{(C, A)}\) as well as the a priori estimates \(\mathrm{V}_i\) of the ultimate claims in the different accident years \(i\) in portfolio A are now scalars. Moreover, it holds that \(\Sigma_j^{(C)}=\left(\sigma_j^{\mathrm{CL}}\right)^2=\left(\sigma_j^{(1)}\right)^2\), \(\Sigma_j^{(A)}= \left(\sigma_j^{\mathrm{AD}}\right)^2=\left(\sigma_j^{(2)}\right)^2\) and \(\Sigma_j^{(C, A)}=\Sigma_j^{(A, C)}=\sigma_j^{\mathrm{CL}} \cdot \sigma_j^{\mathrm{AD}} \cdot \rho_j^{(1,2)}=\sigma_j^{(1)} \cdot \sigma_j^{(2)} \cdot \rho_j^{(1,2)}\).

Table 3 shows the estimates of the ultimate claims for the two subportfolios A and B as well as the estimates for the whole portfolio consisting of both subportfolios.

Since \(I=J=13\) we do not have enough data to derive estimates of the parameters \(\Sigma_{12}^{(C)}, \Sigma_{12}^{(A)}\) and \(\Sigma_{12}^{(C, A)}=\Sigma_{12}^{(A, C)}\) by means of the proposed estimators. Therefore, we use the extrapolations

\[ \begin{aligned} \hat{\Sigma}_{12}^{(C)} & =\min \left\{\hat{\Sigma}_{10}^{(C)},\left(\hat{\Sigma}_{11}^{(C)}\right)^{2} / \hat{\Sigma}_{10}^{(C)}\right\}, \\ \hat{\Sigma}_{12}^{(A)} & =\min \left\{\hat{\Sigma}_{10}^{(A)},\left(\hat{\Sigma}_{11}^{(A)}\right)^{2} / \hat{\Sigma}_{10}^{(A)}\right\}, \quad \text { and } \\ \hat{\Sigma}_{12}^{(C, A)} & =\hat{\Sigma}_{12}^{(A, C)}=\min \left\{\left|\hat{\Sigma}_{10}^{(C, A)}\right|,\left(\hat{\Sigma}_{11}^{(C, A)}\right)^{2} /\left|\hat{\Sigma}_{10}^{(C, A)}\right|\right\} \end{aligned} \tag{71} \]

to derive estimates of \(\Sigma_{12}^{(C)}, \Sigma_{12}^{(A)}\) and \(\Sigma_{12}^{(C, A)}= \Sigma_{12}^{(A, C)}\). Moreover, so that \(\hat{\Sigma}_{11}\) and \(\hat{\Sigma}_{12}\) are positive definite, we estimate \(\Sigma_{11}^{(A)}\) and \(\Sigma_{11}^{(C, A)}=\Sigma_{11}^{(A, C)}\) by

\[ \begin{aligned} \hat{\Sigma}_{11}^{(A)} & =\min \left\{\hat{\Sigma}_{9}^{(A)},\left(\hat{\Sigma}_{10}^{(A)}\right)^{2} / \hat{\Sigma}_{9}^{(A)}\right\}, \\ \hat{\Sigma}_{11}^{(C, A)} & =\hat{\Sigma}_{11}^{(A, C)}=\min \left\{\left|\hat{\Sigma}_{9}^{(C, A)}\right|,\left(\hat{\Sigma}_{10}^{(C, A)}\right)^{2} /\left|\hat{\Sigma}_{9}^{(C, A)}\right|\right\} . \end{aligned} \tag{72} \]

Table 4 shows the estimates for the parameters. The one-dimensional estimates \(\hat{\mathbf{m}}_j\) and \(\left(\hat{\Sigma}_j^{(A)}\right)^{1 / 2}\) are the parameter estimates used in the univariate ALR method applied to the individual subportfolio A. Analogously, the one-dimensional estimates \(\hat{\mathbf{f}}_j\) and \(\left(\hat{\Sigma}_j^{(C)}\right)^{1 / 2}\) are the parameter estimates used in the univariate CL method applied to the individual subportfolio B. From the estimates \(\hat{\Sigma}_j^{(C, A)}\) of the covariances \(\Sigma_j^{(C, A)}=\Sigma_j^{(A, C)}\) we obtain estimates \(\hat{\rho}_j^{(1,2)}\) of the correlation coefficients \(\rho_j^{(1,2)}\) by \(\hat{\Sigma}_j^{(C, A)} / \sqrt{\hat{\Sigma}_j^{(A)} \cdot \hat{\Sigma}_j^{(C)}}\).

Note: Since both the CL method and the ALR method are applied to one-dimensional triangles, the parameter estimates \(\hat{f}_j\) and \(\hat{m}_j\) can be calculated directly (using the univariate methods) and one can omit the iteration described in Section 5.

The first two columns of Table 5 show for each accident year the reserves for subportfolios A and B estimated by the (univariate) ALR method and the (univariate) CL method, respectively. The last column, denoted by “Portfolio Reserves Total,” shows the estimated reserves for the entire portfolio.

Table 6 shows for each accident year the estimates for the conditional process standard deviations and the corresponding estimates for the coefficients of variation. The first two columns contain the values for the individual subportfolios A and B calculated by the (univariate) ALR method and the (univariate) CL method, respectively. The last column, denoted by “Portfolio Total,” shows the values for the entire portfolio.

The same overview is generated for the square roots of the estimated conditional estimation errors in Table 7.

And finally the first three columns in Table 8 give the same overview for the estimated prediction standard errors.

Moreover, the last two columns in Table 8 contain the results for the estimated prediction standard errors assuming no correlation and perfect positive correlation between the corresponding claims reserves of the two subportfolios A and B. These values are calculated by

\[ \begin{aligned} \widehat{\operatorname{msep}}_{\mathbf{C}_{i, J} \mid \mathcal{D}_{I}^{N}}= & \widehat{\operatorname{msep}} C_{i, J}^{(1)}\left|\mathcal{D}_{I}^{N}+\widehat{\operatorname{msep}} C_{i, J}^{(2)}\right| \mathcal{D}_{I}^{N} \\ & +2 c \widehat{\operatorname{msep}}_{C_{i, J}^{1(1)} \mid \mathcal{D}_{I}^{N}} \widehat{\operatorname{msep}}_{C_{i, J}^{(2)} \mid \mathcal{D}_{I}^{N}}^{1 / 2} \end{aligned} \tag{73} \]

with c = 0 and c = 1, respectively. Except for accident year 3, for all single accident years and aggregated accident years, we observe that the estimates in the third column are between the ones assuming no correlation and perfect positive correlation. Note that accounting for the correlation between subportfolios adds about 9% to the estimated prediction standard error for the entire portfolio (295,038 vs. 271,015).