1. Introduction
Actuaries are frequently relied upon to make forecasts and predictions across time periods. This can be as a forecast for a future period, such as in ratemaking; an interpretation of the past, as in reserving; or both together, as in profitability studies. Despite this, methodology used is often ad hoc or not properly suited for making statistical forecasts.
This type of behavior is best modeled via a state space model (SSM), a flexible and powerful time series forecasting method. But besides being less familiar to many practitioners, SSMs have other drawbacks, depending on how they are solved.
This paper shows how a subset of SSM functionality can be added to penalized regression models to make them better equipped to interpret historical data and make forecasts. Such an approach incorporates distributional flexibility and credibility as well as time series components. With these modifications, forecasting and interpretation of historical results can be improved and streamlined.
1.1. Research context
SSMs and penalized regression methods will be explained and used throughout this paper. On the SSM side, De Jong and Zehnwirth (1983) were the first to introduce their use into the actuarial literature and use them to smooth development patterns. Zehnwirth (1996) and Wüthrich and Merz (2008) both use SSMs to smooth reserving estimates, and Evans and Schmid (2007) use them to smooth trend estimates. De Jong (2005) gives a nice overview of SSMs and also shows examples of their use in mortality modeling and claims reserving. Korn (2016) uses a simplified SSM to smooth loss ratios by year.
On the penalized regression side, see Hastie, Tibshirani, and Friedman (2009). Hastie and Qian (2014) give a nice overview of these models and their use in the R modeling language. Williams et al. (2015) show the benefit of using these models for variable selection. And recently, Frees and Gee (2016) showed how these models can be used to price policy endorsements. These lists are not meant to be comprehensive; refer to the mentioned papers for further references.
On the pure actuarial side, this method can be thought of as an extension to the generalized Cape Cod method (Gluck 1997) in that it can consider changes while accounting for development. This concept is discussed further in Section 7.
1.2. Objective
The goal of this paper is to show an approach that fits within a regression framework, is capable of handling time series effects, works well with volatile data having relatively few periods, is capable of handling big data, and produces results suitable for presentation. The proposed method will be referred to as a (linear) regression–based SSM, or RSSM for short. Code that implements the method is shown in Appendix B.
1.3. Outline
Section 2 gives an overview of SSMs. Section 3 discusses some alternative methods for handling changes over time and estimates their performance using simulation results. Section 4 explains how to implement a random walk using RSSM. Sections 5 and 6 discuss more SSM functionality that can be implemented with this approach, including changing trends and momentum. Section 7 gives an overview of how insurance loss data, which emerge over time, can be accommodated in this framework. Section 8 discusses standardization of time series components, something that is necessary for penalized regression models. Section 9 discusses some practical implementation issues, and Section 10 demonstrates a case study for performing a profitability or reserve study on yearly loss ratios.
2. An overview of SSMs
SSMs are a commonly used methodology to model how phenomena change over time. They are expressed as a series of related equations. Their flexibility and ease of interpretation make them a common modeling choice. They are usually solved for using either a Kalman filter or a Bayesian-type model (both of which are discussed in the next section). The proposed approach provides another means of solving for a subset of SSMs within a generalized linear model (GLM) framework.
A simple linear trend model (known as “drift” in SSM terminology), for example, can be expressed as follows (Kim and Nelson 1999):
Yt=Xt+et.
Xt=Xt−1+u.
The first equation (also known as the measurement or observation equation) relates the actual data (Y) to the fitted values (X) with an error term (e). In the second (also known as the state or transition equation), the fitted values are increased by the trend (u) each period.
Another type of SSM is a random walk, which is a way to model gradual changes that can occur over time. The complement of credibility for each period is the fitted result of the previous period, which is an intuitive way to model changes over time. Such a model balances goodness of fit to the data versus having smaller or smoother changes from period to period. A random walk could be represented as follows:
Yt=Xt+et.
Xt=Xt−1+rt.
These equations are equivalent to the above except that in the second, the fitted values, instead of increasing by the same amount each period, are increased by varying amounts (r). This variable is another error term whose values are minimized. The result is a model that balances goodness of fit to the data with as little change as possible, depending on the ratio of the error terms. The first term (e) represents the volatility of the data, while the second (r) represents the variance or average magnitude of the period-to-period changes.
A model wherein the trend (or drift) itself changes via a random walk can be modeled as well. An example is as follows:
Yt=Xt+et.
Xt=Xt−1+ut.
ut=ut−1+rt.
Here, the third equation allows for the trend itself (u) to follow a random walk. Both e and r are error terms that are minimized.
More types of models are discussed as well. Even though the proposed models are based on SSMs, they still can be used without a complete familiarity with SSMs.
3. Comparison with existing methods
3.1. An overview
Perhaps the most common way that actuaries control for changes over time is to model the year within a GLM as a categorical variable. If a mixed model or penalized regression is used, credibility weighting is performed against the overall mean. But such an approach ignores the relationships between consecutive years. The complement of credibility for each year (i.e., what the presumed value would be if there were no data) should be the fitted value of the previous year, which is much more intuitive than the overall mean. Figure 1 shows some randomly created data that illustrates this point.[1] (A penalized regression model was used so that credibility is taken into account. This is similar to adding the year as a random effect in a mixed model.) Note the behavior in years 7 and 8, for example; even though the fitted curve should most likely be decreasing in this range, this does not occur since it is constrained to fall in between the data points and the overall mean. It can be seen that using an RSSM results in more intuitive behavior. Note how the former is also further off in the latest period, making forecasts of future periods less accurate.
SSMs are another way to model changes over time. The most common methods of solving for an SSM are the Kalman filter[2] and Bayesian Markov chain Monte Carlo(MCMC) modeling. The Kalman filter uses formulas to calculate the amount of credibility to be assigned to each period, using the previous period’s prediction as the complement of credibility. The model requires three parameters, which are estimated via maximum likelihood: the value of the first period and two variance parameters that help determine the credibility. The calculations are made easier by assuming that the distributions of both the errors in the data and the period-to-period changes are normally distributed. (This model is essentially the time series equivalent of Buhlmann-Straub credibility.) For a more thorough review of the Kalman filter, refer to Korn (2016).
One problem with using the Kalman filter to model insurance data is its lack of distributional flexibility such as a GLM provides. Errors are assumed to be normally distributed, and changes additive. There are some ways of fixing these issues (see Taylor and McGuire 2007), but these solutions are still not as robust, flexible, and/or simple as the one proposed. Using the Kalman filter to fit the example data produces a fitted result with no changes, equal to the overall mean.[3] This is because this model requires more than just 10 data points to adequately adapt to and fit the data.
A more flexible framework is provided by Bayesian models, which are capable of modeling SSMs, such as random walks, as well as incorporating any type of distribution assumption. A Bayesian model implementing a random walk has parameters for every period, unlike the Kalman filter, which has a parameter for only the first period. Parameters are typically solved via MCMC techniques, which are simulations that are guided by the overall likelihood of the model. The downsides to these models are the specialized expertise required as well as the time needed to build and run each model. These models also do not scale well to large datasets or to a large number of parameters.
As shown in Figure 2, running a Bayesian model on the example data set performs satisfactorily, although it produces a much bumpier line than the proposed approach. This makes it more difficult to interpret and analyze and not as suitable for presentation. Multiple changes are shown before year 6, despite insufficient support in the data. The verbal explanation for this line would be something similar to “an increase followed by a decrease, followed by a large decrease, followed by an increase, followed by another large decrease.” The RSSM shows a decreasing trend starting from year 6, which seems to be the general trend of the data; the Bayesian line is still bumpy after this point. The explanation for the RSSM would be “mostly flat followed by a sharp decrease,” which is a much simpler and more intuitive explanation given the data. (Note that this model is further improved upon in section 5.3 to be even more intuitive.)
Another approach is to use an additive model, which uses a smoothing function, often a cubic spline, to adapt to the data. This type of model does a good job of fitting to the example data (using the mgcv package in R), as shown in Figure 3.
A problem with splines is that even though the historical data may seem to fit well, they often show high trends at the end points, implying historical and prospective patterns that may not exist. Related to this, small changes in the data or a few new data points often can result in large changes. They are also very susceptible to outliers, as shown in the next section. Figure 4 shows another example from simulated data that demonstrates these issues.[4]
Finally, there are autoregressive integrative moving average (ARIMA) models. These models can be similar to a random walk (namely, an AR(1)), but a significant difference is that forecasts are based off of the latest actual value – as opposed to the latest predicted value for random walks – which make them less suitable for handling volatile data, especially when development is present and the latest points are even less certain. Further, besides not being as intuitive as the methods discussed, they lack the flexibility of SSMs (Carlin 1992). Because of these issues, they will not be elaborated upon further.
3.2. Simulation results
Simulations were conducted during a 10-year period to compare these various methods to each other and to the proposed method, which will be elaborated on in the remainder of the paper. The first simulation exercise was fairly straightforward and did not attempt to mimic real data by including outliers and so forth. The second simulation was meant to be more realistic and used t distributions instead of Gaussian and included occasional outliers to account for the fact that distribution fits are usually not exact. The results are shown in Table 1. The code used to run the simulations can be found in Appendix A.
The Bayesian model was the best performing, followed closely by the proposed. Note the poor performance of using the year as a factor (even with credibility’s being taken into account, as was the case here); when outliers were present, it was even slightly worse than taking a simple average. The differences in the root mean square error numbers are shown to the right as a rough measure of the robustness to outliers of each of the methods. It can be seen that the RSSM is the most robust to outliers. This is because the Kalman filter, Bayesian model, and additive model all depend on various formulas and assumptions to estimate the appropriate credibility, whereas the proposed uses cross-validation and determines the optimal credibility from testing on the data themselves.
4. Implementing a random walk
4.1. Dummy encodings
The proposed approach uses a GLM framework to implement a subset of SSM functionality, such as random walks. This provides a relatively simple and familiar modeling environment and also allows for distributional flexibility and credibility.
To explain the approach, when a categorical variable is added to a GLM, dummy encodings are created, such as those shown in Table 2. (The data values are shown on the left-hand side, and the created model variables are shown across the top.)
To implement a random walk, dummy encodings like those shown in Table 3 can be used instead.
With these, the coefficient value for 2014 affects not only that year but the subsequent years, 2015 and 2016. Likewise, the coefficient value for 2015 affects both 2015 and the next year, 2016. If some form of credibility is applied (which is discussed in the next section), the starting point for each year is the previous year’s fitted value. This allows for the fitted value of each year to be used as the complement of credibility for the following year. So, for example, if the 2015 coefficient is 0, its fitted value will match the 2014 fitted value.
Relating this back to SSMs, it can be seen that doing this is equivalent to the random walk, where r is the coefficient value for each year. The first equation (which relates the empirical data to the fitted values) is identical as well, except that here, the distribution of the error term (e) is determined by the GLM family.
Yt=Xt+et.
Xt=Xt−1+rt.
Most statistical packages have methods for modifying the default dummy encodings of certain variables. Appendices A and B show an example of doing this in R.
4.2. Penalized regression and cross-validation
Penalized regression will be used as the credibility technique for both the random walk and other coefficients. This works by imposing a penalty to the likelihood the more a coefficient deviates from 0, thus reducing the coefficient values. This pushes the fitted values back toward the intercept, which is the overall mean, and thus credibility is applied.
Unlike mixed models, for example, which use likelihood-based formulas and a number of assumptions to determine the magnitude of the penalty parameters, penalized regression uses k-fold cross-validation. K-fold cross-validation works as follows: the data are randomly divided into k chunks, or “folds.” The model is fit on k – 1 of these folds, using different values for the penalty parameter, and then each of these fitted models is tested on the remaining fold. This process is repeated k times, each time using a different fold for the validation. The penalty parameter that performs best on the test data is chosen. For smaller data sets, this process even can be repeated multiple times, and the average penalty parameter selected. This procedure is implemented in many statistical packages.
As mentioned, this approach differs from Bayesian models, mixed models, and the Kalman filter, all of which use different assumptions and formulas to estimate the penalty parameters. Another benefit of cross-validation is that it provides an excellent framework for testing the results of the model as the cross-validated predictions (i.e., the predictions made on the holdout or test folds) can be compared against the actual data to calculate various metrics that are less affected by any possible overfitting.
Another benefit is their ability to fit on a large number of variables, even with large data sets. This is because of the efficient fitting algorithm: the model is initially fit using a large penalty value that causes most of the coefficients to be near 0, making the model easy to solve for. This penalty is then gradually decreased, and the model is refit, each time using the results of the previous model as the starting point for the coefficients. Because of this, changes to coefficient values are small at each step, making it easier for the fitting procedure to find the optimal values (Friedman, Hastie, and Tibshirani 2009). Mixed models and Bayesian methods often do not scale as well with large data sets having a large number of parameters. The run time for mixed models, especially, deteriorates rapidly as the number of variables or data points increases.
4.3. Types of penalized regression methods
Penalized regression methods apply a penalty to the coefficient values to stabilize them. There are two types of penalty functions frequently used. Ridge regression is based on the squared value of the coefficients, also known as L2 regularization. This is similar to a mixed model or to using a normal distribution as the prior in a Bayesian setting.
The other type is the lasso, which penalizes based on the absolute value of the coefficients. A benefit of this type of model is that it can aid in variable selection. This is because the absolute value penalty will approach 0 much faster than the squared values, so some coefficient values are set to 0, thus taking out their effect in the model. The downside of this model is that it does not handle correlated variables well. A compromise model called an elastic net provides the benefits of both by imposing a weighted average of both types of penalties (Zou and Hastie 2005). Such a model can handle correlated variables and perform variable selection.
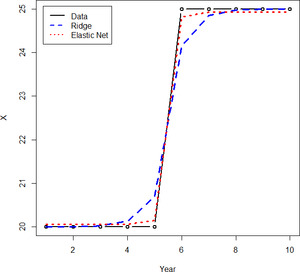
There is another benefit of the elastic net for time series models. Because ridge regression does not shrink its coefficients down to 0, when using it to model a random walk, it will often show small changes in each year, even if it seems that there have not been any real changes. But the lasso cannot be used, since time series variables have correlations, thus making the elastic net the ideal choice.[5] A comparison of the use of ridge regression and the elastic net is shown in Figure 5. Note how ridge regression produces the bumpier line, which as mentioned does not lend itself as well to interpretation.
Related to this, because the square of a large number is an even larger number, if the data have a large jump in a single year, ridge regression often will model smaller changes over the course of several years. An elastic net model typically handles this scenario much better, as shown in Figure 5. The ridge model shows the decreasing trend as starting from year 4, whereas in reality it seems that the decreasing trend did not start until year 6. A starker example is shown in Figure 6. It can be seen that a one-time increase is modeled over a period of three years.
For these reasons, the elastic net is the recommended model to use when fitting RSSMs.
4.4. Multiple segmentations
Using the modified dummy encodings shown to model a random walk within a GLM framework makes it easy to model not only the overall changes but also the changes by various segmentations. This can be done by including an interaction term between the segmentation and the random walk variable. Including a random walk variable by itself as well as an interaction term between the segmentation and the random walk produces a model that credibility weights each segment’s changes using the overall average changes as the complement. This can be a powerful tool for handling yearly or quarterly data in a hierarchical fashion—much more detailed than simply modeling on an average trend. This also can be a way to implicitly model correlations between segments that share common characteristics.
A problem exists, however, when using the simple random walk dummy encoding shown above (see Table 3) to model multiple segmentations. The issue is demonstrated using created data in Figures 7 and 8. In this example, several segments are fit with their changes modeled using a random walk (using an interaction term as described) as well as a term for each segment.
The segment shown in Figure 7 is moving away from the overall mean, and in Figure 8, it is moving toward the mean, as can be seen. Note how the fits using the simple encodings give rise to a steeper curve than expected when moving away from the mean and a flatter than expected curve when moving toward the mean. This is because when the simple encodings are used, the first point of each segment is determined by the value of the segment coefficient (since all of the random walk variables are 0 at this point). The subsequent points are determined from the interaction between the segment and the random walk variable, all of which are shrunken toward 0 due to the penalty. Because of this, the model will often “take a shortcut” and gradually approach the data points over several periods to reduce the total value of this penalty, which results in the pattern mentioned.
To fix this issue, the random walk dummy encodings can be modified so that the mean of each year is 0 (which can be done by simply subtracting the mean from each column). If these encodings are used instead, the segment coefficients now represent the average value of each segment, since the net effect of the random walk parameters is 0. Doing this fixes the tendency to take a shortcut and results in behavior that is more intuitive, as can be seen.
On another note, it is worth mentioning that both the random walk and the segment parameters share the same penalty value. This does not mean that they will receive the same amount of credibility since this depends on other factors as well. But still, this should not be a concern as it is consistent with the penalized regression methodology, which uses the same penalty value for all parameters. If the variables are on the same scale (which they should be—see Section 7), this will give them equal treatment in the model. An equal amount of explanation is penalized the same amount regardless of which variable it comes from. However, it still may be advisable to use a different penalty for the random walk components. This can be accomplished by setting the penalty of these variables to a factor of the overall penalty and using another round of cross-validation to determine this factor.
4.5. Using cross-validation with longitudinal data
Longitudinal (or panel) data is the term used to describe data that both use explanatory variables and have multiple observations across time periods, such as the data being described here. One of the assumptions of cross-validation is that the folds are not correlated with each other. But this may be violated for this type of data, since the same entity may exist in different folds at different time periods, and these observations are correlated with each other.
To address this issue, instead of randomly selecting individual rows for inclusion in each fold as is normally done, the entities themselves can be randomly assigned to folds along with all of their corresponding rows. This will reduce the correlation across folds when using panel data with cross-validation. (Note that this is necessary only when a corresponding variable is not included in the model.)
4.6. Numeric variables
This section illustrated how a random walk can be used to allow the coefficients of categorical variables to change over time. It is possible to do the same with numerical variables. Instead of including interactions, as done above, a new variable can be created and added to the model that is the product of the random walk and that variable. This works since
Coef1×V+Coef2×V×RW=V×(Coef1+Coef2×RW),
where V is the desired variable, RW is a random walk variable, and Coef1 and Coef2 are two model coefficients. This allows for modeling how the relationships of numerical variables can change over time.
5. Extending the random walk
5.1. Random walk with drift
The random walk model discussed in Section 4 assumes that the expected change for each period is zero, and this serves as the complement of credibility. If this is not the case, a trend (or drift) term can be added, and this value will serve as the effective complement of credibility instead. Such a term can be added to a GLM by including the time period as a numerical variable. (It is a good idea to set the mean of this variable to 0 for the reasons mentioned in Section 4.4. This variable also should be standardized, as illustrated in Section 8.)
5.2. Modeling a changing trend
All of the discussion above focuses on a random walk on the level of a variable. It is possible to model a changing trend (or drift, also known as a second-order random walk) by using dummy encodings like those shown in Table 4.
Using these, the 2014 coefficient, for example, will cause increases in years 2014 to 2016, and the 2015 coefficient will cause increases in years 2015 and 2016. This will cause a change to the slope. A trend term should be added for the starting slope unless it is assumed to be 0. (Once again, coefficients that sum to 0 should be used. The variable also should be standardized, as illustrated in Section 8.)
5.3. Mean reversion and momentum
It is possible to build a model that uses the concept of mean reversion. Allowing for mean reversion on the trend, for example, allows the trend to change but also causes any changes to gradually decay over time and revert to the long-term average trend. This can be used to model shorter-term changes in the trend that gradually revert toward a long-term average value. An example of dummy encodings with 25% mean reversion is shown in Table 5.
As can be seen, instead of adding 1 to each subsequent year, the added amounts decay exponentially. (As mentioned, after these dummy encodings are created, the mean should be subtracted from all columns so that they all equal 0. They should be standardized as well, as discussed in Section 8.)
This concept of mean reversion can be used to relate a random walk on the level of a variable to a random walk on the trend. If the mean reversion is set to 0, no mean reversion will occur, and the result is identical to a random walk on the trend. Alternatively, if the mean reversion is set to 1, the changing trend will immediately revert to its long-term value after one period, so each change affects only a single period. This is identical to a random walk on the level of a variable. Any value between 0 and 1 can be viewed as a compromise of the two models.
One way of looking at these models (with perhaps a higher mean reversion value, although not necessarily) is as a random walk on the variable’s level, but with momentum. In these models, the complement of credibility for the change of each period is a value between 0 and the previous period’s change. This will cause changes to continue in the same direction the following period, unless they are reversed. This is often a more realistic expectation since, quite often, changes display serial correlation over time.
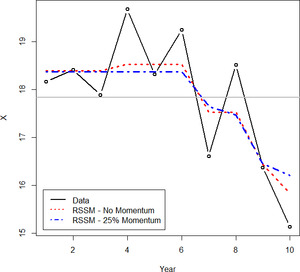
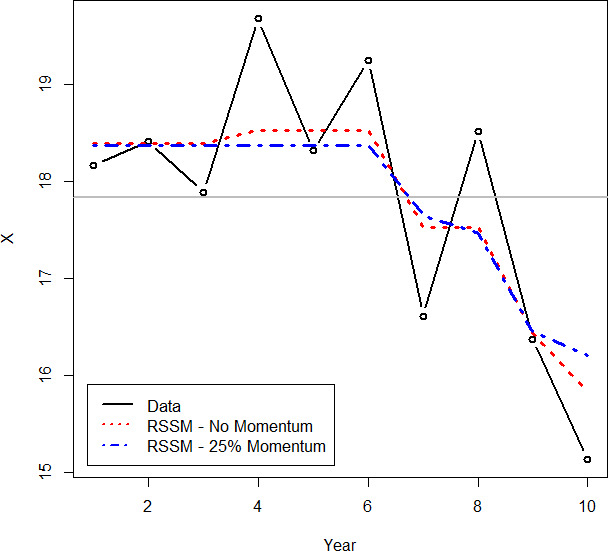
Fitting the example data with this type of model produces the result shown in Figure 9. Note how this model both improves the fit to the data and results in a smoother, nicer-looking curve.
Cross-validation can be used for choosing the optimal momentum for a model. Values can be tested in jumps of 5%, 10%, 25%, and so forth, with all random walk variables sharing the same value.
The SSM equations for this mean reversion model are as follows (wherein the average long-term trend is assumed to be 0 for simplicity). It is easy to verify that these will produce identical results as using the dummy encodings shown above.
Yt=Xt+et.
Xt=Xt−1+ut.
ut=aut−1+rt.
It can be seen that if the mean reversion parameter (a) is set to 1, these equations will be equivalent to those of a changing slope. If a is set to 0, then, and these equations are equivalent to a random walk on the level. If a is set to a value between 0 and 1, the trend will gradually decay back toward 0 (or to the long-term trend, if specified in the model).
5.4. Level mean reversion
It is worth mentioning that mean reversion can be used on the level of a variable as well, not just on the trend. This would cause any changes in the random walk to gradually decay, causing the level to revert toward its long-term average over time. If a trend or drift component were included, the level would gradually revert toward the trended long-term average. This would be done by having the encodings of the random walk start at 1 as usual and having subsequent values multiplied by a factor causing them to decay exponentially back toward 0 over time.
5.5. Extra dispersion
It is worth mentioning that another time series component can be added to provide some extra flexibility. A random walk models changes by period that are expected to continue in the next period. In contrast, another component can be added for spikes and dips to the fitted values that occur only within a single period and that do not continue to the next. The SSM equations for this model are the following:
Yt=Xt+et;
Xt=Zt+dt;
Zt=Zt−1+rt;
where is another state variable and d_t is this new component, which is an error term that is minimized. This component can be added to a GLM by including the year as a factor. However, doing so in addition to including a random walk variable usually results in poorer performance (in my experience), and using it is not recommended unless perhaps a greater penalty is applied to these variables. Another way to view this component is as a random walk with full level mean reversion.
6. More SSM components
6.1. Seasonality
If one is modeling on a period of less than a year, it may be necessary to account for the different levels of each month, quarter, or other unit, depending on the data. This can be accomplished simply by adding another categorical variable, adding another random walk, or using splines.[6]
6.2. Predictive variables
Sometimes, the causes of yearly changes are understood and can be related to external variables. When this is the case, the variable can be incorporated in the model to help improve the predictions. This variable should be included as an index so that only changes in the variable affect the level during each period, not the actual value of the variable.
For example, if yearly loss ratios by country are correlated with the interest rate, an index based on the interest rate can be used. This index can be created by dividing all values by the interest rate of the first year for that country. Note that the index was based on the interest rate itself and not the change in the interest rate, so changes in the interest rate will cause changes to the yearly loss ratios. If the interest rate has a lagged effect on the loss ratios, it is possible to insert it lagged by the appropriate number of periods, which can be determined via another round of cross-validation.
Including a random walk variable along with a predictive variable index will allow for both unexplained and explained changes to affect the variable of interest.
6.3. Multidimensional random walks
A two- (or more-)dimensional random walk can be constructed by interacting two random walks with each other. Depending on the packages used, the columns may need to be constructed manually. (The columns should be multiplied together while still in 1s and 0s, and they can be made to sum to 0 afterward.) This can be useful for geographical smoothing, for example.
7. Accounting for development
To account for the delay in insurance losses, a Cape Cod approach can be used. Inputs to the model should be the paid or reported loss ratios or loss costs multiplied by the loss development factors (i.e., chain ladder), and the regression weights should be set to the premiums or exposures divided by the loss development factors (i.e., the “used premiums” or “used exposures”). This procedure accounts for development while taking into account the extra volatility of the greener years. This causes the model to give less weight to these years, but all years are still taken into account for determining the fitted loss ratios for each year.
Once the model is run and the predictions are made, profitability studies and pricing models can use these predictions directly. Forecasted periods that are not in the data will need to be carried forward using the state-space modeling equations or alternatively by adding rows to the original data set that are excluded from the fitting. For reserving studies, since the model predictions represent the expectation for each period, they can serve as the a priori estimates for the remaining development, i.e., for use in a Bornhuetter-Ferguson method.
It should be noted that using a Bornheutter-Ferguson or similar method pushes the data points toward the mean, which artificially lowers the volatility and is not appropriate for model inputs. It is acceptable to use such a method for the final results, as mentioned, but not for modifying the inputs into the model, which should be true to the actual data.
An interesting feature of such an approach is that it can be thought of as a credibility weighting between the chain ladder and Cape Cod or Bornhuetter-Ferguson methods. If full credibility is given to the historical changes, results will match the chain ladder estimates. Alternatively, if no credibility is given to the changes, the results will equal the used premium weighted average, which is the Cape Cod method. In a reserving context, if a Bornhuetter-Ferguson method is applied to these predictions, the final results will match the chain ladder predictions in the former case and the Bornhuetter-Ferguson in the latter. Anywhere in between can be thought of as a credibility weighting between these two extremes. This is similar to the Generalized Cape Cod method (Gluck 1997) except that here, changes and optionally credibility are determined within a penalized regression framework.
8. Standardization
This section discusses standardization of different time series components. Standardization is important for penalized regression models since the same penalty is applied to every model variable. Therefore, they should be on the same scale so that they receive equal treatment; otherwise, equal coefficient values will cause greater changes to the variable with higher values. For example, if one variable is stated in pounds and another in ounces, the one stated in pounds has a larger scale and is likely to have a greater effect on the fitted results.
The most common approach is to normalize each variable by subtracting the mean and dividing by the standard deviation. This applies to numerical variables only. When dealing with both numerical and categorical variables, Gelman (2008) suggests dividing each numerical variable by twice the standard deviation instead. This is because a binary variable with 50% ones has a standard deviation of 0.5.
None of these approaches are designed for handling time series variables, however. These also need to be adjusted so that they can receive equal treatment. The following rules will be used to standardize time series variables to put them on the same scale as the other variables in the model and as each other:
-
A random walk variable (with no momentum, which is discussed later) does not need to be adjusted, since it is similar to a categorical variable, which will not be modified. Since this random walk variable is not adjusted, all other time series variables can be compared to it for calculating their relative scaling factor.
-
Instead of comparing the standard deviations from the mean, the scale of a time series variable should be determined by calculating the square root of the average squared differences between each time period. This is similar in nature to the common practice of using the standard deviation but more properly reflects the nature of these variables.
When calculating these averages, since the denominator is the same for all time series variables (equal to the number of time periods), it will cancel out when being compared and can be ignored. This means that instead of comparing the average squared differences, the sum of the squared differences will be compared. This quantity is equal to 1 for a plain random walk (with no momentum), which is the point of comparison. Therefore, the standardization divisor for each variable is equal to the square root of the sum of the squared differences.[7]
Applying these rules to a simple trend (or drift) variable, which is a numerical sequence from 1 to the number of time periods, this variable would be divided by the square root of one less than the number of time periods. So, for example, a 10-year series would be divided by 3, and a 26-year series would be divided by 5. (Note that the longer series receives a greater divisor. To explain, if both a trend and a random walk variable are in a model, the total penalty for using the random walk equals [n – 1] times the average change, where n is the number of time periods [assuming a lasso penalty for simplicity]. The penalty for using the standardized trend variable equals √[n – 1] times the selected trend. Using the trend instead of the random walk can result in a lower penalty but is less flexible than the random walk. Since the total penalty for using the random walk grows with the length of the sequence, to put the variables on equal footing, it is necessary for the trend penalty to do the same. Also, as the number of data points grows, a trend parameter is capable of having a greater impact on the likelihood and so can withstand a larger penalty value.)
Both Appendix A and Appendix B show R code that uses these standardization rules. When using it in a penalized regression model, it is recommended that one manually standardize all variables as described and make sure that the penalized regression function used does not apply any additional standardization by default.
To recap, categorical variables should not be adjusted, numerical variables should be divided by twice the standard deviation, and time series variables should be divided by the square root of the sum of the squared differences.
9. Some notes on implementation
The method presented can be implemented using most existing elastic net packages. To do so, the default dummy encodings for random walk variables can be changed, as discussed. See Appendix B for example R code. The random walk variables for each period also can be created and added manually.
It is important to verify that the selected penalty value is not the last value tested, because if it is, it may not be the true optimal value. If this occurs, the procedure should be rerun to smaller penalty values.
Before a GLM solving algorithm is run, a matrix is created for the specified independent variables. Many GLM functions do this implicitly. Just as a separate column is created in this matrix for each possible value of a categorical variable, a separate column is created for each period in a random walk variable, except for the first. If interactions with some segmentation are included, separate columns will be created for every combination of year and segment. Because of this, the resulting matrix can become quite large for models that use a large number of predictors and that have a large number of data points. For most models, this is not an issue, but for very large ones, if memory issues are encountered, instead of creating a standard matrix that utilizes memory for each cell value, a sparse matrix can be created instead, which utilizes memory for only non-0 cells. This can reduce the amount of memory required dramatically since most of the values in a typical modeling matrix are usually 0. (The example shown in Appendix A takes this approach.)
Some sparse matrix implementations (such as the sparse.model.matrix function in the Matrix package in R), when building a sparse matrix, will initially create a non–sparse matrix and convert it to a sparse matrix only at the very end. This can create memory issues for very large models. If issues are encountered, the matrix can be constructed manually one variable at a time so that sparse matrices can be used even during construction, which will save memory.
10. Loss ratio case study
The proposed method will be demonstrated with an example profitability or reserve study involving yearly loss ratios in which both credibility and smoothing/forecasting are employed.
Three segments are used in the example, each having two subsegments, making six subsegments in all. Each of these segments and subsegments is affected by various changing factors, both on the premium side and on the loss side, which cause the loss ratios to vary by year. Premium is affected by rate changes, which are easily accounted for, but the recorded rate changes are usually not 100% accurate and do not take everything into account, such as changes in policy wording. On the loss side, aside from a longer-term trend that affects the losses by a (perhaps) similar amount each year, social, legal, economic, and other factors can cause changes during shorter periods. Some of these may affect the entire book, and others can be limited to various segments or subsegments.
Another consideration is that claims take time to be reported and settled, so our current snapshot of losses will develop over time. Our goal is to estimate the ultimate loss ratio for each year and for future years for a reserving or profitability study.
The ultimate chain ladder loss ratios are shown in Figure 10. This example assumes that premiums have already been on-leveled for rate changes and that losses have been trended by the long-term average trend (although it is possible to use the procedure to fit this as well). For simplicity, the on-level premiums for each subsegment for each year are assumed to be $1,000, although varying premiums can be accommodated as well.
To fit these data, an elastic net with variables for a random walk is used. The model will account for the different loss ratio levels for each segment and subsegment as well as the changes to each by year, incorporating credibility for both the level and changes. A Tweedie family is used to fit the aggregated losses.
A Cape Cod–like approach is used to account for development, as discussed in Section 7. Loss ratios inputted into the model are the reported loss ratios multiplied by the loss development factors (i.e., the chain ladder loss ratios), and the premiums divided by the loss development factors (i.e., the used premiums) are used as the regression weights. This procedure accounts for development while taking into account the extra volatility of the greener years.
The code used to generate and fit the data is shown in Appendix B. The regression formula used was as follows, where a colon is used to indicate interaction effects, ult.lr are the ultimate loss ratios, intercept is an intercept term, seg is the variable for the segment, subseg is the variable for the subsegment, and yr.rw is a random walk variable:
log(ult.lr)=intercept+seg+subseg+yr.rw+seg:yr.rw+subseg:yr.rw.
This is a hierarchical credibility model. The overall average level of the loss ratio is determined by the intercept. The average relativities for each segment are determined by the seg coefficients, and the additional relativities for each subsegment are determined by the subseg coefficients. Since each coefficient value is penalized and pushed back toward 0, each level is credibility weighted back toward the previous, i.e., each segment is credibility weighted back toward the overall mean, and each subsegment is credibility weighted back toward the segment.
The same can be said for the changes by year. The yr.rw variable creates a random walk on the intercept, which affects all segments and subsegments. The interaction of this variable and the segment allows for additional changes that affect only particular segments, and these changes are credibility weighted back toward the overall changes by year. The same occurs at the subsegment level, and these changes are credibility weighted back toward the indicated segment changes.
The model just discussed does a good job of fitting all segments and their changes by year but does not take into account any possible autocorrelation between years, i.e., momentum of the yearly changes. Stated another way, if a change is observed in a period, then instead of using no change as the complement of credibility for the next period, perhaps the complement should be set to somewhere between 0 and the previous indicated change. This can be tested by redefining the random walk variable with different amounts of momentum and then refitting the model (as discussed in section 5.3). The momentum value having the lowest cross-validated error is then selected. The cross-validated error (using the deviance as the error measure) for the model with no momentum is 0.0999. Testing in increments of 0.1, the next value tested is 0.1. This model has a cross-validated error of 0.0984, which is better than the first model. Testing a momentum value of 0.2 yields an error of 0.1015, worse than the previous. So the selected value is 0.1. The final fitted results for each segment and subsegment are shown in Figure 11.
Looking at this figure, some common trends can be seen. Most of the subsegments start increasing in year 3 and decrease in year 7, although this increase is delayed a year in subsegment 3. Common patterns can be seen by segment as well. Subsegments in segment 1 show an initial increase followed by a decrease, segment 2 shows a generally increasing pattern, and segment 3 shows a decrease followed by an increase, and then no change from year 7. (All of this can be seen by looking directly at the fitted coefficients as well.) It also is apparent that less weight is given to the more recent years due to the additional uncertainty of these immature years.
11. Conclusion
This paper shows a method of incorporating a subset of SSM functionality into a linear regression framework. In addition to the improved performance and ease of use of this method, the resulting models are intuitive, and the corresponding parameters lend themselves easily to interpretation. This can be a useful tool when one is attempting to “dig deeper” and discover changes or trends that may be affecting particular segments or entities. It can make forecasts into future periods more accurate as well. The results are suitable for presentation, which is an important consideration since findings often need to be communicated to other parties. Last, it is incorporated in a framework that scales well to large data sets, an important consideration in the age of big data.