1. Background

Overparameterized models tend to be less accurate in their predictions than those with fewer parameters. For instance, the popular textbook by Burnham and Anderson states, “Overfitted models … have estimated (and actual) sampling variances that are needlessly large (the precision of the estimators is poor, relative to what could have been accomplished with a more parsimonious model)” (2002). Also see J. Frost (2015). Such discussions are framed in terms of fitting the model to the sample versus to the population. Getting the right balance between these two fits is the goal of a lot of statistical methodology.

Fitting parameterized curves to row or column factors is one way to mitigate overfitting, but finding the right curves can be an issue. Often actuaries keep a parameter for every row and every column, in part because it is not clear how to eliminate them, even though many of them are not statistically significant. The methodology discussed in this paper—of shrinking fitted values toward the overall mean—addresses that issue by reducing the predictive variance.

Credibility theory shrinks class estimates toward the mean using the average for the variance of individual classes over time and the variance of the class averages. The James-Stein estimator (described in Stein 1956) does so as well, but it uses model assumptions to quantify the average individual variance. Starting with Hoerl and Kennard (1970), statisticians have developed methods that shrink the estimated mean for each observed point toward the overall mean by using a shrinkage parameter, λ, which is selected based on how well the model works on predictions for holdout samples. Typically λ is tested by dividing the data set into 4–10 groups, which are left out one at a time and predicted by the model fit on all the other groups, with various values of λ. This procedure is called “cross-validation.”

The original regularization method is ridge regression, which uses parameters β_j to minimize the negative log-likelihood (NLL) plus λΣ\(\beta_{j}^{2}\). More popular recently is the least absolute shrinkage and selection operator, or LASSO, which minimizes NLL plus λΣ|β_j|. This has the practical advantage that as λ increases, more and more parameters, and eventually all but the mean, go to exactly 0. This makes LASSO a method of variable selection as well as estimation, so the modeler can start with a large number of variables and the estimation will eliminate most of them. As λ gets smaller, the parameter size penalty vanishes, and thus the maximum likelihood estimate is obtained. Hoerl and Kennard (1970) proved that some λ > 0 always produces a lower error variance, so shrinkage can always improve predictive accuracy.

Usually all the variables are standardized by a linear transformation to make them mean 0, variance 1. That way parameter size is comparable across variables. The additive part of the variable transformations is picked up by the mean, which is not included in the penalty for the sum of the parameters and so is not shrunk. The other parameters end up being pushed toward zero, which in turn pushes each fitted value toward the mean. Blei (2015) and Hastie, Tibshirani, and Wainwright (2015) are good references.

A straightforward application of regularization would be to apply it to generalized linear model (GLM) modeling in ratemaking. Such modeling is just like regular GLM except that shrinking the parameters shrinks the fitted values toward the mean; thus, it is like GLM plus credibility, but with the shrinkage coming from the method instead of from within and between variances. Adding interaction terms would be convenient with shrinkage, as many of them would be shrunk to or toward zero unless they actually have predictive value. It would be easy to extend this method to distributions beyond those that GLM uses. Loss reserving, however, as discussed below, takes a little more doing to get into a regression form to which shrinkage can be applied.

Bayesian versions of regularization work by giving the parameters shrinkage priors, which are mean-zero priors—normal distributions for ridge regression and double exponential for LASSO. There are generalizations that use other shrinkage priors. The advantages of the Bayesian form are that it gives a distribution of parameters for parameter uncertainty calculations and that it has a goodness-of-fit measure analogous to the Akaike information criterion (AIC) for model comparisons. AIC, the Bayesian information criterion (BIC), and others do not work with regularized models due to parameter counting problems with shrinkage. Markov chain Monte Carlo (MCMC) estimation can numerically produce samples of the posterior distribution without needing to specify conjugate posteriors for the priors.

A classical approach similar to Bayesian estimation is random effects modeling. Instead of parameters having distributions, the effects being modeled have shrinkage distributions, such as a mean-zero normal distribution. The terminology used is that this method projects effects instead of estimating parameters. For instance, the differences between the frequency of an event in a territory and the statewide frequency of the same event could be a mean-zero random effect. The only parameter would be the variance of these effects, but the model projects each territory’s effect. One common method of projection is to maximize the product of the likelihood function with the probability of the effects. This turns out to be the same thing as computing the posterior mode in the Bayesian interpretation, but it can be done as a classical optimization. Ridge regression and LASSO are special cases of random-effects modeling.

A typical assumption in random effects is that each random effect has its own variance parameter. However, using the generalized degrees of freedom approach of Ye (1998), Venter, Gutkovich, and Gao (2017) found that having so many scale parameters can use up many degrees of freedom—that is, including them in the model makes the fitted values much more responsive to hypothetical small changes in the data points. Most random effects software allows users to specify the existence of just one variance parameter for the whole model, which seems to give a considerably more parsimonious model without sacrificing too much in goodness of fit. This procedure would get to the same result as ridge regression or LASSO.

For reserve applications, the starting point is a row-column factor model. To make it applicable in this context, the fitted value is the row parameter times the column parameter times a constant. For identifiability, there is no parameter for the first row or column other than the constant—that is, the factor for that row and column is 1.0. The problem with applying parameter shrinkage in this form is that if any parameter is eliminated, that row or column also gets only the constant. However, if the model is set up so that each parameter is the change in the row or column factor from the previous one, then when a variable is eliminated, that row or column just gets the factor for the previous row or column. Since the first row and column get 1.0 anyway, the factor for the second row or column is its parameter change plus 1.

This paper takes this activity one step further—instead of the parameters being these first differences, they are the second differences in the factors at each point. Then if one of these is 0, the modeled first difference does not change at that point, so the factor is on a line defined by the previous two factors. This seems to be a bit more realistic in actual triangles and allows for more parsimonious models.

The row-column model is a special case of the row-column-diagonal model. The latter is actually in wide use in the social sciences, where it is called the age-period-cohort (APC) model. The history of these models traces back to Greenberg, Wright, and Sheps (1950), who in turn referred to data analysis by W. H. Frost (1939). In actuarial work, a column-diagonal model was discussed by Taylor (1977), who called it the “separation model,” a term still used. The first actuarial reference to the full APC model appears to be the reserve model of Barnett and Zehnwirth (2000). Mortality modelers have been using various forms of APC models since Renshaw and Haberman (2006).

Parameter shrinkage methodology is starting to be applied in actuarial modeling. Venter, Gutkovich, and Gao (2017) modeled loss triangles with row, column, and diagonal parameters in slope change form fitted by random effects and LASSO. Venter and Şahın (2018) used Bayesian shrinkage priors for the same purpose in a mortality model that is similar to reserve models.

Gao and Meng (2018) used shrinkage priors on cubic spline models of loss development. Some precursors include Barnett and Zehnwirth (2000), who applied shrinkage to reduce or omit piecewise linear slope changes in reserve modeling; Gluck (1997), who did something similar for the Cape Cod model; and England and Verrall (2002), who used cubic spline modeling for loss triangles.

Section 2 discusses the row-column model for cell means and goes into more detail on applying parameter shrinkage. Section 3 discusses loss distributions for individual cells given their fitted means. The fitting methods and properties of the distributions are illustrated in Section 4 by fitting to frequency, severity, and aggregate loss data from a published triangle. Extensions of the row-column model are discussed in Section 5. Section 6 concludes. Appendices 1, 2, and 3 cover, respectively, distribution details, coding methods including examples and output, and the sensitivity of goodness of fit to the degree of shrinkage used.

2. Parameter shrinkage methodology

The data are assumed to be for an incremental paid triangle. A constant term, C, is included, and the first row factor and first column factor are set to 1.0. In the basic row-column model, the mean (or a parameter closely related to the mean, depending on the distributional assumptions) for the (w,u) cell is the product of row and column factors:

\[\mu_{w,u} = A_w B_u C\]

Here A_w is the parameter for accident year (AY) w and B_u is the parameter for lag u. This basic model will be used for frequency, severity, and aggregate losses by cell.

There can get to be a lot of parameters, with one for every row and column. Parameter shrinkage aims at getting more parsimonious models that avoid overfitting and so predict better. This is the goal of regularization in general. Here there will still be a parameter for every row and every column, but several adjacent parameters could be on line segments.

When all of the observations are positive, an exploratory fit can be done using regression with shrinkage on the logs of the losses. Then the fitted values are the sums of the row and column log parameters, plus a constant. This can be set up in regression format with (0,1) dummy variables identifying the row and column an observation is in. This allows the use of commonly available estimation applications. The model in which the parameters are second differences can still be set up this way, but the variables become sums of more complicated dummies. This is illustrated in the example. For the distributions in the examples, an exponential transformation of this model is done, with the dependent variable being the dollar losses.

Some background on MCMC will help clarify the methodology. MCMC numerically generates a collection of samples from the posterior distribution when only the likelihood and prior are known. With data X and parameters β, Bayes’ theorem says the following:

\[p\left( \beta \middle| X \right)\mathbf{=}\frac{p\mathbf{(}X\mathbf{|}\beta\mathbf{)}p\mathbf{(}\beta\mathbf{)}}{p\mathbf{(}X\mathbf{)}}\]

The left side is the posterior distribution of the parameters given the data, and the numerator of the right side is the likelihood times the prior. The denominator p(X) is a constant for a given data set, so maximizing the numerator maximizes the posterior. In random effects, the numerator is called the “joint likelihood,” so maximizing it gives the posterior mode. The original MCMC methodology, that of the Metropolis sampler, uses just the numerator. It has a proposal generator to create a possible sample of the parameters from the latest accepted sample. If this increases the numerator, it is added to the collection of samples. If it doesn’t, there is an acceptance rule to put it in or not, based on a (0,1) random draw. After a warm-up period, the retained samples end up being representative of the posterior.

A refined version of the Metropolis sampler, the Metropolis-Hastings sampler, is more efficient. Further refinements include Hamiltonian mechanics and the no-U-turn sampler, which evolve the proposal generator dynamically. The latter is the basis of the Stan MCMC package, which is available in R and Python applications. Another methodology is the Gibbs sampler, which draws parameters sequentially from the posterior distribution of each parameter given the data and the latest sample of all the other parameters. The JAGS (Just Another Gibbs Sampler) package uses that method.

Basically, then, MCMC is looking for parameters that give relatively high values to the log-likelihood plus the sum of the logs of the probabilities of the parameters, using their priors. The posterior mode is at the set of probabilities that maximizes this sum. (This is also called the “maximum a posterior,” or MAP.) The posterior mode using the normal or Laplace prior gives the parameters estimated by the ridge or LASSO regression.

2.1. Posterior mean versus posterior mode

While classical shrinkage methods agree with the Bayesian posterior mode, the posterior mean is the basic Bayesian estimator. The mode is very similar to classical estimation in that both methods optimize some probability measure—such as the NLL or joint likelihood.

The posterior mean is a fundamentally different approach. It does not maximize a probability. Instead it looks at all the parameter sets that could explain the data, and weights each according to its probability. The most likely set of parameters has appeal, but it has more risk of being a statistical fluke. If it is similar to many other possible parameter sets, then it would probably be only very slightly higher in posterior probability and not much different from the mean. But if it is very different, it could be overly tailored to that specific data set. In that case, only a small percentage of the MCMC samples would be close to that point. The posterior mean is aimed at getting an estimate that would still perform well on other samples.

2.2. Measuring goodness of fit

Traditional goodness-of-fit measures, such as AIC, BIC, and so on, penalize the log-likelihood with parameter-count penalties. This is already problematic for nonlinear models, as the parameter count does not necessarily measure the same thing for them. Ye (1998) developed a way to count parameters using what he called “generalized degrees of freedom,” which measures how sensitive the fitted values are to slight changes in the corresponding data points. This is accomplished by taking the derivative of each fitted value with respect to the data point, usually numerically. It agrees with the standard parameter count given by the diagonal of the hat matrix for linear models.

Parameter shrinkage also makes the parameter count ambiguous, and from Ye’s perspective, the shrunk parameters do not allow as much responsiveness to changes in the data, so they do not use up as many degrees of freedom. For LASSO, the gold standard of model testing is leave-one-out, or LOO, estimation. The model is fitted over and over, each time leaving out a single observation, with the log-likelihood computed for the omitted point. The sum of those log-likelihoods is the LOO fit measure.

Both LOO and Ye’s method are computationally expensive and do not work well with MCMC anyway because of sampling uncertainty. To address these shortcomings, Gelfand (1996) developed an approximation for a sample point’s out-of-sample log-likelihood using a numerical integration technique called “importance sampling.” In his implementation, that probability is estimated as its weighted average over all of the samples, using weights proportional to the reciprocal of the point’s likelihood under each sample. That methodology gives greater weight to the samples that fit the point poorly, which would be more likely to occur if that point had been omitted. The estimate of the probability of the point comes out to be the reciprocal of the average over all samples of the reciprocal of the point’s probability in the sample. This is the harmonic mean of the point’s probabilities. With this calculation, the sample of the posterior distribution of all of the parameters as generated by MCMC is enough to do the LOO calculation.

That technique gives good, but still volatile, estimates of the LOO log-likelihood. Vehtari, Gelman, and Gabry (2017) addressed that issue using something akin to extreme value theory—fitting a Pareto to the probability reciprocals and using the fitted Pareto values instead of the actuals for the largest 20% of the sample. They called this technique “Pareto-smoothed importance sampling.” It has been extensively tested and has become widely adopted. The penalized likelihood measure is labeled \(\widehat{{elpd}}\)_loo, standing for “expected log pointwise predictive density.” It aims at doing what AIC and the other measures were trying to address as well—adjusting the log-likelihood for sample bias.

The Stan software provides a LOO estimation package that can work on any posterior sample, even those not from Stan. It outputs \(\widehat{{elpd}}\)_loo as well as the implied log-likelihood penalty and something Stan calls LOOIC—the LOO information criterion—which is ‑ \(\widehat{{elpd}}\)_loo, in accordance with standards of information theory. Since the factor is not critical, here the term “LOOIC” is used for \(\widehat{{elpd}}\)_loo, which is the NLL increased by the penalty.

2.3. Selecting the degree of shrinkage

Selecting the scale parameter of the Laplace or Cauchy prior for MCMC, or the λ shrinkage parameter for LASSO or ridge regression, requires a balancing of parsimony and goodness of fit. Taking the parameter that optimizes \(\widehat{{elpd}}\)_loo is one way to proceed, and that was the approach taken by Venter and Şahın (2018). However, this approach is not totally compatible with the posterior mean philosophy, as it is a combination of Bayesian and predictive optimization. An alternative would be to give a sufficiently wide prior to the scale parameter itself and include that in the MCMC estimation. This is called a “fully Bayesian” method and produces a range of sample values of λ. Gao and Meng (2018) is a loss reserving paper using the fully Bayesian approach. That is the approach taken here.

LASSO applications, such as the R package glmnet, use cross-validation to select a range of candidate λ values. An alternative is to build in more of the Bayesian approach. The Laplace (double exponential) prior is discussed in Appendix 1. There, the log density is given as log[f(β|σ)] = ‑log(2) – log(σ) – |β|/σ, with σ = 1/λ. Summing over the k parameters makes the negative log probability = k * log(2) – k * log(λ) + λΣ|β_j|. This is the LASSO penalty on the NLL of the data, but if λ is a given constant, the first two terms are dropped. In addition, if λ itself is given a uniform prior with density = C over some interval, the second term needs to be included, but the uniform density is a constant that can be dropped. Thus the quantity to be minimized over λ, β_j is as follows:

\[NLL - k * \log \left( \lambda \right) + \lambda \sum | \beta_j |\]

The uniform prior is an arbitrary but reasonable choice, so values of λ that are not at the exact minimum of this are possible candidates as well.

2.4. Estimation issues

Instead of doing MCMC, a nonlinear optimizer such as the Nelder-Mead method could be used to get the posterior mode through classical estimation. Good starting parameters seem to be needed, however. One advantage of MCMC is that it seems to be able to find reasonable parameter sets better than classical optimization. That might in fact be one of its historical attractions. However, MCMC can also find a lot of local maximums that are not very good fits. The lingo of MCMC appears to be that this will happen if the model is “poorly specified.” In practice, that seems to mean if the priors are too wide. Running the estimation with starting values from the previous better fits also can help avoid bad local maximums.

Starting with LASSO can give a starting point for MCMC. Stan is good at pointing out which parameters are not contributing to the fit, but the second-difference variables are negatively correlated and thus work in groups, which makes some individual parameter ranges less indicative of the value of those parameters. LASSO gives parameter sets that work together at each value of λ.

The Stan software used here is not able to include R packages such as tweedie and gamlss.dist. With good starting parameters from related Stan fits, classical estimation in R can maximize the posterior mode for the Tweedie and Poisson–inverse Gaussian (PiG) distributions discussed in Appendix 1, and it can at least compare fits by the posterior mode probabilities. Some of that was done in the examples below. Unfortunately, neither the posterior mean nor the LOOIC can be computed this way, so the comparisons are essentially suggestive.

3. Distributions for reserve modeling

The LOOIC measure provides a way to compare the fits for different residual distributions. In addition, MCMC—and to some extent maximum likelihood—makes it easy to estimate distributions that are not in the linear exponential family that GLM modeling requires. This feature allows better modeling of the residual distributions and better estimation of reserve range distributions. The distributions explored here provide more flexible modeling of mean-variance relationships across the triangle as well as skewness and higher moments.

Detailed distribution formulas are included in Appendix 1, but there are a few key takeaways:

• Development triangles are subject to a unique form of heteroskedasticity. The variance is not constant among the cells, but it often decreases less than the mean does across the triangle, due to volatile large losses paying later. This phenomenon is addressed by introducing an additional variance parameter. The easiest example is that of the normal distribution—instead of a constant variance, the variance, and so the standard deviation, is sµ^k. If k < 1, the variance decreases more slowly than the mean. Something similar can be done for any distribution and is labeled as the “k form.” The Weibull k is particularly interesting as its skewness changes more than is seen in other distributions, often in a helpful way. In GLM the mean-variance relationship also determines the skewness and other shape features, but now these can all be modeled independently.

• The Tweedie distribution, usually parameterized with variance = φµ^p, p ≥ 1, is reparameterized in a, b, p to have mean = ab, variance = ab², and skewness = pa^‑1/2. Then the distribution of the sum of variables with the same b and p parameters is Tweedie in Σa_j, b, p. Also, if Z is Tweedie in a, b, p, then cZ has parameters a, bc, p. This puts the focus on controlling the skewness with the p parameter. In the usual form, the skewness is still p times the coefficient of variation (CV), but the skewness relationship is overshadowed by the variance. This additive feature makes it possible to fit a severity distribution even if only the number and total value of payments are known for each cell—the individual payments are not needed. This is the case for the normal k as well, but with a slightly different formula. The reparameterization also makes it easier to represent mixtures of Poissons by a Tweedie, which generalizes the negative binomial and PiG.

• Choosing which parameter of a distribution to fix among the cells can also change the mean-variance relationship across the triangle. For example, the gamma with mean µ = ab and variance ab² has variance = bµ = µ²/a, so fixing a in all the cells makes the variance proportional to the mean squared, but fixing b makes it proportional to the mean. This then works the same way with any Tweedie distribution, which allows either mean-variance relationship with any skewness/CV ratio, as determined by p. The form with variance proportional to mean often works fairly well, depending on how the larger loss payments are arranged. The Tweedie-mixed Poissons, such as the negative binomial, are related to this. They come in two forms with different mean-variance relationships, which arise from the mixing Tweedie having a or b fixed across the cells. When fitted to a single population—that is, to only one cell—the fits from the two forms are identical.

• The typical overdispersed Poisson (ODP) assumption has variance proportional to mean, but the actual ODP in the exponential family takes values only at integer multiples of b, which is not what is needed for losses. Thus the ODP is usually applied to reserving with the quasi-likelihood specified but without any identified distribution function. The essential feature of this method is that the variance is proportional to the mean, so any Tweedie with fixed b, p could represent such an ODP, and in fact the gamma is often used in ODP simulations, where an actual distribution function is needed. But the gamma can be fitted directly by maximum likelihood estimation, which would allow the use of the Fisher information for parameter uncertainty instead of bootstrapping. (The parameters are asymptotically normal, but for positive parameters and usual sample sizes, a gamma with a normal copula usually works better for the parameter distribution.) Here we fit this form of the gamma by regularization.

Details are also given for the shrinkage distributions used in MCMC, and generalizations of classical LASSO and ridge regression are discussed along with them.

4. Example

As an example of this methodology, we model a loss triangle, including exposures, counts, and amounts, from Wüthrich (2003). With the additive property of the Tweedie, only counts and amounts are needed to model the severity distributions across the cells, and with exposures, the frequency distributions can also be modeled. The respective triangles are shown in Tables 1 and 2.

4.1. Exploratory analysis

It is often useful before fitting models to do some simple fits on an exploratory basis. The row-column factor model expresses the (w,u) cell mean as the product of row and column factors:

\[\mu_{w,u} = A_w B_u C = \exp \left( p_w + q_u + c \right).\]

The log additive form is often set up as a linear model, and before getting into the distributional issues, multiple regression on the logs of the losses can reveal much of the structure of the data. This step can be done if there are no 0 or negative data points, and in fact some conditional distributions for the data given the fitted means, such as the gamma, also require positive observations.

4.1.1. Design matrix

To set up multiple regressions, the whole triangle has to be put into a single column as the dependent variable. In building the design matrix, it is also helpful to have three columns that identify the row, column, and diagonal, respectively, that each data point comes from.

The design matrix has a column for each variable. Here, for specificity, the first row and column are not given parameters, and therefore design matrix columns are needed for the variables in triangle rows 2–9 and columns 2–10. It usually helps to put in a name for each column and the triangle row or column number above each name. For a typical regression or GLM model for a triangle, the variable for a row will be 1 for a cell if the cell is from that row, and 0 otherwise, and similarly for the columns.

The model favored here, where the variables are slope changes, can also be represented by a design matrix with dummy variables, but they are no longer (0,1) dummies. A row parameter is the sum of its previous first differences, written as \(p_{w} = \sum_{j = 2}^{w}f_{j}\), and the first differences are sums of the previous second differences, so \(f_{j} = \sum_{i = 2}^{j}a_{i}\). Then p₂ = f₂ = a₂, p₃ = f₂ + f₃ = 2a₂ + a₃, p₄ = f₂ + f₃ + f₄ = 3a₂ + 2a₃ + a₄, and so on. Then the row parameter dummy a_i is set to max(0, 1 + k − i) for a cell in row k. The same formula holds for column parameters, with slope changes denoted by b_i. The entry for an observation in the design matrix is the number of times any slope change is added up for that observation. Table 6 shows the design matrix for the initial model.

Regressions can be done on both matrices. Calling the log column y and the design matrix x, this is easy enough to do in Excel with matrix functions, giving the parameter vector β = (x’x)^‑1x’y. It is even easier with regression functions such as those available in the package Real Statistics. It and, in fact, all packages used here assume that the constant term is not in the design matrix, so from now on, x refers to the design matrix without the constant term.

4.1.2. Regression

Both the levels regression and the slope change regression give the same overall fit—see Table 3—but the t-statistics are different. Tables 4 and 5 show these for the two regressions. Usually t-statistics with absolute values greater than 2 are considered significant. By that measure, most of the row parameters in the levels regression are not significant, although those in the columns are. That might make this triangle a good candidate for the Cape Cod model. Parameter reduction will end up allowing some degree of variability among the rows, much in the same way as the generalized Cape Cod of Gluck (1997).

The trend regression parameters are in general less significant, but a lower threshold for t may be appropriate in that adjacent parameters are strongly negatively correlated—raising one and lowering the next would offset each other in all but one row. Thus they are more significant together than they are individually. When a trend change is low, that means the previous trend continues. The a2 parameter is probably significant, which would show a general upward trend from the first row. The column trend changes are significant in the beginning, with some fluctuation in direction, and then lose significance, which would mean a continuing trend.

4.1.3. LASSO

For large design matrices of second-difference variables, Stan can have difficulty finding good initial parameter values. In those cases, LASSO is often more efficient at identifying variables that are likely to end up with parameters close to zero and thus with no change in slope for the fitted piecewise linear curve. These variables can then be eliminated, producing the same effect. Usually I like to use a low shrinkage value, λ, for this purpose, so that not too many variables are eliminated in LASSO. Generally some more can be eliminated later—those that Stan estimates to have posterior distributions centered near zero—as long as omitting them does not degrade the LOOIC. This isn’t variable selection in the usual sense, as the variables eliminated would have parameter values of 0 if left in, so the whole design matrix is being used. It is more a matter of tidying up the model. The design matrix can feed right into LASSO software to get a start on parameter reduction. This step was not needed here since it is a pretty small triangle, but it is shown for possible use in other models.

Appendix 2.1 shows code for the R package glmnet. The program estimates the parameters for up to 100 values of λ, depending on some internal settings. It can print a graph of the parameter values as a function of decreases in λ, also shown in Appendix 2. Cross-validation is done in a function called cv.glmnet, which produces a target range for λ between lambda.min and lambda.1se, for this example the range (0.0093,0.1257). Here the variables with nonzero parameters for values of λ near 0.03 were passed on to Bayesian LASSO.

The range of λs is not passed on to Stan. I usually start Stan with a fairly wide prior for s = 1/λ, which is the Laplace scale parameter, but allowing s to be too high can lead to divergent estimation. After seeing the posterior distribution I might tighten the prior to exclude ranges that aren’t being used for the sake of efficiency. This seems to have no effect on the posterior distribution of s.

Bayesian LASSO has several advantages over classical, including giving a sample distribution of parameters for risk analysis, being able to include a distribution of values of λ, and having a goodness-of-fit measure, the LOOIC. The second and third columns of coefficients shown in Appendix 2 have the same nonzero variables, except for V10, V11, and V15. Keeping the variables in the second column except for V15 leaves the seven variables a2, a6, b2, b3, b4, b5 and b7, plus the constant. These are used in a reduced design matrix in Stan to do the MCMC estimation.

4.2. Aggregate triangle

The models to be estimated by MCMC are coded in Stan. Appendix 2.2 shows the code used for estimating the gamma distribution with fixed b, so with variance proportional to mean, from any design matrix x1. The model is as follows:

• c is uniform(‑4,16)

• logbeta is uniform(‑20,20)

• beta = exp(logbeta)

• logs is uniform(‑5, ‑0.2)

• s = exp(logs)

• v is double exponential(0,s)

• alpha = exp(x1 * v + c) * beta

• y is gamma(alpha,beta), where in Stan, beta = 1/b

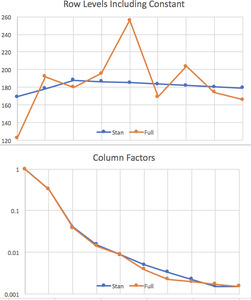
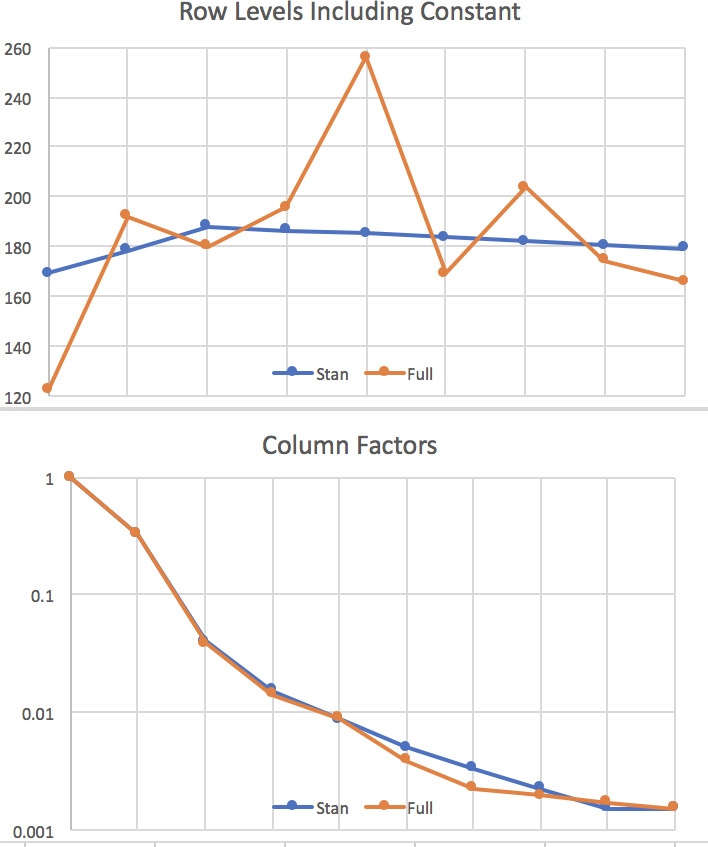
The output includes a graph of (0.05,0.95) and (0.2,0.8) percentile ranges for the parameters, shown in Figure 1. This is where parameters that are near zero with large positive and negative ranges can be reviewed for removal from the model. None of our results are like that. The resulting row and column parameters are compared with those from the full lognormal regression (Tables 3 and 4) in Figure 2. Not shown is the s parameter, which is in the range (0.32,0.77).

Figure 1.Parameter ranges, Stan gamma fit v = (a2,a6,b2,b3,b4,b5,b7)

Normal k, GiG, gamma, and Weibull k distributions were fitted to the triangle. All have very similar row and column parameters but different LOOICs, due to the different distribution shapes. Table 7 shows the LOOIC, the NLL, and their difference, the parameter penalty. All except the gamma have a parameter for the power in the variance = s * meank relationship, but here all of those powers came out very close to 1.0. The gamma was fitted with the b parameter constant across the cells, so it also has the power k = 1 implicitly. This procedure thus saves a parameter. The GiG has one more parameter for the percentage normal, which is 30%.

Figure 2.Row and column parameters for gamma in Stan and full regression, lognormal

The best-fitting distribution is the Weibull k, which is the Weibull with an adjustment fitted to the mean-variance relationship. It has the most variability by cell in skewness, which apparently helps for this data set. The 0 skewness of the normal k does not work well for these data even though the variance is proportional to the mean.

The Weibull k and gamma fits have about the same mean and CV by cell, but the skewnesses are different. Figure 3 graphs the common CV and the two skewnesses by lag for the second row, the last row that has all columns. Because the rows are all pretty similar, this graph would look about the same for any row. The gamma skewness is twice the CV, but the Weibull is consistently lower than the gamma. This appears to provide a better representation of the observations under the row-column model.

Figure 3.Fitted CV and skewness for gamma and Weibull k fits

Appendix 3 looks at the sensitivity of the LOOIC measure to changing values of λ.

4.3. Severity

The data do not have individual payment observations, but due to the additive property of the Tweedie, the counts and total payments in a cell are enough to model the severity distribution. Severity is typically modeled with a constant CV across the cells. That requires the Tweedie severity a parameter to be constant. Each cell gets its own b parameter from the row-column model. Then the losses in a cell are modeled as Tweedie in a times the number of payments in the cell and the b for the cell, with any p. Here p = 2 and p = 3, so the gamma and the inverse Gaussian are fitted. The model with constant b, so with variance proportional to mean, is tested for comparison. If severity is normally k–distributed in µ_w,u, s, k, the payment total is distributed normally with mean = µ_w,u ∗ (counts) and variance = \(s\mu_{w,u}^{k}\) ∗ (counts).

For the gamma, the model equations are similar to those shown in 4.2 for aggregate losses, but now α is fixed across cells, not β, and counts are used in the calculation of severity. The y variable is the observed severity means by cell, which have variances of ab²/count, given the gamma claims severity with mean ab = α/β and variance ab² = α/β². This makes the severity mean gamma with both α and β multiplied by the counts. The model equations are as follows:

• c is uniform(‑30,0) for the severity

• logalpha is uniform(‑30, ‑1)

• alpha = exp(logalpha)

• s is uniform(0.01,0.02), although it was wider in earlier runs

• v is double exponential(0,s)

• beta = alpha/exp(x1 * v + c), so alpha/beta is mean

• y is gamma(alpha * counts, beta * counts), where in Stan, beta = 1/b

The starting point is to use the same seven variables that were optimal for aggregate losses. For the gamma distribution, the parameter graph with (5%,95%) and (20%,80%) ranges is shown in Figure 4. From the graph, v[6], which is the coefficient for the column 5 slope change, has a mean close to zero and a wide range—just the sort of graph that indicates a parameter is not needed. Indeed, eliminating that parameter improves the LOOIC slightly. The remaining variables are the slope changes for rows 2 and 4, and for columns 2, 3, 4, and 7.

Figure 4.Gamma severity parameter ranges, v = (a2,a4,b2,b3,b4,b5,b7)

The design matrix for those data is now used for the three distributions. The gamma with a fixed is the best fit. For the inverse Gaussian, holding b constant, which makes the variance proportional to the mean, is actually slightly better than fixing a. Fit measures and the fitted moments are in Table 8, showing that the variance power appears to bear an inverse relationship to the skewness—that is, the more skewed distributions have the lowest power.

Figure 5 graphs the resulting level factors (not differences) for the gamma and the inverse Gaussian. The column factors are indistinguishable for the two distributions. Severity grows fairly steadily across AYs, and it is highest at the fifth lag. The raw severity mean is highest for the seventh and eighth columns but is also highly volatile there.

Figure 5.Row and column severity level parameters

It is not possible to use the R Tweedie package within Stan, but it can be used with a nonlinear optimizer, such as optimx, to estimate the posterior mode parameters. That requires a short R program to compute the product of the prior, which takes a closed form, with the density from the Tweedie package for the cells, whose means come from the linear model. We now try that for the Tweedie with a fixed across the cells using a Cauchy prior with σ = 0.1. It produces an estimate of p = 2.1. This is close to the gamma distribution value of p = 2 and therefore looks pretty good.

4.4. Frequency

Cell counts and AY exposures are in the available data, so mean frequency in a cell is modeled with the row-column model, and the number of claims is modeled with its mean equal to the cell frequency mean times the row exposure. The Poisson distribution and two forms of the negative binomial (NB) are fitted. NB1 is the one with variance proportional to the mean, and NB2 has variance as a quadratic function of the mean.

The fit measures are shown in Table 9. NB2 is clearly the best fit. Its row and column factors for six chains are graphed in Figure 6. Payment frequency declines slightly by row and sharply by column.

NB2 takes two parameters, µ, φ, with mean µ varying by cell and with variance = µ + µ²/φ for constant φ. As usual, µ comes from the exponentiation of the linear model but then is multiplied by exposures by cell. The log of φ is given a uniform prior.

The PiG probability mass function is technically of closed form, but it uses modified Bessel functions that cannot be computed for large arguments in double-precision arithmetic by the usual methods. However, the dPIG function in the R package gamlss.dist is able to calculate it. We use this method to maximize the posterior mode as was done above for the Tweedie severity. The PiG’s NLL is a little worse than that of NB2, and its LOOIC is probably similar, assuming the shrinkage is comparable. It is a more skewed distribution, so the NB2 appears to have enough skewness for these data.

Figure 6.Frequency row and column factors

5. Extensions of the row-column model

We now discuss a few extensions of the basic row-column model for this methodology. The aggregate triangle with the gamma distribution is used with fixed b, so variance is proportional to mean, as it is a good-fitting model and its estimation is fast—one or two seconds typically.

5.1. Additive component

Müller (2016) suggested expanding the multiplicative model with an additive component. He argued that some part of loss development is from late-reported claims, and these could be more related to exposure than to losses that have already emerged. Any AY exposure variable, such as premium or policy count, would be the starting point. This would be multiplied by coefficients by column and then added to the row-column mean for the cell. Even a constant exposure for all the rows could be used if exposure is not available or has already been included, as in a loss ratio triangle. Also, the coefficients could be on a curve fitted across the columns, just as the other parameters are. The resulting model for the cell mean, µ_w,u, is

\[\mu_{w,u} = A_w B_u C + D_u E_w,\]

where E_w is the exposure for AY w (or just a constant) and D_u represents column parameters.

The idea that this comes from late-reported claims suggests that the coefficients would all be positive, but another possible interpretation is that this is an additive term to adjust for bias from a purely multiplicative model. Then it would not have to be positive.

Next, we fit a positive factor by column and apply it to AY exposures, with the result added to the row-column means. This can be done in logs with another design matrix, x2, for the slope changes for the column parameters. This design matrix is the same as the column parameter design matrix, except that it includes a dummy variable for the first column as well. There is also a vector called expo that has the exposures by row, scaled down by 100,000 so the coefficients don’t have to be too minuscule. Key model steps are these:

• logbeta is uniform(‑20,20)

• beta = exp(logbeta)

• v is double exponential(0,s)

• w is double exponential(0,s)—this represents the additive column parameters

• alpha = exp(x1 * v + c) * beta + expo * exp(x2 * w) * beta (one could use the dot product for expo)

• y is gamma(alpha,beta), where in Stan, beta = 1/b

The resulting additive parameter ranges are shown in Figure 7. Most of these are centered near zero, with wide ranges. Keeping just the first three gives a good fit to the triangle, with LOOIC and NLL of 99.9 and 90.1, respectively, compared with 103.6 and 93.8 for the row-column gamma model. There are nominally three extra parameters here, but the LOO parameter penalty is about the same, at 9.9, as the 9.8 of the base model. The penalty comes from the out-of-sample fit, which is apparently better with the exposures included. Perhaps the exposures allow more shrinkage of the other parameters. The exposure factor is 0.653 for the first column and 0.606 for the second. After that, it falls by a multiple of 0.545 for each subsequent column. This is believable as an effect of claims incurred but not reported, as it is strongest early on and then practically disappears by the end.

Figure 7.Columns 1–10 parameter ranges for exposure log slope change variables

5.2. Calendar-year effects

Inflation can operate on payment years more than on AYs per se, as jury awards and building costs are typically based on price levels at the time of payment. This phenomenon can be modeled by adding calendar-year factors to the model or by using them instead of AY factors. With just diagonal and column factors, this approach has been called the “separation model” since Taylor (1977).

Another type of calendar-year effect comes from changes in loss processing, which could speed up or slow down payments in just a few diagonals. Only one or two diagonal parameters are able to model this. Such effects do not need to be projected, but adjusting for them can reduce estimation errors on the other parameters. Venter (2007) applied that principle to the triangle of Taylor and Ashe (1983), for example.

Either way, the mean for the multiplicative model with calendar-year effects included is

\[\mu_{w,u} = A_w B_u G_{w+u-1} C\]

The cell in row w and column u will be on diagonal w + u – 1, assuming the columns start at 1, and rows and diagonals start with the same number. G_w+u–1 is thus the trend factor, and in this framework it is the exponentiation of a cumulative sum of the modeled second differences that have shrinkage priors, just as the As and Bs are.

Including diagonal parameters can make row and column factors ambiguous, so some constraints are needed if all row, column, and diagonal factors are to be used. One approach is to adjust for row levels by such means as dividing by premiums or exposures. In that case, it is fair to assume there is no overall trend in the AY direction and therefore all the trend is on the diagonals. We can still have row factors, but in the estimation we make them the residuals to a trend that runs through them, so that a trend line fitted to them would simply be the x-axis. This idea is discussed in more detail by Venter and Şahın (2018). But if parameter reduction eliminates a fair number of parameters, this step might not be necessary.

A good starting point for the exploratory analysis is to fit both the row-column and the diagonal- column models with log regressions in second-difference form. This can give an indication as to whether the row or the diagonal factors are more explanatory. Usually before this procedure, the triangle should be divided by an appropriate AY exposure measure, such as premiums, policy counts, or similar. In a row-column model, the row parameters can pick up such known row effects, but even in that model, adjusting for them first can help with parameter reduction. We apply this method to the sample triangle using the exposures above (divided by 100,000 to keep the loss numbers in the same range).

This triangle with 9 rows actually has 11 diagonals, as 2 short rows usually found at the bottom of the triangle are not provided. The two initial regressions, with all rows and columns or all columns and diagonals, have very similar R squared values: 95.75% for rows and 95.76% for diagonals. But since there are more diagonals, the respective adjusted R squared values reverse, at 94.1% and 93.8%. But none of the row or diagonal t-statistics are greater than 1.8 in absolute value. This again suggests a Cape Cod model. Just small differences among row effects end up as an aspect of the resulting MCMC estimation.

Again LASSO is a good starting point for parameter reduction. The negatively correlated variables make it difficult to know which individually insignificant variables to leave out. LASSO selects groups of variables for each λ. Running it for each of the two regressions gives possible variable sets for use in MCMC. Since all of the row and diagonal parameters are individually insignificant, the lambda.min variables are taken; with the choices set out above, this λ gives the largest set of variables, some of which can be eliminated later. All of the columns except 6, 8, and 9 are included, as are rows 2, 3, and 6, and diagonals 5, 8, and 11.

The best row model is with rows 2 and 3 and columns 2, 3, 4, 5, 7, and 9. It gives a LOOIC of 103.3 with an NLL of 92.6 and a penalty of 10.7. These are not strictly comparable to the results obtained without dividing the triangle by the exposures. The best diagonal model is not as good, with a LOOIC of 111.1, an NLL of 101, and a penalty of 10.1. This includes only diagonal 5, although including 5 and 8 works about as well. Thus the rows provide a better account of this triangle than do the diagonals. In fact, when the calendar-year trend is fairly constant, there is usually no need for diagonal parameters, since the trend is projected on the row and column factors.

Since there are only a few row and diagonal parameters, they can all be included in a single model. Doing so and then eliminating parameters near zero leaves just row 2; columns 2, 3, 4, 5, and 7; and diagonals 5 and 8. The LOOIC and NLL are 99.0 and 89.7, respectively, with a penalty of 9.3. This is easily the best-fitting model by these measures. Similarly to the exposure adjustment, a lower penalty results, even with the same number of nominal parameters.

5.3. Calendar-year effects with exposure adjustment

Finally, putting it all together, the exposure adjustment is included in the row-column-diagonal model. Since the whole triangle has already been divided by the exposures, just a constant is used instead of the actual exposures by row. This simplifies the coding. To keep factors in the same scale, the constant used is 10. The code is in Appendix 2.2.

In this model, column 7 is no longer significant. Table 10 shows the estimated parameters, and the resulting factors for rows, columns, diagonals, and exposures are in Figure 8. The exposure factors by column are denoted by d. The resulting LOOIC and NLL are 97.4 and 87.1, respectively, with a penalty of 10.3. The exposure parameters do increase the penalty a bit in this case. There are nominally 12 parameters in this model, but since they have been shrunk, fewer degrees of freedom are used—probably about 7. This is thus a fairly parsimonious model to produce the 40 row, column, diagonal, and exposure factors plus the constant and β.

Figure 8.Factors

5.4. Parameter distributions

It is easy in Stan to extract the sample distributions of the parameters. Code for this procedure is in Appendix 2.3. It is used here to make a correlation matrix of the parameters, shown in Table 11.

The diagonal parameters c5 and c8 have a lot of correlations with row and column parameters, as does the constant. The exposure parameters d1, d2, and d3 are negatively correlated with each other, as they represent adjacent slope changes and thus somewhat offset each other. The first row and column parameters, a2 and b2, have a degree of correlation as well, and they are both negatively correlated with the constant, which offsets them to some degree—especially a2, as it is the only row parameter.

6. Conclusion

Reducing overparameterization is known to improve the predictive accuracy of models, and parameter shrinkage is a proven way to reduce the error variances by reducing the actual and effective number of parameters. In loss reserving, eliminating factors is not usually possible, but making factors from the cumulative sum of slope changes facilitates parameter reduction. Building a design matrix of slope change variables is the starting point, and then LASSO and Bayesian parameter shrinkage can be applied to do the estimation. There are R packages for these operations that require minimal programming.

In the end, LASSO is more or less a feeder to the MCMC estimation, as MCMC provides better tools for determining the degree of shrinkage and for measuring predictive accuracy as well as providing parameter uncertainty distributions. MCMC also can handle most probability distributions. Still, the negative correlation of the slope change variables makes it harder to tell which combination of variables to eliminate. LASSO is a good starting point for this purpose, especially in big data sets.

Extensions of the row-column factor model can improve performance. Here, using diagonal trends and including an additive exposure-based component both prove helpful. These are not unusual findings—including an exposure component almost always seems to help, and correcting for diagonal events often does.

The gamma distribution with the scale parameter held constant across cells makes the variance proportional to the mean, which is useful for reserve modeling. The variance-mean relationship can be further controlled by adding a parameter for it, as in the normal k and generalized inverse Gaussian distributions. Modeling skewness can improve the range predictions. Special cases of the Tweedie distribution are useful for that, and they also allow for modeling of the severity distribution with only counts and amounts in total, not individual claims. The Weibull k distribution provides a different skewness effect, which can sometimes be appropriate. Mixing Poissons by the Tweedie gives two versions of popular frequency distributions.

6.1. Ideas for further research

After the bulk of the work on this paper was completed, a new R MCMC package became available. BayesianTools does MCMC estimation with a version of the Metropolis sampler for any probability distribution whose likelihood can be computed in R. This would include the Tweedie and PiG distributions along with the Sichel—a more generalized, heavy-tailed count distribution. It is not mature software like Stan and seems to crash easily by getting parameter values that generate infinities, but it is promising. Preliminary tests confirm the random effects–posterior mode results for the Tweedie and PiG discussed in Sections 4.3 and 4.4 by getting the posterior mean fits. The main difficulty is the package’s delicacy in needing good starting points.

The heavy-tailed count distributions can be useful to actuaries now and then, but the reparameterized Tweedie would appear to have a lot of potential applications, for both severity and aggregate samples. Most triangles have aggregate losses. This Tweedie variance and mean use just the a and b parameters, and the skewness needs just a and p. This makes it easy to get a desired moment combination. It is more convenient this way than using most of the transformed beta-gamma family, for instance.

For 1 < p < 2, the Tweedie has a positive probability at 0 and so can accommodate data with some 0 values, which occur often in triangles. The standard parameterization also accommodates 0 values of p, with slightly different moments, so the two could be compared to fine-tune the fit. Both parameterizations will work with the R Tweedie package and so could have parameter shrinkage applied. Quasi-likelihood is usually used for the standard version, but it is not clear how to apply shrinkage there. Probably it could be done by adapting the random effects–posterior mode approach, and there might be a way to get MCMC to treat the quasi-likelihood as a likelihood. But there seems little reason to do that if the density is already calculable in R.

Appendices

Appendix 1. Prior and Conditional Probability Distributions

A1.1. Aggregate loss distributions

A1.1.1. Tweedie

The Tweedie distribution is usually parameterized so that EX = µ and VarX = \(\phi \mu^p\). However, its derivation starts out as a member of a class called the “exponential dispersion family,” with parameters p, λ, and θ having EX = λθ and VarX = λθ^p. Then taking µ = λθ and φ = λ^1−p gives the usual form. This form has computational advantages relating to quasi-likelihood estimation, but as computation gets less expensive, this issue declines in importance. Good references for these distributions include Jørgensen (1987, 1997) and Renshaw (1994). The Wikipedia article on the Tweedie distribution gives a good summary as well.

Getting the variance = \(\phi \mu^p\) requires making φ a function of p. Using parameters s, k with \(s = \theta^{p - k} \lambda^{1 - k},\) the variance becomes

\[s \mu^k = \theta^{p - k} \lambda^{1 - k} \left( \lambda \theta \right)^k = \lambda \theta^p\]

for any k, which is an additional parameter.

For a single cell, it is meaningless to say the variance is proportional to a given power of the mean, because you can make two fixed numbers proportional with any power you want. It is when you make some parameters constant across all the cells that the variance can be proportional to a power of the mean for the whole data set. So if you make φ and p constant across the cells, you get the variance proportional to \(\mu^p\). But if you make s, k, and p constant across the cells, the variance is then proportional to µ^k across the data set.

The Tweedie family in the original parameterization with fixed p, θ is closed under addition of independent variates, with ΣX_j having parameters λ₀ = Σλ_j, θ, p. In the common parameterization, λ = φ^1/(1–p), the φ parameter for ΣX_j is

\[\phi_{0} = \left\lbrack \sum_{}^{}\phi_{j}^{\frac{1}{1 - p}} \right\rbrack^{1 - p}\]

This supposes that θ = µ_j/λ_j = \(\mu_{j}\phi_{j}^{1/(p - 1)}\) is constant among the summands. Then µ₀ = θλ₀.

The family with fixed p, λ is closed under multiplication by a constant, c. In the φ, µ, p form, suppose that the resulting parameters are φ₀, µ₀, p. Since E(cX) = cEX and Var(cX) = c²VarX, we must have µ₀ = cµ and

\[\phi_0 \left( c \mu \right)^p = c^2 \phi \mu^p.\]

This leads to φ₀ = c^2−pφ.

Another parameterization, which makes the sum and scale results much more convenient, has parameters a, b, p with a = θ^2−pλ and b = θ^p−1. Then ab = λθ = EX, and ab² = λθ^p = VarX. Looking at ΣX_j with fixed θ, p: since λ_j = θ^p−2aj, we have

\[a_{0} = \theta^{2 - p}\lambda_{0} = \theta^{2 - p}\sum_{}^{}{\lambda_{j} = \theta^{2 - p}\sum_{}^{}{\theta^{p - 2}a_{j} = \sum_{}^{}{a_{j}.}}}\]

For cX, we have EcX = cEX = cab = a₀b₀ and Var(cX) = c²ab² = \(a_{0}b_{0}^{2}\). Then dividing variance by mean and dividing mean squared by variance produces b₀ = cb and a₀ = a, respectively. Thus b is a scale parameter, and the a shape parameters add across independent distributions. This procedure can be used, for instance, in simulating the sum of individual claims from a Tweedie severity.

Although p does not appear in the mean and variance formulas, it is still part of the distribution. In fact, Skw(X) = \(\frac{p}{\sqrt{a}}\). More generally for the Tweedie, Skw(X) = pCV(X), where CV is the coefficient of variation, that is, the standard deviation divided by the mean. This follows from a more general formula of Renshaw (1994) for skewness in the linear exponential family. Thus in the µ, φ, p parameterization, Skw(X) = \(p\sqrt{\phi}\mu^{\frac{p}{2 - 1}}\). In the µ, s, k, p parameterization, Skw(X) = \(p\sqrt{s}\mu^{\frac{k}{2 - 1}}\). The p parameter may or may not appear in the variance of the Tweedie, but it is key in the skewness. That is the fundamental significance of the choice of p.

In the a, b, p parameterization, fixing b across the cells makes the variance proportional to the mean for any choice of p. This is possibly useful for modeling aggregate losses. On the other hand, fixing a across the cells makes the variance proportional to the mean squared, which could be useful for severity. In this parameterization, the mean and variance are the same as those usually given for the gamma distribution. Thus the Tweedie can be looked on as a generalization of the gamma wherein there is another parameter, p, for the skewness.

In general, E(X − EX)³ = EX³ − 3EX²EX + 2(EX)³ and Skw(X) = E(X − EX)³Var(X)^‑1.5. In terms of a, b, p, some moments are these:

• EX² = ab² + a²b²

• EX³ = b³(pa + 3a² + a³)

• E(X − EX)³ = pab³

These combine to give Skw(X) = \(\frac{p}{\sqrt{a}}\).

The Tweedie with 1 < p < 2 in particular has been used for aggregate losses. It can be derived as a Poisson frequency and a gamma severity with frequency and severity both smaller in smaller cells. See Meyers (2009) or Venter (2007). In loss triangles, however, the smaller cells often have larger severity. The gamma/Poisson interpretation is not necessary to use these values of p, but there still will be a positive probability at 0.

The gamma distribution is the Tweedie with p = 2, and p = 3 gives the inverse Gaussian. With p = 1, the probability is positive only at integer multiples of b. This is sometimes called the “overdispersed Poisson,” but it could be underdispersed as well. The Poisson occurs when b = p = 1. The only other closed-form density is p = 0, the normal distribution. For the inverse Gaussian density in the a, b, p = 3 parameterization, the density is

\[f \left( x \middle| a,\ b \right) = \sqrt{\frac{a^{2}b}{2\pi x^{3}}}\exp\left( \frac{- (x - ab)^{2}}{2bx} \right).\]

The R package Tweedie has distribution and density functions and inverses for simulation with p ≥ 1. It uses the µ, φ, p parameterization, so to use it for the a, b, p parameterization, set µ = ab and φ = a^1−pb^2−p. To use the µ, s, k, p parameterization, set φ = sµ^k−p.

There is no Tweedie with 0 < p < 1. For p < 0, the Tweedie is very heavy tailed but is shaped like a negatively skewed mean-zero distribution on the real line. It is a generalization of the standard normal called an “extreme stable distribution.” The density contains an infinite sum and is a function of p and λ in the original parameterization (Jørgensen 1997). For the standard normal, (X₁ + … + X_n)/\(\sqrt{n}\) is also standard normal. For the Tweedie with p ≤ 0 and X_j independent and identically distributed in λ, p, (X₁ + … + X_n)n^{(p−1)/(2−p)} is also Tweedie in λ, p. This is the basic requirement for a distribution to be stable. The standard normal is the case p = 0.

A1.1.2. Normal k

The constant variance of the normal does not work for triangle fits because the variance decreases for the later cells. One way to address this heteroskedasticity is to set \(\sigma_{w,u}^{2} = s\mu_{w,u}^{k}\) for parameters s, k. This method adds an additional parameter. It is not meaningful when fitting a normal to a single distribution, because for any two values of k, you can find two values of s that will give the same σ². It is only when you need distributions for each cell that this procedure becomes useful. The main drawback of this distribution is that it has zero skewness.

A1.1.3. Gaussian–inverse Gaussian, or GiG

The inverse Gaussian distribution is the Tweedie with p = 3. The name arises for some abstract reason not usually relevant. It has skewness = 3CV, which is more skewed than the gamma but less than the lognormal. Most reserve cell distributions have less skewness than this, so a weighted average of the Gaussian and inverse Gaussian distributions with the same mean and variance can encompass a good number of the triangles actuaries have to deal with. The GiG here is built around \(\sigma_{w,u}^{2} = s\mu_{w,u}^{k}\), so the parameters will be s, k, the row and column parameters defining the cell means, and a parameter v in (0,1) for percentage Gaussian.

The inverse Gaussian density is closed in form but a bit complicated, so it is often easier to use a packaged function. Most published density functions and programmed software use the µ, φ parameterization, often in 1/φ, so set 1/φ = a²b to match mean and variance.

A.1.1.4. Weibull k

The Weibull distribution with parameters λ, h has f(x) = \(\frac{{hx}^{h - 1}}{\lambda^{h}}e^{- (x/\lambda)^{h}}\) and F(x) = \(1 - e^{- (x/\lambda)^{h}}\). The moments are gamma functions and are more compact with the notation n! = Γ(1 + n), which agrees on the integers. Then EX = \(\lambda\frac{1}{h}!\) and VarX = \(\lambda^{2}\left\lbrack \frac{2}{h}! - \left( \frac{1}{h}! \right)^{2} \right\rbrack\). These give CV² = \(\frac{\frac{2}{h}!}{\left( \frac{1}{h}! \right)^{2}}\) – 1. The skewness is \(\left\lbrack \frac{\frac{3}{h}!}{\left( \frac{1}{h}! \right)^{3} - 1} \right\rbrack\)/CV³ − 3/CV. The skewness is negative for h > 3.60235 or so and gets large for small h. This gives a range of distribution shapes. For the heteroskedasticity in a reserve triangle, it again might be helpful to be able to set VarX = s(EX)^k. This would require

\[1 + CV^{2} = \frac{\frac{2}{h}!}{\left( \frac{1}{h}! \right)^{2}} = 1 + s(EX)^{k - 2} \]

Unfortunately, this would have to be solved numerically. There are various root finding programs that can solve for h inside of an estimation routine. This is easier in logs due to limitations of double-precision numbers. Calling the right side v, the equation to solve is

\[g(h) = \log\left( \frac{2}{h}! \right) - 2\log\left( \frac{1}{h}! \right) - \log(v) = 0\]

This can be done, for example, by iterating with Newton’s method starting at some value h₀ and setting h_j+1 = h_j – g(h_j) / g’(h_j). For this purpose, g’(h) is easy enough with the digamma function ψ(x) = ∂logΓ(z)/∂z, which is widely available in software packages. Using this function,

\[g^{'}(h) = \frac{2\left\lbrack \psi\left( 1 + \frac{1}{h} \right) - \psi\left( 1 + \frac{2}{h} \right) \right\rbrack}{h^{2}}.\]

Stan has a function called algebraic_solver that is a root finder for nonlinear systems of equations. The root of g(h) can also be found by defining g(h) as a function, using a strict protocol, and then calling algebraic_solver. It uses a reliable and efficient derivative-free search routine called Powell’s hybrid algorithm to find the root. Both using this function and writing a custom function to do the Newton’s method calculation work fine, but both are very slow.

A1.2. Severity distributions

Severity in loss triangles does not usually have the same heteroskedasticity problems that aggregate loss has, so any severity distribution can be tried. Typically the variance is proportional to the mean squared for severity. Thus the a, b, p form of the Tweedie with a fixed across cells is a good starting point. The tail is not usually as heavy for individual cells as it is for the whole severity distribution used for pricing. The additive form property of the a, b, p parameterization makes it easy to use when the data include only the number of payments, n_w,u, and total payments, x_w,u, for the cell. Then x_w,u is distributed as n_w,ua, b_w,u, p. For the normal k, x_w,u is normal with mean µ_w,un_w,u and variance \(n_{w,u}s\mu_{w,u}^{k}\).

A1.3 Frequency distributions

A1.3.1. Poisson

The Poisson is the Tweedie with p = b = 1, and a is usually called λ. Some moments are as follows:

• EN = Var(N) = λ

• Skw(N ) = \(\sqrt{\lambda}\)

• EN² = λ + λ²

• EN³ = λ + 3λ² + λ³

• E(N − EN)³ = λ

One problem is that the variances of the cells have to pick up the Poisson variability as well as any specification error in the mean, and the Poisson variance can be too limited for this purpose.

A1.3.2. The Tweedie mixture of Poissons, or “TweeP”

Adding some variability to the Poisson is often done by assuming the Poisson λ is itself uncertain, and assigning a distribution for that. The most common case is to use a gamma distribution for λ, which yields the negative binomial. But this is often misapplied. If there is a population of drivers, for example, each with a Poisson distribution for number of accidents in a year, with λ_j for driver j, then the number of accidents for the whole population is Poisson in Σλ_j. This is just a case of the additive property of the Tweedie. The negative binomial arises if a driver is chosen at random, with unknown λ_j that is gamma distributed.

Assume λ is distributed as Tweedie a, b, p. To get the moments, use the formula Eg(N ) = EE[g(N)|λ]. Then

• EN = EE[N|λ] = Eλ = ab

• EN² = EE[N²|λ] = E[λ + λ²] = ab + ab² + a²b²

• Var(N) = ab(1 + b)

• EN³ = EE[N³|λ] = E[λ³ + 3λ² + λ] = pab³ + 3a²b³ + a³b³ + 3ab² + 3a²b² + ab

• E(N − EN)³ = EN³ − 3EN²EN + 2(EN)³ = pab³ + 3ab² + ab

The last item requires a bit of algebra. After a little more,

\[{Skw}(N) = \frac{pb^{2} + 3b + 1}{(1 + b)\sqrt{{ab}(1 + b)}}\]

In the frequency world, some, such as Mathematica documentation, use the notation r = a, q = b/(1 + b). Then b = q/(1 – q), 1 + b = 1/(1 – q), and b(1 + b) = q/(1 – q)². It is even more common to use p instead of q, but here p is already used for the Tweedie skewness parameter. Substituting this notation produces the following:

\[{Skw}(N) = \frac{(p - 2)q^{2} + q + 1}{\sqrt{{rq}}}.\]

Hougaard, Lee, and Whitmore (1997) discussed the TweeP and provided a formula for computing the probabilities for any p > 1 except 2, which they reported works up to about n = 150 before running into problems with double-precision representations. This would be fine for distributions with small counts, such as claims per policy, but it would not handle aggregate claims from larger business units. Some special cases discussed below have closed-form distributions for any n.

Hougaard, Lee, and Whitmore (1997) started by introducing three transformed parameters to simplify the formulas, defined by α = (p − 2)/(p − 1), 1/δ = \(\sqrt{2\phi}\), and 1/θ = 2µ²φ. Then they defined the coefficients c_n,j(α) recursively by solving c_n,0(α) = Γ(n − α)/Γ(1 − α) and c_n+1,j+1(α) = (n − (j + 1)α)c_n,j+1(α) + c_n,j(α). Finally,

\[f(0) = exp\left\lbrack - \frac{\delta}{\alpha}\left( \lbrack\theta + 1\rbrack^{\alpha} - \theta^{\alpha} \right) \right\rbrack\]

\[f(n) = \frac{f(0)}{n!}\sum_{j = 1}^{n}c_{n,j}(\alpha)\delta^{j}(\theta + 1)^{\alpha j - n}.\]

A1.3.3. Negative binomial

The negative binomial is the TweeP with p = 2. It has a closed-form probability mass function. In the q, r form it is

\[f(n;r,q) = \frac{\Gamma(r + n)}{n!\Gamma(r)}q^{n}(1 - q)^{r}.\]

It has mean = ab = m = qr/(1 – q), variance = ab(1 + b) = qr/(1 – q)² = m/(1 – q) and skewness = (1 + q)/\(\sqrt{{qr}}\) = (1 + q)CV.

As with the Tweedie, two basic forms for cell distributions come about by fixing either a or b across the cells. If b, and therefore q, is fixed across the cells, then the variance is proportional to the mean. If a, and therefore r, is fixed, it is convenient to eliminate q by qr = m – qm, so q = m/(r + m). Then 1 – q = r/(r + m). The variance m/(1 – q) then becomes m(r + m)/r or m + m²/r. Thus the variance is a quadratic function of the mean.

The second is the form used in GLM and often works better as a distribution of residuals, perhaps because the part of the residual distribution that comes from estimation error for the mean is large enough in large cells to benefit from the mean squared term. The probability mass function then is as follows:

\[f(n;m,r) = \frac{\Gamma(r + n)m^{n}r^{r}}{n!\Gamma(r)(m + r)^{n + r}}.\]

A1.3.4. Poisson–inverse Gaussian, or PiG

The Poisson mixed by the inverse Gaussian is the TweeP with p = 3. It has the same mean and variance as the negative binomial. The skewness is (1 + q + q²)/ \(\sqrt{{qr}}\). It is thus a slightly more skewed alternative to the negative binomial. It also has the two forms of parameterization across a data set. As usual, they both give the same distribution for a single sample—that is, a sample not involving multiple cells, such as statewide accident frequency. The density has calculation issues, but the probability-generating function in the m, r parameterization is this:

\[P(z) = e^{r - r\sqrt{1 - \frac{2m}{r}(z - 1)}}\]

See Dean, Lawless, and Willmot (1989), who also gave a recursive algorithm for calculating f(n; m, r), which is a bit simpler than the algorithm of Hougaard, Lee, and Whitmore (1997), with p = 3, α = ‑1/2. There is an exact probability mass function involving modified Bessel functions. However, these can run into problems with double-precision representations if there is a large number of claims. Perhaps 40- to 50-digit precision could be needed to calculate them in some cases. R does have specialized functions for arbitrary-precision numbers, but not every Bessel function application uses them. The modified Bessel function of the first kind is defined as follows:

\[I_{\alpha}(x) = \sum_{j = 0}^{\infty}{\frac{1}{j!(\alpha + j)!}\left( \frac{x}{2} \right)^{2j + \alpha}}.\]

The modified Bessel function of the second kind, which is the same thing as the modified Bessel function of the third kind—an obsolete but stubborn term—is this:

\[K_{\alpha}(x) = \frac{\pi}{2}\frac{I_{- \alpha}(x) - I_{\alpha}(x)}{\sin\left( {απ} \right)}.\]

In light of this calculation (see Zha, Lord, and Zou 2016), the PiG probability mass function is

\[f(n;m,r) = \sqrt{\frac{2\alpha}{\pi}}\frac{m^{n}e^{r}K_{n - 1/2}(\alpha)}{(\alpha/r)^{n}n!},\]

where α = \(\sqrt{r^{2} + 2mr}\).

The dPIG function in the R package gamlss.dist seems to be able to calculate this with any m, so it probably uses arbitrary-precision numbers.

A1.3.5. Sichel distribution

The Sichel is a three-parameter distribution that comes from mixing the Poisson by a generalization of the inverse Gaussian. Its skewness is greater than that of the negative binomial and can be greater than that of the PiG as well. Rigby, Stasinopoulos, and Akantziliotou (2008) is a good source for this and other heavier-tailed count distributions. Venter (2011) applied the Sichel to mortality data relevant for workers compensation and found that it fit slightly better than the negative binomial.

The Sichel probability function is also closed in form using the Bessel functions. It is as follows:

\[f(n;m,r,v) = \frac{K_{n + v}(\alpha)\left( {mc} \right)^{n}}{K_{v}(r)n!(\alpha/r)^{n + v}},\]

where α = \(\sqrt{r^{2} + 2mrc}\) and c = K_ν(r)/K_ν+1(r).

It has the same mean and variance as the PiG, which is the special case ν = ‑1/2. The parameter ν can be any real number. The negative binomial is a limiting case. Higher moments are shown in the appendix of Rigby, Stasinopoulos, and Akantziliotou (2008), but the c there is 1/c here, and σ is 1/r. The density function is available in the R gamlss.dist package.

A1.3.6. Others

The zero-truncated frequency distributions, which eliminate the positive probability at zero, provide further choices, and there are other mixtures as well. The appendix of Klugman, Panjer, and Willmot (2008) is a good starting point for these.

A1.4. Distributions for use as shrinkage priors

Shrinkage priors are mean-zero priors that push parameters toward zero, which can be offset by the likelihood increase if the parameter is important to creating a better-fitting model. In both classical and Bayesian estimation, these offsetting priorities are balanced by finding parameters that give high values to the sum of the log-likelihood plus the log of the prior probabilities of those parameters. Shrinkage can be done toward any value, but only the mean-zero versions are used here.

A1.4.1. Normal distribution

If the parameter β is distributed as normal(0,σ), the log of the density is as follows:

\[\log\left\lbrack f\left( \beta|\sigma \right) \right\rbrack = - \frac{\log(2\pi)}{2} - \log(\sigma) - \frac{\beta^{2}}{2\sigma^{2}}.\]

Constants—meaning any terms whose parameters are not being estimated—can be ignored in the estimation. In fact, with a fixed value of σ, the estimation would look for higher values of
\(\left\lbrack \text{loglikelihood} - \frac{1}{2}\sum_{}^{}\frac{\beta_{j}^{2}}{\sigma^{2}} \right\rbrack\). This value is what is maximized in ridge regression, for selected values of γ = 2/σ².

A1.4.2. Laplace distribution

The Laplace density on the real line is

\[f\left( \beta|\sigma \right) = \frac{1}{2\sigma}\exp\left( - \frac{|\beta|}{\sigma} \right)\]

It has variance = 2σ² and kurtosis = 6.

Also, log[f (β|σ)] = ‑log(2) – log(σ) – β|σ. With a fixed value of σ, the estimation seeks high values of [log-likelihood – Σ|β_j|σ]. This is maximized in LASSO. Shrinkage with the Laplace prior is thus called Bayesian LASSO.

A1.4.3. Cauchy distribution

The Cauchy is just the Student’s-t distribution with 1 degree of freedom, so it is heavy-tailed. In fact, the mean does not even exist, as the integral defining it does not converge. The density and its log are as follows:

\[f\left( \beta|\sigma \right) = \frac{\sigma}{\pi}\frac{1}{\sigma^{2} + \beta^{2}}\]

\[\log\left\lbrack f\left( \beta|\sigma \right) \right\rbrack = \log(\sigma) - \log(\pi) - \log\left( \beta^{2} + \sigma^{2} \right).\]

Thus, ignoring constants and for a fixed value of σ, the optimization would be on [log-likelihood − Σlog(\(\beta_{j}^{2}\) + σ²)]. This is not a common classical method, but perhaps it should be.

The Cauchy prior is usually used with a smaller value of σ than the one used for the Laplace prior. It then puts more weight on small values of the parameters but still allows occasional larger values if they provide enough improvement in the log-likelihood. In this way, it usually produces more parsimonious models than the Laplace does, but often with only a slight reduction in log-likelihood. It is becoming more popular as a shrinkage prior, and the classical analogue could provide a similar improvement over LASSO.

A1.4.4. Scaled t prior

The scaled t distribution with ν degrees of freedom and its log are expressed in the following equations:

\[f\left( \beta|v,\sigma \right) = \frac{\Gamma\left( \frac{1}{2} + \frac{v}{2} \right)}{\sigma\sqrt{{πv}}\Gamma\left( \frac{v}{2} \right)}\left( 1 + \frac{\beta^{2}}{v\sigma^{2}} \right)^{- \frac{(v + 1)}{2}}\]

\[\begin{align} \log\left\lbrack f\left( \beta|v,\sigma \right) \right\rbrack = &\log\left\lbrack \frac{\Gamma\left( \frac{1}{2} + \frac{v}{2} \right)}{\Gamma \left( \frac{v}{2} \right)} \right\rbrack \\ &- \frac{1}{2}\biggl\lbrack \log\left( \sigma^{2} \right) + \log(v) + \log(\pi) \\ &+ (v + 1)\log\left( 1 + \frac{\beta^{2}}{v\sigma^{2}} \right) \biggr\rbrack. \end{align}\]

This distribution has variance = σ²ν/(ν – 2) for ν > 2 and kurtosis = 3 + ν/(ν – 4) for ν > 4. The Cauchy is the special case ν = 1, and the normal is the limiting case as ν → ∞. The case ν = 6 provides a reasonable approximation of the Laplace. For this ν, it and the Laplace have kurtosis of 6, and a Laplace σ of \(\frac{\sqrt{3}}{2}\) matches the variance of the t with σ = 1. As there are no odd moments and only five moments exist for ν = 6, the Laplace thus matches all existing moments of this t. Figure 9 graphs the densities.

Figure 9.Student’s t with 6 degrees of freedom versus Laplace densities

A1.4.5. Estimating σ

The fully Bayesian approach includes σ as a parameter to be estimated. If it has a uniform prior with density K over an appropriate interval, the log density in the Laplace case becomes this:

\[\log \left\lbrack f \left( \beta | \sigma \right) \right\rbrack = \log \left( K \right) - \log \left( 2 \right) - \log \left( \sigma \right) - | \beta | / \sigma\]

In the estimation, K drops out as a constant, but now the log(σ) has to be included, since σ is a parameter. The posterior mode with n parameters then maximizes [log-likelihood − n ∗ log(σ) − Σ|β_j|/σ]. This is one possibility for a classical LASSO estimate of σ, and so λ, but the uniform prior is just one possible choice, so other values of λ might be worth considering as well.

Initially I also tried putting a prior on the ν parameter of the scaled t distribution. That would provide a Bayesian estimate of how heavy a tail the prior should have. Initial model runs always ended up with ν somewhere between 0.8 and 1.2 for the data here, which is pretty close to the value of 1.0 that produces the Cauchy. However, estimates for the Laplace and Cauchy priors were very close for these small models, and LASSO was used as an intermediate step, so the Laplace prior was used in the estimates in the example.

Appendix 2. LASSO and Stan code

This appendix discusses how to design the package code for a project. The code I used here is given as an example, with package output connected, but it is not necessarily optimal for processing speed.

A.2.1. LASSO

The design matrix can feed right into LASSO software to get a start on parameter reduction. Illustrated here is the R package glmnet. The data y and the design matrix x are put in text files swissy.txt and swissx.txt first. This R code sets up and runs glmnet, given that it has already been installed. Standardization is turned off because the design matrix consists of dummy variables that count how many times a slope change is added in.

library(glmnet)
y = scan('swissy.txt')
x = read.table('swissx.txt', header = FALSE)
x = as.matrix(x)
N = length(y)
U = ncol(x)
fit1 = glmnet(x, y, standardize = FALSE)

The program estimates the parameters for up to 100 values of λ, depending on some internal settings. This function prints out (Figure 10) a graph of the parameter values as λ decreases, going from left to right, with the variables numbered 1–19. The top axis is the number of nonzero parameters, and the bottom is the L1 norm, Σ|β_j|, both of which increase as λ decreases.

plot(fit1, label=TRUE)

Figure 10.LASSO parameter growth with shrinkage reducing

The parameters can increase and decrease as λ changes since they are negatively correlated and thus, to some degree, can substitute for each other. Variable 9, in green at the bottom of Figure 10, is the parameter for the second column of the matrix, which is a significant drop, and it is the last one to leave the model as λ increases.

In the next block of R code, print(fit1) calculates and prints out three columns (not shown) for each λ: df, the number of nonzero parameters; %Dev, the R squared in this regression case; and then λ itself, in decreasing order of λ and increasing order of df. I call these dof, rsq, and lambda, and use them to calculate NLL + λΣ|β_j| – k * logλ, the quantity to be minimized if λ has a uniform prior, for each row. That is called min and is printed out with λ next.

answer = print(fit1)
lambda = answer[,3]
rsq = answer[,2]
dof = answer[,1]
sst = sum((y-mean(y))^2)
ssr = (1-rsq)*sst
sigsq = ssr/(N-dof)
NLL = N*log(sigsq)+ssr/2/sigsq
beta = fit1[[2]]
h=dim(answer)[1]
k=dim(x)[2]
L1 = c(1:h)
for(i in 1:h) L1[i] = sum(abs(beta[2:k,i])) #sum 
    of absolute values
min = NLL-dof*log(lambda)+lambda*L1
lambda

##   [1]    5.6980000    5.1920000    4.7310000    
  4.3110000    3.9280000    3.5790000    3.2610000
##   [8]    2.9710000    2.7070000    2.4670000    
  2.2480000    2.0480000    1.8660000    1.7000000
##  [15]    1.5490000    1.4120000    1.2860000    
  1.1720000    1.0680000    0.9729000    0.8865000
##  [22]    0.8077000    0.7360000    0.6706000    
  0.6110000    0.5567000    0.5073000    0.4622000
##  [29]    0.4212000    0.3837000    0.3496000    
  0.3186000    0.2903000    0.2645000    0.2410000
##  [36]    0.2196000    0.2001000    0.1823000    
  0.1661000    0.1514000    0.1379000    0.1257000
##  [43]    0.1145000    0.1043000    0.0950500    
  0.0866100    0.0789200    0.0719100    0.0655200
##  [50]    0.0597000    0.0543900    0.0495600    
  0.0451600    0.0411500    0.0374900    0.0341600
##  [57]    0.0311300    0.0283600    0.0258400    
  0.0235500    0.0214500    0.0195500    0.0178100
##  [64]    0.0162300    0.0147900    0.0134700    
  0.0122800    0.0111900    0.0101900    0.0092870
##  [71]    0.0084620    0.0077100    0.0070250    
  0.0064010    0.0058320    0.0053140    0.0048420
##  [78]    0.0044120    0.0040200    0.0036630    
  0.0033380    0.0030410    0.0027710    0.0025250
##  [85]    0.0023000    0.0020960    0.0019100    
  0.0017400    0.0015860    0.0014450    0.0013160
##  [92]    0.0011990    0.0010930    0.0009958    
  0.0009073    0.0008267    0.0007533    0.0006864
##  [99]    0.0006254    0.0005698
min

##   [1]  139.1546578  128.5099482  
    119.2727479  110.2654986  101.5464556
##   [6]   93.1729916   85.1716841  
     77.6168526   70.5099937   63.9140876
##  [11]   57.8211853   52.2532368  
     47.2379003   42.7012551   38.6963721
##  [16]   35.1559199   32.0395586  
     29.3520893   27.0057140   25.0460777
##  [21]   23.3507511   21.9024199  
     20.6774497   19.6905216   18.8214565
##  [26]   18.1204360   17.5483675  
     17.0637192   16.7143903   16.4110022
##  [31]   16.1538759   15.9435496  
     15.8276049   15.7128830   13.4839918
##  [36]    9.3518397    5.5858747  
      4.4655629    1.1074878   -2.3413246
##  [41]   -5.3021017   -5.2037415  
     -7.4618867   -9.2628828  -10.8067730
##  [46]   -9.2122464  -10.2469277  
    -14.1664652  -14.8062671  -15.2758039
##  [51]  -15.5672680  -12.3776308  
    -12.9763013  -13.3960749   -9.7473662
##  [56]  -10.0955550  -10.3551425  
    -10.4168976  -10.4854673   -1.7043340
##  [61]   -2.0199045    1.9086412  
      1.3079381   -3.7673173   -4.0607240
##  [66]   -4.1319612    0.8366980  
      0.8321761    0.9443275    1.1637626
##  [71]    1.5035898    1.8398307  
      2.4239278    2.8805064   15.0096378
##  [76]   15.2633089   15.7676314  
     16.3980934   23.1392631   30.4838019
##  [81]   37.3736464   44.8752963  
     45.7278083   53.3901917   54.6076325
##  [86]   55.6780471   56.8859274  
     58.2370121   59.5790237   60.9277201
##  [91]   62.2826403   63.6308198  
     64.9699640   66.4593997   67.8064965
##  [96]   69.2943538   70.6396882  
     80.2739272   81.8555927   83.4379203

The minimum of this function is at the 51st cell, where λ = 0.05439. Since the uniform prior is only one possible choice, other values of λ should be considered as well. Adding a few more variables is a sound choice, as they can be eliminated later in Bayesian LASSO if they are not needed. The 59th value is at the end of the area of low values of min, with λ = 0.02584. Cross-validation is done in a function called cv.glmnet, which produces its own target range for λ between lambda.min and lambda.1se.

cvfit = cv.glmnet(x, y, standardize = FALSE)
cvfit$lambda.1se

## [1] 0.1256568

cvfit$lambda.min	

## [1] 0.01019241

The variables and coefficients for selected values of λ are given by the coef function.

coef(cvfit, s=c(0.01118616, 0.02584, 0.05439, 
    0.11449))

## 18 x 4 sparse matrix of class "dgCMatrix"
##                       1             2 
                3            4
## (Intercept)  4.96801195  5.014613e+00 
     4.960018e+00  4.775570560
## V1           0.13797768  7.511297e-02 
     1.940272e-02  0.003674287
## V2          -0.03868051  .            
     .             .
## V3           .           .            
     .             .
## V4           .           .            
     .             .
## V5          -0.17133069 -1.153241e-01 
    -5.443126e-06  .
## V6           .           .            
     .             .
## V7           .           .            
     .             .
## V8           .           .            
     .             .
## V9          -1.30479742 -1.442692e+00 
    -1.321330e+00 -1.157271291
## V10         -0.48333616 -1.432428e-06 
     .             .
## V11          0.65565734  1.302843e-01 
     .             .
## V12          0.50612353  6.865177e-01 
     6.936972e-01  0.373278485
## V13          .           .            
     .             0.136026729
## V14          0.09814611  1.273081e-01 
     6.540153e-02  .
## V15          .           1.700821e-06 
     .             .
## V16          .           .            
     .             .
## V17          0.48927296  .            
     .             .

A.2.2. Stan

A2.2.1. Aggregate example

Below is the code used for estimating the gamma distribution with fixed b, so with variance proportional to mean, from the reduced design matrix. Most of the code is for setup purposes—declaring the variable types and dimensions, and so on. Now the y variable is in monetary units, but the model is still fitted in logs. The cell gamma mean is the exponentiation of the sum of the log parameters for that cell, which makes the parameters slightly different than they would be for estimating the mean of the log.

data {
int N; // number of obs
int U; // number of variables
vector[N] y;
matrix[N,U] x1;  //design matrix with U columns
}
parameters { // all except v will get uniform 
    prior, which is default real<lower=4, 
    upper=16> cn;  //constant term, starting 
    in known range vector[U] v;  // the parameters
real<lower=-5, upper = -0.2> logs; //log of s, 
    related to lambda, not too high real<lower
    =-20, upper = 20> logbeta;  //log of beta
}
transformed parameters { 
real beta;
real s;   // shrinkage parameter, like lambda 
vector[N] alpha;  //fitted means
beta = exp(logbeta); //for positive parameter, 
    uniform on log is like 1/X
s = exp(logs); // 1/X gives more weight to lower 
    values, which is good if X not big 
alpha = exp(x1*v+cn)*beta;
}
model { // gives priors for those not assumed 
    uniform. Choose this one for lasso. 
for (i in 1:U) v[i] ~ double_exponential(0, s); // 
    more weight to close to 0 
for (j in 1:N) y[j] ~ gamma(alpha[j], beta);
}
generated quantities { //outputs log likelihood 
    for testing purposes vector[N] log_lik;
for (j in 1:N) log_lik[j] = gamma_lpdf(y[j] | 
    alpha[j],beta);
}

Stan parameterizes the gamma with parameter beta = 1/b, and alpha_w,u is set, so the mean is alpha_w,u/beta. Stan also uses the parameter s = 1/λ for the Laplace = double exponential prior, and here s is taken as a parameter to be estimated. Unless otherwise stated, all parameters are taken to have uniform priors over their defined ranges. The transformed parameters are intermediate calculations, do not have priors, and are not estimated. The generated quantities section creates additional outputs, here the log-likelihood for each point for each parameter sample for the LOOIC calculation.

The range defined for the constant was informed by the LASSO result but is wider than it needs to be. Beta is defined by giving its log a wide uniform prior. That is similar to giving it a prior of 1/x. This is appropriate for a parameter that can be either a number or that number’s reciprocal. 1/beta would have the same prior—its log would be uniform on the real line (limited by ±10³¹⁰ or so by double-precision numbers). Also, the 1/x prior often gives the classical unbiased estimate for a positive parameter. This is similar for s, but it was given a smaller range. Too high a value can get into convergence problems. After some experimentation, a6 was replaced with a4, which gives a better fit by LOOIC and NLL.

A2.2.2. Including exposure

In the code below, w is the vector of coefficients for the exposure column parameters, and x_expo is the corresponding design matrix. The exposure by row is in a vector expo, but this is divided by 10,000 to put it on a more useful scale. The alpha by cell is built up from the row-column mean, the exposure component, and beta. Losses are assumed to be gamma distributed.

alpha = exp(x_expo*w); //expo design matrix for 
    log 2nd diff * parameters 
for (i in 1:N) alpha[i] = alpha[i]*expo[i]/10000; // 
    multiply by row exposure
alpha = (alpha + exp(x1*v+cn))*beta; // add in 
    row-col mean to give mean, alpha
}
model { // gives priors for those not assumed 
    uniform. This one for lasso. 
   for (i in 1:U) v[i] ~ double_exponential(0, s);
   for (i in 1:V) w[i] ~ double_exponential(0, s); 
for (j in 1:N) y[j] ~ gamma(alpha[j], beta);
}

Here the exposure adjustment is included in the row-column-diagonal model. Since the whole triangle has already been divided by the exposures, just a constant is used instead of the actual exposures by row. This simplifies the coding. To keep factors at the same scale, the constant used is 10.

alpha = (10*exp(x_expo*w) + exp(x1*v+cn))*beta;
for (j in 1:N) y[j] ~ gamma(alpha[j], beta);

A2.3 Extracting samples from Stan output

fit3p_ss = extract(fit3p, permuted = FALSE) #Need 
    FALSE to get array
fit3p_ss = fit3p_ss[,,1:14] #Only need first 14
dim(fit3p_ss) = c(4000,14) #Collapses dimensions
corrM = cor(fit3p_ss) #Correlation matrix
write.csv(corrM, file = "cormatAPCexp.csv")

The extract function gives every variable or transformed variable plus other things. Here it is a (1,000, 4, 139) array, so it goes by sample and then by chain. The parameters are in the first 14 elements, so only those are needed here. R keeps an array in a long vector with notation on how it is arranged. The dim function can collapse adjacent dimensions, giving just a table. Then the correlation matrix is computed by the cor function.

Appendix 3. Sensitivity of LOOIC penalized likelihood to \(\lambda\)

Usually it is not considered good practice to select regression variables by maximizing AIC and so on, as that would increase the chance of getting a spurious result. There is a similar risk involved in choosing λ to maximize LOOIC. Putting a prior on λ and then taking the posterior mean, not the mode, is the fully Bayesian approach. That was done in the examples. Nonetheless it is interesting to see how LOOIC responds to changes in λ. We look at that here for the gamma row-column fit to aggregate losses.

Instead of λ, we vary s = 1/λ, which is the scale parameter and is proportional to the standard deviation of the Laplace prior. Lower values of s are more parsimonious, as are higher values of λ. For a fixed random seed of 10,000, the model in the example had a posterior mean s of 0.54, with a 5%–95% range of (0.32,0.77). The LOOIC was 103.6, with a parameter penalty of 9.8. The standard deviation of the LOOIC was about 13 for this and all the tested fits, and the standard deviation of the penalty was usually about 3.3. The testing found that the LOOIC improved with higher s up to a value of s = 0.14, and then it was flat for higher values of s. See Table 12 for the results.

There were seven slope-change parameters in this model. Often, with more parameters, we see the LOOIC level off at some point although the parameter penalty keeps increasing for higher values of s. This result might not hold for the posterior mode or for classical LASSO. I prefer the lowest λ for any given LOOIC for the sake of general parsimony. No matter how high s is, parameters with values closer to zero still get the highest prior probability, so the sample sets might all have similar parameters in them, once s is high enough. I even more prefer to set a prior for s and let MCMC determine a posterior range for it. Here, that actually gives the lowest LOOIC, but only by about 1/40 of a standard deviation.

The prior used in the examples is proportional to 1/s on a range of about (0.007,0.82), which is (‑5,‑1/5) for log s. I like a 1/x prior for a positive parameter, particularly if the prior is wide, as that prevents it from being biased upward when the top of the range is far larger than the parameter should be. This prior is equivalent to a uniform prior on log x. It is not so different from a uniform prior when used on a small range, however. Large values of s can make convergence more difficult for some models, so I usually try to avoid them.