1. Introduction
1.1. The classical concept of credibility
The century-old concept of credibility presumes combining real data (also referred to in actuarial literature as “current observations”, “subject experience”, or “sample mean”) with a hypothetical source (“external information”, “collective experience”, “relevant experience”, or “prior mean”) through a compromise estimator
C=ZR+(1−Z)H,
where is the credibility factor (Longley-Cook 1962; Klugman 1992; Hickman and Heacox 1999; Bühlmann and Gisler 2005; Klugman, Panjer, and Willmot 2012; Herzog 2015). This approach is a standard method of valuation of insurance contracts in a typical situation in which the actual history of an insured is insufficient to assure any reasonable estimation accuracy. In order to estimate the pure premium, a company needs a reliable predictor of the total loss, the amount it will have to pay in order to cover claims due to the occurrence of insured events such as traffic accidents or hospitalizations.
The total loss depends on the frequency and severity of insured events that are estimated from the past experience of the insured. When this experience is too short to produce a sufficient number of claims, the company supplements it with a prior distribution that is often based on the collective history of a risk group and other plausible sources. Similar situations often arise in business and finance, when new contracts are valuated in the presence of insufficient data or in a rapidly changing environment.
Credibility theory determines the minimal conditions under which a prediction for a cohort is fully credible. Full credibility (i.e. a credibility factor is assigned in the case of a compromise estimator, that is computed from the actual data only. When full credibility is not possible, the compromise estimator is based on both the actual data and the (hypothetical) prior distribution information, and partial credibility is applied, with a credibility factor Credibility factor thus plays a vital role in credibility estimation. It determines the portions of the compromise estimator, attributed to the real and to the hypothetical data.
The limited fluctuation credibility approach is a standard way of determining allowed values of It requires that in order to deserve a credibility factor the real data must satisfy the following condition,
P{Z|R−E(R)|>cE(R)}≤α,
for a given probability and desired relative precision
Under the classical frequency-severity model, when the total loss consists of a Poisson number of individual losses condition (1.2) is satisfied by a sufficiently large frequency of insured events It follows from rather simple probability arguments that the frequency satisfying the inequality
λ≥λF=(zα/2c)2(1+γ2)
suffices for the full credibility, where is a coefficient of variation of losses is the mean loss, is the standard deviation of losses, and is the upper -quantile of the standard normal distribution. It is assumed here that is sufficiently large to allow normal approximation of (Herzog 2015, chapter 5; Klugman, Panjer, and Willmot 2012, chapter 17).
When the partial credibility condition (1.2) is satisfied with frequency
λ≥λP=Z2λF.
Either full or partial credibility can always be assigned under these conditions because the hypothetical estimate equal to the prior mean with probability 1, is assumed without any error or uncertainty. When the history of real data is short, (1.2) always holds with a zero or very small credibility factor. One can always compensate for the lack of information contained in real data by using “infinite information” contained in the prior distribution because it is assumed to be known completely, without any error or any uncertainty.
1.2. Two pointed limitations of the classical concept
Limitation 1: Assumption of error-free prior. The classical limited-fluctuation credibility approach accounts for uncertainty in the real data only, assuming no uncertainty in the hypothetical prior data – that is, considering the prior data as fully credible. Tindall and Mast (2003) and Atkinson (2019) pointed out that this assumption is misleading and unrealistic in practical settings.
In actuarial practice, it is unrealistic to expect to know prior parameters exactly, without any error or uncertainty. More typically, they are estimated from past experience, such as the frequency and severity of claims in a given risk group. As Tindall and Mast (2003) noted, in practice, the amount of confidence in the prior mean (called the “current expectations” in the Tindall and Mast paper) “drives the extent to which the actuary relies on credibility theory” (2003, 47). If the prior mean was obtained as “purely a guess”, then the actuary will rely more heavily on the current real data (i.e., what the authors call the “emerging experience”). “Another potential flaw is that the Prior Rate may be less than fully credible”, according to Atkinson (2019, 9). “Since the Limited Fluctuation method assumes that the Prior Rate has full credibility, it may receive more weight than it deserves.”
In this paper, we introduce uncertainty in the prior distribution parameters and express it in terms of a non-zero variance of the corresponding hyper-prior (i.e., the second-level prior), which is the prior distribution of the prior mean of the loss model. We then revisit the limited-fluctuation condition under this generalized model, deriving corrected conditions for full and partial credibility. Several approaches are proposed; each of them provides a compromise estimator with a credibility factor determined by the relative uncertainty of real and hypothetical data. The standard criteria (1.3) and (1.4) for full and partial credibility both appear as a special case of a fully credible prior, when the hyper-prior variance is 0.
A new third scenario then emerges, in addition to full and partial credibility. In cases in which the degree of uncertainty is too high in both the real and the hypothetical data, even a partial credibility sometimes may not be possible. For example, this situation takes place when a totally new type of events is insured, with insufficient data as well as little or no past experience.
Limitation 2: Agreement and homogeneity. Tindall and Mast (2003) also mentioned another limitation of the standard credibility practice. They emphasize a typical heterogeneity within the insured groups. Credibility depends on the degree of agreement between the actual data and the prior distribution. “The closer the data lean toward homogeneity and comparability with current expectations, the higher the credibility is likely to be” (Tindall and Mast 2003, 47). At the same time, the authors noted that “experience, however, rarely matches contemporary expectations” (47).
Actuarial Standards of Practice No. 25 requires that “in carrying out credibility procedures, the actuary should consider the homogeneity of both the subject experience and the relevant experience. Within each set of experience, there may be segments that are not representative of the experience set as a whole” (Actuarial Standards Board 2011, 4). Indeed, as long as variability exists within a risk group, it is possible for a given insured to have distribution parameters different from those of the relevant risk group. For example, a driver with the same driving record, type of a vehicle, and family structure as the rest of the risk group may still be on the safer side or on the riskier side of the group. As a result, for the given insured is no longer equal to the hyper-prior mean That is, the real data and the hypothetical data may have different means.
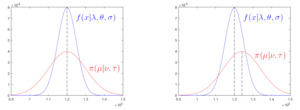
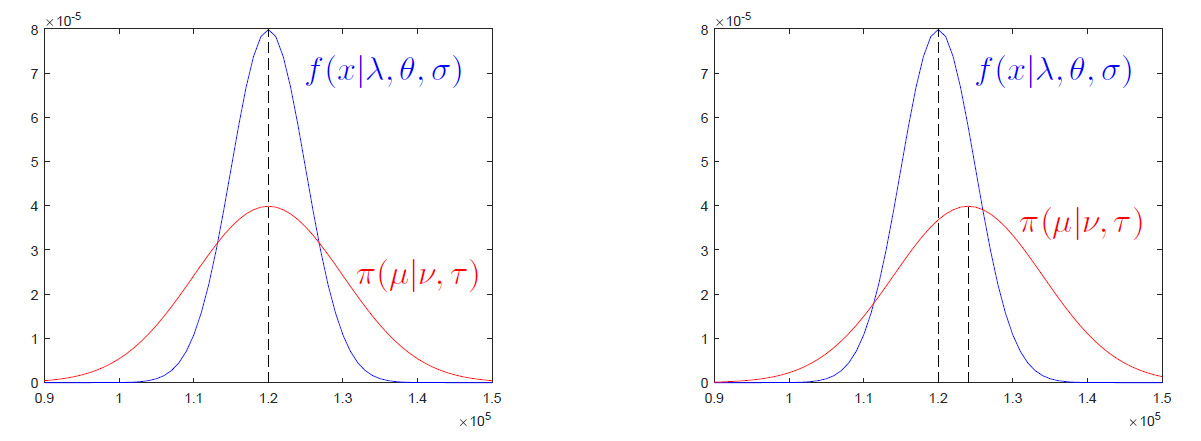
We address this issue in Section 2 by accounting for heterogeneity – different distributions of real data within each group. In Section 2, we assume “typical” or “random” members of risk groups, for whom the prior mean agrees with the actual expectation. An example of a perfect agreement is shown in Figure 1, left-hand side. Then, in Section 3, we consider insureds with some deviation from the prior mean, as depicted in Figure 1, right-hand side. Since the prior mean is no longer assumed to be fully known with no error, such deviations occur inevitably. The impact of a disagreement between the real data and the prior mean is apparent. In the extreme case, when discordance between the current experience and expectations is too high, there may be no room even for a partial credibility. The last two sections of the paper contain an illustration of the proposed methods with specific scenarios, followed by a summary and conclusions.
2. Limited Fluctuation under Uncertainty in Hypothetical Data
Actuarial Standards of Practice No. 25 state, “The actuary should use an appropriate credibility procedure when determining if the subject experience has full credibility or when blending the subject experience with the relevant experience. The procedure selected or developed may be different for different practice areas and applications” (Actuarial Standards Board 2011, 3). We propose three limited-fluctuation methods that account for uncertainty in hypothetical data, and then we discuss the situations appropriate for each method.
To quantify this uncertainty, we assume that the prior mean, of the total loss, is no longer deterministic. Rather, it has an approximately normal distribution, with mean and variance Sample mean and sample variance of losses within the risk group are often used to generate an estimate of in which case is inversely proportional to the group size. To summarize, we have
Total loss:X=∑Ni=1Yi≈Normal,Frequency of claims:N∼Poisson(λ),Severity parameters:θ=E(Yi),σ2=Var(Yi),γ=σ/θ,Prior distribution:μ∼Normal(ν,τ2).
Under this general setting, the distribution of the total loss, has mean and variance expressed as:
E(X)=EE{∑N1Yi|N}=E(Nθ)=λθ,Var(X)=EVar{∑N1Yi|N}+VarE{∑N1Yi|N}=E(Nσ2)+Var(Nθ)=λσ2+λθ2.
Parameters and are generally unknown. Thus, the chosen prior distribution and the component of the compromise estimator (1.1) may agree or disagree with the actual distribution of
By agreement, we understand that the chosen prior distribution of has a mean, that actually equals the mean of Notice that this does not always have to be the case. On one hand, actuaries have the real data. On the other hand, they choose a prior distribution, or they obtain it from some data source such as based on the past experience of a relevant risk group.
In case of an agreement, This can be understood as an unbiased choice of the prior distribution. For example, suppose the prior distribution is generated by the relevant risk group, and the given insured is a typical member of the associated risk group, in which case the expected total loss is This is justified when an insured is selected from a group at random. Then the expected total loss agrees with the expectation across the risk group, as on Figure 1, left.
Consider a general situation in which years (or insured periods) of data are available, The real component of the compromise estimator will then consist of the sample mean
We now have two estimators of the expected total loss that complement each other - the sample mean and the prior mean Each of them can be used to estimate but it is most efficient to combine them, in accordance with the credibility and Bayesian principles. Combining them results in the compromise estimator
In this respect, we introduce three limited-fluctuation credibility conditions that differ in their interpretation of precision while estimating the expected total loss. These conditions restrict deviations of estimates from the expected total loss in three different ways, forcing the sample mean and the prior mean to be close to separately, as in (2.3), or jointly, as in (2.5), or having the compromise estimator, close to as in (2.6).
In this section, we assume that a given insured is a typical member of the associated risk group, in which case the expected total loss is This assumption is justified, for example, when an insured is selected from a group at random. Then the expected total loss agrees with the expectation across the risk group.
2.1. Method 1: Fluctuations of real and hypothetical data
The standard form of the compromise estimator contains two credibility factors. Factor shows the credibility of the real data, whereas corresponds to the credibility of the prior. Uncertainty in both and requires symmetric conditions on coefficients and
Thus, the classical condition (1.2) is now replaced by a combination of two conditions
{pR=P{Z|ˉX−E(X)|>cE(X)}≤αRpH=P{(1−Z)|μ−E(X)|>kE(X)}≤αH
for chosen probabilities and and relative precision factors and The first inequality in (2.3) is the classical limited-fluctuation condition on the permissible deviation of real data, from their expected value. The second inequality represents a similar condition on the hypothetical data.
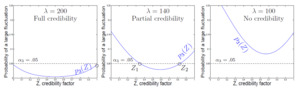
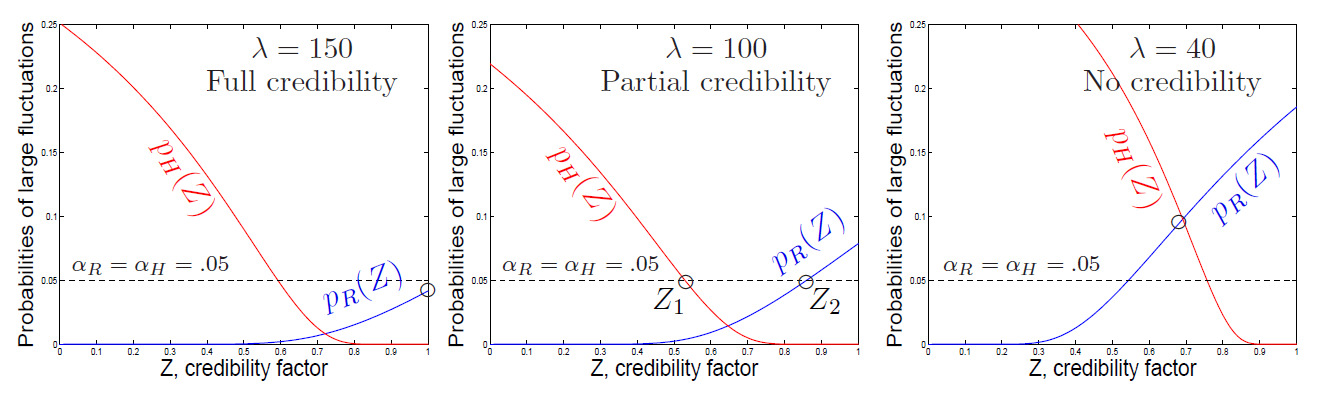
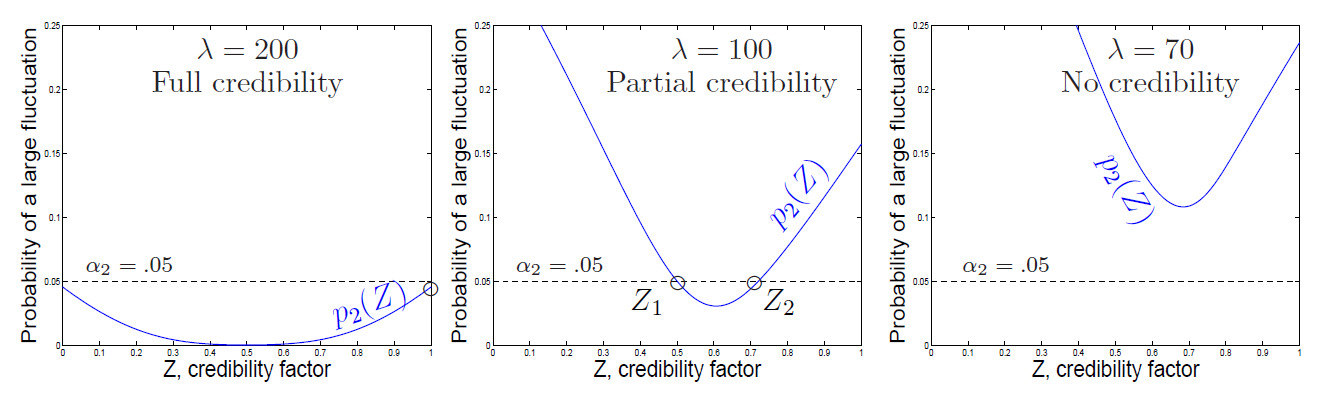
Let us look at the probabilities in (2.3) that are depicted in Figure 2, with and different values of Clearly, increases with whereas decreases. Regions where both curves appear below the threshold contain the allowed credibility factors For different frequency parameters we notice three distinct cases.
-
Full credibility. When the expected frequency, is sufficiently large, the solution set of (2.3) includes The data are fully credible, and the pure premium can be estimated solely from the real experience (Figure 2, left).
-
Partial credibility. With a lower solutions of system (2.3) form an interval, with Any credibility factor from this interval can be chosen. In practice, underwriters will often choose The interval does not contain and therefore, the observed data are not fully credible (Figure 2, middle). Partial credibility applies in this case.
-
No credibility. Reducing even further, we enter the situation in which there are no solutions to (2.3) in This happens when the variability of both the real and the prior data is so high that no -factor can satisfy both limited-fluctuation conditions simultaneously.
In Figure 2 (right), the intersection point of the two curves appears above and thus, conditions (2.3) are not satisfied together for any
This case will never appear if the prior mean is (unrealistically) assumed to be exactly known. Such a 100% reliable estimate can always satisfy the limited-fluctuation condition. On the other hand, if both and are unreliable, then no compromise combination of them can “magically” become reliable!
2.1.1. Analytic solution
To solve inequalities (2.3) analytically, we use the mean and variance of losses derived in (2.2) based on the assumptions (2.1). Then, inequalities in (2.3) are equivalent to
cE(X)ZStd(ˉX)≥zαR/2 and kE(X)(1−Z)Std(μ)≥zαH/2.
Solving them for and using (2.2) and assumed agreement we obtain a solution in the form of two inequalities,
{Z≤cE(X)zαR/2Std(ˉX)=cλθzαR/2√λ(θ2+σ2)/n=c√λnzαR/2√1+γ2Z≥1−kE(X)zαH/2Std(μ)=1−kνzαH/2τ
The interval of solutions
Z∈[Z1,Z2]={[1−kνzαH/2τ,c√λnzαR/2√1+γ2]if1−kνzαH/2τ≤c√λnzαR/2√1+γ2∅otherwise
represents all credibility factors that can be assigned.
Similarly to the classical credibility theory, a higher expected frequency of insured events makes the real data more credible by increasing the upper bound of (2.4). As seen in Figure 2, increasing moves an insured from the “no credibility” category into a “partial credibility” and further, into a “full credibility”. When the interval of (2.4) contains full credibility can be assigned.
When the hypothetical mean is (unrealistically) considered fully credible, it corresponds to In this case, the lower bound of (2.4) becomes converting (2.4) to the classical solutions for full and partial credibility (Klugman, Panjer, and Willmot 2012; Herzog 2015).
We can also see that the solution in (2.4) exists when the expected frequency of claims is high, reflecting informative real data, or when variance is low, reflecting informative hypothetical data. When both sources and lack information, the interval is empty, and there no solution.
2.2. Method 2: The jointly limited fluctuation
Here we require that the real and prior estimates attain the desired relative precision simultaneously with a high probability In other words,
p2=P{Z|ˉX−E(X)|>cE(X)∪ (1−Z)|μ−E(X)|>kE(X)}≤α2.
Assuming independence of the real data and the prior parameters (such as independence of the given insured from all the other members of the risk group), condition (2.5) results in the inequality
p2=1−(1−pR)(1−pH)=1−{1−2Φ(−c√λnZ√1+γ2)}⋅{1−2Φ(−kν(1−Z)τ)}≤α2,
where denotes the standard normal distribution function. Notice that probability accounts for uncertainty in the present experience as well as the hypothetical mean Hence, the probability in (2.5) is understood with respect to the joint distribution of and
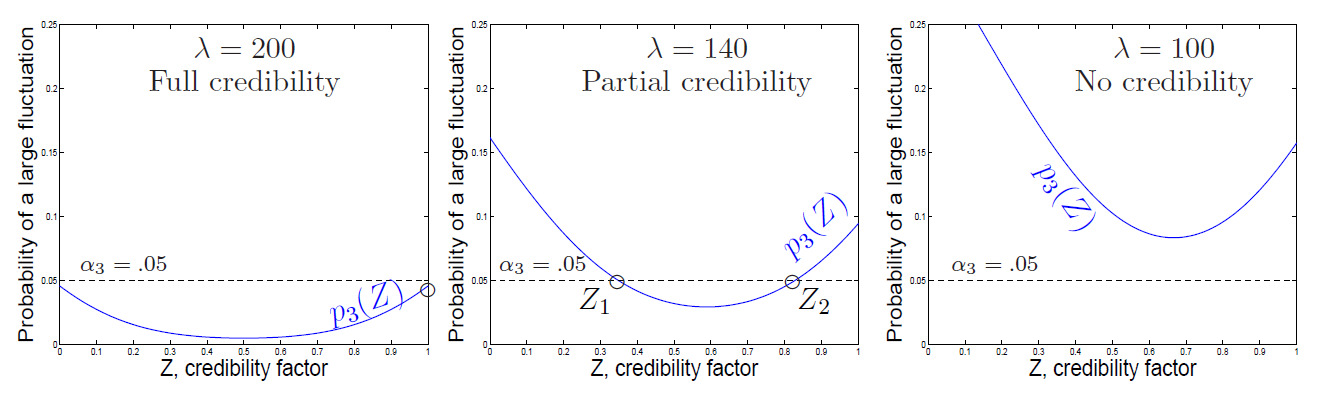
Similarly to Method 1, this may result in full credibility, partial credibility, or no credibility at all, and credibility increases with the expected frequency as seen in Figure 3.
2.3. Method 3: Fluctuation of the compromise estimator
Besides conditions on each component of the compromise estimator, it is natural to require a certain relative precision of the whole estimator After all, the compromise estimator is the one to be used by the insurance company as the final estimator of the pure premium. Therefore, as the third approach, we require that
p3=P{|C−E(X)|≥cE(X)}=2Φ(−cλθ√Z2λ(θ2+σ2)/n+(1−Z)2τ2)≤α3.
This condition can also result in full, partial, or no credibility. These three scenarios are seen in Figure 4.
The intervals of credibility factors solving (2.5) and (2.6) do not admit closed-form expressions. Both inequalities can be solved numerically.
3. Heterogeneity of Risk Groups
Kelliher and colleagues defined heterogeneity risk as one of the components of insurance risk that is related to “heterogeneity within risk groups used to set expectations, with variations in the profile of each risk group distorting experience” (2013, 13). Due to heterogeneous groups, there are insured customers or cohorts whose expected loss differs from the prior mean – that is, their actual experience is in a strong or weak disagreement with the prior distribution, as in our example at the end of Section 1 and in the right-hand panel of Figure 1. This discordance affects obtained solutions of limited-fluctuation inequalities (2.3), (2.5), and (2.6) in the previous section, because now the prior mean is a biased estimator of the pure premium for the given insured.
Let be the relative difference between the hyper-prior (risk group) mean and the expected loss In terms of the large fluctuation probability of the prior mean in (2.3) becomes
pH(δ)=P{(1−Z)|μ−E(X)|>kE(X)}=Φ(−kλθ(1−Z)τ+δ)+Φ(−kλθ(1−Z)τ−δ).
The methods presented in Sections 2.1 and 2.2 make use of this probability, and thus, disagreement affects the credibility factors computed according to both of them. Method 3 in Section 2.3 requires bounding the probability
p3=p3(δ)=P{|C−E(X)|≥cE(X)}=Φ(−cλθ+τ(1−Z)δ√Z2λ(θ2+σ2)/n+(1−Z)2τ2)+Φ(−cλθ−τ(1−Z)δ√Z2λ(θ2+σ2)/n+(1−Z)2τ2)
which is now also dependent on the relative deviation of the prior mean from the actual mean of the real data.
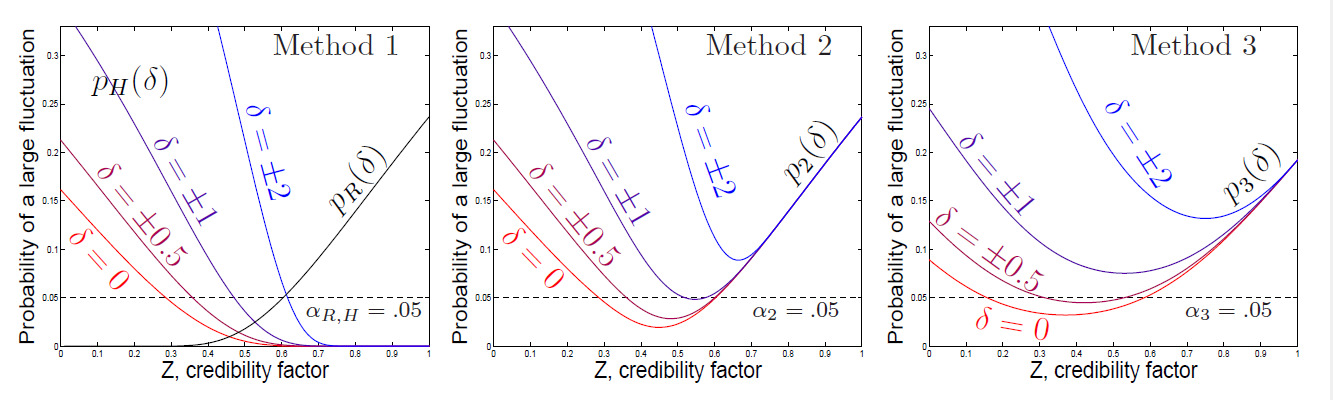
The impact of on credibility estimates is seen in Figure 5 for all three of the methods introduced. Larger differences between the expectations for an insured and the risk group cause the probability of a large fluctuation to increase. In this depicted case, a relative difference of results in no available credibility estimator.
Figure 5 also shows that the current experience appears more credible so long as it agrees more with the prior distribution.
4. Illustration
To illustrate the proposed methods, here we consider several scenarios with different severity and frequency parameters, and and hyper-parameters, and of the prior distribution. In all scenarios, we suppose that years of data are available for an insured. The tolerable error probabilities are set to be for individual deviations in (2.3) for Method 1. For joint events in (2.5) and (2.6) for Methods 2 and 3, to have a fair comparison of the three methods. However, the last two examples have to illustrate a point stated a few paragraphs below. Precision thresholds are
Table 1 gives the maximum credibility factors, that satisfy the corresponding limited-fluctuation credibility conditions. The first six scenarios reveal an agreement between the real data and the prior information, in the sense of Section 2. Disagreement is introduced in the next three scenarios. The last two cases illustrate that all the three methods converge to the classical case when the prior distribution is assumed to be known with no error.
Full credibility, is assigned in scenario 1, in which there is a sufficiently high frequency of claims, under a low severity standard deviation Scenarios 2-6 are modifications of scenario 1. A high prior variance in scenario 2 has no impact on the full credibility because the compromise estimator is based solely on the real data in this case. On the other hand, a lower frequency, in scenario 3 and a higher loss standard deviation, in scenario 4 increase the degree of uncertainty in the real data. As a result, only partial credibility can be assigned. In the case of both a lower claims frequency and a higher standard deviation of losses, as in scenario 5, we reach the critical level of uncertainty where no credibility is possible. This situation can be rescued when the uncertainty in real data is compensated for by a more reliable prior information with a low prior standard deviation as in scenario 6.
Disagreement, in the sense of Section 3, does not affect the full credibility of scenario 1a, in which estimation of the pure premium is based on the real data without using the prior distribution. On the other hand, disagreement may reduce the partial credibility. For Method 1, the maximum partial credibility factor, is determined by probability in (2.3). If the prior satisfies its limited-fluctuation condition, then partial credibility can be assigned, as in scenario 6a. Otherwise, there is no credibility factor that satisfies both conditions in (2.3), and this case results in no credibility, as in scenario 3a. Scenarios 1a, 3a, and 6a are blueprints of scenarios 1, 3, and 6, only with some disagreement between the real data and the prior.
The last two examples, 3b and 6b, repeat scenarios 3a and 6a with the only difference being practically no uncertainty in the prior distribution. Notice a very low prior standard deviation, We observe two facts here. The “no credibility” situation in scenario 3a is now corrected in scenario 3b. In general, credibility estimation is always possible when the prior distribution is known without any error (perhaps, unrealistically), because even in the extreme case of no history of real data, the option of is still available, and the pure premium is estimated from the prior only. Second, we see that in the case of a completely known prior distribution, all three methods converge to the same credibility, and it coincides with the classical partial credibility factor in Klugman, Panjer, and Willmot (2012) and in Herzog (2015).
Densities of actual data and the prior mean used in Scenarios 1 and 1a are shown in Figure 1.
5. Summary and Conclusions
According to Actuarial Standards of Practice No. 25, “The actuary should apply credibility procedures that appropriately consider the characteristics of both the subject experience and the relevant experience” (Actuarial Standards Board 2011, 3). In actuarial practice, characteristics of real data (subject experience) are typically fully addressed by developing and fitting appropriate loss models. At the same time, uncertainty of the prior distribution (relevant experience) is often neglected, and the prior is assumed to be absolutely known without any error.
In this article, we propose three methods under three limited-fluctuation conditions that account for the uncertainty of the prior. Conclusions include the following:
-
Uncertainty of the real data, as well as uncertainty of the prior, affects credibility factors and decisions concerning full and partial credibility. Credibility increases with the expected frequency of losses.
-
When much uncertainty exists in both the real data and the prior, there may be a case in which no credibility can be assigned, even a partial one. A larger experience or a more informative prior is required to assign credibility. This situation will not exist when the prior is considered fully credible, with no uncertainty.
-
Accounting for the heterogeneity of risk groups, credibility also depends on the location of the insured’s expected loss relative to the prior mean. The current experience is more credible if the actual expected loss agrees with the prior.
Examples given in the previous section suggest that all three methods essentially agree on their assignment of high/full or low/no credibility. Indeed, in order to obtain a credible estimator of the expected total loss, both the real and the hypothetical components and and sample and prior, individual and collective experience, and so on) must be credible, and the three methods express these requirements in three different ways.
Method 1 expresses this credibility separately for and For example, if one of the two components fails to be credible, an estimator based solely on the other component may be considered, giving the estimate full credibility. This can happen when the real history of an insured is too short to contain any events, or when the prior mean is “purely a guess”, as put by Tindall and Mast (2003). In such cases, one should see if there is an acceptable combination of and that leads to an interval in (2.4) that contains for the full credibility of the prior, or for the full credibility of the real data. Then the credibility problem still has a solution.
Methods 2 and 3 impose joint conditions on the credibility of real and hypothetical data. In general, these conditions may be considered milder than those of Method 1 because a high credibility of one source of data may compensate for a low credibility of the other, a feature that Method 1 does not have. Method 3 does not consider credibility of and at all. Instead, it goes directly to the compromise estimator and states the low-fluctuation credibility criterion in terms of its precision. If this is the only goal, Method 3 is appropriate. However, if credibility can be improved by expanding one or the other source of data or enhancing the quality of such data, one may find Methods 1 and 2 more appropriate for this approach.
Acknowledgements
The authors are grateful to the editor, referees, and the proofreader for their professional handling of our manuscript and a number of detailed and constructive suggestions. This research is sponsored by The Actuarial Foundation. We greatly appreciate its support and encouragement.
Funding
This research is supported by The Actuarial Foundation.