1. Introduction[1]
Many claim data sets are modeled, and estimates of loss reserve produced, by means of simple statistical structures. The chain ladder model, and its simple derivatives, such as Bornhuetter-Ferguson, Cape Cod, etc. (Taylor 2000; Wüthrich and Merz 2008) may be singled out for special mention in this respect.
Other data sets are modeled by means of more complex statistical structures. For example, Taylor and McGuire (2016) describe in detail the application of generalized linear models (GLMs) to claims data. This approach is especially suitable for data sets that contain features such that the chain ladder model is inapplicable.
More recently, interest has been growing in machine learning (Harej, Gächter, and Jamal 2017; Jamal et al. 2018). This category of model includes the artificial neural net (ANN), which has been studied in earlier literature (Mulquiney 2006), and shown to be well adapted to data sets with complex features, such as those modeled with GLMs.
The drawback of a GLM is that its fitting to a complex data set requires a skilled resource, and is time-consuming. Many diagnostics will require programming, much time will be absorbed by their review, and many iterations of the model will be required.
For a data set such as that described in Section 4.4.1, a total of 15 to 25 hours may be required, even assuming that all diagnostics have already been programmed, and excluding documentation. The cost of this will vary from place to place, but a reasonable estimate of the consultancy fee in a developed country might be US$5,000-10,000.
The time and cost might be cut if an ANN could be applied. However, the ANN model will not be transparent. It will provide only limited revelation of the claim processes and mechanics (e.g., superimposed inflation (SI)) generating the data set. Although the ANN might produce a good fit to past data, the absence of this information on claim processes might render their extrapolation to the future difficult. This can induce considerable uncertainty in any estimate of loss reserve.
A GLM, on the other hand, is a structured and transparent model that rectifies these shortcomings, but, as mentioned above, at a cost.
The question that motivates this work is whether it is possible to produce a model similar in structure, transparency and interpretability to a GLM, but in a mostly automatic fashion. For this, we turn to regularized regression, specifically the lasso, which provides a compromise between the GLM and the ANN, with the potential to achieve the best of both worlds. Given a set of input features and a degree of regularization or penalty, the lasso will select a subset of the features to generate a model that resembles a GLM, without any further intervention.
A key phrase above is “given a set of input features.” The lasso will perform feature selection to construct a model, but will not generate the initial set of features. Therefore, much of the focus of this paper is in determining a framework to construct a set of initial features for consideration by the lasso. Specifically, our aim here is to establish a framework in which the lasso may be automated for application to claim modeling in such a way as to cut the modeling cost to a small fraction of that required by a GLM, but with an output equivalent to that of a GLM, and with all of the latter’s transparency.
In order to achieve these objectives, the model is to be self-assembling in the sense that, on submission of a data set to the lasso-based software, the model will assemble itself in a form that may be read, validated, understood and extrapolated exactly as would a GLM.
Beyond this very practical motivation, regularization is possessed of some very useful theoretical properties. Hoerl and Kennard (1970), in their discussion of ridge regression (a special case of regularization), noted that there is always a shrinkage constant which gives lower estimation and prediction variances than the maximum likelihood estimate (which is the minimum variance unbiased estimate). The same observation applies to the lasso.
This bias-variance trade-off property is an important justification of regularization techniques. The result is that while estimates are biased relative to the overall mean, they are also closer to the individual means. This is a concept well understood by actuaries familiar with credibility theory.
The lasso has found its way into recent actuarial literature, though not always in application to loss reserving. Venter (2018) uses a Bayesian lasso for loss reserving where, for the most part, the model structure is one of multiplicative accident and development year effects. A later section of the paper considers some variations of this structure, such as the inclusion of some additive effects or a multiplicative payment year effect.
Li, O’Hare, and Vahid (2017) and Venter and Şahın (2018) apply the lasso to age-period-cohort models, a classical lasso in the first case and a Bayesian lasso in the second. The “age-period-cohort” terminology is used in mortality studies, but, as those authors point out, precisely the same concept arises in insurance claim modeling, where the translation is accident year-development year-payment year.
On the other hand, the model structures required for mortality and claim modelling are quite different, so the mortality papers do not consider some of the issues required in loss modeling.
A somewhat related paper is that of Gao and Meng (2018), who construct a Bayesian model of a loss reserving triangle. This resembles the present paper to the extent that it uses natural cubic splines as basis functions for the construction of curves describing the development of an accident year’s claim cost over development years. The present paper uses linear splines as basis function for describing this type of development and much else.
Neither of the loss reserving papers mentioned here considers the issue of loss development patterns that vary from one accident period to another, an issue that arises in practice. Gao and Meng obtain their data from a particular NAIC data base (Meyers 2015) and demonstrate the reasonableness of their assumption of a common development pattern for all accident years. However, it is also true that examples can be found in the same data set that fail this condition (Taylor and Xu 2016). The example of Section 4.4 is of this type.
In short, although the lasso has been introduced into the loss reserving literature, it has as yet been applied to some of the less challenging problems. The present paper endeavors to fill that gap, illustrating that it can also be applied successfully to more complex loss reserving exercises.
The innovations of the paper to lasso implementation include:
-
the use of an individual claim data base, aggregated only to a low level at which little of the individual claim information is lost;
-
the incorporation of claim development patterns that vary substantially from one accident period to another;
-
the incorporation of claim finalization data;
-
the use of explanatory variables other than accident year, development year and payment year;
-
exploration of standardization of explanatory variables.
Section 3 describes the construction of a lasso model aimed at these objectives, after Section 2 deals with notational and other preliminaries. Section 4 illustrates numerically the application of the model to both synthetic and real data, and Section 5 discusses the prediction error associated with this type of forecasting. Section 6 examines a couple of possible areas of further investigation, and Section 7 closes with some concluding remarks.
2. Framework and notation
Many simple claim models use the conventional data triangle, in which some random variable of interest is labeled by accident period and development period In this setup, the combination is referred to as a cell of the triangle, and the quantity observed in this cell denoted The durations of the accident and development periods will be assumed equal, but need not be years. As a matter of notation, A realization of will be denoted
The real data set used in this paper consists of individual claim histories. These are capable of representation in the above triangular form but, for most purposes, this is unnecessary. However, some aggregation of claims occurs, as explained in Section 4.4.1, simply in order to reduce computation. The quantity of interest throughout will be individual claim size at claim finalization, converted to constant dollars on the basis of wage inflation. A claim often involves multiple payments on various dates. The indexation takes account of the different dates.
Claim size for individual claim will be denoted A vector of labeling quantities will also be associated with claim These quantities may include calendar period in cell and others.
One non-routine quantity of interest later is operational time (OT) at the finalization of a claim. OT was introduced to the loss reserving literature by Reid (1978), and is discussed by Taylor (2000) and Taylor and McGuire (2016).
Let the OT for claim be denoted defined as follows. Assume that claim belongs to accident period and that is an estimator of the number of claims incurred in this accident period. Let denote the number of claims from the accident period finalized up to and including claim Then In other words, is the proportion of claims from the same accident period as claim that are finalized up to and including claim
There will be frequent reference to open-ended ramp functions. These are single-knot linear splines with zero gradient in the left-hand segment and unit gradient in the right-hand segment. Let denote the open-ended ramp function with knot at Then
RK(x)=max(0,x−K).
For a given condition define the indicator function when is true, and when is false.
3. Regularized regression
3.1. In general
Consider an ordinary least squares regression model
y=Xβ+ε
where is the response vector, is the parameter vector, is an error vector subject to and is the design matrix. The parameter vector is estimated by that which minimizes the loss function It will be convenient to express this as where, for vector with components denotes the -norm
\left\| x \right\|_{q} = \left(\sum_{m}^{\mathstrut}\left| x_{m} \right|^{q} \right)^{\frac{1}{q}}
Regularized regression includes in the loss function a penalty for large regression coefficients (components of The regularized loss function is
L \left(y; \widehat{\beta} \right) = \left( \left\| y - X \widehat{\beta} \right\|_2 \right)^2 + \lambda \left( \left\| \widehat{\beta} \right\|_q \right)^q \tag{3.2}
for some selected where is a tuning constant.
The generalization of (3.1) to a GLM assumes the form
y = h^{-1} (X\beta) + \varepsilon \tag{3.3}
where is the (possibly non-linear) link function, operates component-wise on the vector and may now be non-normal, but still with and independence between observations still assumed. The parameter vector is estimated by the maximum likelihood estimator which minimizes the loss function (negative log-likelihood)
L\left( y;\widehat{\beta} \right) = - \sum_{m = 1}^{n}{l\left( y_{m};\widehat{\beta} \right)} \tag{3.4}
where the summand is the log-likelihood of observation when
The regularized form of (3.4) is similar to (3.2):
L\left( y;\widehat{\beta} \right) = - \sum_{m = 1}^{n}{l\left( y_{m};\widehat{\beta} \right)} + \lambda\left( \left\| \widehat{\beta} \right\|_{q} \right)^{q} \tag{3.5}
The effect of variation of is as follows. As (3.5) tends to revert to the unregularized form of GLM. As the penalty for any nonzero coefficient increases without limit, forcing the model towards one with a single coefficient, in which case the model consists of just an intercept term and all predictions are equal to the mean response.
3.2. The lasso
3.2.1. Loss function
There are two recognizable special cases of (3.2):
(a) Here the second member of (3.2) reduces to just multiplied by the number of nonzero terms in the model. This is a computationally intractable problem, although it is noteworthy that setting produces a metric equivalent to the Akaike information criterion.
(b) In this case, (3.2) is recognized as the ridge regression (Bibby and Toutenburg 1977) loss function. All included covariates will be nonzero in this approach.
A further case of interest arises when This is the least absolute shrinkage and selection operator (lasso) (Tibshirani 1996), which is the modeling device used throughout this paper. Its loss function (3.5) may be written explicitly as
\begin{align} L\left( y;\widehat{\beta} \right) &= - \sum_{m = 1}^{n}{l\left( y_{m};\widehat{\beta} \right)} + \lambda\left\| \widehat{\beta} \right\|_{1} \\ &= - \sum_{m = 1}^{n}{l\left( y_{m};\widehat{\beta} \right)} + \lambda\sum_{r = 1}^{p}\left| {\widehat{\beta}}_{r} \right| \end{align} \tag{3.6}
The appearance of absolute values of coefficients in the loss function will generate many corner solutions when that function is minimized. Hence, the covariates included in the model will be a subset of those included in the regression design, and the lasso acts (as its full name suggests) as both a selector of covariates and as a shrinker of coefficient size. Efficient algorithms such as least angle regression (Efron et al. 2004), which generates a path of solutions across all make the lasso computationally feasible.
The strength of the shrinkage of covariate set can be controlled with the tuning parameter as discussed at the end of Section 3.1, with the number of covariates decreasing as increases.
An obvious generalization of loss function (3.6) is
L\left( y;\widehat{\beta} \right) = - \sum_{m = 1}^{n}{l\left( y_{m};\widehat{\beta} \right)} + \sum_{r = 1}^{p}{\lambda_{r}\left| {\widehat{\beta}}_{r} \right|} \tag{3.7}
where the may differ with This generalization will be discussed further in Sections 3.2.2 and 4.4.3.
3.2.2. Lasso interpretations
The lasso has been presented in Section 3.2.1 rather in heuristic terms. However, it is useful for some purposes (see, e.g., Section 4.4.3) to consider specific models for which the lasso is the optimal estimator in some sense. There are two main interpretations (Tibshirani 1996).
Bounded coefficients. Consider the optimization problem:
\widehat{\beta} = \underset{\sum_{r = 1}^{p}\left| \beta_{r} \right| \leq B}{\text{arg min}}\; {\sum_{m = 1}^{n}{l\left( y_{m};\beta \right)}}
i.e., maximum likelihood subject to the bound
This problem is soluble by the method of Lagrange multipliers, then (3.6) is the Lagrangian, and the Lagrange multiplier. So the solution is as for the lasso.
It is straightforward to show by a parallel argument that, if the problem is modified to the following:
\widehat{\beta} = \underset{\left| \beta_{r} \right| \leq B_{r},r = 1,\ldots,p}{\text{arg min}}\; {\sum_{m = 1}^{n}{l\left( y_{m};\beta \right)}}
then the solution is as for the lasso with loss function (3.7).
Bayesian interpretation. Suppose that each parameter is subject to a Bayesian prior that follows a centred Laplace distribution with density
\pi\left( \beta_{r} \right) = (2s)^{- 1}\exp\left( \frac{- \left| \beta_{r} \right|}{s} \right) \tag{3.8}
where is a scale parameter. In fact, All priors are supposed stochastically independent.
The posterior negative log-density of is
- \sum_{m = 1}^{n}{l\left( y_{m};\beta \right) + s^{- 1}\sum_{r = 1}^{p}\left| \beta_{r} \right|} \tag{3.9}
up to a normalizing coefficient, and this is the same as (3.6) with The lasso, in minimizing this function, maximizes the posterior density of so that is the maximum a posteriori (MAP) estimator of
It is straightforward to show by a parallel argument that if the prior (3.8) is replaced by
\pi\left( \beta_{r} \right) = \left( 2s_{r} \right)^{- 1}\exp\left( \frac{- \left| \beta_{r} \right|}{s_{r}} \right) \tag{3.10}
then the posterior negative log-density of becomes
- \sum_{m = 1}^{n}{l\left( y_{m};\beta \right) + \sum_{r = 1}^{p}{s_{r}^{- 1}\left| \beta_{r} \right|}} \tag{3.11}
and MAP estimation lasso is equivalent to the lasso with loss function (3.7) and
3.2.3. Covariate standardization
Standardization of covariates, and hence associated coefficients, is often moot in regression analysis. In the case of regularized regression, however, it is usually desirable. Without it, the true values of some coefficients will be large and some small, but the penalty applied in (3.6) will be the same for all cases.
This would favor the exclusion of covariates whose coefficients are large by their nature. And it would lead to the undesirable situation in which the regularized model would change as a consequence of mere rescaling of covariates.
It is assumed that all covariates in a regression take numerical values with physical meaning, or are categorical. A categorical variate is converted into a collection of Boolean variates for the purpose of the regression.
Covariates are also classified as of three types:
-
fundamental;
-
derived;
-
interaction.
Fundamental covariates do not depend on others (e.g., accident period), while derived variates are functions of fundamental variates (e.g., It will be assumed that any derived covariate depends on just one fundamental covariate, and the latter will be called its parent.
Three types of standardization were tested for the present investigation. All took the form
{\overline{\overline{x}}}_{{ms}} = \frac{x_{{ms}}}{f_{s}}
where
-
is the standardized form of the element of the unstandardized design matrix i.e., value of the -th covariate associated with the -th observation; and
-
is a scaling constant for given
Further, let be the centered version of i.e.,
{\overline{x}}_{{ms}} = x_{{ms}} - \eta_{s},\eta_{s} = \frac{\sum_{{l =}1}^{n}x_{{l}s}}{n}
and let denote the design matrix after centering of covariates and excluding any column relating to an intercept coefficient.
Note that standardization here consists of scaling but not centering. While centering is common in regularization problems, we elected not to center our features since many of our basis variables were Boolean variables and we wished to preserve the zero-valued levels.
The three versions of scaling constants assumed the following forms (nomenclature in the first two cases from Sardy 2008):
-scaling:
-scaling: where is the s-th diagonal element of
-scaling:
For all continuous fundamental covariates, the scaling factors are as set out here. A derived covariate takes on the same scaling factors as its parent. Note that we consider accident, development and payment periods to be continuous for this purpose, even though, strictly speaking, they are restricted to integer values.
The scaling for Boolean variables is a little more complex. Booleans that are derived from continuous fundamental covariates take the same scaling as their parent. On the other hand, Boolean variables that are derived from the one-hot encoding of a categorical variable with n levels into (n-1) Boolean covariates use the scaling factors as set out above.
Of the three forms of standardization, that generated by -scaling appeared most effective in terms of goodness-of-fit, and is the only one pursued further here.
3.2.4. Cross-validation
The parameter in (3.6) is free, and its value must be selected with suitable compromise between goodness-of-fit (small and parsimony of parameters (large A common approach to this selection is -fold cross-validation (Hastie, Tibshirani, and Friedman 2009). This procedure is as follows:
-
Select a maximum value of to be considered.
-
Run the lasso on all the data to generate a sequence of values to be considered.
-
Randomly partition the data set into (roughly) equal subsets.
-
Select one of these subsets as the validation set, and aggregate the remaining subsets to form the training set.
-
Fit the model to the training set.
-
Compute a goodness-of-fit statistic for this model. In the present exercise, this is the Poisson deviance where runs over all observations in the validation set, and is the value fitted by the model to the -th observation. Note that this is an out-of-sample comparison.
-
Repeat steps (5) and (6) times, in each case using a different one of the subsets as the validation set.
-
Average the goodness-of-fit statistics thus obtained and produce an average error and standard deviation over the folds. This is referred to as the CV error.
-
Select a new (lower) value of and repeat steps (3) to (8). Continue until the selected attains its chosen minimum value.
Step (6) is motivated as follows. The Poisson deviance goodness-of-fit measure would be for known means In fact, the means are unknown, and are replaced by fitted values in the deviance.
Note that the results of this cross-validation process are random due to the partitioning of the data into k subsets. This randomness may be reduced by running the cross-validation many times and averaging the error curves; however, this has not been carried out here.
At this point, one has obtained a collection of ordered pairs and can plot CV error against The curve will usually take a vaguely U-shaped form, with high values resulting in poor fit, and low values of resulting in over-fit. The optimal value of may be taken as that which minimizes CV error. The model based on this value of will be referred to as the min CV model. For the purpose of the present investigation,
The choice of statistic (Poisson deviance) given above is equivalent to out-of-sample log-likelihood estimation using cross-validation and in our computational work we use the built-in package feature to perform this tuning.
An alternative choice of optimal intended to recognize the sampling error in the CV error, proceeds as follows. In step (8) of the above procedure, the standard error of the goodness-of-fit statistic replications is also calculated. Let the value obtained from the model defined by be denoted The optimal value of is then taken as the least for which CV error Evidently, the requirement implies that the model with will be more parsimonious than the min CV model.
This alternative was tested for the data sets discussed here, but the resulting models appeared overly parsimonious, tending to model inefficiently features that were known to exist in the data. As a compromise, other intermediate models were tested, in which the optimal was selected as the least for which CV error for various e.g. Again, however, such models appeared to confer no advantage over the min CV model. Henceforth, only min CV models will be considered.
3.2.5. Training error
The training error is another metric of fitting error that may be of interest. This is based on a model trained on the entire data set and is defined as the mean squared error, where the are taken from the model trained on the entire data set, and the summation runs over all in that data set.
This is a goodness-of-fit test only, with no regard to the predictive power of the model.
In the application of the lasso, although the CV error is taken as the most efficient criterion for selection of the tuning parameter the training error is routinely computed and displayed in results obtained from synthetic data (Section 4.3.2).
4. Application of the lasso to claim modeling
4.1. Preamble on covariate selection
Section 4.3 studies the application of the lasso to a number of synthetic data sets, while Section 4.4 studies its application to a well understood real data set. But, before that, some general commentary on covariate selection is pertinent.
A typical claims data set will cover two independent time dimensions, accident and development periods (“row and column effects”), and a third dimension, payment period (“diagonal effects”), which is constructed from the other two. A necessary decision in any modeling of the data set will be the number of dimensions to be included within covariates.
It will usually be essential to include at least two. Moreover, some data sets exhibit all three effects: accident, development and payment. Nonetheless, inclusion of a third dimension should always be approached with caution. It clearly introduces collinearity between covariates, and therefore the potential for an ill-behaved model and poor prediction.
Further, the number of potential terms in a lasso linear predictor can become very large in models that include all possible covariates plus interactions, with obvious implications for computational load.
Even when the model fits well to data, the inclusion of all three effects may lead to mis-allocation between them. For example, data containing SI as a payment period effect, but no accident period effect, may return a model in which SI is allocated partly to each. The ramifications of this for forecasts require careful consideration. More on that shortly.
In the meantime, one may note that collateral information, external to the model itself, might exist with a bearing on the covariates to be included in the model. If, for example, there existed such information, indicating a high likelihood of payment quarter effects but low likelihood of accident quarter effects, then payment quarter might be included as a model covariate and accident quarter excluded.
This preliminary selection of covariates is referred to as feature selection. It may not be essential in some cases, but is a means of exploiting collateral information to reduce computational load.
Section 4.3 approaches the synthetic data set as if blind to any features. It therefore employs a saturated lasso, in which accident quarter (AQ), development quarter (DQ) and payment quarter (PQ) effects are all included in the models, together with all possible interactions of a defined type.
On the other hand, the real-world example of Section 4.4 comes accompanied by a legislative background, involving major changes to the conditions affecting claim sizes, with these changes taking effect from a particular accident date. Any potential AQ effects are muted by the fact that this is a model of average claim sizes, and so AQ effects due to changing exposure are absent.
There are no other known major AQ effects, so feature selection has been employed, with AQ excluded from main effects and included in only a few very specific interactions related to the legislative change. PQ effects are included in full.
As already mentioned, decisions on feature selection carry ramifications for forecasts. Intuition may be derived here from the operation of the separation method (Taylor 1977). Consider a claim triangle constructed to contain only the column and diagonal effects contained in the separation method and model the resulting triangle with a GLM containing only these effects. Call this “Model ” Suppose the diagonal effect is an increase of 5% from each diagonal to the next. The model will produce an estimate of this.
Now model the same triangle with the same GLM, augmented to contain a row effect. Call this “Model ” This model may misallocate the diagonal effect, partitioning it between rows and diagonals, say 3% per diagonal and 1.0194% per row
Models and are distinctly different. However, their forecasts will be identical if the forecast assumes 5% inflation per future diagonal, and the forecast assumes 1.94%.
The point of this discussion is that it hints at the following proposition.
Proposition. Consider a data set containing DQ and PQ effects but no AQ effect. Let denote a model that contains explicit DQ and PQ effects but no AQ effect, and let denote a model that is identical except that it also contains explicit AQ effects. Then, in broad terms, and will generate similar forecasts of future claim experience if each extrapolates future PQ effects at a rate representative of that estimated for the past by the relevant model.
The saturated lasso of Section 4.3 corresponds to model and so forecasts from that model incorporate future PQ effects at rates consistent with those estimated for the past, despite the fact that misallocation might have caused their understatement.
The lasso of Section 4.4 largely excludes AQ effects, and so corresponds to model There is little scope for misallocation of PQ effects, and the model estimates of these are genuine. In accordance with the proposition, they may be extrapolated to the future at face value. Alternatively, the allowance for future inflation may be reduced to zero, giving estimates in the currency values of the valuation date (closing date of last observed diagonal). This latter course is the one followed in the forecasts of Section 4.4.
4.2. Implementation
All work was carried out using R (R Core Team 2018) on a Windows PC. The lasso was fitted using the glmnet package (Friedman, Hastie, and Tibshirani 2010). We used the glmnet() function to estimate an initial vector of penalties to consider and then used the cv.glmnet() function with an extended penalty vector to produce the models. cv.glmnet() returns models for all penalty values considered, including the models for the and penalties as discussed in Section 3.2.4.
glmnet v3.0-2 supports normal and Poisson distributions. Of these, we selected the latter as more applicable to our loss reserving data, which contains positive values only and is heavier-tailed than a normal. For a Poisson distribution, cv.glmnet() uses the deviance as the loss measure.
ggplot2 (Wickham 2009) was used to produce the figures.
A worked example (including code) illustrating the use of the methods in this paper may be found at https://grainnemcguire.github.io/post/self-assembling-claim-reserving-models.
4.3. Synthetic data
4.3.1. Data sets
The lasso was first applied to several synthetic data sets. The advantage of this is that the features of the data sets are known, and one is able to check the extent to which the lasso identifies and reproduces them. The data sets can be manufactured to include specific features, identifiability of which is marked by differing degrees of difficulty.
Four synthetic data sets were constructed and analyzed. Each consisted of a quarterly triangle of incremental paid claims In each case, it is assumed that is subject to a log normal distribution with mean and variance :
Y_{ij} \sim \log N \left( \ln \mu_{ij} - \frac{1}{2} \tau_{ij}^2, \tau_{ij}^2 \right) \tag{4.1}
where
It is assumed, other than where specifically noted, that
\ln \mu_{ij} = \alpha_i + \beta_j + \gamma_t \tag{4.2}
for parameters so that (4.1) amounts to a GLM with AQ (row), DQ (column) and PQ (diagonal) effects.
The cell variances are set as
\sigma_{ij}^2 = C \mu_{ij} \tag{4.3}
for constant selected so that i.e., This is considered a not-unrealistic variance structure, and (4.3) accords with the variance assumption of the Mack chain ladder model (Mack 1993).
Data set 1: Cross-classified model chain ladder model
In this model, and so (4.2) reduces to
\ln \mu_{ij} = \alpha_i + \beta_j \tag{4.4}
and the model includes accident and development quarter, but not calendar quarter, effects. The mean and variance structure are the same as for the cross-classified chain ladder models (Taylor 2011).
The numerical values of are:
\begin{align} \alpha_i = &\ln 100,000 + 0.1R_1 (i) + 0.1R_{15} (i) \\ &- 0.2 R_{20} (i) - 0.05 R_{30} (i) \end{align}\tag{4.5}
\beta_j = (a - 1) \ln j - bj \text{ with } \frac{a}{b} = 16, \frac{a}{b^2} = 48 \tag{4.6}
Here the AQ effects exhibit an upward trend initially, with an increase in gradient at AQ 15, and then a downward trend from AQ 20. The DQ effects follow a Hoerl curve with delay to payment subject to a mean of 16 quarters, and a standard deviation of quarters.
Data set 2: Addition of payment quarter effect
The model is as for data set 1 except that term of (4.2) is now manifest, specifically
\gamma_{t} = 0.0075\left( R_{1}(t) - R_{12}(t) \right) + f(t)
with
\mathrm{\Delta}f(t) = 0.001\left( R_{12}(t) - R_{24}(t) \right) + 0.002R_{32}(t)
where is the backward difference operator
This represents a PQ effect that increases at the rate of 0.0075 per quarter from zero at PQ 1 to 0.0825 at PQ 12. The rate of increase then increases linearly from 0.0010 at PQ 13 to 0.0120 per quarter at PQ 24; the PQ effect is then flat up to PQ 32, after which its rate of change increases linearly to 0.0160 per quarter up to PQ 40. This represents SI at a continuous rate of 0.75% per quarter for the first 12 payment quarters, at a steadily increasing rate for the next 12 quarters, at a constant rate over the next 8 quarters, and finally at a steadily increasing rate over the last 8 quarters.
Since is linearly related to and there is potential for multicollinearity when predictors related to all three are included in the linear response, as in (4.2) (see, e.g., Kuang, Nielsen, and Nielsen 2008; Venter and Şahın 2018; Zehnwirth 1994). Selection of predictors that avoid this is often difficult in such models. The lasso offers an automated procedure for predictor selection, although it obviously does not always guarantee a correct parametric description of multicollinearity.
Data set 3: Addition of a simple interaction
The model is as for data set 2 except that an additional term is added to the linear predictor (4.2), thus:
{\ln μ}_{{ij}} = \alpha_{i} + \beta_{j} + \gamma_{t} + 0.3H_{17}(i)H_{21}(j)\beta_{j}
where is the Heaviside function
\begin{align} H_{k}(x) &= 0,x < k \\ &= 1,x \geq k.\end{align}
This data set is the same as data set 2, except that all DQ effects are increased to wherever AQ exceeds 16 and DQ exceeds 20. It may be verified that the interaction, while a large step change for affected cells, affects only 10 cells (those in the subtriangle with vertices at (17,21), (17,24) and (20,21)) out of the 820 constituting the triangle, so this is a subtle effect within the data set, and its identification by a model can be expected to be difficult.
Data set 4: Addition of more complex interactions
The model is as for data set 2 except that the diagonal effect there is now modified:
\ln \mu_{\text{ij}} = \alpha_{i} + \beta_{j} + \frac{\lbrack 40 - j\rbrack}{39}\gamma_{t} \tag{4.7}
where is as in data set 2. This means that the strength of the diagonal effect is greatest at where it is the same as for data set 2. The strength of the effect declines linearly with until it vanishes at This may be interpreted as SI that is large in respect of early claim settlements, and small in respect of late settlements (as well as varying over PQ).
4.3.2. Results
A data set amounts to a surface of observed values, as functions of a number of explanatory variables. In the present case, it is a surface of quarterly paid claim amounts as a function A priori, the function may assume any shape.
It will be assumed that the observations can be adequately approximated by a vector space with a finite basis of functions (the basis functions of the space). Let observations be arranged in a vector (the ordering is unimportant), and hence denoted Then observation will be approximated by some linear combination of these basis functions:
y_{m} \cong \sum_{r = 1}^{p}\beta_{r}X_{r}\left( i_{m},j_{m},t_{m} \right),m = 1,\ldots,n \tag{4.8}
where = for observation
An alternative representation of this is
y = X\beta + \varepsilon \tag{4.9}
where are vectors with components respectively, is the matrix with elements and the approximation errors in (4.8) are represented by components of the vector assumed to be stochastic subject to a defined distribution.
This is the same as (3.1), and so the whole discussion of Section 3 may be applied to the estimation of the surface in question here. The lasso may be applied, yielding a parameter estimate vector and a vector of fitted values
\widehat{y} = X\widehat{\beta}.
Any application of this structure requires a selection of the set of basis functions. Basis functions for the present investigation were chosen as:
-
for main effects; and
-
for interactions.
This produces a total of 117 main effects basis functions and 4,563 interaction basis functions. The values of K, were selected to remove redundant terms (for example, everywhere for though these would be automatically eliminated by a lasso model in any case.
The main effects basis functions generate the vector space of all linear splines in respectively, with knots at integer values in their domains. The interaction basis functions relate to 2-way interactions in each of which two of the three row, column and diagonal effects undergo a step change.
The use of ‘ramp’ functions in the set of basis functions bears some similarities to the multivariate adaptive regression splines (MARS) approach (Friedman 1991), which also uses ramp functions to build up a multivariate fit. Our proposed approach has some notable differences.
First, the respective model-building procedures of MARS and lasso are different. MARS uses a stepwise procedure, adding one ramp at a time. Each addition is unpenalized, i.e., with no shrinkage of regression coefficient. On the other hand, the lasso proceeds by means of steps, each of which gradually adjusts all coefficients simultaneously, and all penalized.
At the “solution point” (best fit), a MARS model will contain K unrestrained effects, whereas a lasso would typically contain more than K parameters, but with smaller coefficients than would be obtained by a refit it on those factors unrestrained. So the lasso “invests” degrees of freedom in partial effects, rather than the all-or-nothing of MARS. The latter approach is also likely to be more stable. Thus, the solution curves are quite different.
Second, the lasso is not restricted to ramps, so can permit a broader range of functional forms, such as our proposed interaction terms. Finally, we believe the penalization setup, and particularly variation of penalty over different effects, is more natural for imposing pre-conceived effects relevant to the data. For example, a known change in claim behavior can be allowed for as an unpenalized, or partially penalized, effect, as discussed in Section 4.4.3.
The lasso is applied thus to the four data sets described in Section 4.3.1, using a Poisson distribution assumption. This choice of distribution was essentially dictated by the lasso software used. See Section 6.1 for further discussion.
In the case of synthetic data, there is another goodness-of-fit metric of interest. This is referred to subsequently as the test error, and is calculated by the same formula as in step (6) of the CV error (see Section 3.2.4) except that the “observations” are taken from the lower triangle consisting of future diagonals These observations are generated as described in Section 4.3.1 with for i.e., nil SI in the future, neither actual nor forecast in the underlying data generative model.
The test error cannot be computed in the case of real data, since the true underlying model is unknown and the actual experience unobserved. It is worthy of note that, even if the actual experience were available, the underlying process generating it might have undergone structural change so that the computed test error would be contaminated with model error.
The results of lasso regression for each of the four data sets follow.
Data set 1: Cross-classified model chain ladder model
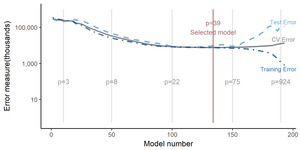
Figure 4‑1 displays the CV error (based on the Poisson deviance, and estimated by the cv.glmnet() function), training error and test error for a sequence of models with various values of decreasing from left to right. Also shown is the number of parameters in the model, steadily increasing as decreases.
The CV error initially decreases with decreasing but then increases. It attains a minimum in a model involving 39 parameters. The test error (usually unavailable in real life) would choose a similar model, which is reassuring. The training error, as pointed out in Section 3.2.5, is a mere goodness-of-fit statistic, and so declines monotonically as the parameterization of the model increases.
Figure 4‑2 illustrates the accuracy with which the model tracks the known AQ and DQ effects included in the data, both in training data (the past, indicated by the grey area in the plots) and the test data (the future, white background). The AQ effect (Figure 4‑2, left), for example, measures the variation of the response variate, and the lasso fit to it, across the range of AQs. In general, this fit will depend on DQ (though not in the case of data set 1), and hence the labeling in the left plot as “AQ effect where DQ=20.”
The values of in the particular instance of synthetic data are labeled as “Simulated” and represented by the narrow grey line. The plotted values of “Underlying” and “Lasso” are It is seen that the fitted values track actuals closely. Similar remarks apply to Figure 4‑2 (right).
Data set 2: Addition of payment quarter effect
In this case, the model involves 59 parameters. Due to space limitations, the plots of AQ and DQ effects are not reproduced here. The model’s tracking of these effects is, however, accurate.
Figure 4‑3 tracks PQ effects at DQ=4 and 14. The PQ effects differ in the two cases because PQ at DQ corresponds to AQ + 1 and, for given the AQ effects differ at and Note that, by (4.2), the true values for PQ at DQ fixed) are given by
{\ln μ}_{t - j + 1,j} = \left( \alpha_{t - j + 1} + \gamma_{t} \right) + \beta_{j},t = 1,\ldots,40
The value is constant as varies, but the bracketed member illustrates how the plotted “PQ effect” is actually a mixture of AQ and PQ effects, and that the plot will vary with the value selected for
The lasso fit of PQ effects is accurate; the “Underlying” and “Lasso” trajectories in the plots are almost indistinguishable except at low payment quarters.
Data set 3: Addition of a simple interaction
The model involves 77 parameters. It was remarked in Section 4.3.1 that the interaction added to the model generating this data set affects only 10 cells out of 820, and so modeling of the interaction was expected to be difficult. However, Figure 4‑4 (left) shows the lasso to be remarkably effective in tracking the sudden increase in paid amounts at DQ 21. On the other hand, the lasso model somewhat overstates the tail of the DQ effect.
Similarly, Figure 4‑4 (right) illustrates the sudden increase in paid amounts at AQ 17 in the AQ effect at DQ 24. AQs 17 to 20 are the only ones for which observations on the increase exist. The lasso recognizes the increase accurately for AQs 17 to 19, but extrapolates a lesser increase to subsequent AQs.
This seems excusable. The data triangle contains no experience of the increase for those later AQs, and in fact provides no particular basis for assuming that those AQs would be subject to the same increase.
The chain ladder is based on an assumption that the payment delay pattern is the same for all accident periods. It can therefore lead to poor modeling, and erroneous forecasting, in the case of data sets that contain abrupt changes in delay pattern. This is illustrated by Figure 4‑5, which plots loss reserves by accident quarter, as given by:
-
The lasso, where future payments are forecast as the
-
The chain ladder, with age-to-age factors estimated from the experience of the last 8 PQs;
-
Actual future payments (simulated)
The chain ladder’s age-to-age factors are influenced by the elevated experience at DQs 21 to 24, but only slightly. As a result, the loss reserve for each AQ after 16 is seriously under-estimated. As explained in connection with Figure 4‑4 (right), the lasso does recognize the increase for AQs 17 to 19, and most AQs from 17 onward are not under-estimated.
The fact that this occurs despite the lasso’s underestimation of accident quarter effect apparent in Figure 4‑4 (right) was investigated further, and the underestimation found to be compensated elsewhere in the model. Specifically, SI was overestimated in the later payment quarters of experience, and then extrapolated into the future. This is an example of the identifiability problem when AQ, DQ and PQ effects are all included in the basis functions.
Data set 4: Addition of more complex interactions
The model involves 53 parameters. The main feature of this data set was SI that varied over both PQ and DQ. Therefore, Figure 4‑6 plots PQ effects for DQ = 5 and 15. These plots correspond to Figure 4‑3 for data set 2 and, as there, the plotted “PQ effect” is actually a mixture of AQ and PQ effects. In any event, the lasso appears to track the true data trends closely.
Of course, the ultimate purpose of the claim modeling here is forecast of a loss reserve. For this reason, Figure 4‑7 (top) plots the lasso loss reserve estimates, separately by AQ, compared with the true expected values. The figure also includes error bars for each reserve. These have been obtained as follows:
-
The simulation of the data set was replicated 500 times, generating a sample of 500 data sets.
-
The lasso has been applied to each replication, in each case with set equal to the min value corresponding to the originally chosen model (strictly speaking, a path of decreasing values of values was used, each corresponding to a different model, from which the model corresponding to the original model’s min value was selected, since it is often faster to fit a whole path in glmnet than compute a single fit).
Some experimentation was conducted with an alternative (and considerably more time-consuming) approach in which the value of was optimized within each of 100 replications, and little change in results was found.
Figure 4‑7 (bottom) gives the corresponding plot for the chain ladder on the same scale.
It is seen that:
-
Both models exhibit some upward bias, except that, for the most recent AQs, the chain ladder underestimates considerably.
-
As is often the case, the chain ladder exhibits large prediction error in connection with the more recent AQs, whereas the lasso produces much tighter forecasts.
It may be possible to shrink the parameter set further in all four of the above examples. The basis functions selected at the start of this subsection for the modeling of column effects are open-ended ramp functions. Some number of these are required to fit the kind of curvature observed in Figure 4‑2 (right).
The profile displayed there resembles a Hoerl curve, for which
\beta_{j} = A + B \ln j + Cj
Thus, the addition of the functions to the set of basis functions might lead to a more economical model. The ramp basis functions could be retained to accommodate deviations from the Hoerl curve.
4.4. Real data
4.4.1. Data set
As explained at the start of Section 4.3.1, synthetic data form a useful test of a model’s ability to detect and reproduce known (albeit complex) features. In the case of real data, on the other hand, the correct model is unknown and so validation of the fitted model is less sure. However, the real data set may have the advantage of challenging the model with subtle, unknown features that may not have been contemplated in the construction of synthetic data.
The real data set selected for use here is drawn from a privately underwritten, but publicly regulated, scheme of Auto Bodily Injury Liability in one of the Australian states. It consists of the claim history from the scheme commencement on 1 September 1994 to 31 December 2014. This totals 82 quarters if the initial month September 1994 is counted as 1994Q3.
The data set comprises a unit record claim file, containing only finalized claims, of which there are about 139,000. Each record includes inter alia the following fields in respect of the claim to which it relates:
-
Date of accident;
-
Date of finalization;
-
Injury severity score at finalization;
-
Legal representation status at finalization;
-
For each individual payment:
-
Date of claim payment;
-
Amount of claim payment.
-
The injury severity score is the Motor Accident Injury Severity (MAIS), which assumes values 1 to 5 for injuries, 6 for a fatality, and 9 in the case where generally there is insufficient information to determine a score. Values 1 to 5 ascend with increased severity. Severity 5 would usually involve paraplegia, quadriplegia, or serious brain injury. Claim sizes vary very considerably according to MAIS.
Legal representation simply notes whether or not the claimant is represented. The great majority of claimants with MAIS 2 to 5 are legally represented, but MAIS 1 includes a substantial proportion of minor injuries for which legal representation has not been obtained. For the purpose of the present investigation, a new covariate maislegal has been created, defined as:
\begin{align} \text{maislegal} = &0, \text{ if MAIS = 1 and the claimant is} \\ &\text{unrepresented;} \\ = &1, \text{ if MAIS = 1 and the claimant is} \\ &\text{represented;} \\ = &\text{MAIS, otherwise.} \end{align}
Claim payments have been summarized into a (finalized) claim size. Each claim payment has been adjusted by the State wage inflation index from the date of payment to 31 December 2014, and all adjusted payments then summed. This produces a claim size expressed in 31 December 2014 dollars.
Most claims involve a sequence of payments, but there is usually a dominant one, and it is usually not greatly separated in time from the finalization date. Hence, for the purpose of the analysis, all payments in respect of a specific claim are regarded as made on the date of finalization (albeit correctly indexed for inflation). This has some implications for the measurement of SI.
Finally, the data have been aggregated into cells labeled by maislegal, accident and development quarter (and, by implication, payment quarter). The number of finalizations in each cell has also been recorded for use as a weight in the analysis.
This step was not essential in principle, but was aimed purely at reducing the computational load so that a greater number of basis functions could be considered. With an additional load, modeling at the individual claim level would be possible.
Two of the authors have worked on the data set continually over a collective period of more than 15 years, conducting quarterly analyses. There are a number of data complexities but, with this experience, the data set is believed to be well understood.
Complexities include the following:
(a) Claim processes undergo change from time to time. In consequence, there have been occasional material changes in the rate of claim settlement.
(b) SI experience has been typical of schemes of this type, with periods of rapid increase in claim sizes, punctuated by periods of quiescence.
(c) It is apparent that SI does not affect all claim sizes equally. The largest claims are largely unaffected by it. These are claims involving the provision of income and medical support for life, and there is little scope for dispute over the extent of liability. The opposite is true of less serious claims. These often involve soft tissue injury for which objective determination of severity is difficult. In the absence of change to the rules of assessment, the trend in claim sizes is usually upward.
(d) The scheme was subject to major legislative change from December 2002. This was the Civil Liability Act (CLA). The changes affected claims with accident dates after that date, and had the effect of elimination of many of the smallest claims, and reducing the cost other relatively small claims. This caused a radical change in the distribution of claim sizes.
(e) As a result of the elimination of a material proportion of claims from the scheme, claim management resources were released to process and settle the remaining claims earlier than had been the case in AQs prior to the CLA.
(f) The reduction in claim sizes resulting from the CLA was gradually eroded in AQs subsequent to 2003Q1, causing further changes in the distribution of claim sizes.
All of these changes are incompatible with the chain ladder model, or indeed with any model that assumes the same payment delay pattern for all accident periods. Some of the changes (specifically, (a) and (d)-(f)) are row effects, whereas some are diagonal effects ((b) and (c)). This creates a challenge for many models.
In view of (a), operational time (OT), as defined in Section 2, is a much more useful metric of time than real development time, such as development quarters. The OT is computed for each claim according to its AQ, and attached to the relevant claim record. In the aggregated data, the operational time for an (accident, development) quarter cell within a particular maislegal is taken as the average of the individual operational times in that cell.
4.4.2. Results
The data were aggregated by quarter, and the lasso was used to model average claim size where
-
maislegal;
-
AQ;
-
DQ;
-
PQ.
-
OT in AQ and DQ for maislegal
-
average claim size (response variate) in AQ and DQ for maislegal
-
number of claim finalizations (weight variate) in AQ and DQ for maislegal
All variates here other than DQ, the response, and the number of claim finalizations are covariates.
The basis functions for main effects in the lasso were chosen as:
where the calendar quarters 1994Q3,…,2014Q4 are labeled 1,…,82 for convenience.
All observations were assumed Poisson distributed, as discussed later in Section 6.1.
The basis functions for interactions were chosen as:
There are 109 main effects basis functions and 26,728 interaction basis functions. Regression problems of this size are computation-intensive. The analyses of the present subsection were performed using a PC with 16Gb RAM, 2 cores, and a 2.9GHz chip using the Microsoft R Open 3.5.0 release. With these resources, a single regression occupied 5 hours.
It should be pointed out that this regression alone is only part of the entire program of loss reserving. For example, the computation of OT requires an estimate of the ultimate numbers of claims incurred in each AQ (see Section 2), so the estimation of IBNR counts is required as a preliminary exercise.
The loss reserve estimate depends on future finalizations in respect of past AQs. These must be assigned to future PQs if SI is to be accounted for correctly, so a forecast of future finalization counts by AQ and PQ forms another preliminary exercise. Moreover, although the lasso model will have provided estimates of past rates of SI, future rates are exogenous and will require forecasts.
The loss reserve consists of the ultimate cost of future finalizations (for past AQs), less the indexed amount already paid in respect of claims open at the valuation date (which will be finalized in future). There may be other subsidiary issues to be addressed. For example, finalized claims may sometimes reopen.
Thus, the loss reserving model of this example consists of multiple submodels. The present subsection deals with just one of those.
The lasso model contained 94 nonzero coefficients including the intercept. Although this is a moderately large number of coefficients, it should be recognised as covering the eight distinct maislegal categories. These were all modeled separately in the consulting exercise described in Section 4.4.1. In this sense, the 94 parameters might be thought of as about 12 per maislegal model.
In the case of analysis of real data, it is not possible to compare actual and fitted effects as in Figure 4‑2 to Figure 4‑4 and Figure 4‑6, since the actual effects are unknown. The following model validation diagnostics therefore compare actual and fitted total cost of finalization.
For example, Figure 4‑8 compares, for each value of maislegal and for each development quarter, the total (inflation indexed) cost of finalizations to 31 December 2014 with the total of the fitted costs of all the claims involved. Note that these values, and all in subsequent figures, have been scaled by a constant value for confidentiality, and, in some cases, the scaled values are shown on a log scale for readability.
Attention is given in the following discussion to maislegal 1, since it is by far the largest category, accounting for 62.5% of all finalizations in the data set.
Figure 4‑9 gives the corresponding plot by payment quarter.
Figure 4‑8 and Figure 4‑9 illustrate a relatively faithful reproduction of the data by the model, at least in aggregate over development and payment quarters, respectively. Similarly, the models tracks the data reasonably well by accident quarter, though there are two notable exceptions for maislegal=1, as may be seen in Figure 4‑10, where there are differences over AQs 2 to 8 (1995Q1 to 1996Q4) and 35 to 40 (2003Q2 to 2004Q3).
An anomaly in the second of these periods is not altogether surprising. Note the mention in points (d) to (f) of Section 4.4.1 of legislative change from late 2002, known to have caused abrupt changes in the cost of claim finalizations. Figure 4‑10 (left) suggests that the model has smeared the abruptness over a year or two.
Figure 4‑10 (right) sheds additional light on this matter. It is a 2-dimensional heat map of the ratio A/F, where A, F denote actual and fitted total finalization costs at the cell level. Several features are prominent:
(a) An abrupt change in fit is indeed apparent at AQ 34 or 35. For 3 or 4 years after this, the model overstates claim costs in the early DQs.
(b) In later AQs, this overstatement persists at a more moderate level in the first development year or so, but then tends to underestimate in the second development year. This is probably explained by the changing payment pattern mentioned in point (e) of Section 4.4.1.
(c) In the early AQs mentioned above, the model exhibits the reverse tendency, with overestimation in the first DQs, and underestimation in the next few.
4.4.3. Adjustment for special circumstances
The legislative change discussed in Sections 4.4.1 and 4.4.2 appears somewhat troublesome in the abruptness of its effects, and is worthy of further discussion. It is accommodated in the model by interactions of main effects with the step function for in the vicinity of 34. These interactions could have been anticipated.
Recall that the lasso applied in Section 4.4.2 used loss function (3.6) in which the same penalty is applied to each covariate. Recall also the Bayesian interpretation of the lasso in Section 3.2.2 in which this relates to the reciprocal dispersion of the prior on each covariate’s regression coefficient.
Such a penalty treats the interactions as no more likely to be non-null in the vicinity of than anywhere else, in contradiction of strong expectations to the contrary. It would be possible to recognize the virtual inevitability of these interactions by using the alternative loss function (3.7) with for these interactions, assuming a lesser value than for other
The objective stated in Section 1 was to automate the modeling of claims experience, and the contemplation of varying with seems to run counter to this objective. On the other hand, it would appear perverse to deliberately overlook the effects of a known material change to the claim environment. For this reason, we are broadly in favor of removing the penalty term corresponding to parameters that would track known discontinuities in the data.
We would also take this a step further and recommend the consideration of customized parameters (i.e., beyond those included in the set of features) that capture specific experience. These customized parameters would be included with a penalty of 0.
In the case of the anomaly relating to the legislative change here, we have conducted a small side experiment by including some customized variables based on the following considerations:
-
The legislative change introduced a discontinuity at AQ 35 for maislegal 1. This suggests including a Boolean covariate for AQ 35 and higher.
-
The effect differed in the first year compared to later years. This suggests including some specific modeling for AQ 35-38.
-
The legislative change had the effect of removing lower value claims but leaving more serious claims unaffected. This translates to an increase in claim sizes at lower operational times, but this increase gradually wears off as operational time increases. This suggests using variables that contain a reverse operational time spline – the spline is nonzero at low operational times but reduces to 0 for higher operational time terms.
To select exact terms to be included in the model, a GLM was fitted with overdispersed Poisson error and using the same covariates as selected by the lasso illustrated above. Additional terms were then added to deal with the special features just identified. A heat map similar to that in Figure 4‑10 was used to guide covariate selection.
The following custom terms were selected for inclusion in the lasso model after a short period of experimentation:
The lasso model was then fitted in the usual way, except that the six variates above were included without penalty, along with the other basis functions described in Section 4.4.1.
After refitting the lasso, the tracking of model and experience for maislegal 1 was re-examined. This has improved, as is apparent from Figure 4‑11.
4.4.4. Comparison of lasso and custom-built GLM predictions
Projections from the model from the previous section (i.e., the lasso model together with the custom modifications for the known legislative effect) were compared with those from a custom-built GLM of the individual claim size data. This model was manually constructed by those intimately familiar with the data, and has previously been discussed by Taylor and Sullivan (2016). As discussed in Section 1, building such a model consumes a significant amount of a skilled resource.
Both models are projected forward, excluding SI. Comparisons of the loss reserve by accident quarter (on a log scale) are presented in Figure 4‑12. Again payments have been scaled.
Overall the comparison is reasonable. The results for maislegal 1 are very similar, while other maislegal groups are generally comparable. Note that the differences in maislegal 9 are magnified due to the scale of that plot. Furthermore, this class contains small numbers of claims.
Evidently, the lasso, with a small amount of customization, has produced numerical results very close to those derived from many hours of a skilled consultant’s time. The lasso might therefore be considered as effective as the consultant in the estimation of quantities such as average claim size, ultimate claim cost, run-off schedules, etc.
However, the lasso model, in common with other machine learning models, is subject to the interpretability problem. This manifests itself in a model that fits well to data, forecasts efficiently, yet is a rather abstract combination of basis functions. A physical interpretation will often be possible, but may be achieved only on by means of some detailed analysis.
While it is true that the lasso produces a more interpretable model than an ANN, for example, it is still the case that modeled effects may be a combination of a number of spline and interaction terms. Additional work would be required to interpret these and translate them to specific data features, which in turn could form the basis for extrapolation to a loss reserve.
The consultant’s modeling, on the other hand, will be more targeted at specific data features, and consequently less abstract and more easily interpretable.
5. Prediction error
Every forecast needs to be accompanied by some information on its dispersion, possibly standard error, but preferably the entire predictive distribution. This can be achieved in relation to a loss reserve generated from a lasso model by a bootstrap of that model.
This approach is well documented in the literature, and can be readily bolted onto the forecasting procedure outlined in Section 4. In view of this lack of novelty, the bootstrap is not followed up numerically in the present paper. However, the following three subsections add a few comments on each.
To consider prediction error, let be the future random variable to be forecast, and let Let be the forecast from the thinned lasso model. The prediction error is
\begin{align} \widehat{Z} - Z = &\left( E \left\lbrack \widehat{Z} \right\rbrack - \mu \right) + \left( \widehat{Z} - E \left\lbrack \widehat{Z} \right\rbrack \right) \\ &+ \left( \mu - Z \right) \end{align} \tag{5.1}
The first of the three members on the right is the error in the long-run model estimate (i.e., the average over many replications of the model estimate), and is the effect of the difference between the selected model and reality. It is called model error. The second member is the component of prediction error arising from the limited size of the data set, and the resulting sampling error in parameters estimates. It is called parameter error. The final member reflects the assumption that the predictand is drawn from a stochastic process, and represents the noise in that process. It is called process error.
It is usual to assume that all three components of (5.1) are stochastically independent, so that the mean square error of prediction (MSEP) of forecast is
\begin{align} MSEP \left\lbrack \widehat{Z} \right\rbrack = &E \left\lbrack \left( \widehat{Z} - Z \right)^2 \right\rbrack \\ = &E \left\lbrack \left( E \left\lbrack \widehat{Z} \right\rbrack - \mu \right)^2 \right\rbrack \\ &+ E \left\lbrack \left( \widehat{Z} - E \left\lbrack \widehat{Z} \right\rbrack \right)^2 \right\rbrack \\ &+ E \left\lbrack \left( Z - \mu \right)^2 \right\rbrack \\ = &MSE_{model} \left\lbrack \widehat{Z} \right\rbrack \\ &+ MSE_{parameter} \left\lbrack \widehat{Z} \right\rbrack \\ &+ MSE_{process} \left\lbrack \widehat{Z} \right\rbrack \end{align} \tag{5.2}
where the last three members are the mean square errors of model, parameter and process errors.
5.1. Bootstrap of a GLM
Bootstrap of a lasso is an extension of bootstrapping a GLM, and so some aspects of the latter are first recalled as background to the former.
The application of the bootstrap to a loss reserving GLM is discussed in some detail in Taylor and McGuire (2016). It is noted there that various forms of bootstrap are available, most notably (nomenclature varies somewhat from place to place):
-
Parametric bootstrap. Bootstrap replications are generated by resampling of model parameters from a selected distribution (usually normal) with first and second moments as estimated by the GLM.
-
Non-parametric bootstrap. A bootstrap replication is generated by resampling of the data set, and the fitting of the GLM form to it.
In these bootstrap procedures, the GLM is taken as the correct model, and so model error is not considered. However, an estimate of may be obtained from replications of and may be estimated by simulation of the noise.
5.2. Bootstrap of lasso
In an analogous process, a non-parametric bootstrap may be applied to the entire lasso. The replications then generate a collection of different data sets, and hence possibly different models (i.e., different subsets of selected covariates). Aggregation of the first two members on the right side of (5.1) yields
\widehat{Z} - Z = \left( \widehat{Z} - \mu \right) + \left( \mu - Z \right) \tag{5.3}
Now, if it is reasonable to assume that the lasso is unbiased, then the average of over all replicates (and therefore over different models) will approximate and an approximate version of (5.3) is
\widehat{Z} - Z = \left( \widehat{Z} - \overline{Z} \right) + (\mu - Z) \tag{5.4}
Then replicates of can be used to estimate An estimate of may be obtained in the usual way.
The computational load from a bootstrap of the entire lasso would vary depending on the number of basis functions considered and the size of the data set. For example, a single run of the glmnet procedure for the synthetic data took 6-10 seconds while the full cross-validation run required approximately 3 minutes. By contrast, the run-times for the real data example were approximately 20 minutes and 4.5 hours, mainly due to the significantly greater number of basis functions. Therefore, bootstrapping using a single glmnet procedure, as described in relation to Figure 4‑7, with cross-validation omitted, will produce acceptable computation times in many, though not all, cases.
Note also that bootstrapping a lasso, as described above, would not enable partition of into its two components. This would require replications within replications, a form of iterated bootstrap (Hall 2013). A single replication, involving a fixed GLM, would be expanded to multiple replications of resampled parameter estimates with that model held fixed. This would provide an estimate of for that single model. Evidently, this would be even more computer-intensive, though the replications to estimate parameter error would run more quickly due to the constrained set of basis functions.
Unfortunately, the above estimate of would probably fall short of its true value in two respects.
First, the universe of models from which any lasso model is selected is only the vector space spanned by the chosen basis functions. This may be smaller than the space of all conceivable models.
Second, resampling of the data set can generate only pseudo-data sets that are broadly consistent with the trends and features of the original data set. For example, it is unlikely to generate a data set consistent with rates of SI that are uniformly double those underlying the original data set. Yet such a regime of high SI might occur in future.
Thus, the model MSE obtained from a bootstrap lasso will include only models of the future that broadly resemble those of the past. This sort of distinction is discussed in some detail in Risk Margins Taskforce (2008), who decompose model MSE into (their nomenclature):
-
External systemic error, which includes model error induced by features that are possible in future data but not present in the data set; and
-
Internal systemic error, which accounts for only error in the selection of a model consistent with the data set.
No model based only on claim data is likely to include allowance for external systemic error, so the most that one can expect of the lasso is inclusion of internal systemic error.
5.3. Model bias
The lasso’s shrinkage of parameter estimates induces bias in model estimates. For this reason, the lasso is sometimes used just for selection of the model form, and then the selected model refitted to the data without penalty. The result should be approximately unbiased.
Some experimentation with this procedure was carried out in relation to the examples of Section 4, but the results were not encouraging in that the refit caused a substantial deterioration in model performance in some cases. Further detail appears in Section 6.1.
Model refitting was not pursued further here, but may be an are worthy of investigation. The relaxed lasso (Meinshausen 2007) might be useful for this purpose, as it considers the set of convex combinations of the lasso and unpenalized regression.
6. Further development
6.1. Model thinning
The lasso is implemented here by means of the R function cv.glmnet(). This provides a limited choice of error distributions. The most appropriate available for analysis of claim experience is Poisson, and this has been used for initial lasso modeling. The result is that a min CV model often includes some number of very small coefficients, seemingly with very little influence on the model.
The statistical significance of these coefficients was tested as follows. In the case of each data set considered here, a GLM was fitted to the full data set, including only those covariates included in the min CV lasso model and assuming, in common with the lasso, a Poisson error distribution. The resulting regression coefficients do not equal those of the lasso, because the GLM is unpenalized. The majority are found to be significant.
However, the conclusion on significance fails to recognize the effect of the very restrictive Poisson assumption that the mean of observations equals the variance. In practice, this can estimate an unrealistically low variance. The standard errors associated with estimated regression coefficients reflect this variance, and can also be unrealistically low.
This creates a very low hurdle for significance of the coefficients, and consequent overstatement of that significance. In order to overcome this shortcoming, an experimental GLM was fitted, again including only those covariates included in the min CV lasso model, but now assuming more realistic error distributions, either overdispersed Poisson or gamma.
The major effect was that the standard errors of coefficients were considerably expanded relative to those of the Poisson GLM, significance was reduced, and a much more economical model resulted. This model is referred to as a thinned model.
In common with other Bayesian estimators that shrink towards a prior mean, lasso estimates of regression coefficients are biased. The thinned model, consisting of an unpenalized GLM, would mitigate this bias. It would, of course, fail to gain the benefit of the variance-reduction inherent in the lasso.
The thinned model is preferable when it does not degrade fit or forecast performance. However, this was not always the case. It usually performed almost as well as the unthinned model in fitting to observations. In forecasting, it usually performed well on the real data set, but poorly on the synthetic, though even this was not consistently the case. Our working hypothesis is that this may be related to the collinearity in basis functions and the resulting misallocation of payment quarter effects to accident quarter in the synthetic data study, but we have not yet rigorously investigated this.
Model thinning might be a useful area of further investigation, and it might be useful in the case of more highly supervised modeling. However, in view of the uncertainty as to its performance, the thinned model is not recommended as a self-assembling model at this stage. A possible future project might consist of revisiting this question and ascertaining whether the collinearity of basis functions is driving the problem, or whether there are other causes.
6.2. Bayesian lasso
The version of the lasso used in this paper is non-Bayesian. A Bayesian version is also available, in which the Bayesian interpretation set out in Section 3.2.2 is made explicit. The so-called fully Bayesian method also sets a prior on and then optimizes it. This avoids the need to optimize by means of cross-validation..
A Bayesian interpretation of the lasso model (where the penalty term is interpreted as a Laplacian prior on the parameters; see equation (3.8)) permits the usage of standard Bayesian machinery to infer distributional properties for the parameters as well as the observation error, which allows a broader estimate of uncertainty.
One common approach is to interpret the Laplacian prior as a mixture of Gaussians which means that the and their corresponding variance parameters can be estimated as a hierarchical model; see, for instance, Park and Casella (2008). This has the added advantage of normal distributions throughout, which is a convenient assumption for conjugacy and Gibbs sampling.
The Bayesian paradigm implemented in software such as Stan (Carpenter et al. 2017) also allows for more flexibility in the choice of loss distributions and priors. For example, a heavy-tailed prior distribution (e.g., Cauchy) could be used to eliminate small parameters.
The joint sampling of the distribution then allows estimation of the full posterior distribution of other statistics, such as the reserve implied by a set of estimates. This might be valuable for the estimation of variability and quantiles of reserve, including allowance for internal systemic error. As in the case of the bootstrap (Section 5.1), such estimates would include no allowance for external systemic error.
The Bayesian approach also presents options for the estimation of the penalty term There are plug-in estimates possible using empirical Bayes approaches, or a low-information prior can be applied to give a posterior distribution for jointly with the other parameters. Again, see Park and Casella (2008).
7. Conclusions
The objective of this paper is to identify an automated system of claims experience modeling that will track complex data sets sufficiently well without supervision. The lasso, with judiciously chosen basis functions as covariates, seems to achieve this. This is subject to the issue of feature selection, discussed in Section 4.1, and which might sometimes require a brief preliminary investigation.
A routine procedure has been developed, and once the basis functions have been specified, no parameter input nor supervision is required. The model will self-assemble the model that is optimal according to the lasso criterion.
This procedure has been applied to both synthetic and real data. The synthetic data contain known complexities, and so form a control against which to assess any model. The lasso-based procedure appears to identify these features and estimate them reasonably accurately.
The real data set relates to Auto Bodily Injury claims, and so is comparatively long tailed. Eccentricities of the data cannot be known with certainty. However, as the authors have more than 15 years’ experience with the data set, a number of features are known with reasonable confidence. Of course, real data might also contain other unknown subtleties.
The data set contains a number of features that are awkward for traditional claim modeling (“traditional” here means those that stop short of a GLM framework). They include changes in all three of row, column and diagonal effects. Even within a GLM, considerable time and effort is required to explore these features thoroughly, and account for them satisfactorily in a model.
But the lasso-based procedure appears to identify them and model them relatively accurately. This reduces a claims modeling assignment from a duration of possibly several days of senior analyst time to a few hours of junior analyst time. It was found that the lasso model closely reproduces the forecasts of a manually and expensively custom built GLM. However, a custom built GLM is likely to provide a less abstract representation of the data, be more interpretable, and yield insight into the dynamics of the claim process with less analysis than would be required by the lasso for the same outcome.
One weakness that emerged was failure of the model to recognize instantaneous material changes such as might result from legislation with a drop-dead date for changes.
However, where the occurrence (though perhaps not the effectiveness nor efficiency) of such changes can be anticipated, as would be the case for legislation, the model is capable of modification in such a way as to enhance its recognition of the changes. This aspect was tested in the case of real data, and found satisfactory.
The proposed procedure is applicable to data at any level of granularity, from traditional aggregation to individual transaction level. The required set of basis functions may vary from one application to another, and time spent in careful choice of these will probably repay itself.
Estimation of prediction error may be performed by one of several bolt-on procedures that are already well known. Of particular note is the fact that one of them, non-parametric bootstrapping of the entire lasso, will provide an estimate of prediction error that includes at least a part of model error, as defined in (5.2).
To the authors’ knowledge, no other documented loss reserving procedure does this. Some papers consider such matters as parameter error in respect of the scale parameter but this does not fall within model error as defined here, which refers to error in the algebraic structure of the model. One might conjecture that some future machine learning methods that contemplate a universe of alternative model forms (e.g., neural nets) will be able to do so.
It must be said that the lasso-based procedure discussed here can be computer-intensive. While a fit to an aggregate triangle data can be relatively fast, a single model fit (with cross-validation) to a large unit record dataset was not possible on a relatively heavy-duty PC.
A few cautionary comments. First, although the model can accurately estimate past effects, such as variations in SI and variations in claim payment delays due to changing rates of claim settlement (and others), it is not an oracle. It cannot pronounce on future rates of SI and claim settlement. These must be inserted “by hand” into any forecasts.
The unsupervised procedure suggested here amounts to a form of machine learning. One would be well advised, in handing control of one’s destiny to a robot, to maintain strict surveillance to ensure adequate performance of the robot.
Although an unsupervised procedure is proposed, it would be advisable to supplement it with strong back-end supervision. This would consist of a number of comparisons of the model with the data to which it is fitted. Examples (by no means exhaustive) appear in Sections 4.3.2 and 4.4.2, and include actual-to-fitted heat maps, plots of actual and fitted response against major individual covariates (AQ, DQ, etc.), and extraction of specific model effects.
Acknowledgment
The authors acknowledge the valuable assistance of Josephine Ngan of the University of New South Wales in the modeling documented in this paper.
The research reported here received financial supported under Australian Research Council’s Linkage Projects funding scheme (project number LP130100723).
An earlier, but similar version, of this paper was posted on the Social Science Research Network (abstract_id=3241906) in 2018.