Pricing Cyber Insurance for a Large-Scale Network

1. Introduction

Over recent years, cyber insurance has become increasingly important as our society has relied more and more on the cyber domain for almost all aspects of daily life and work. However, there have been only a few research projects dealing with modeling and assessing cyber risks. Among the obstacles that have prevented the cyber insurance market from achieving maturity are the absence of reliable actuarial data and the reluctance of IT to reveal its infrastructures, both of which make actuarial modeling even more challenging (Betterley 2017; Kosub 2015; Xu and Hua 2019).

Traditionally, ratemaking relies on actuarial tables constructed from experience studies. Unlike traditional insurance policies, cyber insurance has no standard scoring systems or actuarial tables. Cyber risks are relatively new, and there are very limited data about security breaches and losses. This difficulty in finding data is further exacerbated by the reluctance of organizations to reveal details of security breaches to avoid losing market shares, reputation, etc. Pricing cyber insurance is still a challenging task, although demand for insurance has been increasing and there are insurance companies providing cyber insurance products. According to Betterley’s report (Betterley 2017), the insurers tend to increase premiums for larger companies, and coverage can be limited and very expensive for companies without good cyber-security protection. The main feature that distinguishes cyber risks from traditional insurance risks is that the information and communication technology resources are interconnected in a network. We are interested in understanding how interconnected risks might affect each other. Most recently, Xu and Hua (2019) proposed a general framework for modeling the infection and recovery processes of a network while accounting for various costs and risks that might arise from those processes. This method models the cyber risk from a micro-level perspective, which works very well if the exact network structure is known. However, in practice, it may be unfeasible to determine the exact structure of a network due to the confidentiality of IT infrastructures, scales, and the complexity of real-world networks. For example, the network for financial transactions of a bank can be extremely complicated, and pricing cyber insurance based on such a network becomes impractical if it is necessary to know the exact structure of the network. Therefore, to tackle this challenging issue, we propose a novel approach that models cyber risk from a macro-level perspective using some basic specifications of a network. But it must be noted that there are some other factors, such as network design principles, that may affect a network’s susceptibility to cyber risks.

The work most closely related to the topic of cyber risk from the macro level is by Eling and Wirfs (2019), in which the cost of cyber risks was studied by using data from SAS OpRisk Global Data. The research adopted a loss-distribution approach, which considers the loss frequency and severity, and deployed the extreme-value theory to study the loss distribution. Although this work provides a deeper understanding of cyber risks, it does not consider the network characteristics, which we believe to have significant effects on the cyber risk of a specific company. Our approach aims to provide further understanding about how network characteristics affect cyber losses on a macro level. Specifically, for a large-scale network, knowing the exact structure is often unfeasible, but knowing some basic quantities, such as the numbers of nodes and edges, could help to describe the basic features of the complex network. For underwriting purposes, it is more practical to be able to consider premiums without knowing the exact structure of the network. Also, physical network structures are likely to be different than logical network topologies, which describe how data flow within a network. To this end, we employ scale-free network structures for the mechanism of generating underling network topologies. The so-called scale-free structures exist widely in the real world; Barabási (2016) offers many real-world examples of scale-free networks. Instead of needing to know the exact network structure, we will only need to know some network statistics, including the number of nodes, the number of edges, and the degree distributions, to abstract the network. One of our main tasks is to understand how those network features affect cyber risks.

We develop a simulation-based approach for assessing potential cyber risks on a large-scale network given a set of underwriting information. The study in this paper is innovative in the following aspects: (1) it accounts for the randomness of networks and only requires summary information about the network to conduct the simulations; (2) it adapts and implements a new and more reasonable mechanism (different from the algorithm of Xu and Hua 2019), for the processes of risk infection and risk recovery, which allows both infection and recovery to continuously evolve over time; and (3) it conducts an extensive simulation study based on the implemented simulation algorithms, uncovering insights into how factors such as network features contribute to the frequency and magnitude of cyber risks.

The paper is organized as follows: Section 2 introduces the proposed approach and algorithm, and Section 2.1 introduces the basic concepts of scale-free networks. Section 3 explains the simulation study we conducted to understand the mechanism of risk spreading and recovering and the statistical effects on cyber risks. Section 3.2 reports the findings about the statistical effects of various predictive variables on the cyber risks to uncover the most important underwriting risk factors. Section 4 demonstrates how to use the proposed approach to price a specific large-scale network. Section 5 concludes the paper with further discussion of the application of the proposed approach.

2. The Proposed Approach

Ratemaking for cyber risks on a large-scale network is very challenging, especially considering that network topology and risk-spreading and risk-recovering mechanisms themselves can be very complicated and that there are very few relevant data sets available. To address these issues, our approach is based on synthetic data that can account for a variety of scenarios with respect to network topology and interactions between infection and recovery activities.

A model for loss frequency and severity based on a large-scale network can be the following. Let G(V, E) denote an undirected graph with n nodes represented by V and m edges represented by E. A node abstracts a computer (or server or working station) at an appropriate resolution depending on the insuring interest, and the graph abstracts the communication network of a company.

Let random variables N and Z be the number of loss events during a unit time period and the loss severity, respectively. For a given graph G and some other covariates X_N, the conditional number of loss events is $N|\left( G,X_{N} \right) \sim F_{N|\left( G,X_{N} \right)}\left( 𝒢,\theta \right)$, where $𝒢$ is the collection of attributes that are associated with the graph itself, such as number of nodes and edges, and θ is the collection of the parameters for the other covariates, such as average waiting time to infection and to recovery, respectively. Further, the loss severity Z, such as the cost of replacing a node, does not depend on the network G, and it may depend on some other predictive variables X_Z. For example, the cost of replacing a node is generally an inconsequential fraction of the cost of a breach event. We can write $Z|X_{Z} \sim F_{Z|X_Z} (\alpha),$ where α is the collection of parameters for the predictive variables. Let Z₁, . . . , Z_n be independent copies of Z, and Z and N are independent. Therefore, the aggregated loss for the graph G can be written as

$$S|\left( G,X_{N},X_{Z} \right) = \sum_{i = 1}^{N|\left( G,X_{N} \right)}{Z_{i}|X_{Z},}$$

and then

$$\mathbb{E}\left\lbrack S|\left( X_{N},X_{Z} \right) \right\rbrack \approx \frac{\sum_{j = 1}^{|J|}\left\lbrack \mathbb{E}\left\lbrack N|\left( G_{j},X_{N} \right) \right\rbrack\mathbb{\cdot E}\left\lbrack Z|X_{Z} \right\rbrack \right\rbrack}{|J|}, \tag{1}$$

where the $(G_1, \dots, G_{|J|})$ is a random sample of G, and using a sampling scheme provided by Goh, Kahng, and Kim (2001), in which G is of a scale-free network, J is the collection of indexes, and $|J|$ is its cardinality (the number of simulated networks). The variability of S can be assessed similarly based on the simulations. The approximation in equation (1) should be sufficiently accurate when J is large enough. (For sampling from a scale-free network, refer to Goh, Kahng, and Kim 2001; Chung and Lu 2002; and Cho et al. 2009).

Here, we notice that the network topology and the risk-spreading scheme are assumed only to affect the loss frequency, while the loss severity Z does not depend on either the network structure or how the cyber risks spread. This assumption is reasonable as loss severity (such as the cost of labor and replacements for recovering a node) has usually been standardized and does not depend on the network itself. That being said, one of the main tasks of this paper is how to tackle the modeling task for the loss frequency $N|(G, X_N),$ for which both network structures and the risk-spreading scheme may play an important role.

2.1. Scale-free network

To account for the randomness of large-scale network structures, we consider using scale-free networks as the underling network structures. (For many examples of scale-free networks in the real world, refer to Barabási 2016.) When a network is too large and its exact structure is impossible to describe, such as a financial transaction network or Internet traffic network, summary statistics often are used to describe the structure of the network. Among those summary statistics associated with a network, the number of nodes, the number of edges, and the degree distribution of the network are the most basic statistics. The degree of a node indicates the number of edges connected to the node, and the degree distribution describes how the node degrees are distributed over a network. Let a random variable K represent the node degrees, and then p_k = $\mathbb{P}$[K = k] is the probability mass function of K. When K follows a power-law distribution in the sense that p_k = ak^−γ with constants a > 0 and γ > 0, the network is referred to as a scale-free network; for most real-world examples of scale-free networks, the range of the index γ is between 2 and 3 (see Barabási and Albert 1999; Barabási 2016). This paper will focus on undirected scale-free networks, as such a property has been found in many different commonly used networks that are relevant to cyber risks, such as the Internet at the router level and email networks in which two directly connected nodes can communicate with each other in both directions. (For details about scale-free networks, refer to Barabási and Albert 1999 and Barabási 2016; and for terminology and statistical inference about network analysis, refer to Brandes and Erlebach 2005 and Kolaczyk 2009.)

2.2. A novel model and its related simulation algorithm

Given the number of nodes, the number of edges, and the degree distribution, networks can be generated from a static scale-free random graph that preserves these given properties (see Goh, Kahng, and Kim 2001; Chung and Lu 2002; Cho et al. 2009). Synthetic data, and thus estimated risks associated with a randomly sampled network, can then be obtained based on a risk-spreading and risk-recovering algorithm that will be discussed in detail in the Appendix. By altering the sets of values of basic network statistics (n, m, γ), as well as the cost functions and the assumptions for infection and recovery processes, various cyber risks associated with the random network (of which only basic network statistics are known) can be assessed. The synthetic data can then be used to calibrate the model so that a relatively flexible, but simplified, pricing model can be developed.

Due to the lack of available data for many of the factors that may affect cyber risks and corresponding losses, our approach and algorithms provide a flexible tool for conducting computer experiments based on the following factors:

• Number of nodes of the network

• Number of edges among the nodes

• Index γ of the scale-free network

• Number of initially affected nodes

• Dependence structure among the nodes

• Distribution of waiting time to infection

• Distribution of waiting time to recovery

To keep our framework more general, an infection is defined to be very broad, which can include infection of a computer by malware or a virus, theft of sensitive information or breach of data, or loss of control of computers or certain software (e.g., ransomware, distributed denial-of-service attack, etc.). The infection time can be interpreted as the time required to have or detect an infection. For example, for a data breach as an infection, the waiting time to infection can be interpreted as the time between two consecutive breaches. Similarly, the waiting time to recovery is also defined to be very broad and dependent on the practical scenario. For a malware infection, the recovery can be interpreted as the time needed to clean the malware, patch security vulnerabilities, and bring the computer back to a functioning status. For a data breach, the recovery can be interpreted as the time needed to contain the breach. For example, the average time to contain a data breach was 69 days in 2018 according to Ponemon Institute (2018).

Although some of these assumptions are not, in general, easy to specify, the simulation models at such a level of granularity provide a useful platform for creating synthetic data while accounting for the uncertainty of those factors. A feasible approach is to consider different possibilities for those assumptions and then employ the proposed model to conduct simulations. Afterward, assessment of potential cyber risks and losses can be done by analyzing the synthetic data. It should be noted that the aim is to develop an efficient and flexible algorithm for understanding how cyber risks might evolve on a complex large-scale network. It is out of the scope of this paper to discuss how to choose assumptions with no available relevant data. We believe that assumptions can be based on experts’ experiences, experienced data (e.g., published reports from Ponemon Institute), or both. When corresponding data is available, statistical inference for the assumptions should be a relatively easier task. The proposed approach is suitable for various assumptions and, in what follows, the models and algorithms will be discussed for cases in which the assumptions are given. After discussing the models, we will conduct simulations and case studies to understand the risk-spreading and risk-recovering mechanism, to uncover the most important underwriting risk factors, and to demonstrate how to use the proposed approach for pricing a large-scale network, for which the uncertainty of the assumptions will have been accounted.

Boguná and colleagues (2014) proposed a method for simulating mutually independent non-Markovian stochastic processes. In this paper, we relax the independence assumption and propose a new method of simulating dependent non-Markovian stochastic processes. The technical details of the proposed model and the algorithm for simulations are included in the Appendix. Here, we briefly summarize the basic idea of the algorithm. Given a network with nodes (e.g., computers) and links (e.g., cables or wireless communication, or both), the proposed simulation algorithm includes two types of stochastic processes: (1) the recovery process, wherein each infected node can be recovered according to a stochastic recovery process; and (2) the infection process, wherein each healthy node can be infected via the vulnerable link in a stochastic infection process. The status of each node, either healthy or infected, is determined by the interaction of these two types of processes. The proposed algorithm allows all the involved processes to evolve during a certain time period, and it allows the node status to change. Based on the algorithm, we can simulate the evolution of infection over a network, that is, how the infection is spreading or recovering, or both, over a network during a time period. Because the assumptions of the stochastic processes, as well as the specifications of the network, may affect how the risks are evolving, we can use the algorithm to simulate different scenarios and generate synthetic data to study risk factors.

3. Simulation Study

In this section, we explain how we conducted extensive simulation studies to understand how network characteristics affect the cyber risks. Section 3.1 explains how we first conducted an exploratory analysis on a network with a fixed number of nodes and edges to focus on understanding the risk-spreading and risk-recovering mechanism. Then, Section 3.2 explains how we conducted a formal statistical analysis on the effects of various factors, including the number of nodes, the number of edges, etc. Sections 3.3 and 3.4 discuss the effects on accumulated infected nodes and accumulated recovered nodes, respectively.

3.1. Exploratory analysis

We first carried out simulations to study the source of variability of cyber risks based on networks with a given number of nodes and edges. Due to its flexible shape and tail behavior, a Weibull distribution in the following form was chosen for both the random time to recovery and the random time to infection:

$$\overline{F}(\tau) = \exp\left\{ - \left( {μτ} \right)^{\alpha} \right\},\ \ \ \ \mu,\alpha > 0$$

As in reality, most scale-free networks have the γ parameter in the range of (2, 3), and we chose 2.1, 2.5, and 2.9 as three values of γ. For the purpose of simulation, without knowing the exact dependence structure of a complex network dependence, we can use a multivariate Gaussian copula in order to gain some basic ideas about how dependence affects overall cyber risks. The following is the cumulative distribution function (CDF) of a d-dimensional Gaussian copula where Σ is the correlation matrix of the d-dimensional standard multivariate normal CDF Φ_d, and Φ is the CDF of the standard univariate normal distribution:

$$C\left( u_{1}, \dots ,u_{d} \right) = \Phi_{d}\left( \Phi^{- 1}\left( u_{1} \right), \dots ,\Phi^{- 1}\left( u_{d} \right),\Sigma \right)$$

The D_k in equation (A.1) can then be written as

$$D_{k}\left( u_{1}, \dots ,u_{d} \right) = \Phi_{d|k}\left( \Phi^{- 1}\left( u_{1} \right), \dots ,\Phi^{- 1}\left( u_{d} \right);\mu_{d|k},\Sigma_{d|k} \right),$$

where $\Phi_{d|k}$ is the CDF of the multivariate normal distribution with mean $\mu_{d|k} = \left( \rho_{{ik}};i \neq k \right)^{\intercal} \cdot \Phi^{- 1}\left( u_{k} \right)$ and correlation matrix $\Sigma_{d|k}$, and the R function partial.r{psych} can be used to get the partial correlation matrix. Because the dependence is the random waiting time to infection on the nodes that are connected directly to the infected node, it is reasonable to assume that there is only positive dependence. Therefore, in what follows, we assumed positive dependence in the Gaussian copula to make the large-scale simulation more tractable. The proposed algorithm was employed to conduct the simulation analysis. Here, we assumed that initially there was 1 infected node, and the correlation coefficient was assumed to be 0.5. We relaxed these assumptions to be more flexible when we studied the statistical effects from various factors in Section 3.2. Table 1 contains the simulation settings and the corresponding results for five different representative cases.

Based on cases A, B, and C from Table 1, the values of γ did not have a strong effect on cyber risks in terms of the average total service-down time per node and per month, denoted as node × month, and the average total number of recovered nodes. However, based on cases C, D, and E, both the random time to infection and the random time to recovery dramatically affected cyber risks. In particular, when the time to recovery is not much smaller than the time to infection, cyber risks can be greatly increased.

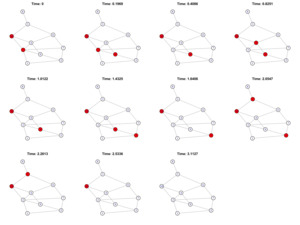
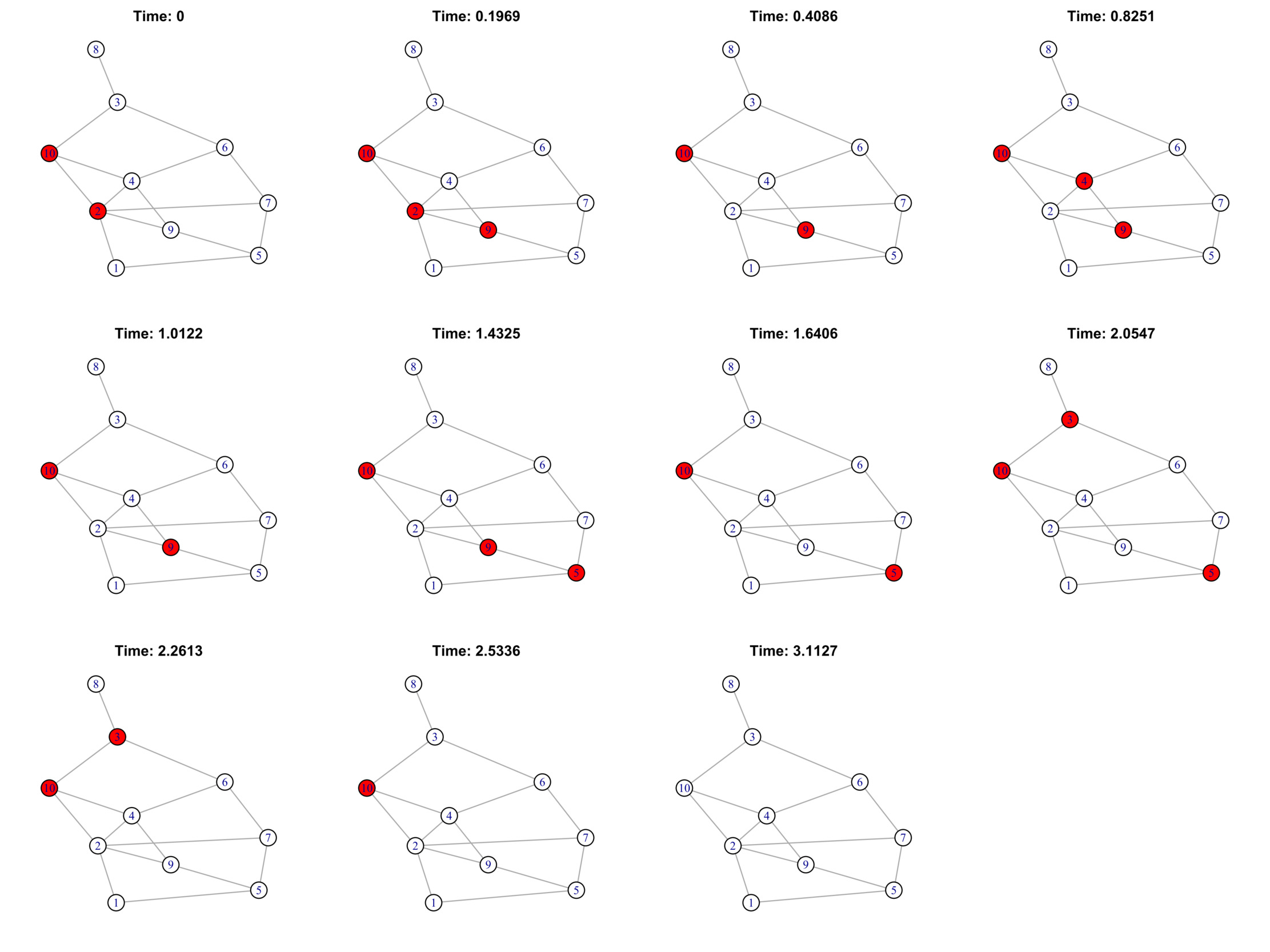
Figure 1 illustrates the trajectories of the numbers of infected nodes for cases A, B and C, respectively, with 800 randomly developed trajectories for each case. Note that with the same number of nodes and the same number of edges, different γ ∈ (2, 3) for the scale-free network does not lead to significantly different development patterns of the infected nodes. This observation is consistent with the numbers reported in Table 1 as well.

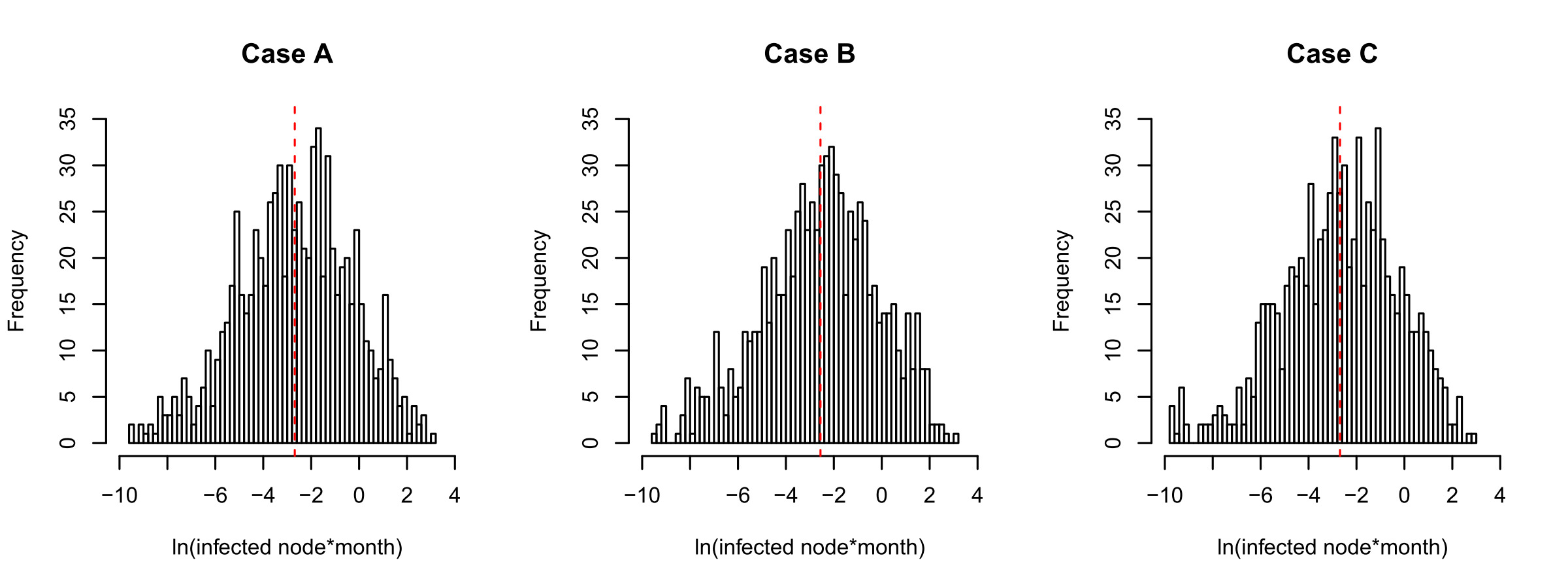
Figure 2 shows the histograms of the natural logarithm of the accumulated infected nodes × month for cases A, B, and C, respectively. The vertical red dashed lines are the corresponding sample means. Again, the patterns are quite similar although the γ’s are different.

We can conclude from the above comparisons that, given that other factors are the same, the γ parameter for the scale-free network may not affect overall cyber risks significantly. In Section 3.2, another study with various factors involved, such as different numbers of nodes and different numbers of edges, suggests that γ is not statistically significant in affecting cyber risks.

Figure 3 illustrates the trajectories of the numbers of infected nodes for cases D and E, respectively, with 800 randomly developed trajectories for each case. Note that with the same number of nodes and the same number of edges, the random time to infection and the random time to recovery play a very important role in affecting the process of risk spreading and recovering. Unlike the cases in Figure 1, cases D and E here have a relatively slower speed for recovery compared with that for infection. Therefore, the number of infected nodes increases significantly over time. When the recovery speed is slow enough, such as in Case E, it is most likely that the number of infected nodes will increase dramatically until almost all are infected. In this case, the whole network will have a very slim chance of complete recovery.

Figure 1.Infected nodes over time, cases A, B, and C

Figure 2.Histograms of the natural logarithm of accumulated infected nodes × month, cases A, B, and C

Figure 3.Infected nodes over time, cases D and E

Figure 4 shows the histograms of the natural logarithm of the accumulated infected nodes × month for cases D and E, respectively. The vertical red dashed lines are the corresponding sample means. It is interesting to note that there tend to be two modes for the distributions of the accumulated infected nodes × month when the time to recovery gets closer to the time to infection, which is clearer in Case E. A possible reason for this is that, in the network system, recovery and infection are competing with each other, and when one of these two competing factors dominates, it tends to dominate the whole system.

Figure 4.Histogram of the natural logarithm of accumulated infected nodes × month, cases D and E

3.2. Statistical analysis

This section explains our formal study of the statistical effects of various factors on cyber risks based on synthetic data. The purpose of using different factors is to identify the important variables that must be included in candidate models for pricing cyber risk insurance. Our approach was to randomly choose the values of the parameters associated with the model, and then conduct simulations to generate synthetic data for further statistical analysis. We generated a random sample size of 800 within the time frame T = 12. The following predictive variables were considered:

• par_cop: the common correlation coefficient ρ of the Gaussian copula (from 0.1 to 0.9)

• mean_rec: the population mean of the Weibull distribution for the random waiting time to recovery (from 0.1 to 1.0)

• var_rec: the population variance of the Weibull distribution for the random waiting time to recovery (from 0.1 to 1.0)

• mean_inf: the population mean of the Weibull distribution for the random waiting time to infection (from 0.1 to 6.0)

• var_inf: the population variance of the Weibull distribution for the random waiting time to infection (from 0.1 to 6.0)

• Nnode: the number of nodes (from 20 to 100)

• Nedge: the number of edges (from 80 to 400)

• Gam: the γ parameter for the scale-free network (from 2 to 3)

• Ninf0: the initial number of infected nodes (from 1 to 5)

In order to check that the predictive variables were roughly balanced and mutually independent, we first standardized them, except for the variable Ninf0, and then drew the scatter plots. Figure 5 shows the scatter plots of 100 randomly chosen points for these covariates, and there seems to be no multicollinearity and the data are roughly balanced.

Figure 5.Scatter plots of standardized covariates

Two main response variables are of interest: Tinf, the accumulated infected nodes × month, and Nrec, the accumulated number of recovered nodes. These two variables directly affect the number of losses. For example, Tinf may lead to losses due to the shutdown of services, and Nrec is directly associated with repair and replacement costs, which, however, are not generally significant costs in a cyber insurance claim.

Based on the ranges of the predictive variables, we used some strictly increasing transformations, such as the logit and natural logarithm (ln) functions, to make the ranges of the variables be (−∞, ∞) in order to have relatively stable numerical performance when regression analyses were conducted with computer software. Refer to tables 2 and 4 for details on how such transformations were employed and for their corresponding estimates.

3.3. Effects on the accumulated infected nodes and time

For the response variable Tinf, we tried several different models, such as linear models and generalized linear models based on the gamma distribution and the inverse Gaussian distribution. After trying the Box-Cox transformation with the help of the R function boxcox(), we found that the optimal value of λ of the Box-Cox transformation was −0.02 for the data. Since this value was very close to zero, we could simply transform the response variable by the natural logarithm. Afterward, a multiple linear regression could be used to assess the effects of the predictive variables. The following linear regression model was chosen to assess the effects of the predictive variables:

$$\begin{align} \ln ( \text{Tinf} ) \sim &\ \text{logit(par_cop)} + \ln ( \text{mean_rec} ) + \ln ( \text{mean_inf} ) \\ &+ \ln ( \text{var_rec} ) + \ln ( \text{var_inf} ) + \ln ( \text{Nnode} ) \\ &+ \ln ( \text{Nedge} ) + \text{logit(Gam-2)} + \text{Ninf0} \end{align}$$

Tables 2 and 3 show the corresponding estimates and the analysis of variance (ANOVA) table, respectively. There are several interesting findings suggested by the analysis. First, from Table 3, we found that average recovery time and infection time contributed most to the variability of the accumulated infected nodes × month, and the initial number of infected nodes played a relatively important role. However, after controlling for the other variables, the number of nodes and the number of edges in the network did not affect the response variable as much as the aforementioned leading factors. This suggests that assumptions about average recovery and infection time are the most critical, while assumptions about network features, such as number of nodes, number of edges, and the γ parameter, are relatively less important. Second, we found that the dependence parameter did play a role here, although it was not very important. Under such a simulation setting, a more mutually dependent network tended to lead to a relatively smaller Tinf (see Table 2). A reasonable interpretation is related to equation (5), where relatively stronger upper-tail dependence might lead to a larger value of $\Phi (\tau | \left\{ t_{j_{s}},r_{j} \right\}$), thus a larger probability that no infection would occur in the next time period of τ. However, in general there were no deterministic results about the direction of the effect from dependence. Third, the directions of the effects from the significant predictive variables were consistent with our intuition based on Table 2. For example, a larger time to recovery and a smaller time to infection tended to increase Tinf, and a larger number of initially infected nodes tended to increase Tinf as well. Fourth, as we already observed from Section 3, the γ parameter for the scale-free network was not significant at all after controlling all the other variables, which removes concern about any influence from the index of scale-free networks.

3.4. Effects on the accumulated recovered nodes

For the response variable Nrec, we tried generalized linear models based on the Poisson distribution and the negative binomial distribution, respectively. A test of overdispersion proposed by Cameron and Trivedi (1990) indicated that the negative binomial was more suitable, and for it, we employed the R function dispersiontest() in the AER package. The following negative binomial model was chosen to assess the effects of the predictive variables:

$$\begin{align} \text{Nrec} \ \sim &\ \text{logit(par_cop)} + \ln ( \text{mean_rec} ) + \ln ( \text{mean_inf} ) \\ &+ \ln ( \text{var_rec} ) + \ln ( \text{var_inf} ) + \ln ( \text{Nnode} ) \\ &+ \ln ( \text{Nedge} ) + \text{logit(Gam-2)} + \text{Ninf0} \end{align}$$

Tables 4 and 5 show the corresponding estimates and the Type III analysis, respectively. The patterns of the effects from the predictive variables on Tinf were quite similar to those on Nrec. For instance, based on Table 5, average infection time and recovery time contributed most to the variability of the accumulated number of recovered nodes, and after controlling the other variables, the number of nodes and the number of edges in the network did not affect Nrec as much as the leading factors. This, again, suggests that assumptions about average recovery and infection time are the most critical ones. Moreover, the γ parameter again did not play a significant role. Like the case for Tinf, the dependence parameter also played a significant role with stronger dependence leading to fewer recovered nodes.

4. Case Study

In Section 3, we used a relatively small network to study the statistical effects of various factors. However, when the network of interest is much larger, simulations need to be conducted accordingly, based on the actual specifications of interest. In this section, we consider a particular case of much larger networks, and we demonstrate how to assess the potential cyber risks under the proposed framework and how to use the proposed model to price cyber insurance for a large-scale network.

The following are the assumptions considered for this particular example:

1. The network is large, with 100 to 5,000 nodes and 400 to 20,000 edges.

2. The network is scale free and the λ parameter is from 2 to 3.

3. The policy term is 12 months (T = 12).

4. The waiting time to both infection and recovery follows a Weibull distribution. Moreover, the average and the standard deviations of the random time to recovery are from 0.1 to 1.0 month, respectively, and those of the random time to infection are from 0.1 to $\sqrt{6}.0$ months, respectively.

5. The dependence structure among the random waiting time to infection of the nodes that are linked to the same affected node is a Gaussian copula with the pairwise correlation coefficient ρ, which can take a value from 0.1 to 0.9.

6. The cost of recovering a node is η and the loss-of-service interruption per node × month is ω.

Note that these assumptions cover a very wide range of cases due to the following aspects: (1) the numbers of nodes and edges are quite flexible; (2) only the distribution family for the random waiting time is assumed, and the mean and variance can be chosen based on the real applications; and (3) the dependence structure covers a wide range of positive dependence.

Similar to the study in Section 3.2, we first generated synthetic data based on the above assumptions and a sample size of 1200. We checked that there was no multicollinearity of the covariates and the data were balanced across different variables.

For Tinf, the Box-Cox transformation was applied to transform the response variable Tinf to roughly follow a normal distribution. A multiple linear regression model was then fitted with all the covariates being included; the ANOVA table is Table 6. It suggests that the following variables do not contribute significantly to the model: par_cop, var_inf, Nnode, Nedge, and Gam.

Then, we excluded the insignificant variables (except var_inf because, otherwise, the exact distribution for the random waiting time to infection cannot be specified). Then, for the candidate model, the estimated parameter $\widehat{\lambda}$ = 0.1818182 for the Box-Cox transformation; the ANOVA table and the estimates are shown in tables 7 and 8, respectively.

For Nrec, the Poisson regression and the negative binomial regression were compared, and the overdispersion test suggested that the negative binomial regression model was more suitable. An initial model with all the variables included led to the Type III analysis shown in Table 9. It shows that par_cop, var_rec, and Nnode did not contribute to the deviance significantly; and although the variables Nedge and Gam appear to be statistically significant, they contributed only marginally to the deviance.

Based on that consideration, we chose the same set of predictive variables for the candidate model for the response variable Nrec that we chose for Tinf, and used the following model:

$$\begin{align} \text{Nrec} \ \sim &\ \ln ( \text{mean_rec} ) + \ln ( \text{mean_inf} ) + \ln ( \text{var_rec} ) \\ &+ \ln ( \text{var_inf} ) + \text{Ninf0} \end{align}$$

The Type III analysis and the estimated regression parameters are reported in tables 10 and 11, respectively.

With estimates from the candidate models for both Tinf and Nrec (tables 8 and 11, respectively), the expected total loss can then be estimated as

$$\mathbb{E}\lbrack S\rbrack = \omega \cdot \mathbb{E}\left\lbrack \text{Tinf} \right\rbrack + \eta \cdot \mathbb{E}\left\lbrack \text{Nrec} \right\rbrack . \tag{2}$$

Knowing the values of ω and η, the predicted total loss $\widehat{S}$ can be trivially calculated based on equation (2). Table 12 contains the predicted Tinf and Nrec and their standard errors (SE). The last two columns of the table are based on a case where the values of ω and η are specified, for which a detailed discussion follows.

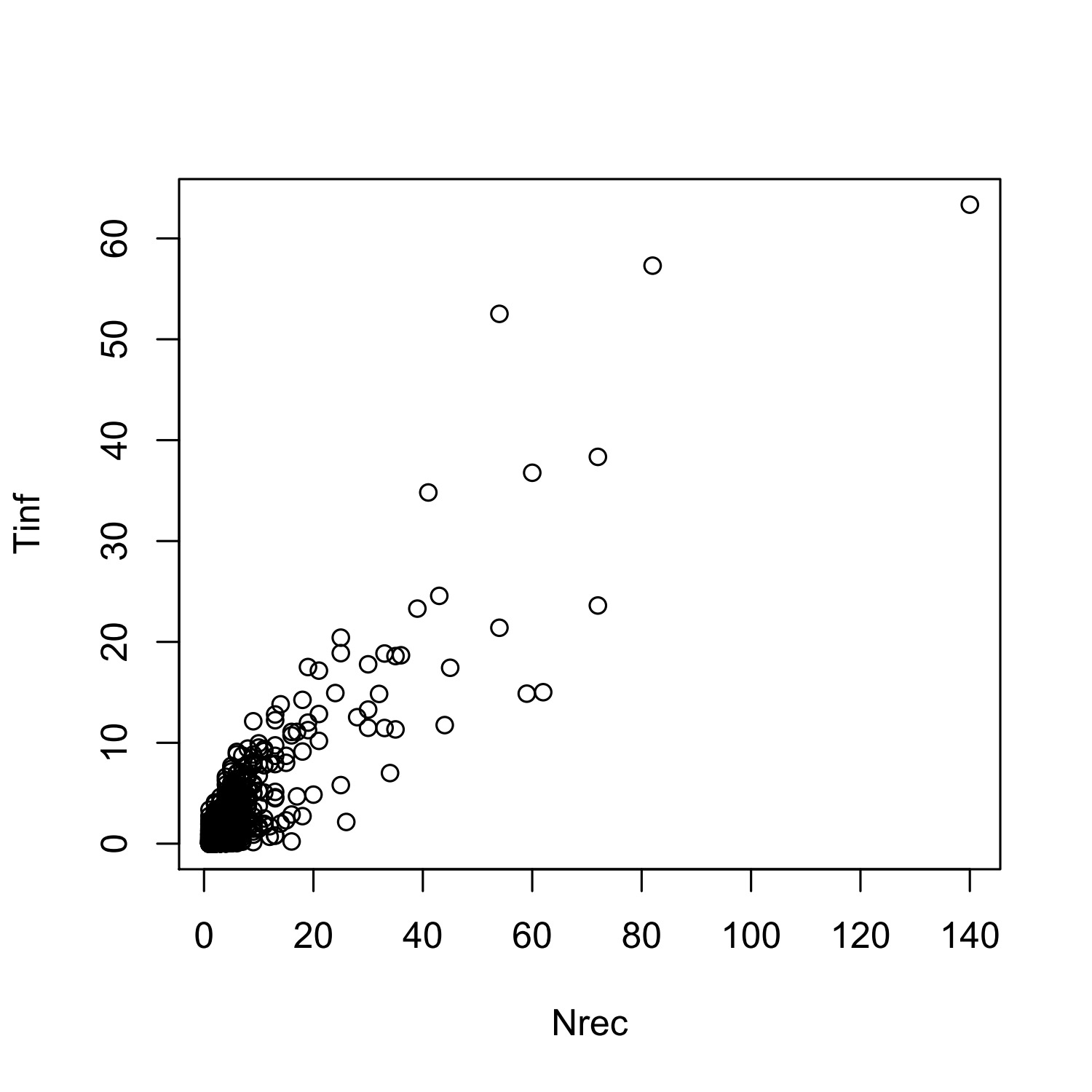
In order to assess the standard error of $\widehat{S}$, the covariance between $\widehat{\text{Tinf}}$ and $\widehat{\text{Nrec}}$ must be considered. A theoretically ideal method is to model the covariance between Tinf and Nrec conditioning on different values of the predictive variables. However, the scatter plot (see Figure 6) between them indicates that the dependence is very strong, and the calculated correlation coefficient is about 0.88. Under such a situation, a conservative method can be used to assess the standard error of $\widehat{S}$, in which an upper bound of the covariance between $\widehat{\text{Tinf}}$ and $\widehat{\text{Nrec}}$ is considered. Therefore, using the Cauchy-Schwarz inequality,

$$\begin{align} \text{var}(S) \leq \ &\omega^{2}\text{var}\left( \text{Tinf} \right) + \eta^{2}\text{var}\left( \text{Nrec} \right) \\ &+ 2\omega\eta\sqrt{\text{var}\left( \text{Tinf} \right)\text{var}\left( \text{Nrec} \right)}. \end{align}$$

For example, assume that ω = USD$50,000 and η = USD$20,000. Then, the predicted $\widehat{S}$ and its standard error are calculated as shown in the last two columns of Table 12.

Figure 6.Scatter plots for Tinf and Nrec in the case study

This case study provided some interesting findings. First, the number of nodes and the number of edges may not be that important in determining the overall cyber risks under the proposed framework and assumptions. This may be because the numbers of nodes and edges are already large enough to allow cyber risks to spread and recover freely. The most important factors are how fast the risks are spreading, how fast the infected nodes are recovered, and how many nodes have initially been infected. Estimates of overall cyber risks can be very sensitive to changes in those factors. Second, although the dependence structure may affect the overall risks, it plays a marginal role. Two aspects should be noticed about the role of dependence structures: (1) the dependence structure is assumed only on the random waiting time to infection, and, in reality, dependence among other factors may exist; and (2) there are no deterministic results about the direction of the effects from the dependence structure; it might increase or decrease the overall risks.

5. Conclusion

To address the shortage of credible data for pricing cyber insurance for a large-scale network, we propose a novel approach based on synthetic data generated by a flexible risk-spreading and risk-recovering algorithm. The proposed algorithm is able to allow the sequential occurrence of infection and recovery over the term and the dependence of the random waiting time to infection. The proposed approach provides a more practical way for assessing the cyber risks of a large-scale network while only requiring a reasonably small set of underwriting information.

After many simulation studies and a case study, we found that, in pricing cyber insurance for a large-scale network, the most important factors that deserve higher attention and priority are (1) the random waiting time to infection, (2) the random waiting time to recovery, and (3) the number of infected nodes at the beginning of the term. Other factors, such as the number of nodes, the number of edges, and the degree of the scale-free network, are much less important compared with those leading factors. This conclusion holds at least within the conducted studies and assumptions, and for it to hold under other scenarios, we think that the number of initially affected nodes must be much smaller than the number of the nodes and edges of the whole network to allow risk spreading and risk recovery without constraint coming from the network topology itself.

A potential limitation of the proposed risk-spreading and risk-recovery algorithm is that it does not account for self-infection or an infection that does not link to any other nodes, such as an infection from USB flash drive attack. Under an intranet environment or some other internal network with restricted access to USB flash drives and any other outside networks, the issue becomes minimal. Otherwise, practically, one can either artificially add one node connected by one edge to each existing node for the simulations or use the aforementioned overall vulnerability score system to factor in self-infection risks.