Approximating the Aggregate Loss Distribution

Dmitry E. Papush; Aleksey S. Popelyukhin; Jasmine G. Zhang

1. Introduction

Aggregate loss distributions have extensive applications in actuarial practice. The modeling of aggregate losses is a fundamental aspect of actuarial work, as it bears on business decisions regarding many aspects of insurance and reinsurance contracts. Our purpose in this study is to determine the best statistical distribution with which to approximate the aggregate loss distribution for property and casualty business with applications to quota share agreements.

When separate data on loss frequency and loss severity distributions is available, actuaries can approximate the aggregate loss distribution using such methods as the Heckman-Meyers method (Heckman and Meyers 1983), the Panjer method (Panjer 1981), fast Fourier transform (Robertson 1992), and stochastic simulations (Mohamed, Razali, and Ismail 2010). However, sometimes only aggregate information is available for analysis. In such a case, the choice of the shape of the aggregate loss distribution becomes very important, especially in the “tail” of the distribution. The tail is often the part of the distribution that is most affected by policy limits, and a failure to model the tail correctly can lead to an overestimation of the discount given to loss ratios due to the application of policy limits.

Previously published papers debate the appropriateness of various aggregate loss distributions. Dropkin (1964) and Bickerstaff (1972) showed that the lognormal distribution closely approximates certain types of homogenous loss data. Pentikäinen (1987) suggested an improvement of the normal approximation using the so-called NP method. He compared this method with the gamma approximation and concluded that both methods yield reasonable approximations when the skewness of aggregate losses is less than 1, but that neither method is accurate when the skewness is greater than 1. Venter (1983) suggested the transformed gamma and transformed beta distributions for the approximation of aggregate loss, while Chaubey, Garrido, and Trudeau (1998) suggested the inverse Gaussian distribution.

Papush, Patrik, and Podgaits (2001) analyzed several simulated samples of aggregate losses and compared the fit of the normal, lognormal, and gamma distributions to the simulated data in the tails of the distributions. This was a deviation from previous research, which was based solely on theoretical considerations. In all seven scenarios Papush, Patrik, and Podgaits tested, the gamma distribution performed the best. Therefore, they recommended the gamma as the most appropriate approximation of aggregate loss.

This research expands upon that 2001 study but retains the same general approach.

2. Method

2.1. Overview of the study

Initially, proceeding as in Papush, Patrik, and Podgaits (2001), we limit our consideration to two-parameter probability distributions. Three-parameter distributions often provide a better fit, but observed data is often too sparse to reliably estimate a third parameter. We compare the fit of five candidate distributions, shown in Table 1.

Table 1.Distributions used for the approximation of aggregate loss

Distribution	Parameters	Probability density function	Mean	Variance
Normal	$\mu$ — location $\sigma > 0$ — scale	$\frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}$	$\mu$	$\sigma^2$
Logistic	$\mu$ — location $s > 0$ — scale	$\frac{e^{-\frac{x-\mu}{s}}}{s \left( 1 + e^{-\frac{x-\mu}{s}} \right)^2} = \frac{1}{4s} \text{ sech}^2 \left(\frac{x - \mu}{2s} \right)$	$\mu$	$\frac{s^{2}\pi^{2}}{3}$
Gamma	$\alpha > 0$ — shape $\beta > 0$ — rate	$\frac{\beta^{\alpha} x^{\alpha - 1} e^{-\beta x}}{\Gamma (\alpha)}$	$\frac{\alpha}{\beta}$	$\frac{\alpha}{\beta^{2}}$
Inverse gauss	$\mu > 0$ — location $\lambda > 0$ — shape	$\left\lbrack \frac{\lambda}{2\pi x^3} \right\rbrack^{1/2} \exp \left\{ \frac{-\lambda (x - \mu)^2}{2\mu^2 x} \right\}$	$\mu$	$\frac{\mu^{3}}{\lambda}$
Lognormal	$\mu$ — scale $\sigma > 0$ — shape	$\frac{1}{x} \cdot \frac{1}{\sigma \sqrt{2\pi}} \exp \left( - \frac{(\ln x - \mu)^2}{2\sigma^2} \right)$	$e^{(\mu + \frac{\sigma^{2}}{2})}$	$e^{(2\mu + \sigma^2)}(e^{\sigma^2} - 1)$

Our analytic procedure is summarized in the following formal steps:

Choose frequency distribution and obtain severity distributions from Insurance Services Office’s (ISO’s) circulars or loss submission data.
Simulate the number of claims (N) and the individual loss amounts $(X_{1}, \ldots, X_{N}),$ put the individual loss amounts into per occurrence layers $(X_{1}^{l} \ldots, X_{N}^{l}),$ and calculate the corresponding aggregate loss $(S^{l} = \sum_{i = 1}^{N}X_{i}^{l})$ in each layer $l.$
Repeat this analysis many times (50,000) to obtain a sample of aggregate loss.
Fit the parameters of different candidate probability distributions.
Test the goodness of fit of the distributions and compare results.

2.2. Choice of software

We used the open-source statistical software tool R (R Core Team 2014) to perform our analysis. R is widely used in different actuarial contexts and is also popular in the sciences and social sciences.

In addition to the base version, R allows users to develop packages of functions and compiled code and upload them to the Comprehensive R Archive Network (CRAN). These packages can be freely downloaded for use. In our project, we used packages lhs (Carnell 2016), fitdistrplus (Delignette-Muller and Dutang 2015), NORMT3 (Nason 2012), gsl (Hankin 2006), actuar (Dutang, Goulet, and Pigeon 2008), and e1071 (Meyer et al. 2017).

2.3. Selection of frequency distribution

In actuarial science, the Poisson distribution is commonly used to represent the frequency of insurance claims. It has a memoryless property—that is, the number of claims in any time interval should not affect the number of claims in any other interval. This is a good approximation to what we observe in real data on claim frequency. We selected different mean frequencies (λ’s) to model small, large, and in some cases medium books of business. The selected mean frequencies can be seen in Tables 2a and 2b.

2.4. Selection of severity distributions

For casualty products, we used curves developed by ISO actuaries. The majority of ISO’s curves are mixed exponential distributions, which can be represented as sums of exponentials $f(x) = \sum_{i}^{}{w_{i}\frac{1}{\theta_{i}}e^{\frac{x}{\theta_{i}}}}.$ Each exponential distribution in the mixture has a different mean $\theta_{i}$ and a weight $w_{i},$ with the weight corresponding to the probability of the individual exponential distribution being chosen.

Table 2a shows the severity distributions we considered for casualty products, along with the means of the claim counts used, and the per occurrence layers we divided the individual losses into. Additional detail may be found in Section 2.6, “Layer descriptions.”

To model typical small commercial, middle market, and large commercial books of non-catastrophe property business, we chose distributions derived from ISO data for increasing amount-of-insurance (AOI) ranges. In addition, we simulated distributions based on representative samples of real-life losses.

Table 2a.Distributions used for casualty products

Distribution	Mean Poisson frequency, λ	Type of Severity distribution	Per occurrence layers
General liability: Premises and operations	100, 500, 1000	Mixed exponential (mean 35K)	250K x 0, 500K x 0, 1M x 0 750K x 250K, 500K x 500K, 4M x 1M
General liability: Products	Same as above	Mixed exponential (mean 135K)	Same as above
Commercial auto	Same as above	Mixed exponential (mean 45K)	Same as above
Errors and omissions: medium lawyers	50, 500	Lognormal (mean 250K)	1M x 0, 5M x 0
Directors and officers: public non–Fortune 500	50, 500	Lognormal (mean 1.3M)	10M x 25M

Table 2b.Distributions used for property, non-catastrophe

Distribution	Mean Poisson frequency, λ	Type of Severity distribution	Layers
Small commercial: AOI 5M to 6M	100, 500	Mixed exponential (mean 95K)	1M x 0, unlimited
Middle market: AOI 25M to 30M	Same as above	Mixed exponential (mean 175K)	Same as above
Large commercial: AOI 100M to 125M	Same as above	Mixed exponential (mean 285K)	Same as above
Non-catastrophe property 1	Same as above	Loss sample (mean 100K)	Same as above
Non-catastrophe property 2	Same as above	Loss sample (mean 110K)	Same as above

2.5. Simulation method

We used Latin hypercube sampling (LHS) to sample frequencies from the Poisson distribution and severities from each exponential component of the mixed exponential distributions before applying corresponding weights. We chose LHS over Monte Carlo simulation because it spreads sample points more evenly across all possible values so that samples drawn using LHS are more representative of the real variability in frequency or severity. In particular, since we were interested in studying the tail of the distribution for this study, LHS ensured that our simulation contained a reasonable sampling of high values. We implemented LHS using the randomLHS() function in the lhs package in R.

We used bootstrapping, the base function sample() in R, to choose which exponential component of the mixed exponential distribution to use and to bootstrap losses from the property loss submissions. This function allows the bootstrapping procedure to run very efficiently.

We sampled the losses from the loss submissions without replacement because we believe this provides a better representation of a true “year” of data: the same loss to the same property should not occur in the same year. Sampling without replacement also ensures that we do not obtain too many small losses in each year’s sample, and it thus prevents the understatement of aggregate loss.

2.6. Layer descriptions

We divided our simulated individual losses into the per occurrence layers included in Tables 2a and 2b. Using the following calculation we determined the amount of penetration of each simulated loss within a layer:

$\begin{align} Loss\ in\ Layer = &Min(Max ( (Aggregate\ Loss \\ &- RETENTION), 0 ), LIMIT), \end{align}$

where ${RETENTION}$ is the lower bound of a layer, possibly equal to zero, and ${LIMIT}$ is the width of the layer. For instance, for the layer $750K excess of $250K, ${RETENTION}$ would be $250,000 and ${LIMIT}$ would be $750,000. For the layer $1M excess of $0, ${RETENTION}$ would be $0 and ${LIMIT}$ would be $1M.

If none of the claims in one simulation penetrated one of the excess layers—i.e., “$4M x $1M” —the aggregate loss for that simulation was zero. This created a mass at zero in our distribution. Thus, the aggregate loss distributions we fitted were of this form:

$p_{0} + p_{1}*Candidate\ Distribution,$

where $p_{0} = \Pr\left\{ Aggregate\ Loss = 0 \right\},$ $p_{1} \equiv 1 - p_{0}$ and $Candidate\ Distribution \in \{ Normal,$ $Logistic,$ $Gamma,$ $Inverse\ Gauss,$ $Lognormal\}$ .

2.7. Estimating the number of simulations to run

Many studies (e.g., Papush 1997) use the central limit theorem to estimate the number of simulations necessary to achieve a reasonable degree of accuracy in the estimate of the mean. However, this study concentrates on approximating the tail of the distribution. To the best of our knowledge, there is unfortunately no established method for finding the number of simulations to run when the values of interest relate to the tail of a distribution. To ensure that we achieved a reasonable degree of accuracy of our results, we followed the method described as follows.

We started by running 1,000,000 simulations and calculating the 99th percentile of the resulting aggregate distribution. We then re-ran the same 1,000,000 simulations this time monitoring two metrics as we went through the simulation process. After each increment of 2,500 simulations we measured two quantities: the change in the 99th percentile of the distribution and the difference between the 99th percentile of the distribution from the cumulative set of simulations, compared with the 99th percentile of the distribution obtained as the result of our first run.

Using this approach, we were able to verify the following two assumptions. First, as the mean frequency of the Poisson distribution used in our simulation increases—that is, the size of our book—the accuracy of the 99th percentile will also increase. Second, as the per occurrence limit of the coverage decreases, the accuracy of the 99th percentile will increase.

Due to those two assumptions, we show only results for small-book scenarios with high per occurrence limits. Under 50,000 simulations, we have found that both metrics suggested an error of 1% or less for nearly all scenarios. For instance, we found that for premises and operations with a $1M per occurrence limit and a mean frequency of 100, we had an error of 0.8% after 25,000 simulations, while 50,000 simulations resulted in an error of 0.6%. Figure 1 shows graphs of the two metrics in this scenario (by number of simulations used). It is noteworthy to mention that the error was greater than 3% in only one scenario.

Figure 1.99th percentile simulation error

2.8. Parameter estimation

Parameter estimation was implemented using the function fitdist() in the R package fitdistrplus (Delignette-Muller and Dutang 2015). Initially, we used both maximum likelihood and the method of moments to estimate parameters for approximating distributions. The parameter estimates for the two methods were similar to one another, but the parameters from the method of moments yielded a better-fitting distribution as measured by both the percentile matching and the expected excess value tests. Therefore, we chose to use the method of moments.

2.9. Testing goodness of fit

Once we had simulated the sample of aggregate losses and estimated the parameters for the distributions, we tested the goodness of fit. We created three tests to compare distributions in their tails. These tests are also relevant to reinsurance pricing.

The aggregate features of proportional reinsurance treaties are usually expressed in terms of the loss ratios, which we substituted by calculating percentages of the mean of the simulated aggregate distribution (e.g., 100% of mean, 125% of mean, etc.). In other words, we expressed values $x$ in the tail of the distributions in terms of the percentages $p$ of means of the simulated distributions: $x = p*mean.$

The percentile matching test compares the survival functions $Prob\{ X > x\}$ of distributions at various values of the argument until the distributions effectively vanish. This test gives a transparent indication of where two distributions are different and by how much. For various percentages of the mean, we tested how much the survival functions $Prob\{ X > x\}$ in the fitted distributions differed from those of the simulated sample.

The excess expected loss cost test compares the conditional means of distributions in excess of different amounts. Specifically, it evaluates the conditional expectations $E\left\lbrack X - x \middle| X > x \right\rbrack*Prob\{ X > x\}$ for different values of $x.$ These values are important for both the ceding company and the reinsurance carrier when considering aggregate loss ratio caps, stop-loss coverage, annual aggregate deductible coverage, profit commission, sliding-scale commission, and other types of aggregate reinsurance transactions with loss-adjustable features. For instance, in the case of an aggregate loss ratio cap, it is important to accurately price the discount given to the cedent based on the cap. For various percentages of the mean, we test the percentage error in the excess expected loss cost in the fitted distributions as compared to the excess expected loss cost in the simulated sample. We call this “Error in Pricing of Aggregate Stop Loss” in the tables and charts presented in the appendix.

Finally, we estimated the accuracy of the five candidate distributions in pricing loss corridors. In other words, we test the amounts $E\left\lbrack X\text{^} \middle| x_{2} > X > x_{1} \right\rbrack$ $*$ $Prob\left\{ x_{2} > X > x_{1} \right\},$ where $X\text{^}$ is loss in an aggregate layer, namely $\max ( \min ( X - x_{1},0 ),$ $x_{2} - x_{1} ).$ In a loss corridor, the reinsurer returns the responsibility for losses between the two loss ratios $x_{1}$ and $x_{2}$ to the primary insurer.

3. Results and conclusion

We illustrate the results of our study in the tables in the appendix. There we show the characteristics of the frequency—denoted as “Size”—and name—denoted as “LoB” (i.e., line of business)—of severity distributions selected in each scenario, the mean aggregate loss in each layer, and the results of the three goodness-of-fit tests. The first column of each table shows the results of each test on the simulated data. In the top portion of each table, the other five columns show the difference in the percentile matching test for the various candidate distributions. The second and third portions in our tables show the error as a percentage of mean aggregate loss for the different distributions in the excess expected loss cost test and error in loss corridor pricing, respectively. The graphs show the results from the first two goodness-of-fit tests. One can clearly see that in every example, gamma (represented by a red line on charts and green background in the tables) shows the smallest error.

Surely, only six examples with measurements at just six points shown in the appendix should not be considered a very convincing argument. That is why we ran our tests for a large sample of reasonable severity distributions (253), for several reasonable layers (13), and for a few reasonable portfolio sizes (3). Among the severity distributions selected for the study were several closed-form ones (ISO’s PremOps Table 1, for example) as well as some empirical ones (losses from a large client’s submission). In the latter case we use bootstrapping to generate an aggregate loss distribution. We measured results at every 5 percentage points from a minimum of 75% of mean to a maximum of 250% of mean.

We found that the gamma distribution provides a fit that is almost always the best for both ground-up and excess layers.

4. Additional comments

Our choices of potential candidates for the aggregate distribution (see Table 1) were not, in fact, random. We chose the normal distribution as a limiting distribution of sums of identically distributed independent losses. We considered the gamma distribution as a distribution of sums of identical exponentials.^[1] We included the lognormal distribution as it is a popular distribution used to approximate the sum of unlimited losses. As we analyzed our choices through the differences in higher moments of the aggregate loss distribution^[2] (since the first two moments were matched), we decided to consider also the logistic distribution, whose skewness and excess kurtosis lie between that of the normal and the gamma distributions, as well as the inverse Gaussian distribution, whose skewness and excess kurtosis lie between that of the gamma and the lognormal distributions.

Table 3 demonstrates the behavior of higher moments of the listed distributions expressed in terms of their coefficient of variation, or CV. The table is important as it provides a comparison of the shape of the different theoretical curves with the same first two moments.

Table 3.Higher moments (skewness and excess kurtosis) in terms of CV

Distribution	CV	Skewness	Ex. kurtosis
Normal	$c$	0	0
Logistic	$c$	0	1.2
Gamma	$c$	$2c$	$6c^2$
Inverse Gauss	$c$	$3c$	$15c^2$
Lognormal	$c$	$c+c^3$	$16c^2 + 15c^4 + 6c^6 + c^8$

Given that we narrowed our consideration to two-parameter distributions, we could only match the first two moments of the empirical distribution by varying parameters of the theoretical one. Consequently, the quality of the approximation depends mainly on how close the higher moments of the theoretical distribution are to the corresponding higher moments of the empirical distribution. Therefore, to decide which theoretical distribution is a better approximation, it is helpful to estimate the ratio of skewness, and, possibly, kurtosis, to the CV.

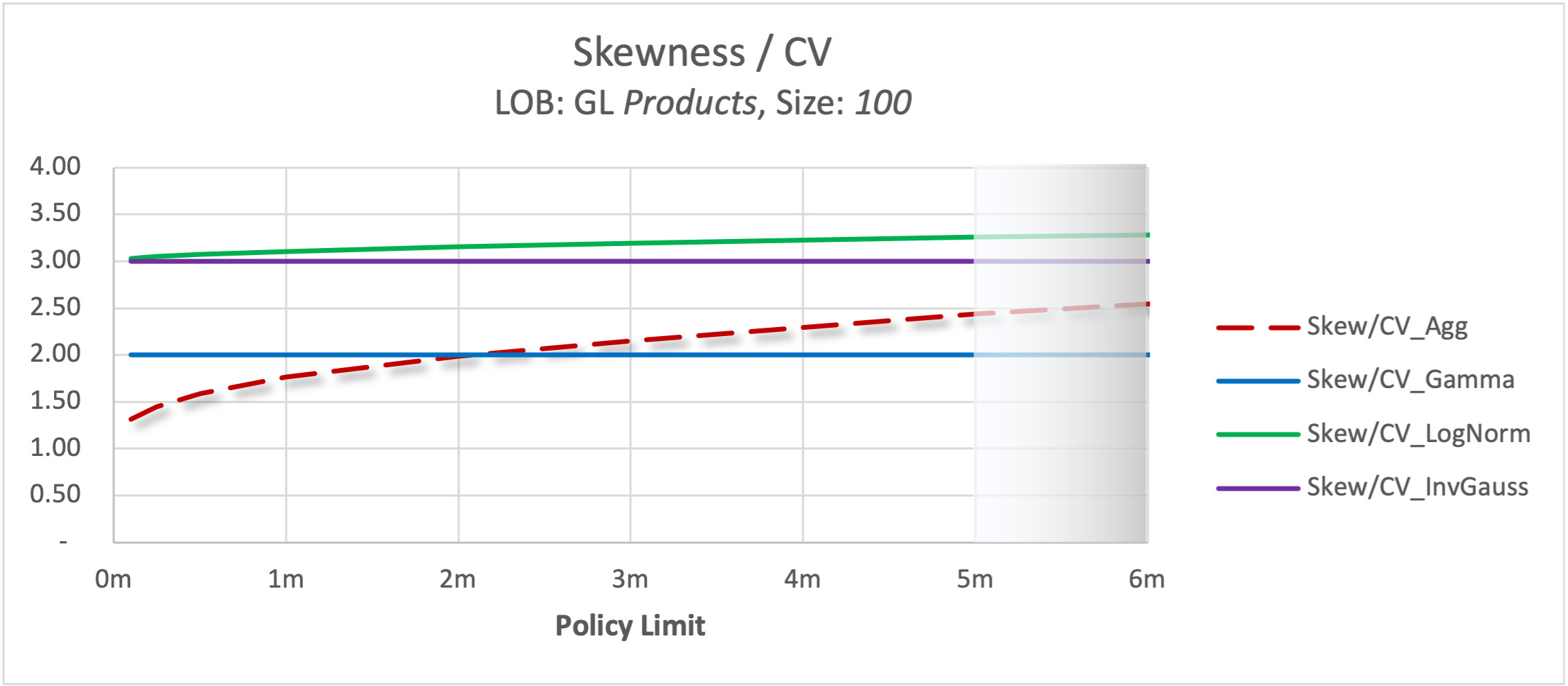
In the case of Poisson frequency and known severity assumptions it is possible to calculate these ratios exactly.^[3] For example, Figure 2 illustrates the behavior of the skewness-to-CV ratio using a GL products severity curve along with a Poisson frequency distribution for different policy limits. The results of the empirical simulation are labeled as CV_agg, and the other three lines are derived from theoretical calculations. As one can see, the ratio of skewness to CV was much closer to 2 than to 3 in the simulation. We could expect the gamma distribution to have a better fit than other distributions because its CV is 2.

Figure 2.Skewness/CV as a function of primary limit

We ran a series of similar tests for a multitude of combinations of appropriate severity curves, layers, and portfolio sizes, 253 x 13 x 3 scenarios overall. In deciding which theoretical distribution provides the best approximation to the simulated, empirical, one, we paid special attention to matching the tail of the distributions.

We were encouraged to see that closeness of higher moments translated to a good fit and that the overwhelming majority of lines of business can be, for all practical purposes, well approximated by a gamma distribution. The same would hold true not only for a series of individual severity curves but also for a mix of several of them. These results lead us to the general conclusion that the gamma distribution provides a uniformly reasonable approximation to the aggregate loss on the interval from the mean to at least two means of the aggregate distribution.