1. Introduction
From the earliest days of Lloyd’s of London, the concept of risk distribution, or aggregating risk to reduce the potential volatility of loss results, has been a prerequisite for an insurance transaction. In the current insurance market, the prevalence of captive insurers – insurance companies owned by one or more of their insureds or other stakeholders – has led to increased scrutiny and consideration of the question, “How much risk distribution is enough for a transaction to qualify as insurance?” While there are many qualitative ways to think about aggregating risk exposures to diversify risk, risk distribution is, at its core, a statistical and therefore actuarial issue. The purpose of this paper is to assist insurance regulators in determining whether or not an insurance company has achieved risk distribution from an actuarial point of view.
From an actuarial point of view the determination of risk distribution would likely focus on the volume of expected claims, among other things. However, it is common in the insurance industry to discuss risk distribution in terms of the number of independent exposures and this has been reinforced by multiple tax court opinions. Therefore we will tend to focus on exposure units throughout our development of a risk measurement risk distribution. There is a direct positive correlation between independent exposure units and the number of expected claims. The use of independent exposure units versus expected claims does not impact the methodology we developed or the results of any risk distribution analysis.
2. Background
To understand risk distribution, one must begin by discussing the concept of insurance. Governments typically interact with insurance on two levels: regulatory oversight and taxation. In the United States, what does and does not qualify as insurance for regulatory purposes may sometimes not align with definitions of insurance for purposes of federal taxation. This is where the notion of risk distribution plays a key role in the conversation.
The National Association of Insurance Commissioners (NAIC) defines insurance as “an economic device transferring risk from an individual to a company and reducing the uncertainty of risk via pooling” (NAIC 2015). So the concepts of risk transfer and risk distribution (or pooling) are the essence of how U.S. insurance regulators understand insurance.
Neither the Internal Revenue Code (IRC), nor regulations promulgated by Congress, nor any rulings issued by the Internal Revenue Service (IRS) provide a definition of what constitutes an insurance arrangement for Federal income tax purposes. Instead, taxpayers have had to rely upon judicial precedent created over the past 75 years, which has developed a framework for when transactions constitute bona fide insurance that results in valid income tax deductions as ordinary and necessary business expenses.
The case that established the foundation of the modern definition of insurance for tax purposes was Helvering v. LeGierse (1941). In LeGierse, Justice Murphy stated that insurance must involve an insurance risk and “(h)istorically and commonly insurance involves risk-shifting and risk distribution.” This four-pronged test of (1) insurance risk, (2) risk transfer, (3) risk distribution, and (4) commonly accepted notions of insurance (Harper Group v. Commissioner 1991) remains essential to the courts’ interpretation of insurance.
Risk transfer and risk distribution are in many ways related topics. In the Harper case (Harper Group v. Commissioner 1991), expert witness Dr. Neil Doherty stated that while risk shifting looks at the arrangement from the perspective of the insured (i.e., has a risk faced by the insured been transferred?), risk distribution looks to the insurer to see if the risks acquired by the insurer are distributed among a pool of risks such that no one claim can have an extraordinary effect on the insurer. The result is that the volatility of results for an insurer is reduced by insuring a large number of discrete risks. One recent article described risk distribution as the idea that “the (actuarially credible) premiums of the many pay the (expected) losses of the few. This is the essence of insurance” (IRMI 2011).
What does and does not constitute risk distribution has been an evolving issue since LeGierse.. Cases initially focused on the number of insured parties. During this era, the Humana case was key (Humana, Inc. v. Commissioner 1989). In Humana, a brother-sister captive model was found to be insurance for federal tax purposes. Humana’s captive model insured between 22 and 48 distinct corporations and 64 to 97 individual hospitals.
Gulf Oil v. Commissioner (1990), another case during that time period, stated in dicta that “risk transfer and risk distribution occur only when there are sufficient unrelated risks in the pool for the law of large numbers to operate… In this instance ‘unrelated’ risks need not be those of unrelated parties; a single insured can have sufficient unrelated risks to achieve adequate risk distribution” (Gulf Oil Corp. v. Commissioner 1990). This is noteworthy in at least two respects. First, it introduces the law of large numbers as an approach to understanding risk distribution (an idea also advanced in Harper the following year). Second, it suggests that unrelated risk might not require unrelated parties.
In the following few years, a number of Tax Court decisions focused on the percentage of risk as measured by premium that was attributable to unrelated parties as a test of risk distribution. In Harper Group v. Commissioner (1991), the Tax Court held that risk shifting and risk distribution were present when 29% to 32% of the captive’s premiums were from unrelated insureds. However, holdings of cases like Kidde Industries v. U.S. (1997) found that insurance payments from subsidiaries, rather than separate corporate entities, of a parent corporation did not constitute deductible insurance premiums for tax purposes.
Kidde further discusses risk distribution and the law of large numbers by stating:
Risk distribution addresses the risk that over a short period of time claims will vary from the average. Risk distribution occurs when particular risks are combined in a pool with other, independently insured risks. By increasing the total number of independent, randomly occurring risks that a corporation faces (i.e., by placing risks into a larger pool), the corporation benefits from the mathematical concept of the law of large numbers in that the ratio of actual to expected losses tends to approach one. In other words, through risk distribution, insurance companies gain greater confidence that for any particular short-term period, the total amount of claims paid will correlate with the expected cost of those claims and hence correlate with the total amount of premiums collected.
This idea of reducing the variability between expected and actual losses is central to actuarial approaches to measuring risk distribution.
The more recent Tax Court decisions appear not to emphasize the number of insured parties, but rather discrete independent risks. For example, Rent-A-Center v. Commissioner (2014) found that the transactions between Rent-A-Center (RAC) and its captive insurance company, Legacy, constituted insurance despite an average of more than 64% of risk coming from one subsidiary (Gremillion 2015). In particular, they noted:
During the years in issue RAC’s subsidiaries owned between 2,623 and 3,081 stores; had between 14,300 and 19,740 employees; and operated between 7,143 and 8,027 insured vehicles. RAC’s subsidiaries operated stores in all 50 states, the District of Columbia, Puerto Rico and Canada. RAC’s subsidiaries had a sufficient number of statistically independent risks. Thus, by insuring RAC’s subsidiaries, Legacy achieved risk distribution. (Rent-A-Center Inc. and Affiliated Subsidiaries v. Commissioner 2014)
Securitas reinforced the concepts presented in Rent-A-Center, specifically citing the number of employees and insured vehicles (Securitas Holdings Inc. and Subsidiaries v. Commissioner 2014). The opinion went on to say, “Risk distribution is viewed from the insurer’s perspective. As a result of the large number of employees, offices, vehicles, and services provided by the U.S. and non-U.S. operating subsidiaries, SGRL was exposed to a large pool of statistically independent risk exposures. This does not change merely because multiple companies merged into one” (emphasis added) (Securitas Holdings Inc. and Subsidiaries v. Commissioner 2014).
Avrahami is the most recent U.S. Tax Court case to highlight the importance of risk distribution in determining if a transaction is bona fide insurance (Avrahami v. Commissioner 2017). In Avrahami, the court found in favor of the IRS that Feedback Insurance Company, Ltd. was not an insurance company for tax purposes, noting “The absence of risk distribution by itself is enough to sink Feedback” (Avrahami v. Commissioner 2017).
In the Avrahami opinion the court provided some valuable discussion on risk distribution. Avrahami reinforced the comments in the Securitas opinion on the law of the large numbers, stating, “The idea is based on the law of large numbers—a statistical concept that theorizes that the average of a large number of independent losses will be close to the expected loss” (Avrahami v. Commissioner 2017).
The Avrahami opinion also included a discussion on the number of affiliated entities a captive would need to insure to achieve risk distribution. The opinion agrees with the Rent-A-Center finding that a captive can achieve risk distribution by insuring only brother-sister entities. However, when the experts in the case disagree on the number of entities required in such an arrangement, the court clearly states, “We also want to emphasize that it isn’t just the number of brother-sister entities that one should look at in deciding whether an arrangement is distributing risk. It’s even more important to figure out the number of independent risk exposures” (emphasis added) (Avrahami v. Commissioner 2017). This focus on exposures from the court is consistent with thinking about risk distribution from an actuarial point of view.
3. Testing for risk distribution
An actuarial approach to quantifying risk distribution faces several challenges. There is no single objective measure, nor bright line indicator, which categorically classifies one transaction as clearly satisfying risk distribution, while another transaction clearly fails. There is some guidance from the IRS, although much of it examines corporate structures, rather than the number of independent risk exposures. There are also several court decisions, with sometimes inconsistent or ambiguous findings. So, although fundamentally assessing risk distribution does have a subjective element, it can be based on analysis and informed judgment.
Based on the Tax Court decisions and guidance provided to date, an actuarial measure of risk distribution should focus on:
-
The size of the pool of statistically independent risk exposures, not the corporate structure, and
-
The reduction in the variability between expected losses and actual losses as a result of aggregating these risks.
4. Criteria for potential risk distribution measures
While there are no prescribed methods for measuring risk distribution, there are several criteria to consider.
A one-sided test is preferable. When determining if risk distribution is present, the test should focus only on downside or negative risk. It should not consider scenarios where the insurance company benefits from positive results, or speculative risk. For the purposes of achieving risk distribution, we are not concerned with whether an insurance company reduces the volatility of their gains.
The test should be transparent and easy to explain. Insurance concepts are not always intuitive and can be difficult to approach for those not in the industry. If a risk distribution test is going to be used in Tax Court to support an insurance company’s position, the underlying assumptions should be clear and the results should be explainable.
The test should be acceptable to regular users. This seems obvious, but the test must be accepted by those in the industry who routinely assess whether a transaction satisfies risk distribution, such as captive attorneys and captive managers. It must also satisfy the scrutiny of insurance and tax regulators charged with oversight of these insurance transactions. For this acceptance to occur, the test must not only be understandable, as mentioned above, but also intuitive. If a transaction at face value appears to satisfy risk distribution, the test should generally produce results consistent with the expectations of professionals practicing in the field.
The test should not be easily manipulated. Any test can be manipulated to some extent; however, a robust test is one where the assumptions are clearly documented and any abuses are easily detected.
The test should focus on process risk. Volatility is reduced with greater numbers of exposures based on the law of large numbers. This reduction in volatility is largely due to a decrease in process risk as opposed to parameter risk. The reduction in process risk is the focus of risk distribution. Modeling parameter risk is inherently difficult and not the focus of the exercise.[1]
5. Potential risk distribution measures
VaR and TVaR methods. Value at risk (VaR) measures the expected loss from some risk, e.g., insurance losses or investments, within a set period of time and at an assumed level of statistical confidence. For example, a portfolio of insurance policies with a VaR of $1,000,000 for one year at a 5% confidence level means there is a 5% probability the net loss for the portfolio will exceed $1,000,000 over the upcoming year (Bodoff 2008; Goldfarb 2006).
Tail Value at Risk, or TVaR, is a related metric that is conditional on the portfolio experiencing a loss. That is, TVaR measures the expected loss given that an event outside of the given probability level has occurred. It focuses on the magnitude of the adverse event and the likelihood of the events. So a TVaR of $1,500,000 at the 5% confidence level means the average loss over the worst 5% of all possible loss scenarios averages $1,500,000.
VaR and TVaR are both rigorous one-sided tests and could be used to test that the insurance company has significantly improved its potential loss at a given percentile through risk distribution. However, the underlying math is not easily explained. In addition, there is heavy reliance on the selected underlying loss distribution models and other assumptions and may therefore be susceptible to manipulation.
Coefficient of Variation (CV). The CV is the ratio of the standard deviation to the mean of a variable. The CV of an insurance company’s expected losses is an easy-to-explain measure of volatility that decreases as the number of independent exposures increases. This makes it an appealing potential risk distribution test. However, the CV can be more easily manipulated than the other tests we have reviewed. It is also a two-tailed statistic as it reflects all risk, not just downside or adverse variability.
Expected Policyholder Deficit (EPD). EPD can be viewed as the probability of the net present value (NPV) underwriting loss for the insurance company multiplied by the NPV of the average severity of the underwriting loss. A test based on the EPD would focus on only the downside risk and would be relatively transparent. The fact that the EPD relies on premiums, though, could lead to results that are not intuitive. The EPD ratio would improve with higher premiums, though this would not necessarily mean more risk has been distributed. It also adds an additional set of assumptions about how premiums are determined that make the statistic more vulnerable to manipulation (Butsic 1992; CAS Research Working Party on Risk Transfer Testing 2006; Freihaut and Vendetti 2009).
Expected Adverse Deviation (EAD). EAD represents the average amount of loss that the insurance company incurs in excess of the expected losses, or the expected amount of adverse deviation to which an insurer or insurance program is exposed. This test has similar benefits to the EPD test but does not incorporate premiums, so it is not as easily manipulated and avoids the counterintuitive results related to higher levels of premium.
To test for risk distribution we normalize the EAD value by dividing by the expected losses. This EAD ratio measures how much volatility or risk an insurance company or program is taking on relative to its expected losses. The higher the EAD ratio, the more loss volatility there is relative to expected losses. As an insurance company diversifies its risk, and increases risk distribution, we would expect to see the EAD ratio decrease. The EAD ratio ranges between 0% and 100%. This allows easier comparisons between different types of insurance and risk exposures. For non-negative random variable X, the EAD ratio can be represented as:
EAD(X)=E(max(X−E(X),0))
EAD Ratio=EAD(X)E(X)
6. How does the EAD ratio work?
When testing the various measures, we found the EAD ratio to be a reliable statistic that satisfies many of the characteristics needed for determining risk distribution. The EAD ratio’s application to common traditional insurance coverages produced intuitive results which were more consistent than other tests considered. A simple example will help to illustrate the computation of the EAD ratio and how adding additional exposures decreases it, consistent with more risk distribution.
EAD Ratio Example
An insurance company writes a policy with a 90% chance of no loss and a 10% chance of a $1,000,000 loss.
The expected losses E(L) are the weighted average of the different loss scenarios. So,
E(L)=90%×$0+10%×$1,000,000=$100,000.
The EAD is the probability-weighted average of the losses in excess of expected losses in each scenario above, if any. So,
EAD=90%×$0+10%×($1,000,000−$100,000)=$90,000.
The EAD ratio is then the EAD divided by expected losses.
EAD ratio=EADE(L)=$90,000$100,000=90%.
If the insurance company wrote two such policies for uncorrelated risks:
E(L)=2×10%×$1,000,000=$200,000
EAD=1%×($2,000,000−$200,000)(Claims on both policies)+18%×($1,000,000−$200,000)(Claims on one or the other policy)+81%×($0)(Claims on neither policy)=$162,000.
EAD ratio=$162,000$200,000=81%.
The addition of a second policy has helped the insurance company diversify and distribute risk. This can be seen in the EAD ratio dropping from 90% to 81%. If the company sold 10 policies, the EAD ratio would drop to 35.1%. If it sold 1,000, the EAD ratio would drop to 3.8%.
To see the effect frequencies might have on the EAD ratio, we calculated the EAD ratio for our simple model described above using two additional frequencies: 1% and 20%. The EAD ratios by number of policies are shown in Table 1.
As the frequency increases, all else being equal, we expect the volatility compared to the expected losses would decrease. The Table 1 shows the intuitive result for the simple model.
Real-world applications will involve larger numbers of policies, more complex loss distributions, and/or more complex coverages, so a simulation approach will be needed in order to quantify the EAD ratio.
7. When is a risk distribution test necessary?
While we have proposed a measure to determine the amount of risk distribution in an insurance company, it may not always be necessary to complete an EAD calculation to determine if the proper level of risk distribution is present. There are currently some “safe harbors” in which no further testing is required, including:
-
Group captives that meet the criteria of existing safe harbors
-
Captive insurance companies that meet the unrelated risk criteria currently in place, either by providing coverage to numerous unrelated parties, e.g., a risk retention group, or via a reinsurance facility
-
First-dollar insurance programs with a large number of claims, particularly if the claims are third party in nature, which tends to increase their statistical independence.
In situations where risk distribution is not readily apparent without further testing, it is important to note that this does not mean it is not present. It only indicates further testing and documentation are necessary. It is also important to remember that it is not feasible to develop a perfect bright line indicator test which will be suitable in every situation. In addition to applying a test such as the EAD ratio, consideration should be given to the number and type of coverage(s) being provided, including the limits, deductibles and other coverage features, the extent of independence between exposures and the extent to which the insurance entity or program is able to diversify risk internally with other programs or by externally using reinsurance. For example, a captive providing a dozen uncorrelated enterprise risk coverages for an insured with hundreds of stores and tens of thousands of customers annually may well have sufficient risk distribution even if its EAD ratio is higher than we might expect.
In proposing the use of the EAD ratio to measure risk distribution, we sought to determine an actuarial metric to identify when it is clear and unambiguous that the result would meet the existing requirements for risk distribution in an insurance company or program.
8. What is an appropriate EAD ratio threshold for risk distribution?
The maximum value for the EAD ratio is 100%. As the insurance company diversifies its risk more and more, the ratio approaches 0%. We have tested the EAD ratio in a variety of common insurance company structures to determine what typical ratios these programs achieve.
Our focus in assessing risk distribution is how much an insurance company can reduce its risk through an increase in the number of independent exposures. Our initial focus was therefore not on the EAD ratio itself but on how additional exposures reduced the ratio. The reason for this is that a particular coverage’s EAD ratio for a base exposure is typically close to 100% but may be lower based on the expected distribution of claims and overall claim frequency. For example, a coverage that has a higher claim frequency per base exposure will have a lower base EAD ratio. However, in testing multiple common scenarios we typically found that the base EAD ratio for a single risk exposure was above 90%. If a coverage has an exposure with a claim frequency of greater than 10%, the base EAD ratio may be lower than 90%.
When testing insurance company structures that are commonly accepted as having risk distribution, we found they had typically reduced the EAD ratio by at least two-thirds (2/3) from the EAD ratio for a single independent risk exposure. We based this finding on testing several traditional insurance contracts, such as personal lines coverages, commercial coverages, and catastrophe coverages. We have included the results for common coverages that shows EAD ratios and reductions for various exposure levels in Table 2. More detail is available in Exhibit 1.
We also tested many alternative risk arrangements, such as group captive structures and small captives participating in reinsurance pooling arrangements that have been historically treated as insurance by the IRS and/or Tax Court and a minimum two-thirds reduction consistently applies to those programs as well.
The selection of the exposure units of statistically independent risk can also impact the EAD ratio per base exposure. For example, a workers compensation insurance program could use $100 of payroll as a unit of independent risk exposure, consistent with traditional workers compensation rating, or perhaps a different exposure unit such as number of employees. However, one could reasonably question whether the loss potential inherent in an employee’s first $100 of payroll is truly independent of the second $100 of payroll. The exposure selection made by the actuary evaluating this program changes the EAD ratio per base exposure.
If the approach of comparing the EAD ratio of an insurance program to the average EAD ratio per base exposure unit is used, we believe that more clearly independent units of risk are preferable. Examples include:
-
Vehicle-powered units rather than thousands of miles driven
-
Number of employees, rather than payroll in $100s
-
Number of customers, transactions or stores, rather than thousands of dollars of revenue
-
Number of patients or procedures for healthcare providers
-
Number of tenants, rather than property values
While each of the more granular exposure bases are perfectly acceptable and commonly used for premium determination, the statistical independence of exposure units are much more easily defended and consistent with the examples provided by the U.S. Tax Court.
This ability to manipulate the EAD ratio improvement by changing the exposure base is potentially a material issue as relates to comparing the overall insurance program’s EAD ratio to that of an average base exposure unit. To address this concern and to simplify the necessary risk distribution testing, we have proposed an EAD ratio threshold of 30% (i.e., 90% *(1/3)). This simplification is reasonable because most base EAD ratios are greater than 90%. It is our finding that risk distribution is present when an insurance company achieves an EAD ratio of less than 30%. As previously noted, if an insurance company is dealing with base exposures that have frequencies greater 10%, a lower EAD threshold may be more appropriate.
9. Details of the EAD ratio calculation using simulation
The calculation of the EAD ratio for an insurer will typically require a simulation of potential future losses. Once projected losses from the various exposures being covered by the insurer are simulated, coverage terms (per occurrence limits and deductibles, aggregate limits, etc.) are applied and the insurer’s expected retained losses over all scenarios are calculated. Once the expected losses for the insurer are estimated, a second simulation must be run to determine the amount of adverse loss in every iteration where simulated losses exceed the expected amount. EAD will be the sum of each of these adverse deviation amounts divided by the number of iterations. Another way to think of EAD is the product of the frequency of adverse loss situations and the average severity of adverse deviation. Once the EAD is calculated, it is divided by the initial expected losses to produce the EAD ratio.
For those familiar with testing for risk transfer in reinsurance contracts this process and the EAD ratio have many similarities to the Expected Reinsurer Deficit (ERD) ratio (Freihaut and Vendetti 2009). Both approaches use simulated cash flows to determine the average loss amount beyond a predetermined level. EAD focuses on the insurance company’s adverse losses relative to expected losses. ERD focuses on a reinsurer’s adverse losses relative to the reinsurance premiums. Where EAD focuses on how an insurance company diversifies its losses to minimize large excess loss situations, ERD is concerned with how likely the reinsurer is to lose money on a deal. While there are many similarities between these two ratios, they are inherently testing two different concepts and sometimes the items they are testing are at odds with each other. It is important to remember that the EAD ratio is a test for risk distribution and provides no insight on whether a contract has the necessary amount of risk transfer to qualify as insurance.
10. Additional EAD ratio examples
We will now examine some additional examples of EAD ratios to demonstrate how risk distribution can be assessed for different types of insurance programs.
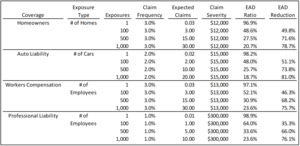
Personal Lines Example (Exhibit 2)
Exhibit 2 shows an example for a hypothetical Florida homeowners insurer covering 10,000 homes. The model was separately parameterized for catastrophe and non-catastrophe claims. Non-catastrophe claims were simulated using a Poisson claims distribution assuming a 3% frequency per insured home and a lognormal severity distribution with a mean of $12,000 and a coefficient of variation of 4.0. A per occurrence limit of $500,000 was also applied with no deductible.
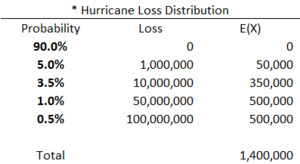
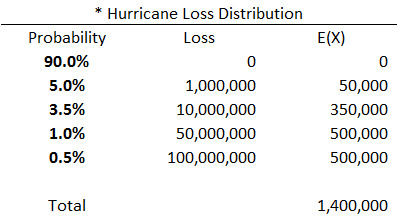
Catastrophe claims were simulated using the simplified loss distribution shown in Table 3.
The initial model results include no reinsurance. The high frequency-low severity non-catastrophe claims have an EAD ratio of 7.0%, suggesting a high level of risk distribution. Conversely, the catastrophe claims result in an EAD ratio of 91.4%, suggesting substantial loss volatility and very little risk distribution. When the two types of claims are combined, the resulting EAD ratio is 26.5%, satisfying our standard of 30%. One way to interpret this result is that the non-catastrophe claims successfully allow the insurance company to diversify or distribute the volatility/risk associated with the catastrophe claims.
One way insurers commonly reduce volatility is by purchasing reinsurance. Examples 2 and 3 in Exhibit 1 show two different reinsurance programs. Example 2 shows a 50% quota share of the non-catastrophe claims and a 50% quota share of the catastrophe losses after a $5,000,000 retention. Example 3 increases the catastrophe reinsurance retention to $10,000,000.
The reinsurance treaties have the desired effect on risk distribution and decrease net loss volatility as can be seen in the resulting EAD ratios. In Example 2, the EAD ratio for all claims types is reduced from 26.5% to 10.3%. Example 3 shows a higher EAD ratio of 14.0%, which is intuitively consistent with the increased retained risk associated with the $10,000,000 hurricane reinsurance retention. It also remains lower than the EAD ratio from the model without reinsurance.
Workers Compensation Example (Exhibit 3)
The second EAD ratio simulation example is for workers compensation coverage. Both payroll and employee counts are included and either could be used to develop the expected claim counts for the Poisson model. A lognormal distribution is again used to model the unlimited claims severities with a mean of $13,000 and a CV of 5.0. Four different exposure scenarios are calculated corresponding to 200, 500, 1,000 and 2,000 covered employees. EAD ratios are computed 1) for the direct insurance policies without reinsurance, 2) for the excess of loss reinsurance contract with a $250,000 attachment, and 3) the losses net of this excess of loss reinsurance. This allows us to assess the risk distribution of both a primary insurer and the reinsurer that assumed only this contract.
The direct scenarios show that the EAD ratio steadily decreases as more exposures, and therefore more expected claims, are added to the insurance program. The EAD ratio approaches the 30% guideline once there are around 500 employees covered.
As one would expect, the EAD ratios associated with a net retention of $250,000 per occurrence decrease due to the removal of volatility associated with claims in excess of retention. However, the ceded excess loss portfolio has extremely high EAD ratios compared to the direct results. Again, this is intuitive as the excess layer has both much more volatility and much lower total expected losses. As a result, the numerator of the EAD ratio, the expected adverse deviations, are much higher, and the denominator, the expected losses, are substantially lower. This results in much larger EAD ratios for all exposure levels tested. One interpretation of this result is that an excess of loss reinsurer needs many more exposures to achieve a comparable level of risk distribution compared to the exposures needed for a primary insurer.
Additional research is needed to assess whether different and higher EAD thresholds may be permissible for assessing risk distribution of reinsurance portfolios. It is worth noting, however, that reinsurers typically insure many different types of coverages and exposures from several different primary insurance companies. The EAD ratio for a reinsurer with a diverse book of business would likely be dramatically lower. Exhibit 2 summarizes the model’s results for this example.
Now that we have presented a couple of traditional insurance examples, let’s move on to examples related to enterprise risk captives which are currently under a great deal of scrutiny for their risk distribution.
Enterprise Risk Captive with Reinsurance Example (Exhibit 4)
Exhibit 3 presents a typical enterprise risk captive (ERC). It provides eight coverages with $20,000,000 in revenue. Revenue is the exposure unit in this example, as many enterprise risk coverages have rates based on revenue. Limits of $1,000,000 per occurrence are applied to all of the coverages. We have used a variety of claim frequency and severity simulation distributional forms, including Poisson-log normal, Bernoulli, and Poisson-discrete. These loss distribution models are generally accepted and among the most commonly used in property casualty insurance modeling. This is to highlight that different coverages, particularly enterprise risk coverages, can and should be modeled using different loss distributions to accurately estimate the underlying claims processes. The underlying loss distributions and parameters are the most important assumptions in the EAD ratio model. As such, insurance regulators and their actuaries focusing on the issue of risk distribution would reasonably be expected to examine the reasonableness and appropriateness of these distributions and parameters within their reviews.
In our example, the loss distributions produce 4.59 expected claims in total across all coverages and expected losses are estimated to be approximately $592,000. The EAD ratio of the direct coverages written by the captive is 39.4%, outside of our recommended 30% guideline. Note that this scenario does not include any high frequency coverages such as property, auto physical damage, medical stop loss or deductible reimbursement for a workers compensation coverage, nor are there any excess of loss insurance coverages. This is common among ERCs where coverages with low frequencies are typically preferred.
A common feature of enterprise risk captives is the use of a reinsurance facility among ERCs offering similar coverages. In this example, we have modeled a reinsurance program among eight essentially identical captives offering the same coverages with the same underlying exposures and loss distributions. Each participant in the reinsurance program cedes 51% of its risk into the reinsurance facility and is retroceded a proportionate quota share of the facility’s aggregated risk. As we would expect, the EAD ratio drops from 39.4% to 13.5% suggesting much more risk distribution. This is reasonable given that the maximum retained risk from any one claim has been reduced from $1,000,000 to $553,750 (the 49% retained loss, plus one eighth of the loss amount ceded into the reinsurance facility). In addition, the portion of the claims assumed from the other reinsurance facility participants further diversifies the captive’s net retained risk.
After our example captive cedes 51% of its risk to a reinsurance facility that includes the example captive and seven other similar captives, the EAD ratio is reduced from 39.4% to 22.4%. This finding that the pooling of the captive’s risks with seven other captives leads to an EAD ratio within our 30% guideline is consistent current case law.
One interesting side note of this model is that there is a minimum EAD ratio a captive can achieve using a quota share reinsurance facility. In essence, even if there were an infinite number of pool participants that completely diversified the pooled losses, the retained risk not subject to the quota share still results in claims volatility.
Enterprise Risk Captive without Reinsurance Example (Exhibit 5)
The last example, shown in Exhibit 5, changes some of the underlying assumptions for an ERC from the one shown in Exhibit 3. A couple of coverages with higher claims frequency, i.e., more claims, have been included in the program. At $50,000,000 in revenue, the overall expected losses are also higher. We continue to show both the direct EAD ratio and the net result of participation in a similar reinsurance facility to Example 3.
In this example the loss distributions produce 40.5 expected claims across all coverages and expected losses are estimated to be approximately $1,388,000. The EAD ratio of the direct coverages written by the captive is 22.9%, inside of our recommended 30% guideline.
As we saw in the Florida Homeowners example, the inclusion of a volume of high frequency, low severity claims reduces the overall loss volatility of the program in total and reduces the EAD ratio. In this case, the direct EAD ratio suggests the captive has sufficient risk distribution on a direct basis and does not need to participate in a reinsurance program solely for the purpose of satisfying risk distribution. However, the captive may well continue to purchase reinsurance for any number of valid risk management reasons.
One can arrive at some important conclusions regarding ERCs from the last two examples: Most importantly, ERCs insuring companies with significant revenue (as a proxy for statistically independent risk exposures), which provide a variety of insurance coverages, including some with higher frequency and lower severity, may not need to participate in a reinsurance facility for the sole purpose of satisfying risk distribution requirements. This would be based on a finding that the EAD ratio for the captive on a direct basis, or after external reinsurance without any retrocession, met the 30% guideline. The contrary may also be true, as smaller ERCs insuring companies with lower revenue may actually need to cede more risk into a reinsurance facility to satisfy a 30% EAD ratio standard for risk distribution.
11. Additional considerations, model enhancements and areas of research
There are some coverage features which cause the EAD ratio to produce results that may be somewhat counterintuitive. For example, a program with an aggregate limit that is close to the expected losses can impact the EAD ratio. Coverages with high claim frequency and very low severities with little variability sometimes resulted in unusually low EAD ratios per exposure unit, making it difficult to show a 2/3 reduction in the EAD ratio. A number of the scenarios we modeled that produced unusual EAD ratios included assumptions that would have raised questions about risk transfer. This makes some sense as risk distribution is focused on reducing the volatility of the losses being assumed, while risk transfer focuses on whether there is enough loss potential being assumed.
The EAD ratio models presented make the simplifying assumption that the potential losses in the insurance program are uncorrelated. If a material positive correlation was identified between coverages, for example, between employment practices liability claims and workers compensation claims (both sensitive to economic downturns), this correlation should be reflected in the simulation model. We point out that the correlation would need to be positive to raise concerns, as negatively correlated coverages would actually increase the amount of risk distribution, thereby making an independent model somewhat conservative.
The impact of positive correlation on the ability to distribute risk has been referenced in previous U.S. Tax Court opinions. The Avrahami opinion noted that the reinsurance company that was utilized, which only insured pooled terrorism coverage, didn’t “distribute risk because the terrorism policies weren’t covering relatively small, independent risks.” Based on our review of EAD ratios for various coverages, it is clear that achieving risk distribution via insuring losses with extremely low frequencies and material positive correlations would require significantly more exposures than more common coverages.
The EAD ratio would not be negatively impacted by a company insuring a heterogeneous book of business. For simplicity, our traditional insurance examples focused on homogeneous books of business but our captive examples clearly had a heterogeneous group of coverages. As we discussed, if a homogeneous book leads to some positive correlation in losses, it would actually require a higher number of exposures to achieve risk distribution.
As previously mentioned, assessing the EAD ratio needed for a reinsurance company to satisfy risk distribution may well require additional research. Because of the substantially greater loss volatility and risk appetite of typical reinsurance companies, a higher EAD ratio than 30% may well still possess risk distribution. In addition, the levels of capitalization of the typical reinsurer allow this higher level of loss volatility in exchange for a higher expected return.
The EAD ratio ultimately depends more directly on the number of expected claims to provide risk distribution than on the number of statistically independent risk exposures. This is consistent with actuarial research in other areas such as credibility theory. However, the basis for the expected claim counts are still ultimately going to be based on the risk exposures. This is consistent with guidance from the U.S. Tax Court and other authorities on risk distribution.
Finally, evaluating the claims on a present value basis, similar to that used for ERD calculations, may be an area for improvement. One difference is that the EAD ratio does not rely on premium and underwriting expenses in the manner ERD does. It is unclear at present whether this enhancement would materially improve the usefulness of the results of the EAD ratio analysis.
12. Conclusion
With the issue of risk distribution squarely in the spotlight as the IRS and U.S. Tax Court assess whether some forms of ERCs are insurance for tax purposes, a rigorous actuarial approach to modeling risk distribution for insurance companies and programs has become necessary. The expected adverse deviation (EAD) ratio is a straightforward, understandable, one-tailed statistic for determining the presence of risk distribution from an actuarial perspective. Using the EAD ratio, actuaries and regulators can assess the level of risk diversification achieved by an insurance program after the application of all coverage features and any applicable ceded or assumed reinsurance. We believe a 30% threshold for the EAD ratio demonstrates sufficient risk distribution for most applications.
Parameter risk “describes the uncertainty in estimating the exact nature of the loss process in which statistical models are used to describe the randomness of the loss process.” Process risk is “a way of expressing the variation in potential outcomes based on the size of the sample” (www.irmi.com/online/insurance-glossary/).