1. Introduction
The question of how to allocate risk capital to different units or lines of business has generated considerable attention in the actuarial literature. This paper reviews the form and the intellectual foundation of a variety of methods and then compares their results in the context of a theoretical loss model and a specific real-world example. The goal is to offer insights on the similarities, differences, and stability of the different methods.
We find considerable variation in the results from different methods, although all of the allocations appear to be geometrically related. More precisely, depending on the example, the allocations seem to constitute a lower-dimensional manifold relative to the dimension of the allocation problem. Expected value (EV) allocations lie at one end of the frontier while extreme tail allocations are at the other. Furthermore, we also find significant differences in stability. Small changes in the underlying data set can have dramatic effects on the allocation results associated with certain methods. In particular, some allocations generated by value-at-risk (VaR), as well as those generated by extreme tail risk measures, prove to be unstable due to their focus on a small number of sample outcomes (in the case of VaR, just one).
There are various surveys on capital allocation techniques and methods (Burkett, McIntyre, and Sonlin 2001; Albrecht 2004; Venter 2004; Bauer and Zanjani 2013). It is important to stress that, in this paper, we are not attempting to endorse or favor any particular method. While we have written elsewhere on the origins of “economic allocations” from a theoretical perspective (Bauer and Zanjani 2016, 2021), the goal here is to gain perspective on practical differences. To elaborate, theoretical differences between two methods are less concerning if, in practice, they produce similar answers. Moreover, a theoretically appealing method is of little use if, in practice, it is unstable. Thus, we view the comparison of different allocation methods as a worthwhile endeavor to inform practice.
This paper is organized as follows. We start in Section 2 by reviewing the foundations of the capital allocation problem. In particular, we address the question of why—or, rather, under which conditions—the capital allocation problem is relevant, and what precisely we mean by a capital allocation. Then in Section 3, we provide details on how capital is allocated. We commence by discussing the most popular conventional allocation approach, the so-called Euler or gradient allocation principle, including its economic underpinnings. However, we also review alternative approaches, including “distance minimizing” approaches, allocation by percentile layers, and economic allocations originating from counterparty risk aversion, and we discuss relationships between the methods. In Section 4, we compare capital allocation methods. In Section 4.2, we present a pedagogical allocation exercise illustrating the connections between economic methods and conventional methods. In Section 4.3, we implement all allocation methods in the context of data provided from a catastrophe reinsurer: first we describe the data and the specifics of the approaches, and then we compare and contrast the resulting allocations, evaluate their effects on pricing, and test their stability. Finally, in Section 5, we offer our conclusions.
2. The foundations of capital allocation
2.1. Why allocate capital?
We must first establish why capital is allocated. The simple answer from the practitioner side is that allocation is a necessity for pricing and performance measurement. By allocating capital costs to each business line, the firm can set the price in each line to cover capital costs and meet financial targets. To utilize an end-of-cycle performance management assessment tool like risk-adjusted return on capital (RAROC), a benchmark needs to be set at the beginning of the actuarial cycle using a capital allocation principle (Farr et al. 2008; Baer, Mehta, and Samandari 2011). When setting benchmarks for lines of business within a multiline firm, one must ensure that the benchmarks put in place are consistent with the firm’s financial targets, specifically the target return on equity (ROE).
This seems logical at first glance, yet some of the academic literature has been skeptical. Phillips, Cummins, and Allen (1998) noted that a “financial” approach to pricing insurance in a multiline firm rendered capital allocation unnecessary, a point reiterated by Sherris (2006). The financial approach relies on applying the usual arbitrage-free pricing techniques in a complete market setting without frictional costs. In such a setting, one simply pulls out a market-consistent valuation measure to calculate the fair value of insurance liabilities. Capital affects this calculation in the sense that the amount of capital influences the extent to which insurance claims are actually paid in certain states of the world, but, so long as the actuary is correctly evaluating the extent of claimant recoveries in various states of the world (including those where the insurer is defaulting), there is no need to apportion the capital across the various lines of insurance.
Once frictional costs of capital are introduced, the situation changes, as seen in Froot and Stein (1998) and Bauer and Zanjani (2013). Frictions open up a gap between the expected profits produced by financial insurance prices and the targeted level of profits for the firm. In such a case, the gap becomes a cost that must be distributed back to business lines, like overhead or any other common cost whose distribution to business lines is not immediately obvious.
As a practical example, consider catastrophe reinsurers. Natural catastrophe risk is often argued to be “zero beta” in the sense of being essentially uncorrelated with broader financial markets. If we accept this assessment, basic financial theory such as the capital asset pricing model would then imply that a market rate of return on capital exposed to such risk would be the risk-free rate. Yet, target ROEs at these firms are surely well in excess of the risk-free rate. The catastrophe reinsurer thus has the problem of allocating responsibility for hitting the target ROE back to its various business lines without any guidance from the standard arbitrage-free pricing models.
Viewed in this light, “capital allocation” is really shorthand for capital cost allocation." Capital itself, absent the segmentation of business lines into separate subsidiaries, is available for all lines to consume. A portion allocated to a specific line is not in any way segregated for that line’s exclusive use. Hence, the real consequence of allocation lies in the assignment of responsibility for capital cost: a line allocated more capital will have higher target prices.
An important point, to which we shall return later, is the economic meaning of the allocation. Merton and Perold (1993) debunk the notion that allocations could be used to guide business decisions involving inframarginal or supramarginal changes to a risk portfolio (e.g., entering or exiting a business line). The more common argument is that allocation is a marginal concept—offering accurate guidance on infinitesimal changes to a portfolio. As we will see, many methods do indeed have a marginal interpretation, but the link to marginal cost is not always a strong one.
2.2. Capital allocation defined
We start by offering notation and defining capital allocation.[1] Consider a one-period model with business lines with loss realizations modeled as square-integrable random variables in an underlying probability space [2] At the beginning of the period, the insurer decides on a quantity of exposure in each business line and receives a corresponding premium in return. The exposure is an indemnity parameter so that the actual exposure to loss is
I(i)=I(i)(L(i),q(i))
We assume that an increase in exposure shifts the distribution of the claim random variable so that the resulting distribution has first-order stochastic dominance over the former:
P(I(i)(L(i),ˆq(i))≥z)≥P(I(i)(L(i),q(i))≥z)∀z≥0,ˆq(i)≥q(i)
For simplicity, we typically consider to represent an insurance company’s quota share of a customer ’s loss:
I(i)=L(i)×q(i)
Other specifications could be considered, but the specification above implies that the claim distribution is homogeneous with respect to the choice of variable The proportional argument may be justified locally by pointing out the availability of proportional reinsurance or by alluding to the idea that claims are proportional in dollars. This simplifies capital allocation, although it should be noted that insurance claim distributions are not always homogeneous (Mildenhall 2004), and the “adding up” property associated with a number of methods depends on homogeneity. Extensions to more general (nonlinear) contracts are possible when generalizing the setting (Frees 2017; Mildenhall 2017).
We denote company assets as and capital as where, to fix ideas, we adopt a common specification of the difference between the fair value of assets and the present value of claims. We denote by the aggregate claims for the company, with the sum of the random claims over the sources adding up to the total claim:
N∑i=1I(i)=I
However, actual payments made amount to only because of the possibility of default. We can also decompose actual payments, whereby (as is typical in the literature) we assume equal priority in bankruptcy, so that the payment to loss is
min{I(i),aII(i)}⇒N∑i=1min{I(i),aII(i)}=min{I,a}
Allocation is simply a division of the company’s capital across the sources of risk, with representing the capital per unit of exposure assigned to the th source. Of course, a full allocation requires that the individual amounts assigned to each of the lines add up to the total amount for the company:
N∑i=1q(i)k(i)=k
It is worth noting that the question of what to allocate is not necessarily straightforward. Are we to allocate the book value of equity? The market value of equity? In general, the answer to this question is going to be guided by the nature of costs faced by the firm. Even then, the costs may be difficult to define, as the decomposition of capital costs offered by Mango (2005) suggests.
3. Capital allocation techniques
Assuming we have answered the question of what to allocate, the remaining question is how to do it. Unfortunately, the answer is not straightforward; there are a bewildering variety of peddlers in the capital allocation market. Mathematicians bearing axioms urge us to adhere to their methods—failure to do so will result in some immutable law of nature being violated. Economists assure us that only their methods are optimal. Game theorists insist that only their solution concepts can be trusted. Practitioners wave off all of the foregoing as the ravings of ivory tower lunatics, all the while assuring us that only their methods are adapted to the real-world problems faced by insurance companies. Everyone has a pet method, perhaps one that has some intuitive appeal or one that is perfectly adapted to some particular set of circumstances.
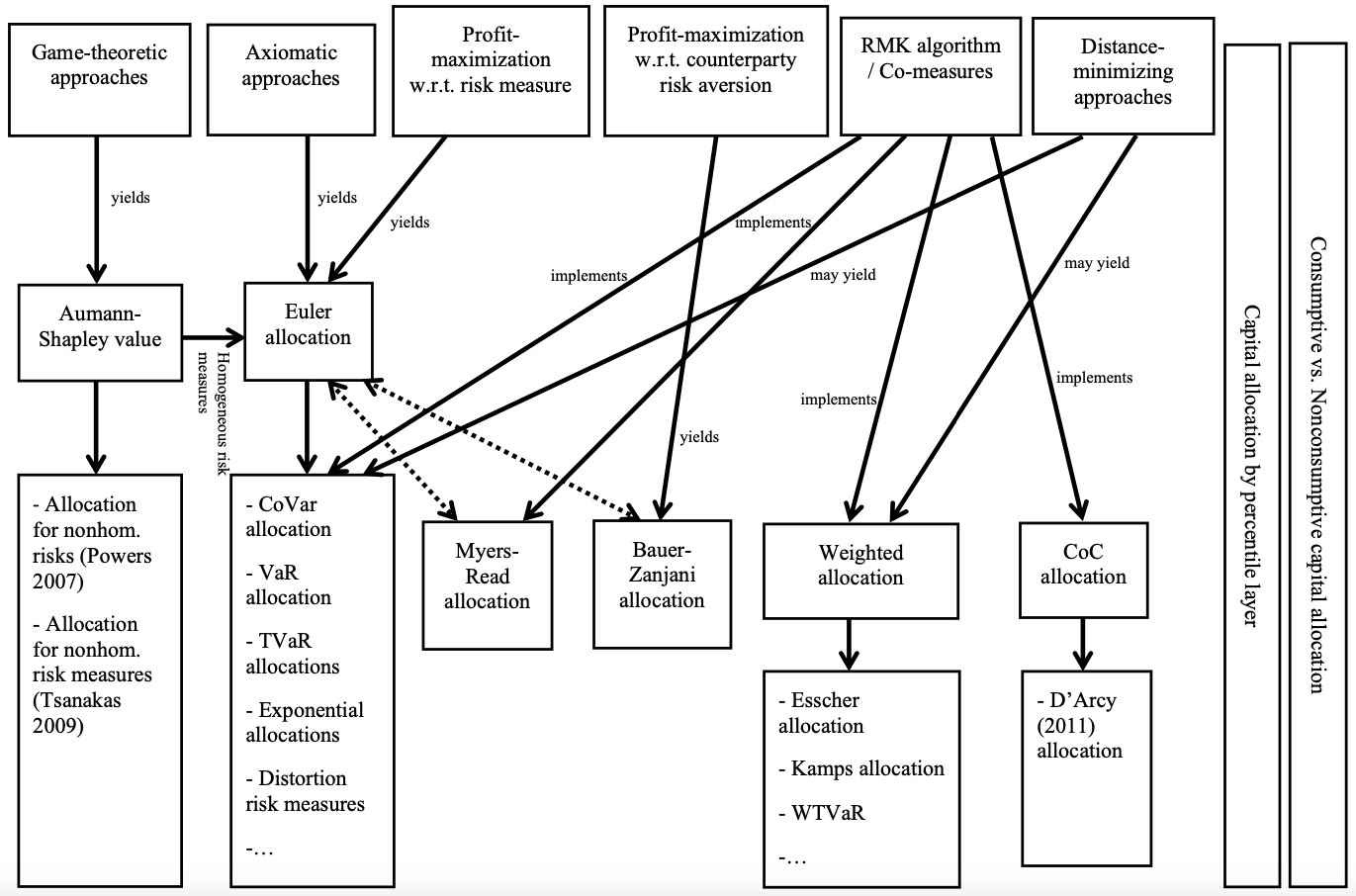
Given such variety, it is not surprising that allocation methods defy easy categorization. Many do end up in essentially the same place—the Euler or gradient method—a convergence noted by Urban and colleagues (2004) and Albrecht (2004). But others do not. In the following section, we attempt to give an overview of the primary approaches. We keep the focus on concepts and examples. Table 1 summarizes the allocation examples, and Figure 1 shows their interrelationship in graphical form.
3.1. The Euler method and some different ways to get there
Consider setting capitalization based on a differentiable risk measure and further imagine allocating capital to line based on
k(i)=∂ρ(I)∂q(i)
This allocation is commonly referred to as the gradient or Euler allocation, the latter being a reference to Euler’s homogeneous function theorem. This theorem states that for every positive homogeneous function of degree 1 —which is equivalent to requiring that the risk measure be homogeneous—we automatically obtain the “adding up” property: The basic Euler approach can be found in Schmock and Straumann (1999) and Tasche (2004), among others.
The Euler or gradient allocation can also be implemented without requiring that by normalizing
k(i)k=∂ρ(I)∂q(i)ρ(I)
One of the major advantages of the Euler allocation is that it is possible to directly calculate (approximative) allocations given an available economic capital framework that allows the derivation of and [3] More specifically, we can approximate the derivative occurring in the allocation rule by simple finite differences (although more advanced approaches may be used)—that is,
∂ρ(I)∂q(i)≈ρ(I+ΔL(i))−ρ(I)Δ
where is “small.”
A number of different paths lead to the Euler allocation. Denault (2001) proposes a set of axioms that define a coherent capital allocation principle when His axioms require the following:
-
Adding up—The sum of allocations must be
-
No undercut—Any subportfolio requires more capital on a stand-alone basis.
-
Symmetry—If risk A and risk B yield the same contribution to capital when added to any disjoint subportfolio, their allocations must coincide.
-
Riskless allocation—A deterministic risk receives zero allocation in excess of its mean (see also Panjer 2002).
Denault shows that the risk measure necessarily must be linear in order for a coherent allocation to exist. This result essentially echoes the findings of Merton and Perold (1993), but shows that allocation based on a linear risk measure constitutes an exception to their indictment of using allocations to evaluate inframarginal or supramarginal changes to a portfolio. Linear risk measures are obviously of limited application, but Denault (2001) finds more useful results when analyzing marginal changes in the portfolio. In particular, he uses five axioms to define a “fuzzy” coherent allocation principle that exists for any given coherent, differentiable risk measure—and this allocation is given by the Euler principle applied to the supplied risk measure.
Kalkbrener (2005) uses a different set of axioms:
-
Linear aggregation—This combines axioms 1 and 4 of Denault.
-
Diversification—This corresponds to axiom 2 of Denault.
-
Continuity—Small changes to the portfolio should have only a small effect on the capital allocated to a subportfolio.
He finds that the unique allocation under these axioms is given by the Gâteaux derivative in the direction of the subportfolio, which again collapses into the Euler allocation:
k(i)=limε→0ρ(I+εL(i))−ρ(I)ε=∂ρ(I)∂q(i)
Some common homogeneous risk measures used in this axiomatic context are
-
the standard deviation, derived from the standard deviation premium principle (Deprez and Gerber 1985);
-
the VaR;
-
the expected shortfall/tail VaR (TVaR);
-
the risk-adjusted TVaR (RTVaR) (Furman and Landsman 2006, and under a different name in Venter 2010);
-
the exponential risk measure (Venter, Major, and Kreps 2006); and
-
the distortion risk measures (Denneberg 1990; Wang 1996), including
-
proportional hazard transformation (Wang 1995, 1998),
-
Wang transformation (Wang 2000), and
-
exponential transformation (McLeish and Reesor 2003).
-
An alternative approach to the capital allocation problem is from the perspective of game theory. Lemaire (1984) and Mango (1998) both note the potential use of the Shapley value, which rests on a different set of axioms, in solving allocation problems in insurance. The Shapley value (Shapley 1953) is a solution concept for cooperative games that assigns each player a unique share of the cost. Denault (2001) formally applies this idea to the capital allocation problem, in particular by relying on the theory of cooperative fuzzy games introduced by Aubin (1981). The key idea here is that the cost functional of a cooperative game is defined via the risk measure :
c(q(1),q(2),…,q(N))=ρ(q(1),q(2),…,q(N))
The problem then is to allocate shares of this “cost” to the players, with the set of valid solutions being defined as (see also Tsanakas and Barnett 2003)
C= {(k(1),k(2),…,k(N))| c(q(1),q(2),…,q(N))=∑k(i)q(i)&c(u)≥∑k(i)ui,u∈[0,q(1)]×…×[0,q(N)]}
Thus, for allocations in this set, any (fractional) subportfolio will feature an increase in aggregated per-unit costs, which connects to the usual solution concept in cooperative games requiring any solution to be robust to defections by subgroups of the players. The Aumann-Shapley solution is
k(i)=∂∂ui∫10c(γu)dγ|uj=q(j)∀j
If the risk measure is subadditive, positively homogeneous, and differentiable, the solution boils down to the Euler method when loss distributions are homogeneous.[4]
The Euler method is also recovered in a number of “economic” approaches to capital allocation, where the risk measure is either embedded as a constraint in a profit-maximization problem (e.g., Meyers 2003 or Stoughton and Zechner 2007) or embedded in the preferences of policyholders (Zanjani 2002). In either case, the marginal cost of risk ends up being defined, in part, by the gradient of the risk measure. As illustration, consider the optimization problem adapted from Bauer and Zanjani (2016):
maxk,q(1),q(2),…,q(N){N∑i=1p(i)(q(i))−V(min{I,a})−C}⏟=Π
subject to
ρ(q(1),q(2),…,q(N))≤k
From the optimality conditions associated with this problem, assuming a nonexplosive solution exists,
∂Π∂q(i)=(−∂Π∂k)×∂ρ∂q(i)
can be obtained at the optimal exposures and capital level. Hence, for the optimal portfolio, the risk-adjusted marginal return for each exposure is the same and equals the cost of a marginal unit of capital More to the point, the right-hand side of Equation (5) allocates a portion of the marginal cost of capital to the th risk, an allocation that is obviously equivalent to the Euler allocation. In this sense, the Euler allocation is indeed “economic,” but it is important to stress that any economic content flows from the imposition of a risk measure constraint.
This economic setup also recovers performance measurement based on the Euler method. Fixing the risk-adjusted marginal return is the same at the optimal exposures. Moving off the optimal values, if a source of risk has a higher-than-average performance (i.e., if in Equation (5) there is a positive sign), one can marginally increase exposure and the risk-adjusted performance of the entire portfolio will increase. This property aligns with theorem 4.4 in Tasche (2000), which states that the gradient allocation method is the only risk allocation method that is suitable for performance measurement.
3.2. Distance-minimizing allocations
Not all approaches lead to the Euler principle. Laeven and Goovaerts (2004), whose work was later extended by Dhaene, Goovaerts, and Kaas (2003); Zaks, Frostig, and Levikson (2006); Dhaene and colleagues (2012); and Zaks and Tsanakas (2014), derive allocations based on minimizing a measure of the deviations of losses from allocated capital. Specifically, Laeven and Goovaerts propose solving
{mink(1),k(2),…,k(N)ρ(∑Ni=1(I(i)(L(i),q(i))−q(i)k(i))+)s.th. ∑Ni=1q(i)k(i)=k
to identify an allocation, whereas Dhaene and colleagues (2012) consider
{mink(1),k(2),…,k(N)∑Ni=1q(i)E[θ(i)D(I(i)(L(i),q(i))q(i)−k(i))]s.th. ∑Ni=1q(i)k(i)=k
where is a (distance) measure and are weighting random variables with
In the approach by Dhaene and colleagues (2012), certain choices for and can reproduce various allocation methods. For instance, for and they arrive at weighted risk capital allocations studied in detail by Furman and Zitikis (2008). Examples include the allocation based on the Esscher transform and the premium principle by Kamps (1998). Other choices lead to other allocation principles, including several that can be derived from the application of the Euler principle, such as weighted TVaR (WTVaR).
3.3. Allocations by co-measures and the RMK algorithm
Euler methods require calculation of gradients of risk measures, which sometimes can present a numerical challenge. An alternative approach is the Ruhm-Mango-Kreps (RMK) algorithm (Ruhm, Mango, and Total 2003; Kreps 2005), a popular approach of capital allocation in practice, partly due to its ease of implementation. According to Kreps (2005), it commences by defining as the total capital to support the company’s aggregate loss where is the mean (reserve) and is the risk load. Then, the capital allocations for risks emanating from the asset or the liability side are defined as
q(i)k(i)=E[I(i)]+Ri=E[I(i)]+E[(I(i)−E[I(i)])ϕ(I)]
where is the riskiness leverage, and “all” that one needs to do is to find the appropriate form of This allocation method adds up by definition, and it scales with a currency change if for a positive constant
Different interpretations are possible, but the key advantage is ease of implementation, since the method solely relies on taking “weighted averages” (Ruhm 2013).
Of course, the RMK algorithm presents only the general framework. The crux lies in the determination of the riskiness leverage Various examples are presented by Kreps (2005), some of which result in familiar allocation principles that can be alternatively derived by the gradient principles.
More generally, Venter (2004) and Venter, Major, and Kreps (2006) introduce co-measures. Specifically, they consider the risk measure[5]
ρ(I)=E[∑jhj(I)ϕj(I)|Condition on I]
where the are linear functions. Then, they define the co-measure as
r(I(i))=E[J∑j=1hj(I(i))ϕj(I)|Condition on I]
which satisfies and thus serves as an allocation.
As Venter (2010) points out, even for one risk measure there may be different co-measures (i.e., the representation is not unique). Some of them yield representations that are equivalent to the gradient allocation, but this is not necessarily the case. In Table 1, the last column lists the riskiness leverage / co-measures of some common allocation methods. We introduce two allocation approaches by directly relying on their implementation via the RMK algorithm and co-measures.
3.3.1. Myers-Read approach
Myers and Read (2001) argue that, given complete markets, default risk can be measured by the default value, i.e., the premium the insurer would have to pay for guaranteeing its losses in the case of a default. Then, they propose that “sensible” regulation will require companies to maintain the same default value per dollar of liabilities and effectively choose this latter ratio as their risk measure.
More precisely, following Mildenhall (2004), the default value can be written as[6]
\begin{align} &D(q^{(1)},q^{(2)},\ldots,q^{(N)}) \\ &= {\mathbb{E }}\left[ \mathbf{\mathit{1}}_{\{I \geq a\}} (I-a)\right] \\ &= {\mathbb{E }}\bigl[ \mathbf{\mathit{1}}_{\{I \geq {\mathbb{E }}[I] + k^{(1)} \,q^{(1)} + \ldots + k^{(N)} \,q^{(N)}\}} \bigl(I - [{\mathbb{E }} [I] + k^{(1)} \,q^{(1)} \\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad + \ldots + k^{(N)}\,q^{(N)}] \bigr) \bigr]\end{align}
and the company’s default-to-liability ratio is
c = \frac{D}{{\mathbb{E }}[I]} = \frac{{\mathbb{E }}[\mathbf{\mathit{1}} _{\{I \geq a\}} (I-a)]}{{\mathbb{E }}[I]}
Myers and Read (2001) verify the adding-up property for —which again shows a relationship to the Euler principle. They continue to demonstrate that in order for the default value to remain the same as an exposure is expanded, it is necessary that
c = \frac{\frac{\partial D}{\partial q^{(i)}}}{{\mathbb{E }}[L^{(i)}]}
which, in turn, yields
\begin{align} c \, {\mathbb{E }}[L^{(i)}] &= {\mathbb{E }}\left[ \left(L^{(i)} - \left({ \mathbb{E }}[L^{(i)}] + k^{(i)}\right)\right)\,\mathbf{\mathit{1}}_{\{I\geq a\}}\right] \\ \Rightarrow k^{(i)} &= {\mathbb{E }}\left[ \left(L^{(i)} - {\mathbb{E }} [L^{(i)}] \right) \big| I \geq a \right] - c\,\frac{{\mathbb{E }}[L^{(i)}]}{{ \mathbb{P }}(I\geq a)} \end{align}
This is similar to the allocation found by Venter, Major, and Kreps (2006), although they allocate assets rather than capital, so does not occur in the first term. As indicated in their paper, it is possible to represent this allocation as a co-measure using and
3.3.2. D’Arcy allocation
D’Arcy (2011) considers allocations by the RMK algorithm but identifies flexibility in choosing the riskiness leverage as its “greatest flaw.” To uniquely identify the “right” function, he proposes to use capital market concepts, particularly cost of capital, to “reflect the actual cost of recapitalizing the firm.” Specifically, he allows the riskiness leverage to depend on both the size of the loss realization and the type of shock leading to the loss (idiosyncratic, industrywide, or systemic). The riskiness leverage factor is the ratio of the cost of capital divided by the normal cost of capital, where the realized cost of capital, in addition to systemic factors, depends additively on the ratio of aggregate losses to the firm’s actual capital:
\phi (I)=\frac{\mathbf{\mathit{1}}_{\{I\geq C\}}(\text{CoC}_{\text{market}}+\frac{I-a}{a})}{\text{CoC}_{\text{normal}}} \tag{7}
It is important to note that D’Arcy (2011) only proposes the RMK algorithm only for the “consumptive” aspect of capital allocation, whereas he also includes a “nonconsumptive” allocation in the spirit of Mango (2005) (see Section 3.4).
3.4. Consumptive versus nonconsumptive capital
Mango (2005) argues that capital costs consist of two parts. An insurer’s capital stock can be depleted if a loss realization exceeds the reserves for a certain segment or line, or when reserves are increased. Mango refers to this part as a consumptive use of capital since in this case, funds are transferred from the (shared) capital account to the (segment-specific) reserve account. The second, nonconsumptive part arises from a “capacity occupation cost” that compensates the firm for preclusion of other opportunities. It is thought to originate from rating-agency requirements in the sense that taking on a certain liability depletes the underwriting capacity.
The importance of this distinction for our purposes is that it complicates practice in cases where the two sources of costs require different approaches to allocation. For example, D’Arcy (2011) follows Mango’s suggestion by first allocating consumptive capital via the RMK algorithm, where the riskiness leverage, or capital call cost factor, is associated with the cost of capital (see also Bear 2006 and D’Arcy 2011). He then allocates capital according to regulatory rules, and the final allocation ends up as an average of the two allocations. Thus, the two different motivations for holding capital are reflected in a hybridization of allocation methods.
3.5. Capital allocation by percentile layer
Bodoff (2009) argues that allocations according to VaR or to tail risk measures do not consider loss realizations at smaller percentiles, even though the firm’s capital obviously supports these loss levels as well. Thus, in order to allocate, he advocates considering all loss layers up to the considered confidence level. His approach considers allocating capital to loss events, but since we are interested in allocating capital to lines, we follow the description from Venter (2010).
Assume the capital is determined by some given risk measure. For instance, VaR is used in Bodoff (2009). Then, the allocation for the layer of capital is
{\mathbb{E }}\left[ \frac{I^{(i)}}{I} \big| I \geq z\right] \times dz
Going over all layers of capital, we obtain the allocation
q^{(i)} \, k^{(i)} = \int_0^k {\mathbb{E }}\left[ \frac{I^{(i)}}{I} \big| I \geq z \right] \, dz
where, obviously,
\sum_{i=1}^N q^{(i)} \, k^{(i)} = \int_0^k {\mathbb{E }}\left[ \frac{I}{I} \big| I \geq z\right] \, dz = \int_0^k dz = k
As Venter (2010) points out, even if is set equal to a risk measure and allowed to change with the volume of the writings, the resulting allocation does not collapse to the gradient allocation in any known cases.
When implementing the approach based on a sample of size obviously it is necessary to approximate the integral formulation above. When we base it on and use the simple empirical quantile for its estimation, we can set
q^{(i)} \, k^{(i)} = \sum_{j=1}^{\alpha\, N} {\mathbb{E }}\left[\frac{I^{(i)}}{I} \big| I \geq I_{(j)} \right] \,\left[I_{(j)} - I_{(j-1)}\right]
where we set Since the conditional expectations within the sum have to be also approximated by taking averages, the implementation in a spreadsheet may be cumbersome (or even infeasible) for large samples.
3.6. Economic counterparty allocation
Sections 3.1 to 3.5 outline so-called 'conventional capital allocation methods. While conventional methods vary in technique, they all consider capital allocation a technical problem but do not contemplate the motivation for holding capital in the first place. In contrast, Bauer and Zanjani (2016) argue that the demand side’s risk preferences would have an impact on the optimal capital and allocation decision. More precisely, Bauer and Zanjani introduce a theoretical framework of capital allocation that is derived from the insurer’s profit maximization subject to counterparty risk aversion. The concept is fundamentally different from that of Equation (4), where the premium and risk measure are exogenously determined. Here, the premium is a choice variable for the insurer, subject to a participation constraint for the counterparty. In particular, there is no risk measure to be imposed in the first place, but an endogenous expression for the risk measure can be derived from the allocation rule. In the remainder of the paper, we will refer to this allocation as the Bauer-Zanjani allocation.
The idea of incorporating a demand function is also raised by Kliger and Levikson (1998) and later on by Zaks, Frostig, and Levikson (2008), where the default probability is considered. To elaborate on the setup, it is assumed that we have a group of consumers/policyholders or business lines. Each consumer or line has wealth and is susceptible to a loss which is random. Each consumer is risk averse by default, and has utility function and expected utility Each consumer can purchase insurance to recover a portion of the loss at premium rate Both and are chosen by the insurer. The insurer will collect the premium up front and deliver a total of for indemnity payments. The expected payback to each consumer is with the latter amount triggered by the insurer’s default or when its assets are less than the total indemnity payment The insurer then solves the following one-period optimization problem:
\max_{a,\{ q^{(1)}...q^{(N)} \},\{ p^{(1)}...p^{(N)} \}} \sum_{i=1}^{N} p^{(i)} - \sum_{i=1}^{N} e^{(i)} - \tau a \tag{8}
This is subject to participation constraints for each consumer:
\begin{align} v_i &= {\mathbb E }[U_i(w^{(i)} -p^{(i)} -L^{(i)} +R^{(i)} )] \\ &\ge {\mathbb E }[U_i(w^{(i)} -L^{(i)} )] \; \forall i \end{align}
The solution suggests that an allocation weight for each consumer/policyholder is
\frac{k^{(i)}}{k} = \frac{{\mathbb E }\left[ \mathbf{1}_{\{I\ge a\}} \sum_{k} \frac{U'_k}{v'_k} \frac{I^{(k)}}{I^2} \frac{\partial I^{(i)} }{\partial q^{(i)} } \right]}{{\mathbb E }\left[ \mathbf{1}_{\{I\ge a\}} \sum_{k} \frac{U'_k}{v'_k} \frac{I^{(k)}}{I} \right]} \tag{9}
The supporting risk measure takes the form
\rho(I) = \exp \left\{ {\mathbb E }^{\tilde{{\mathbb P}}} \left[ \log (I) \right] \right\}
where the measure is given by its likelihood ratio:
\frac{\partial \tilde{{\mathbb P}}}{\partial {\mathbb P}} = \frac{{\textbf{1}}_{\{ I \ge a \}} \sum_{k} \frac{U'_k}{v'_k} \; \frac{I^{(k)}}{I}}{{\mathbb E }\left[ {\textbf{1}}_{\{ I \ge a \}} \sum_{k} \frac{U'_k}{v'_k} \; \frac{I^{(k)}}{I} \right]}
It turns out that this risk measure does not satisfy the common axioms of coherence and convexity. It is important to note that within this framework, the allocation results are determined through optimization. In particular, the exposure parameters are not fixed but determined in the optimization procedure—unlike in the conventional approaches.
3.7. Some connections between the allocations
Table 1 presents the implementation of all allocation methods mentioned in the previous sections. As a side note, there are several connections between the various allocation methods beyond what has been pointed out so far in this section:
-
For elliptical distributions, the Euler allocation yields to the same relative amounts of capital allocated to each line, irrespective of which (homogeneous) risk measure we use (corollary 6.27, McNeil, Frey, and Embrechts 2015).
-
Asimit and collegues (2012) show that risk capital allocation based on TVaR is asymptotically proportional to the corresponding VaR risk measure as the confidence level goes to 1.
Moreover, Figure 1 graphically illustrates the relationship between various methods discussed in this section. In the next section, we compare the methods based on two example settings.
4. Comparison of capital allocation methods
In this section, we analyze the allocation problems and methods discussed in the previous sections in the context of (1) a binomial loss model and (2) real-world catastrophe insurance losses. Specifically for the second context, we gained access to (scaled) simulated loss data for a global catastrophe reinsurance company.
We use the binomial loss model as a pedagogical tool to compare allocations in a lower dimension and to gain an understanding of allocation characteristics that may also be found in higher dimensions. With regard to the second context, we believe our data offers a degree of realism missing from previous contributions in which proposed allocation methods are studied only in the context of stylized examples or based on normal distributions (which is particularly limiting, as discussed in Section 3.7).
In Section 4.1, we start by outlining the allocation approaches. In the next two sections, 4.2 and 4.3, we present the implementation in the two settings. In Section 4.3, we also present a pricing exercise to show the impact of allocations and a sensitivity analysis to examine the stability of allocations.
4.1. Allocation approaches
For allocation techniques in both examples, we consider the following approaches:
-
Allocation by EVs
-
A covariance allocation (Here we choose the parameter 2 due to the similarities of the supporting risk measure to a quantile for a normal distribution, where 2—or, rather, 1.96 for a two-sided confidence interval of 95%—is a common choice.)
-
TVaR (expected shortfall) allocations for confidence levels 75%, 90%, 95%, and 99%
-
VaR-based allocations for confidence levels 95% and 99% (In the real-world context, in addition to estimating the allocations based on splitting up the corresponding empirical quantile into its loss components, labeled “simple,” we consider an estimation that takes into account the surrounding realizations by imposing a bell curve centered at the quantile with a standard deviation of three, labeled “bell.” In both examples, we also apply the kernel estimator method found in Tasche 2009 for computation of VaR and its allocations.)
-
Exponential allocations for parameters 0.10, 0.25, and 1.00
-
Allocations based on a distortion risk measure, in particular the proportional hazard transformation, Wang transformation, and exponential transformation (For the proportional hazard transformation parameters, we use 0.60 , 0.80 , and 0.95, where we follow Wang 1998 indicating that a typical transformation parameter ranges from 0.5 to 1.0, depending on the ambiguity regarding the best-estimate loss distribution. For the Wang transformation parameters, we use 0.25, 0.50, and 0.75, where we follow Wang 2012 indicating that a typical transformation parameters in the reinsurance domain range between 0.50 and 0.77, whereas 0.25 is a typical assumption for long-termed Sharpe ratios in the financial market. For the exponential transformation, we use parameters 0.50, 0.75, and 1.00.)
-
Myers-Read allocations for different capital levels (Section 3.3.1) (In particular, we choose capital equal to the 99.94% quantile, which roughly depends on capital levels to support an AM Best AA+ rating; three times the premium, which is roughly consistent with National Association of Insurance Commissioners aggregate levels; and the 99% VaR just for comparison purposes.)
-
Weighted/transformation-based allocations based on the Esscher and Kamps transformation (Here we choose transformation parameters such that a nonexplosive evaluation is possible, but sufficiently different from the EV allocation, which results in
-
The D’Arcy (2011) implementation of the RMK algorithm (Section 3.3.2), where we rely on the same (first) two capital levels as for the Myers-Read allocation
-
Allocations based on the percentile layer (Bodoff in Section 3.5), where we allocate the 90%, 95%, and 99% VaR
-
RTVaR allocations with 75%, 90%, and 95%, and (as with the covariance allocation)
-
Allocation on the (simple) average of the four considered TVaRs
-
Bauer-Zanjani allocations (Since their approach relies on the solution of an optimization problem, we need to specify the necessary ingredients. We provide details on the solution within both settings in the appendices.)
4.2. The case of heterogeneous Bernoulli losses
We consider individuals that face Bernoulli-distributed losses to belong to three groups. More precisely, we assume
-
groups of identical consumers with the same probability of loss, and
-
differing sizes of loss among groups, with and
We demonstrate results using groups of 5 consumers and groups of 100 consumers
For conventional allocation, we consider allocation of capital to three groups of consumers and assume full exposure in all groups. Therefore, the total loss indemnity in each group is where and the total indemnity of the company is The computation of expectation, standard deviation, VaR, TVaR, and other moments of are trivial and those statistics are used to calculate allocation weights. The results are listed in Table 2.
For the Bauer-Zanjani allocation, we assume that all groups have the same constant absolute risk aversion (CARA) preferences and absolute risk aversion parameters and we solve the allocation problem using from 0.1 to 2.0. It is well known that with CARA preferences, initial wealth is irrelevant. We impose a frictional cost of We optimize the objective function of Equation (8), obtain the parameters, and use Equation (10) in Appendix A to obtain the allocation weights. The optimization and allocation results are shown in Table 7.
Figure 2 provides a direct comparison of the different allocation methods (except for exponential c = 1). More precisely, since we have three different groups and allocation percentages add up to 1, we can depict allocations by two numbers. We choose the allocation percentages for Groups 1 and 3, and then, of course, the allocation to Group 2 can be calculated as the difference between their sum and 1.
Surprisingly, all methods lie along a line that shows a trade-off between allocating more to Group 3, which has the biggest loss size, and allocating more to Group 1, which has the smallest loss size. We observe that the tail-focused allocations such as Myers-Read lie on one extreme end and allocate the most to Group 3, while the EV allocation lies on the other extreme end and allocates the least to Group 3. Methods with distortion risk measures and weighted distribution transformations result in allocations closer to those of the EV method. The VaR, TVaR, and RTVaR methods are in between, with RTVaR (more tail focused) allocating more to Group 3, followed by TVaR and VaR. In the case of 100 consumers per group, the trade-off of allocation weight between Group 1 and Group 3 happens in a much smaller range compared with the case of 5 consumers per group. This is likely due to the diversification effect of 100 consumers and the fact that binomial risk is not a tail-focused loss distribution. Now, Group 3 is relatively less risky and therefore requires relatively less capital support. The weights of capital allocation shift from Group 3 to Groups 1 and 2.
The Bauer-Zanjani allocations also adhere to the same relationship, where a higher risk-aversion parameter pushes toward the tail risk measures—e.g., BZ-2.0 (the Bauer-Zanjani allocation with resembles the TVaR 95% allocation (seen in Figure 2a). For smaller risk aversion, the allocation is closer to the allocations focusing on the whole distribution—e.g., BZ-0.1 (the Bauer-Zanjani allocation with resembles the allocations of Bodoff, Wang transformation with large proportional hazard with small and Kamps (seen in Figure 2b).
Overall, despite the variety of capital allocation methods proposed, it appears that they produce rather similar results; their differences are explained by a single parameter that roughly corresponds to how much the tail scenarios are emphasized.
4.3. Catastrophe reinsurance losses
For this application, we begin by describing in detail the data and the approach to aggregation in Section 4.3.1. In particular, for our analyses, we limit the presentation to an aggregation to four lines only in order to facilitate interpretation of the results. Here, we follow Bauer and Zanjani (2021), where the same data and aggregations are used. We then compare allocation methods in Section 4.3.2. Finally, we consider their stability in Section 4.3.4.
4.3.1. Description of the data
The data is supplied by a catastrophe reinsurance company and it has been scaled. We are given 50,000 joint loss realizations for 24 distinct lines differing by peril and geographical region. Figure 3 provides a histogram of the aggregate loss distribution, and Table 3 lists the lines and provides some descriptive statistics about each line. The largest lines for our reinsurer (by premiums and expected losses) are “US Hurricane,” “N. American EQ West” (North American Earthquake West), and “ExTropical Cyclone” (Extratropical Cyclone). The expected aggregate loss is $187,819,998 with a standard deviation of $162,901,154, and the aggregate premium income is $346,137,808.[7]
We consider an aggregation to four lines, with line numbers listed in the column “Agg,” where we lump together all lines by perils. In particular, we can think of Line 1 as “earthquake,” Line 2 as “storm and flood,” Line 3 as “fire and crop,” and Line 4 as “terror and casualty.” In order to keep the results comprehensible, we limit the exposition to this four-line aggregation level. Table 4 provides descriptive statistics for four aggregated lines. Figure 4 shows histograms for each of these four lines.
We notice that Line 1, the “earthquake” distribution, is concentrated at low loss levels with only relatively few realizations exceeding $50 million (the 99% VaR only slightly exceeds $300 million). However, the distribution depicts relatively fat tails with a maximum loss realization of only slightly under $1 billion. The (aggregated) premium for this line is $46,336,664 with an expected loss of $23,345,695.
“Storm and flood” (Line 2) is by far the largest line, in terms of both premiums ($243,329,704) and expected losses ($135,041,756). The distribution is concentrated around loss realizations between $25 and $500 million, though the maximum loss in our 50,000 realizations is almost four times that size. The 99% VaR is approximately $700 million.
In comparison, the “fire and crop” (Line 3) and “terror and casualty” (Line 4) lines are small with aggregated premiums (expected loss) of about $34 ($19) million and $22.5 ($11) million, respectively. The maximal realizations are around $500 million for “fire and crop” (99% VaR = $163,581,546) and around $190 million for “terror and casualty” (99% VaR = $103,201,866). We consider the same allocation approaches outlined in Section 4.1. For the Bauer-Zanjani allocations, we again consider CARA preferences with different absolute risk aversion levels. The results of the optimization procedure are provided in Table 8. For details on the implementation procedure, refer to Appendix A.
4.3.2. Comparisons for the unmodified portfolio
Table 5 presents conventional allocation results for the (unmodified) portfolio of the company. Here, for each allocation method, we list the capital levels for each line, their sum, and the risk measure evaluated for the aggregate loss distributions. Obviously, the last two numbers should coincide—which can serve as a simple check for the calculations.
These aggregate risk measures vary tremendously, and thus so do the by-line allocations. For instance, it is trivial that the quantile VaR is far greater than the 95% quantile VaR. Therefore, in the second row for each method, Table 5 again lists the allocations as a percentage of the aggregate risk measure. These are the percentages on which we will base our comparisons. This is not only because it facilitates comparisons, but also because this is in line with practice, where the actual capital of a company may not be given in terms of a risk measure at all, or even if it is, it may not be the measure used for allocation.
The first observation when comparing the allocations is the realization that many of them look quite similar, which resonates with observations in other studies. For instance, in the context of the assumptions used for the Casualty Actuarial Society Dynamic Financial Analysis modeling challenge, Vaughn (2007) points out that a variety of methods, including allocations based on “covariance, Myers-Read, RMK with variance, Mango capital consumption, and XTVaR99 are all remarkably similar.” We find similar results in the context of an example from life insurance (Bauer and Zanjani 2013). There are a few outliers, however, most notably the exponential allocation with (Exp3). The reason is that, in that case, there is an extreme weight on the extreme tail, which, in turn, is driven by very extreme realizations of Line 2. Indeed, there are various realizations in the aggregate tail where the line realizations for Lines 1, 3, and 4 are under the expected loss, which explains the resulting negative allocations to these lines.
For comparing the remaining allocations, in analogy to the comparison in Section 4.2, we note that each allocation in our four-line context is characterized by three—not four—real numbers, since the fourth follows by subtracting the sum of the others from 100%. Hence, as in Figure 2, we can visualize allocations graphically, now as points in three-dimensional space. Moreover, we can evaluate the distance between two allocations using the Euclidean norm.
Figure 7a in Appendix B plots all of our allocations except for the aforementioned Exp3. From this, we see that there are a few other outliers in the sense that the distance to other allocation methods is quite significant: three VaR allocations—namely the “simple” calculation (VaR1S, VaR2S) for both confidence levels and the bell curve–based calculation for the higher confidence level (VaR2B)—and the Esscher allocation for the (high) parameter of 1E-7 (Essch1). The intuition for the latter is, again, the exponential weight pushing all relevance to the extreme tail where Line 2 dominates the others. Hence, both the exponential allocation and the Esscher allocations are extremely sensitive to the choice of the parameter (although this sensitivity does not appear to apply to the Kamps allocation). For VaR, on the other hand, it is well known that estimation based on Monte Carlo simulation is erratic (Kalkbrener 2005), so it may be numerical errors driving these outliers (at least for VaR1S). Two VaR allocations calculated using the kernel smoothing method (VaR1K, VaR2K) fall closer to the EV and other allocation methods.
Interestingly, aside from the “outlier” allocations mentioned above and two Myers-Read allocations, the points all appear to lie on a parabola-shaped curve in three-dimensional space that is suggestive of a systematic pattern. Hence, like the findings in Section 4.2, the differences among allocations seem to be explained by a single parameter. In order to zoom in on the remaining allocations, Figure 7b replots the same points, but this time we exclude outlying allocations as well as the two outer Myers-Read allocations. Again, the allocations seem related, and we find that the EV allocation plays an “extreme role.” This may not come as a surprise since suitable allocation methods should penalize risk “more than linearly” (Venter 2010).
A number of allocation methods are very close to the EV allocation: the Kamps, Wang, Bodoff, and covariance allocations are all within 0.06 of the EV allocation. In contrast, all the TVaR, RTVaR, average TVaR, D’Arcy, and Myers-Read allocations (except one) are bunched together between 0.07 and 0.19—and all roughly along the parabola-shaped curve, where the order appears to be driven by the parameters. The former allocation methods close to the EV are all driven by the entire distribution, whereas the latter allocation methods are all focused on the tails (though the Myers-Read allocation does depend on the entire distribution).
Figure 7a shows that Bauer-Zanjani allocations (BZ roughly lie along the parabola when the risk-aversion parameters are large, so that the allocations roughly coincide with many tail-based allocations when the counterparty is more risk averse. However, when the counterparty is approaching risk neutrality, or when is small, Bauer-Zanjani allocations produce results that deviate from other allocations. A key reason for this finding lies in the underpinning optimization problem that delivers an optimal portfolio on which the allocation is based. As is evident from Table 8, especially for smaller choices of the portfolio weights vary in their values. In particular, the weight for line 3, is relatively low, explaining why less capital is allocated to it.
Two key observations emerge. First, we observe a dissonance between allocations based on the tail and allocations based on the entire distribution. But which one is more appropriate? Should we, or should we not, focus on tails? Venter (2010) argues that from an economic stance, risk taking is not risk free—any modification to risk taking should carry some charge, so a focus on the tails is misguided. He supports using marginal (i.e., Euler-based) methods that are based on the entire distribution, such as the Wang transformation, since they are “the most commensurate with pricing theory.” However, D’Arcy (2011) and Myers and Read (2001) also present approaches with economic motivations. Second, we observe that conventional allocations behave in a qualitatively different manner from the economic Bauer-Zanjani allocations.
4.3.3. Comparisons of pricing under different risk measures
In this section, we explore pricing implications of different risk measures using the catastrophe reinsurance data. More precisely, we calculate prices using premium principles. Premium principles assume that the (net) premium is set with a positive loading on expected losses corresponding to a risk measure. A further discussion on some of the basic methods and premium principles is offered by Kaas and colleagues (2008). Here, we set the aggregate net premium to meet a profit-loading requirement, calibrate the risk measure so that the risk measure on losses meets the target aggregate net premium level (i.e., we solve for and then generate by-line prices using capital allocation techniques.[8] For VaR-based and TVaR-based pricing, we use the following formula for calibration:
{\mathbb E }[I] + \tau \; \text{VaR}_{\alpha}(I) = (1 + \text{profit loading}) \times {\mathbb E }[I]
where is the capital cost, and we assume it to be 8% in our calculation.
First, we need to obtain the profit loading on aggregate expected losses from the data. The data provider does not reveal expenses allocated to each business line, so the true profit loadings are unknown to us. We assume a constant expense loading on expected losses across the four lines. We calculate allocations using expense loads of 30% and 60%, with the former corresponding to the approximate all-line U.S. industry average for 2017 and the latter chosen for comparison purposes. Our data suggests an 84.29% margin of aggregate premiums over aggregate expected losses. Therefore, when assuming a 60% expense loading, the profit loading on expected losses is 24.29% in aggregate and 38.48%, 20.19%, 22.19%, and 48.62%, respectively, by line. When assuming a 30% expense loading, the profit loading on expected losses is 54.29% in aggregate and 68.48%, 50.19%, 52.19%, and 78.62%, respectively, by line. For each risk measure, we solve for the parameter in the risk measure. Finally, we use the calibrated risk measures to calculate net premium by line using capital allocation methods and to deduce profit loadings by line. We do not include the Myers-Read, D’Arcy, and Bauer-Zanjani methods here because these methods do not directly correspond to a risk measure. Table 6 provides the results.
In Table 6, we also include the provided aggregate premium markups, although—as noted in Footnote 7—these should be interpreted with care. At first glance, these markups suggest that Line 4 is the most profitable and Line 2 the least profitable. However, under the various capital allocation methods and the assumption of a common underwriting expense load across lines, Line 2 appears to be priced with the largest profit loadings, while Line 4 has the smallest loadings.
Comparing the results across methods, we see substantial variation in the implied loadings for Lines 3 and 4. This is not surprising, given their small size relative to the other lines: the variation between the methods is less pronounced for the larger lines, Line 1 and Line 2. VaR-based pricing, for which we again use the kernel smoothing method, stands out from the other methods as it implies a larger loading for Line 1 than for Line 2 in the case of 30% expense loadings. TVaR-based pricing produces results similar to those of VaR for a 60% loading, but it produces significantly lower loadings for Line 1 in the case of 30% expense loadings. Distortion risk measures, standard deviation, the Esscher transformation, and the Kamps transformation all produce similar pricing results in terms of ranking, with Line 2 Line 1 Line 3 Line 4. So, an important takeaway here is that, although the four lines come with significant differences in terms of relative size, risk measures can yield different rankings and weights in pricing. Tail-focused risk measures, including VaR and TVaR, yield qualitatively different results than measures considering the entire distribution.
4.3.4. Stability of the methods
In this section, we study the stability of the allocation methods. In particular, we recalculate the allocations from Subsection 4.3.2 for two distorted portfolios:
-
Sensitivity 1: We eliminate 1,000 arbitrary sample realizations, leaving us with 49,000 realizations.
-
Sensitivity 2: We replace the five worst-case (aggregate) scenarios with the sixth-worst aggregate scenario (so that our sample now contains six identical scenarios).
The intuition behind the first stability test is clear: an allocation should be robust to unsystematic changes in the sample. When adding, changing, or subtracting from the sample in an unsystematic way, we would hope to see the allocation stay more or less the same. And since we cannot add to or change the sample because we do not know the data-generating process, we subtract.
The second test is motivated by ideas from Kou, Peng, and Heyde (2013), who discuss robustness properties of risk measures and—based on the observation that coherent risk measures are not always robust—define so-called natural risk statistics. It is important to note that our angle is different in that we consider allocations and not risk measures, even though the underlying issues are the same. Specifically, extreme tail scenarios are very hard to assess—for instance, even with 5,000 observations one cannot distinguish between the Laplace distribution and the distributions (Heyde and Kou 2004). Therefore, modifications in the extreme tail should not have a tremendous impact on the allocation.
As indicated in the previous subsection, we can identify allocations for our four business lines with points in three-dimensional space, and we can identify the difference between two allocations with the (Euclidean) distance between the corresponding points. As a yardstick when assessing allocations, note that the difference between the 90% and the 99% TVaR is 0.056, which is thus a sizable difference. The difference between the 95% and the 99% TVaR is 0.026, which is still considerable.
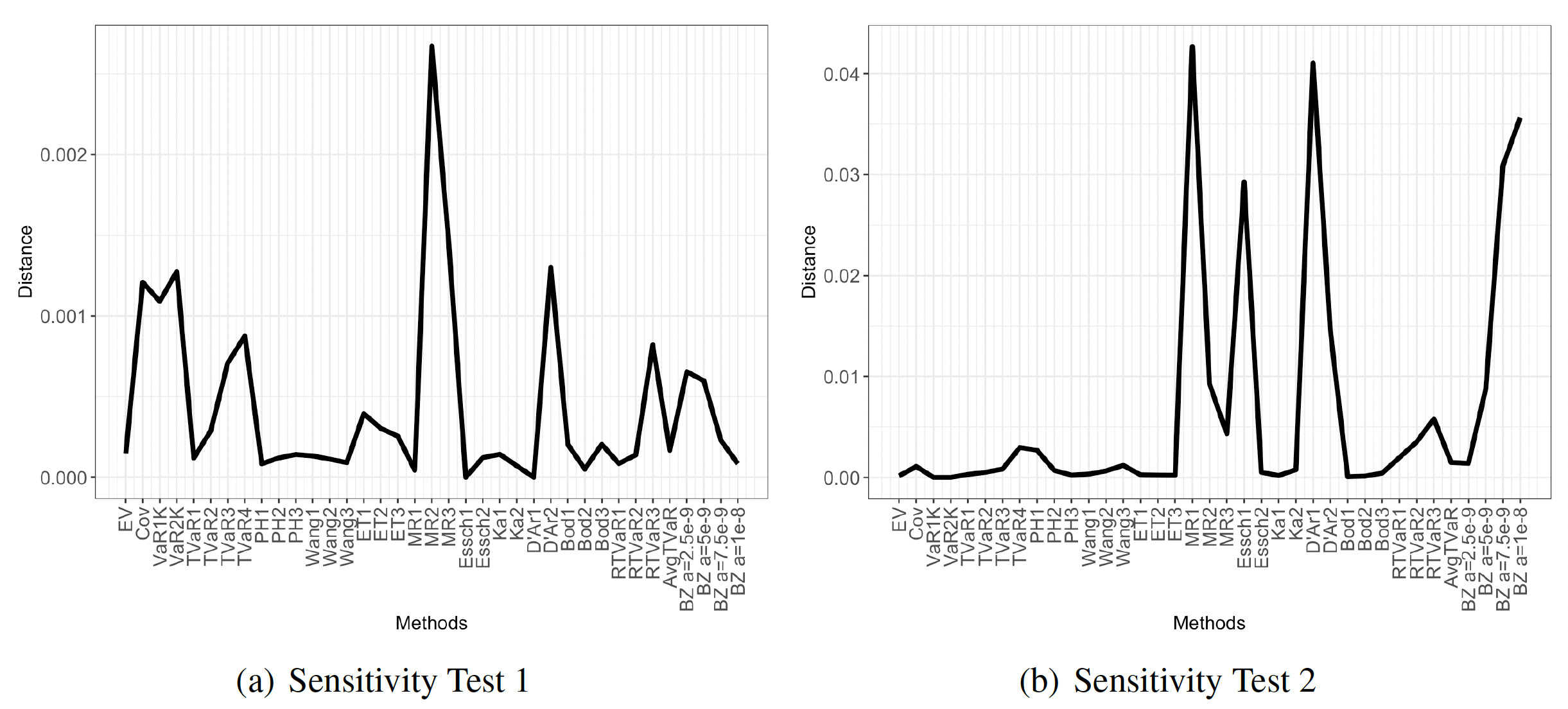
Figure 5 plots distances between the allocations for the original portfolio and the modified portfolio for both sensitivity portfolios and all considered allocations methods. Again, we find that VaR-based allocations and the Exp3 allocation stand out as extreme outliers, though on different tests. More specifically, VaR allocations respond particularly poorly to unsystematic changes in the portfolio, whereas the exponential allocation is particularly sensitive to changes in the tail. This contrasts with the findings of Kou, Peng, and Heyde (2013), who argue that VaR has good robustness properties for risk measurement. VaR allocations based on the kernel estimator are stable at both the 95% and the 99% levels. We eliminate VaR-based (except for VaR kernel) and exponential allocations and plot the differences for the remaining methods for both tests separately. Figure 6 displays the results.
Figure 6a shows the results for the (unsystematic) modification via the elimination of 1,000 samples. We find that all methods are relatively stable (ignoring VaR1S). The maximal difference now is about 0.0025, which is not too sizable for the Myers-Read 2 allocation: the corresponding allocation vectors are (7.56%, 88.98%, 4.44%, -0.97%) and (7.78%, 88.85%, 4.38%, -1.01%), respectively.
In contrast, when eliminating tail scenarios, the impact can be considerable. Figure 6b shows that, in some cases, it can amount to more than 0.04. The most sensitive allocation methods are the Myers-Read, D’Arcy, Esscher, and the Bauer-Zanjani for high —all of which are tail-focused allocations. However, we do not find the same for TVaR-based allocations, which is contrary again to the findings from Kou, Peng, and Heyde (2013) for risk measurement. Also noteworthy is the stability of the proportional hazard, Wang, Kamps, and Bodoff allocations, so it appears that stability is less critical for methods that are not tail focused.
5. Conclusion
Actuarial literature contains numerous contributions on the subject of capital allocation. While theoretical questions are not settled and deserve continued attention, implementation questions have received much less attention but are of great importance to practitioners. This paper attempts to contribute by exploring differences and commonalities between various methods that have been proposed.
We find substantial differences across the universe of methods, although we find that all allocations appear systematically related in the context of our examples. Stability issues arise, predictably, in methods whereby allocations are keyed to one outcome or to a small set of outcomes—as is the case with some VaR-based allocations and allocations based on tail-risk measures. While the analysis here is based on specific data, we find the systematic relationship surprising and also encouraging in view of companies’ problem of choosing the “correct” method. More research is needed to verify whether these findings carry over to other situations.
_and_(.png)




_and_(.png)