1. Introduction

Insurance companies are subject to numerous regulatory standards to which they must comply to guarantee their financial engagements arising from insurance policies. In particular, they must follow the IFRS 17 Insurance Contracts issued by the International Accounting Standards Board (IASB) for the recognition, measurement, and disclosure of insurance contracts. For non-life insurance companies, this results in the establishment of a loss reserve covering the liability for incurred claims, i.e., the unpaid part of insured claims that have occurred. Significant parts of this nonfinancial risk are the frequency risk (the uncertainty related to the number of claims) and the severity risk (the uncertainty related to the total amount of each claim).

Most of the loss reserving models proposed in the literature can be classified into two categories: collective approaches and individual approaches. This is mainly due to the granularity of the underlying data set. Collective loss reserving models are better known, more used in practice, and have been investigated more extensively by researchers. These models rely on aggregated data, usually collected by accident year and development year, whose dynamic researchers try to capture. The information is usually gathered in a table referred to as a run-off triangle (see Table 4). The actuarial literature on such models is vast: we refer readers to the overviews by Wüthrich and Merz (2008) and England and Verrall (2002).

Individual loss models aim to explain the dynamic of the development on a claim-level basis, before the claims are aggregated (see Figure 1). These approaches advantageously use detailed information on each payment and each contract to model the reserve of the portfolio. The first individual models were developed in the 1980s by Bühlmann, Schnieper, and Straub (1980), Hachemeister (1980), and Norberg (1986), but it was really at the turn of the century that such a loss reserving approach became popular. Many modeling strategies were pursued in parallel: in particular, the parametric or semiparametric approaches presented by Antonio and Plat (2013), Pigeon, Antonio, and Denuit (2013), Larsen (2007), Zhao, Zhou, and Wang (2009), and Zhao and Zhou (2010), and the approaches based on machine learning techniques, such as those of Wüthrich (2018), Baudry and Robert (2019), and Duval and Pigeon (2019). The idea to replace the Poisson distribution by a Cox process has been investigated by Avanzi, Wong, and Yang (2016), Badescu, Lin, and Tang (2016), and Badescu et al. (2019). The goal is to account for dependence in the claim arrival process to refine the estimate of the incurred but not reported reserve. Finally, a few research papers have compared collective and individual approaches; for example, Huang, Qiu, and Wu (2015), Hiabu et al. (2016), and Charpentier and Pigeon (2016).

In this paper, we introduce a model that has many features patterned on the basic structure of the models proposed by Antonio and Plat (2013) and Pigeon, Antonio, and Denuit (2013). We thoroughly analyze a portfolio from a Canadian casualty and property insurer, focusing on three popular car insurance coverages: automobile physical damage (APD), bodily injury (BI), and accident benefit (AB). The main objectives of this paper are threefold:

• Propose a generalization of an existing parametric model that allows more flexibility in the modeling of the dependence structure.

• Discuss model implementation strategies.

• Analyze the differences and similarities of the models obtained for the three available coverages.

Note that there is dependence between the three coverages, but in the data set considered, there are too few relevant observations for a model to be statistically valid at the individual level. Collective approaches, for example, Shi and Free (2011), De Jong (2012), Zhang and Dukic (2013), Abdallah, Boucher, and Cossette (2015), and Côté, Genest, and Abdallah (2016), have been proposed to model such dependence and, with an adequate data set, these approaches could be adapted to an individual setting.

In Section 2, we present the structure of the individual model proposed here, highlighting the generalizations of Antonio and Plat (2013) and Pigeon, Antonio, and Denuit (2013). In Section 3, we implement the model on a data set and we analyze the results. We conclude the paper in Section 4.

2. Individual Loss Reserving

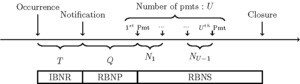
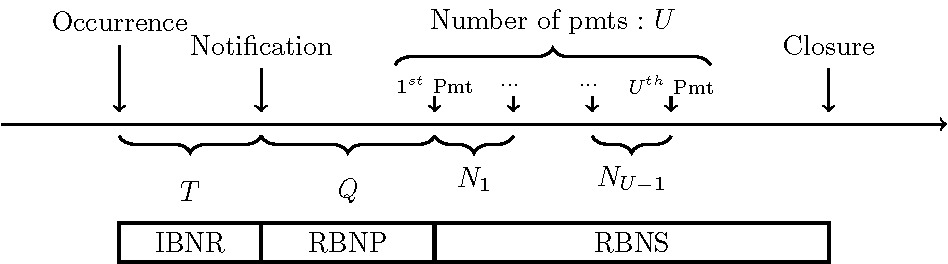
In this section, we summarize the structure of the model, mainly inspired by Pigeon, Antonio, and Denuit (2013). In Figure 1, we illustrate a typical development pattern of a claim and show the different reserves that must be modeled: incurred but not reported (IBNR), reported but not paid (RBNP), and reported but not settled (RBNS).

Figure 1.Typical development pattern of a claim in non-life insurance

Identically to Pigeon, Antonio, and Denuit (2013), time is discretized in periods, which will be years in our case. Each claim is uniquely identified by \((i,k)\) where \(i\in \left\{1, \ldots, I\right\}\) corresponds to the \(i\)th occurrence period and \(k\in \left\{ 1, \ldots, K_{i}\right\}\) is the \(k\)th claim from occurrence period \(i.\) To simplify the notation throughout, note that we do not make reference to \((i,k)\) if unnecessary. To model such a claim, three basic components are needed: a model for the occurrence of a claim, which is the starting point of its development (see Subsection 2.2); a series of discrete random variables (rvs) representing the time structure, meaning the delays between the different events (see Subsection 2.1); and a random vector for the development of the severity of a claim (see Subsection 2.3).

2.1. Time components

Let us characterize the evolution of a claim \((i,k)\) from its occurrence to its settlement through the following three random variables:

• \(T_{i,k}\) representing the reporting delay (in years or, more generally, in periods) for the \(k\)th claim of the \(i\)th occurrence period, i.e., the number of periods between the occurrence period of a claim and the reporting time to the insurance company;

• \(Q_{i,k}\) representing the first payment delay (in periods) for the \(k\)th claim of the \(i\)th occurrence period, i.e., the number of periods between the reporting time to the insurance company and the first payment; and

• \(U_{i,k}\) representing the total number of payments made for the \(k\)th claim of the \(i\)th occurrence period.

In practice, we often observe claims for which the file is closed without payment \((U_{i,k} = 0).\) In order to have more flexibility to model this situation, we introduce a dichotomous rv \(I_{i,k}\) to take into account the occurrence of a first payment and we define

\[\begin{aligned} U_{i,k} = \begin{cases} 0, &\qquad \text{if } I_{i,k} = 0\\ U_{i,k}^{\ast} + 1, &\qquad \text{if }I_{i,k} = 1 \end{cases}\end{aligned}\]

where \(U_{i,k}^{\ast}\) corresponds to the number of payments made after the first one. Remember that \((i,k)\) is a unique identifier for each independent claim. Therefore, each claim is associated with a unique value for each time component \(T_{i,k},\) \(Q_{i,k},\) and \(U_{i,k}.\)

Because we are interested solely in the total amount of the reserve and not in the payment calendar, it is not necessary to construct a model for the delays between each payment. Each of the time components \(T_{i,k},\) \(Q_{i,k},\) and \(U_{i,k}\) is a discrete rv with a cumulative distribution function (cdf) denoted by \(F_{1}\left(\cdot ;\mathbf{\nu}\right),\) \(F_{2}\left(\cdot ;\mathbf{\psi}\right),\) and \(F_{3}\left(\cdot ;\mathbf{\beta}\right),\) \(\mathbb{N}\rightarrow \left[0, 1\right],\) with respective probability mass function (pmf) given by \(f_{1}\left(\cdot ;\mathbf{\nu}\right),\) \(f_{2}\left(\cdot ;\mathbf{\psi}\right),\) and \(f_{3}\left(\cdot;\mathbf{\beta}\right).\) Finally, we assume that \(I_{i, k} \sim \text{Bernoulli}(p).\)

Depending on the stage of development, each observation of the data set provides more or less information on the distribution of each of these components. Indeed, given the category (IBNR, RBNS, RBNP, or closed, see Figure 1) to which a claim at the evaluation date belongs, Table 1 presents the information available for the estimation of the parameters of the models. This information will be used to derive the likelihood functions maximized in Subsection 2.4.

2.2. Occurrence of a claim

Let the rv \(K_{i}\) represent the number of claims for the occurrence period \(i\) with cdf denoted by \(G_{i}:\mathbb{N\rightarrow }\left[ 0,1\right]\) such that \(\text{E}\! \left[ K_{i} \right] =\int xdG_{i}\left( x\right) =\theta \omega _{i},\) where \(\omega _{i}\) corresponds to the exposure for the occurrence period \(i.\) In order to choose and estimate a model for \(K_{i},\) it is important to note that only the claims reported to the insurer are observed. This means that the distribution of \(K_{i},\) \(i = 1, \ldots, I\) must be adjusted as follows:

\[\begin{aligned} \text{Pr}\! \left( K_{i} = k\left\vert T_{i,1}\leq t_{i}^{\ast }-1,\ldots,T_{i,k} \leq t_{i}^{\ast }-1\right. \right),\end{aligned}\]

where the evaluation takes place \(t_{i}^{\ast }\) periods after the occurrence, and the evaluation is done at the beginning of the period before payments are made by the insurer. In the simplest case, \(K_{i}\sim \text{Poisson}\left(\theta \omega_{i}\right)\) and

\[\begin{aligned} &\left( K_{i}\left\vert T_{i,1}\leq t_{i}^{\ast }-1, \ldots,T_{i,k}\leq t_{i}^{\ast }-1\right. \right) \\ &\ \sim \text{Poisson}\left( \theta \omega _{i}F_{1}\left( t_{i}^{\ast }-1; \mathbf{\nu}\right) \right),\end{aligned}\]

where \(F_{1}\) is the cdf of the reporting delay rv \(T_{i,k}.\)

2.3. Severity model

We have chosen to model the severity of the claims based on development factors like those of the chain-ladder method but adequately adapted in an individual loss reserving framework. In the well-known chain-ladder, or Mack’s, model for aggregated data, the multiplicative development factors link cumulative payments from one development period to the next. In the model here, the development factors link the cumulative payments for each claim individually.

Let \(Y_{i,k,j},\) \(j \in \left\{ 1, 2, \ldots, U_{i,k}\right\}\) denote the severity of the \(j\)th incremental payment of claim \((i,k)\) and \(\mathbf{\Lambda}^{\left(i,k\right)}\) be a random vector of dimension \(U_{i,k},\) assuming that a vector of dimension 0 is simply equal to 0.

More precisely, let \(\mathbf{\Lambda }^{\left( i,k\right) }\) be given by

\[\begin{aligned} \mathbf{\Lambda}^{(i,k)} &= \begin{bmatrix} Y_{i,k,1} & \lambda^{(i,k)}_1 & \cdots & \lambda^{(i,k)}_{U^*_{i,k}} \end{bmatrix}^T,\end{aligned}\]

where \(\lambda_{j}^{\left(i, k\right)} = \sum_{r=1}^{j+1}Y_{i,k,r}/\sum_{r=1}^{j}Y_{i,k,r}.\) Thus, the ultimate amount of claim \((i,k),\) denoted by \(C_{i,k},\) is given by

\[\begin{aligned} C_{i,k} &= \displaystyle{\prod_{j = 1}^{U_{i,k}} \Lambda^{(i,k)}_{j}} = Y_{i,k,1} \times \displaystyle{\prod_{j = 1}^{U^*_{i,k}} \lambda^{(i,k)}_{j}},\end{aligned}\]

where \(\mathbf{\Lambda }_{j}^{\left(i, k\right)}\) corresponds to the \(j\)th component of \(\mathbf{\Lambda }^{\left(i, k\right)}.\)

In this paper, we choose a multivariate distribution for \(\mathbf{\Lambda }^{\left(i,k\right) }\) defined through a copula, i.e.,

\[\begin{aligned} F_{\mathbf{\Lambda}}\left(\mathbf{\lambda}\right) &= \mathcal{C}\left( F_{Y_1}(y_1), \ldots , F_{\lambda_{u^*}}(\lambda_{u^*})\right),\end{aligned}\]

where \(\mathcal{C}\) is the copula and \(F_{Y_{1}}, F_{\lambda _{1}}, \ldots, F_{\lambda _{u^*}}\) are the marginal cdfs of each component of the development vector \(\mathbf{\Lambda },\) respectively. For the sake of simplicity, we assume that \(U_{i,k}\) only affects the dimension of the copula, but not the joint distribution of \(\mathbf{\Lambda}\) in the same way as the multivariate skew normal distribution in Pigeon, Antonio, and Denuit (2013). This assumption should be challenged in future research. We assume these distributions to be continuous on \(\mathbb{R}^{+}.\) For the first payment \(Y_{1},\) various classical distributions such as the gamma and lognormal distributions are considered, while for the development factors, a wide range of distributions are investigated. For the choice of the marginal distributions as well as for the dependence structure, this approach is more flexible than multivariate distributions used in other papers.

For the choice of the copula, we consider first and foremost elliptical copulas. The normal and Student copulas have the advantage of being defined through a correlation matrix \(\mathbf{\alpha }\) that allows us to consider diversified correlation structures. The Student copula may be preferable given its ability to capture dependence in the extreme values. The degree of freedom obtained will be an indicator of the more suitable model.

In practice, to establish the model, we have to choose the maximum dimension \(M\) of the random vector \(\mathbf{\Lambda}^{\left(i, k\right)}\) beforehand. This will be done considering the data set used and a tail factor, e.g., a geometric mean could be defined for cases where the number of payments exceeds \(M.\)

2.4. Estimation

Let us now define the likelihood functions that will be maximized to estimate the parameters of the models. Of course, these functions will consider the use of the density \(c\) of the corresponding copula \(\mathcal{C}\) for the dependence structure linking the components of \(\mathbf{\Lambda }^{\left( i,k\right) }.\) For closed claims, the likelihood function, denoted by \(L^{\text{Cl}},\) is given by

\[\begin{aligned} L^{\text{Cl}} \propto& \prod_{(i,k)_{\text{Cl}}} c \left( F_{Y_1}(y_1), \ldots , F_{\lambda_{u^*_{i,k}}}(\lambda_{u^*_{i,k}}) ; \mathbf{\alpha} | u_{i,k} \right) \\ &\quad \quad \times f_{Y_1}(y_1) \times \ldots \times f_{\lambda_{u^*_{i,k}}}(\lambda_{u^*_{i,k}}) \nonumber \\ \times& \prod_{(i,k)_{\text{Cl}}} f_1(t_{i,k};\mathbf{\nu}|T_{i,k} \le t^*_{i,k} -1) \\ &\quad \quad \times f_2(q_{i,k}; \mathbf{\psi} |Q_{i,k} \le t^*_{i,k} - t_{i,k} -1) \nonumber \\ \times& \prod_{(i,k)_{\text{Cl}}} f_3(u_{i,k};\mathbf{\beta} | U_{i,k} \le t^*_{i,k} - q_{i,k} - t_{i,k} - 1). \nonumber \end{aligned}\]

For RBNS claims, the likelihood function, denoted by \(L_{c}^{\text{RBNS}},\) is given by

\[\begin{aligned} L^{\text{RBNS}} & \propto \prod_{(i,k)_{\text{RBNS}}} c \left( F_{Y_1}(y_1), \ldots , F_{\lambda_{u^*_{i,k}}}(\lambda_{u_{i,k}^*}) ; \mathbf{\alpha} | u_{i,k}^{ed} \right) \\ &\quad\quad\quad\quad\times f_{Y_1}(y_1) \times \ldots \times f_{\lambda_{u_{i,k}^*}}(\lambda_{u_{i,k}^*}) \nonumber \\ \times& \prod_{(i,k)_{\text{RBNS}}} f_1(t_{i,k};\mathbf{\nu}|T_{i,k} \le t^*_{i,k} -1) \\ &\quad \quad\quad\times f_2(q_{i,k}; \mathbf{\psi} |Q_{i,k} \le t^*_{i,k} - t_{i,k} -1) \nonumber \\ \times & \prod_{(i,k)_{\text{RBNS}}} (1-F_3(u_{i,k}^{ed}-1;\mathbf{\beta})), \nonumber \\\end{aligned}\]

where \(u_{i,k}^{ed}\) represents the observed number of payments at the evaluation date. Finally, for RBNP claims, the likelihood function, denoted by \(L_{c}^{\text{RBNP}},\) is given by

\[\begin{aligned} L^{\text{RBNP}} & \propto \displaystyle{\prod_{(i,k)_{\text{RBNP}}}} f_1(t_{i,k};\mathbf{\nu}|T_{i,k} \le t^*_{i,k} -1) \\ &\quad\quad\quad\quad\times ( 1 - F_2(t^*_{i,k}-t_{i,k}-1 ; \mathbf{\psi})).\end{aligned}\]

The likelihood functions are evaluated considering all observations classified in the respective categories, \((i,k)_{\text{Cl}},\) \((i,k)_{\text{RBNS}},\) and \((i,k)_{\text{RBNP}}\) at the evaluation date. The marginal cdfs \(F_{Y_{1}}, \ldots, F_{\lambda _{u^*_{i,k}}}\) and their associated probability density functions (pdfs) \(f_{Y_{1}}, \ldots, f_{\lambda _{u^*_{i,k}}}\) can be estimated by the fully parametric inference function for margins (IFM) method. This parametric two-step procedure is more flexible than the maximum likelihood method and more amenable to computations. A pseudo maximum likelihood method can also be used by first estimating each marginal nonparametrically by the empirical distribution function, not requiring specifying functional forms for the marginals. Then, the dependence parameters of the parametric copula family are estimated by the values that maximize the log pseudo likelihood function. See Joe (2014) and Genest and Favre (2007) for more details on these estimation methods.

2.5. Predictions

Once all components of the model are estimated, we can proceed with the prediction of the total reserve amount. An approach by Monte Carlo simulation allows us to find the predictive distribution of the reserve and, for the insurer, to use different risk measures to determine its economic capital. For each reserve category, we simulate the missing part of the development, based on observed information. We will obtain a reserve for each claim, for each category, and, hence, for the entire portfolio. Here is a summary of the components to be simulated for each reserve category:

1. For the IBNR reserve, we will need to simulate, for each occurrence period, a realization of the conditional rv

   \[\begin{aligned} (K| &T_1 \leq t^*-1, \ldots, T_{k^*} \leq t^*-1, \\ &T_{k^* + 1} > t^*-1, \ldots, T_{K} > t^*-1), \end{aligned}\]

   where \(k^{\ast }\) represents the observed number of claims in the considered period. For the case where \(K_{i}\sim \text{Poisson}\left( \theta \omega_{i}\right),\) we obtain a conditional rv with a \(\text{Poisson}\left( \theta \omega_{i}F_{1}\left( t_{i}^{\ast }-1;\nu \right) \right)\) distribution. Then, for each IBNR claim, we simulate a realization of the total number of payments \(U\) and of the development vector \(\mathbf{\Lambda}.\) Finally, the IBNR reserve amount is given by \(Y_{1} \times \prod\limits_{j=2}^{U}\Lambda_{j}.\)

2. For each observed RBNP claim, we simulate a realization of the number of payments \(U\) and a realization of \(\mathbf{\Lambda }\) of dimension \(U.\) We obtain a realization of the RBNP reserve with \(Y_{1}\times \prod\limits_{j=2}^{U}\Lambda_{j}.\) The only difference between the IBNR reserve and the RBNP reserve is that the number of claims is not known in the former case, whereas it is known in the latter case.

3. For each observed RBNS claim, we simulate a realization of the conditional rv \(\left( U\left\vert U\geq u^{ed}\right.\right)\) to obtain the number of missing payments. Note that the development vector \(\mathbf{\Lambda}\) can be written as

   \[\begin{aligned} \mathbf{\Lambda} &= \begin{bmatrix} \mathbf{\Lambda}^{\ast } & \mathbf{\Lambda}^{-}\end{bmatrix}, \end{aligned}\]

   where \(\mathbf{\Lambda }^{\ast }\) corresponds to the observed part of \(\mathbf{\Lambda }\) and \(\mathbf{\Lambda }^{-}\) to the unobserved development factors. We will then have to simulate a realization of the complete vector conditionally on the observed values \(\left( \mathbf{\Lambda }\left\vert \mathbf{\Lambda }^{\ast } = \mathbf{\ell}\right. \right)\) where \(\mathbf{\ell} = \left( Y_{1}, \lambda_{1}, \ldots, \lambda_{(u^{ed}-1)}\right).\) We sum all the claims to obtain an estimation of the RBNS reserve given by \(Y_{1} \times \left(\prod\limits_{j=2}^{U}\Lambda_{j}-\prod\limits_{j=2}^{u^{ed}}\Lambda_{j}^{\ast }\right).\)

3. Numerical Analysis

3.1. Data set

In this section, we provide a detailed analysis of a personal auto insurance data set from a Canadian property and casualty insurance company. The initial data set contains information regarding more than 100,000 car insurance claims for a period running from 2004 to 2016. We consider claims for three well-known types of coverage in the data set: automobile physical damage (APD), bodily injury (BI), and accident benefit (AB). APD coverage includes all guarantees regarding the loss or the partial loss of the car, such as collision or theft. BI and AB coverages are related to medical expenses and other related fees for insureds and a not-at-fault third party. All calculations have been done in R, using the copula package. This package is mainly used to manipulate elliptical and Archimedean copula families. More specifically, the function cCopula based on the Rosenblatt transformation (see Rosenblatt 1952 and Hofert, Mächler, and McNeil 2012) has been used to generate realizations of rvs conditionally on what has been observed, i.e., to compute \(\mathcal{C}(u_d | u_1, \ldots, u_{d-1}).\)

We will distinguish two types of statuses for a claim: open and closed. Because the data set did not explicitly include information regarding the status of a claim, a claim will be considered open if the amount of the reserve of the current period is nonzero or if the annual paid amount in the current year is different from zero. Also, for BI coverage, we consider as being open any claim with the following two additional characteristics:

• The development year is below or equal to 3, and

• No payment or reserve has ever been allocated to the claim.

Otherwise, the claim is considered closed. Adding these conditions for the BI coverage is justified given the slower development of these claims, as observed in Table 5, in which the most important payments occur in the third or even fourth development year. The absence of a payment or a reserve in the first years does not guarantee that there will be no future development. Finally, a claim whose status goes from closed to open is considered reopened. In Table 2, we present other characteristics of the data set, such as the number of claims with a refund, with multiple refunds, with a reopening, with multiple reopenings, etc.

Many reopenings tend to indicate that the claim is complicated to settle because its development differs from the typical development pattern of a claim presented in Figure 1. Indeed, there is something uncommon about the claims that required further developments from the original settlement. The coverage with the most reopenings is BI. Table 3 presents descriptive statistics for total payments of closed claims. The total payments for the BI coverage vary greatly, yet it is the class for which we have the fewest observations. The median total payment for BI is the lowest, while the average is the highest. Those statistics show that under the BI coverage, a large number of small payments are made as well as a non-negligible number of large payments, leading to the very large standard error observed. In comparison with the other two classes, these statistics illustrate how much riskier AB and BI coverages are: standard deviations and maximums are much higher than for APD. We also notice low minimums for all three classes, which are most likely administration fees that cannot be separated from the actual indemnity, adding to the complexity of the data set.

To validate the results, we consider January \(1^{\text{st}},\) 2012 as the evaluation date. Hence, only the information known at that date will be used for the model adjustment and for the analysis. The incremental loss development triangles for the three types of coverages AB, BI, and APD are given in Tables 4, 5, and 6, respectively.

The amounts in gray correspond to those observed and are used only to validate the results. We note that the development of claims for AB and BI is slower than for APD claims. The amounts paid for AB claims are more important in the first two to three years and then decrease slowly thereafter. For BI claims, we observe the opposite: the development of the claims is rather slow in the first two to three years and then accelerates before slowing down again around the seventh year. Unlike BI claims, APD claims take essentially two years for their development, leaving only minor payments thereafter. From the information available between 2012 and 2016 (in gray in Tables 4, 5, and 6), it is possible to obtain an approximation of the total paid amount for each coverage: $206,253,310 for the AB reserve, $246,404,599 for the BI reserve, and $5,015,952 for the APD reserve. It is important to note that the true reserve amounts should be slightly higher than these amounts, in particular for AB and BI coverages, given that the total amount of claims that occurred between 2004 and 2011 are not completely settled at the end of 2016.

For comparison purposes, we present the results obtained with classical collective approaches in Subsection 3.2 before presenting the results obtained with the individual copula-based approach in Subsection 3.3.

3.2. Collective approaches

We compare our individual loss reserving approach to classical collective models such as Mack’s model and parametric models based on the Poisson, gamma, and Tweedie distributions (see Wüthrich and Merz 2008 for a detailed presentation). These generalized linear models (GLMs) are benchmarks that insurers use to evaluate solvency. Results obtained are given in Table 7. We have also included in Table 7 the 95th and 99th percentiles of the distribution of the approximated reserve obtained by a bootstrap approach.

For AB claims, we note that the results are rather interesting as the observed total amount is within one standard deviation of the expected value, and the variance represents less than \(10\%\) of the expected amount predicted. Otherwise, the estimated parameter \(\widehat{p}\) of the Tweedie model is approximately 1.01, which explains the similarity of the results of the Poisson and Tweedie models. However, the quantiles are considerably above the true value of the reserve. In fact, the values are in the same range as the observed value.

For BI coverage, the estimations are much higher than the true value of the reserve, and the variance is high compared with the estimated value (more than \(15\%).\) The estimated parameter \(\widehat{p}\) of the Tweedie model is 1.72. The parametric models perform better than Mack’s model in that the 99th quantiles are not unreasonably higher than the 95th quantiles. As can be seen in the incremental loss development triangle (see Table 5), the highest amounts are not in the first years of development. This is due to claims with a large first payment, for which the delay for the first payment was longer than claims with a smaller first payment. For BI coverage, there are numerous dynamics for the settlement of claims, which complicates the treatment of aggregated data. Indeed, if the proportion of claims between these different dynamics change, adjustments must be made to pursue a common settlement dynamic for all claims. However, incorporating this type of information is not consistent with the ideas behind such models. Also, the quantiles are considerably higher than the realizations for this type of coverage. In such a case, an insurer using this model would set aside a reserve amount much higher than truly needed.

Results for GLM models are not given for APD claims. Such models are not appropriate due to numerous negative entries, which leads to the conclusion that these models do not generally capture the dynamic behind the data. As for Mack’s model, it underestimates the necessary reserve. We could explain this underestimation by the fact that the negative elements of the development triangle (see Table 6) lead to development factors below 1, starting from the fourth factor. Refunds are specific to each file and evolve over time. For instance, the insurance company can sell the iron from a car destroyed in an accident to recover some money from the total loss. More generally, an insurer can use its right of subrogation to regain money from insured loss payments. Collective approaches cannot easily handle this kind of portfolio characteristic because it is not consistent over time. Given the number of refunds received for APD claims (see Table 2) and the short settlement time (see Table 9), it is not surprising to have negative entries in Table 6.

Considering an individual approach would be more appropriate in this context given that a collective approach is based on the idea of stability through time. However, this portfolio contains many settlement patterns and a significant variation in the number of insured exposure units. In Tables 4, 5, and 6, unsteady variation can be observed down the first column (especially for year 2011), when more stability could have been expected for the first development year.

3.3. Individual approaches

3.3.1. Time structure

Various parametric models were tested to model rvs \(T_{i,k},\) \(Q_{i,k},\) and \(U_{i,k}^{\ast }.\) Besides the classical counting distributions, we considered mixtures with degenerate components such as

\[f\left(x;\mathbf{\xi }\right) = \sum\limits_{s=0}^{p}\xi _{s}\mathbb{I}_{\{x=s\}}+\left( 1-\sum\limits_{s=0}^{p}\xi _{s}\right) g\left(x\right), \tag{3.1}\]

where \(g()\) can be the pmf of the Poisson, negative binomial, or binomial distribution, \(\mathbf{\xi} = \begin{bmatrix}\xi_0 & \cdots & \xi_p \end{bmatrix}\) is a vector of parameters, and \(p = 0, 1, 2,\) or 3. Final choices were made using the AIC and BIC criteria. We present the results in Table 8.

As suggested in Subsection 2.1, we included a Bernoulli distribution to model the possibility of closure without any payment \((I = 0).\) Estimated values and standard deviations of the Bernoulli parameter for each class are \(\widehat{p}_{AB} = 0.356 \, (0.004),\) \(\widehat{p}_{BI} = 0.140 \, (0.003),\) and \(\widehat{p}_{APD} = 0.658 \, (0.004)\) for IBNR claims and \(\widehat{p}_{AB} = 0.111 \, (0.003),\) \(\widehat{p}_{BI} = 0.066 \, (0.002),\) and \(\widehat{p}_{APD} = 0.170 \, (0.005)\) for RBNP claims. The probability that a claim closes with a payment is significantly higher for an IBNR claim than for an RBNP claim. Therefore, we concluded that the additional information that no payment has been made during the first year was relevant to predict the probability that payments would be made on that claim.

In the data set used, we observed that a nonnegligible number of claims were closed without payment. When we modeled the occurrence of claims, all claims in the data set were included since we are interested in a claim being open and not being settled. However, we used this distribution to predict the number of IBNR claims, whereas the number of predicted IBNR claims and RBNP claims does not reflect the number of claims for which the insurer will have to make a payment to settle the claim. We will determine the number of predicted IBNR claims and RBNP claims for which we will have to simulate a claim severity by making an adjustment for the number of predicted IBNR claims and observed RBNP claims.

We used a binomial distribution to model the number of claims for which a development would occur. To estimate the parameter \(p\) of the binomial distribution, we considered only claims that had been in the data set for at least five years. This allowed us to have a reasonable amount of protection against future claim developments. We estimated this parameter by its empirical counterpart.

The probability that an RBNP claim is not settled varies depending on whether we possess the additional information that no payment was made in the first year. We therefore estimated the probability that an RBNP claim would eventually lead to a payment by calculating the ratio of the number of closed claims for which no payment was made in the first year but the total amount paid was not zero to the total number of closed claims with no payment in the first year.

It could be possible to refine this method if we had the underwriting rules or information concerning the construction of the data set. Individual models allow such targeted adjustments to be handled. This kind of analysis is not possible in a collective approach. For example, Table 2 shows for BI coverage that more than \(35\%\) of closed claims had been settled without payment. In a collective approach, such a particularity in the data set would certainly have been missed because only the aggregated information was used in the modeling process.

3.3.2. Development structure

Modeling the development vector \(\mathbf{\Lambda}\) constitutes one of the key questions in our analysis, given the potential strong associations between the components of this vector. We present, in Table 9, descriptive statistics of \(\mathbf{\Lambda}\) for closed claims. First, we observed, at an individual level this time, a situation similar to that observed in Tables 4, 5, and 6 with respect to the development pattern. Indeed, we saw faster development for APD coverage than for the other coverages. We also noted the same slower development of the claims at the beginning for BI coverage, with a higher development factor \(\lambda_{1}\) on average. Moreover, high values for standard errors of the development vector \((1269, 91.03, 12.63, 11.87)\) seemed to support the idea that it could be risky to model the development of a BI claim from an aggregated point of view.

Marginal distributions. To adjust and select a marginal distribution for each component of the development vector \(\mathbf{\Lambda},\) we included all available information, independently of the claim status (open or closed). We considered various distributions such as the gamma, normal, lognormal, Weibull, Gumbel, Pareto Type I, Pareto Type II (Lomax), generalized Pareto, loggamma, etc. We estimated all parameters using maximum likelihood techniques and appropriate R functions. We made our final choice based on the AIC and BIC. For each rv, Table 10 presents the selected distribution with the estimated values of the parameters (see Appendix for the parametrization of the distributions). For the third component of the development vector, \((\lambda_2),\) for AB coverage, we found that the loglogistic distribution was slightly better than the Burr distribution (AIC of 8,123 versus 8,147). The latter was selected in order to avoid complicating the model unnecessarily. Further, the same distribution (lognormal) was selected to model the first payment for the two coverages for medical expenses and other related fees while a different distribution (Pareto II) was chosen for material damage coverage.

Dependence. To characterize the strength of the dependence relation between the components of the development vector \(\mathbf{\Lambda},\) we estimated Spearman’s rho and Kendall’s tau empirically, and the results are presented in Table 11. We estimated only the components for which we had at least 150 observations in the data set. These results guided the choice of the dependence structure within the individual models.

To estimate the dependence structure, we used a semiparametric estimation method based on ranks (see, e.g., Genest and Rivest 1993 and Genest and Favre 2007) since the marginal distributions were unknown. For indication only, we also considered a classical parametric estimation method, IFM, proposed by Joe and Xu (1996). The values obtained for the different association measures indicated that a copula allowing negative dependence within the model had to be chosen. For AB and BI claims, a copula flexible enough to permit a level of association that differs between the components of the development vector \(\mathbf{\Lambda}\) also had to be considered. For that reason, we tried to adjust only elliptical copulas for these two types of coverages. For APD claims, we also tested the Frank copula. Finally, the Gumbel copula was not appropriate to model negative dependence, and the atypical behavior of the Clayton copula when the dependence parameter is negative excludes it from being considered in dependence modeling for a claim.

To estimate the dependence structure, we only used closed claims for which we had the complete information. The dependence structure could be different for claims needing only a few payments and claims with a long settlement period. However, it must be mentioned that by taking out the censored data, claims that were paid and closed rapidly necessarily represented a larger proportion of the data used in the estimation, which could impact the results.

Table 12 presents the AIC criteria for each copula and each estimation method, and Table 11 presents the estimation results obtained for each coverage with the semiparametric method for a normal copula with parameter \(\Sigma^{\text{Normal}}\) and a Student copula with parameters \(\Sigma^{\text{Student}}\) and \(\upsilon.\) Note that for the latter copula, we obtained \(\upsilon =\) 9,800, 47.7, and 11.2 for the AB, BI, and APD claims, respectively. The results for the Frank copula for APD claims have not been included given that it was the copula with the worst adjustment.

Predictive distribution. Figure 2 presents the predictive distribution for AB and BI coverages using the normal copula, and Figure 3 presents the predictive distributions for BI and APD coverages using the Student copula. As expected \((\upsilon = 47.7),\) both graphs for BI coverage are quite similar. This is confirmed with the values given in Table 13, which shows that the two models are not significantly different than the expected value, the standard deviation, and the 95th and 99th quantiles.

Figure 2.Predictive distribution based on a normal copula for AB (left) and BI (right) claims

The solid vertical line represents the observed reserve and the broken lines represent the simulated average value and the 99th quantile.

Figure 3.Predictive distribution based on a Student copula for BI (left) and APD (right) claims

The solid vertical line represents the observed reserve and the broken lines represent the simulated average value and the 99th quantile.

We note that the model for AB claims gives good results. The estimation of the expected value is slightly lower than its realization, but only by $2 million, which is less than the standard deviation. Furthermore, the variability represents more than an acceptable proportion of the estimated value of the reserve. The empirical coefficient of variation is around \(4\%.\) Consequently, the upper quantiles of the predictive distribution represent a considerable amount to be put aside as a reserve to cover possible future developments or reopening of claims, without being excessively high. For BI claims, the estimated value of the reserve is around $50 million over the realization, which represents a little more than \(20\%\) of the observed reserve. Finally, for APD coverage, the predicted amount is again slightly higher than the realization, but the performance of the model is satisfactory given that it predicts an amount above the observed reserve in a similar range of values.

Out of the three coverages, AB provided the best overall results for both individual and collective approaches. The prediction for the individual model was closer to the observed value. On data containing numerous reopenings, like BI coverage, the advantages of an individual model are more perceptible. Even though neither approach could easily get the average close to the observed value, the results from the individual approach are a lot more sensible, especially in the upper quantiles. As for APD coverage, refunds affect this coverage considerably, and no special adjustment was made in the individual model to take into account the numerous refunds, even though it was possible to do so. We did not pay special attention to this characteristic because it was negligible for bodily injury coverage, leading to a slightly conservative loss reserve for APD coverage. The model uses the total number of payments without necessarily considering if the payment has been made after a reopening. In our situation, the information about the claim status (open or closed) was an approximation. With a data set including reliable information on the claim status, this should be part of the model.

4. Conclusion

In this paper, we propose a generalization of the loss reserving model introduced in Pigeon, Antonio, and Denuit (2013). Compared with the existing model, estimating the marginals and the dependence structure separately increases flexibility and facilitates the estimation procedure, given that fewer parameters must be optimized simultaneously. However, this strategy has a price: the total number of parameters increases and, therefore, so does the complexity of the model. However, an individual parametric approach makes it possible to better understand and model the complexity of the underlying data set.

We also performed a detailed case study based on a micro-level data set from the industry. Our main conclusions are that

• the presented individual parametric model allows us to capture the complexity of claims development for AB and BI coverages, yet it is less relevant for APD coverage; and

• closed claims without payment must be modeled separately given their divergent behavior with respect to the coverage (AB/BI/APD) and the reserve stage reached by the development (IBNR/RBNP).

In future research, it would be interesting to add covariates in the three components of the model and to slightly expand the model to allow the prediction of the insurer’s payment schedule. Finally, it seems essential to perform a meta-analysis, like the one carried out by Huang, Qiu, and Wu (2015), which would compare different individual parametric approaches as well as models based on statistical learning techniques.

Acknowledgments

The authors thank an anonymous referee and the associate editor for useful comments that helped to improve the paper. Roxane Turcotte would like to thank the Natural Sciences and Engineering Research Council of Canada and the Fonds de recherche du Québec - Nature et technologies for financial support under grant 200418. Hélène Cossette would like to thank the Natural Sciences and Engineering Research Council of Canada for financial support under grant 04273. Mathieu Pigeon would like to thank the Natural Sciences and Engineering Research Council of Canada for financial support under grant 07094. The authors would also like to thank the industrial partner for supplying the database.

Appendix: Distributions

The pdf of a lognormal rv is

\[\begin{aligned} f(x) &= \frac{1}{x \theta_2 \sqrt{2 \pi}} \exp\left( \dfrac{- \left(\ln(x) - \theta_1\right)^2}{2 \theta_2^2} \right)\mathbb{I}_{(0,\infty)}(x)\end{aligned}\]

where \(\theta_1 \in \mathbb{R}\) and \(\theta_2 \in \mathbb{R^*_+}.\)

The pdf of a Pareto Type II rv is

\[\begin{aligned} f(x) &= k \frac{\theta_1^{\theta_2}}{(\theta_1+x)^{\theta_2+1}}\mathbb{I}_{(0,\infty)}(x)\end{aligned}\]

where \(\theta_1 \in \mathbb{R^*_+}\) and \(\theta_2 \in \mathbb{R^*_+}.\)

Finally, the pdf of a Burr rv is

\[\begin{aligned} f(x) &= \theta_1 \theta_2 \times \frac{x^{\theta_2-1}}{ \left( 1 + x^{\theta_2} \right)^{\theta_1 + 1}}\mathbb{I}_{(0,\infty)}(x)\end{aligned}\]

where \(\theta_1 \in \mathbb{R^*_+}\) and \(\theta_2 \in \mathbb{R^*_+}.\)