1. Introduction
In property and casualty (P&C) reserving practice, the estimation of reserves is a learning task: how to use the history of paid claims to predict the pattern of emergence of future claims. A major ongoing challenge is to quantify the respective uncertainty, or distribution, of future claims emergence. This is important for determining the required reserves, risk capital, and the resultant solvency of an insurance company.
In this paper, we explore the use of Gaussian process (GP) models for loss development. GP regression is a powerful machine learning technique for empirical model building that has become a centerpiece of the modern data science tool kit. GP approaches now form an extensive ecosystem and are fast being popularized across a wide range of predictive analytics applications. We posit that GPs are also highly relevant in the context of risk analytics by offering both full uncertainty quantification and a hierarchical, data-driven representation of nonlinear models. The proposed GP framework for loss triangles revolves around viewing the emergence of claims by accident and development year as a random field, bringing to the forefront a spatial statistics perspective. More precisely, we provide a fully Bayesian GP approach for the modeling of claims development that yields a full probabilistic distribution regarding future losses. We then show how GPs can be adapted to deal with the considerable complexities of loss development distributions including nonstationarity, heteroskedasticity, and domain constraints.
1.1. Models for Loss Development
The loss development challenge is to project from the “upper triangle” of historical claims the distribution of the lower triangle of future claims. The mean of that distribution is typically used to determine the level of loss reserves, and its tail is used to set the desired level of allocated risk capital. The fundamental objects available in loss development are cumulative paid claims (CC), indexed in terms of accident year (AY) and development lag (DL). In the National Association of Insurance Commissioners (NAIC) data set used below (see Section 1.5), we have for where denotes the full development horizon (10 years in NAIC data). Two derived quantities are the incremental payments
Ip,q:={CCp,1,q=1;CCp,q−CCp,q−1,q=2,…,Q,
and the year-over-year loss development factors (LDFs), i.e., the consecutive ratios between cumulative paid claims,
Fp,q:=CCp,qCCp,q−1,q=2,….
The advantage of LDFs is that they are normalized in terms of overall claims volume. A metric related to incremental claims is the incremental loss ratio (ILR),
Lp,q:=Ip,q/Pp,
where is the premium for the th accident year. We refer to LDF and ILR as “modeling factors” in this paper and denote them by
The training, or historical, data are presented via a triangle of development claims. We view the triangle as a collection of cells, indexed by two “inputs,” namely (i) and (ii) and one “output,” for example, We are interested in linking inputs to the outputs (or converting the loss development triangle/square into a columnar set of data with a single index The paradigm we adopt is a response surface approach, i.e., construction of a statistical latent surface representing the “true” output, which is then noisily observed in actual data. Thus, we postulate that there is an underlying function such that
yi=f(xi)+ϵi.
Following the triangular structure, we henceforth index cells by their year and lag writing For concreteness, we focus on the ILRs as the outputs; then is a true incremental loss development structure that describes the completed square, and are the observation noises, which are independent, with state-dependent variance For example, the chain ladder (CL) method assumes that the LDF is log-normal with a mean (i.e., independent of accident year), prescribed via the CL formula, and variance dependent on More generally, we construct a statistical model relating the observed factors ’s to the true latent input-output relationship, plus observation noise where captures the likelihood of realized observations.
In this paradigm, forecasting future losses translates into the double step of inference on the latent and then constructing the predictive distribution of future modeling factors s that is based on inferring the structure of For instance in the CL, the inferred logarithmic loss development factors are added together to inflate to the ultimate log development factor, combined with the (additive on the log scale) noises and finally exponentiated to obtain
1.2. Uncertainty Quantification
Our primary goal is to extrapolate existing losses to complete the full loss square given experience up to the present date This extrapolation must recognize that loss development is subject to stochastic shocks, and hence the forecasted should be represented as random variables. Indeed, beyond providing the expected modeling factor (or the more commonly expected cumulative ultimate losses we wish to quantify the respective distribution, so that we may, for example, assess the quantile of as needed in solvency computation. Since we have the fundamental relationship that
CCp,Q={CCp,qQ−1∏ℓ=qCCp,ℓ+1CCp,ℓ=CCp,qQ−1∏ℓ=qFp,ℓorCCp,q+Pp(Q∑ℓ=q+1Lp,ℓ)
to forecast unpaid claims, we need to forecast future s or s.
The overall task discussed above of constructing a predictive distribution of conditional on losses so far introduces the fundamental distinction between extrinsic and intrinsic uncertainty. The extrinsic uncertainty, also known as process variance, is linked to the fact that in equation (1.4) observed losses are noisy, so one must first forecast the latent surface and then overlay the extrinsic noise Thus, extrinsic uncertainty is the variance In contrast, intrinsic, or model or parameter, uncertainty refers to the impossibility of fully learning the true data-generating process given a finite amount of loss data. Traditionally, extrinsic uncertainty is fitted through a parametric assumption (e.g., log-normal LDFs or Poisson incremental claims), while intrinsic uncertainty is obtained from the standard error of a point estimate inferred through maximum likelihood estimation (MLE) or via ad hoc formulas such as the CL.
Many existing models tend to underestimate intrinsic uncertainty, which Track changes is on 40 leads to underpredicting the variance of ultimate claims. As a result, the models do not statistically validate in large-scale out-of-sample tests for reserving risk, due to being light-tailed. Thus actual ultimate claims are frequently too far above or too far below the mean forecast, relative to the estimated predictive variance. One popular remedy has been Bayesian frameworks (England, Verrall, and Wüthrich 2012; Kuo 2019; Taylor 2015; Wüthrich 2018; Zhang and Dukic 2013; Zhang, Dukic, and Guszcza 2012) that more explicitly control the residual randomness in through the respective priors. In this article, we contribute to this strand by developing a machine-learning-inspired, hierarchical approach that includes three layers of uncertainty.
First, we adopt a semiparametric extrinsic uncertainty, prescribing the distributional family of but allowing for cell-dependence. As our main example, we take to be normally distributed, but with variance depending on development year.
Second, we model in terms of a Gaussian random field. This offers a natural quantification of model risk through the two-step process of conditioning on the observed loss triangle and then computing the residual posterior variance in The latter posterior variance summarizes our confidence in correctly inferring given the data and is referred to as intrinsic uncertainty.
Third, we account for the misspecification risk regarding the spatial structure of by a further Bayesian Markov chain Monte Carlo (MCMC) procedure. Specifically, we employ MCMC to learn the distribution of the hyperparameters, especially the lengthscales, of the Gaussian process representing This is the correlation uncertainty layer. We show that in aggregate these three uncertainty layers not only properly account for overall predictive uncertainty (which is no longer underestimated), but also generate nonparametric predictive distributions while maintaining computational tractability afforded by the Gaussian structure.
To summarize, in our GP-based framework, completing the triangle comprises (i) sampling, via MCMC, hyperparameters of consistent with observations (ii) sampling a realization of s conditional on and (iii) sampling a realization of future observation noise and (iv) combining s and s to return the (sample-based) distribution of via equation (1.5). Importantly, while observation noises are a priori independent across cells, the spatial dependence in creates correlation in modeling factors across both accident years and development lags. This is a major distinction from traditional methods, where no such correlation is available. Moreover, the GP paradigm allows one to produce directly the whole vector which gives a full projection of the claims between today and the ultimate development date.
1.3. Related Literature
Stochastic loss reserving addresses uncertainty quantification of unpaid non-life insurance losses. The vast literature is centered around the CL method (Mack 1993, 1994), which provides analytic predictive distributions based on empirical plug-in estimates, and Bayesian methods (England and Verrall 2002), which extract posterior distributions through bootstrapping or MCMC approaches. We refer to the Wüthrich and Merz (2008) and Meyers (2015) monographs for an overview of the state of the art.
The CL approach provides empirical formulas for the latent LDFs that are then commonly injected into a log-normal model for Of note, the CL mean can be interpreted as a weighted average of across accident years, To provide statistical underpinnings to the CL formulas, analysts have developed Bayesian CL frameworks—see Merz and Wüthrich (2010). The latter derive as the posterior mean of a certain Bayesian conditioning expression. In turn, this allows the natural extension to consider intrinsic uncertainty, i.e., to use the full posterior of to capture model risk. Another notable extension of CL considers correlation in across accident years to remedy the respective independence assumption in the original CL, which does not validate well. Such correlation is also a popular way to boost the variance of ultimate claims. A related issue is the inclusion of a payment year trend.
In the multivariate Gaussian reserving models (Wüthrich and Merz 2008, Ch. 4), the cumulative claims are modeled as a log-normal random variable with mean/standard deviations The typical assumption is that the logged mean is of the form decomposing the true surface as an additive combination of one-dimensional accident year and development lag trend factors (an idea similar to the age–period decomposition of mortality surfaces). The variances are then directly specified via a correlation matrix In the most common version, they are taken to be independent across cells; see, for instance, Meyers (2015), who proposed the leveled CL (LCL) approach whereby the observation variance is constant across accident years and decreases in lag The three latent vectors are estimated via MCMC (implemented in Stan) after specifying certain structured priors on them. In the alternative correlated chain ladder proposed by Meyers (2015), the mean structure is augmented with generating across-year correlation between cumulative paid claims. However, in his results the posterior of the estimated correlation coefficient is quite wide, being both positive and negative, precluding drawing a clear conclusion regarding the across-year dependence. Zhang and Dukic (2013) and Zhang, Dukic, and Guszcza (2012) employ another parameterization, whereby they forecast cumulative losses with a prescribed nonlinear functional form, fitted through a hierarchical Bayesian model. Statistically similar is the approach of England and Verrall (2002), who used generalized additive models based on cubic splines; see also the extension to a GAMLSS model in Spedicato, Clemente, and Schewe (2014).
An alternative is to model directly. This paradigm dispenses with the existence of a “true” data-generating loss process and views triangle completion directly as an extrapolation task: given we seek to build an extrapolating surface that matches the observed upper triangle and smoothly extends it into the bottom half. In this framework, there is no observation noise, but rather the surface is viewed as a random field that intrinsically “vibrates.” Projected losses are then obtained by conditioning on historical observations but otherwise taking the remaining intrinsic variability in as the measure of the randomness of future LDFs. This approach will lead to correlated fluctuations in due to the spatial covariance.
This idea was recently implemented by Lally and Hartman (2018) (henceforth LH), who proposed applying GP regression to run-off triangles. In their framework the conditional residual variance of is precisely the predictive uncertainty. This idea exploits the fact that for far-out extrapolation. LH construct GP regression models for viewing cumulative losses as a smooth function of accident period and development lag. The inherent spatial nonstationarity of the run-off triangle is handled through input warping that is learned as part of fitting the GP model. LH work in a Bayesian framework, capturing hyperparameter uncertainty, as well as uncertainty about the best warping function.
1.4. Contributions
Our proposal to employ GP models for loss development combines the existing concept of a Bayesian chain ladder with a spatial representation of loss emergence. Thus, we model the development triangle as a random field; the inferred correlations across development lags and accident years allow for consistent stochastic extrapolation of future claims in both dimensions. In particular, this allows a statistical investigation of the trend/correlation in both the AY and DL dimensions.
The GP framework brings multiple advantages relative to existing loss development approaches. Having a coherent statistical framework for capturing all three uncertainty layers—extrinsic observation noise, intrinsic model uncertainty, and intrinsic correlation uncertainty—is the first distinguishing feature of our method. This combination offers a rigorous way to describe the predictive distribution of ultimate claims In particular, we can generate nonparametric, empirical distributions of any subset of s. To that end, the basic GP structure implies that a forecasted ILR is normally distributed. When modeling ILRs, the additive form in equation (1.5) implies that ultimate cumulative claims is also normally distributed. However, incorporating hyperparameter uncertainty leads to a mixture-of-Gaussians distribution of and hence a much more flexible description for the tails of
Second, the spatial structure of GPs allows us to generate consistent multiperiod trajectories of future losses, offering a full uncertainty quantification not just of a specific but of the entire vector Such joint draws of the full ILR path are necessary to capture the covariance structure not only of future capital requirements and risk allocation but also of the timing of the emergence of claim payments. Many existing models are either unable to generate full scenarios for the time-path or would generate wildly infeasible ones. For instance, since the Mack (1993) model only assumes that each LDF is log-normal and is otherwise independent and identically distributed, consecutive draws of as changes will almost certainly lead to nonsensical, non-monotone cumulative paid claims.
Third, we discuss coherent ways to adjust the GP model to respect the constraints of the development data, in particular the declining variance as losses develop, asymptotic convergence to ultimate losses, and paid incremental claims that are almost always positive. These constraints are especially important for far-into-the-future forecasts. To implement them, we built a custom hurdle model, augmented with virtual observations. As far as we know, this is a new methodology for GP surrogates of truncated data and is of independent interest to the GP community. Let us remark that in extrapolation tasks, which are necessarily mostly assumptions-driven, professional judgment can be conveniently encapsulated into the GP model via both the mean and the spatial kernel structure. Moreover, the corresponding forecast accuracy is then neatly encoded in the GP predictive variance, transparently showing to what extent the forecast is data-driven or assumption-based.
Fourth, the spatial structure extends naturally to analysis of multiple triangles, and hence brings a consistent way to handle multivariate losses. In Section 4.5 we show how GPs offer a ready-made mechanism to borrow strength (i.e., actuarial credibility) from the experience of related firms.
From the empirical side, we systematically check the efficacy of point estimates and distributions across a wide range of business lines and companies based on the paid claims in the full NAIC database. In particular, we present a variety of assessment metrics that go beyond the standard root-mean-square-error measures to assess the accuracy of the predictive distribution and predictive intervals (CRPS, NLPD, and K-S metrics, see Section 4.1). To our knowledge, these are new tools for uncertainty quantification of loss development and yield a detailed aggregate analysis.
Relative to Lally and Hartman (2018), who also investigated GPs for loss emergence, we note several key differences in the setups. First, LH work with cumulative losses, only mentioning incremental losses in passing. In our opinion, this is much less clear conceptually since it is difficult to disentangle the intrinsic dependence from cumulating claims from a true spatial correlation across DL and AY. Second, in LH the model for has no provision for ensuring monotonicity or convergence to full development. Instead, LH address this nonstationarity through input warping that reduces as grows. Lack of any monotonicity constraints implies that when computing the predictive distribution of ultimate losses, implausible values of are averaged. Third, LH eschew the issue of noisy losses—their model includes (taken to be constant), but it essentially serves as a numerical regularization device, bundling the randomness of claim emergence with the average pattern of loss development. In contrast, our approach distinguishes between the “true” loss development pattern and the observations. Fourth, LH present only a very limited study of three triangles; our analysis of the whole NAIC data set offers much more comprehensive conclusions.
Finally, we mention that other Bayesian spatial models have been proposed to represent the loss development surface; see, for instance, Gangopadhyay and Gau (2003), who proposed using bivariate smoothing splines combined with Gibbs sampling. However, a spline model is less suited for extrapolation (as it does not allow specifying a prior mean function), which is the main task in completing the triangle, and is furthermore more awkward for uncertainty quantification, necessitating the use of expensive MCMC compared with the parsimony of equation (2.3).
Our R and Stan code is available for inspection via a public repository at https://github.com/howardnewyork/gp_ilr. That folder also contains the data set described below and a brief guide through a README file.
1.5. Data Set
For our data set we use the NAIC database. That database was originally assembled by Meyers and Shi (2011) who built it using Schedule P triangles from insurer NAIC annual statements reported in 1997. These annual statements contain insurer-level run-off triangles of aggregated losses by line of insurance. The data in Schedule P include net paid losses, net incurred losses (net of reinsurance), and net premiums. The triangles were completed using subsequent annual statements from 1998–2006; a complete description of how it was constructed and how the insurers were selected is available on the CAS website (Meyers and Shi 2021).
The rectangles encompass 200 companies across six different business lines (not all companies have all lines): commercial auto comauto (84 companies), medical malpractice medmal (12), private passenger auto ppauto (96), product liability prodliab (87), other liability othliab (13), and workers compensation wkcomp (57). Each rectangle consists of 10 accident years and 10 development years, covering accident years 1988–1997 and development lags 1 through covering the period 1988 to 2007 (for the 10th development year for claims originating in 1997). To construct our training set we use the upper triangle, i.e., the data as it would appear in 1997, for a total of 45 LDF observations per triangle and 55 ILR observations. From the provided data, we use only those companies that have a full set of 10 years of data without any missing fields. We also exclude companies that have negative premiums in any year. Throughout, we focus on paid claims.
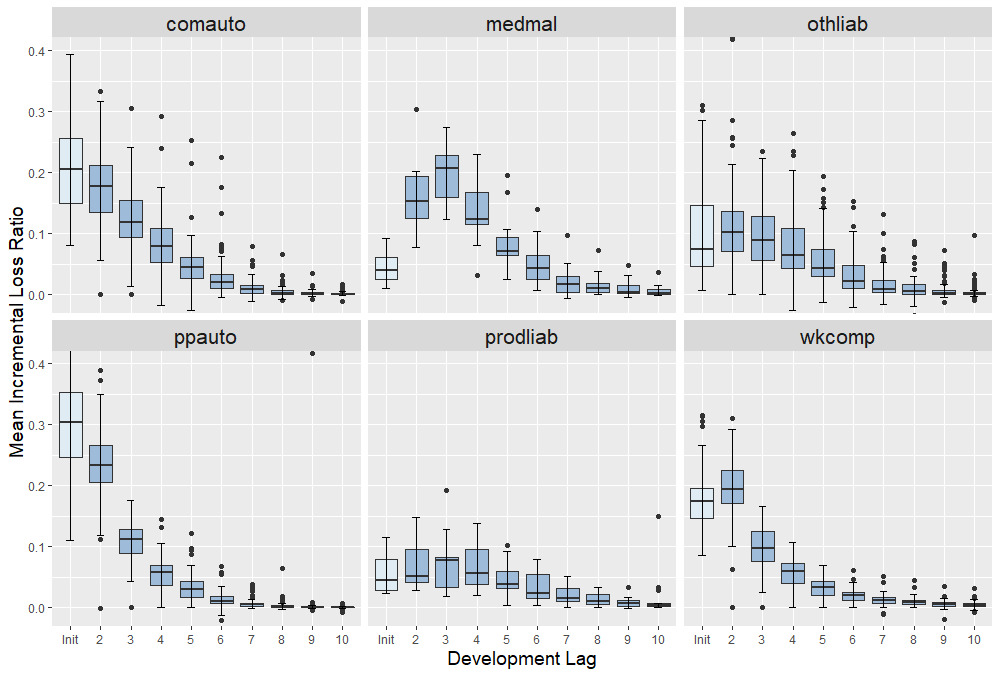
Figure 1 shows the typical shape of incremental loss ratios across different business lines (see also Table 2 in Appendix C that shows a typical triangle in terms of raw and the corresponding ILRs The boxplots show the distribution of across the companies of a given line. We observe that, as expected, ILRs tend to decrease in lag (with the notable exception of medmal where tends to peak at and prodliab where ILRs are essentially flat for the first 3 years). The auto insurance triangles tend to develop by or so; however, all other lines exhibit a significant proportion of positive ILRs even at We also observe that there is a nontrivial, frequently non-monotone pattern to the dispersion of which implies the need for a careful statistical modeling of
2. Gaussian Processes for Development Triangles
2.1. Gaussian Processes Overview
Gaussian process modeling (see, e.g., Rasmussen and Williams 2006; Forrester, Sobester, and Keane 2008) is a nonparametric machine learning framework to probabilistically represent input-output relationships. The GP has proven to be one of the best-performing methods for statistical learning, providing flexibility, tractability, and a fast-growing ecosystem that incorporates many extensions and computational enhancements. Moreover, compared with other machine learning methods, such as neural networks or random forests, GPs are highly suited for actuarial applications thanks to their intrinsic probabilistic structure that provides fully stochastic forecasts.
In the description that follows we adopt the abstract perspective of inputs and outputs Recall that our input cells are bivariate and the outputs are certain transformations of observed losses so far.
In traditional regression, including linear, generalized linear, and generalized additive modeling, in equation (1.4) is assumed to take on a known parametric form. Under the GP paradigm, is deemed to be latent and modeled as a random variable. Formally, a GP is defined as a set of random variables where any finite subset has a multivariate Gaussian distribution with mean and covariance A key difference between a GP and a standard multivariate normal distribution is that the latter is defined by a mean vector and a covariance matrix, whereas a GP is defined by a mean function and a covariance function.
GP regression recasts the inference as computing, using Bayes’ rule, the posterior distribution of conditional on the observed data where A key insight of the theory is that if the prior for is a GP, then so too is the posterior over new inputs namely In the standard setup, closed form expressions can be obtained for the posterior mean and the posterior covariance If ’s are normally distributed, then the posterior for the outputs, will also be a GP.
To construct a GP model, the user must specify its (prior) mean function and the covariance structure as well as the noise structure, i.e., the likelihood This is usually done by picking a parametric family for each of the above, so that inference reduces to learning the hyperparameters governing the structure of There are two broad approaches to fitting a GP to data. The first is an optimization-based approach, and the second is a Bayesian approach. The optimization approach entails using MLE to solve for the hyperparameters underlying the GP mean and covariance functions. The Bayesian approach requires establishing priors for each of the parameters and then solving for the posterior distribution of each of the hyperparameters. This is done by Markov chain Monte Carlo, generating a chain of samples drawn from the marginal distribution of each of the parameters. These samples can then, in turn, be used to generate a posterior distribution for on the training inputs as well as new inputs The primary advantage of the optimization is that the method is fast compared with the Bayesian approach. The Bayesian approach is, however, more flexible, and with judicious choices of priors can produce substantially more robust solutions. In sum, the steps involved in modeling with a GP entail:
-
Pick a prior mean and covariance function, plus noise specification.
-
Use MLE or a Bayesian approach to solve for the hyperparameters.
-
Use multivariate normal identities to condition on data + conditional simulations to generate forecasts of (both in- and out-of-sample).
-
Test the goodness of fit of the model.
-
Try alternate mean and covariance functions, repeat steps 2–4.
Practically, as our primary computing environment we have used the probabilistic programming language Stan (Carpenter et al. 2017) to build a fully Bayesian GP model. Stan uses Hamiltonian Monte Carlo as its core algorithm for generating a chain of samples drawn from the marginal distribution of each of the parameters. Those samples can then, in turn, be used to generate a posterior distribution for on the training inputs as well as new inputs (Betancourt 2017). In addition, we also compared with alternative implementation of GPs in R via the DiceKriging package (Roustant, Ginsbourger, and Deville 2012) that employs MLE-based hyperparameter optimization.
2.2. Determining the Posterior of a Gaussian Process
As mentioned previously, if the prior then the posterior, over new inputs is a multivariate normal random vector and has a closed form expression. That is, for any cell is a random variable whose posterior given is
f∗(x∗)|y∼N(m∗(x∗),s2(x∗))
m∗(x∗)=m(x∗)+C∗C−1(y−m(x))
s2(x∗)=C(x∗,x∗)−C∗(x∗)C−1C∗(x∗)T,
where the matrix covariance matrix and the vector are
C:=[C′(x1,x1)C(x1,x2)…C(x1,xN)C(x2,x1)C′(x2,x2)…C(x2,xN)⋮⋮⋱⋮C(xN,x1)C(xN,x2)…C′(xN,xN)],C∗(x∗)T:=[C(x∗,x1)C(x∗,x2)⋮C(x∗,xN)],
and Consequently, the point forecast at is and provides a measure of uncertainty (akin to standard error) of this prediction. The role of can be thought of as (spatial) credibility—posterior variance is low when is in the middle of the training set and grows as we extrapolate further and further away from Our interpretation is of as the intrinsic model uncertainty, which is then overlaid with the observation noise so that the predictive distribution of is
Y(x∗)∼N(m∗(x∗),s2(x∗)+σ2(x∗))
where the additive structure is thanks to the independence between the intrinsic uncertainty of the ILR surface and the extrinsic noise in realized paid losses. Note that equation (2.1) can be vectorized over a collection of inputs providing a multivariate Gaussian distribution for the respective In contrast to chain ladder–like methods, where loss development is done step by step, with a GP model we can complete the entire loss square (or any subset thereof) in a single step through the same universal multivariate Gaussian sampling. From another perspective, the GP posterior variance (2.3), which is specified indirectly through the spatial smoothing imposed by is to be contrasted with the direct specification of the correlation between and in the multivariate Gaussian models (Wüthrich and Merz 2008, Section 4.3.2).
2.3. A Conceptual Introduction to Gaussian Processes
The covariance structure captures the idea of spatial dependence: for any cells and if and are deemed to be “close” or in the same “neighborhood,” then we would expect the outputs, and to be “close” too. This idea is mathematically encapsulated in : the closer is to the larger the covariance and hence knowledge of will greatly affect our expectations of For example, model factors for consecutive accident years are expected to have high covariance, whereas factors 10 years apart would likely have lower covariance. Learning the covariance function (through, for example, likelihood maximization or a Bayesian procedure) quantifies this relationship, ultimately allowing for highly nonlinear modeling of claims by location.
Among many options in the literature for the covariance function, arguably the most popular is the squared exponential kernel,
C(xi,xj)=η2exp(−12(xi−xj)Tρ−2(xi−xj)),
where is a diagonal matrix. Traditionally, diagonal elements of the matrix are known as the lengthscale parameters, and is known as the signal variance. Together they are referred to as hyperparameters. While the lengthscale parameters determine the smoothness of the surface in the respective dimension, determines the amplitude of the fluctuations.
To provide intuitive insight into how a simple GP can model a relatively complex nonlinear function, we show an example in which the underlying data are generated from the following distribution (note input-dependent noise):
Y(x)∼N(0.1(x−1)2+sin(2x),0.1⋅1{x<3}+0.25⋅1{x≥3}).
To start, we could arbitrarily assume for the GP prior a mean function and a covariance function as in equation (2.6) with its entry defined via Now suppose our training data consist of a single point with being the observation noise. The observation at provides “strong” information for future measurements in that vicinity, and weak information for measurements far away. The covariance values of for new inputs will be close to 1 near but close to zero for values far away from 2, e.g., but at Thus we are more confident in our predictions for inputs close to 2 than further away, reflected in the “sausage-like” posterior 95% credible interval shown in the left-most graph in Figure 2. Note that on the right side of the plot, the lack of any nearby data points implies that approximately
When there are more data in our training set, the model gets “stronger” in the vicinity of the data points—see the middle panel in Figure 2 where we train on 40 data points. Here the trained GP model (dashed orange) matches quite well the true response (solid blue). We see that even with a very simple kernel definition (2.6), we are able to model a complex nonlinear model with noisy measurement. As we receive more data on which to train the model, the credible intervals shrink.
To give a sense of the effect of the lengthscale hyperparameter on the model, we fit another GP to the same data maintaining the square exponential kernel. The first model has and the second has shorter lengthscale The smaller decorrelates the observations faster and hence makes more “wiggly”—see the right panel of Figure 2. Here the smaller clearly overfits visually, confirming the need to have a rigorous procedure for picking the hyperparameters. Below we discuss how to specify the parametric structure or kernel of the covariance function; how to learn the parameters of the kernel; how to use GPs to conduct extrapolation, not just interpolation, tasks; and what special features are required for modeling paid loss development data.
2.4. Mean Function
The prior mean function stands in for the prior belief about the structure of in the absence of observed data. This resembles the approach described in Clark (2003) that prescribes a parametric growth curve for (or for The role of the mean is to guide the inference by detrending observations against a known structure. One can also combine such parametric trend assumptions with the GP framework through the so-called universal kriging that takes where ’s are the prescribed basis functions, and simultaneously infers the trend coefficients in conjunction with solving equation (2.1).
As can be seen from the example shown in Figure 2, a posterior GP will revert to the prior GP or will be more heavily influenced by the prior GP when the projection is conducted for inputs that differ materially from the observed data. An alternative for guiding the data is to dispense with the mean function (by using and adjust the kernel to incorporate a linear regression component. For example, in a Bayesian linear regression setting, is a linear function, and the priors for unknown and are Then can be trivially seen to be zero and for any inputs is determined as
Cov(Y(x1),Y(x2))=E[Y(x1)Y(x2)]−E[Y(x1)]⋅E[Y(x2)]=E[(ax1+b)⋅(ax2+b)]=σ2a⋅x1x2+σ2b.
Thus, a Bayesian linear regression can be modeled as a GP (although rather inefficiently), with mean function and covariance known as the linear kernel.
It can be shown (Rasmussen and Williams 2006, Ch. 4) that a quadratic function can be modeled in a GP setting by multiplying together two linear kernels. Furthermore, a range of more complicated functions can be modeled as combinations (namely, adding or multiplying) of simple kernels, such as linear or periodic kernels. In such a way, compound kernels provide structure to GP regression, which can be particularly useful for conducting extrapolation rather than just interpolation predictions. Details of working with compound kernels can be found in Duvenaud et al. (2013) and Rasmussen and Williams (2006). By creating compound kernels, a GP can model nonlinear data locally and then blend into a linear or quadratic regression model for distant extrapolations.
In this paper, we employ the compound kernel
C(x,x′)=C(SqExp)(x,x′)+C(lin)(xAY,x′AY)+C(lin)(log(xDL),log(x′DL)).
The squared exponential component will dominate in areas where there are lots of training data. For distant extrapolations, the former will trend toward zero and so the linear kernel will be dominant. Other kernel families, such as Matern, could also be straightforwardly used. In our experiments, the choice of kernel family is of secondary importance, in part because the triangle is in tabular form and therefore does not possess the fine local correlation structure that is most affected by kernel choice.
3. Structural Constraints of ILRs
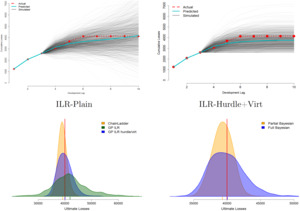
The left panel of Figure 4 shows a basic GP fit of ILR for a typical triangle. It illustrates the inherent smoothing of the GP approach that converts noisy observations from the upper triangle, (red dots), into a smooth latent surface of the modeling factor, here ILR. It also highlights several key features of ILRs:
-
as generally decreasing monotonically;
-
cumulative paid claims are generally increasing so that the true ILR should satisfy for any cell;
-
as generally monotonically, so there is little intrinsic and extrinsic uncertainty for long lags; and
-
as decreases rapidly, so ILRs are highly volatile for short development lags but have minimal variance for longer lags.
These features create the double challenge of constraints. First, the generated predictive distributions of must satisfy these constraints. In particular, it implies that the observation noise must be structured appropriately. Second, it might be desirable to have the latent also satisfy the constraints. For example, one might challenge the assumption of having a Gaussian prior on
3.1. Overall Procedure
For the latent surface after trying multiple approaches, we recommend using a plain GP structure. In particular, we do not impose any constraints on the latent surface—for example, we allow for ILR modeling. At the same time, it is critical to enforce that the predictive mean/standard deviation as the lag increases. Due to the spatial structure of the GP, without that constraint, forecasting ILR far into the future, i.e., far bottom right of the completed triangle, will intrinsically reduce to the prior, i.e., In turn, this leads to extremely wide predictive intervals, as the model would suggest a high degree of uncertainty about the posterior distribution of far into the future. Rather than more complex work-arounds, such as nonconstant GP process variance we found that the combination of a hurdle model, decreasing and virtual observations, all described in Section 3.2 below, ensures that at large lags (see right panel of Figure 4). This also offers a convenient, albeit ad hoc, way of handling the desired mixed distribution of realized ILRs for large
3.1.1. What to Model
Given that many quantities might be derived from the developed losses, the question of which quantity to model is nontrivial. In our analysis, we found that incremental loss ratios work best. This is partly justified by the fact that the spatial dependence assumption (in particular, across accident years) is most appropriate.
In contrast, other approaches have worked with unscaled quantities, such as the cumulative losses or the incremental claims For example, the Meyers (2015) LCL approach postulates that is log-normal with mean and standard deviation Lally and Hartman (2018) also directly model The overdispersed Poisson method is based on modeling
The choice of the object to model strongly influences the shape of the respective latent surface and the appropriate noise distribution. Incremental paid loss amounts tend to be skewed to the right and are occasionally negative, while is much more volatile as it is strongly affected by the overall claim volume. The fact that claims settle and hence eventually stabilize leads to different asymptotics: and
3.1.2. Variable Transformations
A natural way (analogous to a link function in generalized linear models) to enforce is via a log-transform. However, we found that the reverse exponentiating to convert predictions to original scale tends to be highly unstable with GPs, in particular generating very high predictive variance. A similar cause is our preference for modeling ILRs (that lead to an additive structure when computing ultimate claims) relative to LDFs, which come with a multiplicative structure. Indeed, our experiments suggest that properly building a GP model for LDFs is quite challenging, as the models tend to generate excessive uncertainty in the LDF at large lags. For example, even a hurdle LDF model will occasionally lead to a nonsensical predictive mean of that is multiple orders of magnitude larger than what is reasonable.
3.2. Noise Modeling
To ensure that progressively decays as we take the variance of to depend on The latter feature forces the estimated ILR surface to closely match observed s for long development lags to capture the full development of losses at At the same time, we allow to deviate far from observations for short lags. To achieve this, the observation variances are viewed as a nonparametric function of the DL The respective hyperparameters are learned with other GP hyperparameters, assuming a decreasing structure in DL. Our experiments suggest that an informative prior for is crucial for the MCMC chains to function well. The right panel of Figure 6 shows the respective posterior distribution, where we see that the fitted ’s rapidly approach as increases. This makes the forecasts get tighter around as lag increases, reflecting reduced uncertainty in incremental losses.
Remark 1. For cumulative models, increases in and should approach some ultimate asymptotic value. For incremental models, the same effect is achieved implicitly, since the uncertainty in ultimate losses is primarily based on the product/sum of individual -terms that progressively become less and less stochastic.
Furthermore, to reflect that generally we had success with the following Gaussian-hurdle-type observation model:
L(x)∼N(m∗(x),σ2(x))∨y_,
where Thus, future ILRs are first sampled from the Gaussian predictive distribution and then are rounded up to zero to directly enforce the nonnegativity constraint. Note that it makes the predictive distribution a mixture of a truncated normal and a point mass at the resulting is skewed and noncentered, i.e., The respective likelihood during the inference step is a mixture of a Gaussian likelihood if and a Bernoulli likelihood which we term the hurdle probability.
The hurdle probability takes care only of the left tail of It is also important to ensure that for at the bottom right of the completed square, otherwise large implies large posterior uncertainty in and hence very wide (right-skewed) predictive intervals even with equation (3.1) in place. To do so, we add virtual observations at namely, that losses fully develop by Computationally we simply augment our training data set with Virtual data points allow for incorporation of professional judgment by including information that lies outside the available loss triangle training data set.
Remark 2. We also tried based on the empirical standard deviation of the available observations at lag which is related to the stochastic kriging approach (Ankenman, Nelson, and Staum 2010). However, this method is highly unstable except for the first couple of DLs as otherwise there are too few observations to estimate the standard deviation with any certainty. Yet another possibility is to adjust based on the credibility of individual loss cells.
3.3. Models Tested
For our tests we have run the following three GP-based ILR models:
-
ILR-Plain: Stan Bayesian GP model with a compound linear kernel (parameterized by trend coefficients that fits We also fit lag-dependent observation variances We use equation (2.7) and take the following weak hyperpriors:
\begin{align} \rho &\sim InvGamma( p_{\rho,1}, p_{\rho,2} ), \\ \eta^2 &\sim \mathcal{N}(0, p_{\eta^2}), \\ \sigma &\sim \mathcal{N}(0, p_{\sigma}), \\ \theta &\sim \mathcal{N}(0, p_\theta).\end{align} \tag{3.2}
To set the hyperpriors for we follow the exposition by Betancourt (2017). The GP model becomes nonidentified when the lengthscale parameter is either below the minimum lengthscale of the covariate or above the maximum lengthscale of the covariate. Our training inputs are equally spaced, and the min and max lengthscales are and We then use these bounds to place light tails for the transformed lengthscale by tuning to obtain yielding a more informative prior. We also scale the training inputs to have zero mean and standard deviation 1.
-
ILR-Hurdle: Bayesian GP for ILRs with a hurdle observation likelihood (3.1) and constrained mean function.
-
ILR-HurdleVirt: Bayesian GP for ILRs with a hurdle likelihood and virtual observations at
For all models we use eight MCMC chains, with a burn-in of several hundred transitions and generating at least 1,000 posterior samples.
To demonstrate performance of GP models relative to “vanilla” loss development frameworks we also employed the ChainLadder (Gesmann et al. 2018) R package to construct a Mack stochastic chain ladder (Mack CL) that fits log-normal distributions to LDF Mack CL is equivalent to an overdispersed-Poisson generalized linear model for incremental claims
Remark 3. In Appendix A we also report the results from using the bootstrap chain ladder in ChainLadder (Gesmann et al. 2018), which replaces the parametric LDF modeling of Mack CL with a nonparametric bootstrap.
4. Empirical Results
4.1. Performance Metrics
In general, all loss reserve models are trained on the upper-left portion of the loss square, with the model being used to project the bottom-right portion. Since loss development forecasts are used for multiple purposes, we identify an appropriate performance metric for each likely broad application of the model. (Below we use to denote a generic random quantity being validated against its realizations This allows for comparison among GP implementations as well as against more standard models. We now describe the intended applications of loss reserve models along with the matching performance metrics. A key feature that we emphasize is the ability of GPs to generate full probabilistic forecasts, i.e., the entire predictive distribution, which allows for more sophisticated tests relative to methods that return only point forecasts.
-
Best estimate reserves: A primary task of loss reserve models is to establish a best estimate reserve for unpaid claims. To measure the accuracy of a model we test the ultimate projected cumulative claims by calculating the root mean square error (RMSE) of the ultimate projected cumulative losses, namely, against the actual amounts. We also calculate the “weighted” RMSE on cumulative paid loss ratio amounts, namely, where are the premiums for AY The latter metric down-weights the larger companies that have higher ’s and provides a more interpretable result. The RMSE captures the accuracy of the point forecast in terms of minimizing bias and controlling for variance and is aggregated (by averaging) across triangles, grouped by line of business.
-
Cash flow projections: A key financial task is to conduct cash flow projections for the emergence of claims payments. This is a core component of an asset–liability management program. To do this, a preliminary step is to calculate the -step-ahead cumulative loss ratios, namely We then calculate the RMSE on this value. We expect s to increase in as uncertainty necessarily rises for longer forecast horizons. Thus, the -year-ahead RMSE offers a more granular assessment and corrects for the tendency of the overall RMSE to be unduly influenced by the errors in the bottom right of the triangle.
-
Risk capital: Risk capital is necessary to cover reasonable worst-case loss scenarios, and the accuracy of the left-hand tail of the ultimate loss distribution is thus important for this measure. A good model, for example, should show 5% of the empirical cumulative claims, being less than the 5% predictive quantiles. To assess the tails of the predictive distribution we report the coverage probability: the empirical frequency that the realized losses land within the -band of the predictive distribution. Below we test for 90% nominal coverage, looking at the 5%–95% predictive quantiles.
-
Sensitivity analysis: This involves analysis of reserves based on reasonable downside and upside cases. In this case, we would want the overall predictive distribution to represent a good model for the data so as to detect potential model misspecifications. This leads us to more formal statistical tests described below.
To assess the quality of the predictive distribution, we use proper scoring functions (Gneiting and Raftery 2007) as implemented in the scoringRules (Jordan, Krüger, and Lerch 2019) R package, which return quantitative scores, such that better models should have (asymptotically) lower test scores than worse models. The proper scoring function ensures that a model is penalized for forecasting too much uncertainty; simpler metrics are typically sensitive only to underestimating the variance of Two specific criteria are the continuous ranked probability score (CRPS) and the negative log probability density (NLPD). CRPS is defined as the squared difference between the predictive cumulative distribution function (CDF) and the indicator of the actual observation,
\begin{align} \text{CRPS}( r) & := \int_{\mathbb{R}} (\hat{F}(z) - 1_{\{ r \le z\}})^2 dz. \end{align} \tag{4.1}
For repeated measurements, CRPS can be interpreted as the quadratic difference between the forecasted and empirical CDF of In our case the distribution of changes from company to company, but we can still average CRPSs across triangles.
NLPD is a popular tool for testing general predictive distributions. For a single triangle, the NLPD is defined as
\begin{align} \notag \text{NLPD} (r) & = -\sum_{i=T+1}^N \log p(y_{i}|y_{1:T}) \\ & = \left(\frac{r -\hat{r}}{\sigma_r} \right)^2 + \log \sigma_r^2,\end{align} \tag{4.2}
in the case where the predictive distribution is Gaussian and where is the number of training samples and is the total number of data samples. The NLPD is analogous to the likelihood function, except that lower values imply better fits of the model to the data. This score can be approximated directly in Stan using MCMC techniques—see Bürkner, Gabry, and Vehtari (2020). We calculate the NLPD on the ultimate losses of each triangle, and then add up across companies.
To further validate the entire forecasted distribution of we consider the realized quantile (i.e., “rank”) of relative to the predicted CDF. If the forecast is correct, those ranks should form a uniform distribution, since —see Figure 5. More formally we implement a Kolmogorov-Smirnov test on the realized sorted percentiles across triangles of a given business line. Let be the respective uniform percentiles. The K-S test rejects the hypothesis that is uniform at the 5% level if is greater than its critical value based on Kolmogorov’s distribution (Carvalho 2015). This can be visualized through a plot by plotting ’s -axis) against ’s -axis) and adding diagonals above and below the 45-degree line—see right panel in Figure 5. The same test was implemented by Meyers (2015) for over the entire NAIC data set.
To recap, we assess our models through multiple test metrics sorted in terms of their specificity: RMSE is based only on the predictive mean, NLPD is based on the predictive mean and variance, coverage is based on the predictive quantile, and Kolmogorov-Smirnov and CRPS are based on the full predictive distribution.
4.2. Predictive Accuracy
Table 1 lists the aggregate results for the wkcomp triangles (see Appendix A for the other lines). We recall that “lower is better” for all metrics other than coverage, which should be at 0.90. First, we observe a broad agreement between the two RMSE metrics (total RMSE based on ultimate cumulative losses and RMSE on the loss ratios weighted by the respective premia). At the same time, the more granular metrics signal that low RMSE is not necessarily correlated with good predictive uncertainty quantification. Indeed, while chain ladder achieves low RMSE scores, it fails to validate across the predictive distribution tests. Specifically, they have low coverage (so frequently actual losses are “extreme” in terms of predictive quantiles), high NLPD, and very high K-S scores, failing the K-S test. This implies that their predictive distribution is not representative of the realized —in particular the predictive variance is “off.” In contrast, GP ILR models perform much better on all of the above and hence more properly capture the predictive distribution. Indeed, in Figure 5 we see that, for example, the ILR-Hurdle+Virt model can reproduce the expected uniform ranks, while the Mack CL model underestimates variance of so that many realizations are completely outside the predicted interval, yielding extreme ranks close to zero or 1 (see the right panel). This is corroborated by the low coverage of the Mack CL and the high coverage (close to the nominal 0.90) by the GP ILR models. (In fact, ILR-Plain has too much uncertainty as its coverage is above 0.90). The last column of Table 1 shows that the Mack CL does not pass the K-S test, while the ILR-Hurdle models do and have K-S statistics that are more than 50% lower. The NLPD metric matches the above discussion, although it is harder to interpret; we also note that the CRPS suggests that the ILR models are worse, likely due to being unduly influenced by outliers. Namely, if a method does not work well in a few triangles then its respective score would be very high, skewing the average CRPS across the entire business line.
Similar patterns are observed for other business lines. We note that GP methods have trouble dealing with the comauto triangles, where they generate worse RMSEs and other statistics, including not passing the K-S test. One conclusion is that no one particular metric provides a full picture, and thus a comprehensive validation analysis is warranted. In Appendix B we also plot the -step-ahead RMSE across different methods. As expected, predictive accuracy drops significantly for many steps ahead—i.e., trying to forecast cumulative loss ratios five or more years into the future leads to large RMSEs.
4.3. Interpreting Gaussian Process Models
Relative to classical models, the parameters in a GP framework are rather different. The key parameters are the lengthscales and the lag-dependent observation variance Figure 6 displays the posterior of those two across three different business lines in our data set. Specifically, we show the distribution of the MCMC posterior means for the lengthscales We observe that in terms of AY, wkcomp has the largest i.e., the most time-stationary ILRs, while medmal has much lower implying that different accident years can yield quite distinct ILRs for the same lag A similar pattern occurs for We observe that suggesting that there is less dependence (as expected) in development lag compared with accident years. We also note lower for medmal, implying that there is limited serial correlation in ILRs even in consecutive years. The middle panel of Figure 6 shows the fitted ’s. As discussed, observation variance generally decreases rapidly in The shape of reflects the spread in raw ILRs as captured in Figure 1. For example, the faster development of wkcomp claims is reflected in the respective observation variances converging to zero faster.
Finally, the right panel of Figure 6 displays the hurdle probabilities We interpret as the likelihood that the observed ILR will be exactly zero, i.e., no new losses will take place. Generally, should be increasing in and approach 1 as losses fully develop and becomes constant. We see that full development generally occurs within 7 years for wkcomp and comauto (with workers compensation converging to zero a bit faster), while medmal develops much slower and even at the chance that is about 5%. The humped shape of ILRs for medmal in Figure 1 clearly manifests itself here, resulting in an inverted-hump shape of ’s. The hurdle probabilities provide a nonparametric, model-based summary of the probability for losses to fully develop after lags.
A major reason for adopting a fully Bayesian approach to loss development is to obtain comprehensive uncertainty quantification. The top row of Figure 7 visualizes predictive distributions of for a fixed accident year In that case, there are three actual observed losses at and we then display 1,000 sample predictions of for Recall that the GP framework directly samples the entire trajectory of the respective loss factors for which are then converted into cumulative losses and finally into the respective empirical predictive distributions. With our Bayesian GP approach the analysis is done empirically with the MCMC samples returned by Stan.
Having direct access to the stochastic scenarios of the completed triangle in turn allows full probabilistic analysis of any given aspect of loss development, from dynamic capital allocation to risk management. This is illustrated in the bottom left of Figure 7 where we plot the forecasted distribution of ultimate losses vis-à-vis the actual realized ultimate loss; the respective quantile is used for the rank testing and CRPS/NLPD computations. Besides the forecasts from ILR-Plain and ILR-Hurdle+Virt that match the same 1,000 scenarios shown in the top row of the figure, we also include the classical Mack CL forecast. The plot clearly conveys that the Mack CL predictive distribution is very narrow, i.e., has much lower predictive variance versus the Bayesian GP fits, which matches its poor predictive coverage and percentile-rank score. On the contrary, the ILR-Plain model overestimates predictive uncertainty, partly due to not accounting for the intrinsic constraints on Note that even if the respective distribution of might look reasonable, the more granular analysis of the generated trajectories of in the top panel reveals the fundamental mismatch between the ILR-Plain model and the nature of loss development. Indeed, a substantial fraction of the trajectories in the top left of Figure 7 feature either decreasing cumulative losses or sudden upward jumps in neither of which is reasonable. In contrast, the trajectories in the top-right panel corresponding to the Hurdle+Virt model look much more realistic. Another important observation from Figure 7 is how the correlation uncertainty leads to a non-Gaussian predictive distribution of —in particular, we observe a strong right skew. In contrast, the Mack CL prediction is essentially symmetric.
Our analysis demonstrates that GP models offer a flexible approach to capturing loss development dependencies. Such models are competitive with existing methods in terms of accuracy (RMSE) and provide better predictive distributions in terms of more sophisticated variance, interval, and rank tests.
4.4. Partial Bayesian Models
It can be difficult to fully disentangle the two intrinsic uncertainty sources of a GP model. Recall that the posterior GP variance reflects the concept that many “true” surfaces can be fitted based on the limited amount of observed loss data. In complement, the hyperparameter or correlation uncertainty reflects the impossibility of fully inferring the correlation between different loss triangle cells.
To better connect to the classical chain ladder, we investigated partial Bayesian models that provide a recipe for learning the true modeling factors and then superimpose stochastic forecasts. In this setup, we view the GP MVN conditioning formula (2.1) as a smoothing mechanism that offers a recipe for extracting a latent ILR surface from a given loss triangle. Such smoothing is very similar to kernel regression, prescribing a translation from to and in fact resembles the chain ladder recipe that represents LDFs as a weighted average of observed empirical year-over-year development factors. However, unlike equation (2.4), the partial Bayesian model then sets “” so that Thus, there is no posterior variance of the latent and the inference step returns a single “best” point estimate of the ILR surface, omitting model risk.
Although the “middle” layer of uncertainty is now turned off, we maintain correlation uncertainty, continuing to employ MCMC to learn the spatial patterns in as encoded in Thus, we keep residual uncertainty quantification by integrating, via MCMC sampling, over potential to take into account that the MLE-based forecast ignores intrinsic correlation risk. Moreover, for forecast purposes, recognizing that future development is uncertain, we still inject randomness by generating realized loss quantities based on and the hurdle model likelihood (3.1).
By construction, the partial Bayesian model will have narrower predictive bands for furthermore those bands would be primarily based on the observation variance rather than on the forecasting distance between the prediction cell and the upper triangle. The bottom-right panel of Figure 7 visualizes this effect by comparing the predictive distribution of from an ILR-Hurdle model relative to a partial Bayesian version of the same. We observe that the predictive variance of a partial Bayesian GP model is broadly similar to that of the Mack CL. Since the latter tends to underestimate predictive variance, we conclude that model uncertainty is a critical piece of the uncertainty quantification puzzle.
4.5. Handling Multiple Triangles
A single triangle yields a very small training data set of just 50 or so observations. As a result, there exists significant model risk, i.e., large uncertainty on how to complete it. This is indeed what we observe, with rather large predictive credible intervals for ultimate losses Note that this effect is in contrast to much existing literature where the predictive uncertainty is underestimated. In turn, the natural remedy is to raise credibility by borrowing information from other triangles. This credibility boost can be quantified through both tighter hyperparameter posteriors, i.e., lower correlation risk, and lower i.e., lower model risk.
To borrow strength from multiple-company data, we augment the original input data with a categorical covariate that is the indicator for the underlying company. Data from multiple companies are combined to form a single training set, with inputs now being trivariate, namely Then the multiple-triangle squared exponential kernel is defined as
\begin{align} C^{(SqExpMlt)}(x^i,x^j) :=\eta^2 \exp (-\rho^{-2}_{AY}(\texttt{AY}^i - \texttt{AY}^j)^2 \\ \quad - \rho^{-2}_{DL}(\texttt{DL}^i - \texttt{DL}^j)^2 ) \\ \quad \cdot e^{-\rho_{Co} \cdot (1-\delta_{ij})}, \\ \text{where} \quad \delta_{ij} = \begin{cases} 0, & \text{Company}^i \neq \text{Company}^j\\ 1, & \text{otherwise} \end{cases} \\ \text{and} \quad \rho_{Co} > 0. \end{align} \tag{4.3}
In effect, the covariance between two data points is “discounted” by when the inputs come from different companies. A low value for implies that statistical gains are available from grouping company data, and a high value implies that the companies are relatively independent. In our approach we use the same and parameters across grouped companies (which, in itself, stabilizes the analysis), although a more sophisticated, hierarchical approach for these parameters could also be adopted. By using this method, the learning of model factors from one company can be influenced by such model factors from other companies. As before, we add linear kernels from equation (2.7) to
An alternative solution is to build a categorical-input GP with a different -correlation coefficient for each company pair that adjusts the squared exponential kernel to
\begin{align} \tilde{C}^{(SqExpMlt)}(x^i,x^j) &= \eta^2 \exp \Bigl(-\rho^{-2}_{AY}(\texttt{AY}^i - \texttt{AY}^j)^2 \\ &\quad - \rho^{-2}_{DL}(\texttt{DL}^i - \texttt{DL}^j)^2 \\ &\quad - \rho_{Co_i,Co_j} \Bigr),\end{align}
where measures the “distance” between Company and Company Thus, is the squared exponential kernel on the trivariate input cells where the first coordinate is interpreted as a categorical factor and has distance (interpreted as cross-triangle correlation) between factor levels Note that this specification leads to hyperparameters to be estimated for a set of triangles, limiting scalability as grows.
Running the multicompany model on a set of five wkcomp triangles (picked randomly from the data set) we obtain the following estimates of :
\begin{align} R^{(Co)}\! := \!\begin{pmatrix} \!1\! & & & & \\ \!0.9553\! & \!1\! & & & \\ \!0.8587\! & \!0.8497\! & \!1\! & & \\ \!0.7467\! & \!0.7389\! & \!0.6641\! & \!1\! & \\ \!0.9498\! & \!0.9398\! & \!0.8449\! & \!0.7346\! & \!1\! \\ \end{pmatrix}.\end{align} \tag{4.4}
Thus, we find that three companies labeled as “1,” “2,” and “5” form a “cluster” with high correlation among their ILRs, but companies “3” and “4” are much less correlated. In comparison, implementing equation (4.3) to infer a single correlation hyperparameter yields the estimate which is roughly the average of the above s. An important takeaway is that the correlation structure is heterogeneous, so that assuming a constant cross-triangle correlation as in equation (4.3) is inappropriate, at least for randomly selected triangles.
Shi and Hartman (2016) investigated a different approach to borrowing strength from other run-off triangles and imposed a hierarchial multivariate normal prior on the LDFs. Thus, development factors from different triangles are empirically correlated by assuming they are all drawn from the common hyperprior. Shi and Hartman postulate a known interpreted as the shrinkage parameter: as the LDFs across triangles will all collapse to the same value, effectively boosting credibility. In contrast to the above, in our analysis we organically determine the between-triangle correlation in ILRs, which is learned like other hyperparameters. We refer to Avanzi et al. (2016), Shi (2017), and Shi, Basu, and Meyers (2012) for further multi-triangle approaches, in particular relying on copula tools.
5. Conclusion and Outlook
Gaussian process models are a powerful centerpiece in the modern predictive analytics/data science tool kit. We demonstrate that they are also highly relevant for actuaries in the context of modeling loss development. The GP approach brings a rigorous Bayesian perspective that is simultaneously data-driven and fully stochastic, enabling precise, nonparametric quantification of both extrinsic and intrinsic sources of uncertainty. Our empirical work with the large-scale NAIC database demonstrates that GP-based models can properly account for the predictive distribution of cumulative claims and loss ratios. While our methods do not necessarily bring material improvement in raw accuracy (leading to similar RMSE measures relative to classical CL approaches), they do significantly improve coverage and percentile rank scores.
As a modeling tool, GPs offer a wide latitude for customization. Above, we illustrated that strength by constructing a special Gaussian hurdle likelihood to match the observed behavior of ILRs. Two other tailorings involved imposing a nondecreasing, yet nonparametric structure on the observation variances and adding virtual observations. There remain several other directions for further investigation that we now briefly discuss.
Advanced kernel modeling: It would be worthwhile to investigate the realized dependence structure in the run-off triangles. Beyond the common “shape” in how claims cumulate over development years (i.e., a common set of ILRs), and the business trend over accident year, further dependence is likely. For example, operational changes in claims management and business practices and in reserving practices, as well as legislative changes, also take place and can potentially introduce calendar-year effects. Within the run-off triangle they could manifest themselves in a “diagonal dependence” for the ILRs—namely, over ILRs for which for a given This also includes incorporating other trends through alternative linear (or polynomial) kernel specifications. One should also investigate alternative kernel families, such as the Matern family, instead of the squared exponential family (2.6) we employed, or alternative compound kernels.
Modeling factors: Our analysis suggests that the incremental loss ratio is the best object to model. In particular, this stems from the resulting additive structure in converting ILRs to cumulative claims, which matches better the additive Gaussian structure intrinsic to GPs. Nevertheless, we expect that successful GP models could also be developed for LDFs or for cumulative loss ratios. As mentioned, Lally and Hartman (2018) achieved good performance with a GP model for Full comparison of these competing frameworks remains to be done. In a related vein, additional analysis is warranted for incurred losses that could be adjusted up or down, in contrast to the paid losses discussed herein that are generally monotone.
Multiple triangles: Finally, although we showed that one may straightforwardly adapt a GP to handle multi-triangle development, full investigation into that topic is beyond the scope of this paper. Multiple triangles raise two issues.
The first is computational tractability. Going beyond 10 to 20 triangles leads to consideration of many hundreds of cells and requires significant adjustments from off-the-shelf GP tools as full Bayesian MCMC with Stan becomes prohibitively expensive. One promising idea is to take advantage of the gridded nature of loss triangles. Such gridded structure implies that the GP covariance matrix has a special “Kronecker” shape. The Kronecker product (Flaxman et al., n.d.) approach decomposes a grid of input data into two sets of covariance functions allowing for a dramatic speedup in the inference models through faster matrix inversion formulas. The use of GPUs in performing GP calculations is also starting to be implemented in Stan and other probabilistic languages (e.g., Greta), and preliminary testing suggests that much larger models can be computationally tractable.
The second issue concerns the fundamental question of how to construct a relevant training data set. For example, the full NAIC data set includes more than 300 triangles, and considering them all at once is still not computationally feasible unless one has a supercomputer. Therefore, an appropriate subset should be identified given a concrete modeling task. This suggests clustering the triangles prior to employing a multi-triangle model. This can be done manually by the analyst, who may identify which companies are likely, a priori, to be viewed as similar, or through a clustering algorithm. Another option would be to follow a two-step hierarchical procedure where single-triangle models are used to identify groupings and then multi-triangle analysis is conducted. Our initial investigations suggest that deciding what to do depends on the aims—for example, boosting credibility of a given triangle forecasting; identifying common trends across triangles (i.e., inference of the covariance structure); or capturing cross-triangle correlation for risk allocation purposes.
Acknowledgment
We thank the anonymous reviewers for many thoughtful suggestions that improved the original manuscript. Support from the CAS Committee on Knowledge Extension Research is gratefully acknowledged.





__observation_variance___sigma_q__(mi.png)






__observation_variance___sigma_q__(mi.png)


