1. Introduction
Creating the target response variable for an insurance loss cost predictive model has traditionally involved two main actuarial treatments: development and trending. Since claims can take a long time before they are settled, development allows the actuary to estimate their ultimate (final) settlement values as of the time of analysis. Trending, which is the main subject of this paper, allows the actuary to adjust for the general changes in loss costs over time particularly due to changes in prices of insurance cost factors such as business mix, inflation, technology, and tort. The interested reader should see Basic Ratemaking by Werner and Modlin for a more in-depth discussion of these two methods (105-121). However, I will show that actuarial trend rates are not suitable for trending target loss variables of actuarial predictive models. This is because they contemplate other dynamics—business mix—which are already contemplated in predictive models, and therefore introduce extraneous modeling complications which bias predictions.
Such bias can be enough to eat away all if not a significant proportion of the underwriting profit margin (given the narrow profit margins of insurance books of business). Or equally regressive, it can cause the book of business to shrink unnecessarily. A trend undershoot of 1% can eat away as much as 10% of margins, with the actual profit corrosion depending on size of profit provision (assumed in this case to be 10%); and the impact of a 1% trend overshoot on the growth of your business will depend on elasticity of demand. Also, the trend bias problem, as I will show, may be so elusive that it may cause an insurance book of business to bleed to its death—a condition I have called Pricing Hemorrhage. This paper discusses the distortionary effects of actuarial trends on predictive modeling target loss variables (loss costs, frequency, severity, loss ratios or any other), and demonstrate ways to avoid them. Therefore, the purpose of this paper is central to driving strong and consistent underwriting results for an insurance book of business. Its – the paper’s—close relationship to pricing precision also renders it relevant to any actuarial department which seeks to promote the standards of pricing excellence.
The paper is arranged as follows: Part 2 is a theoretical exposition of how an inappropriate trend such as the actuarial trend rate can distort the target loss variable in a predictive modeling framework; Part 3 presents a solution to the distortion; Part 4 uses simulated data to demonstrate Parts 2 and 3; Part 5 concludes by restating the major themes of the paper and their ramification on the profitability of an insurance book of business.
2. The distortion of target loss costs by actuarial trends
Assume the ultimate loss cost of the ith risk in an insurance book of business in year t (denote evolves as follows[1]:
E(Yit|xi)=exp(β0)exp(∑k>0xiktβk)exp(αt)
Where:
is the model parameter associated with the constant term;
is the model parameter associated with the kth model variable;
is the kth model variable (such as insurance score) of the ith risk in exposure period t; and
the general inflation parameter, is the rate of change of loss costs over time due to changes in general economic and social climate such as monetary inflation, technology, insurance laws, and other related factors; it does NOT however include changes in business mix or distribution as that is rather accounted for by the risk attributes, In this paper, we call such general inflation parameter the econometric trend rate. It should be noted that even though I focus on loss costs in this section, all insights and conclusions apply freely to other target loss variables such as frequency, severity and loss ratios.
The above is a generalized linear model (GLM) specification. The interested reader can consult with McCullagh and Nelder 1989 for a thorough treatment of the topic, or Duncan, Feldblum, Modlin, Shirmacher, and Neeza 2004 for a casual treatment. It must however be pointed out that, an understanding of GLMs is not required to follow the rest of the paper. It is typical in actuarial predictive modeling for the target loss costs to be trended to the level of the current year or a specified future year in which the model will be implemented (called trend-to year in actuarial argot). It is also typical for an actuarial trend rate to be used for this purpose. This section shows that this culture of trending target loss variables with an actuarial trend rate creates a subtle wrinkle in the target response variable that biases loss cost predictions. To see this, notice that the actuarial trend, which we will denote r, is a sum of and hence contemplates two main dynamics:
-
The changes in aggregate loss costs over time driven by general economic and social factors which we have denoted by and called the econometric trend rate above; and
-
The changes in aggregate loss costs driven by changes in business mix or distribution such as policy limits, deductibles, tenure and other risk characteristics over time. We will denote such change
Thus,
The reader should note that, in an actuarial predictive model, changes in business mix are already accounted for by the risk variables —We specifically build predictive models so that rates can automatically change with risk characteristics. Hence, while applying to aggregate loss costs is in order, applying it to the granular (risk-level) target loss cost in a predictive model is unnecessary and even distortionary. To explicitly show the distortionary effect of an actuarial trend on predictive model predictions, let us introduce a new term, , to denote the level of the target loss cost of ith risk at period t when trended to period T with the actuarial trend rate. Mathematically,
E(Ya,Tit∣→xi)=E(Yit∣→xi).exp(r(T−t))=exp(β0)exp(∑k>0xiktβk)exp{(α+δ)T−δt}=exp(β∗0)exp(∑k>0xiktβk)exp(−δt)
Where:
β∗0=β0+(α+δ)T
Three things are worth pointing out to the reader about (1) and (2). The reader should remember that (1) provides us with the true values of loss cost for an insurance risk in any period and is hence the reality the pricing actuary seeks to estimate.
i. (1) and (2) differ by two main parameters: The constant term and trend parameters In other words, if we fit the raw (non-trended) and trended target loss costs on the risk variables and trend term, all model factors will be equal except for the ones associated with the constant and trend terms.
ii. The presence of a residual trend term, in (2) even after trending all loss costs to the same exposure year is concerning and highlights the elusive distortion, call it wrinkle, that is introduced by the actuarial trend factor. A target variable, correctly trended to the same level, should have no correlation with time. Additionally, this residual trend term is not only elusive but also a bane to modeling: As we will show in Part 4, when target loss costs are trended with the actuarial rate, model predictions will still be biased whether a trend term is included in or excluded from the model. The modeler, unaware of the inappropriateness of the actuarial trend rate, will not expect any such nuisance trend term, let alone be inspired to rectify its distortions.
iii. (1) and (2) differ in loss cost predictions for all but exposure year T (the trend-to year). This implies that the predictions from (2) are almost always biased. Particularly, the bias factor, measured as the ratio of predicted loss cost under (2) to that under (1), can be calculated as:
bias factor=E(Ya,Tit|xi)E(Yit|xi)=exp{(α+δ)(T−t)}=exp{r(T−t)}
The following implications about the bias factor should also be noted:
I. If the actuarial trend rate, r, is positive, then the predictions under (2) will be overbiased for all exposure periods prior to the current exposure year (T), and underbiased for all exposure periods afterwards; whereas if r is negative, it will be underbiased for all exposure periods prior to the current exposure year (T), and overbiased for all periods after. The level of bias is proportional to the actuarial trend rate and the distance between the exposure and current (trend-to) years, implying the bias would continue to worsen over time if unchecked, a phenomenon I call, a Pricing Hemorrhage. The relationship between the bias and exposure year is shown by the bias curve in Exhibit 1.
II. To eradicate the bias caused by trending, the loss cost predictions attained under (2) must be trended back to their exposure levels with the actuarial trend rate (i.e., multiplied by )—A treatment that is elusive and will not be obvious to the modeler. This is one of the punchlines that the article seeks to make: That trending target loss costs with an actuarial trend rate in predictive modeling presents an extraneous pricing trap which the pricing team can do without. It will therefore be in the modeler’s interest to rather model non-trended than trended loss costs as we will demonstrate below.
3. The econometric trend— An efficient way to adjust for trends in predictive model target loss variables
A solution to the trend bias trap presented in Part 2 is to model non-trended ultimate loss costs (or frequency or severity) on an econometric trend term (time t variable) and other relevant risk covariates As can be observed in equation (1) and is also shown with the simulations in Part 4, this provides unbiased loss cost estimates for all risks in all time periods. Because the econometric trend effect is estimated simultaneously with the other risk covariates, it correctly measures the magnitude of the general inflation rate. In addition, the modeling team is saved from the burden of having to trend loss costs and any corresponding costs of falling into the pricing trap discussed above.
A befitting question is why has the suboptimal trending culture—modeling target loss costs trended with actuarial trend rate—been so prevalent in actuarial predictive modeling? The first reason is what I call, The Occasional Trap of Intuition (TOTI): The concept of trending target loss costs (just as we do with aggregate loss costs) sounds so intuitive that it has not attracted a serious consideration or study, and thus, has maintained its popularity despite its sub-optimality. The other is the expertise asymmetry between the pricing actuary and predictive modeler in each other’s body of work: The superficial knowledge of the predictive modeler about actuarial subject matters such as actuarial trends makes it hard for him or her to analyze their effects on predictive model outcomes. I know of many fellow predictive modelers who used actuarial trends liberally but did not know what they contemplated or how they differed from an econometric trend. Likewise, most actuaries are not statisticians and may hence not be able to see the subtle effects of actuarial applications in a predictive model framework. It takes a professional who has pursued a deep training in both fields to catch such subtleties and arrange a healthy marriage between the products of the two fields.
4. Showing the trend bias with simulations
Assume we simulate a book of insurance business which follows the dynamics below:
-
Age group (young vs old) is the only relevant risk variable; and that a young insured is 3 times as risky as an old insured.
-
The proportion of young insureds increases by 5% every year, from 20% of the book in year 1 to 80% in year 13.
-
Loss severity increases exponentially by 3% per annum due to general inflation.
-
Loss severity for a given risk i in exposure year t, follows an exponential distribution, and per 1, 2, and 3, is defined as:
E(Yit|age,t)=exp{ln(6)+t(0.03)+ln(3)∗(young=1)}
-
40,000 claims are filed every year.
-
Exposure years 1 through 8 are the historic years whose data will be used for actuarial and predictive modeling analyses; and exposure years 9 through 13 are the prospective years in which the proposed model will be implemented.
The reader should note that even though simple, the above simulation captures the major dynamics of an insurance book of business.
4a. Deriving the actuarial trend rate
An actuary derives his (her) trend rates by examining severity of ultimate claims at periodic intervals such as monthly, quarterly, or yearly. He (She) would then assess the magnitude and direction of the periodic changes in ultimate claim severities to estimate a suitable trend rate he (she) believes will apply to future years. Using the simulated data above, Exhibit 2 shows the average severity estimates and their natural logs for the historic exposure years.[2]
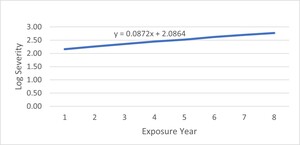
In a log-link model specification, it is easier to rather estimate trends in the logged- than the raw-variable space. Exhibit 3 fits a trend line to log of loss severity to estimate the trend rate.
Per the above trend line, the actuary will select 8.7%—the coefficient of the time variable—as the trend rate for severity. As mentioned in Part 2 and evidenced here, it is different from the general inflation rate because it also contemplates the continuous distribution changes in the book—increasing proportion of young insureds in this example. It therefore follows that the trend due to changes in mix only, is roughly 5.7% (8.7%-3.0%). We show how the trend distortion and bias in predictions occur using the case analyses below.
4b. Case analyses
In this section, we analyze four different ways of dealing with trends in actuarial predictive models. For each case, we will present the GLM parameter estimates, and compare the means of predicted and actual outcomes for the historic (t=1-8) and prospective (t=9-13) exposure years. These should help the reader build a vivid picture of the wrinkles caused by trending target loss variables with the actuarial trend rate and how they can be unraveled. The following definitions will be handy:
Mean Actual Severity is the average value of the actual loss severities of the insured risks for the exposure year of interest. The actual loss severity for any risk in any exposure year is given by equation (5) above.
Mean Modeled Severity is the average value of the modeled loss severities of the insured risks for the exposure year of interest. This is the mean of the dependent variable that was modeled. The reader should note that, when we trend the target loss severity, the mean actual and mean modeled severities diverge.
Mean Predicted Severity is the average value of the predicted loss severities of the insured risks for the exposure year of interest.
It is also worthy to point out that the effect of the trend-induced biases on pricing in each case will depend on how the actuarial team uses the GLM output for ratemaking. In this article, we will focus on two major approaches: In the traditional approach, the pricing team fetches only the GLM coefficients of the risk variables as relativities and combine them with the actuarially derived base rate to calculate the proposed premiums. In the evolutionary approach (argued as superior and recommended in the paper, Ratemaking Reformed: The Future of Actuarial Indications in the Wake of Predictive Analytics), the pricing team uses the risk’s GLM prediction—as the best estimate of the risk’s pure premium— and inflate with fixed and variable expense provisions to calculate the risk’s proposed premium. Also, while traditional ratemaking exercise is performed at least once every year for most insurance products, actuarial GLMs can remain in production without major changes for 3-5 years. Therefore, defects in GLMs tend to persist for a longer period.
Case 1 (most common scenario): Target loss severity is trended with actuarial trend rate and a trend term is added to the set of covariates.
When we model actuarially trended loss severity with a trend term and a dummy for age group, the model parameter estimates are shown in Exhibit 4.
The results are consistent with what was discussed in Part 3: The parameter for young is unbiased (1.0977=ln(3)), and the trend term parameter is the negative of the distribution (business mix) trend rate Also, as discussed above and shown in Exhibit 5, predictions of severity for both retrospective years and prospective years are biased (except for the year to which the target loss severity was trended, year 8 in this case), and the biases are directly proportional to the absolute difference between the exposure and trend-to years.
The bias is vivid in the above table: Loss severity is overstated for historic years and understated for future years. The reader should see that, since the GLM risk relativities are unbiased in this case, the traditional pricing approach will not be affected. However, the evolutionary pricing approach which rather uses the GLM predictions to make premiums will suffer the biases created by this trending culture.
The above trend bias is not a defect to be taken lightly by the actuary. It can stealthily rupture the veins of an insurance book of business and cause it to bleed increasingly to death: A malady I have named as Pricing Hemorrhage! The problem is that the pricing team (unaware of this distortionary effect) will not know that the target (modeled) severity is a contorted reality, and that even though their predictions match this target, they deviate from actual severity. Sadly, the deviations worsen as time passes. This defect can go undetected for years. Even when the imprecision is detected, it is likely to be misdiagnosed as a base rate inadequacy and consequently be treated, albeit ineffectively, with a constant base rate offset. But as can be inferred by the trending values of the bias, the effective remedy should have a trend component. In fact, as noted in Part 2, we get the correct mean severity value for each exposure year by multiplying the GLM predictions by which equals in this case, with t denoting the exposure year of interest. The need to remedy may also not be obvious to the pricing team because the presence of a trend term in the model creates a false notion that the GLM estimates are already trended to their right exposure year levels!
Case 2: Target loss severity is trended with actuarial trend rate and a trend term is NOT added to the set of covariates.
Exhibit 6 shows the results when we trend our target loss severity with the actuarial trend rate but do not include a trend term in our predictive model.
As you can see, the age parameter is biased (1.0332=ln(2.81) < ln(3)). The reason for the bias is due to trending the target variable with trend rate which does not equal the econometric trend rate. As shown in Part 3, the inappropriateness of the actuarial trend rate inhibits it from ridding the model of its trend effects and rather creates a distortionary residual trend effect; hence, when the modeler excludes a trend term in his model, the residual trend effect is picked up by the intercept term and the age variable through a phenomenon which statisticians call the Omitted Variable Bias. The intuition for this is simple: With the old segment being disproportionately larger in the earlier years, the application of an overstated trend rate exaggerates their—the old segment’s— current-level severities, thereby dampening the disparity in severity of claims between the two groups.
The predicted estimates are also biased against the actual and even the modeled severities, as shown in Exhibit 7.
Unlike in case 1, both the traditional and evolutionary pricing approaches will be adversely impacted by the bias in this case since both the relativities and the predictions are biased.
In case 3, we see that these biases evaporate when we appropriately trend the target severities with the econometric trend rate.
Case 3: Target loss severity is trended with econometric trend rate and a trend term is included in the model.
As expected and observed in Exhibit 8, when the target loss severity is trended with the appropriate factor, all trend effects are flattened; thus, adding a trend term will be found to be statistically insignificant as evidenced in the model output. The predictive modeler ideally should remove the trend term from the model for two main reasons. The first is to save a statistical degree of freedom; but even more importantly, to eliminate any trace of false impression, albeit the almost zero trend coefficient, that trending has been already contemplated in the predictions. That way, he or she will remember accordingly that, predictions are as of the trend-to year (i.e., year 8 in our example) and thus have to be de-trended back to their respective exposure years with the same econometric trend rate:
Detrended Predicted = exp(0.03*(year-8)) * predicted
With respect to impact on the pricing approaches, the traditional approach will not be adversely affected since the relativities are unbiased and the evolutionary approach will also not be biased if the detrended predictions are used.
This method, however, has application challenges. Finding the correct econometric trend rate to trend the target loss variable is difficult in practice. And as pointed out in Part 2, any inaccuracy in the economic trend rate, like the actuarial trend rate, will lead to distortionary effects. Also, even though the trap presented here is less convoluted than case 1 (especially when the modeler accordingly excludes the trend term), the extra step of detrending GLM predictions back to their exposure years is still a bane. It is a requirement induced by unnecessarily trending the target loss severity to the same level of the trend-to year before modeling. Case 4 shows how we can accurately predict actual severity without trending the target loss variable.
Case 4: Target loss severity is NOT trended, and a trend term is added to the set of covariates.
This is the most preferred way for dealing with trends in an actuarial predictive modeling framework. No time or resource is wasted on trending the target loss variable before modeling; the model parameters as well as target loss variable are accurately estimated; and no time or resource is wasted on detrending the GLM predictions back to their respective exposure years. See Exhibits 10 and 11.
Since the relativities and the predictions are unbiased in this case, none of the two pricing approaches will be adversely affected.
Part 5: Concluding remarks
The three nonnegotiable metrics of business success —Underwriting Profit, Renewal Retention and New Business Production—have a special bond with prices (premiums) in insurance. Insurance underwriting profit margin is one of the thinnest among industries, with even 10% being on the gracious side. Slight errors in premiums therefore have pronounced impact on profits. For instance, underpricing customers by 1% can eat away as much as 10% of your profits, and even higher percentages with lower underwriting profit provisions. Also, given the low concentration (market power) of most insurance industries, customer retention and demand can be highly elastic especially among the youthful and low-income segments; and lastly, the high cost of acquiring new business, ranging from 10% to 30% of premiums, makes the loss of a renewal or quoted business expensive, especially when due to an evitable pricing bias. Pricing adequacy and accuracy, the two major goals in insurance pricing, are thus paramount!
It is therefore the obligation of the pricing actuary to espouse practices which allow him or her to climb up the rungs of pricing excellence and eschew the ones which bring him or her down that ladder. Trending the predictive model target loss variable is one such regressive culture. Apart from being an extraneous toll on resources and time, it introduces a stealthy pricing trap which produces biased predictions, with the biases worsening by the year after model implementation—A condition I have called Pricing Hemorrhage! The good news is that Pricing Hemorrhage is preventable: Simply model non-trended target loss variable as a function of a trend term and model covariates.
The use of a log-link and a GLM framework is only for simplicity’s sake, and without a loss of generality.
Quarterly periods are the most used as it allows for seasonality effects to be controlled for. However, in this example, we would use yearly periods to keep it simple and avoid general trend complications not relevant to our topic.
.jpg)




.jpg)