1. Introduction
Insurance companies run capital models to quantify risk, assess capital adequacy, allocate capital, and assist in enterprise risk management. For such purposes, a capital model needs to capture all risk sources that may cause large swings in financial results. One-year capital models calculate changes in financial variables during one calendar year. Although multiyear models should provide a more complete view on capital usage, one-year models are more common because of their ease of implementation. For a property and casualty (P&C) insurance company, catastrophic events and investment volatilities are usually the main considerations in a one-year model. Catastrophic events—of which earthquake and hurricane are the worst perils—are unpredictable in timing and may affect many policyholders at once and produce huge losses. A company typically invests its assets in stocks, bonds, and other financial securities. Market values of securities can vary wildly, and bonds can default. In a short time horizon, catastrophe losses and investment losses are the greatest threat to a company’s net worth. Over a longer term, however, inadequate pricing, adverse reserve development, or strategic and operational failures may cause greater damage. Not being able to capture fully the effects of those risks is a limitation of one-year models. Nonetheless, most of the concepts and mathematical formulas we discuss in the paper are applicable in multiyear models.
We study the probability distributions of catastrophe and investment losses, and their joint impact on the one-year change in net worth. Other sources of risk, including adverse development of loss reserves, rate inadequacy, market cycle, and large fire or other non-catastrophe claims, are also important. During a single year, however, such risks have relatively small volatilities. Their contributions to tail values of company net worth are insignificant. When we calculate the required sample size related to tail risk measures, such risk sources can be ignored.
We are interested in stochastic models as opposed to static, scenario-based models. A one-year stochastic model produces probability distributions of financial variables at the end of a year. To quantify risk, we use such statistical measures as variance, standard deviation, value at risk (VaR), or tail value at risk (TVaR). The latter two are called tail risk measures. Because capital is usually considered a cushion for preventing insolvency, VaR and TVaR are more common risk measures in capital modeling.
Statistical measures can rarely be calculated with mathematical formulas. They are typically estimated through simulation. To run a simulation is to draw random samples simultaneously from all random variables contained in a model. When the sample size is large, the probability distribution of a sample is near the distribution of the original random variable. So a statistical measure of the sample can be used as an estimate of the same measure of the original variable (e.g., a sample VaR as an estimate of the VaR of the original variable). The larger the sample size, the better the approximation.
We usually have some expectation regarding the accuracy of an estimation, although it is not always explicitly spelled out. For example, economic capital may be defined by a VaR measure on a modeled surplus loss distribution. We may want to ensure, with a probability close to 1, that a sample VaR is less than $100 million off the true VaR (the true VaR, of course, is unknown). If, instead, a sample VaR can easily deviate from the true VaR by $100 million, then two back-to-back model runs with different seeds can produce estimations with a $200 million difference. Many of us working in capital modeling have been asked to explain why the modeled economic capital can vary so much even though the underlying exposures have changed little. We may attribute it to sampling error and to the limitation of computing resources that does not allow larger samples. However, such explanations are weak if we cannot quantify the error range or the necessary sample size.
In this paper, we study the problem of required sample size for achieving a given precision with a given (high) probability. Our method is to use mathematical theories about distributions of sample measures. For statistical measures we are interested in, including the mean, VaR, and TVaR, when the sample size is large, sample measures are distributed normally around the targeted true measures. Variances of the normal distributions shrink as the sample size increases, giving us more accurate estimations. A threshold of sample size can be found using the normal distributions.
It is well known that capital modeling necessitates a much larger sample size than many other fields. This is mostly due to the skewness and fat tail of probability distributions of catastrophe losses and the length of return periods (e.g., 1 in 1,000 years or 1 in 2,000 years) we use to quantify the economic capital. Capital modelers routinely run 100,000 trials. Our calculation shows that even a sample of that size sometimes is not enough.
We offer some general comments on modeling to put the present study into perspective. Capital modeling, or any stochastic modeling for that matter, is a two-step process. The first is to construct a model to fit the reality, and the second is to generate sample points to approximate the model. The first step is difficult and often results in a mismatched model. That is known as the model risk. But that topic is beyond of the scope of the paper. We take a model as given and attempt to quantify and control the sampling error. Constructing a model is equivalent to specifying a set of random variables with interactions among them. To estimate a statistical measure of the model, we use a corresponding sample measure. For example, a VaR of a catastrophe loss is approximated by a corresponding sample VaR. Sample VaRs with various seeds form a probability distribution around the true VaR. The distribution is determined by the shape of the catastrophe loss distribution. It is not, however, affected by the specific way the catastrophe model is constructed (i.e., random variables and dependencies used). Therefore, this study does not refer to any specific model construction. We also assume that running simulations produces truly random samples, although actual simulation engines may have slight imperfections.
The paper is divided into seven sections. In Section 2 we single out two risk drivers—investment loss and catastrophe loss—for further study. Mathematical theories on the normal approximation of statistical measures are reviewed in Section 3. The theories are applied to sample-size questions related to investment and catastrophe risks in Section 4. Some extensions to simultaneous estimation of two risk measures are given in Section 5. In Section 6 we illustrate the dominating effect of catastrophe losses in tail events. We conclude the paper in Section 7, where we suggest a method of increasing the sample size and discuss problems for further study.
2. Sources of Risk in a Capital Model
In this section we break down a capital model into components and look at their respective risk characteristics. A one-year capital model produces sample points for the one-year change in every financial variable. Investment gains and underwriting gains are equally important variables for evaluating economic capital. They drive the volatility in modeled surplus change. (We are not concerned with specific accounting rules. Surplus here may mean the U.S. statutory surplus, U.S. GAAP [generally accepted accounting principles] equity, or other measures of net worth.) So a capital model, at the highest level, should include two components—investments and underwriting. We typically model many classes of assets. For each class, the model generates a random variable representing its one-year change in market value. The random variables are usually correlated, and they sum up to the total investment gain, denoted by IG. On the underwriting side, we model several lines of business. The one-year underwriting gain (earned premiums minus the sum of incurred losses and incurred expenses) of each line is a random variable, and they sum up to the total underwriting gain, denoted by UG. The sum, SG = IG + UG, is the one-year change in surplus. The economic capital is usually defined by applying some risk measure on the probability distribution of surplus change.
Our main endeavor in this paper is to find a lower bound of sample sizes that, in a probabilistic sense, ensures a low sampling error when estimating a statistical measure. Such lower bounds, as will be seen in Section 3, depend on the shape of the probability distribution and the specific measure. In this paper, we discuss estimation of mean, VaR, and TVaR as applied to investment gains and underwriting gains. VaR and TVaR are measures of tail risk, as opposed to variance or standard deviation, which quantify the overall volatility.
Note that when we speak of a probability distribution of investment gain or underwriting gain, or any financial variables, we refer to a distribution generated by a model, not one in the real world. Whether the model fits the real world is out of our scope. For any financial quantity, different model developers may build different models, which produce different distributions. To discuss a feature of a financial variable in general terms, say the tail behavior of catastrophe loss, we imply that it is a common feature regardless of the model. Fortunately, it is often the case that distributions of a financial variable from well-built models all have similar shapes and key features. This is not surprising given that model developers likely use the same theories and the same empirical data. Thus, we may discuss a financial variable without referring to a particular model.
It is common for an insurance company to build some models itself and to purchase others in the software market. Investment models, given the large number of variables with complex dynamics and correlations, are usually purchased from specialized software vendors. A good investment model is capable of simulating interest rates, bond spreads, defaults, and market value changes. Typically, in an insurance company, the investment portfolio is well diversified among bonds and stocks. Most models would produce a near-normal distribution for the one-year total return of such a portfolio. This is consistent with one of the stylized features of financial returns called aggregational Gaussianity (Cont 2001). Recent empirical studies on stock market returns continue to support the normality (Egan 2007) (Hebner 2014). Bond returns have more skewness (to the left), probably because of the value loss at default (Rachev, Menn, and Fabozzi 2005). But they can still be described as nearly normally distributed with slight skewness and a fat tail. Note that daily returns of stocks or bonds are known to be highly skewed and fat-tailed. As the time horizon increases, however, the central limit theorem sets in and distributions of returns become more normal-like. So, for one-year returns, near-normal distributions are conceptually acceptable. The normal distribution has the property that VaRs in the deep tail do not deviate far (measured by multiples of the standard deviation) from the mean. In this sense we say normal distributions do not have great tail risk.
For P&C insurance companies with a sizable property book, extremely large underwriting losses are usually produced by catastrophic events. Probability distributions of catastrophe losses are defined by catastrophe models. Few insurance companies build their own stochastic catastrophe models, especially for rarer perils, such as hurricane and earthquake, for which historical loss data are sparse. Most employ one or more third-party models. Distributions of catastrophe losses are highly skewed toward large losses. The likelihood of occurrence of large losses decays slowly as loss increases. This property is called the fat tail and is characteristic of high-risk risk sources.
In contrast, other underwriting components, including reserve change, premiums, expenses, and non-catastrophe losses, vary with much smaller magnitude within one year. They have small standard deviations and do not have fat tails. Since our concern is the tail risk of the underwriting gain, catastrophe must be the dominating component. Let CL represent the annual catastrophe loss. Then the one-year underwriting gain is where the “other variables” term equals earned premium minus the sum of incurred expenses, non-catastrophe losses, and reserve development. The left tail of UG and the right tail of CL have similar shapes and decay at similar rates. This says that the required sample size for approximating VaR or TVaR of UG (in its left tail) almost equals that for approximating corresponding VaR or TVaR of CL (in its right tail). Therefore, the only underwriting component we need to examine is the catastrophe loss.
In parallel with catastrophe loss we define the investment loss as the negative investment gain, Thus, the right tails of IL and CL both represent large losses. The variable equals the negative change in surplus (or surplus loss) minus some variables with relatively small variations. We omit the less important variables and write the “reduced” surplus loss as These three loss distributions are the focus of the rest of the paper.
3. Mathematical Preliminaries
Our calculation of required sample size is based on the normal approximation—that is, as the sample size approaches infinity, the probability distribution of a sample statistic approaches a normal distribution. There is a large volume of mathematical work on the normal approximation. We review some results in this section and apply them later to solve sample-size problems. As explained in the previous section, random variables in this paper represent losses. A loss random variable may take positive or negative values, as underwriting loss or investment loss does. The right tail of a loss distribution represents large losses, which determine risk. For technical reasons we always assume that losses are continuous random variables, which means they have continuous cumulative distribution functions (CDFs). Additional assumptions are also needed for some results, including that losses have continuous probability density functions and have finite variances.
We use and to denote the mean, the variance, and the standard deviation of The value at risk of at a tail probability (meaning is near 1) is denoted by It is more commonly known as the th percentile of is sometimes simplified as The tail value at risk at denoted by is the expected value of under the condition i.e., and are some of the most common risk measures (Venter 2003; Rachev, Menn, and Fabozzi 2005; Hardy 2006).
We now introduce notations for some sample statistics. Let …, be a random sample of size drawn from the distribution of The sample mean is To define sample VaR and sample TVaR we rearrange the sample points in an ascending order, Then for the sample distribution we may define the VaR at a tail probability to be an for some near Precise definitions of sample VaR vary slightly in publications (Cramer 1957; Hardy 2006). When is large all the definitions produce almost equal values. For convenience we simply assume is an integer and the sample VaR is Accordingly, the sample TVaR at is defined as and is denoted by
A sample statistic is generally a good approximation of the corresponding measure of the original distribution if the sample size is large. Mathematically, we say that the sample measures converge to the true measures as sample size approaches infinity, which has been rigorously proved for the mean, VaR, TVaR, and many other statistical measures. Convergence in a probabilistic sense is a more complex concept than convergence of a number sequence. There are several ways of defining it. A sequence of random variables is said to converge in probability to a constant if for any Convergence to a constant is easy to understand. But for our purpose a more sophisticated concept is necessary. A sequence of random variables is said to converge in distribution to a random variable if at every point which is a continuity point of the CDF of In this case the CDF of is called the limiting distribution. These concepts can be found in standard textbooks (Hogg and Craig 1978).
Consider each sample point as a random variable. Then all s have the same distribution as the original and are independent. The sample measures and are also random variables. Below are convergence results about sample means. (We assume all technical conditions required for mathematical proofs hold.)
Convergence of sample means. As converges in probability to the mean of In addition, converges in distribution to a normal variable where is the variance of
The first statement is the familiar law of large numbers. It says that is a good estimate for when is large. The second statement is the central limit theorem. It is a stronger result as it gives a limiting distribution. Both theorems can be found in many textbooks (Hogg and Craig 1978).
The limiting normal distribution is the basis for calculating the required sample size. In capital modeling we routinely run a large number of trials, 100,000 or more. This is necessary because our models include highly skewed distributions, like catastrophe losses, and we are interested in VaR and TVaR in the deep tail. With a sample size so large, the limiting distribution is a good approximation to the distribution of the random variable It implies that the estimation error is normal with variance If we increase then the variance decreases. There is a threshold so that for any sample size greater than the error is within, in a probabilistic sense, a given bound. In notation, our task is, for a given error bound and a confidence level near 1, to find a large integer so that when As a common practice, we choose
It is known that if is a standard normal variable then If is distributed as then So, for large enough, the following equation holds with good precision: Solving the equation for gives us a threshold
N = \left( \frac{1.96\sigma}{a} \right)^{2}.\tag{1}
This formula is easy to understand intuitively. A greater means sample points are more dispersed, so the sample mean is less accurate. To achieve a given accuracy level, more sample points are needed. The formula is identical to the full credibility standard for severity—see formula (2.3.1) in Mahler and Dean (2009). Note that, in addition to the variance, other characteristics of the distribution may potentially influence the threshold, like higher moments or tail thickness. They do not appear in equation (1) but may affect its validity. If the distribution of is skewed and fat-tailed, a larger may be needed for the distribution of to be approximately normal. This seems to be a minor issue as the sample size in capital modeling is generally very large.
The following is a similar result for VaR.
Convergence of sample VaRs. Let As converges in distribution to where and is the probability density function of
This is a classic result, whose proof can be found in Chapter 28 of Cramer (1957). For a recent discussion, see Manistre and Hancock (2005). It is interesting to note that the statement is very similar to the central limit theorem, although is not a sum of independent variables.
We now apply the same argument as that used in deriving equation (1). First, substitute the limiting distribution for the distribution of Then, for a given error bound and a tail probability we solve for the threshold The result is as if plugging in the expression of into equation (1):
N = \left( \frac{1.96}{af\left( x_{p} \right)} \right)^{2}p(1 - p).\tag{2}
It is no surprise that the density function appears in equation (2). Recall that a quantile function is defined as where is the inverse function of In other words, A sketch of graph is given in Figure 1. A random sample …, drawn from can be considered obtained in two steps. First draw a random sample …, from a standard uniform distribution and then transform them into …, using the function In Figure 1, the true VaR and the sample VaR, are plotted on the vertical axis. equals where is the th value when the s are ordered from smallest to largest. The error on the horizontal axis is transformed to an error on the vertical axis. The ratio is approximately the slope This explains why the size of the error and thus the in equation (2), is directly related to
To understand the meaning of factor in (2), we define Then is a binomial variable with and For a fixed if is large then has a large chance to deviate far from is large when is near ½ and is small when is near 1.) A larger implies that is a less precise estimate of Thus, the required sample size should increase with
Lastly, we have the following statement for TVaR.
Convergence of sample TVaRs. Let and As converges in distribution to where
Since equals zero when is essentially determined by the values of greater than A relationship between and the conditional variance can be found in Manistre and Hancock (2005). By definition, is a mean (to be more precise, a conditional mean) and is the corresponding sample mean. So the statement here is just a variation of the central limit theorem. (Its proof, however, is trickier.) Trindade et al. (2007) is another recent paper in finance that uses this normal approximation result.
Now we derive a threshold to ensure that, if the error is within a given error bound with a probability The formula is
N = \left( \frac{1.96}{a(1 - p)} \right)^{2}V\left( \left( X - x_{p} \right)^{+} \right).\tag{3}
The similarity between equation (3) and equation (1) is obvious. In this case, only the variance beyond matters.
We may use equations (1) through (3) directly to compute a required sample size. Conversely, for a given sample size, we can use them to compute an expected error range. If, limited by time or resources, we cannot run a model for as many trials as desired, the error range would be larger than what is expected. Then it helps to know if such an error range is still acceptable.
4. Estimation of a Single Risk Measure
We now use these mathematical formulas to estimate the required sample size related to mean, VaR, and TVaR in a capital model. As pointed out in Section 2, investment loss and catastrophe loss are the two risks that dominate the search for sample size. Their probability distributions have very different overall shapes and tail behaviors. The investment loss is normal-like with some skewness. The catastrophe loss is highly skewed with a fat right tail. In this section we show how these characteristics lead to differences in required sample sizes. A large sample is required for estimating the mean of investment loss. We need an even larger sample for estimating a tail VaR of catastrophe loss.
The formulas in Section 3 contain some parameters of the original distribution that are not readily available. This appears to create a chicken-and-egg situation. For example, to use equation (1) to compute a sample size, we need the standard deviation of the original distribution (the distribution defined by the model). To get however, we need to first decide on a sample size, then run the model, generate sample points, and compute the sample standard deviation. But how do we choose this initial sample size? Several ways exist to get around the difficulty in practice. First, the parameters need not be accurate. A rough and slightly conservative estimate should suffice. If we overestimate then we overestimate the required sample size, which still gives a useful guideline. To obtain a rough estimate of we may need only a relatively small number of trials. Sometimes, a priori knowledge of the shape of a distribution may help. For a near-normal distribution, we may estimate a confidence interval for using the sample distribution theory for a normal population (Hogg and Craig 1978). It is also likely that we can run a component model many more times than we can run the full capital model. It allows us to get good parameter estimates for each component. Lastly, a parameter may be derived from other information. For example, if the current investment portfolio is greater than last year’s, which has a known standard deviation then is a reasonable pick for this year.
In the remaining discussion we use a hypothetical capital model to demonstrate calculations. It is adapted from some actual capital models for a P&C insurance company, and we make sure important characteristics of the actual models are kept. The model represents a midsized insurance company with $1 billion in property premium and $5 billion in invested assets. It is a one-year model, consisting of an investment component and a catastrophe component. The two components are summed up independently. The investment portfolio consists of many different stocks and bonds with a total modeled mean one-year gain of about Catastrophe losses are generated by a catastrophe model with a modeled mean loss of about $160 million. (The 4% and the $160 million are meant to provide relative sizes of investment risk and catastrophe risk. Their precise values can only be estimated using sample statistics.)
We first calculate the sample size for estimation of the means of investment loss IL and catastrophe loss CL. The mean is often considered among the easiest to estimate, meaning that it can be more accurately estimated with a smaller sample size. Hence, we want to set a smaller error bound. The mean of investment loss is about and the mean of catastrophe loss is about 160 million. Let us set the range of error for each to be about of the mean.
To obtain an estimate of the standard deviation we take a large sample separately from each component model. The investment model is run times and the catastrophe model, times. Then we estimate with the sample variance formula where is the sample mean. We get, for the investment loss, million and for the catastrophe loss, million. (Here and below, dollar amounts are stated in millions.) Substituting these s and into equation (1) gives the required sample sizes: and
The calculation shows that the required sample size for mean investment loss is many times larger than that for mean catastrophe loss, as the standard deviation of investment loss is three times as large. It should not be a surprise that the investment return has a greater standard deviation than the catastrophe loss, although the latter has much greater tail risk. An insurance company usually holds a large investment portfolio ($5 billion in this example), and thus may suffer big losses in a market downturn. Asset mix also influences volatility. Holding more stocks or more low-grade bonds increases the volatility. Since the one-year return is nearly normally distributed, the variance or standard deviation fully quantifies the risk. For example, the 99.9% VaR, minus the mean return, is three times the standard deviation. In contrast, the shape of a typical catastrophe loss distribution renders that its standard deviation is small relative to its tail VaRs. For our catastrophe loss, which is derived from a book of business that is well diversified geographically and among several covered perils, we calculate that the 99.9% VaR, minus the mean loss, is 11 times the standard deviation. This multiple would be larger for a less diversified book. Of course, if a company adopts a conservative investment strategy, its investment return may have a smaller standard deviation than its catastrophe loss.
We now discuss sample size related to VaR. We are interested in long return periods: 1 in 1,000 and 1 in 2,000 years. For investment gain, VaRs in those return periods are in the $600 million to $800 million range, and for catastrophe loss, they are between $1 and $2 billion. If we choose an error range to be no more than 5% of the VaR, then we may set the parameter in equation (2), to equal 40 for investments and 100 for catastrophe. However, to compare results across all scenarios and show the influence of the shape of the tail, we use the same
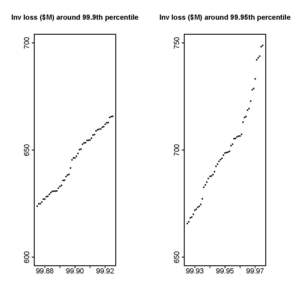
To use equation (2), the only parameter to be estimated is It is the slope of the quantile function at a probability near 1, where the graph of is very steep (see Figure 1). We use the same initial model runs to estimate the slopes, where we have sample points from the investment model and from the catastrophe model. Figure 2 plots the sample points for the investment loss around the two return periods, 1 in 1,000 years (99.9th percentile) and 1 in 2,000 years (99.95th percentile). Similar plots of sample points for the catastrophe loss are in Figure 3. (We exaggerate the scales of horizontal axes to make the graphs more readable. We also choose the pair of windows in each figure to have the same size.) Clearly, sample points around the 99.95% sample VaR form a steeper pattern than those around the 99.9% sample VaR.
Our method of estimating the slope is to run linear regressions through some sample points around the sample VaR. For example, one regression uses 21 sample points consisting of 10 sample points immediately below the sample VaR, 10 immediately above it, and the sample VaR itself. We do this for several different sets of sample points, each time getting a different slope, and we then select a slope slightly on the conservative (large) side. We obtain the following results. For investment loss, For catastrophe loss, The distribution of the catastrophe loss has a fatter tail than that of the investment loss, so its quantile function has larger slopes. Substituting these numbers into equation (2), together with we obtain the required sample sizes: for investment loss, and for catastrophe loss, and As expected, estimating VaRs for the catastrophe loss requires much more sample points than for the investment loss. If we run the catastrophe model just 100,000 times, then the error range would be larger than the expected $100 million. Using equation (2) we obtain that, with probability 0.95, the 99.9% sample VaR has an error bound of $122.3 million and the 99.95% sample VaR, $176 million.
Lastly, we look at sample-size calculation for TVaR. Both VaR and TVaR are measures for tail risk. Each has some advantages over the other (Venter 2003; Rachev, Menn, and Fabozzi 2005; Hardy 2006). When choosing TVaR, we usually calculate it at relatively shorter return periods, like 1 in 500 or even 1 in 100 years (99.8th percentile or 99th percentile). One reason is that TVaR is greater than VaR at the same return period. TVaR at too long a return period may be too large for determining economic capital. Also, as a rule, we try to avoid using samples from the deep tail. Extremely large losses produced by a model are not reliable. They are likely far away from corresponding real-world-event losses. In addition, samples from a deeper tail have larger sampling errors. Since TVaR is the average of all losses exceeding a threshold, lowering the threshold would give less weight to extremely large losses. This results in more accurate and stable estimates. In the following example, we examine and The latter is chosen to compare with corresponding VaRs discussed previously.
The key parameter in equation (3) is the tail variance If a random sample is drawn, a sample version of this variance, denoted by is easy to compute. For example, if the sample size is and then the sample VaR is and among the values only 200 are nonzero. Its variance is vastly smaller than the full variance The random sample of size 100,000 from the hypothetical investment model gives us and The 1,000,000 sample points from the catastrophe model give us and
Select an error bound Plugging the parameters into equation (3) we get required sample sizes. For the investment loss, and for the catastrophe loss, and As expected, attaining the same level of precision is much harder for catastrophe loss than for investment loss. Comparing with our previous calculation, we see that to get the same level of precision at the same return period, a larger sample is needed for TVaR than for VaR. Note that the last statement appears to be true for every long return period on our investment and catastrophe loss curves. But we have found probability distributions for which sample TVaRs are more accurate than corresponding sample VaRs.
Since and are greater than 100,000, if we run only 100,000 trials, then the error bound (with probability 0.95) is more than 100 million. It is easy to compute that and
5. Simultaneous Estimation of Two Risk Measures
Running a capital model generates random samples simultaneously from all the variables defining the model. The three equations in Section 3 let us calculate required sample sizes for a single risk measure on one variable. They can also be used to determine error ranges when given a sample size. For example, we calculated error bounds for sample VaRs when running the catastrophe model 100,000 times. We showed that, with a 0.95 probability, the error of a 99.9% sample VaR is less than $122.3 million, while the error of a 99.95% sample VaR is less than $176 million. However, when we draw a sample and compute both sample VaRs, the two error bounds generally do not hold simultaneously. That is, the probability of the following joint conditions is less than 0.95: and In this section, we show how to derive an error range for a simultaneous estimation of two statistical measures.
We calculated standard deviations of the investment loss and the catastrophe loss in Section 4. They are and Substituting the s and into equation (1) and solving for we obtain the 0.95-probability error bounds and (million dollars). The sample mean of the catastrophe loss is more accurate than that of the investment loss.
A sample for the (reduced) surplus loss, SL = IL + CL, is the sum of the above two samples, which are paired up independently. The mean of SL is the sum of the means of IL and CL. Because IL and CL are independent, so This gives an error bound for SL, slightly greater than Obviously, investment volatility has a larger influence on the sampling error when estimating the mean of the surplus loss.
Let us review some mathematical theories on joint distributions of two sample statistics. Suppose and are two risk measures on the same random variable We have learned that each sequence of sample VaRs, or tends to a normal distribution centered at and respectively. But for each and are correlated. Whether the two sequences of sample VaRs can jointly converge is a harder question. The following theorem provides a positive answer.
Joint convergence of two sample VaRs (Cramer 1957). As the sequence of random vectors converges in distribution to a bivariate normal distribution where the covariance matrix is
\Sigma = \begin{pmatrix} p(1 - p)\text{/}f\left( x_{p} \right)^{2} & p(1 - q)\text{/}f\left( x_{p} \right)f\left( x_{q} \right) \\ p(1 - q)\text{/}f\left( x_{p} \right)f\left( x_{q} \right) & q(1 - q)\text{/}f\left( x_{q} \right)^{2} \\ \end{pmatrix}.
Thus, for a large the joint distribution of and can be approximated by a bivariate normal with Let us apply the formula to our catastrophe loss. Setting and and using the values of and derived in Section 4, we obtain
\Sigma_n=\left(\begin{array}{ll} 3896.4 & 3962.5 \\ 3962.5 & 8063.6 \end{array}\right).
A bivariate normal distribution with zero mean is symmetric about the origin. We intend to find a rectangle such that its probability is 0.95. For separate estimations of 99.9% VaR and 99.95% VaR, the error ranges are and respectively. It motivates us to look for a number so that and Let be the CDF of the bivariate normal. The equation for solving is For a given there are many software programs to numerically compute the left-hand side. Using such a program and a trial-and-error approach, we find which gives and Thus, we obtain a joint error range for the two sample VaRs.
The following result is about joint convergence of sample VaR and sample TVaR at the same percentile. Let and In Section 4 we learned that the sample VaR, and the sample TVaR, each converge to a normal distribution centered at and respectively. Further, and are correlated, their covariance also converges, and the following statement holds.
Joint convergence of sample VaR and sample TVaR (Manistre and Hancock 2005). As the sequence of random vectors converges in distribution to a bivariate normal distribution where the covariance matrix is
\Sigma=\left(\begin{array}{cc}p(1-p) / f\left(x_p\right)^2 & p\left(t_p-x_p\right) / f\left(x_p\right) \\ p\left(t_p-x_p\right) / f\left(x_p\right) & V\left(\left(X-x_p\right)^{+}\right) /(1-p)^2\end{array}\right).
For a large sample, the joint distribution of and is near a bivariate normal where We can use the bivariate normal distribution to solve problems related to simultaneous estimation of VaR and TVaR. Look at the hypothetical catastrophe loss distribution, for example. Assume we run 100,000 trials. At 99.9%, we found in Section 4 estimates of the tail variance 1,188.6 and the slope 624,526. We also estimate with a sample that approximately equals 695.8. These together provide
\Sigma_{\mathrm{n}}=\left(\begin{array}{cc} 3896.4 & 4340.9 \\ 4340.9 & 11885.9 \end{array}\right)
The separate error bounds for 99.9% VaR and TVaR are 122.3 and 213.7, respectively. We seek a rectangle of the size that has a probability 0.95 under the bivariate normal distribution. Using trial and error, we get It provides a joint error range when estimating the VaR and TVaR simultaneously.
6. Tail Behavior of Surplus Loss
Assuming IL and CL are independent, we calculated in Section 5 that and where SL = IL + CL is the (reduced) surplus loss. Note that is only slightly larger than (and is much smaller), which means the overall variation of the surplus loss is dominated by investment loss.
Figure 4 shows how the investment loss and the catastrophe loss influence the distribution of surplus loss, using our hypothetical model. Sample quantile functions of the IL, CL, and SL are plotted in the same window. Each quantile function is shifted vertically so that its mean value equals zero. (That is, they are graphs of and In the left window, the entire range of probability is shown. We see that the IL curve and the SL curve are almost indistinguishable, but at the right tail, SL appears to rise faster than IL. (The two curves also differ, to a lesser degree, at the left tail.) We conclude that investments dominate the distribution of surplus except at the tails.
In the right window of Figure 4, only the extreme right tails of the three quantile functions are shown. We see that the surplus curve starts to bifurcate from the investment loss and converge toward the catastrophe loss. So catastrophe dominates the right tail of the surplus loss distribution. In addition, the catastrophe loss curve appears to be “catching up” to the surplus loss curve. (These trends are made clearer by our shifting the three curves to zero out the means.) This means the slope of the latter, is less than that of the former, for near 1. This observation is consistent with a theoretical insight. The sum CL + IL should vary less at the tail than CL itself, because it gets diversification benefit from mixing up with IL. Therefore, estimation of VaR by a sample is more accurate for surplus loss than for catastrophe loss. For example, in Section 4 we derived that, for estimating the catastrophe loss VaR, to within a 100 million error bound, we need about 150,000 trials. We provide evidence here that this sample size is good enough for estimating the corresponding surplus loss VaR, to the same level of accuracy.
We believe the properties demonstrated in Figure 4 hold in a typical capital model. The distribution of surplus loss is dominated by investments overall, but by catastrophe in the extreme tail. At what point the surplus loss curve starts to deviate from the investment curve and merge with the catastrophe curve depends on the relative size of the components. This happens sooner (at a smaller if the catastrophe risk is larger.
We have discussed only the “reduced” surplus loss so far. Omitting the low-volatility components (premium, expense, non-catastrophe loss, and reserve development) allows us to easily compare loss curves in Figure 4 and draw clean conclusions about the influence of investment and catastrophe losses. Obviously, the complete surplus loss, with the low-volatility components added back in, has a different probability distribution. However, its distribution should have a similar shape, tail behavior, and risk characteristics to those of the reduced surplus loss. In particular, their variances and corresponding VaRs and TVaRs are close. The investment loss and the catastrophe loss have similar dominant effects on the complete surplus loss.
7. Conclusions
In this paper we discussed sample-size problems in capital modeling. We reviewed mathematical theories relating the sample size to sampling errors. We demonstrated calculation of required sample sizes and error bounds for estimating VaR and TVaR, focusing on investment losses and catastrophe losses. In particular, we showed that catastrophe losses, because of their skewness and fat tail, require very large samples to estimate VaRs and TVaRs in the deep tail.
In practice, sample sizes often are limited by runtime restriction and computer resources. If the minimum sample size that keeps sampling errors small is not attainable, we need to find remedies. One method is to select “better” random seeds. Some modeling software allows users to arbitrarily fix seeds. Assume each simulation is limited to 100,000 trials. Instead of running one simulation, we run it 20 times with seeds randomly chosen by the software. We record only the surplus change variable to save time and storage space. Using the 2,000,000 sample points we estimate the 99.9% VaR and 99.95% VaR of the surplus loss (or any number of other metrics that we think are important). Since the sample size is much larger than that from a single simulation, these sample VaRs have much smaller error ranges. Next, among the 20 simulations, we pick the one that gives us best estimates of the two VaRs and use its seeds to run a 100,000-trial simulation to calculate other interested variables and metrics. The selected simulation, although not having the required sample size, produces good estimation for the important statistical measures. We have used this process as a practical workaround. It would be interesting to understand statistical properties of such an estimator.
In Section 5, we studied sample-size problems in simultaneous estimation of more than one risk measure. In the mathematical literature, the normal approximation technique has been developed to solve more complex sample-size problems, such as in cases involving several correlated random variables. However, a more useful and challenging problem is to determine a required sample size for obtaining accurate risk allocation. As an example, assume the 1-in-500-year TVaR of catastrophe loss is to be allocated among several lines of business using the co-TVaR method. (For co-TVaR allocation, see Venter 2003.) What is a minimum sample size that ensures, with probability 0.95, that all co-TVaRs have errors less than 5%? Intuitively, the sample size here ought to be larger than what is needed for the estimation of the TVaR alone and depends on the distribution of each component and correlations among them. Given the widespread use of risk allocation or capital allocation, this is an important problem.