1. Introduction

The finance and insurance industries rely heavily on the use of models in decision making (e.g., in the determination of regulatory capital requirements and pricing). However, such models are subject to error. Specifically, model risk can be defined as the potential loss that can result from the misspecification or misuse of models (inspired by the definition in Capital Requirements Directive IV, Article 3.1.11). Model failures have had serious consequences in the past—e.g., in 1997, the hedge fund Long-Term Capital Management lost around $4.5 billion as a consequence of relying on normality assumptions while neglecting the importance of stress testing (Lowenstein 2008). In 2008, investors that had a poor understanding of the Gaussian copula in the David Li’s pricing formula relied on it excessively in pricing credit derivatives. That over-reliance was one of the drivers of the 2008 financial crisis (Salmon 2009). Nowadays it is well understood that model risk is a key concern, and hence its quantification is of vital importance.

Recent regulations related to model risk management

Regulators nowadays regard the calculation of capital requirements based on models that are neither challenged nor backtested as not being credible. We cite Deloitte Center for Regulatory Strategy (2018): “Supervisors will neither approve nor place reliance on the firm’s strategic and operational use of a model, including for risk assessment and capital planning, unless satisfied with a firm’s model risk management.” In 2011, the first supervisory guidance on model risk management, SR 11-7, was published by the Office of the Comptroller of the Currency and the Federal Reserve (Board of Governors of the Federal Reserve System 2011). The key focus of SR 11-7 is on ensuring an effective challenge of models. In 2013, the Basel Committee on Banking Supervision expressed its concern about model uncertainty. It conducted surveys and found that risk weightings for the same assets may differ among banks—that observation undermines the credibility of the models used by banks (Basel Committee on Banking Supervision 2013). In its discussion paper on the review of specific items in the Solvency II Delegated Regulation, the Actuarial Association of Europe insists on focusing more on model risk assessment (Actuarial Association of Europe 2017). A recent supervisory statement from the Prudential Regulation Authority of the Bank of England highlights the necessity of understanding and accounting for the assessment of model uncertainties. That document also presents some model risk management principles that the authority deems important to apply when using stress test models (Prudential Regulation Authority 2018). Whereas regulators stress the necessity of accounting for model risk assessment in the decision-making processes of financial institutions, in practice such an accounting is not always obvious, and if it is done, it tends to be of a qualitative rather than a quantitative nature. A major obstacle is that the quantitative methods developed by researchers so far are either not well suited to deal with the assessment of model risk in practice or not yet recognized by practitioners.

Current practices of model risk assessment

Banks and insurance companies around the globe tend to employ risk management frameworks that are similar to the ones that local or international professional organizations have proposed. For example, insurance companies in the United States, Canada, and most other countries in North and South America are known to follow the frameworks suggested by the Society of Actuaries (SOA) and the Canadian Institute of Actuaries. Three main approaches to model risk assessment can be distinguished.

First, the practice most commonly demanded by and applied in the market is to assess model risk using what is called a risk-rating scheme—a practice commonly known as the qualitative scoring method (Dionne and Howard 2017). In other words, to assess a model, one evaluates various common inherent risk factors, such as model complexity, the expertise of the model’s users, the quality of its reporting, the frequency of its usage, its financial impact, and so on. The risk manager assigns a score to each factor and sums up the individual scores to get a comprehensive view of the model risk. Although such an approach is easy to understand and to implement, it is also very imperfect. Indeed, this methodology may confuse the risk that results from improper implementation of the model with the risk that results from model uncertainty—the first risk is in principle already accounted for in the operational risk assessment, but the second one needs particular consideration. Moreover, the scores and weights attributed to each factor are highly subjective, as they depend heavily on expert judgment, which makes this approach far from robust. Finally, risk mitigation controls can be misleading. To decrease the model risk in accordance with the qualitative scoring methodology, one would aim to decrease the final score by, say, decreasing the complexity of the model; however, a decrease in complexity does not necessarily decrease the model risk.

Second, a method known as modern operational risk management offers practitioners a quantitative approach to modeling risk measurement. In this approach one views model risk as a type of operational risk and measures it by modeling the frequency and severity of model risk events. A presentation of this approach can be found in Samad-Khan (2008) and OpRisk Advisory and Towers Perrin (2010). Although modern operational risk management offers consistency with the way other types of risk are assessed and allows for interdependencies among risks, it has some serious drawbacks. Empirical data on model risk losses can be scarce and inaccurate. In addition, the approach in itself is subject to potential high model risk. These major limitations hinder the use of this approach in practice.

Third, the Institute and Faculty of Actuaries’ (IFoA’s) Model Risk Working Party opined recently that a quantitative assessment based on model comparison is highly preferable but unfortunately is not ready for practical use; in their words, “Where alternative methodological choices to those employed in a model are plausible, the impact of method changes on model outputs can also be tested … However, … methodological changes (e.g., a change in dependence structure or valuation method) are too time-consuming to implement for test purposes” (Black et al. 2017). A quantitative approach along the lines of what IFoA suggests is the model uncertainty approach (MUA). That approach is based on the principle of model risk sensitivity. Such sensitivity is measured using benchmarking, backtesting, and comparison with alternative models (Jacobs 2015). In addition, it is a bottom-up approach to aggregating model risk in that it consists of evaluating the model risk inherent in each individual modeling and then aggregating individual model risks using models’ dependencies. Compared with the other aforementioned approaches, the MUA offers various advantages. It is much less subjective and provides a clear and traceable process with the ability to provide guidance on the level of capital that is needed to account for model risk. However, the expertise, time, and resources this approach requires make it less desirable by practitioners.

In this paper, we develop a quantitative approach to model risk assessment that aligns with the MUA. Our approach is based on the theory of risk bounds that studies the behavior of a model under worst-case and best-case scenarios. To compute risk bounds, one first selects the model assumptions that can be fully trusted, hence distrusting all other assumptions. Next, one determines a model (a worst-case scenario) that is consistent with those trusted assumptions and that leads to the highest possible value for the risk measure. Similarly, one determines the model that yields the lowest possible value. Those two extreme values are the risk bounds. Our contributions are as follows. First, we define a new notion of model risk that enables one to quantify the model risk contribution of each assumption by making use of the extensive literature on risk bounds. Second, we extend the notion of risk bounds by assigning a “credibility score” to each assumption of interest instead of making a binary decision on whether it is fully trusted or distrusted. This results in tighter bounds that better reflect experts’ opinions and are more useful in practice. Our third contribution is to propose new measures that make it possible to establish the capital buffer for model risk.

The paper is organized as follows. In Section 2, we review the recent academic literature on risk bounds. To ensure that the paper is self-contained and to facilitate its use, we recall the main theorems on risk bounds in the extended Appendix C. In Section 3, we present our model risk assessment approach that incorporates the abovementioned contributions. Section 4 consists of a case study where we apply our approach to a real-world data set, the SOA medical data set (Grazier 1997). Section 5 concludes.

2. Review of the literature on risk bounds

The quantitative approach to model risk assessment aims to assess the uncertainty arising from the choice of the probability model (e.g., the assumption that the loss distribution belongs to the exponential family of distributions), the adoption of parameter calibration techniques (since different techniques may actually lead to different parameter estimates), and the limitation of the collected data. Over the past decades, many researchers have explored this topic. A standard approach to assessing model risk consists of comparing the capital value (or more generally speaking, the value of a risk measure) resulting from the model used with the one resulting from extreme models—extreme models are the models adopted in worst- and best-case scenarios. The extreme values taken by the adopted risk measure are referred to as risk bounds. In this approach to model risk assessment, a first step consists of specifying which assumptions we can be certain about and which ones we cannot. The bounds thus clearly depend on the model assumptions that are considered fully reliable. For instance, one might trust that the distributions of the portfolio components are fully known, but not the interdependence. Or, one might be certain that the loss distribution is unimodal and has a known mean and variance.

Researchers have bestowed special attention on dependence uncertainty bounds—i.e., risk bounds when the dependence structure is unknown but information on the marginals is available. This stream of the literature finds its pedigree in Rüschendorf (1981) and Makarov (1982). In the homogeneous case—i.e., when the distribution functions of the marginals are identical—B. Wang and Wang (2011) and Puccetti and Rüschendorf (2013) obtained sharp tail bounds in the case of monotone densities and concave densities, R. Wang, Peng, and Yang (2013) found explicit formulas for the worst value-at-risk when the marginal densities are monotone or tail-monotone, and R. Wang (2014) studied asymptotic bounds. In the inhomogeneous case, the analysis becomes more complicated, and approximations of bounds were needed. Therefore, Puccetti and Rüschendorf (2012a) and Embrechts, Puccetti, and Rüschendorf (2013) developed a new algorithm, known as the rearrangement algorithm, that can numerically approximate value-at-risk sharp bounds (i.e., attainable bounds) for the distribution of the aggregate risk. Furthermore, Bernard, Rüschendorf, and Vanduffel (2017) provided explicit (but non-sharp) upper and lower bounds of the value-at-risk of the portfolio loss when we have information only on the marginal distributions (see Theorem 1 in Appendix C).

Various attempts to include dependence information have been made in the literature. Puccetti and Rüschendorf (2012b) offered an improvement on some existing bounds for the distribution function and the tail probabilities of portfolios by adding a positive dependence restriction on the dependence structure. Bignozzi, Puccetti, and Rüschendorf (2015) and Rüschendorf (2017) showed that an assumption of a negative dependence would mainly affect the upper bound of the value-at-risk but an assumption of a positive dependence would affect the lower bound (see Theorems 2 and 3). Puccetti, Rüschendorf, and Manko (2016) considered the value-at-risk upper bounds in the case where positive dependence information is assumed in the tails or some central part of the distribution function. In Puccetti et al. (2017), independence among (some) subgroups of the marginal components is assumed, a fact that leads to a considerable improvement in the value-at-risk bounds as compared with the case where only the marginals are known (see Theorems 4 and 5).

In practical situations, estimating the dependence structure can be challenging and can lead to inaccurate results. In contrast, one can perform moment estimates with a reasonable degree of accuracy (note that the accuracy decreases with the increase in the order of the moment). This observation constitutes a motivation for the many papers that replaced the assumption on the dependence structure with a constraint on the variance as some source of dependence information. In fact, it is intuitive to see that adding variance and higher-order moments constraints to a setting in which only the marginals are fully known is likely to improve the risk bounds as that addition captures information that cannot be represented by the marginals. Bernard, Rüschendorf, and Vanduffel (2017) derived value-at-risk bounds based on the knowledge of the marginal distributions and the variance of the portfolio risk (see Theorem 6). Bernard et al. (2015) studied these bounds under the knowledge of higher-order moments (skewness, for instance). Interestingly, Bernard, Denuit, and Vanduffel (2018) provided evidence that replacing the knowledge of the marginal distributions with the knowledge of the collective mean does not cause a significant loss of information. In fact, a considerable number of papers have studied risk bounds in scenarios in which information on the mean and higher-order moments of the portfolio risk is assumed instead of assuming knowledge on marginal distributions and dependence structure—see, for example, Kaas and Goovaerts (1986), Hürlimann (1998), Hürlimann (2002), De Schepper and Heijnen (2010), and Zymler, Kuhn, and Rustem (2013), among others. Bertsimas, Lauprete, and Samarov (2004) derived value-at-risk bounds when only the mean and a maximum variance of the portfolio loss can be trusted (see Theorem 7). Moreover, Puccetti et al. (2017) derived bounds when information on the maximum variance of the portfolio loss is assumed in addition to the knowledge of the marginals and the independence among some subgroups of the marginals (see Theorem 8).

Another case of interest is the factor model in which each individual risk depends on a common risk factor. Many important models in risk management can be seen as factor models, e.g., the multivariate normal mean-variance mixture model. Bernard et al. (2017) derived risk bounds (mainly of the value-at-risk and the tail value-at-risk) when factor models are only partially specified (see Theorems 9 and 10).

Other sets of assumptions that were considered in the literature are the shape and the domain of the loss distribution. Bernard, Rüschendorf, and Vanduffel (2017) derived the upper bound of the value-at-risk of a nonnegative portfolio loss whose mean is the only assumption that can be fully trusted (Theorem 11). Bernard, Denuit, and Vanduffel (2018) derived risk bounds when the portfolio loss is bounded and information on marginals and maximum moments are available (see Theorems 12 and 13). Bernard, Kazzi, and Vanduffel (2020) derived risk bounds for unimodal portfolio distributions and considered the case of nonnegative portfolios with possibly a theoretically infinite variance (see Theorems 14, 15, and 16). Additional results can be found in the literature, such as in Li et al. (2018) and Bernard, Kazzi, and Vanduffel (2022), where information on the shape (unimodality and symmetry) of either the individual risks or the total risk is taken into account.

3. Model risk assessment

An adopted model is composed of a set of adopted assumptions. The traditional way, as seen in the academic literature, of assessing the model risk inherent in an adopted model consists of following a three-step approach. First, one specifies all assumptions that can be fully trusted. In general, there exist many models that are consistent with these assumptions, and the adopted model is merely one among them. Next, one maximizes and minimizes the risk measure over the set of all plausible models—that is, one determines the worst-case and best-case values (i.e., the bounds). Finally, in the third step, one compares the risk bounds with the value the risk measure takes under the adopted model.

Under the traditional approach, however, all the assumptions that are not fully credible are completely neglected. In this section, we work on improving the traditional approach by overcoming that drawback. First, we propose a method to assess the contribution of each assumption to the total model risk. This analysis will provide the modeler with insight as to how risky it is to adopt each of the assumptions in terms of model risk. Second, we present a novel approach to improve the risk bounds by making use of the assumptions that are not fully credible. Finally, we introduce a new measure for the model risk capital buffer.

3.1. Setting

Consider a portfolio of $n$ individual risks $\{X_i\}_{1\leq i \leq n}$, and denote the portfolio loss variable by $S = \sum_{i=1}^{n}X_i$. Note that unless otherwise stated we do not assume the portfolio to be homogeneous.

We write $X \sim F_X$ to express that $F_X$ is the cumulative distribution function of $X$. And we denote by $E[X]$, $\text{var}[X]$, and $\text{std}[X]$ the mean, variance, and standard deviation of $X$, respectively.

Let $\rho: \mathcal{M} \rightarrow \mathbb{R}$ be a risk measure where $\mathcal{M}$ is the set of all real-valued random variables defined on a probability space (i.e., $\mathcal{M}$ is a set of measurable functions). Let $F^*$ be the cumulative distribution function of the adopted model and let $\{ a_i \}_{i \in \{1,...,n\}}$ be a set of assumptions that characterizes $F^*$—i.e., adopting the set of assumptions $\{ a_i \}_{i \in \{1,...,n\}}$ is equivalent to adopting $F^*$. We define a decreasing sequence of sets $\{ \mathcal{A}_k \}_{k \in \{1,...,n\}}$ with $\mathcal{A}_k = \{X \in \mathcal{M} \text{ }| \text{ }X \text{ respects assumptions } \{ a_i \}_{i \leq k}\}$.

In a scenario where only the assumptions $\{ a_i \}_{i \leq k}$ are adopted, we define the corresponding upper and lower bounds of the risk measure $\rho$ by

$$\overline{\rho}_k = \underset{{X\in \mathcal{A}_k }}{\sup}{\rho(X)},\tag{3.1}$$

and

$$\underline{\rho}_k = \underset{{X\in \mathcal{A}_k }}{\inf}{\rho(X)},\tag{3.2}$$

respectively.

Without loss of generality of the methods we propose, the risk measure that we consider in this paper is the value-at-risk (VaR). Note that VaR is indeed commonly used as the reference measure for computing the capital requirement in the industry. In fact, the VaR at a probability level $\alpha$ represents the amount of capital necessary to ensure with a confidence level $\alpha$ that the insurance company or financial institution will not be technically insolvent after a specific period. Formally, VaR is defined as

$$\small{ \mathrm{VaR}_\alpha(S)=\text{inf}\{x \in \mathbb{R} \text{ } | \text{ } F_S(x) \geq \alpha \}\text{, } \alpha \in (0, 1), }\tag{3.3}$$

where $F_S$ is the cumulative distribution function of the aggregate risk $S$.

3.2. Model risk allocation

A fully trusted model (i.e., when the assumptions leading to the model are all fully trusted) poses no model risk. However, such a model does not exist. Typically, only some of the assumptions can be fully trusted, say $\{a_{i} \}_{{i} \leq {k}}$. The risk bounds ($\overline{\rho}_{k}$ and $\underline{\rho}_{k}$) corresponding to those fully trusted assumptions reveal the uncertainty coming from the non–fully trusted assumptions $(\{a_{i} \}_{{k}<{i} \leq {n}})$; the wider the bounds, the more uncertainty we have in the non–fully trusted assumptions. This uncertainty is seen as a representation of the total model risk entailed by the non–fully trusted assumptions.

However, if we calculate only risk bounds in the one scenario where we split fully trusted versus non–fully trusted assumptions, we will be assessing only the uncertainty that arises from completely distrusting the whole set $\{a_{i} \}_{{k}<{i} \leq {n}}$. Such an approach is incomplete as it ignores the actual impact of each assumption on the total model risk.

In order to reveal the impact of a specific set of assumptions, say $\{a_{i}\}_{{k}<{i} \leq {l}}$, on the total model risk inherent in $\{a_{i}\}_{{k}<{i} \leq {n}}$, it would be intuitive to observe how sensitive the risk bounds are to the addition or removal of $\{a_{i} \}_{{k}<{i} \leq {l}}$ from the set of assumptions responsible for the total model risk.

In other words, to assess the model risk contribution of a subset of the non–fully trusted assumptions, we can assume knowledge of that subset and translate it into additional constraints in the maximization and minimization of the adopted risk measure. We can then compare the newly derived risk bounds with the risk bounds derived before adding the new constraints. The risk bounds, if changed, will get tighter as the uncertainty decreases when more information is added. The decrease in uncertainty will reveal the contribution this subset of non–fully trusted assumptions had to the total model risk. Following this reasoning, we can define a measure of the contribution of any set of assumptions to the total model risk conditional on the knowledge of another set of assumptions. This measure is introduced in mathematical terms in Definition 3.1.

Definition 3.1 (Conditional model risk contribution measure). Let $\rho: \mathcal{M} \rightarrow \mathbb{R}$ be a risk measure. Let $F^*$ be the cumulative distribution function of the adopted model and let $\{a_{i}\}_{{i} \leq {n}}$ be a set of assumptions that characterizes $F^*$. Let us define a decreasing sequence of sets $\{\mathcal{A}_{k}\}_{{k} \leq {n}}$ with $\mathcal{A}_{k} = \{X \in \mathcal{M} \text{ }| \text{ }X \text{ respects assumptions } \{a_{i}\}_{{i} \leq {k}}\}$. Then, for ${k}<{l}$, we can define a measure of the contribution of assumptions $\{a_{i}\}_{{k}+1 \leq {i} \leq {l}}$ to the total model risk given full knowledge of $\{a_{i}\}_{{i} \leq {k}}$ when using the risk measure $\rho$ as follows:

$$\mathcal{C}(\rho, \mathcal{A}_k, \mathcal{A}_l) = 1- \frac{\overline{\rho}_{l} - \underline{\rho}_{l}}{\overline{\rho}_{k} - \underline{\rho}_{k}},\tag{3.4}$$

where $\overline{\rho}_j = \underset{{X\in \mathcal{A}_j }}{\sup}{\rho(X)}$ and $\underline{\rho}_j = \underset{{X\in \mathcal{A}_j }}{\inf}{\rho(X)}.$

3.3. Example

Let us consider an adopted model $F^* = \mathcal{N}(10,4)$ where the assumptions of interest are $\{ a_i \}_{i \in \{1,2,3,4\}}$ = {$a_1$ = the mean is 10, $a_2$ = the variance is equal to 4, $a_3$ = the distribution is unimodal, $a_4$ = the distribution is normal}. Let $\mathrm{VaR}_{95\%}$ be the adopted risk measure. To assess how much the unimodality assumption contributes to the total model risk left after fully trusting that the mean and the variance are equal to 10 and 4, respectively, we calculate $\mathcal{C}(\mathrm{VaR}_{95\%}, \mathcal{A}_2, \mathcal{A}_3)$. Using the bounds of Theorems 7 and 14, $\mathcal{C}(\mathrm{VaR}_{95\%}, \mathcal{A}_2, \mathcal{A}_3)= 1 - \frac{28.75 - 10}{38.21 - 9.86} = 33.44\%$. Hence, given the knowledge of the mean and the variance, the unimodality assumption constitutes 33.44% of the total model risk.

We can see that $\mathcal{C}(\rho, \mathcal{A}_k, \mathcal{A}_l)$ is a relative measure of model risk contribution whose value is between 0 and 1. Specifically, we observe $\mathcal{C}(\rho, \mathcal{A}_k, \mathcal{A}_l)= 0$ only when $\overline{\rho}_{l} = \overline{\rho}_{k}$ and $\underline{\rho}_l = \underline{\rho}_k$, which means that assuming $\{ a_i \}_{k < i \leq l}$ after already having assumed $\{ a_i \}_{i \leq k}$ does not bring any additional model risk. In the case of the other extreme, we observe $\mathcal{C}(\rho, \mathcal{A}_k, \mathcal{A}_l) = 1$ when $\overline{\rho}_{l} = \underline{\rho}_{l}$, which means that assuming $\{ a_i \}_{k < i \leq l}$ constitutes the whole model risk conditional to the knowledge of $\{ a_i \}_{i \leq k}$.

Remark 3.1. We actually have, in several cases, explicit formulas for the risk bounds, which leads to an explicit formula for the conditional model risk contribution $\mathcal{C}(\rho, \mathcal{A}_I, \mathcal{A}_{J})$. For instance, in the previous example, in order to calculate the model risk contribution of adding a unimodality assumption, given the information on the mean and the maximum variance when using the risk measure $\mathrm{VaR}_\alpha$ ($0<\alpha<1$), we used the bounds of Theorems 7 and 14 and easily obtained an explicit form of $\mathcal{C}$. In this particular scenario, interestingly, the conditional model risk contribution $\mathcal{C}$ depends only on the probability level $\alpha$—i.e., if we assume knowledge of the mean and the maximum variance, the model risk contribution of adding the unimodality assumption is independent of the values of the mean and the maximum variance.

Remark 3.2. Note that, based on the difference between the sets $\mathcal{A}_k$ and $\mathcal{A}_l$, different types of risk can be assessed. For example, if the difference in the sets results from adding an assumption on the parameter, then a parameter risk is being assessed and so on.

Furthermore, the measure in Definition 3.1 can be used sequentially to perform what is called a “model risk allocation.” This can be explained as follows:

• We look at the adopted model, and we try to disassemble the assumptions upon which it was built. This can be done in a backward order in the sense that we start with a set of assumptions that fully define the adopted model and then we start to remove one assumption or subset of assumptions at a time until we obtain a set of the most basic and credible assumptions (i.e., the set of the fully trusted assumptions).

• After arriving at the most basic scenario, a comparison of the distance between the upper and lower bounds among the different relevant scenarios can be performed. Specifically, the comparison can be performed using $\mathcal{C}(\rho, \mathcal{A}_k, \mathcal{A}_{l} )$ by moving forward from the most basic scenario to the adopted model. This would reveal the marginal effect on model risk of adding each assumption conditional on the already adopted assumptions.

This idea will become clearer as we present and explain the methodology of model risk allocation more thoroughly using diagrams in the following subsection.

3.3. Summary diagrams

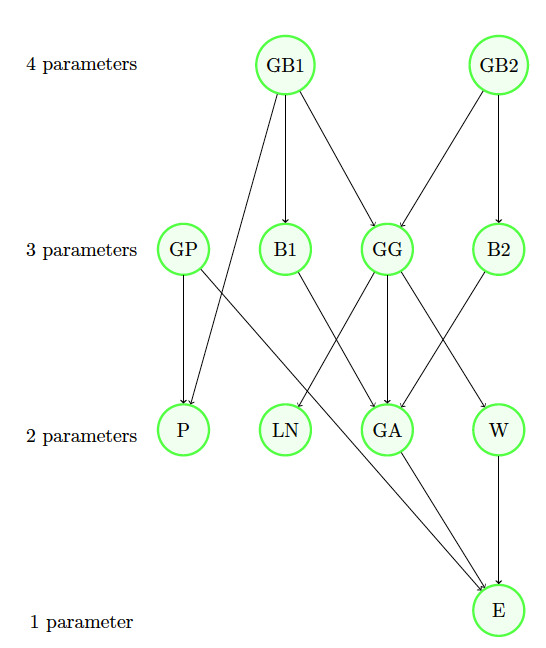
The literature offers risk bounds in many scenarios of interest. We present here a few of them with their interrelations in diagrams. Indeed, we present three diagrams that can be useful in performing the model risk allocation. Note that we use VaR as the risk measure $\rho$. Each scenario of the first two diagrams corresponds to a theorem that stems from the literature. To ensure that the paper is self-contained and to facilitate its use, we recall each theorem in Appendix C using consistent notations. The first diagram (in Figure 1) presents particular assumptions that can be made for the dependence among the individual components of a portfolio, whereas the other two diagrams serve to deal particularly with assumptions made for the portfolio loss when seen as a univariate random variable.

Figure 1.Diagram showing linkages between scenarios adopted in the academic literature.

The scenarios consist of assumptions made on the portfolio loss and its components on aggregate and marginal levels. Each number refers to a scenario for which the bounds are derived and presented in the appendix by a theorem of the same number. The notations are consistent with those in the theorems. The assumptions considered are the assumptions of knowledge of the marginals (m), sequential negative cumulative dependence (ncd), partial independence (pind), maximum standard deviation of the portfolio loss (s), having a partially specified factor model (pf), sequential positive cumulative dependence (pcd), and independent subgroups (ind). The symbols above the root node refer to the assumption adopted in the node. The notation on each arrow refers to the assumption added when following that arrow.

To perform the model risk allocation on an adopted model described by a specific probability distribution, we can begin by relaxing some of its assumptions while staying in the same distribution family, i.e., by studying the position of our model compared with its family of distributions (e.g., Diagram in Figure 3). Then we can make a bigger relaxation to drop the family of distribution assumptions and move backward to the more basic assumptions (e.g., Diagrams 1 and 2, respectively, displayed in Figures 1 and 2). Note that the assumptions of at least one of the root scenarios should be respected during the whole backward path—that root scenario is often seen as easy to fully trust. Note also that the assumption of knowledge of the portfolio mean $\mu$ in Diagram 2 can easily be replaced by an assumption of knowledge of an interval of the mean; this would be calculated by maximizing/minimizing the bounds as functions of the mean.

Figure 2.Diagram showing linkages between scenarios adopted in the academic literature.

The scenarios consist of assumptions made on the portfolio loss considered as a univariate random variable. Each number refers to a scenario for which the bounds are derived and presented in the appendix by a theorem of the same number. The notations are consistent with those in the theorems. The assumptions considered all refer to the portfolio loss random variable and are the assumptions of knowledge of the mean (μ), maximum standard deviation (s), nonnegativity (+), unimodality (U), minimum portfolio loss value (a), maximum portfolio loss value (b), minimum positive portfolio loss value (+), infinite variance (h), setting the infimum and supremum of the portfolio loss to 0 and infinity respectively (R+), and adding k-2 higher moments than the second moment (dk). The symbols above the root nodes refer to the set of assumptions adopted in the corresponding nodes. The notation on each arrow refers to the set of assumptions added when following that arrow. The asterisk on 12* refers to the fact that Theorem 12 was restricted to the case where only the maximum value of the second moment is known.

Figure 3.Diagram showing linkages between some families of distributions.

The position of two distributions on the two endpoints of an arrow refers to the fact that the one on the head of the arrow is a special case of the other distribution. The distributions set on the same horizontal line share the same number of parameters as depicted on the left. The distributions considered in the diagram are as follows: the generalized beta of first and second kind (GB1 and GB2, respectively), the beta of the first and second kind (B1 and B2, respectively), the generalized gamma (GG), the generalized Pareto (GP), the lognormal (LN), the gamma (GA), the Weibull (W), the Pareto (P), and the exponential (E) distributions.

Illustration

We present a toy example to illustrate the methodology. Assume that a variable of interest $X$ is modeled using an exponential distribution with mean $E[X] = 10$ and variance $\text{var}[X]= 100$, i.e., $X \sim Exp(\lambda= 0.1)$. Then the third quartile of $X$ is equal to $\mathrm{VaR}_{75\%}(X) = \frac{-ln(1-0.75)}{0.1}= 13.86$. Assuming an exponential distribution with a specific parameter is a rather strong and restrictive assumption. If the data allow being fully confident only about the fact that the mean belongs to the interval $[8,12]$ and the variance is less than 196, then all other assumptions that led to the adopted model should be tested. Disassembling assumptions by walking backward in the graphs would lead to several paths. We provide a few examples for illustrative purposes:

• If we consider that we trust only the intervals of the mean and the variance, the risk bounds based on Theorem 7 are (-0.08, 36.25). Those bounds are very wide and very far from 13.86, which makes them, if used on their own, almost useless in practice.

• We start by choosing one simple backward path, say, E $\rightarrow$ GA $\rightarrow$ 15 $\rightarrow$ 14 $\rightarrow$ 7 (see Figures 2 and 3).

• At this step, we start the allocation of model risk. Moving from the bounds of 7 to the ones of 14, we compare the two bounds to assess how much model risk is allocated to the unimodality assumption assuming that we trust the information on the intervals of the mean and the variance. The bounds of 14 are in this case (1.27, 27.87). Using the notations introduced in Definition 3.1, we have that $\rho = \mathrm{VaR}_{75 \%}$, $\mathcal{A}_2 = \{X \in \mathcal{M} \text{ }|\text{ } E[X] \in [8,12],\mathrm{var}[X] \in [0, 196]\}$, and $\mathcal{A}_3 = \{X \in \mathcal{M} \text{ }|\text{ } E[X] \in [8,12], \mathrm{var}[X] \in [0, 196], X$ is unimodal}, and we obtain $\mathcal{C}(\rho, \mathcal{A}_2, \mathcal{A}_{3}) = 26.78\%$. Hence, assuming that we trust the intervals of the mean and the variance, the unimodality assumption constitutes 26.78% of the total model risk.

• The bounds in 15 are (1.27, 23.68). Since the lower bound is not sharp, the conditional model risk contribution of the nonnegativity assumption, i.e., $\mathcal{C}(\rho, \mathcal{A}_3, \mathcal{A}_4)$, is at least 15.75%. However, for simplicity, we take here the exact value of 15.75% (for more details on the sharpness of bounds refer to Appendix 6).

• It is interesting as well to study the model risk inherent in the choice of a bigger family of the exponential and gamma distributions. This is aimed to answer the question of whether the risky choice was the adoption of the gamma family or the choice of the exponential among the gamma family members. The VaR bounds for a gamma distributed random variable whose mean and variance respect the given intervals are (8.11, 16.64). The conditional model risk contribution of choosing a gamma distribution after having knowledge of the intervals on the mean and the variance and of the unimodality and nonnegativity, i.e., $\mathcal{C}(\rho, \mathcal{A}_3, \mathcal{A}_4)$, is 61.94%.

• Let us now assess the parameter risk inherent in choosing an exponential distribution family. The lower and upper bounds of the $\mathrm{VaR}_{75\%}(X)$ within the exponential distribution while respecting the intervals of the mean and variance are $(11.09, 16.64)$. The conditional parameter risk contribution is 34.94%.

To formally summarize the results using the notations of Definition 3.1, we express the assumptions in Table 1, where the notations are as defined in Figures 2 and 3, but with $\mu$ and $s$ referring particularly to $E[X] \in [8,12]$ and $\mathrm{var}[X] \in [0, 196]$, respectively.

We then display our estimates for the conditional risk contributions in Table 2. The first three columns of Table 2 reflect what was discussed previously. The last column of Table 2 presents how much the aggregate assumptions constitute of the total model risk. This measure is conditional only on the basic scenario, which we assume fully credible by default. Hence, $\mathcal{C}(\rho, \mathcal{A}_{2}, \mathcal{A}_{k+1})$ can be seen (in some sense) as the unconditional measure of model risk contribution of assumptions $\{ a_i \}_{i \leq k+1}$.

3.4. Credibility-based bounds

In the literature, risk bounds are based on assigning either full or zero credibility to the assumptions on which the adopted model is built. As a result, the bounds are usually either very wide (because of trusting very few assumptions) or unrealistic (because of assigning full credibility to assumptions that cannot be fully trusted). A solution to this problem would be to assign partial credibility to the assumptions and calculate the bounds accordingly. This can be expressed formally in the following analysis.

Our analysis is based on having a non-null set of assumptions $\{a_i\}_{i \leq r}$ that we can easily consider as almost sure, i.e., $P(\{a_i\}_{i \leq r} \text{ are correct}) = 1$. Hence, for an adopted model $F^*$ and a set of assumptions $\{ a_i \}_{i \leq n}$, we can compute $n-r+1$ upper bounds—i.e., we can calculate the decreasing sequence of upper bounds estimates $\{\overline{\rho}_i\}_{ r \leq i \leq n}$ where $\overline{\rho}_k$ is the corresponding risk value for the set of assumptions $\{ a_i \}_{i \leq k}$. We see these values as the possible realizations of a random variable UB, and we aim to estimate the mean of UB. We find that

$$\scriptsize{ \begin{aligned} P(\text{UB} \leq \overline{\rho}_k) & = P(\{ a_i \}_{i \leq k} \text{ are correct})\\ &= \left\{ \begin{array}{cl} P(a_k \text{ is correct}\backslash \{ a_i \}_{i \leq k-1} \text{ are correct}) \\ \times P(\{ a_i \}_{i \leq k-1} \text{ are correct}) & \text{for } k \in \{ r +1,...,n\}, \\ 1 & \text{for } k \in \{ 1,...,r\}, \end{array} \right.\\ &= \left\{ \begin{array}{cl} \prod_{j=r+1}^{k} P(a_j \text{ is correct}\backslash \{ a_i \}_{i \leq j-1} \text{ are correct}) & \text{for } k \in \{ r+1, ...,n\}, \\ 1 & \text{for } k \in \{ 1,...,r\}. \end{array} \right. \end{aligned} }$$

Indeed, $P(a_j \text{ is correct}\backslash \{ a_i \}_{i \leq j-1} \text{ are correct})$ can be seen as a conditional credibility factor and can be denoted as $z_j$. Thus, we can express the cumulative distribution function of UB as

$$\small{ P(\text{UB} \leq \overline{\rho}_k) = \left\{ \begin{array}{cl} \prod_{j=r+1}^{k}{z_{j}} & \text{for } k \in \{ r+1, ...,n\}, \\ 1 & \text{for } k \in \{ 1,...,r\}. \end{array} \right. } \tag{3.5}$$

After specifying the credibility factors, the cumulative distribution function of UB can be calculated and therefore the $E[\text{UB}]$ can be determined; we denote it as the credibility-based upper bound (CUB). The same analysis can be performed to determine the credibility-based lower bounds (CLB). We provide explicit expressions for the CUB and CLB in the following definition.

Definition 3.2 (Credibility-based upper and lower bounds). Let $\rho: \mathcal{M} \rightarrow \mathbb{R}$ be a risk measure. Let $F^*$ be the cumulative distribution function of the adopted model and let $\{ a_i \}_{ i \leq n }$ be a set of assumptions that characterizes $F^*$ where $\{ a_i \}_{i \leq r \leq n}$ can be fully trusted. Let us define a decreasing sequence of sets $\{ \mathcal{A}_k \}_{ k \leq n}$ with $\mathcal{A}_k = \{X \in \mathcal{M} \text{ }| \text{ }X \text{ respects assumptions } \{ a_i \}_{i \leq k}\}$. Let us denote by $z_{j}$ the credibility assigned to $a_j$ given the knowledge of $\{a_i\}_{i \leq j-1}$. Then we can define the credibility-based upper bound CUB and lower bound CLB as follows:

$$\scriptsize{ \mathrm{CUB} \left(\rho, \{\mathcal{A}_{m} \}_{m}, \{z_{j}\}_j \right) = \overline{\rho}_r + \sum_{m=r+1}^{n}{\left(\prod_{j=r+1}^{m}{z_{j}}\right)} {\left( \overline{\rho}_{m} - \overline{\rho}_{m-1} \right)}, } \tag{3.6}$$

and

$$\scriptsize{ \mathrm{CLB} \left(\rho, \{\mathcal{A}_{m} \}_{m}, \{z_{j}\}_j \right) = \underline{\rho}_r + \sum_{m=r+1}^{n}{\left(\prod_{j=r+1}^{m}{z_{j}}\right)} {\left( \underline{\rho}_{m} - \underline{\rho}_{m-1} \right)}, } \tag{3.7}$$

where $\overline{\rho}_j = \underset{{X\in \mathcal{A}_j }}{\sup}{\rho(X)}$ and $\underline{\rho}_j = \underset{{X\in \mathcal{A}_j }}{\inf}{\rho(X)}.$

The credibility factors $\{z_j\}_j$ are to be assessed/specified differently according to each type of assumptions. For example, one may use a specific statistical test to demonstrate confidence about the unimodality property (e.g., the dip test of unimodality—see J. A. Hartigan and Hartigan (1985) and P. M. Hartigan (1985)), another test to demonstrate how trustworthy a specific parameter estimation is (e.g., hypothesis testing), yet another test to see how credible the normality assumption is (e.g., the numerous normality tests), and so on. Nevertheless, the assessment of credibility factors based on statistical tests or expert opinion is considered out of the scope of this paper.

Remark 3.3. The traditional approach to risk bounds can be seen as a particular case of the credibility-based approach where the credibility factors $\{z_j\}_j$ are dummy variables (i.e., can take only the values 0 or 1).

Illustration

Let us elaborate on our toy example introduced in Section 3.3. We specify the conditional credibility factors in Table 3. The sequence of fully trusted initial assumptions in this case is $\{a_1, a_2$}, i.e., the intervals on the mean and the variance, and hence we have $r=2$. The adopted model is reached after adding the assumption $a_7$, and we thus have $n=7$. The credibility-based bounds would then be $\mathrm{CLB}= A_7= 5.69$ and $\mathrm{CUB}= B_7= 21.09$.

Remark 3.4. Table 4 helps us examine the reasoning behind Definition 3.2 from a different angle. In the first column, the bounds improve (i.e., become tighter) when assumptions are added (i.e., when $k$ increases). However, this improvement (shown in the fourth column) cannot be realized when adding assumptions that cannot be fully trusted. A reasonable way of incorporating these improvements is to adjust each improvement according to the credibility (shown in the third column) that the corresponding added assumption holds. This perspective automatically leads to the bounds $(A_k, B_k)$ shown in the fifth column.

Model risk measures

One of the ultimate objectives of assessing model risk is to discover a possible buffer we can use to calculate the corresponding capital requirement. In this section, we propose an intuitive formula that can be used for that purpose.

Following the early work of Cont (2006) on model risk measurement, Barrieu and Scandolo (2015) define the absolute and the relative measures of model risk. The absolute measure reflects the position of the value of the risk measure applied to the adopted model compared with the upper risk bound derived based on the scenario of fully trusted assumptions, whereas the relative measure reflects the position of the adopted model compared with both the lower and the upper risk bounds. In formal terms, if $X^* \sim F^*$, and $\{ a_i\}_{i\leq r}$ is the set of fully trusted assumptions, then the two measures are defined as follows:

Definition 3.3 (Absolute measure of model risk, (Barrieu and Scandolo 2015). $$\mathrm{AM}(\rho, \mathcal{A}_r, X^*) = \frac{\overline{\rho}_r- \rho(X^*)}{\rho(X^*)}. \tag{3.8}$$

Definition 3.4 (Relative measure of model risk, (Barrieu and Scandolo 2015).

$$\mathrm{RM}(\rho, \mathcal{A}_r, X^*) = \frac{\overline{\rho}_r- \rho(X^*)}{\overline{\rho}_r - \underline{\rho}_r}. \tag{3.9}$$

However, in practice, $\overline{\rho}_r$ and $\underline{\rho}_r$ are very different from $\rho(X^*)$ (i.e., the risk bounds are wide), meaning that in many cases of interest these two model risk measures are not very informative. We thus propose using the credibility-based upper and lower bounds to extend these definitions to the credibility-based absolute and relative measures of model risk as follows.

Definition 3.5 (Credibility-based absolute measure of model risk).

$$\mathrm{CAM}(\rho, \mathrm{CUB}, \mathrm{CLB}, X^*) = \frac{\mathrm{CUB} - \rho(X^*)}{\rho(X^*)}.\tag{3.10}$$

Definition 3.6 (Credibility-based relative measure of model risk).

$$\mathrm{CRM}(\rho, \mathrm{CUB}, \mathrm{CLB}, X^*) = \frac{\mathrm{CUB} - \rho(X^*)}{\mathrm{CUB} - \mathrm{CLB}}.\tag{3.11}$$

The four measures are positive increasing functions of model risk with a value of 0 for no model risk. CRM, similar to RM, is unitless and reaches 1 when the model risk is maximal. Indeed, CRM incorporates information on the worst-case and best-case models, on the adopted model, and on the credibility assigned to each assumption. Hence, it would be interesting to incorporate CRM as a factor in the model risk capital formula. In addition, the difference between the CUB and the CLB represents the maximum model risk capital that could be required when using a model that adopts the corresponding assumptions and credibility factors. These ideas lead us to Definition 3.7.

Definition 3.7 (Model risk capital). For a continuous increasing function $f: [0,1] \rightarrow [0,1]$, with $f(0)=0$ and $f(1)=1$, we can define the model risk capital (MoRC) by

$$\small{ \begin{align} \mathrm{MoRC(CRM, CUB, CLB, f)}&= f(\mathrm{CRM}) \\ &\quad \times \mathrm{(CUB - CLB)}. \end{align} } \tag{3.12}$$

We can look at $f(\mathrm{CRM})$ as the percentage of the maximum capital that can be allocated to model risk, starting from 0 for no model risk and reaching 100% for full model risk. The regulator and the model risk manager decide on the degree of conservatism toward model risk. This can be translated into the choice of $f$, i.e., how the percentage of the maximum capital increases with the increase in model risk. One suggestion would be to use the convex function $f(x)=x^n, \text{for } n\geq 1$; then the higher the $n$, the less conservative the MoRC. Indeed, any continuous increasing function $g$ can lead to an admissible function $f= \frac{g - g(0)}{g(1)-g(0)}$.

Illustration

In our toy example, $\mathrm{CAM}= \frac{21.09-13.86}{13.86}= 52.16\%$ and $\mathrm{CRM}= \frac{21.09-13.86}{21.09-5.69}= 46.96\%$. If we choose $f(x) = x^2$, then $\mathrm{MoRC}= 3.4$.

Sometimes it is interesting to compare the model risks of two possible models. This can be done by comparing the corresponding CAMs and CRMs. In addition, noting that the CUBs and CLBs are basically model specific, it can be meaningful to compare the width of the credibility-based bounds of two different models adopted for the same data set; a higher difference is an indicator of a higher uncertainty in the model.

Interestingly, the more assumptions that are challenged and the more credibility a modeler can assign to his or her assumptions, the lower the CAM and (CUB $-$ CLB) are expected to be. That fact encourages the modeler to strive for higher credibility in his or her assumptions and to challenge as many assumptions as possible.

Remark 3.5. The measures presented in definitions 3.3, 3.4, 3.5, and 3.6 focus on the risk of underestimation of the risk measure. Even though this is the case that calls for a buffer in the capital requirement, one can easily construct complementary measures to reflect the risk of overestimation of the risk measure.

4. Case study: SOA medical dataset

In this section, we present an application of the ideas developed in this paper to an SOA Group Medical Insurance Large Claims Database described thoroughly in Grazier (1997). The data are collected from 26 insurers and cover the total claim amounts exceeding $25,000 over the year 1991. We study the total claim amounts as a univariate variable, which makes it possible to challenge the two different univariate models suggested for this same data set by two scientific papers, namely, Cebrián, Denuit, and Lambert (2003) and Zisheng and Chi (2006).

4.1. Data and model description

The data set is composed of 75,789 observations. The average total claim amount is $58,413 and the largest observed total claim is $4,518,420. The standard deviation among the total claims is $66,005, and the VaR at a probability level of 99.5% is $406,190.

Both Cebrián, Denuit, and Lambert (2003) and Zisheng and Chi (2006) adopted an extreme value theory perspective and fit a generalized Pareto distribution (GPD), which is known as the “natural” distribution for modeling the excess-of-loss over high thresholds.

Let $S$ denote the random variable of the total claim and $u$ the threshold after which the data are fit to a GPD, and let $G_{\zeta, \theta, \lambda}$ represent the generalized Pareto distribution function with a shape parameter $\zeta$, a location parameter $\theta$, and a scale parameter $\lambda$. Then, one can easily prove that $S | S\geq u \sim G_{\zeta, u, \lambda}$ implies $\mathrm{VaR}_\alpha (S)= u + \frac{\lambda}{\zeta} \left[ \left( \frac{1- \alpha}{\widehat{P}(S> u)}\right)^{- \zeta} - 1 \right]$ for $\alpha \geq 1- \widehat{P}(S> u)$ (see Appendix B for more details on the GPD). To fit the GPD model to the data set, one has to choose a threshold $u$ and then fit the GPD to the conditional distribution of the excesses above the threshold $u$. Typically, $\widehat{P}(S>u)$ is calculated empirically.

Cebrián, Denuit, and Lambert (2003) found that the best choice for the threshold is $u_1 =$ 200,000, which gives 2,013 exceedances. The estimated parameters are $\zeta_1 = 0.314$ and $\lambda_1 =$ 93,901. The mean, standard deviation, and VaR at 99.5% of $S$ under the adopted model are $\mathrm{E}_1[S] =$ 58,405, $\mathrm{std}_1[S] =$ 66,178, and $\mathrm{VaR}_{99.5\% , 1} =$ 406,161.

On the other hand, Zisheng and Chi (2006) chose a threshold of $u_2 =$ 162,402, which gives 3,083 exceedances and leads to the estimated parameters $\zeta_2 = 0.311962$ and $\lambda_2 =$ 82,652.07. The mean, standard deviation, and VaR at 99.5% of $S$ under this model are $\mathrm{E}_2[S] =$ 58,422, $\mathrm{std}_2[S] =$ 66,110, and $\mathrm{VaR}_{99.5\% , 2} =$ 406,928.

4.2. Model risk allocation

The first step in the model risk assessment is to disassemble the assumptions upon which the adopted model was built and try to assess the model risk contribution of each assumption of interest. Using the tools provided in the literature (many of which are stated in Figures 1, 2, and 3), some of the assumptions that are of interest to challenge are questioned as follows:

• Given the threshold, what is the parameter risk in the estimation of the scale and shape parameters of the GPD?

• Given that a GPD is adopted, what is the parameter risk in choosing the threshold?

• Given mean, variance, nonnegativity, and unimodality, how risky is it, in terms of model risk, to choose a GPD?

• How much does each of the assumptions on the moments, nonnegativity, and unimodality contribute to the total model risk of the adopted model?

The diagram in Figure 4 shows some possible paths from two basic scenarios to the adopted models. Motivated by the large number of observations, we calculate the interval on the mean and the maximum standard deviation based on the standard confidence interval procedure. Indeed, $\mu'$ refers to the assumption that the average total claim amount belongs to the interval $(58,413 - 1.96 \text{ } \frac{66,005}{\sqrt{75,789}}, 58,413 + 1.96 \text{ } \frac{66,005}{\sqrt{75,789}})$ $\simeq$ $(57,940, 58,880)$, and $s$ refers to the assumption that the standard deviation is lower than or equal to 66,339 calculated based on the formula of the upper limit presented on pages 197–198 of (Sheskin 2003).

Figure 4.Diagram showing linkages between the scenarios that underlie a GPD model.

The scenarios consist of assumptions made on the portfolio loss considered as a univariate random variable. Each number refers to a scenario for which the bounds are derived and presented in the appendix by a theorem of the same number. The considered assumptions all refer to the portfolio loss random variable and are the assumptions of knowledge on the following: an interval of the mean (μ′), a maximum standard deviation (s), nonnegativity (+), unimodality (U), positive portfolio loss value (+), a maximum value for the third moment (d3), fitting a GPD (GP), choosing the threshold of Cebrián, Denuit, and Lambert (2003) for the GPD (GP/u1), choosing the threshold of Zisheng and Chi (2006) for the GPD (GP/u2), adopting the model of Cebrián, Denuit, and Lambert (2003) (Model 1), and adopting the model of Zisheng and Chi (2006) (Model 2). The symbols above the root nodes refer to the set of assumptions adopted in the corresponding nodes; the notations on each arrow refer to the set of assumptions added when following that arrow. The asterisks on 12* and 12** respectively refer to the fact that Theorem 12 was restricted to the case where only the maximum values of the second moment or the second and third moments are known.

The value of the maximum third moment is calculated by bootstrapping; we simulated 100,000 samples of 10,000 data points each taken from the set of 75,789 observations, calculated the third moment of each bootstrap sample, and then calculated the third quartile of the set of third moment values and adopted the third quartile as the upper limit for the third moment. Indeed, $d_3$ refers to the assumption that the upper limit of the third moment of the portfolio loss random variable is equal to $4.78\times 10^{15}$.

The feature of unimodality can easily be detected from the data and in the two adopted models when complemented by the empirical distribution for the values that are lower than the threshold (the GPD model is usually fitted to the tail of the distribution starting at the threshold, whereas the rest of the distribution is usually modeled empirically).

Remark 4.1. It is important to note that the methods adopted in the estimation of the moments intervals are just a choice from many others; indeed, this case study does not aim to adopt the best estimation methods but rather solely to assess the model risk.

The risk measure adopted in this case study is the one that is most used in the calculation of the capital requirement in Solvency II, the value-at-risk at a probability level of 99.5% ($\mathrm{VaR}_{99.5\%}$). In the diagrams of Figure 5, the risk bounds and the conditional model risk contributions under the various assumptions are presented. At this step, one can directly make several observations:

• The nonnegativity assumption does not contribute to the model risk (0%).

• Assuming a maximum value for the third moment after already having information on the first two moments is not risky in terms of model risk (2.02%).

• Adding information on the variance after having already assumed an interval for the mean has a great effect on the model risk and should be done cautiously (92%).

• Being able to trust the unimodality feature of the data inspires much more confidence in choosing the GPD compared with being able to trust some information on the third moment (56.29% vs. 70.3%).

• Even when one trusts the information on the moments, nonnegativity, and unimodality, the choice of GPD still contributes significantly in the total model risk (56.29%).

• Choosing a threshold after having already chosen to adopt a GPD model can have a relatively higher contribution to the model risk than choosing the GPD itself after having already trusted the unimodality property and some information on the moments (e.g., 78.12% vs. 56.29%).

• The threshold chosen by (Zisheng and Chi 2006) is a stronger assumption (in terms of model risk) than the one chosen by (Cebrián, Denuit, and Lambert 2003) (78.12% vs. 68.38%).

Figure 5.Diagrams showing the VaR99.5% bounds and the corresponding conditional model risk contributions that are relative to the scenarios shown in Figure 4.

The conditional model risk contribution of the last assumption that leads to the adopted model is by definition 100% and hence is not very helpful in interpreting specific assumptions. For that, one can use the relative measure of model risk (RM) defined in Definition 3.4. The parameter risk inherent in choosing the couple $(\zeta_1, \lambda_1)$ after already having chosen the threshold $u_1$ can be presented by $RM_1 = \frac{458,458 - 406,161}{458,458 - 371,825} = 60.37\%$, whereas in the case of Model 2 we have $RM_2 = 52.4\%$. This directly implies that the parameter risk in choosing the scale and the shape parameters of Model 1 after having already chosen the threshold of Model 1 is greater than the one in choosing the scale and shape parameters of Model 2 after having already chosen the threshold of Model 2.

4.3. Model risk measurement

The next step in our model risk assessment framework is to assess the model risk in the model as a whole. We can do that using the credibility-based bounds defined in Definition 3.2. We first choose the assumptions ($a_i$) we will use in the calculation and assign the corresponding conditional credibility factors ($z_i$). Based on the results obtained so far, a meaningful set of assumptions that leads to the adopted model is $\{a_i\}_i = \{ (\mu', s), \text{U}, \text{GP}, u, (\zeta, \lambda)\}$.

Before proceeding to the assessment of credibility factors, it should be noted that this case study does not aim to show the best way of assigning credibility factors but rather to give a simplistic illustration of how the framework works.

The interval on the mean and the maximum variance are both calculated based on a 95% confidence level, so it is not unreasonable to start with this information as the fully trusted basic assumptions.

The sample of observations clearly features unimodality; we can even verify this by performing some unimodality tests (e.g., the dip test of unimodality—see J. A. Hartigan and Hartigan (1985) and P. M. Hartigan (1985). Hence, one can confidently give a 95% credibility to the unimodality property.

Our risk measure is evaluated at the very end of the tail, at a probability level of 99.5%, which makes the GPD a good choice for the model. We choose to assign a 50% conditional credibility factor for the GPD assumption.

To choose the threshold, Cebrián, Denuit, and Lambert (2003) used the Gerstengarbe plot proposed in Gerstengarbe and Werner (1989), whereas Zisheng and Chi (2006) used the goodness-of-fit test for the GPD developed in Choulakian and Stephens (2001). A statistician would have to compare the two tests and assign the corresponding conditional credibility factors. In this illustrative example, we choose to correlate the credibility of the method with the number of times it was cited. Choulakian and Stephens (2001) is currently cited 390 times, whereas Gerstengarbe and Werner (1989) is cited only 24 times, and hence we will consider the goodness-of-fit test as more credible. The Gerstengarbe plot and the goodness-of-fit test are respectively given 50% and 75% as conditional credibility factors.

The scale and shape parameters are estimated in both models using maximum likelihood estimation. However, the parameters are estimated based on 2,013 and 3,083 data points in (Cebrián, Denuit, and Lambert 2003) and (Zisheng and Chi 2006), respectively. Hence, the estimates of the second model are more reliable, and we choose to give conditional credibility factors of 60% and 80% to the estimates of Model 1 and Model 2, respectively. A summary is presented in Table 5 and Table 6.

We can now apply the formula for the credibility-based bounds of Definition 3.2 and obtain the following: $\mathrm{CLB}_1=$ 168,833, $\mathrm{CUB}_1=$ 587,001, $\mathrm{CLB}_2=$ 194,876, and $\mathrm{CUB}_2=$ 576,548. Hence, the credibility-based absolute and relative measures of model risk for the two models are $\mathrm{CAM}_1=$ 44.52%, $\mathrm{CRM}_1=$ 43.25%, $\mathrm{CAM}_2=$ 41.68%, and $\mathrm{CRM}_2=$ 44.44%. The widths of credibility-based bounds of the two models are $\Delta_1 = \mathrm{CUB}_1 - \mathrm{CLB_1}=$ 418,168 and $\Delta_2 = \mathrm{CUB}_2 - \mathrm{CLB_2}=$ 381,672. The two CRMs are very close, but the comparisons of the CAMs and the $\Delta$s show that Model 2 has the least model risk.

Finally, we calculate the suggested MoRC for each of the two models. To theoretically eliminate the model risk, one should add a buffer that, as a percentage of the risk value, is equal to the CAM. However, the CAM is quite high in our case and amounts to more than 40% of the value of the risk measure. Additionally, the CAM may misrepresent the model risk since it does not account for the position of the risk value compared with the CLB. A solution would be to adopt the MoRC in Definition 3.7 with a convex function $f$. The choice of $f$ is based on how conservative the risk management team or the regulators are. If $f(x)=x^n, \text{for } n\geq 1$, then the higher $n$ the less security is required. If we take $f(x)=x^3$ for example, we get $\mathrm{MoRC}_1 = 33,821$ and $\mathrm{MoRC}_2 = 33,500$, i.e., respectively $8.33\%$ and $8.23\%$ of the risk values of the two adopted models.

5. Conclusion

In this paper, we establish a practical framework for quantitative model risk assessment that builds on the literature of risk bounds (theory of model risk). First, we disassemble an adopted model into a set of assumptions and use our novel model risk contribution measure to allocate the model risk to the various assumptions. In so doing, we aim to enlighten the modeler on how cautious he or she is expected to be when making every assumption in the model-building process. Second, we acknowledge that every single assumption can have its own level of credibility and we incorporate this information into the model risk assessment. Third, we define new measures of model risk that the modeler can use for model risk capital allocation. Last, we conduct a case study in which we apply our framework to a real-world data set, the SOA Group Medical Insurance Large Claims Database.

Our framework incorporates previous findings from the literature on risk bounds and is built in a way to embrace future findings in this currently active research area.

Funding

The authors acknowledge funding from the 2019 Individual Grants Competition of the CAS.

Appendices

Appendix A Definitions and notations

Basic notations

We consider a portfolio of individual risks with a portfolio loss variable $S = \sum_{i=1}^{n}X_i$, where $X_i$ is the $i$th individual loss and $n$ is the number of individual risks. We write $X_i \sim F_i$ to express that $F_i$ is the marginal distribution of $X_i$, and we denote the vector of $n$ individual risks by $\boldsymbol{X} = (X_1, X_2, ..., X_n)$.

Our approach to model risk assessment is based on the derivation of upper and lower risk bounds in each of the scenarios of interest. Specifically, for the value-at-risk (VaR) defined in 3.3, and for $\alpha \in (0, 1)$, we denote the risk bounds as follows:

$$\begin{align} \overline{\mathrm{VaR}}_\alpha^v &= \sup_{S\in V}{\mathrm{VaR}^+_\alpha(S)},\\ \underline{\mathrm{VaR}}_\alpha^v &= \inf_{S\in V}{\mathrm{VaR}_\alpha(S)}, \end{align} \tag{A.1}$$

where $\mathrm{VaR}^+_\alpha(S)=\text{sup}\{x \in \mathbb{R} \text{ } | \text{ } F_S(x) \leq \alpha \}$ and $V$ stands for the set of random variables that respect a given set of assumptions denoted by $v$.

Sharpness of bounds

A risk bound is called sharp if it is attainable, i.e., if there exists a random variable in the set of plausible random variables for which the risk measure reaches the value of the bound. In some scenarios, the sharp bounds $\overline{\mathrm{VaR}}_\alpha^v$ and $\underline{\mathrm{VaR}}_\alpha^v$ are hard to derive analytically and thus are replaced by non-sharp bounds. To underscore the difference, we denote the not-necessarily-sharp bounds by $\overline{\overline{\mathrm{VaR}}}_\alpha^{v}$ and $\underline{\underline{\mathrm{VaR}}}_\alpha^v$.

Risk partitions

Let $I_1, .., I_n$ be mutually exclusive sets. We denote by $\bigcup_{i=1}^{k}I_i =\{1,...,n\}$ a partition and by $\boldsymbol{X_{I_i}} := (X_j, j \in I_i)$ the $i$th subgroup of the risk vector $\boldsymbol{X}$.

Specific dependence structures

We denote by $S^c = \sum_{i=1}^{n}X_i^c$ the comonotonic portfolio sum with $X_i^c \sim F_i$. We denote by $S^\perp = \sum_{i=1}^{n}X_i^\perp$ the independent portfolio sum with $X_i^\perp \sim F_i$. We denote by $S_i = \sum_{j \in I_i}X_j$ the sum of a subgroup $I_i$ of individual losses, and by $S^{c,k} = \sum_{i=1}^{k}S_i^c$ the comonotonic version of the portfolio sum $S = \sum_{i=1}^{k}S_i$.

Additional risk measures

Throughout the paper, we concentrate on assessing model risk using VaR. However, to do so, we need to refer to two other risk measures, the tail value-at-risk (TVaR) and the left tail value-at-risk (LTVaR), which are defined as follows:

$$\small{ \mathrm{TVaR}_\alpha(S)= \frac{1}{1-\alpha} \int\limits_\alpha^1 \mathrm{VaR}_u(S) du\text{, } \alpha \in (0, 1), } \tag{A.2}$$

and

$$\mathrm{LTVaR}_\alpha(S)= \frac{1}{\alpha} \int\limits_0^\alpha \mathrm{VaR}_u(S) du\text{, } \alpha \in (0, 1).\tag{A.3}$$

Dependence intensity

A strong notion of positive dependence is the sequential positive cumulative dependence (PCD) defined in Rüschendorf (2017) as a sequential version of the initial PCD defined in Denuit, Dhaene, and Ribas (2001). $\boldsymbol{X}$ is sequential PCD if

$$\scriptsize{ \begin{align} P\left(\sum_{i=1}^{k-1} X_i > t_1 | X_k > t_2 \right) \geq P \left( \sum_{i=1}^{k-1} X_i > t_1 \right) \forall k &\in [2, n] , \\ \forall t_1,t_2&\in\mathbb{R}. \end{align} } \tag{A.4}$$

Similarly, $\boldsymbol{X}$ is sequential negative cumulative dependence (NCD) if

$$\scriptsize{ \begin{align} P\left(\sum_{i=1}^{k-1} X_i > t_1 | X_k > t_2 \right) \leq P \left( \sum_{i=1}^{k-1} X_i > t_1 \right) \forall k &\in [2, n], \\ \forall t_1,t_2&\in\mathbb{R}. \end{align} } \tag{A.5}$$

Factor model

In a factor model, the individual risks $X_i$ are expressed in a functional form as

$$X_i = f_i(Z, \epsilon_i), 1 \leq i \leq n,\tag{A.6}$$

where $\epsilon_i$ are idiosyncratic risk components and $Z$ is a common risk factor taking values in a set $D \subset \mathbb{R}^d$. A partially specified factor model refers to the case where the marginal distributions $F_i$, the conditional distributions of $X_i$ given $Z=z$ denoted by $F_{i|z}$, and the joint distribution of $(X_i, Z)$ denoted by $H_i$ are all known. We denote by $S_z = \sum_{i=1}^{n} X_{i,z}$ the sum of the conditional marginal variables $X_i$ given $Z=z$, and by $S_z^c$ the corresponding comonotonic sum.

Appendix B Properties of the beta and generalized Pareto distributions

Beta distribution

If $X \sim$ Beta$(a,b)$ with $a>0$ and $b>0$, then the density function of $X$ is given by

$$f_{X}(x) = \frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)} x^{a-1} (1-x)^{b-1} \text{ for } 0<{x}<1,$$

where $\Gamma(x) = \int_0^{+\infty} t^{x-1} e^{-t} dt \text{ for } x >0.$ The first two central moments of $X$ are $E[X] = \frac{a}{a+b} \ \text{and var} [X] = \frac{ab}{(a+b)^2(a+b+1)}.$

Generalized Pareto distribution

If $X \sim$ GPD$(\zeta, \theta, \lambda)$ with $\zeta \in \mathbb{R}$, $\theta \in \mathbb{R}$, and $\lambda >0$, then the cumulative distribution function of $X$ is given by

$$\small{ G_{\zeta, \theta, \lambda}(x) = \left\{ \begin{array}{cl} 1 - \left( 1+ \frac{\zeta(x- \theta)}{\lambda} \right)^{-\frac{1}{\zeta}} \text{ for } \zeta \neq 0, &\\ 1 - \exp{\left(-\frac{x-\theta}{\lambda}\right)} \text{ for } \zeta = 0, \end{array} \right. } \tag{B.1}$$

for $x \geq \theta$ when $\zeta \geq 0$, and $\theta \leq x \leq \theta - \lambda/\zeta$ when $\zeta <0$. The first two central moments of $X$ are $E[X] = \theta + \frac{\lambda}{1-\zeta} \text{ for } \zeta <1,$ and $\text{var}[X] = \frac{\lambda^2}{(1-\zeta)^2(1-2\zeta)}$ for $\zeta < 1/2.$

Appendix C Value-at-risk bounds

In this section, we present a review on the value-at-risk (VaR) bounds derived in the literature. Although the section is designed to be read on its own, the theorems presented here are ordered based on their position in the literature review in Section 1. In the banking and insurance practice, actuaries usually have better techniques and more data with which to estimate one-dimensional distributions versus estimating an overall dependence structure. Hence, there is a tendency to give full trust to the marginal distributions and distrust all additional assumptions. We start with the bounds in this basic scenario, where only the marginal distributions are known.

Theorem 1. (Bernard, Rüschendorf, and Vanduffel 2017) (VaR bounds with given marginals) Let $\alpha \in (0,1)$ and $X_i \sim F_i$. Then

$$\scriptsize{ \begin{align} \mathrm{VaR}_\alpha(S)\leq \overline{\overline{\mathrm{VaR}}}^m_\alpha &:= \mathrm{TVaR}_\alpha(S^c) = \sum_{i=1}^{n}\mathrm{TVaR}_\alpha(X_i), \end{align} } \tag{C.1}$$

$$\scriptsize{ \begin{align} \mathrm{VaR}_\alpha(S) \geq \underline{\underline{\mathrm{VaR}}}^m_\alpha &:= \mathrm{LTVaR}_\alpha(S^c) = \sum_{i=1}^{n}\mathrm{LTVaR}_\alpha(X_i). \end{align} } \tag{C.2}$$

The individual risks of portfolios faced in risk management do often show some positive dependence structure. However, some types of insurance products can show some negative dependence, e.g., weather-related insurance products. Hence, an assumption of negative dependence may be realistic. We present in the following two theorems presented in (Rüschendorf 2017).

Theorem 2 (VaR bounds with given marginals and sequential positive cumulative dependence). Let $\alpha \in (0,1)$ and $X_i \sim F_i$, and let $\boldsymbol{X}$ be sequential positive cumulative dependent (PCD). Then

$$\begin{align} \underline{\underline{\mathrm{VaR}}}^{m,pcd}_\alpha &:= \mathrm{LTVaR}_\alpha(S^\perp) \leq \mathrm{VaR}_\alpha(S) \\ &\quad \leq \sum_{i=1}^{n}\mathrm{TVaR}_\alpha(X_i) \\ &= \overline{\overline{\mathrm{VaR}}}^m_\alpha. \end{align} \tag{C.3}$$

Theorem 3 (VaR bounds with given marginals and sequential negative cumulative dependence). Let $\alpha \in (0,1)$ and $X_i \sim F_i$, and let $\boldsymbol{X}$ be sequential negative cumulative dependent (NCD). Then

$$\begin{align} \underline{\underline{\mathrm{VaR}}}^m_\alpha &= \sum_{i=1}^{n}\mathrm{LTVaR}_\alpha(X_i) \leq \mathrm{VaR}_\alpha(S) \\ &\quad \leq \mathrm{TVaR}_\alpha(S^\perp) =: \overline{\overline{\mathrm{VaR}}}^{m,ncd}_\alpha. \end{align} \tag{C.4}$$

Additionally, some subgroups of the portfolio can prove to be independent. One can easily check such a relation statistically and by intuition. In the following theorems we present VaR bounds derived in Puccetti et al. (2017) in scenarios where all or some of the subgroups of the portfolio are assumed independent.

Theorem 4 (VaR bounds with given marginals and independent subgroups). Let $\alpha \in (0,1)$ and $X_i \sim F_i$, and let $\bigcup_{i=1}^{k}I_i =\{1,...,n\}$ be a partition. If the risk subvectors $\boldsymbol{X_{I_1}},..., \boldsymbol{X_{I_k}}$ are independent, then

$$\begin{align} \underline{\underline{\mathrm{VaR}}}^{m,ind}_\alpha &:= \mathrm{LTVaR}_\alpha(S^{c,k}) \leq {\mathrm{VaR}_\alpha(S)} \\ &\quad \leq \mathrm{TVaR}_\alpha(S^{c,k}) =: \overline{\overline{\mathrm{VaR}}}^{m,ind}_\alpha. \end{align} \tag{C.5}$$

Note that $\underline{\underline{\mathrm{VaR}}}^{m,ind}_\alpha$ and $\overline{\overline{{\mathrm{VaR}}}}^{m,ind}_\alpha$ are TVaR and LTVaR functions of independent sums, and hence can be obtained by Monte Carlo simulation.

The following theorem considers the case where only some of the risk subvectors are independent.

Theorem 5 (VaR bounds with given marginals and partial independent substructures). Let $\alpha \in (0,1)$ and $X_i \sim F_i$. Let $\bigcup_{i=1}^{k}I_i =\{1,...,n\}$ be a partition and let $H \subset \{1,...,k\}$, and $Y_i = \sum_{j \in I_i} X_i$. If the risk subvectors $\boldsymbol{X_{I_i}}, i \in H$ are independent, then

$$\small{ \begin{align}{\mathrm{VaR}_\alpha(S)} \leq \overline{\overline{\mathrm{VaR}}}^{m,pind}_\alpha &:= \sum_{i \notin H} \sum_{j \in I_i}\mathrm{TVaR}_\alpha(X_j) \\ &\quad + \mathrm{TVaR}_\alpha(\sum_{i\in H} S_i^c), \end{align} } \tag{C.6}$$

$$\small{ \begin{align}{\mathrm{VaR}_\alpha(S)} \geq \underline{\underline{\mathrm{VaR}}}^{m,pind}_\alpha &:= \sum_{i \notin H} \sum_{j \in I_i}\mathrm{LTVaR}_\alpha(X_j) \\ &\quad + \mathrm{LTVaR}_\alpha(\sum_{i\in H} S_i^c). \end{align} } \tag{C.7}$$

Again, the bounds above can be obtained by Monte Carlo simulation since $\sum_{i\in H} S_i^c$ is an independent sum.

The following theorem considers the case where we can trust the marginal distributions of the individual risks and a maximum variance of the portfolio loss. The fact that, instead of taking an exact value, an upper bound is considered for the variance allows us to capture the presence of statistical uncertainty in the second moment estimation.

Theorem 6. (Bernard, Rüschendorf, and Vanduffel 2017) (VaR bounds with given marginals and maximum variance) Let $\alpha \in (0,1)$, $X_i \sim F_i$, and $\mathrm{var}[S] \leq s^2$. Then

$$\small{ {\mathrm{VaR}_\alpha(S)} \leq \overline{\overline{\mathrm{VaR}}}^{m,s}_\alpha := \min \left( \mu +s \text{ }\sqrt[]{\frac{\alpha}{1-\alpha}} , \overline{\overline{\mathrm{VaR}}}^{m}_\alpha \right), } \tag{C.8}$$

$$\small{ {\mathrm{VaR}_\alpha(S)} \geq \underline{\underline{\mathrm{VaR}}}^{m,s}_\alpha := \max\left( \mu -s \text{ } \sqrt[]{\frac{1-\alpha}{\alpha}}, \underline{\underline{\mathrm{VaR}}}^{m}_\alpha \right). } \tag{C.9}$$

Replacing the information on the marginals with the information on the collective mean alongside having information on the maximum variance simplifies the scenario with no considerable loss of information for the calculation on the bounds, especially for “not-too-large” maximum variances (Bernard, Denuit, and Vanduffel 2018). The bounds derived in this scenario are known as the Cantelli bounds (Bertsimas, Lauprete, and Samarov 2004).

Theorem 7. (VaR bounds with given mean and maximum variance) Let $\alpha \in (0,1)$, $E[S]=\mu$, and $\mathrm{var}[S] \leq s^2$. Then

$$\begin{align} \underline{\mathrm{VaR}}^{\mu,s}_\alpha &:= \mu -s \text{ } \sqrt[]{\frac{1-\alpha}{\alpha}} \leq {\mathrm{VaR}_\alpha(S)} \leq \mu \\ &\quad +s \text{ }\sqrt[]{\frac{\alpha}{1-\alpha}} =: \overline{\mathrm{VaR}}^{\mu,s}_\alpha. \end{align} \tag{C.10}$$

Going back to the independent subgroups, a maximum variance assumption can be added leading to the following theorem derived in (Puccetti et al. 2017).

Theorem 8 (VaR bounds with given marginals, partial independent substructures, and variance information). Let $\alpha \in (0,1)$, $X_i \sim F_i$, and $\mathrm{var}[S] \leq s^2$. Let $\bigcup_{i=1}^{k}I_i =\{1,...,n\}$ be a partition and let $H \subset \{1,...,k\}$ and $Y_i = \sum_{j \in I_i} X_i$, . If the risk subvectors $\boldsymbol{X_{I_i}}, i \in H$ are independent, then

$$\scriptsize{ {\mathrm{VaR}_\alpha(S)} \leq \overline{\overline{\mathrm{VaR}}}^{m,pind,s}_\alpha := \min \left( \mu +s \text{ }\sqrt[]{\frac{\alpha}{1-\alpha}} , \overline{\overline{\mathrm{VaR}}}^{m,pind}_\alpha \right), } \tag{C.11}$$

$$\scriptsize{ {\mathrm{VaR}_\alpha(S)} \geq \underline{\underline{\mathrm{VaR}}}^{m,pind,s}_\alpha := \max \left( \mu -s \text{ } \sqrt[]{\frac{1-\alpha}{\alpha}}, \underline{\underline{\mathrm{VaR}}}^{m,pind}_\alpha \right). } \tag{C.12}$$

Bernard et al. (2017) offers TVaR-based bounds for the value-at-risk of the portfolio risk in the partially specified factor model with and without variance information. Indeed, the TVaR-based representation of the bounds significantly simplifies the simulation process.

Theorem 9 (VaR bounds in a partially specified factor model). Let $\alpha \in (0,1)$, $X_i \sim F_i$, $X_{i,z} \sim F_{i|z}$, and $(X_i, Z) \sim H_i$. Then

$$\small{ \begin{align} \underline{\underline{\mathrm{VaR}}}^{pf}_\alpha &:= \mathrm{VaR}_\alpha(\mathrm{LTVaR}_V(S^{c}_Z)) \leq {\mathrm{VaR}_\alpha(S)} \\ &\quad \leq \mathrm{VaR}_\alpha(\mathrm{TVaR}_V(S^{c}_Z)) =: \overline{\overline{\mathrm{VaR}}}^{pf}_\alpha, \end{align} } \tag{C.13}$$

where $V \sim U(0,1)$.

Theorem 10 (VaR bounds in a partially specified factor model with variance information). Let $\alpha \in (0,1)$, $X_i \sim F_i$, $X_i,z \sim F_{i|z}$, $(X_i, Z) \sim H_i$, and var$[S|Z=z] \leq s^2(z)$. Then

$$\scriptsize{ \begin{align} &{\mathrm{VaR}_\alpha(S)} \leq \overline{\overline{\mathrm{VaR}}}^{pf,s}_\alpha \\ &\quad := \mathrm{VaR}_\alpha \biggl( \min \bigl( \mu(z) +s(z) \text{ }\sqrt[]{\frac{V}{1-V}} , \mathrm{TVaR}_V(S^{c}_Z) \bigr) \biggr), \end{align} } \tag{C.14}$$

$$\scriptsize{ \begin{align} &{\mathrm{VaR}_\alpha(S)} \leq \underline{\underline{\mathrm{VaR}}}^{pf,s}_\alpha \\ &\quad := \mathrm{VaR}_\alpha \biggl( \max \bigl( \mu(z) -s(z) \text{ } \sqrt[]{\frac{1- V }{V}}, \mathrm{LTVaR}_V(S^{c}_Z) \bigr)\biggr), \end{align} } \tag{C.15}$$

where $V \sim U(0,1)$ is independent of $Z$ and $\mu(z) = E[S|Z=z]$.

In most situations, we can be sure about the range of values of the portfolio loss—e.g., we know that the portfolio loss is nonnegative or we have information on the minimum and maximum loss. We start by presenting the VaR bounds for a nonnegative portfolio loss of which we can trust only the mean (Bernard, Rüschendorf, and Vanduffel 2017). These bounds are straightforward to prove and are very wide; hence they are useful only for comparative purposes.

Theorem 11 (VaR bounds for nonnegative random variables with given mean). Let $\alpha \in (0,1)$, $E[S]=\mu$, and let $S$ be nonnegative. Then

$$\begin {align} \underline{\mathrm{VaR}}^{+, \mu}_\alpha &:= 0 \leq {\mathrm{VaR}_\alpha(S)} \leq \frac{\mu}{1-\alpha} \\ &=: \overline{\mathrm{VaR}}^{+, \mu}_\alpha. \end{align} \tag{C.16}$$

The following theorem, derived in Bernard, Denuit, and Vanduffel (2018), presents the VaR bounds in a scenario where we know the range of values of the portfolio loss, the collective mean, and the maximum value of some higher moments. The idea of considering a maximum value for the moments instead of the exact values accounts for the statistical uncertainty of the moments estimation.

Theorem 12 (VaR bounds with a given range of portfolio values, mean, and maximum moments). Let $\alpha \in (0,1)$, $E[S]=\mu$, and $E[S^k] \leq d_k$ for $k = 2, 3,...,r$. If $S$ is valued in $[a,b]$ then

$$\begin{align} \underline{\mathrm{VaR}}^{ab,\mu, d_k}_\alpha &:= \mu -\psi \frac{1-\alpha}{\alpha} \\ &\quad \leq {\mathrm{VaR}_\alpha(S)} \leq \mu + \psi \\ &=: \overline{\mathrm{VaR}}^{ab,\mu, d_k}_\alpha, \end{align} \tag{C.17}$$

where $\psi$ is the maximum value in the interval $\left[ 0, \mathrm{min} \left\{b-\mu, (\mu - a)\frac{\alpha}{1-\alpha} \right\} \right]$ such that the inequalities

$$(\mu + \psi)^k (1-\alpha) + \left( \mu - \psi \frac{1-\alpha}{\alpha} \right)^k \alpha \leq d_k\tag{C.18}$$

hold for $k=2,...,r$.

In many practical situations, the first two moments of the individual risks can be trusted. Incorporating this information leads to the bounds derived in Bernard, Denuit, and Vanduffel (2018) and presented in the following theorem.

Theorem 13 (VaR bounds with a given range of portfolio values, mean, maximum portfolio loss moments, and first two individual moments). Let $\alpha \in (0,1)$, $E[S]=\mu$, $E[X_i]=\mu_i$, var$[X_i]=v_i^2$, $E[S^k] \leq d_k$ for $k = 2, 3,...,r$. If $S$ is valued in $[a,b]$ then

$$\scriptsize{ {\mathrm{VaR}_\alpha(S)} \leq \overline{\mathrm{VaR}}^{ab,\mu, d, im}_\alpha := \mathrm{min} \left( \mu + \psi, \mu + \sum_{i=1}^{n} v_i \text{ } \sqrt{\frac{\alpha}{1-\alpha}} \right), } \tag{C.19}$$

$$\scriptsize{ \begin{align} {\mathrm{VaR}_\alpha(S)} \geq \underline{\mathrm{VaR}}^{ab,\mu, d,im}_\alpha &:= \mathrm{max} \biggl( \mu -\psi \frac{1-\alpha}{\alpha}, \\ &\qquad \quad \mu - \sum_{i=1}^{n} v_i \text{ } \sqrt{\frac{1-\alpha}{\alpha}} \biggr), \end{align} } \tag{C.20}$$

where $\psi$ is the maximum value in the interval $\left[ 0, \mathrm{min} \left\{b-\mu, (\mu - a)\frac{\alpha}{1-\alpha} \right\} \right]$ such that the inequalities

$$(\mu + \psi)^k (1-\alpha) + \left( \mu - \psi \frac{1-\alpha}{\alpha} \right)^k \alpha \leq d_k \tag{C.21}$$

hold for $k=1,...,r$.

Most distributions used in financial and insurance risk modeling are unimodal by nature, as unimodality is a very common feature in real-world insurance data sets. Bernard, Kazzi, and Vanduffel (2020) derives VaR bounds for unimodal distributions with given mean and variance.

Theorem 14 (VaR upper bounds for unimodal distributions with given mean and variance).

Let $\alpha \in (0,1)$, $E[S]=\mu$, and $\mathrm{var}[S] \leq s^2$, and let $S$ be unimodal. Then

$$\scriptsize{ {\mathrm{VaR}_\alpha(S)} \leq \overline{\mathrm{VaR}}^{u,\mu,s}_\alpha := \left\{ \begin{array}{cl} \mu + s \text{ }\sqrt[]{\frac{4}{9(1-\alpha)}-1} \ \ \text{for }\alpha \in [5/6, 1), \\ \mu + s \text{ }\sqrt[]{\frac{3\alpha}{4-3\alpha}} \ \ \ \ \ \ \ \ \text{for }\alpha \in (0, 5/6), \end{array} \right. } \tag{C.22}$$

$$\scriptsize{ {\mathrm{VaR}_\alpha(S)} \geq \underline{\mathrm{VaR}}^{u,\mu,s}_\alpha:= \left\{ \begin{array}{cl} \mu - s \text{ } \sqrt[]{\frac{1-\alpha}{1/3+\alpha}} & \text{for }\alpha \in (1/6, 1), \\ \mu - s \text{ }\sqrt[]{\frac{4}{9\alpha} -1} & \text{for }\alpha \in (0, 1/6]. \end{array} \right. } \tag{C.23}$$

Taking into account the nonnegativity of the portfolio loss, Bernard, Kazzi, and Vanduffel (2020) derive the following analytical bounds.

Theorem 15 (VaR upper bounds for nonnegative unimodal distributions with given mean and variance). Let $\alpha \in (0,1)$, $E[S]=\mu$, and $\mathrm{var}[S] \leq s^2$, and let $S$ be nonnegative unimodal. Then

$$\scriptsize{ \underline{\underline{\mathrm{VaR}}}^{+,u,\mu,s}_\alpha := \mathrm{max}\left(\underline{\mathrm{VaR}}^{u,\mu,s}_\alpha , 0 \right) \leq {\mathrm{VaR}_\alpha(S)} \leq \overline{\mathrm{VaR}}^{+,u,\mu,s}_\alpha, } \tag{C.24}$$

where

$$\scriptsize{ \overline{\mathrm{VaR}}^{+,u,\mu,s}_\alpha := \left\{ \begin{array}{cl} \frac{\mu}{2(1-\alpha)} & \text{for } (\alpha;s) \in A_1, \\ \frac{3}{8}\mu \bigl( - 3 \left(\frac{s}{\mu} \right)^4 (1-\alpha) \ + \\ 2 \left(\frac{s}{\mu} \right)^2 (3 \alpha-1) +3 \alpha+1\bigr) & \text{for } (\alpha; s) \in A_2, \\ \mu + s \text{ }\sqrt[]{\frac{4}{9(1-\alpha)}-1} & \text{for } (\alpha; s) \in A_3, \\ \frac{2\mu}{2-\alpha} & \text{for } (\alpha; s) \in A_4, \\ \mu + s\text{ }\sqrt{\frac{3 \alpha}{ 4 - 3\alpha}} & \text{for } (\alpha; s) \in A_5, \end{array} \right. } \tag{C.25}$$

in which

$$\small{ \begin{aligned} A_1&= \left[ \frac{2}{3},1 \right) \times \left [\mu \text{ } \sqrt{\frac{\alpha -\frac{1}{3}}{1-\alpha}}, +\infty \right ),\\ A_2&= \left[ \frac{5}{7} , 1 \right) \\ &\quad \times \left[ \mu \text{ } \sqrt{ \frac{\alpha -\frac{5}{9}}{1-\alpha}}, \mu \text{ }\sqrt{\frac{\alpha -\frac{1}{3}}{1-\alpha}} \right) \cup \left[ \frac{2}{3} ,\frac{5}{7} \right) \\ &\quad \times \left[\mu \text{ } \sqrt{\frac{3 \alpha - 1 - 2 \sqrt{\frac{3\alpha - 2}{2-\alpha}}}{3(1-\alpha)}}, \mu \text{ }\sqrt{\frac{\alpha -\frac{1}{3}}{1-\alpha}} \right ),\\ A_3 &= \left[ \frac{5}{6},1 \right) \\ &\quad \times \left [0 , \mu \text{ } \sqrt{\frac{\alpha -\frac{5}{9}}{1-\alpha}}\right ) \cup \left[ \frac{5}{7}, \frac{5}{6} \right) \\ &\quad \times \left [\mu \text{ } \frac{\alpha}{2-\alpha} \sqrt{\frac{9 (1 - \alpha)}{9\alpha -5}} , \mu \text{ } \sqrt{\frac{\alpha -\frac{5}{9}}{1-\alpha}}\right ),\\ A_4 &= \left[ \frac{5}{7}, \frac{5}{6} \right) \\ &\quad \times \left [ \mu \text{ }\frac{\sqrt{\alpha \left(\frac{4}{3} - \alpha \right)}}{2-\alpha}, \mu \text{ } \frac{\alpha}{2-\alpha} \sqrt{\frac{9 (1 - \alpha)}{9\alpha -5}} \right ) \\ &\quad \cup \left[ \frac{2}{3} ,\frac{5}{7} \right) \\ &\quad \times \left[ \mu \text{ }\frac{\sqrt{\alpha \left(\frac{4}{3} - \alpha \right)}}{2-\alpha}, \mu \text{ } \sqrt{\frac{3 \alpha - 1 - 2 \sqrt{\frac{3\alpha - 2}{2-\alpha}}}{3(1-\alpha)}} \right ) \\ &\quad \cup \left( 0 , \frac{2}{3} \right) \times \left[ \mu \text{ }\frac{\sqrt{\alpha \left(\frac{4}{3} - \alpha\right)}}{2-\alpha}, \infty \right),\\ A_5 &= \left( 0 , \frac{5}{6} \right) \times \left[0 , \mu \text{ } \frac{\sqrt{\alpha \left(\frac{4}{3} - \alpha\right)}}{2-\alpha} \right). \end{aligned} }$$

In heavy-tailed portfolios, the variance is sometimes large enough to be considered theoretically infinite. To treat that particular scenario, Bernard, Kazzi, and Vanduffel (2020) proved the following theorem.

Theorem 16 (VaR upper bounds for nonnegative unimodal distributions with given mean and infinite variance).

Let $\alpha \in (0,1)$ and $E[S]=\mu$. Let $\mathrm{var}[S]$ be infinite and let $S$ be nonnegative unimodal. Then

$$\small{ \begin{align} \underline{\underline{\mathrm{VaR}}}^{+,u,\mu,h}_\alpha &:= 0 \leq {\mathrm{VaR}_\alpha(S)} \leq \overline{\mathrm{VaR}}^{+,u,\mu,h}_\alpha \\ &:= \left\{ \begin{array}{cl} \frac{\mu}{2(1-\alpha)} & \text{for } \alpha \in \left [ \frac{2}{3},1 \right),\\ \frac{2\mu}{2-\alpha} & \text{for } \alpha \in \left ( 0, \frac{2}{3} \right ). \end{array} \right. \end{align} } \tag{C.26}$$