1. Introduction
The first significant catastrophe bond was issued in 1994. During the next quarter century, the market has evolved and grown more than USD45 billion in outstanding catastrophe bonds with more than USD10 billion new issuances per year. Today catastrophe bonds cover hundreds of sponsors for a wide range of perils. The basic mechanics of catastrophe bonds are described in Cummins (2008), Cummins and Trainar (2009), and Cummins and Barrieu (2012). The website www.artemis.bm provides a wealth of relevant, up-to-date information about the market and individual issues.
The problem of pricing a catastrophe bond is a subset of insurance risk valuation, which is a vast and complicated topic. The complication stems in part from different objectives. Babbel, Gold, and Merrill (2002) summarize three approaches to valuation via (1) adjusting the discount rate, (2) adjusting event probabilities, or (3) adjusting cash flows. Within these approaches, some determine general or partial equilibrium insurance market prices under specific conditions (Borch 1962; Meyers 1996). Many authors assume a complete market setting for insurance risk, which produces a “magic pricing machine” risk-adjusted measure, method (2), and then focus on allocating the costs of market frictions; see Phillips, Cummins, and Allen (1998), Myers and Read (2001), Sherris (2006), and Ibragimov, Jaffee, and Walden (2010). These models are silent about how the adjusted measure is determined. Another approach suggests the actuary can be most useful just focusing on the present value of insurance liabilities (Babbel and Merrill 1998) and avoiding the “slippery slopes that surround the quagmire of equity valuation” (Babbel 1997). Philosophically we follow Babbel’s advice.
Cox and Pedersen (2000), Tilley (1997), and Jarrow (2010) all provide a general valuation methodology for catastrophe bonds. Cox and Pedersen assume that financial aspects of a bond, which drive discounting, are independent from the catastrophe components, producing a pricing formula that is risk adjusted in discount but objective in cat. Jarrow produces a “simple closed form solution” using market-observable interest rate inputs and two critical inputs: the likelihood of an event triggering the bond and the loss given default. His formula is an intricate four-part expression. Beer and Braun (2019) turns Jarrow’s formula around and suggest that bond default intensities should be derived from market pricing.
The existing approaches to analyzing catastrophe bond pricing generally apply inferential statistical models to a database of observed prices using bond, sponsor, and market explanatory variables; see Braun (2016) for a very thorough recent example and Major (2019) for a general survey and critique.
In this paper we do four things.
First, we apply two simplifications to catastrophe bond pricing formulas. The first relates to multiyear contracts. A catastrophe bond is a multiyear contract with variable premium and loss. Property casualty actuaries usually price products with a single-year premium and are generally not concerned with expected premium over multiple years. Life actuaries, in contrast, work with multiyear contracts and have developed a useful equivalence principle for pricing: the expected present value of premiums should equal the expected present value of losses (plus expenses) (Jewell 1980). Explicitly separating premium and loss cash flows and valuing each separately, understanding they are driven by a common peril, produces a transparent and understandable pricing formula. The second simplification results from identifying the economically meaningful cash flows as exactly those of a fully continuous term life insurance policy. This involves realizing the collateral cash flows have no economic significance when collateral is held in a market-priced instrument. The LIBOR adjustments in Jarrow’s expressions do not apply to more recent catastrophe bonds that use a Fed Funds money market instrument as a collateral account. The result is a pricing formula expressed in terms of standard actuarial life insurance and annuity notation (Dickson, Hardy, and Waters 2015), which can be understood by any actuary.
Second, we extend the Cox and Pedersen (2000) pricing model to allow catastrophe risk to be explicitly priced, in an incomplete market setting, by adjusting the event intensity process. In general such an adjustment is not unique, which is what makes the market incomplete. For Poisson processes, this is well known to be the case (Delbaen and Haezendonck 1989). We split the event intensity process into an annual rate variable and an event time distribution, which varies by hazard type. The latter reflects the seasonality of perils such as U.S. hurricanes or EU winter storms. We estimate the distribution for U.S. hurricane from a database of events since 1851. We argue the event time distribution component should be estimated objectively from historical data and meteorological studies and should not have a market risk adjustment. This leaves the annual rate as a free market-determined variable. In a more general setting, the rate is replaced by the distribution of size of loss, allowing a further degree of freedom. We assume that the size of loss distribution is fixed and only the rate varies. Thus, our model is midway between a fully comprehensive model and the Cox model.
Third, we show how the issue price of a seasonal-peril bond varies with its effective date through the year and how the future value of the bond also varies. The variation depends on the objective event time distribution. We show bond prices for U.S. hurricane vary as much 10 percent depending on effective date, with bonds issued furthest from peak event intensity priced the cheapest. Implied secondary market prices vary in the same way and by similar amounts. We show how this variation could be neutralized if the bond paid a variable coupon that is proportional to the event time distribution. The seasonal nature of catastrophe bonds provides an interesting application of the Doob-Meyer decomposition in the derivation of a risk-neutral event intensity equivalent martingale measure. The adjustment is analogous to adjusting the return on a stock in the Black-Scholes model, with seasonal event intensity taking the place of the constant risk-free rate. It also provides an interesting example of an inhomogeneous Poisson process. Life actuaries use these models for survival distributions, where the process has an increasing hazard rate reflecting increased mortality with aging. Casualty actuaries typically assume a constant hazard rate, or an underlying Markov model wherein insureds can switch state, for example, moving from preferred to nonstandard, but with a constant rate within each cell. Catastrophe bonds provide an example wherein the hazard rate varies in a predictable way throughout the year: there are no U.S. hurricanes in the winter or European winter storms in the summer.
Fourth, we show the base model produces a flat term structure of bonds. Some studies have suggested there is an increasing term structure in market and secondary market prices. We consider whether market anticipation of secular intensity increases from climate change or whether asymmetric price fluctuations in the reinsurance and catastrophe bond market could produce an upward-sloping term structure. The former can; the latter are unlikely to.
The paper demonstrates the power and simplicity of applying life contingencies methods and notation to a problem from an orthogonal, property-casualty (P&C) domain. It highlights the synergies between property casualty and life insurance actuarial practice groups and shows the benefits of a broad and general actuarial education.
The remainder of the paper consists of four sections presenting the pricing formula, the annual rate/event time distribution model, the impact of seasonality on bond prices and values, and a brief discussion of the term structure.
2. Pricing formula
A catastrophe bond is structured as a single reinsurance contract written by a fully collateralized special purpose vehicle (SPV) reinsurer. The investor funds the SPV. The SPV invests the collateral in low-risk instruments with all income passed back to the investor. The sponsor pays the investor an additional risk premium interest spread, or coupon. The coupon is the price of the reinsurance protection provided by the bond, so we refer to it also as the price of the bond. Bonds are typically written for a 2- to 5-year term to lower average fixed transaction expenses.
Excluding expenses, there are six cash flows on an year occurrence catastrophe bond. The timing of each cash flow is either fixed or a function of a random variable giving the waiting time until the first claim. Cash flows are from the investor’s perspective; indicates a flow to/from the investor. The cash flows are shown in Table 1.
In life contingency mathematics, is the future lifetime random variable. It depends on the age of the insured at issue and is denoted by We will use to denote the date the bond is issued. We will give a stochastic model for later, once we have seen how it can be used to simplify the cash flows.
In the event of a claim, steps 4 and 5 are obviously netted against one another to provide the sponsor full assurance of being paid and to remove all credit risk. Since catastrophe bonds tend to cover large, industrywide events, sponsors are especially sensitive to counterparty credit risk, and the collateralization of a catastrophe bond distinguishes it from traditional reinsurance. However, from an economic perspective, the funding of the collateral account is meaningless: it does not change the contractually agreed cash flows. It is less well appreciated that the SPV also protects the investor from the possibility of sponsor default. If collateral funds were passed directly to the sponsor, then they could become intermingled with other assets, and the investor could lose priority. Employing an SPV ensures this does not occur.
Today, almost all catastrophe bonds follow New York Regulation 114 Trust guidelines, which require the collateral be invested in cash, a bank CD, U.S. federal or state government obligations, or similar highly rated instruments. A Fed Funds money market account is very common. It can be regarded as paying the risk-free rate. Pre-2008 bonds used a more complex arrangement involving a floating-fixed LIBOR total return swap backed by an investment bank; see Cummins (2008, Figure 1). These complicated structures are a testament to the sales prowess of investment bankers since they lower the credit quality of the collateral and increase fees. Four Lehnmann-backed bonds defaulted in 2008 (Beer and Braun 2019). This irrational behavior has now ceased. As a result, the collateral account earns a market-based risk-free rate Let be the corresponding force of interest. For simplicity we assume is fixed.
Catastrophe bonds can be regarded as paying interest continuously since interest is due up to the date of a claim even if interest is actually remitted quarterly. Any claims are settled as soon as practical and can also be regarded as settling at the date of the claim. In the language of life insurance, the bond is fully continuous.
Assume the investor incurs no additional frictional costs from funding the collateral trust account: the account earns a market-risk-free return, and the investor is indifferent between holding assets inside or outside the trust. If other investors voluntarily hold the collateral instrument, there can be no cost to do so. As a result, the cost of posting collateral, when the interest is credited back to the investor, is zero. Formally: the present value of market-driven risk-free interest paid continuously until time plus return of principal at equals the amount of principal, for all This holds even if the rate of interest is not constant. However, for simplicity, we assume a constant rate. We can demonstrate this equality as follows. Assume principal of 1. The interest is a continuous annuity at rate which has a present value Return of collateral at has a present value Thus, the sum equals 1.
We will use the actuarial equivalence principle (Jewell 1980) to determine the required premium rate. To understand what the equivalence principle says and how it is appropriate for catastrophe bonds, we need to start by comparing P&C and life insurance.
P&C insurance writes short-duration contracts, usually with a 6-month or 1-year term. A rate is an estimate of the expected value of future costs, where costs can include a profit provision. The premium rate is usually fixed, and there is no premium uncertainty.
Life insurance writes long-duration contracts with fixed premiums over a number of years. A premium is redundant in early years and deficient in later years because mortality increases with age and the policy provides intertemporal smoothing for the insured. The actual premium collected by the insurer is random: it is a function of the random future lifetime of the insured. The benefit payment or face value amount is usually known with certainty. There is timing risk. Thus, life policies have considerable premium risk and much less present value amount risk; in contrast, P&C polices have no premium risk but considerable amount risk. To accommodate these differences, the equivalence principles require at issue that the expected present value of premiums equals the expected present value of benefits plus expenses. We use the equivalence principle to determine premium rates for catastrophe bonds to account for the uncertainty in the amount of premium collected.
An obvious objection to using the equivalence principle is the apparent absence of a risk load in expected present values. How can it be appropriate that premium for a highly volatile, one-off catastrophe bond not include a risk load? The resolution is that expected value does not imply actuarial, or objective, expected value. Instead, we can use a risk-adjusted expected value. Life actuaries regularly add implicit risk loads through the use of margins, via conservative mortality and interest crediting assumptions. More generally, financial economics says that arbitrage-free prices are given by expected values with respect to a set of risk-neutral, adjusted probabilities. Actuarial probabilities are usually denoted and risk-neutral probabilities The two probabilities are required to agree on the set of possible and impossible events (they are equivalent measures). is used to compute actuarial loss costs or pure premiums. is used to compute a risk-loaded loss cost, i.e., a technical premium net of expenses. adds a risk load by making bad outcomes more likely and good ones less likely. For example, the Black-Scholes formula does this by lowering the expected return on a stock to the risk-free rate. When we apply the equivalence principle to price catastrophe bonds, we use risk-adjusted probabilities to include a risk load. The use of risk-adjusted probabilities to price catastrophe bonds is standard in the literature (Jarrow 2010). We will discuss the details of the adjusted probability below; for now, assume that the expectation operator is applied using an appropriate probability.
With that background, we apply the equivalence principle. Recall is the spread paid by the sponsor to the investor, is the face amount of the bond, is the loss given default random variable, and is the size of loss distribution. Table 2 provides formulas for the present value of each flow at issue as functions of
Adding up all six flows shows
PV at issue=(cˉa¯Tx∧n|−Ye−δ(Tx∧n)1Tx<n)L.
As we have already discussed, flows 1, 2, 4, and 6 net to zero.
Now apply the expectation operator over outcomes and the equivalence principle to see
Expected PV at issue=0=(cˉaTx,¯n|−E[Ye−δ(Tx∧n)1Tx<n])L.
If and are independent then E[Ye−δ(Tx∧n)1Tx<n]=E[Y]ˉATx,¯n| and Eq. 1 simplifies to
c=E[Y]ˉATx,¯n|ˉaTx,¯n|,
which is the net premium rate for a fully continuous year term life with face value Note is a rate per dollar of cover.
If and are not independent, the rate can be written
c=E[Y]ˉATx,¯n|+Cov(Y,e−δTx1Tx<n)ˉaTx,¯n|.
Some recent bonds include a guarantee of the first-year premium. This can be incorporated into our framework by replacing the present value premium factor with the present value of a 1-year guaranteed, -year continuous annuity, which in standard notation has value
Before proceeding, we briefly consider the impact of frictional and transaction costs.
Cummins (2000) explains that investors can incur frictional costs when they invest in an insurance entity, in this case the SPV reinsurer. He highlights double taxation, principal agency problems with management, and regulatory restrictions as the three most important. Double taxation occurs when an insurer’s income is taxed before stock dividends are paid and the investor is further taxed on dividend income. Catastrophe bonds are careful to avoid this possibility by choice of a tax-free domicile for the SPV. The SPV has no management: all its actions are contractually specified with no discretion allowed. As a result, there are essentially no principal agent problems. Finally, regulatory issues are largely avoided because the SPVs are unregulated entities. Catastrophe bonds are carefully and deliberately structured to reduce frictional costs of capital as close to zero as possible.
Investors could still incur a small frictional cost driven by regulatory restrictions (New York Regulation 114 Trust guidelines) on assets in the collateral account. These restrictions can result in suboptimal portfolios or lost liquidity. The related costs can be modeled as a continuously payable tax on assets with instantaneous rate per year. With frictional costs, the equivalence principle gives cˉax:¯n|=E[Y]ˉA1x:¯n|+τˉax:¯n| and so c=E[Y]ˉA1x:¯n|ˉax:¯n|+τ. Frictional costs are equivalent to a variable expense proportional to the face value.
Finally, issuing the bond may result in transaction expenses. These are generally fixed costs related to setting up the SPV and intermediation costs. They are easily modeled in the same way as initial selling expenses in life insurance. If the total expenses are then the revised price is c=E[Y]ˉA1x:¯n|+Eˉax:¯n|.
Frictional and transaction costs are not analyzed further owing to the relative ease with which they can be incorporated into the pricing formula. We assume below.
3. The event intensity process
In order to calculate the premium rate in Eq. 1, we must specify and estimate a model for the time until a claim for a bond written with effective date a fraction of a year after January 1. We use an inhomogeneous Poisson point process, a standard approach; see Cox and Pedersen (2000), Jarrow (2010), Braun (2011). This means there is an an intensity rate process (what life actuaries call the force of mortality) and that
Pr(Tx>t)=(tpx=exp(−∫t0λx+sds).
We start by estimating objectively -measure) based on the historical record and then discuss a market risk adjustment -measure) to match market prices.
The event rate for an individual bond is derived from the annual ground-up event rate and the probability of attaching. There is a distribution of insured event sizes given by where is the occurrence event loss distribution. is sometimes called the exceeding probability distribution (Mitchell-Wallace et al. 2017). Therefore, the event rate for a bond attaching at is given by where is the ground-up rate. When we discuss the event rate for a specific bond, we assume it has been adjusted for the bond’s attachment point.
Earthquake events are often modeled using a constant hazard intensity Anagnos and Kiremidjian (1988) state constant intensity models are popular because of their simplicity, the small number of parameters, and the ease of combining hazards. Eq. 2 yields the hazard intensity. Equating with the market price and adjusting for allows us to interpret as a risk-adjusted market loss intensity. Comparing to the estimated objective probability of first loss for the bond gives the loss multiple which is a common pricing benchmark.
Event intensity is more interesting for bonds covering seasonal perils. The most important seasonal peril, indeed the single most important peril for reinsurance markets, is U.S. hurricane exposure. In addition to U.S. and EU winter storms, U.S. severe convective storms, Japanese and Australian typhoons, and U.S. wildfires are all seasonal. Because of their significance to the catastrophe bond market, we focus on U.S. hurricanes.
We model as where is the annual event rate estimated using information available at time 0 and is the event time distribution. Time is measured in years. Seasonality means that i.e. is 1-periodic. The annual event rate estimate can evolve over time, and therefore may not be 1-periodic. With this specification, the events are generated by a time-inhomogeneous Poisson process. The probability there are no events between and given no events up to equals
Table 3 shows the number and distribution of landfalling U.S. hurricanes by month. It shows the empirical ground-up event intensity. There have been 292 hurricane landfalls between 1851 and 2018. or an average of 1.74 per year. More than 60 percent occur in August or September, and none have occurred between December and April. It also shows the distribution of major, Saffir-Simpson category 3-5, hurricanes by month. Figure 1 shows a kernel density smoothing of the event density along with a rug plot of the underlying data. The kernel uses a bandwidth factor of 0.5, selected judgmentally. The 1-periodic event density corresponding to an event intensity process is
The impact of seasonality on the survival time (time to event) of the bond is shown in Figure 2. There is no chance of an event from December through April, corresponding to the flat portion of the blue line. But the period from April through November has much higher risk (steeper line). Survival probabilities over a full year are the same as a constant hazard rate (orange line) : the lines cross at Similar phenomena occur with human mortality, where winter illnesses such as influenza cause mortality to vary through the year.
When is a risk-adjusted process, we argue the adjustment is captured in and leaves the temporal event frequency density unchanged. The rationale for this is simple. Risk-adjusted processes capture overall market risk aversion and are driven by a consistent marketwide consensus on good and bad outcomes. The risk-adjusted probability measure lowers the probability of the good outcomes and raises the probability of the bad ones. For catastrophe bonds, all market participants recognize a high annual event rate as bad, so under a risk-adjusted measure, will increase. However, there is no corresponding consensus for the event time distribution. Shifting the average time of an event forward is good for bond holders with effective dates prior to peak intensity because it puts them further from loss. But it is bad for holders with later effective dates because they move closer to loss. Therefore, we model the risk-adjusted event process as The annual rate is adjusted, but the event time distribution is estimated objectively from the data in Table 3.
It is important to realize that the adjustment from to actually combines two parts: the base event rate and the exceeding probability distribution The market could take a different view of overall event frequency at a given point in time and of the size of those events. Delbaen and Haezendonck (1989) show there are infinite ways of adjusting a compound Poisson distribution to another compound Poisson, all producing an equivalent martingale measure. This reflects the fact that the underlying market is incomplete: all equivalent measures produce arbitrage-free pricing, but there is no unique way to choose between them. The situation is in contrast to the Black-Scholes model, wherein there is a unique way of adjusting a stock price process to have the risk-free return. The difference is driven by the fact that the standard deviation of a Brownian motion is known with certainty after observing it for any short period of time. In contrast, no aspect of a Poisson process is known after observing it for a short period of time since generally there are no events! This is why insurance pricing is theoretically more difficult than asset pricing.
Going forward, we will assume where is either an actuarial (objective) annual event intensity or a risk-neutral market price implied intensity for the bond and is the objective estimated 1-periodic hazard density at time given in Figure 1. In real applications, and will be chosen appropriately for the bond being analyzed, perhaps considering only major hurricanes or those making landfall in a particular geography. The rate reflects the bond’s attachment probability.
4. The impact of varying event intensity on price and value
This section determines the impact of seasonal event intensities on price, i.e., coupon, and value as a function of effective date and valuation date. The term is an integer number of years. Fix the annual event rate so where is a 1-periodic event time distribution. From Eq. 2, we need to compute the benefit and annuity present value factors We continue to assume is independent of the other variables. A more sophisticated model could consider different densities by event intensity, each with a different distribution. Figure 1 suggests the distribution of major hurricanes is more clustered in August-October. This will make the timing effects reported in this section more pronounced for higher attaching bonds, which are more likely to be triggered by major events.
By conditioning on surviving through the first year and iterating ˉax:¯n|=ˉax:¯1|+(1Exˉax+1:¯n−1|=(1+(1Ex+⋯+(n−1Ex)ˉax:¯1|, where is the -year deferral factor (pure endowment) for both time and survival, ˉax:¯1|=∫10e−δs(spxds is the value of a 1-year, continuous temporary annuity, and (npx=exp(−λ∫n0μx+sds)=exp(−nλ∫10μx+sds)=pnx. With this model, for integer (tEx=((1Ex)t. Therefore ˉax:¯n|=1−((1Ex)n1−(1Exˉax:¯1|, and similarly ˉA1x:¯n|=1−((1Ex)n1−(1ExˉA1x:¯1|. As a result the indicated price for a bond with effective date is
cx=EY]ˉA1x:¯1|ˉax:¯1|,
irrespective of the (integer) term. However, the price varies with Bonds written in May-September will have a higher than those written on January 1 because they are closer to the peak of the hurricane season, reducing the present value of premium income and increasing the present value of loss. Our formula allows us to quantify the impact of this important timing effect, which has not appeared in the literature before as far as we know. For example, effective date is not considered a factor in Braun (2015). Note that the economic cost of the bond is independent of the effective date; just the coupon price varies.
The results are shown in Figure 3 for a representative bond with risk-adjusted event intensity (the median price for U.S. hurricane bonds issued between 1997 and May 2017) and Remember the difference between ground-up frequency of 1.74 in the previous section and here reflects the bond attachment point as well as the risk adjustment. The left plot shows the expected present value of benefits as a function of the effective date in years, The middle shows the expected present value of coupon factor The right shows the price The plot assumes for simplicity. The assumption holds exactly for an Industry Loss Warranty. For catastrophe bonds, the expected loss to the layer is often 80 percent or more of the probability of first loss, indicating the distribution of is skewed toward 1.
The top panel of Table 4 shows the price for and at January, April, May, June, and July 1, which are the most common U.S. hurricane bond effective dates, and November 1, which is close to the “cheapest” issue date. The selected values of are the 20th, 40th, 60th, 80th, and 90th percentiles of U.S. hurricane catastrophe bond pricing spreads between 1997 and May 2017. Recall, if is constant, then irrespective of term.
The middle panel shows the difference in price compared to a November 1 issue, and the bottom panel shows the change, For a low-risk bond with the price varies by 16 basis points when (21 basis points when representing 3.59 (4.72) percent of the lowest price. For a high-risk bond with the price varies by 142 (159) basis points, representing 9.79 (10.99) percent of the lowest price. These ranges are material for sponsors. When bonds are marketed, they are given indicative price ranges. For a low-risk bond, the range may be 4.25 percent to 4.75 percent, or 50 basis points. Thus, the effective date effect is about one-third of the indicative range. For a higher-risk bond, the range may be 8 percent to 8.75 percent, and the date effect is 48 basis points, or nearly two-thirds of the indicative range.
A multiperil bond can be modeled with a multidecrement model, using a different event density for each peril. The event densities should be risk adjusted. Obviously the seasonal effect will be smaller the more evenly events are distributed throughout the year.
The exact relationship between and is surprisingly complex, with several drivers, especially for a large For a in a reasonable range, say the relationship is very close to the identity, see Figure 4. For a much larger “certain death” the trends and rationale are easier to identify; see Figure 5. As the effective date moves closer to the time of peak intensity, moves from being a concave to a convex function of since the time available to collect premium gets shorter and shorter. While the relationship is obviously always upward sloping, it is not uniformly convex or concave.
We also can compute the policy value for a bond over time, which will determine the secondary market value of the bond. The calculations and results are analogous to pricing. For example, the value of a U.S. hurricane bond will fluctuate cyclically through the year: it will be lowest near the start of the hurricane season and will reach a peak immediately after the end. For a nonseasonal bond, such as earthquake, the policy value will be constant throughout the year.
From the investor’s perspective the policy value at time after issue, is given by the expected present value of income less the expected present value of benefits[1]:
\begin{aligned} {\mathstrut}_tV &= (c + \delta) \bar a_{x+t:\overline{n-t}\kern{-1.0pt}|} + \bar A_{x+t:\overline{n-t}\kern{-1.0pt}|} -\mathrm{E}[Y] \bar A^{1}_{x+t:\overline{n-t}\kern{-1.0pt}|} \\ &= 1 + c \bar a_{x+t:\overline{n-t}\kern{-1.0pt}|} - \mathrm{E}[Y] A^{1}_{x+t:\overline{n-t}\kern{-1.0pt}|}.\end{aligned}
This is simply 1 plus the reserve for a fully continuous term life insurance. We assume that the collateral funding has already occurred at The additional 1 is the return of collateral, which is not a feature of a term life policy. As usual, is expressed per unit of limit.
If is set using the equivalence principle (or is determined by the issue price), then
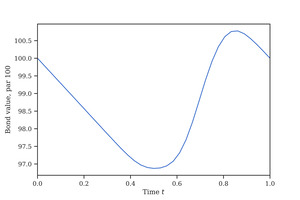
Figure 6 shows how the value of a representative bond varies throughout the year. The bond is written on January 1 with and no partial losses, At issue, the bond has par value of 100. Its value declines steadily as the peak hurricane season approaches, reaching a low point at midyear of 96.9. As the hurricane season progresses, its value recovers, peaking around November 1 at 100.8. Its average value throughout the year is 98.7, indicating a 1.3 percent liquidity haircut for investors in new issues who may need to trade out of their positions. Similarly, a bond issued on July 1 would trade above its par value for almost all the year. Thus, investors concerned about the liquidity of their bonds have a preference to invest in bonds issued closer to peak event intensity time periods.
Bearing in mind the underlying assets are in a net asset value 1 money market account, these swings represent a significant and unwelcome price variation driven solely by the underlying seasonality of the covered peril. The variation could be neutralized if the bond paid a variable coupon[2] proportional to the event time distribution With a variable coupon, the annual present value of premium factor becomes
\begin{aligned} \bar a_{x:\overline{n}\kern{-1.0pt}|} &= \int_0^1 (\mu_t e^{-\delta t})_{t}p_x \, dt \\ &= \frac{1}{\lambda} A^{1}_{x:\overline{n}\kern{-1.0pt}|}.\end{aligned}
As a result, independent of issue date and the value of the bond will be constant over time. The variable coupon corresponds to paying a constant coupon using operational time proportional to the hazard density.
Thiele’s differential equation can be used to track the evolution of the value of a bond. It reads \begin{aligned} \frac{d}{dt}{\mathstrut}_tV &= \delta\, {\mathstrut}_tV - (c + \delta) - \lambda_t(1 - \mathrm{E}[Y] - {\mathstrut}_tV),\end{aligned} where the first term is earnings on the reserve, the second premium and pass-through investment income, and the last the unfunded cost of a claim, what life actuaries call the death strain at risk. The second and third terms lower the value of the bond. Integrating this differential equation gives the same values shown in Figure 6. Integrating Thiele’s equation provides a simple and numerically efficient way of valuing bonds.
5. Term structure
The base model implies a flat term structure: varies with effective date but not with term There are two plausible mechanisms to introduce a term structure, but we argue only one would be effective.
First, the market could anticipate a change in hurricane frequency over the term of the bond caused by climate change, El Niño, or another macrodynamic weather pattern. A forward estimate of spot annual intensities can be incorporated into the model using rather than a fixed This effect could produce a nonflat pricing curve with duration. It works on the same basis as flat premium term life insurance, i.e., it becomes more expensive with increasing term because of the aging effect.
Second, there could be a concern about reinsurance market dynamics where prices jump up but drift down; therefore, locking into a fixed-price multiyear bond increases investor risk. Market dynamics following a large event can result in sudden price increases because short-term capacity shortages create sudden price shocks. A large event’s occurring close to a major renewal date could cause significant price disruption, as seen in the January 1, 2006, market following Katrina, for example. However, since properly anticipated prices fluctuate randomly (Samuelson 1965), and since does not exhibit material nonlinearities over the range of realistic (see Figure 4), this effect would not produce a term structure since Jensen’s inequality would not apply. Therefore, it is unlikely reinsurance dynamics can drive a term structure. Recent bonds have been issued with a call feature that allows the issuer to cancel at anniversary dates to capture lower market pricing. The downside for sponsors is a shorter period to amortize structuring and issuance fees. This also argues against a market-induced term structure.
6. Conclusions
A catastrophe bond’s economically meaningful cash flows are the same as a fully continuous term life insurance policy. As a result, we have a simple catastrophe bond pricing formula expressed in standard actuarial notation.
Catastrophe bonds covering seasonal perils have a periodic event intensity, so their issue price varies with effective date during the year. We quantify this variation, showing it can be more than 10 percent for the most risky bonds. We also show the current value of a seasonal bond varies during the year by more than 3 percent for a median bond, a significant swing given the collateral is in a fixed value money market fund.
A simple seasonal model produces a flat term structure. We show how a nonflat pricing yield curve can be produced by market anticipation of climate change effects but not by an asymmetric forward distribution of event intensities.
These results have implications for sponsors and investors in catastrophe bonds. Investors should prefer bonds issued closer to peak perils because they will trade at a premium for most of the year. Bonds issued further from peak intensity will trade at a discount for most of the year. This effect can be neutralized by paying a variable coupon proportional to the event time distribution.
Finally, the results are important for future studies of bond pricing as they show effective date is a material driver of pricing. Any price time series used to evaluate catastrophe bond pricing should adjust for effective date using an appropriate event time distribution.
_of_landfall_for_all_u.s._hurricanes_based_o.png)




_of_landfall_for_all_u.s._hurricanes_based_o.png)




