1. Introduction
Misrepresentation is a type of insurance fraud in which a policy applicant makes a false statement about a risk factor (or rating factor) that determines insurance eligibility or rates. In insurance ratemaking, information about certain rating factors may be acquired through self-reporting, possibly due to the high cost of verifying the information through alternative channels. For instance, in auto insurance, major rating factors such as vehicle use and annual mileage are usually self-reported by insurance applicants. In health and life insurance, information about smoking status and preexisting medical conditions is acquired mainly through voluntary disclosures. Due to the financial incentive for insureds, self-reported rating factors are usually subject to misrepresentation, giving rise to additional costs for insurance companies and unfair insurance rates for consumers.
In the era of big data, predictive analytics has attracted enormous attention from both the insurance industry and academia. In the insurance industry, predictive analytics has been widely applied in the areas of marketing, underwriting, and claims modeling (Nyce 2007). In actuarial literature, Frees, Derrig, and Meyers (2014) gave a comprehensive review of traditional statistical learning methods and their applications in actuarial science. Quan and Valdez (2018) proposed multivariate decision trees for predictive analytics of insurance claims. With the availability of big data on demographics, socioeconomic status, social media usage, and geolocation, predictive analytics has proven very useful in identifying and predicting insurance claims fraud. There are abundant examples of predictive analytics use for healthcare fraud detection (e.g., Ekin et al. 2018; Bauder and Khoshgoftaar 2017; Bayerstadler, van Dijk, and Winter 2016; Joudaki et al. 2015; and Thornton et al. 2013).
When it comes to underwriting misrepresentation, however, predictive modeling is deterred by the unobserved feature of misrepresentation at the policy level, and the literature available on quantitative methods tailored to the problem is very limited. Recently, Xia and Gustafson (2016) formulated the problem of unidirectional misrepresentation under the regression setting and proved the identifiability of the conditional distribution of the loss outcome given the observed risk status for nonbinary loss outcomes. They showed that consistent statistical inference can be obtained on the parameters of interest, including the risk effect (i.e., the relativity) and the misrepresentation probability, using regular ratemaking data without information on the misrepresentation status. For mathematical convenience, they only studied situations in which there was only one risk factor in the ratemaking models. Xia, Hua, and Vadnais (2018) extended the misrepresentation models to more realistic situations in which there were multiple risk factors in the generalized linear model (GLM) ratemaking framework. Moreover, they relaxed the assumption that the misrepresentation probability does not change with other risk factors and thus allowed for predictive analytics on the misrepresentation probability. With the aid of the aforementioned models, insurance companies can predict the misrepresentation probability at the policy level based on historical ratemaking data.
For the models’ implementation, Xia and Gustafson (2016) and Xia, Hua, and Vadnais (2018) relied on Bayesian inference based on Markov chain Monte Carlo simulations. To facilitate the industrial application of the misrepresentation models, Akakpo, Xia, and Polansky (2019) considered the maximum likelihood inference and proposed using the expectation maximization (EM) algorithm for the lognormal model from Xia and Gustafson (2016) with only one risk factor. (Maximum likelihood inference is more commonly used for GLM ratemaking models due to advantages such as computational efficiency.) Owing to the simplicity of the problem and the tractability of the normal likelihood function, they derived explicit formulas for iterating between the expectation step (E-step) and the maximization step (M-step), along with the observed Fisher information matrix for large-sample inference on the risk effect (relativity) and normal variance parameters. Recently, Chen, Su, and Xia (2021) extended the normal model and its EM algorithm to include zero claims based on a two-part process, and Li, Song, and Su (2021) proposed robust estimation of insurance misrepresentation based on kernel quantile regression mixtures. For the sophisticated misrepresentation predictive models from Xia, Hua, and Vadnais (2018), we aim to incorporate a more general exponential family of distributions under the GLM ratemaking framework. Thus, the maximum likelihood inference will be more involved and the explicit formulas from Akakpo, Xia, and Polansky (2019) will no longer be available for the EM algorithm and large-sample inference.
In this paper, we accept the challenge and use the maximum likelihood method to implement the misrepresentation predictive models from Xia, Hua, and Vadnais (2018) that allow latent binary regression on the prevalence of misrepresentation. Specifically, we introduce a set of latent binary factors on the occurrence of misrepresentation for policies reporting a negative risk status, and we derive general forms of the partial and complete data likelihood functions for the misrepresentation predictive models from Xia, Hua, and Vadnais (2018). We use the EM algorithm (Louis 1982; McLachlan and Krishnan 2008) based on the complete data likelihood function to estimate the parameters in the misrepresentation predictive models. The proposed estimation algorithm enables the frequentist predictive analytics on the misrepresentation status by allowing the prevalence of misrepresentation to vary with certain risk factors. For the sake of illustration, we implement the EM algorithm with some commonly used loss severity and frequency distributions such as the lognormal, gamma, Poisson, and negative binomial. The standard errors of the estimators are obtained for large-sample inference using numerical approximation of the Hessian matrix (Yang et al. 2005) associated with the partial data log-likelihood function. We perform simulation studies to compare the parameter estimates of the proposed EM algorithm and its Bayesian counterpart while assessing the ability of the proposed misrepresentation models to learn parameters, including the misrepresentation prevalence. The simulation studies demonstrate the computational efficiency of the EM algorithm as well as the importance of misrepresentation modeling in practical scenarios where misrepresentation is possible.
Applying the EM algorithm based on the aforementioned loss frequency and severity distributions, we perform model comparisons for the purposes of assessing misrepresentation and predicting claims at the policy level. The application study uses healthcare expenditure and utilization data from the Medical Expenditure Panel Survey (MEPS) to demonstrate the usefulness of the proposed methodology for claim prediction and misrepresentation risk assessment. The analysis obtains a statistically significant test for the presence of misrepresentation and the effects of risk factors on the prevalence of misrepresentation based on the loss severity models on total medical expenditures and the loss frequency models on the number of office-based visits. All the criteria, including goodness-of-fit statistics, in-sample and out-of-sample prediction, and statistical tests, confirm the significance of the test on misrepresentation. For insurance applications, including claims analytics and ratemaking, the application study reveals the importance of model selection in misrepresentation models used for the prediction of future losses fitted using historical data.
The rest of this paper is organized as follows: Section 2 reviews the embedded misrepresentation predictive models from Xia, Hua, and Vadnais (2018). Section 3 considers the EM algorithm for maximum likelihood estimation of the model’s parameters, including those concerning the risk effects (relativities) on the loss frequency/severity and the misrepresentation prevalence. Section 4 discusses the large-sample inference with respect to the risk effects and the misrepresentation parameters and compares models with different distribution choices. Section 5 evaluates the EM algorithm and its Bayesian counterpart based on the parameter estimates and computation speed. Section 6 applies the proposed algorithm and model comparison tools for assessing misrepresentation risk in the healthcare expenditure and utilization variables collected in the MEPS. (For the MEPS data, model validation is performed using various methods, including those commonly adopted for ratemaking models.) Section 7 concludes the paper.
2. Predictive models for misrepresentation
We first review the notation and models from Xia, Hua, and Vadnais (2018) that enable embedded predictive analytics on misrepresentation risk at the policy level based on observed data from regular ratemaking.
2.1. Misrepresentation
We first formulate the statistical problem of misrepresentation for a binary rating factor (e.g., on smoking). For the risk factor, denotes an insured with a positive risk status and denotes a negative risk status. The corresponding reported status that is subject to misrepresentation is denoted as Due to the financial incentive of denying a positive risk status, misrepresentation is assumed to happen only in the direction that is beneficial to the applicant. This unidirectional property translates mathematically to and with Here, the conditional probability is referred to as the misrepresentation probability. Thereby, the conditional probability distribution of quantifies the severity of misrepresentation.
In regular ratemaking data, the reported status is the surrogate version of the risk status that is observable. From a practical point of view, it is more meaningful for insurance companies to study the conditional distribution of (i.e., given an observed status, the true risk attribute of the insured). This conditional probability distribution can be obtained using Bayes’ theorem. Denoting by the true probability of a positive risk status, it is straightforward to obtain the observed probability of a positive risk status as
Application of Bayes’ theorem yields that is, given that an applicant reports a positive status, the true risk status must be positive. Another quantity of particular interest is the percentage of misrepresented cases within those applicants who reported a negative status. In Xia, Hua, and Vadnais (2018), the conditional probability is referred to as the prevalence of misrepresentation. Using Bayes’ theorem, the misrepresentation prevalence can be obtained as
P[V=1∣V∗=0]=λ=θp1−θ(1−p).
Note that the misrepresentation prevalence quantifies the misrepresentation risk given the reported negative status and determines the total number of misrepresented cases in the whole book of policies. Due to the unobserved feature of the conditional probability cannot be estimated directly from regular ratemaking data. Even if fraud investigations are conducted to identify the misrepresented cases, the information may not be credible for estimating the misrepresentation prevalence in the overall book of business due to the selection bias inherent in the investigation process.
2.2. GLM ratemaking
Under the GLM ratemaking framework (Bermúdez and Karlis 2011; Frees 2009; Brockman and Wright 1992), Xia, Hua, and Vadnais (2018) proposed a class of embedded predictive analytics models based on regular ratemaking data for studying misrepresentation risk. For the purpose of ratemaking, we use the random variable to denote the loss outcome that can be either continuous (e.g., for modeling loss severity on the mean of the claim amount given that a claim has occurred) or discrete (e.g., for modeling loss frequency on the average number of claims per policy period). Assume there are additional risk factors that are predictive of the loss outcome denoted by Examples of risk factors that are commonly used in personal property and casualty insurance include age, sex, credit rating, and claim history. For specific product lines such as personal auto insurance, commonly used risk factors include vehicle use, annual mileage, traffic violations, and geographic location.
In GLM ratemaking, a generalized linear model is assumed for the relationship between the mean of and the rating factors in We use the set notation to describe the sets of rating factors in the GLM ratemaking model and the misrepresentation prevalence model, respectively. Thus, we have where can be one of For a GLM ratemaking model, we may specify the conditional probability distribution of as
Y∣V,XS∼D(μV,Xs,φ)g(μV,XS)=α0+∑j∈SαjXj+αk+1V,
where denotes a distribution in the exponential family with the mean and a dispersion parameter The function is referred to as the link function that connects the mean to the linear predictor In GLM ratemaking, may take the form of a gamma or lognormal (i.e., normal for the logarithm of the loss) distribution for loss severity modeling, and it may take the form of a Poisson or negative binomial distribution for frequency models. For ease of interpretation and rate calculation, a log link function is commonly assumed in both severity and frequency models. Under a log link function, the exponential of the coefficient quantifies the relative effect on the mean of with one unit increase in the risk factor and is thus referred to as the relativity associated with Interested readers may refer to standard references such as Goldburd, Khare, and Tevet (2020) for commonly used GLM ratemaking models based on lognormal, gamma, Poisson, and negative binomial distributions. In addition, Xia, Hua, and Vadnais (2018) give examples of distributional specifications for GLM ratemaking models incorporating misrepresentation.
For the implementation of the aforementioned GLM ratemaking models, the difficulty lies in the fact that the true risk status cannot be directly observed due to the presence of misrepresentation in self-reported rating factors. Ignoring the problem of misrepresentation usually leads to bias in the estimate of the risk effect (Xia and Gustafson 2016), resulting in unfairness in the calculated premiums for consumers. Furthermore, the misrepresented status may cause the insurance company to accept high-risk customers who would be ineligible based on their true status. In order to study the severity of the misrepresentation problem and perform predictive modeling at the policy level, we consider the conditional loss distribution given the observed variables treating as a latent variable depending on
2.3. Predictive models on misrepresentation
Denote by the conditional probability function of where which contains the set of regression coefficients. In loss severity modeling, the conditional distribution function usually takes the form of the probability density function of gamma and lognormal distributions. In loss frequency modeling, the function usually takes the form of the probability mass function of Poisson and negative binomial distributions.
Regarding the conditional distribution of the observed variables, Xia and Gustafson (2016) and Xia, Hua, and Vadnais (2018) derived a general form
fY(y∣α,φ,λ,V∗=1,XS)=fY(y∣α,φ,V=1,XS)fY(y∣α,φ,λ,V∗=0,XS)=(1−λ)fY(y∣α,φ,V=0,XS)+λfY(y∣α,φ,V=1,XS),
where is the prevalence of misrepresentation defined in Equation 1 that directly determines the total number of misrepresented cases in the book of policies and thus is of particular interest to insurance companies. From Equation 1, the prevalence of misrepresentation is determined by the prevalence of the risk factor and the misrepresentation probability Note that the mixture structure in Equation 3 cannot be caused by a binary confounding factor unless individuals with a positive reported status all have the same status for this confounding factor. Here the unique feature of misrepresentation data is that the conditional distribution in the first line of Equation 3 is a single distribution instead of a mixture distribution that would typically arise in the case of a binary confounding factor not captured in the model.
Under real insurance settings, either of the probabilities may vary with certain risk factors in That is, it is reasonable to assume that the probability of a true positive status and/or the occurrence of misrepresentation depends on certain risk factors. Hence, we may assume that the prevalence of misrepresentation depends on the risk factors in This can be achieved by assuming a latent binomial regression model on For the purpose of predictive modeling on the misrepresentation prevalence, Xia, Hua, and Vadnais (2018) proposed a latent binomial regression structure given by
\begin{aligned} \left(V \mid V^*=0, \boldsymbol{X}^{\mathcal{\tau}}\right) & \sim {Bernoulli}\left(\lambda_{\boldsymbol{X}^{\boldsymbol{\tau}}}\right) \\ g\left(\lambda_{\boldsymbol{X}^{\mathcal{T}}}\right) & =\beta_0+\sum_{j \in \mathcal{T}} \beta_j X_j, \end{aligned} \tag{4}
where the prevalence of misrepresentation depends on the risk factors in and is a link function that may take the logit, log, or probit form. Here, the logit link function enables us to estimate the risk effect in terms of the odds ratio, while the log link function gives risk effect in terms of the relative risk. The parameters of the logit model, quantify the effects the additional risk factors have on the prevalence of misrepresentation and thus describe the mechanism of misrepresentation. Since the true status is unobserved, the binomial regression model in 4 is a latent model.
From Equation 3, the conditional distribution of the observed variables is a single distribution for applicants who reported a positive risk status (i.e., and it takes the form of a mixture distribution for applicants who reported a negative risk status. The mixture model in the second line of Equation 3 is called a mixture regression model (Grün and Leisch 2007) when there are additional covariates (risk factors) in the model. When the prevalence of misrepresentation (i.e., the mixture weights) depends on some additional covariates as in the case of Equation 4, the model in the second line of 3 is called a mixture of experts model (Jiang and Tanner 1999), or a mixture regression model with concomitant variables (Grün and Leisch 2008).
For distributions in the exponential family, including gamma, normal, Poisson, and negative binomial distributions, Jiang and Tanner (1999) proved that the mixture of experts model is identifiable up to permutation when the true risk factor has a nonzero effect. From the first line of Equation 3, parameters in the conditional distribution can be learned separately from the data with The permutation of the two components in the second line of 3 can be learned from the combined data, and the model given in Equations 3 and 4 thus possesses identifiability. This implies that all the parameters, including those for the risk effects on the loss distribution in Equation 2 and those for the logit model on the prevalence of misrepresentation in Equation 4, can be consistently estimated from regular ratemaking data without observing the true risk status
The estimated regression coefficients from the loss model in Equation 2 allow actuaries to understand the true risk effects on the loss outcome, while those from the misrepresentation model in Equation 4 enable actuaries to assess the prevalence of misrepresentation under the policy level for the purpose of predictive modeling. Based on the models fitted against the historical data, prediction of misrepresentation risk can be made on the new policies. The underwriting department can then undertake a cost-benefit analysis for potential misrepresentation investigations while making informed decisions on the selection of policies for investigation.
3. Maximum likelihood estimation
Because of the unobserved feature of the misrepresentation status, we may implement the misrepresentations predictive models using either Bayesian inference based on Markov chain Monte Carlo simulations or maximum likelihood inference based on the EM algorithm. Both types of implementation use the complete data likelihood function that includes the latent status on the occurrence of misrepresentation at the policy level. Compared with the Bayesian approach, the maximum likelihood method seems to have gained more popularity for ratemaking purposes in the insurance industry. Hence, in this paper, we place our special focus on the maximum likelihood inference for the predictive misrepresentation models presented in Section 2.
3.1. Partial and complete data likelihood
In order to derive the EM algorithm, we first introduce the partial and complete data likelihood for the misrepresentation models of interest. For notational convenience, we denote
\begin{aligned} f_0(y;\boldsymbol{\alpha},\,\varphi)&=f_Y(y\,|\,{\boldsymbol{\alpha},\,\varphi},V=0,\,\boldsymbol{X}^{\mathcal{T}})\notag\\ f_1(y;\boldsymbol{\alpha},\,\varphi)&=f_Y(y\,|\,{\boldsymbol{\alpha},\,\varphi},V=1,\,\boldsymbol{X}^{\mathcal{T}}).\notag \end{aligned}
Suppose there is a random sample of size for the observed variables denoted respectively by and with
Set The prevalence of misrepresentation for the th observation is and which contains the regression coefficients from the misrepresentation model 4. The partial data likelihood function can be written as
\scriptsize{ L^p\left(\boldsymbol{\theta} \mid \boldsymbol{y}, \boldsymbol{v}^*, \boldsymbol{x}\right)=\prod_{i=1}^n\left[v_i^* f_1\left(y_i ; \boldsymbol{\alpha}, \varphi\right)+\left(1-v_i^*\right) \sum_{j=0}^1 \lambda_{i j}(\boldsymbol{\beta}) f_j\left(y_i ; \boldsymbol{\alpha}, \varphi\right)\right] }, \tag{5}
with the corresponding partial log-likelihood function given by
\small{ \begin{align} l^p\left(\boldsymbol{\theta} \mid \boldsymbol{y}, \boldsymbol{v}^*, \boldsymbol{x}\right)&=\sum_{i=1}^n v_i^* \log f_1\left(y_i ; \boldsymbol{\alpha}, \varphi\right)\\ &\quad +\sum_{i=1}^n\left(1-v_i^*\right) \log \sum_{j=0}^1 \lambda_{i j}(\boldsymbol{\beta}) f_j\left(y_i ; \boldsymbol{\alpha}, \varphi\right). \end{align} } \tag{6}
In order to obtain the complete data likelihood for the EM algorithm, we need to introduce the latent status on the occurrence of misrepresentation. For observations where denote by the unobserved binary indicator on whether the th observation is misrepresented (i.e., whether the observation comes from the second component distribution). Similarly, we use to indicate whether the observation comes from the first component distribution. Denote by the vector containing all for different values of and The complete data likelihood function can be written as
\scriptsize{ \begin{align} L\left(\boldsymbol{\theta} \mid \boldsymbol{y}, \boldsymbol{v}^*, \boldsymbol{x}, \boldsymbol{z}\right) \propto \prod_{i=1}^n \biggl\{&v_i^* f_1\bigl(y_i ; \boldsymbol{\alpha}, \varphi\bigr) \\ & +\bigl(1-v_i^*\bigr) \prod_{j=0}^1\left[\lambda_{i j}(\boldsymbol{\beta}) f_j\left(y_i ; \boldsymbol{\alpha}, \varphi\right)\right]^{z_{i j}}\biggr\}, \end{align} } \tag{7}
with the corresponding complete data log-likelihood function given by
\scriptsize{ \begin{align} l\left(\boldsymbol{\theta} \mid \boldsymbol{y}, \boldsymbol{v}^*, \boldsymbol{x}, \boldsymbol{z}\right) = C &+ \sum_{i=1}^n v_i^* \log f_1\left(y_i ; \boldsymbol{\alpha}, \varphi\right)\\ &+\sum_{i=1}^n\left(1-v_i^*\right) \sum_{j=0}^1 z_{i j} \log \left[\lambda_{i j}(\boldsymbol{\beta}) f_j\left(y_i ; \boldsymbol{\alpha}, \varphi\right)\right]. \end{align} } \tag{8}
where is a constant that can be ignored for the numerical procedures in the later sections.
3.2. EM algorithm
In order to obtain the maximum likelihood estimates (MLEs) of the simplified misrepresentation models in Xia and Gustafson (2016), Akakpo, Xia, and Polansky (2019) proposed using the expectation maximization (EM) algorithm that has been commonly used for mixture models in which there are no analytical forms for the MLEs. Due to the tractability of the normal likelihood function, Akakpo, Xia, and Polansky (2019) obtained explicit forms for the iterative formulas involved in the EM algorithm. For other loss frequency and severity distributions such as the ones considered in this paper, there is no explicit form available for the iterative steps in the algorithm. Using numerical optimization methods such as the Newton-Raphson algorithm, we derive the EM algorithm for the predictive models of interest where the prevalence of misrepresentation depends on additional risk factors. The algorithm can be conveniently implemented in the statistical software R for the loss frequency and severity models mentioned previously.
3.2.1. Expectation step
In the expectation step (E-step), the algorithm calculates the expectation of the complete data log-likelihood function with respect to the conditional distribution of given the observations and the latest estimates for Specifically, in iteration we have the conditional expectation
\small{ \begin{aligned} l^*\left(\boldsymbol{\theta} \mid \boldsymbol{\theta}^{(s)}\right) & =\mathbb{E}_{\boldsymbol{z} \mid \boldsymbol{y}, v^*, \boldsymbol{X}, \boldsymbol{\theta}^{(\boldsymbol{s})}}\left[l\left(\boldsymbol{\theta} \mid \boldsymbol{y}, \boldsymbol{v}^*, \boldsymbol{x}, \boldsymbol{z}\right)\right] \\ & =\sum_{i=1}^n v_i^* \log f_1\left(y_i ; \boldsymbol{\alpha}, \varphi\right)\\ &\quad +\sum_{i=1}^n\left(1-v_i^*\right) \sum_{j=0}^1 \mathbb{E}_{z \mid y, v^*, x, \boldsymbol{\theta}^{(s)}}\left[z_{i j}\right] \\ &\quad \cdot \log \left[\lambda_{i j}(\boldsymbol{\beta}) f_j\left(y_i ; \boldsymbol{\alpha}, \varphi\right)\right], \end{aligned} } \tag{9}
where is the density function of the loss distribution evaluated at By Bayes’ theorem, we have for and
\small{ \begin{aligned} \mathbb{E}_{\boldsymbol{z} \mid \boldsymbol{y}, v^*, \boldsymbol{X}, \boldsymbol{\theta}^{(s)}}\left[z_{i j}\right] & =\mathbb{P}\left[z_{i j}=1 \mid \boldsymbol{\theta}^{(s)}, y_i\right] \\ & =\frac{f\left(y_i \mid z_{i j}=1, \boldsymbol{\theta}^{(s)}\right) \mathbb{P}\left[z_{i j}=1 \mid \boldsymbol{\theta}^{(s)}\right]}{f\left(y_i \mid \boldsymbol{\theta}^{(s)}\right)}\\ &=\frac{f_j\left(y_i ; \boldsymbol{\alpha}^{(s)}, \varphi^{(s)}\right) \lambda_{i j}\left(\boldsymbol{\beta}^{(s)}\right)}{\sum_{l=0}^1 f_l\left(y_i ; \boldsymbol{\alpha}^{(s)}, \varphi^{(s)}\right) \lambda_{i l}\left(\boldsymbol{\beta}^{(s)}\right)}, \end{aligned} } \tag{10}
where is the density function evaluated at and is the prevalence of misrepresentation at the policy level evaluated at Note that the posterior probability only appears in the second part of Equation 9, so we only need to calculate it for observations with Based on Equations 9 and 10, we can derive an explicit expression for the expected complete data likelihood function that will be used to update the parameters in the maximization step of the EM algorithm.
3.2.2. Maximization step
In the maximization step (M-step) of the EM algorithm, an update is obtained for the parameters in by maximizing the expected complete data log-likelihood in Equation 9. In iteration of the M-step, the update of the parameters is obtained by
\begin{aligned} \boldsymbol{\theta}^{(s+1)}&=\mathop{\text{argmax}}_{\boldsymbol{ \theta}}\Big[l^*\left(\boldsymbol{\theta}\,|\,\boldsymbol{\theta}^{(s)}\right)\Big]\notag\\ &=\mathop{\text{argmax}}_{\boldsymbol{ \theta}}\mathbb{E}_{\boldsymbol{z}|\boldsymbol{y},\boldsymbol{v^*},\boldsymbol{X},\boldsymbol{\theta}^{(s)}} \Big[l(\boldsymbol{\theta}\,|\,\boldsymbol{y},\boldsymbol{v^*},\boldsymbol{x},\boldsymbol{z})\Big]\notag. \end{aligned}
For the M-step, Akakpo, Xia, and Polansky (2019) derived analytical forms for the lognormal severity model when neither the loss severity nor the prevalence of misrepresentation depends on any other risk factor (i.e., when the model does not involve a logit regression structure 4, or, alternatively, when does not depend on or for any For commonly used loss frequency and severity models including Poisson, negative binomial, gamma, and lognormal models with a logit structure on the prevalence of misrepresentation, no explicit formulas can be derived for estimating the parameters in the M-step. In such situations, we may resort to numerical optimization based on Newton-type methods. For example, according to our extensive numerical experiments, the Newton-Raphson method implemented in the R function performs well for the misrepresentation predictive models based on the aforementioned loss distributions of interest.
Starting with the initial values from a regression analysis without adjusting for misrepresentation, the EM algorithm iterates between the E-step and M-step until the change in the partial data log-likelihood is below a prespecified threshold. For illustration purposes, in the Appendix, we provide the R implementation for a gamma model when does not depend on any risk factor. For the R implementation, we specify 0.4 and 0 as the default values of the starting values for the misrepresentation parameters and each element in respectively. The starting values are specified as input variables of the R functions to allow for changes when needed (e.g., for checking algorithm convergence).
4. Statistical inference and model selection
In this section, we discuss the statistical inference on the risk effects of the rating factors (including the misrepresented ones), the statistical tests on the presence and mechanism of misrepresentation, and model selection with regard to loss distributions and model structures.
4.1. Inference on risk effects
For the purpose of statistical inference on the risk effects of the rating factors, the MLEs have a large sample multivariate normal distribution with the mean converging to the true values of the parameters and the variance-covariance matrix converging to the inverse of the Fisher information matrix, which is the Hessian matrix with respect to the partial data log-likelihood function. For the lognormal loss severity model, Akakpo, Xia, and Polansky (2019) derived explicit forms of the observed Fisher information using the complete data log-likelihood function. For the predictive misrepresentation models of interest, we may evaluate the Hessian matrix of the partial data log-likelihood function using numerical derivatives. Note that numerical derivatives are widely used for obtaining the Hessian matrix in situations where the MLEs do not have explicit forms (e.g., in the case of GLM ratemaking).
Denote by the MLEs of and by the partial data log-likelihood function evaluated at The observed Fisher information evaluated at the MLEs is defined as
\small{ \mathcal{I}_n(\widehat{\boldsymbol{\theta}})=-\left(\begin{array}{cccc} \frac{\partial^2}{\partial \alpha_0^2} & \frac{\partial^2}{\partial \alpha_0 \partial \beta_0} & \cdots & \frac{\partial^2}{\partial \alpha_0 \partial \varphi} \\ \frac{\partial^2}{\partial \beta_0 \partial \alpha_0} & \frac{\partial^2}{\partial \beta_0^2} & \cdots & \frac{\partial^2}{\partial \beta_0 \partial \varphi} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{\partial^2}{\partial \varphi \partial \alpha_0} & \frac{\partial^2}{\partial \varphi \partial \beta_0} & \cdots & \frac{\partial^2}{\partial \varphi^2} \end{array}\right) l^p(\boldsymbol{\theta})|_{\boldsymbol{\theta}=\widehat{\boldsymbol{\theta}}}. } \tag{11}
When the sample size is large, the MLEs have an approximate multivariate normal distribution with being the inverse of the observed Fisher information matrix evaluated at the MLEs (i.e., Thus, for the purpose of statistical inference, the standard error of the th parameter can be approximated by the square root of the th diagonal element of Interested readers may refer to Chapter 7 of Frees (2022) for details regarding the asymptotic properties of MLEs that justify the use of the aforementioned normal distribution for large-sample inference on MLEs.
For the partial log-likelihood function in Equation 6, there are no analytical forms available for the partial second derivatives. For loss frequency and severity distributions, including Poisson, negative binomial, lognormal, and gamma distributions, we resort to numerical derivatives for obtaining the observed Fisher information for the misrepresentation predictive models that can involve a logit structure on the prevalence of misrepresentation. There are a variety of methods implemented in R that can be used to approximate the Hessian matrix. Examples include the complex-step derivative approximation (Martins, Sturdza, and Alonso 2003) implemented in the hessian() function of the numDeriv package and the hessian_csd() function implemented in the pracma package, along with various versions of finite difference approximation (Yang et al. 2005) (e.g., the Secant method in the optim() function, the Richardson’s method implemented in the hessian() function of the numDeriv package, and the three-point central difference formula in the hessian() function of the pracma package). For the misrepresentation predictive models with Poisson, negative binomial, lognormal, and gamma loss distributions, for example, the hessian() function based on the complex-step derivative approximation performs well and provides reasonable standard errors given various data generation mechanisms and in comparison with the standard errors from the corresponding unadjusted models.
Using the standard errors obtained from the observed Fisher information, we can perform statistical inference, including the Wald tests and Wald confidence intervals, on the risk effects of the rating factors that are predictive of the loss distribution and the misrepresentation prevalence.
4.2. Inference on misrepresentation
Regarding inference on the misrepresentation, our first question is whether we can construct a test to assess statistical evidence on the presence of misrepresentation based on observed data. For assessing the presence of misrepresentation, we cannot use the standard error of to perform a statistical test, as the null value lies on the boundary of the parameter space Instead, we may perform a likelihood ratio test (LRT) between the unadjusted model assuming (the null model) and the adjusted model with (the alternative model). The null model is simply a regular GLM ratemaking model that is nested within the misrepresentation model of interest with Denote by the partial data log-likelihood function (5) evaluated at the MLEs and evaluated at the MLEs obtained with the restriction The LRT statistic is given by
G^2=2(l^p_a-l^p_0).
For mixture models, the LRT does not have an asymptotic chi-squared distribution for the test on the order of the mixture (i.e., the number of mixture components) (Hartigan 1985). Due to the involvement of a mixture model structure in the partial data likelihood function (5), the property is also true for the misrepresentation models that contain a mixture regression model under a hybrid structure. Hence, we resort to the parametric bootstrap from McLachlan (1987) to obtain the null distribution of the LRT statistic for hypothesis testing on the presence of misrepresentation. The parametric bootstrap approach fits a null model (i.e., an unadjusted model assuming using the original data and obtains the empirical distribution of the LRT statistic based on repeatedly generated pseudo data according to the fitted null model (e.g., for times). For each simulated data set, an LRT statistic is calculated. The empirical distribution of the LRT statistics are then used to obtain the critical value, or the -value, of the LRT on the original data.
If the LRT on the presence of misrepresentation is significant, then we can perform predictive modeling on the misrepresentation risk by including a logit regression structure on the misrepresentation prevalence according to Equation 4. Since the logit model in 4 is a latent model that can have weak identification (Xia and Gustafson 2016), we recommend a forward selection procedure on risk factors that are significant in predicting the loss distribution. For such variable selection, we may use the -value from either the Wald test based on the observed Fisher information or the LRT based on the parametric bootstrap.
4.3. Model selection with different loss distributions
For selecting models based on different loss frequency or severity distributions, we may resort to model selection criteria, including the Akaike information criterion (AIC), Bayesian information criterion (BIC), and their extended versions. Unlike the LRT that requires the models to be nested (see Section 6.2 of Goldburd, Khare, and Tevet 2020), Lindsey and Jones (1998) and Burnham and Anderson (2002, Section 6.7) noted that AIC and BIC are valid for GLM model comparisons involving different response distributions when the likelihood functions are calculated based on the same sets of observed variables/records. Based on the type of likelihood functions given in the previous section, we may use these criteria to compare the goodness of fit of the different loss models considered in this paper.
The AIC is defined based on the maximized partial data log-likelihood and the number of parameters in the model. It penalizes the complexity of the model when comparing the goodness of fit (i.e., the maximized partial data log-likelihood). In particular, the AIC is given by
AIC=2m-2l,
where the maximized log-likelihood for the regular GLM ratemaking models and it is given by for the misrepresentation models, and is the number of parameters in the model. To avoid overfitting in small sample scenarios, a penalty term is added, giving rise to the corrected AIC (AICc).
An alternative to the AIC is the BIC, in which the penalty depends on both the sample size and the number of parameters in the model. The BIC can be computed via BIC=\log(n)m-2l.
For AIC, AICc, and BIC, a lower value is associated with better goodness of fit, that is, a larger value of the maximized partial data log-likelihood function. These three types of criteria may yield different suggestions for the model selection. There is no golden rule regarding which one is superior to the others. When they favor different models, we may choose the one that has the most recommendations among different criteria. Interested readers may refer to papers by Burnham and Anderson (2002), Fonseca and Cardoso (2007), and Vrieze (2012) for detailed comparisons of the three under various model settings.
4.4. In-sample and out-of-sample prediction
In addition to the AIC/BIC, we may compare and validate predictive models based on in-sample and out-of-sample prediction. Similar to the AIC/BIC that are valid for non-nested models, out-of-sample prediction may be used to compare the predictive power of traditional rating plans as well as regular ratemaking models and those adjusting for misrepresentation.
In predictive analytics and statistical learning, commonly used criteria for evaluating out-of-sample prediction include mean squared error (MSE) and mean absolute error (MAE), which have been widely used for continuous outcomes (see, e.g., Section 2.2 of James et al. 2021). For loss severity and frequency models, including those adjusting for misrepresentation, we use to denote a total of observed values of the claim outcome in Section 3. For defining the MSE, we denote the corresponding predicted values of the claim outcome by where denotes the conditional expectation of claim outcome given the observed risk factors and estimated parameters. For the misrepresentation models, for example, is the conditional expectation of the th observation based on the fitted model with distributional form given in Equation 3. For the sample, the MSE is defined as
M S E=\frac{1}{n} \sum_{i=1}^n\left(y_i-\hat{y}_i\right)^2, \tag{12}
which is a measure of the average distance between the observed values and predicted values of the claim outcome. Alternatively, we may use the root-mean-square error (RMSE), defined as the square root of the MSE.
This formula gives the training MSE since the estimated parameters are fitted from the same observations (i.e., training data) and The training MSE measures the quality of in-sample prediction. For predictive models, such as those used in ratemaking and claim analytics, it is important to ensure the quality of out-of-sample prediction since the models are usually fitted from historical data. Thus, in practice, it is common to divide the data into two subsets: training data for estimating the model and test data for evaluating the model’s predictive power in unseen data. Assuming we have an additional samples as test data, then the test MSE is simply the MSE of the additional test samples given the earlier parameters from the training samples.
From Equation 12, we note that the MSE (RMSE) is an appropriate measure of model fit for normal responses in linear regression settings where the variance does not change with the mean. A similar criterion that works for response variables with constant variance is the MAE, defined as Compared with MSE (RMSE), MAE is less impacted by outliers with large magnitudes of residuals. MSE and MAE criteria, however, may not be appropriate for ratemaking models, including those based on lognormal, gamma, Poisson, and negative binomial distributions. In such ratemaking models, as well as in real loss severity/frequency data, the variance typically increases with the mean, causing larger observations to carry higher weights in the MSE and MAE formulas.
In order to alleviate such concerns, ratemaking actuaries typically assess prediction accuracy using rank-based methods based on actual and fitted values for nonbinary loss responses that exhibit the nonconstant variance feature (e.g., from residual checking). Such assessments usually involve visual examination of plots, including double lift charts (quintile plots) and Lorenz curves (Gini index values), introduced in Chapter 7 of Goldburd, Khare, and Tevet (2020). Interested readers may refer to their book for a comprehensive review of methods that can be used for validating ratemaking plans, including those based on GLM.
5. Simulation studies
Using simulation studies, we compare the proposed EM algorithm for the misrepresentation models with the Bayesian implementation from Xia, Hua, and Vadnais (2018) in terms of parameter estimation and computation speed. For correctly specified models, the simulation studies serve as an internal consistency test of the ability of the proposed estimation procedures to learn the parameters used to generate the data.
For data generation, we consider severity models based on lognormal and gamma distributions, as well as frequency models based on Poisson and negative binomial distributions. We assume multiplicative rating models with the frequency/severity mean structure given in Equation 2 with a log link function. We generate the true status of the risk factor from a Bernoulli trial with probability Using a misrepresentation probability we generate the corresponding samples of by modifying the samples of These parameter values imply a prevalence of misrepresentation of Regarding the correctly measured risk factors, we assume there are three additional risk factors denoted by the vector We generate these risk factors based on the following distributions: and For Equation 2, we assume the regression coefficients to be different for the severity and frequency models. Table 1 presents the values of parameters used for generating the loss severity and frequency outcomes.
Using data simulated from the above mechanisms, we compare the proposed EM algorithms with the Bayesian approaches from Xia and Gustafson (2016) and Xia, Hua, and Vadnais (2018) in terms of parameter estimates and computation time. For the lognormal, gamma, Poisson, and negative binomial misrepresentation models, we use the settings of parameter values from Table 1 for generating samples of size In Tables 2 and 3, we report the parameter estimates, standard errors (in parentheses), and computation times in seconds, respectively, for the loss severity and frequency models using the Bayesian and proposed maximum likelihood approaches based on the EM algorithm. In order to assess the impact of ignoring misrepresentation, the first column provides MLEs from unadjusted analysis using regular GLM.
From Tables 2 and 3, we observe that the estimates of the parameters are essentially the same for the Bayesian and EM approaches in the current large-sample scenarios when the vague priors from the Bayesian approach have minimal effects on the estimation. When compared with the true values in Table 1, both the Bayesian and EM approaches provide estimates of parameters that are close to the true values used to generate the sample (with differences within twice the standard error), demonstrating the ability of the proposed misrepresentation models to learn all parameters without requiring labeled data on misrepresentation. The unadjusted GLM approach, on the other hand, provides biased estimates of parameters. In particular, the estimates of from the unadjusted analysis are biased toward zero for all the models, confirming the attenuation effect expected from ignoring the misrepresentation. The similarity of the estimates is consistent with the asymptotic theories on the equivalences of estimators from Bayesian and maximum likelihood approaches (Strasser 1975). In terms of computation time, we observe that the proposed EM approach can be 50 to 400 times faster for estimating the misrepresentation models of concern when compared with the Bayesian approaches from Xia and Gustafson (2016) and Xia, Hua, and Vadnais (2018). This conclusion about the computation speed is consistent with that of the lognormal algorithm based on closed forms proposed by Akakpo, Xia, and Polansky (2019).
6. MEPS misrepresentation analysis
In this section, we perform an empirical study using the 2014 full year consolidated data from the MEPS (AHRQ 2016). In particular, we apply the gamma and lognormal severity models to total medical expenditures and the negative binomial and Poisson models to the number of office-based visits in order to assess the presence and mechanism of misrepresentation in the data. We perform risk effect assessment, misrepresentation testing, model comparison, and model validation using the methods introduced in Section 4.
6.1. Data and background
The MEPS comprises a series of large-scale surveys on the U.S. population regarding medical expenditures, healthcare utilization, and health insurance coverage that are conducted by the Agency for Healthcare Research and Quality. The MEPS data have been used extensively in the actuarial literature for studying the loss severity and frequency patterns of healthcare expenditures and utilization. For example, Hua (2015) used the MEPS data to study the dependence between the medical loss frequency and severity, and Frees (2009, Chapter 16) demonstrated the fitting of the two-part model combining loss severity and frequency (occurrence) with the MEPS data.
In the misrepresentation literature, earlier papers such as those by Xia and Gustafson (2018) and Akakpo, Xia, and Polansky (2019) assessed the presence of misrepresentation in self-reported uninsured status in the 2012, 2013, and 2014 MEPS data. Due to the individual insurance mandate of the Patient Protection and Affordable Care Act (PPACA), the authors suspected that there was a financial incentive for MEPS respondents to misrepresent their status due to the tax penalty that was introduced in 2014. Based on an empirical analysis treating uninsured status as a response variable, Xia and Gustafson (2018) did not find a statistically significant test of misrepresentation in the 2012 data. Using a simplified lognormal model including only the risk factor subject to misrepresentation, Akakpo, Xia, and Polansky (2019) performed an LRT on the existence of misrepresentation and found the test to be insignificant with the 2013 data but significant with the 2014 data (when the PPACA took effect). The simplified model from Akakpo, Xia, and Polansky (2019) ignored other risk factors in the MEPS data that are predictive of total medical expenditures and overlooked the potential influence other risk factors might have on the prevalence of misrepresentation.
Here, we conduct a more extensive empirical study on the presence of misrepresentation in uninsured status from the 2014 MEPS data using loss severity and frequency models based on lognormal, gamma, Poisson, and negative binomial distributions. Moreover, in an effort to understand the mechanism of the misrepresentation, we study whether the prevalence of misrepresentation varies in response to some of the risk factors. The response variables of interest are the total medical expenditures variable for the loss severity model and the number of office-based visits for the loss frequency model. In addition to uninsured status, risk factors we consider in the analysis include sex, age, smoking, and health status. For the analysis, we exclude adults over 65 who are eligible for Medicare.
For the loss severity misrepresentation model on total medical expenditures, the total sample size is 13,301 after excluding records with missing values and zero total expenditures. For the loss frequency model on total number of office-based visits, we use the same 13,301 records in order to obtain comparable results from the two models with different loss outcomes. The health status variable contains five levels, representing a range of excellent to poor health. The summary statistics of the variables are given in Table 4.
From the table, we observe that a representative individual in the data is an insured 40-year-old nonsmoking female who has an average health condition. From Figure 7 in Akakpo, Xia, and Polansky (2019), the logarithm of the total medical expenditures variable has an empirical distribution that is approximately normal. For the frequency analysis, the variance of the number of office-based visits variable is substantially larger than the mean, raising a concern of potential overdispersion even after adjusting for the risk factors we consider. There are a total of 2,122 zeros (16%), consisting of individuals with no office-based visits but with other types of medical expenditures such as outpatient care and emergency services.
6.2. Severity misrepresentation analysis
We first perform a loss severity analysis and thus set the total medical expenditures variable as the response variable The first set of models we consider are the unadjusted GLM ratemaking models based on the gamma and lognormal loss severity distributions. We specify the uninsured status as the variable that is subject to misrepresentation. The additional risk factors of concern, include sex, age, smoking, and health status. We then consider two types of adjusted models from Section 2.3 that account for the misrepresentation. The first type assumes that the prevalence of misrepresentation is fixed, whereas the second type assumes that the prevalence changes with one of the aforementioned risk factors under consideration. For each of the loss severity distributions, we consider a total of models for the analysis on the total medical expenditures variable. For the two distributions, the MLEs of the parameters for the models are obtained using the proposed EM algorithm implemented in R, with the inference and model comparison tools introduced previously.
Since the models we consider assume different loss distributions, we first perform a model selection based on the AIC, AICc, and BIC introduced in the previous section. Based on the AIC, AICc, and BIC, we choose the lognormal distribution over the gamma distribution due to the corresponding smaller values for all models. In Table 5, we present the goodness-of-fit statistics for the six severity misrepresentation models based on lognormal and gamma distributions. From the table, we observe that according to the BIC, the model with the best goodness of fit is the lognormal misrepresentation model without a latent logit structure on the prevalence of misrepresentation (Model II). According to the AIC and AICc, however, the model with a logit model on the relationship between the prevalence of misrepresentation and age has better goodness of fit (Model IV).
Note that the AIC and BIC consider the goodness of fit of the data based on the maximized (partial data) log-likelihood as well as the complexity of the models. They serve a different purpose than the test on the presence of misrepresentation. In order to obtain statistical conclusions that take into consideration the uncertainty in the estimation, we may perform statistical tests on the presence and mechanism of the misrepresentation and the risk effects using the lognormal misrepresentation models favored by the AIC and BIC.
In Table 6, we present the results from the LRT on the presence of misrepresentation and the Wald test on the effect of each risk factor on the prevalence of misrepresentation for the lognormal misrepresentation model.
From Table 6, the LRT test on the presence of misrepresentation is significant at the 5% level. According to the parameter estimates, the odds of misrepresentation decreases by a factor of when the age of the participant increases by one standard deviation (i.e., 13.3 years). The confidence interval for the relativity is (0.640, 0.984) for the age variable, with the effect being significant at the 5% level. All the other risk factors are insignificant in predicting the prevalence of misrepresentation. After combining results from Tables 5 and 6, we compare the estimates of the unadjusted lognormal model, the adjusted misrepresentation predictive model without a logit structure, and the estimate with the prevalence of misrepresentation depending on the age. Using the three models, we can then compare the estimates on the true risk effects that uninsured status, sex, age, smoking, and health have on average total medical expenditures.
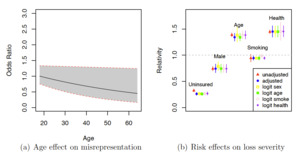
In Figure 1, we present the estimated relativity and the 95% confidence intervals on the relative effect of the risk factors on the odds of misrepresentation and the loss severity as measured by average total medical expenditures. Figure 1a presents the relative effect of the age variable on the odds of misrepresentation for the adjusted model with a logit structure. We set age 18 as the reference level associated with a relativity of 1. We observe that the odds (prevalence) of misrepresentation decreases with age for the individuals with positive medical expenditures. Figure 1b presents the estimated relativity and the 95% confidence intervals of the relativity, that is, the relative effect of each risk factor on average total medical expenditures for the six models of interest. For the age variable, relativity corresponds to an increase of one standard deviation (13.3 years). For the health variable, relativity corresponds to an increase of one unit of health level (from 1 to 5, increasing as the health condition deteriorates).
From Figure 1, we observe that the adjustment to the severity and mechanism of misrepresentation seems to result in a difference in the estimated relativity of uninsured status (a larger negative effect with relativity further away from 1) for all adjusted models. Note that the driver of incentive to deny an uninsured status differs from that of insurance misrepresentation, in which policyholders tend to not disclose risk-increasing statuses to avoid higher premiums. For insurance misrepresentation in the ratemaking context, the effect would be a mirror image of what is shown in Figure 1, with the unadjusted estimate showing attenuation regardless of the direction of error (Xia and Gustafson 2016). Misrepresentation modeling also results in smaller age and smoking effects (with relativity closer to 1) estimated from the adjusted model with a prevalence of misrepresentation based on the age. For all adjusted models, modeling misrepresentation seems to result in noticeable differences in estimated standard errors of sex, age, smoking, and health effects. Whereas earlier papers, such as Xia and Gustafson’s (2016), have demonstrated the identifiability of misrepresentation models guaranteeing statistical consistency, the unobserved feature of misrepresentation does result in an efficiency loss manifested by wider confidence intervals in most parameters. Except for the smoking variable (associated with relativity around 1), uninsured individuals and males have substantially lower average total medical expenditures, while older individuals and those with worse health conditions have much higher average total medical expenditures after adjusting for other risk factors in the model.
Based on the significance of the LRT on we may conclude that the test on the presence of misrepresentation is statistically significant, suggesting potential misrepresentation. Regarding the misrepresentation mechanism, however, we select the simpler misrepresentation model without a logit structure based on BIC.
6.3. Frequency misrepresentation analysis
For the loss frequency analysis, we set the number of office-based visits as the response variable Since the response variable is a count variable, we consider unadjusted GLM ratemaking models based on the Poisson and negative binomial loss frequency distributions. The risk factors (subject to misrepresentation), and are the same as those for the severity models. For each of the loss frequency distributions, we consider the same six unadjusted and adjusted models for the analysis of the number of office-based visits variable. For the two distributions, the MLEs of the parameters for the models are obtained using the proposed EM algorithms implemented in R, with the inference and model comparison tools introduced previously.
Similar to the misrepresentation severity analysis, we first perform a model selection based on the AIC, AICc, and BIC introduced in the previous section. In Table 7, we present the goodness-of-fit statistics for the six frequency misrepresentation models based on the Poisson and negative binomial distributions. From the table, we observe that according to all three types of criteria, the model with the best goodness of fit is the negative binomial misrepresentation model without a latent logit model on the prevalence of misrepresentation (Model II), followed by the model with a logit structure between the prevalence of misrepresentation and the age of the participant (Model IV). Consistent with the lognormal model on total medical expenditures, the goodness-of-fit statistics favor Models II and IV.
Similar to the severity misrepresentation model, we perform statistical inference on the presence and mechanism of the misrepresentation and the risk effects using the negative binomial misrepresentation models. In Table 8, we present the results from the LRT in the presence of misrepresentation and the Wald test on the effect of each risk factor on the prevalence of misrepresentation based on the negative binomial misrepresentation models. The better goodness of fit for the negative binomial models (when compared with the Poisson models according to the AIC and BIC) is consistent with the fact that the variance of the number of office-based visits variable is substantially larger than the mean.
From Table 8, the LRT test on the presence of misrepresentation is significant at the 5% level. The sex and health variables are significant based on the Wald tests on their effects on the prevalence of misrepresentation. According to the model estimates, each increase in age of one standard deviation (13.3 years) is associated with an increase of odds of 1.05 times for misrepresentation, with the confidence interval of relativity being (0.924, 1.185). Despite the difference in the sign of the age effect, the confidence interval overlaps with that of the severity analysis using the lognormal model, meaning that the difference in the estimates is not significant for the two models. Indeed, the confidence intervals of all the variables of sex, age, smoking, and health status overlap, revealing that the estimates of the effects are not significantly different for the lognormal and negative binomial models on the mechanism of misrepresentation when two different response variables are used. Based on the results from the goodness-of-fit and the Wald tests, we compare the unadjusted negative binomial model with the adjusted misrepresentation models with and without a logit model on the sex, age, and health variables. Using these models, we then compare the estimates of the effects of uninsured status, sex, age, smoking, and health status on the average number of office-based visits.
In Figure 2, we present the estimated relativity and the 95% confidence intervals on the relative effect of the risk factors on the odds of misrepresentation and the average number of office-based visits. Figure 2a presents the relative effect of age on the odds of misrepresentation We set age 18 as the reference level associated with a relativity of 1. Figure 2b presents the estimated relativity and the 95% confidence intervals of the relativity of each risk factor on the average number of office-based visits for the six models under consideration.
The results on the frequency relativities (Figure 2b) are very similar to those from the lognormal misrepresentation models on the total medical expenditures. From Figure 2a, we observe that the estimated odds (prevalence) of misrepresentation slightly increases with age, according to the misrepresentation model on the number of office-based visits. The confidence region (the shaded area), however, overlaps with that from the lognormal model, indicating that the estimates are not significantly different for the two models with different loss outcomes. Regarding the risk effects on the loss frequency (Figure 2b), we observe that the adjustment to the severity and mechanism of misrepresentation seems to result in a difference in the estimated relativity of uninsured status (a larger negative effect with relativity further away from 1), age (a larger effect with relativity further away from 1), sex (a slightly larger negative effect), and health status (a smaller relativity). Due to the aforementioned difference in the misrepresentation incentive, the effect would be a mirror image of what is shown in Figure 2 in a ratemaking context. Modeling of misrepresentation seems to result in noticeable differences in estimated standard errors of sex, age, smoking, and health effects. The wider intervals we observe for most parameters are a manifestation of the efficiency loss caused by not observing the misrepresentation status at the policy level. Except for the smoking variable (associated with relativity around 1), uninsured individuals and males have a substantially lower average number of office-based visits, while older individuals and those with worse health conditions have a much higher average number of office-based visits.
Based on the significance of the LRT on we conclude that the statistical test on the presence of misrepresentation is significant, suggesting potential misrepresentation. Due to the inconsistency of results from the loss severity and frequency models concerning the misrepresentation mechanism, we select the misrepresentation models without a logit structure based on the AIC/BIC that penalize model complexity.
6.4. In-sample and out-of-sample validation
For the MEPS analysis, the conclusions on the presence of misrepresentation and risk effects from the previous subsections are made using statistical tests and goodness-of-fit criteria based on (in-sample) data used to fit the models. For the severity models on total medical expenditures and the frequency models on the number of office-based visits, it would be helpful to conduct model validation based on both in-sample and out-of-sample prediction. For predictive analytics purposes, we evaluate each of the six models under each loss distribution, including models that perform less favorably based on in-sample tests. Using the actual and predicted values from the models, we conduct comprehensive in-sample and out-of-sample assessments based on RMSE and MAE criteria, as well as double lift charts and Lorenz curves (Gini index values) typically adopted for ratemaking (Goldburd, Khare, and Tevet 2020).
For both loss severity and frequency modeling, we use the first 10,000 observations to train each model and the remaining 3,301 samples to evaluate out-of-sample prediction. For the lognormal models, we fit normal models on the logarithm of total medical expenditures, and calculate a first set of RMSE and MAE based on the normal residuals using the predicted normal mean and logarithmic transformed actual expenditures at the individual level. The corresponding lognormal residuals are obtained based on the original medical expenditures and the predicted lognormal mean given by The gamma model residuals are obtained from the original expenditures and the predicted gamma mean at the individual level, while the gammalog residuals (comparable to normal ones) are obtained from the logarithm of expenditures and the predicted mean calculated from where denotes the logarithmic derivative of the gamma function. We plot the normal and gammalog residuals against the corresponding predicted values, and the variance seems to stay constant across different predicted values. In Tables 9 and 10, we report, respectively, in-sample (train) and out-of-sample (test) RMSE and MAE for the severity and frequency models. Due to the equivalence of MLEs and least squared estimates (LSEs) under linear regression settings, we may expect the in-sample RMSE to be smaller for normal residuals that correspond to the lognormal models selected from LRT and AIC/BIC based on maximized likelihood functions.
Based on the residual assessment, the RMSE and MAE criteria seem to be appropriate for the normal and gammalog residuals, with variance staying constant across different predicted values. Hence, we may use the results from the top block of each table with better confidence. For the severity models, the normal model on the transformed expenditures (i.e., lognormal model evaluated using residuals from the log scale) with a logit structure on age seems to give the best prediction based on both in-sample and out-of-sample RMSE/MAE criteria. The gammalog results are also consistent with those from AIC/BIC regarding the mechanism of misrepresentation under gamma models. The results are consistent with the in-sample results from Tables 5 and 6 on the selection of loss distribution and mechanism of misrepresentation per the AIC/AICc and LRT. For the MEPS expenditure data, AIC/AICc seems to perform better than BIC for anticipating out-of-sample performance. The in-sample and out-of-sample performance is consistent, confirming that the selected lognormal misrepresentation model provides a reasonable representation of MEPS total expenditures.
From the two blocks at the bottom of Tables 9 and 10, we observe that the conclusions on the misrepresentation mechanism and loss distributions contradict those from the LRT and BIC/AIC reported in the previous subsections. Particularly for the frequency models, even the in-sample results contradict those from the LRT and BIC/AIC regarding nested model comparisons on the choice of distribution and mechanism of misrepresentation (e.g., the Poisson and negative binomial models are nested given the same model structure in each column, and those considered in the LRT are nested in each row). When we experiment by replacing the raw residuals with standardized (working or Pearson’s) residuals for the frequency models, the conclusions are contradictory to those from Tables 7 and 8. This suggests that the RMSE/MAE criteria may not be appropriate for loss frequency models, probably owing to the discrete nature of data.
Hence, we may resort to graphical methods commonly used for ratemaking plans that may be less impacted by the residual magnitudes. We use the double lift charts and Lorenz curves along with the Gini index (Goldburd, Khare, and Tevet 2020) to compare the in-sample and out-of-sample prediction of the severity and frequency models under consideration. We implement the graphical methods based on the R code from the study note for Exam 3 for the Certified Specialist in Predictive Analytics certification offered by the Casualty Actuarial Society Institute (iCAS 2019).
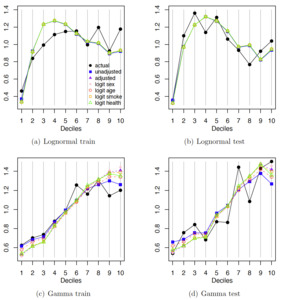
We first create double lift charts comparing unadjusted models with misrepresentation models without a logit structure on the prevalence of misrepresentation. The sort ratio is calculated based on the predicted values from two models from the same loss distribution. The observations are divided into deciles to plot the average observed values and the average predicted values from the models for comparing prediction accuracy within each decile. Since the misrepresentation models seem to provide similar predictions regardless of the misrepresentation mechanism, we decide to plot models within each row of Tables 9 and 10 in the same plot in order to reduce the total number of plots. Figure 3 reports the double lift charts for comparing the unadjusted and adjusted severity models on the total medical expenditures.
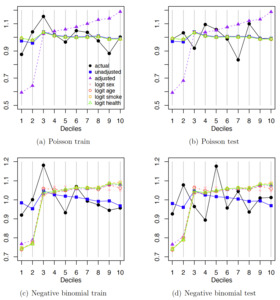
From Figure 3a and 3b, we observe that the results are similar for the unadjusted model and adjusted models with different misrepresentation mechanisms when the lognormal distribution is assumed for the total medical expenditures. In Figure 3c and 3d, the adjusted gamma models seem to capture the actual expenditures better than the unadjusted models at the lower and upper bins where the two types of models disagree the most. Figure 4 reports the double lift charts for comparing the unadjusted and adjusted frequency models on the number of office-based visits.
From Figures 4a and 4b, we observe that the adjusted models seem to work better in capturing the actual numbers of office-based visits under the Poisson distribution, except for the one without a logit structure. In Figures 4c and 4d, the unadjusted negative binomial model gives predictions that are relatively flat and better at capturing the slight decreasing trend at upper bins, while the adjusted counterparts give predictions that better capture the overall increasing trend at the lower bins. Due to the volatility in the frequency data, it seems to be harder to make a clear decision on model performance.
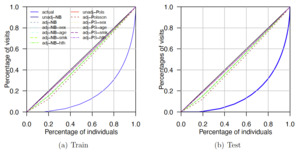
We further resort to the Gini index and Lorenz curves to measure the lift of severity and frequency models. For each model, the Lorenz curve plots the cumulative percentage of predicted values (in expenditures or numbers of visits) against the total percentage of individuals after sorting the individuals based on their predicted values. The Gini index is defined as twice the area between the Lorenz curve and the diagonal line (the line of equality). For model validation, the Gini index quantifies the ability of the model to segment the worst and best risks based on predicted values. In order to facilitate comparisons of Gini index values and to reduce the total number of figures, we plot the Lorenz curves of different severity (or frequency) models in the same figure, along with the one based on the actual experience data. Figure 5 presents the Lorenz curves for comparing loss distributions and misrepresentation mechanisms under the severity models on total medical expenditures.
From Figure 5, we observe that all the models seem to provide Gini index values of about half of those of actual expenditures, suggesting a larger number of risk factors may be needed for achieving better risk segmentation. The best performing model seems to be the gamma misrepresentation model with the health variable affecting the prevalence of misrepresentation. The conclusions are consistent for in-sample and out-of-sample prediction. In Figure 6, we present the Lorenz curves for comparing loss distributions and misrepresentation mechanisms under the frequency models on the number of office-based visits.
From Figure 6, we observe that all of the frequency models seem to provide Gini index values much smaller than those of actual numbers of office-based visits, indicating additional difficulty of achieving good risk segmentation for the discrete frequency models. The best performing model seems to be the Poisson misrepresentation model without a logit structure on the prevalence of misrepresentation. The conclusions are consistent for in-sample and out-of-sample prediction. Table 11 presents the corresponding Gini index values associated with the Lorenz curves for comparing loss distributions and misrepresentation mechanisms under the severity and frequency models.
From Table 11, the Gini index criteria indicate that the severity model with the best ability to segment worst and best risks based on in-sample and out-of-sample prediction is the gamma misrepresentation model with a logit structure (with health variable) on the prevalence of misrepresentation. Among the frequency models, the Poisson misrepresentation model without a logit structure seems to have the best ability to differentiate risks according to the Gini index for both in-sample and out-of-sample prediction. For the lognormal and negative binomial models, the misrepresentation models (with or without a logit structure) have better ability to segment risks compared with their unadjusted counterparts. The ranks of predictive ability are consistent for in-sample and out-of-sample prediction. Although the model validation criteria considered in this subsection seem to favor distributions and mechanisms different from those in the previous subsections, all the criteria seem to reveal the advantage of misrepresentation models in enhancing predictive power, both in-sample and out-of-sample.
6.5. Practical considerations
Using the 2014 MEPS data, we have illustrated the use of proposed algorithms in estimating parameters on the risk effects as well as those related to the existence and mechanism of misrepresentation under models with different loss frequency and severity distributions. For model comparison purposes, we have provided various quantitative methods based on goodness of fit and in-sample and out-of-sample prediction. In addition to these quantitative methods, we would like to emphasize the importance of professional judgment from actuaries and predictive modelers for making the ultimate decision and interpretation of misrepresentation models using their practical knowledge. The following are some important practical considerations related to misrepresentation modeling.
Regarding inference on the presence of misrepresentation, the statistical significance of the LRT indicates that the data favor a mixture distribution in Equation 3 over a regular GLM without accounting for misrepresentation. The LRT and model comparison criteria, however, cannot provide information on the potential source of heterogeneity suggested by the mixture structure. In the case of the MEPS analysis, for example, individuals with high-deductible healthcare plans might behave more like uninsured individuals. Hence, the significance of the test might be caused by both potential misrepresentation on the insurance status and the low protection level of some insurance policies. To assess potential evidence on misrepresentation, we fit the lognormal misrepresentation models using the 2012 and 2013 MEPS data collected before the individual insurance mandate. The analysis confirmed that the LRT statistics reduce by 78% to 82%, respectively, for the two models when compared with the values from Table 6 with BIC criteria favoring the unadjusted lognormal severity models for the 2012 and 2013 data. This suggests misrepresentation to be a potential major contributor to the significance of the 2014 misrepresentation tests.
Like all statistical models, the ability of misrepresentation models to reveal the true values of parameters, including the risk effects and those related to misrepresentation, also relies on the assumption that the model is correctly specified. Misspecification of the distributional assumptions, such as omitting important risk factors or interaction terms, can result in potential bias in the estimation of such parameters. For the MEPS analysis, we tried estimating the prevalence of misrepresentation on the sex indicator, which is unlikely to be subject to misrepresentation, and obtained an insignificant LRT on the presence of misrepresentation with both AIC/BIC favoring regular GLM without accounting for misrepresentation. In specific actuarial applications, we caution that it may be possible for the LRT or model comparison criteria to favor misrepresentation models concerning risk factors unlikely to be subject to misrepresentation, in which case we recommend trying to improve ratemaking models by refining the existing risk factor(s) or adding additional predictors, polynomials, and interaction terms.
Regarding the latent logit model on the prevalence of misrepresentation, we found that the age variable has a significant effect on the prevalence of misrepresentation for the lognormal severity model based on the 2014 MEPS data. According to Equations 3 and 4, the mixture of experts model under misrepresentation has a different distributional form when compared with an unadjusted GLM with an interaction effect between uninsured status and age. In particular, the latent logit model features the prevalence of misrepresentation (i.e., mixture weights) that varies with the individual’s age, whereas the interaction model features constant prevalence of misrepresentation but with the difference of the and distributions (i.e., component distributions) varying with age. For the misrepresentation models considered in this paper, we could include interaction terms between and other risk factors from and Although the misrepresentation models would still possess the general mixture forms given in Equations 3 and 4, the EM algorithms would need to be redesigned since the interaction terms involving are additional latent factors that need to be addressed in the E-step and M-step. Given that interaction terms are commonly included in ratemaking models, this would be an interesting future research topic for misrepresentation modeling. For the MEPS analysis, we would then be able to compare the unadjusted GLM to the corresponding misrepresentation model with the interaction of age and uninsured status in the component distributions, with and without a latent logit model with age as a predictor. The model comparison tools introduced previously could be used for assessing the presence and mechanism of misrepresentation in the presence of an interaction effect between and another risk factor.
7. Conclusions
In this paper, we proposed the EM algorithm for obtaining the MLEs of the parameters from GLM ratemaking models that embed predictive analytics on the misrepresentation risk. The EM algorithms were developed and implemented in R for commonly used loss severity and frequency distributions including lognormal, gamma, Poisson, and negative binomial distributions, with the models allowing the prevalence of misrepresentation to change with certain risk factors. Furthermore, we proposed statistical techniques for inference on the presence of misrepresentation and the effects of various risk factors on the prevalence of misrepresentation and the loss severity or frequency (i.e., ratemaking relativities). The comprehensive simulation studies we performed demonstrated the advantages of the maximum likelihood approach against its Bayesian counterpart and the importance of misrepresentation modeling.
By fitting different loss severity and frequency models using the MEPS data, we performed model selection based on goodness-of-fit statistics that penalize model complexity. The selected models confirmed the statistical significance of the tests on the presence of misrepresentation in the self-reported uninsured status, a conclusion consistent with the previous literature. Regarding the effects that the risk factors have on the loss outcomes, the lognormal loss severity model and negative binomial loss frequency model selected for the two loss outcomes give consistent statistical conclusions. Regarding the misrepresentation mechanism, there is inconsistency in the two models concerning the significance and effect of the age variable on misrepresentation. Thus, we resorted to other criteria such as the BIC and selected the lognormal and negative binomial models without a logit structure on the prevalence of misrepresentation. For model validation, we adopted various numeric and graphical methods to evaluate in-sample and out-of-sample prediction of unadjusted ratemaking models and those adjusting for misrepresentation. Such model validation procedures can be useful for assessing the predictive ability of claims analytics and ratemaking models that are fitted from historical data.
For the current study, the severity and frequency models were fitted, respectively, on the two different response variables. For future studies, it would be interesting and promising to study joint learning of the statistical evidence and mechanism of misrepresentation from a methodological standpoint by combining the frequency and severity models at the policy level. This would be particularly helpful in assessing the overall effect and significance of the risk factors on the prevalence of misrepresentation. The extension would lead to different structures of the complete data and partial data likelihood functions required for the EM algorithm. By resorting to numerical optimization and numerical derivatives, the implementation of the EM algorithms and inference techniques for future joint frequency and severity misrepresentation models would be feasible and promising for obtaining integrated conclusions regarding the presence and mechanism of misrepresentation.
Acknowledgments
The authors are grateful to the editor, anonymous referees and Dr. Jianxi Su for their valuable comments and suggestions that helped significantly improve the quality of this paper. The authors are grateful to the Casualty Actuarial Society for its generous support at the 2018 Individual Grant Competition.