1. Introduction
Climate-smart agriculture
Global food systems, food security, and human health are highly vulnerable to extreme weather and climate events such as windstorms, heatwaves, floods, and droughts (Myers et al. 2017; Tack and Ubilava 2015; Gobin, Tarquis, and Dalezios 2013). The frequency and intensity of extreme events continue to increase as global warming accelerates. Many agricultural production areas are experiencing longer growing seasons and warmer winters due to the climate changes now taking place. This increases variability and losses in yield quantity and quality due to waterlogging, crop heat stress, invasive pests, and overwintering diseases (Bush and Lemmen 2019; Newlands 2016). Reliably attributing specific events in space and time to broader climate variability and climate change is a challenging problem. Accurately predicting the frequency, duration, and intensity of future extreme events is also a major challenge (NAS 2016; Sillmann et al. 2013; Zhang et al. 2011; Easterling et al. 2000). Climate-smart adaptation strategies for the Canadian Prairies, one of the major agricultural growing areas for the global supply of wheat and canola, will very likely be required to mitigate yield risks posed by climate change, such as late seeding decisions due to increased spring precipitation (Renard and Tilman 2019; Carew et al. 2018; Martens, Entz, and Wonneck 2015). Historically, past adaptation strategies explain observed trends in yield (across years 1976–1998), whereby farmers extended and diversified their cropping systems, allocating larger areas to oilseed and pulse crops for extended periods in more humid regions with less risk of yield depression and drought, instead of leaving the areas fallow (i.e., summer fallow) (Campbell et al. 2002). Projected climate change is expected to increase yield variability in both the medium term (2034–2050) and long term (2079–2095), under both low- and high-carbon emission scenarios with production variance effects differing in space and time, as evidenced across crop districts in the province of Manitoba (Carew et al. 2018).
Weather index-based insurance, basis risk, and copulas
Index-based insurance refers to insurance policies with payoffs contingent on the value (e.g., mean or threshold) of an underlying index such as temperature, rainfall, satellite-derived vegetation, or crop stress measurement indices. Index models are typically based on a single variable (i.e., univariate), not multiple variables (multivariate). More complex insurance products use multiple indices at once or apply a statistical model to compute insurance basis risk, premiums, and payoffs. For example, Erhardt and Engler (2018) developed and validated a multivariate model for spatially-dependent predictions of temperature—an autoregressive moving average model with generalized autoregressive conditional heteroscedasticity of residuals (ARMA(3,0)-EGARCH(3,1))—that used bootstrapping to incorporate parameter uncertainty into the simulations. This model demonstrates how actuarial risk measures of the portfolio can be estimated from bootstrap distributions. To be a reliable indicator, an index must be representative of crop loss across many locations having diverse climate regimes and agricultural practices. We refer readers to recent reviews by Lyubchich et al. (2019), Vyas et al. (2021) and Abdi et al. (2021) on copulas, agricultural insurance, and risk management.
The problem of spatial basis risk is fundamental to index insurance and yet is still largely unexplored in the literature (Yu et al. 2019; Jensen, Barrett, and Mude 2016; Norton, Boucher, and Verteramo Chiu 2015; Norton, Turvey, and Osgood 2012). One reason it may have been underexplored is a practical knowledge gap that exists between the application of more advanced multivariate statistical methods and satellite-derived indices in insurance, despite advances in such methods for joint multivariate modeling of risk in agriculture (Newlands 2016). Recent findings of Salgueiro (2019) indicate that weather index–based insurance policies based on copulas that cover both extreme and non-extreme adverse weather can effectively reduce risk exposure, measured by grape yield variance and expected shortfall. Liu et al. (2020) confirm that MODIS vegetation indices, such as normalized difference vegetation index (NDVI), are better predictors of yield at crop peak growing stages, with multiple linear regression model root-mean-squared error (using leave-one-out cross-validation, hereafter LOOCV) in the range of 18%–28% at the municipality scale (using data for the province of Saskatchewan for years 2000–2016). Deep learning has been more recently shown to better explain spatial dependence at a higher spatial resolution (regional or municipal scale) and to further improve the accuracy of the CAR regional yield forecasts (Tanguy et al. 2015; Newlands 2016). Findings demonstrate that, while deep learning outperforms classical methods at higher spatial resolution, it requires hyperparameter tuning and a sufficient amount of yield data for model training.
The copula is a “mathematical tool for modeling the joint distribution of simultaneous events. From the perspective of tail and systemic risk, the copula allows the decoupling of the marginal distribution (that which is associated with tail risk) from the dependence structure (that which is associated with systemic risk),” and enables modeling them separately with a greater precision (Staudt 2010). Copula methods have been widely applied in energy, finance, hydrology, and insurance because they have proven to be both flexible and accurate when accounting for deviations from the normal distribution—particularly, heavy tails. However, copulas have only recently been applied in agricultural risk assessment and insurance for capturing yield–climate dependence and quantifying the occurrence of extreme events (tail dependencies) (Lyubchich et al. 2019; Nguyen-Huy et al. 2018; Sadri and Burn 2014; Woodard et al. 2011). Staudt (2010) highlights the selection of copulas to appropriately capture distribution tail dependence and account for skewness and kurtosis of underlying data, but also the importance of a natural interpretation of the copula.
Earth observation–based indices
Indices derived from direct observation of crop growth from satellites (i.e., remotely-sensed or Earth Observational (EO) monitoring) may better track the variability in crop response due to weather and climate. EO monitoring provides data for model training and validation, and typically offers data that are free and publicly available. From an operational monitoring and forecasting standpoint, models based on satellite-derived indices can detect and track changes in crop condition (e.g., growth and stress) more quickly than those that rely on ground-based yield surveys (Zhao et al. 2020; Petersen 2018; Newlands et al. 2014; Lobell 2013). NDVI is a satellite-based vegetation index that measures plant greenness or plant chlorophyll content and photosynthetic activity as a proxy for plant health and biomass, or yield. Healthy plants absorb visible light for use in photosynthesis and reflect near-infrared radiation (NIR) (700–1300 nm wavelengths). When a plant is stressed (e.g., due to heat waves, nitrogen deficiency, or being in senescence or waterlogged from flooding), it reflects less NIR and absorbs less visible light (red portion of the spectrum, 600–700 nm wavelengths) as photosynthetic activity is less efficient due to damaged or poorly developed cell structure. The NDVI is (NIR – Red)/(NIR + Red), ranging within the interval [0, 1], with higher values representing more “green” biomass, cover type, or quantity and vigor of green biomass associated with healthier plants. Vegetation indices such as NDVI are influenced by soil background reflectance, crop type, physiographic region, crop and land management practices, and climate. The use of such vegetation indices alongside historical climate variability (i.e., temperature and precipitation) has provided valuable insights into changing growing conditions across agricultural landscapes in Canada (Kouadio et al. 2014; He et al. 2012; Wall, Larocque, and Léger 2008; Guo 2003), China (Pei et al. 2019; Yuan et al. 2019), the United States (Wang, Rich, and Price 2003), and Africa (Petersen 2018). Turvey and Mclaurin (2012) emphasize the need to calibrate NDVI based on its spatial dependency on temperature and precipitation before it can be widely applied as a useful tool in index-based insurance product design. They highlight the importance of determining the optimal period and spatial extent best suited for maximizing the strength of relationship between NDVI, climate variables, and crop yields.
1.0.1. Objective
Our goal is to investigate the utility of multivariate copula modeling (MCM) for capturing the spatiotemporal dependence between NDVI, yields, and climate variables, and its potential for reducing basis risk. That is, we are interested in exploring whether MCM is a viable new alternative to improve insurance ratemaking involving model-based indices for setting payoff level and risk loaded premiums, based on more robust estimation and prediction of the probability of yield loss. We illustrate the utility of the MCM using a multi-scale dataset comprising validated and interpolated climate (daily, 1 km), Earth observational NDVI (weekly, 250 m), and crop yield (annual, municipal-scale) data. The MCM approach is benchmarked against the most popular competing algorithms—namely, multivariate regression with ARMA errors (MR with ARMA errors), generalized least squares (GLS), the Bayesian network (BN) approach, and the ARMA EGARCH model.
The paper is organized as follows. Section 2 describes the multivariate data in detail. In Section 3, we detail the competing models (including the MCM approach) and outline how crop yield–NDVI bias can be estimated. In Section 4, we describe training and validation of the models. In Section 5, we demonstrate and evaluate the use of the MCM model for pricing crop insurance premium, benchmarking its performance against a classic burn analysis approach. In Section 6, we present and discuss the modeling results, and Section 7 concludes the paper.
2. Data description
Crop yield
Historical panel data on crop yield (tonnes per acre) (2000–2018) were obtained from the Manitoba Agricultural Services Corporation (MASC) via their publicly available online MMPP Variety Yield Data Browser.[1] Spring wheat (i.e., hard red spring wheat (Triticum aestivum L.)) is selected as a representative crop having high spatial coverage as it is historically one of the major crops grown in Manitoba (alongside canola and barley) (Campbell et al. 2002). A subset of 37 municipalities distributed across the province were selected based on the previously assembled yield and climate data (Tanguy et al. 2015). The municipal regions vary substantially by their harvested area, from 2 to 3,572 km. The municipalities of Stuartburn, West St. Paul, La Broquerie, Dauphin, and Kelsey were removed because they had insufficient annual-yield data for spring wheat, leaving a total of 32 regions.
Climate
Climate data for Manitoba were acquired from Daymet,[2] providing spatially-interpolated estimates of daily maximum and minimum temperatures C) and precipitation (mm) at 1 km spatial grid resolution (Thornton et al. 2017). Daily maximum and minimum temperatures are aggregated into weekly means, and daily precipitation is aggregated into weekly total precipitation, to correspond to the weekly timescale of the NDVI. A boundary file (LCSD00a16a ESRI shapefile) available from Statistics Canada is used to delineate the municipalities as census subdivisions.[3] Centroids of each municipality (i.e., shapefile polygon) are references to obtain values of the climate variables for each region. Some municipalities have multiple centroids that consist of spatially disconnected areas. To reduce potential error in referencing centroid values, the shapefile is processed to ensure only one centroid point corresponds to each municipality, using the “Feature to point” (inside) tool in ArcGIS (ESRI Inc.). See Figure 1 showing variability of the aggregated data.
Normalized difference vegetation index (NDVI)
Statistics Canada’s Crop Condition Assessment Program (CCAP) provides weekly-composite NDVI data at a 250 m spatial resolution from the AVHRR (Advanced Very High-Resolution Radiometer) and the MODIS (Moderate Resolution Imaging Spectroradiometer; instrument of the Terra satellite). The CCAP NDVI product correlates well with other value-added products, such as the Canadian Drought Monitor (DroughtWatch, AAFC), and is used by Statistics Canada in national crop production reporting and by Agriculture and Agri-Food Canada (AAFC) in operational forecasting of crop yield of the major crops (wheat, canola, soybean, corn) across Canada through the growing season (Canadian Crop Yield Forecaster, CCYF) (Chipanshi et al. 2015; Kouadio et al. 2014; Newlands et al. 2014). Data derived from the MODIS satellite imagery at the 250 m resolution[4] are used in this modeling study. The MODIS sensor’s red and NIR channel ranges are 630–670 nm and 841–876 nm, respectively, and lie within the red and NIR spectrum bands of 600–700 nm and 700–1300 nm indicated earlier. The NDVI dataset consists of quality-controlled weekly data (i.e., 7-day composites, Monday to Sunday) during 2000–2018 for the growing season months of April to mid-October or Julian weeks 14 (April 9–15) through week 41 (October 8–14). The aggregation into weekly composites reduces error due to cloudy days among other error corrections required for the satellite imagery. A subset of the data for the 2000–2018 reference period for the months April to September (i.e., weeks 14 to week 36) was processed for input to models coded using the R statistical language and open-source R libraries. NDVI values are extracted from the data files using the ArcGIS “Extract values to table” tool.
NDVI typically increases at the beginning of the growing season, then peaks and levels off in mid-season, then decreases to the end of season (Wall, Larocque, and Léger 2008). Basnyat et al. (2004) have determined that the optimal time when NDVI is most correlated with spring wheat yield of spring-seeded crops maturing in August in the Canadian Prairies (southern Saskatchewan semi-arid field sites) is between July 10–30. During late July to early August, crops have generally completed vegetative growth and are in the grain-filling stage, when crop ripening differences within a farmer’s field can enhance NDVI, pointing to its use for delineating in-field management zones. For the data used in this study, the NDVI response shows a consistent growing season peak each year between Julian weeks 25–27, (i.e., June 18–July 8), which is slightly earlier than the reported optimal time of July 10–30 estimated by (Basnyat et al. 2004). The maximum value of NDVI can be computed over an entire growing season and used to predict crop yield, as an alternative metric to mean NDVI that is computed through the weeks of the growing season. For this reason, we construct and test models for both mean and maximum NDVI. Maximum NDVI varies spatially and symmetrically with most values clustered within 0.95–1.2 t/acre of the yield and with yield estimates corresponding to high NDVI (0.87–1.00), with some regions having consistently higher/lower yields. In Canada, the average farm size in 2011 was 778 acres (i.e., 315 ha or 3.15 km whereby NDVI at the 250 m resolution can enable vegetation monitoring of conditions within a single field. If a field is cropped during one week, remaining neighboring fields in the pixel can influence the resulting NDVI so that the index does not fluctuate substantially. Such an effect has been calibrated and error-corrected by Statistics Canada, along with other corrections to minimize effects of atmospheric residual contaminants and cloud cover.
3. Methods
Exploratory analysis of the multivariate data included quality checks, standard variable importance, pair-wise correlation, spatial correlation analysis, and distribution normality tests. These tests are either detailed in this section or alongside test results presented in the Results and Discussion (Section 6).
Yield–NDVI calibration
Crop yield data bear inherent spatial and temporal uncertainty. Field survey–based estimates, for example, may have coefficients of variation of up to 1%–5% for major crops like wheat, and between 6% and 25% for specialty crops and small areas[5] (Paliwal and Jain 2020). Crop yields also tend to increase through time due to technological change, improvements in seed biotechnology, and better management practices. Such trends are typically removed (yield data are detrended) using various detrending techniques. However, assumptions behind detrending typically do not consider spatial correlation and temporal correlation between yield and climate, and are typically unrealistic and oversimplified (e.g., trends are assumed to be linear in time and spatially homogeneous). Such assumptions often lack independent, evidence-based support and are linked with many confounding variables that vary substantially across complex agricultural landscapes, such as crop genetics/cultivar type, soil, water management, fertilizer and soil nutrient availability, herbicide use for pest control and disease-related yield loss, and energy and other historical technical improvements in farming equipment. Detrending yield and modeling yield anomalies do not necessarily provide greater model explanatory power and reliability, if the data are detrended under unrealistic assumptions unsupported by data evidence (e.g., linearity, normality, spatial independence).
Crop yield and its variability in time and space are driven by both climate and non-climate variables that include harvesting technology, genetics, weather patterns, soil, and agronomic management practices (e.g., farmer decisions on fertilizer application, tillage and crop hybrid selection, irrigation management, row spacing, planting date and depth) (Kukal and Irmak 2018). To account for non-climate drivers, we specify a link function that relates crop yield to the remotely-sensed index as
\[Y_{t}=g(\mathrm{NDVI}_{t}),\]
where is a specified functional relationship between crop yield and NDVI. We utilize a first-order, linear function, where is the slope parameter and is the intercept for estimating bias in the yield and NDVI relationship that takes into account non-climate variables. The and coefficients are assumed to be spatially independent (i.e., constant for all municipalities). Analysis performed in the prior field studies shows that NDVI is near-linearly related to photosynthetically active radiation absorbed by a plant canopy, and hence in light-dependent physiological processes, such as photosynthesis, occurring in the upper canopy (Panek and Gozdowski 2021; Liu et al. 2019; Glenn et al. 2008).
In some modeling studies, crop yield is assumed to depend on and climate variables independently (separability assumption) (Deines et al. 2021), while others assume NDVI, as a measure of vegetative growth, itself depends on climate variables (Pei et al. 2019; Wang, Rich, and Price 2003) (non-separability assumption) (Yuan et al. 2019). Here, we assume the general case of non-separability of the –climate relationship. The same crop yield–NDVI calibration relationship is assumed. For a given yield–NDVI calibration, different models are then used to model the relationship of NDVI to climate and to benchmark our MCM approach against traditional multivariate regression approaches.
Multivariate regression model with ARMA errors
We consider a multivariate regression model with autoregressive and moving average (ARMA) errors (Bianco et al. 2001; Gomez and Maravall 1996) given by
\[\begin{aligned} NDVI_{t}&=\sum_{k=1}^{m}\beta_{k}x_{tk}+\epsilon_{t},\\ \epsilon_{t}&=\phi_{1}\epsilon_{t-1}+\dots+\phi_{p}\epsilon_{t-p} + \theta_{1} a_{t-1}\\ &\quad +\dots+\theta_{q}a_{t-q}+ a_{t}, \end{aligned}\]
where and are autoregressive and moving average coefficients, respectively; is the autoregressive order, is the moving-average order and are selected using the lowest value of Akaike information criterion), and is white noise (i.e., NDVI is the response, are regressors with regression coefficients The regressors are: minimum temperature C), maximum temperature C), total precipitation amount (mm), municipality, and year.
Generalized least squares (GLS) model
We employ the method of generalized least squares (Nelder and Wedderburn 1972) to estimate parameters of a linear regression model when the residuals are correlated with possibly non-constant variance:
\[NDVI=X\beta +\epsilon, \qquad \mathrm{E}[\epsilon]=0,\; \mathrm{Var}[\epsilon]=\sigma^2 \Sigma.\]
NDVI is a vector of observations of the dependent variable (either mean NDVI or maximum NDVI across the growing season); is a matrix of predictors (i.e., minimum temperature C), maximum temperature C), total precipitation amount (mm), municipality, and year); is a vector of the unknown parameters; and is a vector of correlated errors with zero mean and heteroscedastic variance, where is a positive constant and is a matrix. We used the R package nlme to fit the GLS model (Pinheiro et al. 2014).
Bayesian network (BN) model
A Bayesian network is a probabilistic graphical model that uses Bayesian inference to compute probabilities (Gao et al. 2019; Huang, Yang, and Jiang 2019; Silander and Myllymaki 2012; Tsamardinos, Brown, and Aliferis 2006; Friedman, Geiger, and Goldszmidt 1997). BN is a directed acyclic graph (DAG) that models conditional dependence where nodes represent the variables and edges represent the conditional dependencies:
\[p(X_1,X_2,\ldots,X_n)= \prod_{i=1}^{N}p(X_{i}| S_{x_i}),\]
where is the set of edges that are parent node in a graph. We use the bnlearn package in R to fit the BN model to data using the Bayes conditional probability strategy for parameter learning (Scutari and Ness 2012). The naive structure (or unstructured) is typically assumed based on all climate variables as predictors (i.e., parent nodes) of crop yield or its proxy NDVI (i.e., child node). The maximum temperature (i.e., C), minimum temperature C), total precipitation mm), and municipality are parent nodes. In the case of max NDVI, the conditional probability is given by
\[P(Max.NDVI \mid Temp.Max,Temp.Min,Municipality,pcp).\]
A structured network is learned from the observed climate and NDVI data and includes the temporal and spatial effects for each municipality based on NDVI and climate variability as parent nodes for both mean and maximum NDVI, alongside other conditional dependencies between the climate variables.
ARMA-EGARCH model
To model a time series using an EGARCH process, let be a white noise process with mean 0 and variance 1. denotes error (return residuals) and is the square root of the conditional variance with non-negative process. The EGARCH model is represented as follows:
\[\begin{aligned} \epsilon_{t}&=\sigma_{t} Z_{t},\\ \ln(\sigma^2_t)&=\alpha_{0}+\sum_{i=1}^{q}{\alpha_{i} \epsilon_{t-i}^2}+\sum_{j=1}^{p}{\beta_{j}\sigma^2_{t-j}}, \end{aligned}\]
where for and for
The ARMA model is the model with p autoregressive terms and q moving-average terms. This model contains the AR(p) and MA(q) models,
\[y_{t}=\mu+\sum_{i=1}^{m}{\phi_{i}y_{t-i}}+\sum_{j=1}^{n}{\theta_{j} e_{t-j}}.\]
ARCH models assume the variance of the current error term to be a function of the previous errors: often the variance is related to the squares of the previous innovations.
The GARCH processes are generalized ARCH processes in the sense that the squared volatility is allowed to depend on previous squared volatilities, as well as previous squared values of the process.
In the real world, the return processes may be non-stationary, so we combine the ARMA model and the EGARCH model, where we use ARMA to fit the mean and EGARCH to fit the log variance.
We utilized an ARMA(3,0)-EGARCH(1,1) model (Lama et al. 2015; Chen and Chen 2016; Erhardt and Engler 2018), specified by:
\[\begin{aligned} y_{t}&=\mu +\phi_{1} y_{t-1}+\phi_{2}y_{t-2}+\phi_{3}y_{t-3}+\epsilon_{t},\\ \epsilon_{t}&=\sigma_{t}Z_{t},\\ \ln(\sigma^{2}_{t})&=\alpha_{o}+\alpha_{1} \epsilon_{t-1}^2+\beta_{1}\sigma^{2}_{t-1}, \end{aligned}\]
where is the response which is the NDVI, and is the lagged NDVI with lag = 3.
Multivariate copula model (MCM)
A copula is a function that links univariate marginal distributions to the joint multivariate distribution of those variables, with the aim of capturing as much of the entire dependence structure in the multivariate distribution as possible. If a joint distribution is multivariate normal, then a Gaussian copula captures the entire dependence structure. Sklar’s theorem provides the theoretical foundation for the application of copulas: where are random variables with continuous distribution functions and joint distribution function then there exists a unique copula a distribution function on with uniform marginals such that for all
\[ \small{ F(x_1,x_2,\ldots,x_n)=C(F_1(x_1), F_2(x_2),\ldots,F_n(x_n)). } \tag{1}\]
We define this joint distribution based on mean NDVI or maximum NDVI, together with maximum temperature, minimum temperature, and precipitation. A multivariate copula of dimension 4 was specified. The two main elliptical copulas, namely Gaussian and -copula, are selected. These copulas do not have a closed form and are restricted to have radial symmetry, whereas Archimedean copulas such as Frank, Joe, Clayton, and Gumbel have a closed form and allow for a number of different dependent structures. Five different copula models for estimating yield-weather dependence are evaluated by Woodard et al. (2011), who report that the Gaussian and -copulas (as well as kernel, bootstrap, and Clayton copulas) tend to perform well in terms of efficiency, although the Clayton copula performs poorly at low coverage levels.
For the marginal distributions, we select normal distributions for NDVI, maximum temperature, and minimum temperature, and gamma distribution for precipitation, based on goodness-of-fit tests. After fitting the multivariate distribution, we select from it a random sample of specific size. The size of the random sample was either 608 for yearly aggregated data for max NGVI, or 13,984 for yearly data for mean NDVI. The dependence structure is captured and specified in the copula function, for example normal and -copula, by specifying the correlation matrix and the degrees of freedom (for -copula). We use the copula package in R to fit the copula function (Hofert et al. 2014), and the function fitCopula in R with the BFGS quasi-Newton variable metric optimization method with 1000 maximum iterations (set the maxit parameter in the optim.control function) to find the value of the correlation matrix, and appears in the copula function like -copula has also degrees of freedom to be specified and normal copula. The correlation matrix is estimated using the maximum likelihood method using simulated pseudo-observations as realizations of the random variables to the copula models. The mvfc R function is next used to generate the multivariate distribution based on the marginals and copula (refer to Equation 1), and then a random sample is drawn from the multivariate distribution using the rmvdc R function.
4. Model training and validation
We train the models using data from year 2000 to year 2017.[6] An out-of-sample forecast validation for the year 2018 is performed that compares the MCM performance in forecasting the NDVI to the other benchmark models. This approach aims to predict maximum NDVI as a proxy of yield for 2018 as a validation or test year in which both yield and climate data are available. The approach uses current and historical values of climate-related predictors. To generate future predictions (i.e., forecasts), the approach would require future, near real-time (NRT) weather forecasts (and/or longer-term climate model projections). The prediction mean square error (PMSE) and prediction mean absolute error (PMAE) are used as two popular validation metrics of dispersion and deviation between model-based forecasts and observational data (Willmott and Matsuura 2005). Let be the observed value and be the corresponding forecasted value, then for a validation set of size
\[\begin{aligned} PMSE &= \frac{1}{n}\sum_{i=1}^{n} (y_{i}-\hat{y}_{i})^{2},\\ PMAE & = \frac{1}{n}\sum_{i=1}^{n} \left|{{y_{i}-\hat{y}_{i}}}\right|. \end{aligned}\]
In addition to forecast validation for the year 2018, leave-one-out cross-validation (LOOCV) is performed as a hindcast validation using all the training data (2000–2017). The LOOCV leaves one year of data out of the training data, i.e., for the 18 years of data in the original sample, 17 years are used to train the model and one year is used for validation. This procedure is iterated so each year is used as the validation year once, then model errors are averaged for all trials, to quantify overall effectiveness.
The Wasserstein distance metric is the distance between two probability distributions on a given metric space (Piccoli and Rossi 2016; Li 2000; Bernton et al. 2019; Bhatia, Jain, and Lim 2019; Olkin and Pukelsheim 1982). Let be a Polish metric space, and let For any two probability measures on the Wasserstein distance of order between and is defined as (Villani 2009)
\[\begin{aligned} W_p (\mu,\upsilon)= \Big(\inf_{\pi \in \Pi(\mu,\upsilon)} \int_{\mathcal{X}}d(x,y)^p d\pi(x,y)\Big)^{1/p}. \end{aligned}\]
In contrast to point-based measures of forecasting performance, Wasserstein distance allows to account for matching between the true and predicted spatiotemporal distributions rather than only for their location. Model performance improves as PMSE, PMAE, and Wasserstein distance decrease.
Spatial dependence
Spatial correlation (i.e., the tendency for regions that are close together to have similar NDVI) is assessed based on a global Moran I test conducted on maximum NDVI values for each municipality (Moran 1950), because insufficient spatial-referenced yield information is available within each region to enable a local Moran’s test within each municipality. The moran.test function in the spdep R package is used (Bivand et al. 2019). This test has the null hypothesis of spatial independence : versus the alternative hypothesis of spatial autocorrelation : Values of usually range from to with values significantly below its expected value indicating negative spatial autocorrelation, and values significantly above this value indicating positive spatial autocorrelation is the sample size).
5. Model-based crop insurance pricing
When an index does not match a farmer’s actual insured losses, basis risk is present. Either the insurance product is poorly designed, or the index itself does not robustly capture spatial and temporal dynamics of the insured variable, e.g., weather variability or extreme events that affect yield. The advantage of the MCM is that it can capture more representative dynamics of yield change through a growing season in relation to weather variables, and can be used to derive statistical information on claims that is not represented in observed values (e.g., historical data) such as extreme events.
The pricing of weather-based crop-yield insurance contracts based on the MCM for NDVI is demonstrated and benchmarked to the classical burn analysis approach (Gyamerah, Ngare, and Ikpe 2019; López Cabrera, Odening, and Ritter 2013; Taib and Benth 2012). We next describe this benchmarking approach in greater detail.
Let an index-based yield insurance claim size or payoff, be given by
\[X(\tau_1,\tau_2)=k\sum\limits_{s=\tau_1}^{\tau_2}\max\left(I(s)-c,0\right),\tag{2}\]
where is the index; is an index over the measurement period, to is the coverage level for the yield insurance contract to be attractive to a farmer; and is a conversion factor between an index to payoff in units of CAD per acre. We set as 0.87 in NDVI units, which in yield units is 0.70 or 70% of actual yield (i.e., 0.87 multiplied by the 0.807 yield–NDVI conversion factor). We compute as the product of a current (2021) crop dollar value for spring wheat of $230 per t of yield ($6.26 lbs/ac) and the yield–NDVI bias calibration factor obtained for the MCM of 0.807 t/index unit to obtain a fixed crop-specific value for of $185.61 per acre. Average farm size in Manitoba was 1,192 acres (2016).[7]
We adopt a standard approach for pricing a yield contract based on the expected value of claim size, that is discounted by an annual interest rate, where and assumed constant (López Cabrera, Odening, and Ritter 2013; Taib and Benth 2012). An insured farmer, who pays a yield insurance premium at time receives the amount of at the end of the measurement period of the index, i.e., time such that if one purchases insurance today and pays the premium then The times and for example, might correspond to the start and end of the growing season, and would mean that a farmer purchases insurance at the start of the growing season, assuming an index is available for pricing over the entire period To obtain the present value with a risk-loaded premium level, for a given probability of exceedance, expressed for contract price, (CAD per acre), as
\[P(t,\tau_1,\tau_2)=\exp(-r(\tau_2-t)\left[X(\tau_1,\tau_2)|F_{t}\right]), \tag{3}\]
where denotes the filtration or all available information (e.g., historical climate or yield records) in an insurance market up to time which the insurance company considers in contract pricing. Continuously compounding discount rates are assumed along with an annual interest rate of 5% (corresponding to a daily discounting factor of or weekly factor of
Burn analysis is used to determine the insurance premium rate benchmark and assumes that the expected loss rate in the future and the past loss distribution are the same. Burn analysis uses historical data to evaluate the value of derivative contracts based on the basic hypotheses that: (1) the time series of temperature is stable; (2) the data of each year are independent and subject to the same distribution (Jewson, Brix, and Ziehmann 2005). In our burn analysis, the empirical distribution of the payoff based on max NDVI values associated with each municipality and years 2000–2018 (i.e., is used to compute contract price. The contract price changes yearly in the burn analysis benchmark, as the historical payoff is measured only once a year, so this approach can only be used at the yearly scale. In contrast, the MCM index can be simulated at the annual or weekly scale. For comparison purposes, an equal number of predicted values of annual max NDVI from the MCM for each year and municipality were used. Recall that the MCM was trained on observed weekly data across the 32 municipalities and 19 years.
The profit (i.e., total loss or gain) for a farmer is the difference between total claim sizes and the price of the contract entered into at time
\[\Pi^{LG}=X(\tau_1,\tau_2) - P(t,\tau_1,\tau_2). \tag{4}\]
The value-at-risk (VaR) at a statistical significance level (i.e., 5%) of the loss distribution, under a fair premium, is used to determine a fair pricing level, as where is the claim size. This level is termed the exceedance probability. The risk-loaded premium is assumed to be a certain fraction of this pricing level (i.e., also 5%) termed the premium risk-loading factor, The risk-loaded contract price, above the fair contract price, based on the risk-loaded premium, compensates an insurance company for bearing the yield risk, and is given by
\[ \begin{align} P_{risk-loaded} = P_{fair}+\gamma_{risk-loaded} =P_{fair}+\beta\gamma_{fair}. \end{align}\tag{5}\]
6. Results and discussion
Correlation analysis of the data shows that mean NDVI (weekly scale) is more strongly (and positively) correlated with the climate variables than maximum NDVI (annual scale) (Figure 2). These results apply standard Spearman and Kendall pairwise rank correlation analysis that is nonlinear and does not carry any assumptions about the data distribution. Correlation coefficients between 0.10 and 0.29 represent a weak association, coefficients between 0.30 and 0.49 represent a medium association, and coefficients of 0.50 and above represent a strong association or relationship. The association between NDVI (mean or maximum) and any individual climate variable alone is weak. This points to the need for a multivariate model that combines variables in an additive way, or a multivariate model with nonlinear assumptions being needed to explain NDVI (i.e., crop vegetation variability) in response to climate variability. Observed distributions for NDVI (unitless), minimum and maximum temperatures C), and total precipitation (mm) are also shown accompanying the correlation results. The climate data were determined to be normally-distributed for both minimum and maximum temperature, and gamma-distributed for precipitation amount at 1% significance level.
Testing for spatial correlation in NDVI across municipalities in the study region resulted in a global Moran’s critical -score with a -value of 0.0116 (for locations). This -score is less than the critical value 2.58 at the 99% confidence level, hence the null hypothesis cannot be rejected, meaning that there is no significant evidence of spatial correlation.
Based on the highly statistically significant results of the Durbin-Watson test and the score test for non-constant error variance, we conclude that the multivariate model with ARMA errors and the GLS model, which allow for correlated errors and unequal variances, are justified to be used as modeling benchmarks. (The tests are performed using the R package lmtest (Hothorn et al. 2019) and the R package car (Fox et al. 2012).)
Variable importance ranking based on the portion of total observed variance explained by each variable, from most to least important, was determined to be: municipality, minimum temperature, maximum temperature, precipitation, and year. In the case of unsupervised, structural learning, a notably different DAG of variable interdependence and spatial dependence (i.e., via an introduced municipality node) resulted, as compared to naive or unstructured learning (Figure 3). The multivariate copula function is able to represent the overall range of inter-annual observed variability reasonably well, but has difficulty in representing higher variability observed in individual years (e.g., 2002, 2004, 2009, 2014), based on 25% and 75% distribution quantiles for both the normal and -copula function (Figure 4).
The performance of MCM, along with the benchmark models, in predicting mean and maximum NDVI across all municipalities is summarized for the out-of-sample validation test year (i.e., 2018) (Table 1), and for LOOCV (2000–2017) (Table 3). The multivariate regression with ARMA errors (MR with ARMA) model had for mean NDVI and maximum NDVI, as this had the lowest Akaike information criterion, an estimator of prediction error, among different orders of autoregressive terms and moving-average terms.
For the test year of 2018, the ARMA-EGARCH model yields the lowest PMAE and PMSE, that is, point-based measures of forecasting utility. In turn, the MCM copula-based approach delivers the best performance in terms of Wasserstein distance, that is, the metric that accounts for deviations among the true and forecasted spatiotemporal distributions rather than only their means (as in the case of PMAE and PMSE). The results are not surprising as MCM particularly targets better forecasting of spatiotemporal distributions.
The LOOCV validation testing shows the BN model predicts well the mean and maximum NDVI, based on the PMSE and PMAE, but the MCM predicts the best, based on the Wasserstein distance.
Overall, the best-fitting MCM prediction error for the 2018 test year and LOOCV testing was smallest for maximum NDVI, compared to mean NDVI. As noted previously by (Turvey and Mclaurin 2012), integrated NDVI and maximum NDVI (i.e., not mean NDVI) have been shown repeatedly to be the best predictors of crop yield. Overall, substantial reductions in prediction error were achieved by the MCM compared to the standard regression models, such as multivariate regression with ARMA and GLS.
Maps of PMSE and PMAE are shown for each model (Figure 5), where darker regions have lower prediction errors. The white regions are municipalities that are not in our study. The BN and MCM and ARMA-EGRACH are able to reduce prediction error across most municipalities, compared to the MR with ARMA errors model and the GLS benchmark models. Stepanov et al. (2020), in a recent study using NDVI and climate data (2010–2018, 9 years) to predict soybean yield also at a municipality or regional scale, obtained RMSE values as high as 16% (see Table 11, page 17). With a longer historical record of data, data for more municipalities, and further modeling work, current prediction error may be further reduced for the MCM and other evaluated models.
The crop yield–NDVI calibration for the BN and MCM best-performing models indicates that bias increases slightly when using the BN model to predict crop yield (spring wheat) but is far more clustered within the 1 confidence ellipse than the MCM (Figure 6). For the MCM, the estimated coefficients intercept, slope) were 0.807348 and -0.006623, respectively, compared to the BN model, which had fitted values of 0.84058 and -0.004879; for ARMA-EGARCH they were 1.28652 and -0.07623. Most of the predicted values for these models lie within the 90% confidence ellipse for the BN model and the 99% (3 ellipse for the MCM. Note there is error in the crop yield estimates that is not quantified for each year and municipality and may contribute to bias.
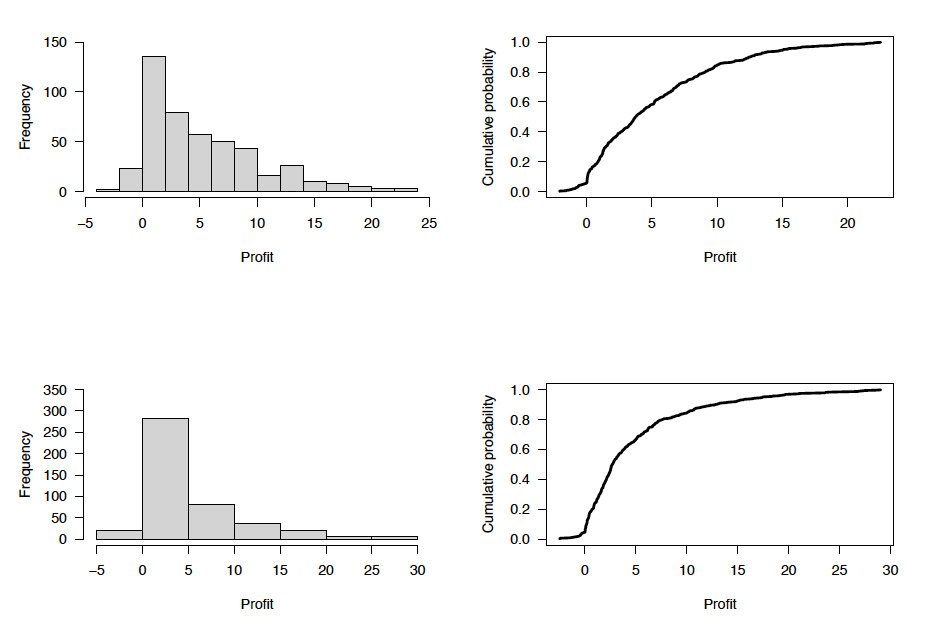
Observed maximum NDVI are more strongly centered between 0.8–0.85 compared with the model-predicted values, which are more broadly distributed between 0.7–1.0 (Figure 7). The associated claim size distribution for the burn analysis is more peaked and clustered around claim sizes between 5–10, but the MCM provides a more uniform distribution of smaller claims and a reduced number of higher claims. Insurance pricing based on the MCM with normal copula shows a wider distribution than the burn analysis benchmark that has most profit values less than 5 $/acre (Figure 8) based on an equal sample size comparison between observed and model predictions
The MCM generated a lower exceedance level (risk loaded at 5%) and a slightly higher premium price, but a much lower loss probability and high gain probability for the farmer, as compared with the burn analysis benchmark based on observed data only (Table 3). For the burn analysis, the probability of loss is only slightly higher than the probability of gain. The resultant premium price of the MCM, 12.5524 $/acre, compares to estimates of actual premiums of 8.59–9.76 $/acre that can be above 10 $/acre in some years.
7. Conclusions
We have evaluated the utility and performance of an MCM approach for forecasting crop yield based on satellite NDVI data and incorporating spatial dependence with climate (temperature and precipitation). Our results illustrate the importance of using validation metrics that measure deviation at distribution extremes, such as the Wasserstein distance. Furthermore, we have found that models incorporating spatial dependence (i.e., BN and MCM) outperform standard or classical regression approaches. Our findings demonstrate that the use of MCM to incorporate complex spatial and temporal dependencies in crop yield is closely linked with the dynamics of confounding variables, like temperature and precipitation. Our results demonstrate that MCM has significant benefits and potential as an objective, consistent, and robust statistical methodology for integrating remote-sensing (such as NDVI), climate, and weather data in the design of novel, improved index-based insurance products. In the future, such insurance products may increasingly utilize satellite-derived indices (i.e., coverage, accuracy, reliability).
Using remote-sensing indices to track basis risk (yield and yield loss) is particularly attractive because they reduce the need for costly and laborious crop yield field surveys, providing better, more timely coverage over large agricultural areas. The use of such data (e.g., vegetation growth/stress indices) can also help to enhance model predictive performance and provide greater temporal and/or spatial coverage and sampling over a region of interest. Rather than just relying on limited historical records of annual yield estimates for model training, the use of satellite data such as NDVI enables developing weekly models for forecasting crop yield and basis risk through the growing season in relation to the timing of extreme events or trends. In tandem with new and improved techniques for data fusion, using data from many satellite image providers, there are anticipated coverage and monitoring capabilities, newly developed remote-sensing indices, and new satellites and constellations of satellites that have been launched with more frequent revisit times than previous missions, having sensors with much higher spatial resolution (e.g., Europe’s Sentinel-2 and Canada’s Radarsat Constellation Mission or RCM). In addition, satellite data could be supplemented by finer-scale imagery collected by drones (i.e., low-cost remotely piloted aircraft systems or RPAS)—a rapidly emerging technology that can also provide high-resolution and timely geospatial data to support model-based agricultural risk decision making.
This study illustrates available R libraries for implementing, fitting, and benchmarking MCMs, for the scientific community and other practitioners who are interested in employing the models. There is increasing interest in the MCM method, as evidenced by a new toolbox called the Multivariate Copula Analysis Toolbox (MvCAT), recently developed for MCM use and application by the statistics and actuarial science community (Sadegh, Ragno, and AghaKouchak 2017). This toolbox employs a Bayesian framework with a Gaussian likelihood function for residuals that infers copula parameters for a wide range of copula families. The findings reported here on MCM performance and utility to multivariate problems support much broader use of MCMs in risk modeling.
In future research, we aim to expand the current MCM to one that has a widely-applicable and flexible network structure (i.e., as a Copula Bayesian Network, CBN). This form could then be compared to Deep Bayesian Networks (DBNs) and recent results obtained for these models (Tanguy et al. 2015). Future research investigations will seek to incorporate data on other agricultural crops and explore the inclusion of multiple satellite remote-sensing indices and indices of weather extremes. Finally, inspired by the recent applications of topological data analysis in actuarial sciences (Jiang et al. 2022; Yuvaraj et al. 2021), we will investigate the utility and limitations of integrating the copula methods with topological summaries of crop yields and atmospheric data.
Acknowledgments
This work is supported, in part, by the Canadian Agricultural Partnership (CAP) of Agriculture and Agri-Food Canada (AAFC) and the Casualty Actuarial Society (CAS). The authors thank Dr. T. A. Porcelli for providing helpful comments and editing of the final manuscript, and Molina Tek (GIS Analyst, AAFC) for assistance in the satellite data manipulation and processing.
MMPP Variety Yield Data Browser, https://www.masc.mb.ca/masc.nsf/mmpp_browser_variety.html
Daymet, https://daymet.ornl.gov
Boundary file, https://www12.statcan.gc.ca/census-recensement/2011/geo/bound-limit/bound-limit-2016-eng.cfm
MODIS NDVI (Statcan), https://open.canada.ca/data/en/dataset/dc700f75-19d8-4913-9846-78615ca93784
Statistics Canada, https://www150.statcan.gc.ca/n1/pub/22-002-x/2011008/technote-notetech2-eng.htm
Data and R code are available by request from the authors.
Manitoba Crop Highlights – 2016 Census of Agriculture, https://www.gov.mb.ca/agriculture/markets-and-statistics/crop-statistics/pubs/crop-highlights-census.pdf
__minimum_and_maximum_temperat.png)

_unstructured__and_b)_learned_structure.png)
_(simulated)_compared_to_observational_data_(green).png)
_and_pmae_(right)_across_the_selected_regional_mu.png)
_(spring_wheat)_and_model_predictions_o.png)
_and_best-fitting_mcm_(top_right)_a.png)

__minimum_and_maximum_temperat.png)

_unstructured__and_b)_learned_structure.png)
_(simulated)_compared_to_observational_data_(green).png)
_and_pmae_(right)_across_the_selected_regional_mu.png)
_(spring_wheat)_and_model_predictions_o.png)
_and_best-fitting_mcm_(top_right)_a.png)