1. Introduction
The concept of systemic risk has gained increasing attention from both regulators and academics. Since 2009, there has been an observable regulatory response to the vulnerability of the banking sector revealed in the financial crisis of 2007–2008 and an attempt to find a solution to the '‘too big to fail’'interdependence between global systemically important banks (G-SIBs) and the economy of sovereign states. In particular, the Financial Stability Board (FSB) started to develop a method to identify G-SIBs for which a set of stricter requirements would apply (FSB 2010, 2011, 2013). A first official version of the G-SIB list was published by FSB in November 2011, and it has been updated each year since.
The debate regarding the systemic nature of financial institutions has been ongoing for many years and has also involved the insurance sector. The International Association of Insurance Supervisors (IAIS) played an important role in this global initiative. The IAIS suggested that the specificities of insurance activity should be duly considered when attempting to extend the definition of systemic risk to the insurance sector, namely regarding the specificities of underwriting (IAIA 2009, 2011). Although it is recognized that insurance is part of the financial sector with significant links to the real economy, it differs from the other financial services by its business model (e.g., the ‘‘inverted cycle of production’’). However, under the leadership and steering of the FSB, the IAIS has focused on the analysis of the potential systemic relevance of insurers.
Both the IAIS and several papers in the literature (Acharya and Richardson 2014; Cummins and Weiss 2013; Eling and Pankoke 2016; Geneva Association 2010; IAA (International Actuarial Association) 2013) have concluded that although insurance companies are less prone to systemic risk and less vulnerable than banks, some nontraditional activities may entail some risk due to the high leverage and implied guarantees associated with them.
To address this risk, the IAIS has developed a methodology to assess and ultimately identify global systemically important insurers (G-SIIs), as well as a range of policy measures to be applied to them (IAIS 2013a, 2013b). An initial list of nine multinational insurance groups that have been classified as G-SIIs was released in 2013. These particular insurers were identified due to the assessment that there could be negative impacts on the stability of the global financial system should one of them become insolvent and fail in a disorderly manner. The IAIS assessment and FSB identification became an annual process, and the FSB and IAIS developed a framework of policy measures to be applied to G-SIIs with the objective of reducing the negative externalities stemming from a potential disorderly failure of a G-SII. This framework of G-SII policy measures consists of three main elements: (1) higher loss-absorbency requirements, (2) enhanced group-wide supervision and group-wide recovery, and (3) resolution planning and regular resolvability assessments.
In November 2019, the IAIS finalized a holistic framework for the assessment and mitigation of systemic risk in the insurance sector (IAIS 2019). The framework moves away from a solely entities-based approach and sets out an activities-based approach for sector-wide risk monitoring and management as a key component of the framework, and it includes tools for dealing with the build up of risk within individual insurers or groups of insurers. The goal is to appropriately implement a framework that will provide an enhanced method for mitigating systemic risk in the insurance sector. In this context, the annual identification of G-SIIs has been suspended and in November 2022, the FSB will determine whether to discontinue or reestablish an annual identification of G-SIIs based on the results of the initial years of implementation of the holistic framework.
One of the key points highlighted in this paper is the prominent role of interconnections in the financial system and the importance of measuring them in terms of risk. This is also apparent within the extensive and varied literature on systemic risk measurement in the banking sector; modeling the interconnections plays a leading role. On the one hand, statistical market-based measures of individual risk such as value at risk (VaR) and expected shortfall (ES)—traditionally employed in risk management but also used for regulation—have evolved to account for tail dependence among banks (for recent survey examples in this field, see Benoit et al. 2016, Bisias et al. 2012, and de Bandt et al. 2013). On the other hand, the structure of financial and economic systems, which are characterized by interacting agents, can be described as a complex system and network indicators have been used to assess systemic risk in the banking sector (for recent surveys about networks and systemic risk, see Caccioli, Barucca, and Kobayashi 2017 or Neveu 2016). Additionally, network indicators have been used to identify the most relevant banks in the system (see, e.g., Clemente, Grassi, and Pederzoli 2019; Rovira Kaltwasser and Spelta 2018 and Spelta, Pecora, and Rovira Kaltwasser 2019).
Less attention has been paid to the measurement of systemic risk in the insurance sector and to the identification of most relevant insurers. A model for systemic risk of insurance companies and banks has been provided by Acharya, Philippon, and Richardson (2016). A rationale for the macroprudential regulation of insurance companies has been described by Gómez and Ponce (2018). Cummins and Weiss (2014) evaluated systemic risk for the U.S. insurance sector, focusing on the interconnectedness of the system. Systemic relevance of the European insurance industry has been explored in Bertin and Sottocornola (2015). The importance of the identification of G-SIIs has been stressed by Guiné (2014). Denkowska and Wanat (2020) proposed combining copula-garch models with minimum spanning trees and then analyzing the contribution of each institution using CoVaR (see also Adrian and Brunnermeier 2016). Fung and Yeh (2018) showed that the recent policy measures proposed by the IAIS are perceived by the market as heading in the right direction and concluded that the regulation partially achieved its intended objective of reducing the systemic risk of G-SIIs. A review of different approaches is given by Jobst (2014).
In this context, we propose to identify the most relevant insurers in the market, combining the network approach with standard risk measures that are based on market data. In this way, we integrate the full picture that is provided by network analysis and the forward-looking approach of market-based statistical measures. We model the insurance market via a weighted network in which vertices represent firms and edges are quantified via market-based measures. Each edge is indeed weighted considering the expected shortfall of the company and the marginal expected shortfall (MES)—proposed by Acharya et al. (2016)—computed on each pair of firms. In this way, the weights allow us to exploit the tail relations between couples of insurers.
To identify most relevant companies in the market, we make use of a suitable network indicator, the effective resistance centrality as defined by Clemente and Cornaro (2020) for unweighted networks as the relative drop of the effective graph resistance (also known as Kirchhoff index) caused by the removal of a vertex from the network. In particular, we extend the version provided by Clemente and Cornaro (2020) to the weighted case. The proposed indicator appears suitable for identifying critical vertices in the network and, therefore, relevant firms in the market. Indeed, the Kirchhoff index has been widely used for assessing the robustness of a network. For instance, Ellens et al. (2011) and X. Wang et al. (2014) showed that this indicator allows assessment of the ability of a network to continue performing well when it is subject to failure and/or attack. Therefore, vertices whose removal mainly affects the value of the Kirchhoff index are critical in terms of the vulnerability of the network. Using this method of analysis, we focus on two aspects of network contagion (i.e., spreading or receiving risk): the local level of interconnection and the dominant position of a firm within a system.
The results show that the networks well capture the behavior of interconnections over time. The pattern of networks’ weights appear to be strictly related to the financial condition of the market. Furthermore, current G-SIIs are identified by this network indicator with only a few exceptions. Indeed, this type of approach can be considered a complement to the more traditional approaches that are based on balance sheet and regulatory data.
The remainder of this paper is organized as follows. Section 2 provides some preliminaries about graph theory and the weighted Kirchhoff index. Section 3 explains how we obtain the network and the weights of edges and defines the weighted effective resistance centrality provided by Clemente and Cornaro (2020). Section 4 describes how we selected the sample of insurance companies over the 2001–2005 period and how we constructed the network for each time period and then presents and discusses results. Section 5 offers conclusions.
2. Preliminaries
2.1. An introduction to graph theory
The scientific study of networks is an interdisciplinary field that brings together ideas from mathematics, physics, biology, computer science, the social sciences, and many other areas. Scientists in a wide variety of fields have, over the years, developed an extensive set of tools—mathematical, computational, and statistical—for analyzing, modeling, and understanding networks. Many systems can be represented by networks and the use of an abstract structure can help capture the patterns of connections between components.
The concept of a network is very intuitive: in its simplest form, a network is a collection of points joined together in pairs by lines. In mathematics, the study of networks is known as graph theory: a graph is, in fact, the mathematical representation of a network (further details on graph theory can be found in Estrada 2011, Harary 1969, and Newman 2010).
In graph theory, the points are referred to as vertices (or nodes) and the lines are referred to as edges (or links) as shown in Figure 1 (a). The number of vertices in a graph are denoted by and the number of edges by Usually, a graph has at most a single edge between any pair of vertices, but there can be more than one edge between the same pair of vertices and those edges are collectively referred to as a multiedge. If there are also edges that connect vertices to themselves, they are called self-edges or self-loops as shown in Figure 1 (b).
A graph that has neither self-edges nor multiedges is called a simple graph. A graph with multiedges is called a multigraph. In the next section, we will neglect self-edges and multiedges.
In a more formal way, a graph can be described as a pair of sets where is the set of vertices and is the set of edges. We consider graphs with fixed order and fixed size The edge connecting vertices is denoted by and by When two vertices share an edge, they are called adjacent.
A nonnegative -square matrix representing the adjacency relationships between vertices of is associated to the graph and it is called the adjacency matrix. The adjacency matrix of a simple graph is the matrix with elements such that
aij={1if there is an edge between vertices i and j0otherwise
If the graph has self-edges, the corresponding diagonal elements of are equal to 1.
In some contexts, it is useful to represent edges as having a weight, or value—usually, a real number. Hence, a weight can be assigned to each edge and, in that case, it would be a weighted graph or valued graph. Moreover, the strength of a vertex is denoted by which equals the sum of the weights of the edges adjacent to it.
A directed graph (or digraph) is a graph in which each edge (called arc) has a direction, pointing from one vertex to another as shown in Figure 2. More formally, it can be said that each edge is an ordered pair of vertices. In general, the adjacency matrix of a directed graph is asymmetric.
An undirected graph is a graph in which if then A path in a network is any sequence of vertices such that every consecutive pair of vertices in the sequence is connected by an edge in the network, as in the red path in Figure 3. More precisely, a path is a sequence of distinct adjacent vertices from vertex to vertex The length of a path in a graph is the number of edges traversed along the path (not the number of vertices). A shortest path (also called a geodesic path) is a path between two vertices such that no shorter path exists. If the graph is weighted, the weighted shortest path is the path with the minimum sum of edge weights. The distance between and is the length of the shortest path joining them when such a path exists, and it is set to otherwise.
A graph is connected if there is a path between every couple of vertices. Figure 4 (a) and 4 (b) show connected and disconnected graphs, respectively.
A graph is complete when every vertex is connected to every other as in Figure 5.
The degree of a vertex in a graph is the number of edges connected to it. The degree of vertex is denoted by and denotes the degree sequence of arranged in nonincreasing order
Given the diagonal matrix of vertex degrees D=(d10⋯00d2⋯0⋮⋮⋱⋮00⋯dn)
the matrix is known as the Laplacian matrix of whose elements are defined as
lij={diifi=j−1ifi≠j and eij∈E0otherwise
The Laplacian matrix is symmetric and positive semidefinite and the rows sum up to that is, its eigenvalues are real and nonnegative and the smallest eigenvalue is zero. The eigenvalues can be ordered and denoted as for such that
For a graph with nonnegative edge weights we denote the weighted adjacency matrix as The weighted Laplacian matrix is defined as where is the diagonal matrix of strengths, with elements To summarize, the elements of the weighted Laplacian are given by
lWij={si=∑jwij if i=j−wij if eij∈E0 otherwise
Since the weighted Laplacian matrix is symmetric and positive semidefinite and the rows sum up to its eigenvalues are real and nonnegative and the smallest eigenvalue is zero. Hence, the eigenvalues can be ordered and denoted as for such that
Recall here a useful result we use in the sequel:
Theorem 1 (Weyl’s Theorem) Let a graph be given and let be obtained by increasing the weight of an edge, the Laplacian eigenvalues of the new graph satisfy This means that increasing edge weights does not decrease the Laplacian eigenvalues.
2.2. The weighted Kirchhoff index and the normalized weighted Kirchhoff index
The Kirchhoff index of a simple connected graph was defined by Klein and Randić (1993) as:
K(G)=∑i<jRij
where is the accumulated effective resistance between vertices and
Briefly, in order to determine the effective resistance, a (simple, undirected, and connected) graph can be seen as an electrical circuit, where a resistor of ohm is associated to each edge For each pair of vertices, the pairwise effective resistance between these vertices—that is, the resistance of the total system when a voltage source is connected across them—can be calculated by means of the well-known series and parallel manipulations (for further details, see Ellens 2011 and Klein and Randić 1993.)
In addition to its original definition, the Kirchhoff index can be rewritten as in terms of the eigenvalues of the Laplacian matrix (see Feng, Gutman, and Yu 2010 and Zhu, Klein, and Lukovits 1996). For a weighted and undirected graph, the weighted Kirchhoff index is defined as (see Klein and Randić 1993)
KW(G)=nn−1∑i=11μWi
Recall here a useful result (see Ellens 2011):
Remark 1 strictly decreases when edges are added or weights are increased.
Remark 1 displays strict monotonicity for when a new edge is added to the graph or when the value of the weight of an edge is increased. This is obviously a desirable property for an indicator aimed at assessing the robustness of the network.
In order to compare the value of the Kirchhoff index for networks with different orders, we can consider the normalized weighted Kirchhoff index. Assuming it can be defined in the following way, extending the indicator provided by H. Wang, Hua, and Wang (2010)to the weighted case:
KWN(G)=KW(G)(n2)
where the denominator considers the maximum sum of the weights.
The Kirchhoff index can be highly informative as a robustness measure of a network, showing the ability of a network to continue performing well when it is subject to failure and/or attack. In fact, this measure can capture the vulnerability of a connection between a pair of vertices because it considers both the number of paths between the vertices and their lengths. A small value of the Kirchhoff index therefore indicates a robust network.
3. Modeling the insurance system
In this section, we model the insurance market as a directed weighted network, which is formally defined as a weighted graph with vertices, representing insurance companies in different countries, and edges, representing the relations between firms. A positive weight, denoted by is associated with each edge
In Section 3.1, we define how the weights on the edges are calibrated using market-based risk measures. In Section 3.2, we provide a new network indicator useful to assess the relevance of each firm in terms of the robustness of the network.
3.1. Risk network of the insurance market
Our purpose is to build a specific risk network that summarizes the tail dependences between insurance companies by considering specific risk measures. The ‘‘tail impact’’ between financial institutions is indeed used in the construction of a network for the insurance system by building on standard market-based measures of systemic risk. These measures are estimated on equity returns; therefore, our model shares various features with correlation networks that are applied to the financial sector and their evolution (e.g., Billio et al. 2012 and Kenett et al. 2012).
In particular, we are interested in quantifying the impact of the distress of an insurance company on the others. This point of view is consistent with the definition of systemic risk. The proposed approach is to use mean expected shortfall (MES) as a measure of the tail influence of a company on another (as proposed by Clemente, Grassi, and Pederzoli 2019). Considering a system with firms, the MES of a firm with is defined by Acharya et al. (2016) in terms of the returns. In particular, we denote the random variables (r.v.) returns of the firm and of the system as and respectively. Hence, the MES is defined as the expected return of the firm conditional on the return of the system being below its VaR level :
MESi=−E(Yi|Ysys≤VaRsys)
It is noticeable that the definition is similar to the CoVaR, which instead quantifies the risk of the system conditional on the distress of a single firm. In this paper, we consider instead pairs of insurers and we define the ES of an insurer conditional on insurer being in distress as
MESi|j=−E(Yi|Yj≤VaRj)
The VaR of a generic firm at a confidence level is here defined as
VaRi=inf{yi:FY(yi)>1−α}
where denotes the realizations of the r.v. and is the cumulative distribution function of (see, e.g., Artzner et al. 1999).
In particular, we consider the difference to quantify the tail influence of an insurer on the insurer This difference is always nonnegative and values that are closer to zero indicate a stronger tail impact of the insurer on insurer In other words, we interpret previous difference as the risk of insurer that is not driven by insurer To assure comparability among institutions, we scale this quantity by a measure of the risk for the insurer that is, the difference between the unconditional expected return and the tail expected return Therefore, we define the following measure of the impact of on as
Ii|j=−E(Yi|Yi≤VaRi)+E(Yi|Yj≤VaRj)E(Yi)−E(Yi|Yi≤VaRi)
is always nonnegative since both the numerator and the denominator are nonnegative. It is noteworthy that in the case the inequality is satisfied, we have a positive reaction of to the distress of the company Our purpose is to analyze systemic risk; therefore, we neglect the positive impact obtaining values of bounded between and
Hence, we construct a network in which each insurance company is a vertex and weights on the edge are defined as follows:
wji={1−Ii|jif i≠j and E(Yi)≥E(Yi|Yj≤−VaRj)0otherwise
It is worth pointing out that in Equation (8), weights reflect the impact of the insurer on insurer Since we are considering a higher value of weight means a high impact between institutions or, in other words, it corresponds to a lower portion of the risk not being driven by the company
3.2. A suitable network indicator: Weighted effective resistance centrality
To identify the most significant insurance companies in the system, we propose a suitable local network indicator that is an extension to weighted networks of the vertex-based effective resistance centrality provided by Clemente and Cornaro (2020, 2019). The vertex-based weighted effective resistance centrality can be defined as follows.
Let be a weighted and connected graph of vertices and edges and the graph obtained by removing the vertex and all its related connections from The eeighted effective resistance centrality of the vertex is defined as
RWK(i,G)=(ΔKWN)iKWN(G)=KWN(Gi)−KWN(G)KWN(G)
In (9) we consider at the numerator the drop of the weighted normalized Kirchhoff index in order to provide a consistent comparison between graphs and that have different orders. Notice that the quantity is not always positive, depending on the relevance of the specific vertex in the network. This measure can be useful to identify strategic vertices, whose failure can affect the resilience of the network. Furthermore, the measure also allows the detection of vertices to be eventually removed in order to improve the robustness of the network.
4. Data, results, and discussion
4.1. Data set description
For our study, we selected the largest insurance companies in terms of asset size and market capitalization. The companies in the sample are listed in Table 2. For each firm, equity returns were collected[1] on a daily basis during the period of January 2001 to the end of December 2015.
Returns were split using monthly windows and then used to construct a time-varying weighted network for each period. To compute weights as defined in Equation (8), ES and MES at the 95% confidence level were estimated for each firm via historical simulation. Additionally, the network was symmetrized using the average effect between the pair of firms involved as the edge weight. To justify this choice, we applied the scaled measure[2] proposed by Fagiolo (2006) to assess whether an empirically observed network is sufficiently symmetric to justify an undirected network analysis. Results provided a negative value of for the whole time period, indicating that the network was only weakly asymmetric and an undirected network analysis was justified.
Hence, we have a network (with where insurance companies are vertices and the weights of the edges are related to the impact between institutions. Notice that the number of assets can vary over time. We considered the 118 firms listed in Table 2, but there was no information available for some of the firms during specific time periods. Therefore, we considered only those insurers for whom the number of observations was sufficiently high to ensure a significant estimation of weights. Specifically, we considered only insurers with a number of observations higher than 90% of trading days. We observed that 14 companies were frequently excluded (i.e., present not more than 75%).[3]
Therefore, we dealt with 180 different networks. On average, they had 105 vertices and more than 4,000 edges. In several windows, the networks were composed by all the firms with more than 6,000 edges. As better detailed in the next subsection, the networks were on average very dense and well clustered, confirming the presence of several triangles. Both binary and weighted assortativity indexes were very close to zero.
4.2. Preliminary results
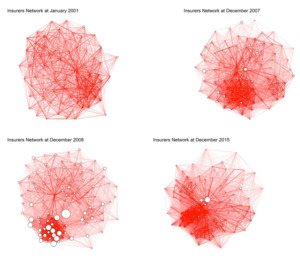
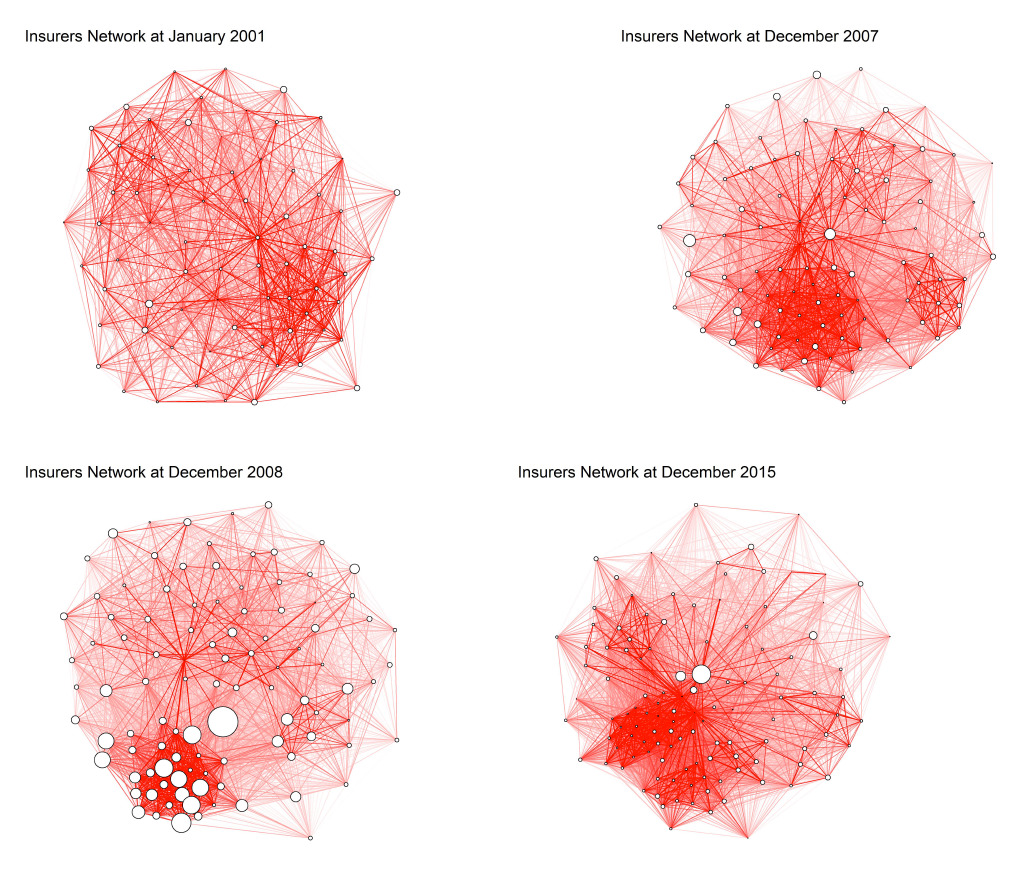
Figure 6 shows 4 of the 180 networks that were analyzed. As previously discussed, each vertex represents an insurance company and the weighted edge measures the average MES-based impact between a company and a company In a preliminary visual inspection, the networks appear to be very dense. Indeed, the density—computed as the ratio of the number of observed edges to the number of potential edges—is equal to 0.7 in the first network (January 2001) and to 0.81 in the last network at the end of the period (December 2015). Although the networks are densely connected, they are not complete because we set a weight equal to zero when minus MES exceeds the expected returns of insurance company in the same time period (see Equation (7)).
Moreover, the networks are denser in periods of crisis, for example, the networks covering data for years 2007 and 2008[4], because of both lower returns and higher dependency (and, hence, higher MES) between companies.[5] In particular, it is noticeable that the situation at the end of 2008—where a very dense subgraph is observed—was characterized by a subset of insurers (mainly U.S. firms) that were highly correlated and had high ES values.
The main measures involved in the computation of are summarized in Figure 7. We analyze how the distributions of the average returns and ESs vary over time.
In this regard, the Distributions of Returns (Figure 7, left) shows the fluctuations of average returns of each company in the sample. As expected, in the periods of the Lehman Brothers failure and the sovereign debt crisis, the average returns are negative and there is higher volatility among firms. According to the Distribution of ES (Figure 7, right), the 2007–2009 crisis is outstanding in terms of the size and frequency of the extreme daily market losses. During 2008, the median of the distribution reaches values close to 10.5%, significantly higher than the values around 3.0% observed in quiet periods. The sovereign debt crisis period (in 2011) is also characterized by a slight increase in the median of ESs distribution (equal to approximately 5.0%).
In Figure 8, we report the distributions of edge weights at four different time periods. The distributions capture the effects of the increased distress that already affected the market in 2007; that is, both MES and ES slowly increased with respect to previous years. The average ratio between MES and ES increased in 2007 and reached a peak in the second half of 2008.
To provide a visualization of the pattern of weights for the whole period, Figure 9 reports mean and confidence intervals at 90% of weights distribution for each year. Another important effect can be detected in 2010 and 2011. There was an average increase in the weights because MES was growing faster than ES and, in particular, the differences in the patterns among the firms in the sample induced higher volatility. At the end of 2011, the standard deviation of the weights was higher than in previous periods. This is mainly because the sovereign debt crisis affected five countries of the Eurozone in a more substantial way. The pattern of the weights also captures the level of contagion for other Eurozone countries, which diminished in the second half of 2012 because of the successful consolidation and implementation of structural reforms in the countries that were most at risk.
4.3. Network robustness indicators and G-SII classification
To measure the level of interconnectedness in the network, at each time period, we computed the clustering coefficient, a well-known network indicator introduced by Barrat et al. (2004) for weighted networks. This indicator has been widely used as a measure of the state of stress of the financial market (see, e.g., Minoiu and Reyes 2013 and Tabak et al. 2014). Since our time span covered very turbulent periods that affected countries in different ways and with different timing, we divided the time period into four different subperiods. Following Lo Duca et al. (2017) and Clemente, Grassi, and Pederzoli (2019), without any pretense of being exhaustive, we defined our four subperiods: pre-crisis (January 2001–December 2007), Lehman Brothers failure (January 2008–December 2009), sovereign debt crisis (January 2010–December 2012) and post-crisis (January 2013–December 2015).
Distributions of clustering coefficients are reported in Figure 10. We observed that the median coefficient evolved consistently with the underlying financial events. It tends to be lower in calm periods and rise before crises. Sharper spikes occur around big events that caused severe stress in the global financial system: for instance, the 2008–2009 Lehman Brothers failure stands out as an unusually large perturbation to the network. Then a decline can be observed until 2010, when a greater focus emerged on sovereign debt in the Eurozone. A smaller peak can be observed in 2011 due to the presence in the sample of several insurance companies from countries that were most severely affected by the sovereign debt crisis.
To assess the relevance of each firm in the system, we computed the weighted effective resistance centrality for each vertex. The aim was to catch the importance of each firm by measuring the relative variation of the normalized weighted Kirchhoff index given by the removal of that vertex from the network. We repeated the procedure for each time period and we ranked firms according to this index. Since the edge weights are based on market-based measures, which are forward looking by nature, our purpose was to identify which firms were the most relevant from a systemic risk perspective.
Figure 11 shows the pattern of the normalized weighted Kirchhoff index over time computed at the network level. Periods such as 2007–2008 and 2011 with higher levels of interconnection in Figure 10 are characterized by a network with a lower degree of robustness in Figure 11. A higher value of means a higher level of network vulnerability, so, in these periods, the failure of a firm can have a larger impact on the whole market.
To focus on the behavior of each insurance company in terms of weighted effective resistance centrality (see Table 1), we ranked firms in decreasing order according to the average assumed by this index for each of the four subperiods. Since we are using a measure of robustness computed on a network that implicitly takes into account the tail dependence between equity returns, the firms in the top quantile can be interpreted to be the most interconnected in the network. We compared them with the insurance companies that were classified as G-SIIs (reported in italics in Table 1). Since Aegon replaced Generali Assicurazioni on the list in November 2015, we labeled all firms that belonged to the list at any time during the period as G-SIIs.
The methodology used by IAIS for identifying systemically important insurers is based on various characteristics, but the sizes of the firms and their interconnectedness with the system are two relevant issues. However, other points, such as global activity, asset liquidation, and substitutability have been considered (see, e.g., EIOPA 2017 and International Association of Insurance Supervisors (IAIS) 2013a). In our comparison, we have taken into account only a single aspect of this classification; namely, we deal with interconnections measured in the tails. We do not intend to propose a new methodology for assessing a G-SII.
It is interesting to note that insurance companies that are classified as G-SIIs also have a relevant impact on the robustness of the network. For instance, considering the whole period, we noticed that AXA, MetLife, AIG, Allianz, and Prudential belong in the top 10 in our ranking. Additionally, we also observed that Aegon increased its ranking, reaching a higher level of importance in the network than Assicurazioni Generali. This seems in line with IAIS’s replacement of Assicurazioni Generali with Aegon in the list of G-SIIs.
The main exception we found was Ping An Insurance, a company that is classified as a G-SII but belongs to very low quartiles of the distribution of the effective weighted resistance centrality in all periods. However, the presence of Ping An Insurance in the G-SII list is mainly justified by its size, which is not considered in our approach.[6]
It is also notable that these results are in line with those of Denkowska and Wanat (2020). Although Denkowska and Wanat used a smaller sample of firms and a different approach based on copula Garch models and a minimum spanning tree, common points are our use of market-based indicators computed on equity returns and application of methodologies to catch the dependence in the tails. As in our case, the authors confirmed the relevance of several firms that belong to the list (as AXA, Allianz, Aegon, Aviva, and Prudential) and the presence of other firms (as Zürich and Legal & General) that are not included in the list.
We also noticed in our analysis that some relevant firms of the U.S. market (see, e.g., Berkshire Hathaway and State Farm) appear to be top players in terms of robustness of the network.
The systemic relevance of reinsurance companies as well as their possible inclusion in the G-SII list (see, e.g., ESRB 2015, Annex 4) was the subject of much discussion. Although we did not consider risk transfer between insurers and reinsurers in this paper, it is interesting to note the presence of the largest reinsurance companies (Munich Re, Swiss Re, and Hannover Re) in Table 1. We can interpret this presence as a confirmation of the relevance of these firms in the market.
We also performed a specific analysis to evaluate possible similarities between the results displayed in Table 1 and the level of interconnection of the firms. To this end, we computed the local clustering coefficients (see Barrat et al. 2004) on each weighted network and we ranked firms according to this indicator. We noticed a general consistency between the results in Table 1 and the ranking based on local clustering coefficient. The correlation between the two rankings is equal to 0.7 if we consider the whole period. In particular, the two methodologies show higher correlation in the '‘pre-crisis’'period (equal to 0.8) and lower correlation in both periods of crisis. In particular, focusing on the G-SII list, we observed that relevant firms in terms of robustness are also highly interconnected in the network. Similarly, the largest reinsurance companies were also well clustered on average. On the other hand, other firms, such as Zürich and Legal & General, that assumed a relevant role both in Table 1 and in the results provided by Denkowska and Wanat (2020), showed lower levels of clustering.
Finally, it is noteworthy that some firms (e.g., Unum Group, Thrivent Financial for Lutherans, and Lincoln National) are clustered at a local level in specific subperiods but have a lower importance when robustness is considered.
Conclusions
Systemic risk is an widely studied issue. In this context, a relevant topic that has been addressed is the need to tighten up supervision on global systemically important financial institutions. We focus in this paper on the insurance sector and we provide a methodology based on a combination of market-based measures and a network approach for assessing relevant firms in the market.
In particular, our aim is to propose a specific network indicator, the weighted effective resistance centrality, that can capture the effect of the removal of a specific firm on the robustness of the network.
Empirical analysis shows how the insurance companies classified as G-SIIs by the IAIS are identified as relevant firms by our indicator with very few exceptions. Our proposal offers a complement to the more traditional approaches based on balance-sheet and regulatory data, not an alternative to the methodology provided by IAIS. Indeed, our results focus on the too-interconnected-to fail perspective using market-based measures whereas the methodology used by IAIS is also driven by size and by overall exposure, focusing on the too-big-to-fail concept and considering balance-sheet data.
Even if size is obviously relevant, the IAIS approach could be improved by combining market and balance-sheet data. For instance, in banking, Varotto and Zhao (2018) suggest classifying as globally relevant only those banks deemed '‘systemic’'by both approaches and focusing on banks for which there is no consistency between the approaches. This type of integration could also help regulators capture the multiple facets of systemic risk in the insurance field.
Acknowledgments
This work has been sponsored by the Casualty Actuarial Society. We thank editor Roger Hayne and two anonymous reviewers for their constructive comments.
_a_simple_graph__with_no_multiedges_or_self-edges_(b)_a_graph_with_both_multiedges_and_.png)


_a_connected_graph_(b)_a_disconnected_graph.png)





__at_different_time_.png)
_a_simple_graph__with_no_multiedges_or_self-edges_(b)_a_graph_with_both_multiedges_and_.png)


_a_connected_graph_(b)_a_disconnected_graph.png)





__at_different_time_.png)