The Actuary Takes the Stand: Compensation for Personal Injury

1. Introduction

Actuarial expert witness work is one of the nontraditional roles that consulting actuaries have been involved in for decades now. Becoming an expert witness has been receiving more attention and recognition worldwide (Wagner 2006). Many consultant actuaries are called upon and take the stand to present their expert opinions in financial lawsuits. These opinions might concern such topics as the pricing and reserving practices of insurance companies, the relationship between risk and return on investments, pension disputes, workers compensation, the cost impacts of claims-made or claims-paid financing, and so on (ASB 2018). Quantifying monetary damages in personal injury cases also falls within the area of actuarial expert witness duties.

Any person injured through the fault of another can claim monetary compensation, in the form of damages, for the injuries sustained, according to the laws of many countries (Lewis et al. 2003). The purpose of compensation is to provide a degree of financial restoration to the injured person’s pre-injury position, and it is often awarded as a lump sum representing discounted future income to the date of settlement, based on assumptions about life expectancy, work life expectancy (WLE), interest rates, and the specific laws and regulations of the country.

The established method for calculation of such damages is generally called the multiplier-multiplicand method. It calculates the product of a multiplicand, the estimated annual loss, and a multiplier, the estimated number of years over which the annual loss is to be paid. When these estimates have been determined by past cases and the previous experience of the judge, it is also called the courts method. However, in the absence of actuarial guidance, there is potential for inaccuracy and inconsistency. Juridical forecasts have become subjective and divorced from the realities of the financial world. While increasing reference to actuarial information over the last 20 years has improved the transparency and consistency of the calculation, the absence of economic reasoning and analysis is a potential source of inaccuracy and bias (Lewis et al. 2002a, 2003).

There has been a long-standing debate in almost all countries between, on the one hand, jurists and lawyers, and on the other, actuarial expert witnesses about the calculation of compensation. Although emerging countries experience more serious problems regarding compensation,^[1] the countries in which actuarial science and the law are well developed still have discrepancies between the parties. The main reason for these problems is that compensation calculations require deep actuarial knowledge as well as awareness of the laws and regulations of a specific country. Determining a fair amount of compensation is very important not only for injured parties but also for insurance companies, which need to keep enough reserves for these non-life insurance payments. Developed countries have specific actuarial compensation tables (e.g., the Ogden tables in the UK) for injury and death, and these tables help actuaries, lawyers, and others calculate the lump-sum compensation due in personal injury and fatal accident cases. However, these tables have been criticized for not including contingencies other than mortality, and for using discrete discount rates.

The practice and perspective of the courts in the UK require the use of the multiplier-multiplicand method based on the Ogden tables. Compared with those of the UK and most European countries, the U.S. tort system relies more on expert-driven damages calculations and less on formal judicial constraints. Nevertheless, the uniform damages methodology used for the U.S. September 11th Victim Compensation Fund to compensate victims and survivors of the World Trade Center and Pentagon attacks on September 11, 2001, can be considered similar to the UK’s Ogden table methodology (Ward 2009). Furthermore, income protection insurance, which has been crucial for millions of people in the course of the COVID-19 pandemic, is another insurance product that could benefit from the methodology discussed in this paper.

The compensation calculation is one of the rare areas in which property and casualty insurance and life and pension insurance intersect and are combined. Although motor vehicle insurance (sometimes referred to as car insurance or traffic insurance) and workers compensation insurance are types of casualty insurance, they also protect insureds from liabilities that arise due to injuries and death. This protection involves actuarial calculations based on life tables and life annuities. The premiums, indemnities, and reserves calculated for those casualty lines require elements of both life and casualty actuarial methodology. That is why this paper might inspire future research and collaboration between actuaries in different fields as well as providing a reconciliation between the jurists/lawyers and the insurance companies.

As a part of their role, actuarial expert witnesses should communicate actuarial matters clearly and concisely to a nonactuarial audience. Individuals who are unfamiliar with actuarial concepts might find it difficult to understand the testimony or the expert witness report. Poor communication of such concepts is one of the fundamental reasons that parties in personal injury cases dispute. In particular, disagreement arises due to lack of a common language and might lead to unfair compensation in terms of the payment period, the amount, or both.

The UK practice in personal injury and wrongful death litigation has a long and established history. It is one of the most settled systems, providing standardized methods and readily applicable actuarial tables, called the Ogden tables. Although such a system improves the practice significantly by ensuring that parties have a comprehensive understanding of the calculations, it is still possible to enhance the methodology. One way is to consider age-earnings profiles for earnings changes over an individual’s life cycle. This paper introduces age-earnings profile tables that are compatible with the Ogden tables, in an effort to improve UK compensation calculations.

The structure of the paper is as follows: Section 2 provides a literature review mainly considering U.S., UK, and European applications. Section 3 focuses on the compensation methodology used in the UK. Section 4 introduces the data used to construct the age-earnings profiles and describes the details of the analysis performed. It presents semiparametric regression and a smoothing splines methodology to obtain fitted, interpolated age-earnings profiles. The section also provides examples to show how the introduced tables can be employed in compensation calculations that use the UK approach, as well as comparisons with calculations based on the Ogden tables alone. Section 5 presents a discussion grounded on the UK and U.S. systems and the implementation of the proposed approach. Finally, Section 6 concludes.

2. Literature review

The literature on compensation for loss of income shows that the calculation is a subject for a multidisciplinary field served by actuarial, economics (especially forensic economics), law, social policy, and demography journals. We present the literature review on compensation for loss of income in two parts: First, we will refer to the book Personal Injury and Wrongful Death Damages Calculations, edited by Ward and Thornton (2009), which was published as a volume of the Transatlantic Dialogue series. It combines 12 original papers that explore common research areas in the calculation of damages in personal injury and death litigation in western Europe and the United States. Second, we will focus on the UK literature to introduce the UK methodology and use of the Ogden tables.

2.1. Western Europe and the United States

Ward and Thornton (2009) edited the book Personal Injury and Wrongful Death Damages Calculations, an important source to understand worldwide implementation of compensation calculations. The book consists of 12 original papers that discuss and compare the different methodologies of different countries. The collection of papers had its origin in a series of annual meetings of the National Association of Forensic Economics held in the UK, Ireland, Italy, and the United States from 2004 to 2008. The papers aim to discuss several aspects of the calculation: Ward (2009) compares the U.S. methodologies for calculating economic damages with the procedures used in the UK and other European Union countries, while Kelly (2009) discusses the future development of the Ogden tables. Wass and McNabb (2009) analyze the labor market effects of disability over a working lifetime, finding a significant employment disadvantage compared with that assumed by the UK courts; they go on to develop a two-state increment-decrement model to estimate WLEs by sex, age, disability, and employment status. This model is used to estimate individual WLEs before and after injury. A similar study is introduced by Butt et al. (2009), focusing on the deficiencies in the estimated employment risks contained in the Ogden tables—that is, the use of unconditional employment rates and the failure to account for the impact of disability. The authors introduce updated estimates of the reduction factors (RFs) for employment risks by using the multiple-state Markov process. These estimates are conditioned on sex, age, disability, and starting employment status. The authors use an additional covariate, educational achievement, which improves the employment estimation. Skoog and Ciecka (2009) provide an overview on work life–related research in the United States over the last 25 years, emphasizing theoretical and empirical developments during this period, such as the switch from life table–based constructs to Markov process models, parametric and nonparametric work life models, models of full-time and part-time work life, and occupation-specific work life models. Cropper and Wass (2009) discuss a fundamental change in the approach to quantifying bodily injury claims: the conversion of lump-sum payments into periodical payments for compensation. This conversion, they argue, may lead to a transfer of the risk of investment returns and uncertain mortality to the tort-feasor. They also discuss further issues related to the indexation of periodical payments. Krueger and Albrecht (2009) concentrate on the level of economic damages that can be recovered based on the difference between the claimant’s pre-injury and post-injury economic output and the methods used to determine economic damages in tort cases. They cover widely accepted economic theories and methodologies, which compose the so-called U.S. approach to computing economic damages.

Although the Ward and Thornton (2009) Transatlantic Dialogue presents a comprehensive literature on compensation calculations, there are many other papers that compare the methodologies and tables of the countries (Lewis et al. 2002a, 2003; Lewbel 2003; Verrall, Haberman, and Butt 2005; Butt et al. 2008; Butt 2014, etc.).

2.2. The UK

In the UK, the compensation calculations for personal injury and wrongful death cases are based on specific actuarial tables called the Ogden tables. These tables, currently in their eighth edition (GAD 2022), are the baseline loss of earnings tables that are disaggregated by age, sex, discount rate, and year of retirement. In the fifth edition of the Ogden tables, Haberman and Bloomfield (1990) introduced RFs as the multipliers for contingencies other than mortality, such as employment. The RFs, presented as supplementary tables that represent the WLE expressed as a proportion of the remaining years until retirement, have been used to adjust the Ogden multipliers by incorporating employment risks based on age, occupation, geographic location, and economic activity.

Lewis et al. (2002a, 2002b, 2003) draw attention to the lack of an attempt to incorporate labor economics in calculations based on the multiplier-multiplicand method applied in England and Wales. They first consider whether the multiplier-multiplicand method produces compensation amounts significantly different from those calculated using a labor economics methodology that is restricted to make it accessible to the courts. Then, to compare these two approaches’ results with those of the method used by forensic economists in the United States, they construct a methodological framework, based on U.S. personal injury cases, that considers the human capital theory of wage determination. This framework measures the lifetime earnings function based on age-earnings profiles that also take into account education, sex, and growth in the level of average earnings over time. Based on these factors, the authors propose the following formula to calculate expected future earnings over an individual’s working life, expressed in present-value terms (Lewis et al. 2002a):

$$P V(W)=\sum_{j=1}^{T} \frac{W_{j}\prod_{i=1}^{j}\left(1+g_{i}\right)}{\prod_{i=1}^{j}\left(1+r_{i}\right)}\tag{1}$$

where $W_j$ denotes the wage an individual receives at each age $j$ over a $T$-year working life and varies by time due to increases in individual productivity; $g_i$ represents the growth rate, reflecting the average productivity growth over time and possible cohort effects; and $r_i$ is the real discount rate. Use of a real discount rate avoids the need to adjust earnings growth for the possible effects of inflation. $g_i$ is based on historical data for movements in average economy-wide earnings and shifts the age-earnings profiles over time.

Further, Lewis et al. (2002b) adjust the methodology to estimate post-injury earnings, hence considering the disability effect, and they calculate employment probabilities as well as estimate the parameters in (1) by using data from the UK Labour Force Survey 1996–1997. They conclude that the difference between the court award and the award calculated by their alternative method, which includes both individual-specific and economy-wide earnings growth, is significant for the sample of 100 adjudicated cases and subgroups they consider. Both women and men are equally undercompensated under the court methodology, and excluding future earnings from the calculations accounts for 70% of the undercompensation, on average. The results vary by age, sex, employment, and education (for more details, see Lewis et al. 2003).

The inverted U–shaped profiles that are produced based on cross-sectional data to measure age-earnings profiles generally underestimate the growth of earnings at younger ages and overestimate the decline in earnings at older ages. Thus, the use of mean earnings to construct age-earnings profiles might be problematic due to this method’s contradictions with the underlying theory. A way to deal with this problem is to estimate empirical earnings functions, which requires the specification of an appropriate functional form to express the way earnings vary with years of experience. Although the quadratic specification is the most commonly used form, the U.S. evidence suggests that fourth-degree polynomials provide better approximations of earnings profiles (Lewis et al. 2002a). In contrast to cross-sectional data, the use of individual longitudinal data might not produce the inverted U–shaped profile, instead yielding earnings profiles that continue to rise until retirement. On the other hand, Rodgers, Brookshire, and Thornton (1996) show that forecasts for the present value of earnings for young employees based on cross-sectional data sets do not differ significantly from those based on panel data sets. As will be seen in Section 3, the cross-sectional UK data also suggests inverted U–shaped age-earnings profiles for both males and females as well as both full-time and part-time employment. We will discuss the nature of the data and the results in detail in Section 3.

Butt et al. (2008) aim to improve the RFs proposed by Haberman and Bloomfield (1990) by considering the current employment status and the disability. They also provide an extended literature review on compensation calculations, introducing substantial research for both the UK and the United States. The authors constrain their own study, however, to the multiplier-multiplicand method of calculations because it is a standardized method and is used by the UK courts. They propose advanced supplementary tables for the nonmortality contingencies, based on two methods: transition probabilities and transition intensities (hazard rates). The main contribution of the paper is to provide a dynamic modeling of employment risks disaggregated by disability, following in the footsteps of Haberman and Bloomfield (1990) by making use of the advancing labor market data in the UK. Taking into account that the WLE is essential to compensation calculations, they derive RFs by calculating the WLE and employment risks disaggregated by disability.

In a more recent study, Chan, Chan, and Li (2012) investigate how the uncertainty surrounding mortality and interest rate assumptions affects the precision of actuarial multipliers, using stochastic mortality and interest rate models for the UK. They draw attention to the lack of any information in the Ogden tables about the underlying uncertainty. They conclude that if both mortality and interest rate risks are taken into account, then the confidence interval for a multiplier can be as wide as 31% of its best estimate, indicating a significant level of uncertainty involved in the actuarial approach to calculating damages.

Building upon this research background, the aim of the present paper is to improve compensation calculations using a hybrid methodology that combines the UK and U.S. systems. The literature suggests that the U.S. system mainly focuses on positive contingencies, such as real wage increases and life cycle earnings, while the UK system focuses more on negative contingencies, such as the RFs related to education level, unemployment, and disability. This paper introduces tables for age-earnings profiles for males and females for the UK as a promotion factor to be inserted in the calculations.^[2] The approach is different from the ones introduced in the U.S. methodology, since the existence of the Ogden tables requires construction of a compatible table. Use of the Ogden tables in the UK courts has achieved a standardization in compensation calculations. However, the tables have been criticized for the absence of real growth in earnings, age-earnings cycle adjustment, and post-injury risk adjustment. This paper discusses the design of promotion tables that can be used, for example, with the Ogden tables. We believe that the proposed approach will fill the gap and can also be improved in a consistent way so that it can easily be adopted by practitioners of the UK compensation methodology.

3. Loss of earnings calculations in the UK

This section introduces the use of the Ogden tables.

3.1. The Ogden tables

The Ogden tables are actuarial tables constructed specifically to assist UK courts in compensation calculations for personal injury and death cases. A working group composed of experts from different fields, including actuaries, lawyers, and accountants, was established in 1984 to work on the calculation of compensation for financial losses or expenses directly caused by personal injury or death. The group published a set of actuarial tables and explanatory notes providing suitable multipliers to be used to calculate lump-sum awards of compensation.

These tables, known as the Ogden tables, have been updated regularly, and the latest version, the eighth edition, was published in 2022 (GAD 2022). As described by government actuary Martin Clarke in his foreword (2022), the tables have been improved and extended since their first publication. Further editions provided multipliers for different retirement ages for males and females based on updated mortality projections. Starting with the fifth edition, additional tables have been introduced for contingencies other than mortality. There have been changes in the discount rates used in the tables, and explanatory notes have been expanded as well as examples provided to assist practitioners. The ultimate aim of the tables is to ensure a balance between accuracy and simplicity in their application, which, among other things, helps the reconciliation process by providing a certain level of understanding of the compensation calculations.

The methodology used in the Ogden tables is based on the construction of the multipliers. Multipliers are the present values calculated for specified discount rates per unit of future annual loss, which is net of tax in the case of loss of earnings and pension. The multiplier is the figure by which an annual loss is multiplied to obtain a capitalized sum by taking mortality risks and accelerated receipt into account. The calculated sum is also discounted by using the RFs, which represent the contingencies other than mortality.

3.1.1. Discount rate

The annual interest rate, after tax and inflation, used to calculate the present values is called the discount rate. Although the discount rate was previously set based on the yields of index-linked gilts, a method that was expected to yield rates close to risk-free returns, since 2001 new statutory discount rates have been set by the lord chancellor. Different discount rates apply in the three UK jurisdictions: -0.75% in Scotland, -0.25% in England and Wales, and +2.5% in Northern Ireland. In the latest edition of the Ogden tables, the discount rates presented in the multiplier tables range from -2% to +3% (GAD 2022).

3.1.2. Mortality data

The eighth edition provides 36 separate Ogden tables as well as several sets of additional tables (GAD 2022). Tables 1 to 34, which present the multipliers for annual loss or expense that are designed to represent three different periods—for life, until retirement, and post-retirement—for men and women separately, use the projections of future mortality rates produced every two years for the UK and its constituent countries by the Office for National Statistics. The eighth edition provides multipliers based on mortality rates from the most recent, 2018-based, projections, which were published at the end of 2019. The last two tables, Tables 35 and 36, are designed to be used for losses with regard to deferred and fixed periods of time. Since the mortality projections are not relevant in these tables, the multipliers are the same for men and women.

3.1.3. Contingencies other than mortality

Tables 3 to 18 of the current Ogden tables (GAD 2022) do not take into account any contingencies other than mortality. In order to calculate more accurate compensations, then, it is necessary to include unemployment risk. To this end, Butt et al. (2008) constructed additional tables to be used as a part of the Ogden tables in order to include unemployment risk as an RF. They built the RFs based on essential features, such as sex, age, employment, disability status, and educational attainment, that affect a person’s future working life. These are presented as Tables A to D in the Ogden tables.

These RFs were initially introduced by Haberman and Bloomfield (1990). Although the deficiencies in their methodology were acknowledged by the authors themselves, the factors were not changed until the sixth edition of the Ogden tables due to lack of data that would enable the estimation of transition probabilities in a multistate model. As briefly discussed above, a related analysis was published by Lewis et al. (2002b); later, with involvement of the Ogden Working Party, Butt et al. (2008) carried out research regarding the RFs and constructed tables that first appeared in the sixth edition. Their research, based on data from 1998 to 2003 published in the Labour Force Survey, provides estimates for the probabilities of movement of females and males between different employment states, depending on age, level of disability, and starting employment state. Essentially, these probabilities allow the calculation of the working life expectancy, which is defined as the working time to retirement. The constructed RFs are applied to the relevant baseline multipliers, presented in Tables 3 to 18 of the Ogden tables (2022), in order to obtain a multiplier that considers the period that the claimant would be expected to be engaged in work, on average.

4. Modeling age-earnings profiles

4.1. Data

We use data from the Annual Survey of Hours and Earnings (ASHE; see ONS 2021, 2022) to construct age-earnings profiles supplementary to the Ogden tables. ASHE provides data in all industries and occupations across the UK, including information regarding the levels and distribution of employees’ earnings and their paid hours worked. ASHE data is based on surveys of businesses each year and covers about 180,000 jobs from around 60,000 responding businesses. The sample of employees from which the data sets are constructed does not change from year to year, except for retirees and new entries, and thus ASHE data sets are combined to obtain a panel data set. Since the data set observes the same employees in each year, provided that they are in employment and their employer responds to the survey, it allows analyzing the hours and earnings of different cohorts of employees. The estimates presented by the ASHE results tables are available by age group, occupation, industry, sector (public or private), full- versus part-time work, and a range of geographies.

Data provided by ASHE is considered to be more accurate than that of the Labour Force Survey since it is based on information provided by employers, rather than being self-reported by employees. ASHE data is used as the main source to analyze the distribution of earnings in the UK because it benefits from a large sample size that allows more detailed analysis than do other sources. It is also the principal source of data to estimate the public- and private-sector pay differential, the gender pay gap, and the number of employees being paid below minimum wage and below living wage. The large sample size also gives ASHE a longitudinal aspect that is not present to the same extent in other surveys of earnings (ONS 2021, 2022).

The estimates vary in quality, particularly depending on the size of the samples. Thus, ASHE provides quality information—the coefficient of variation—about the estimates. For each combination of full-time/part-time and male/female workers, estimates for hours and earnings are given separately. We use median as the measure of typical earnings in our analysis since it is the preferred measure of the Office for National Statistics. In earnings distributions, a relatively small number of high-paying jobs may have a disproportionate impact on the mean. On the other hand, the median is less affected by a skewed distribution and provides a more accurate picture of typical pay than the mean.

4.2. Semiparametric regression and smoothing splines

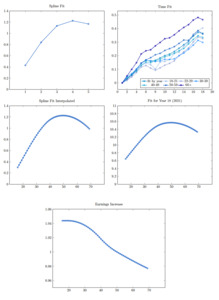
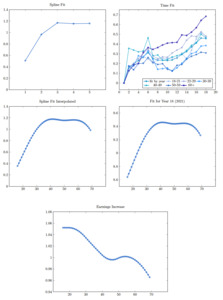
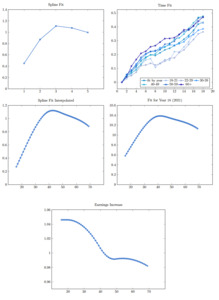
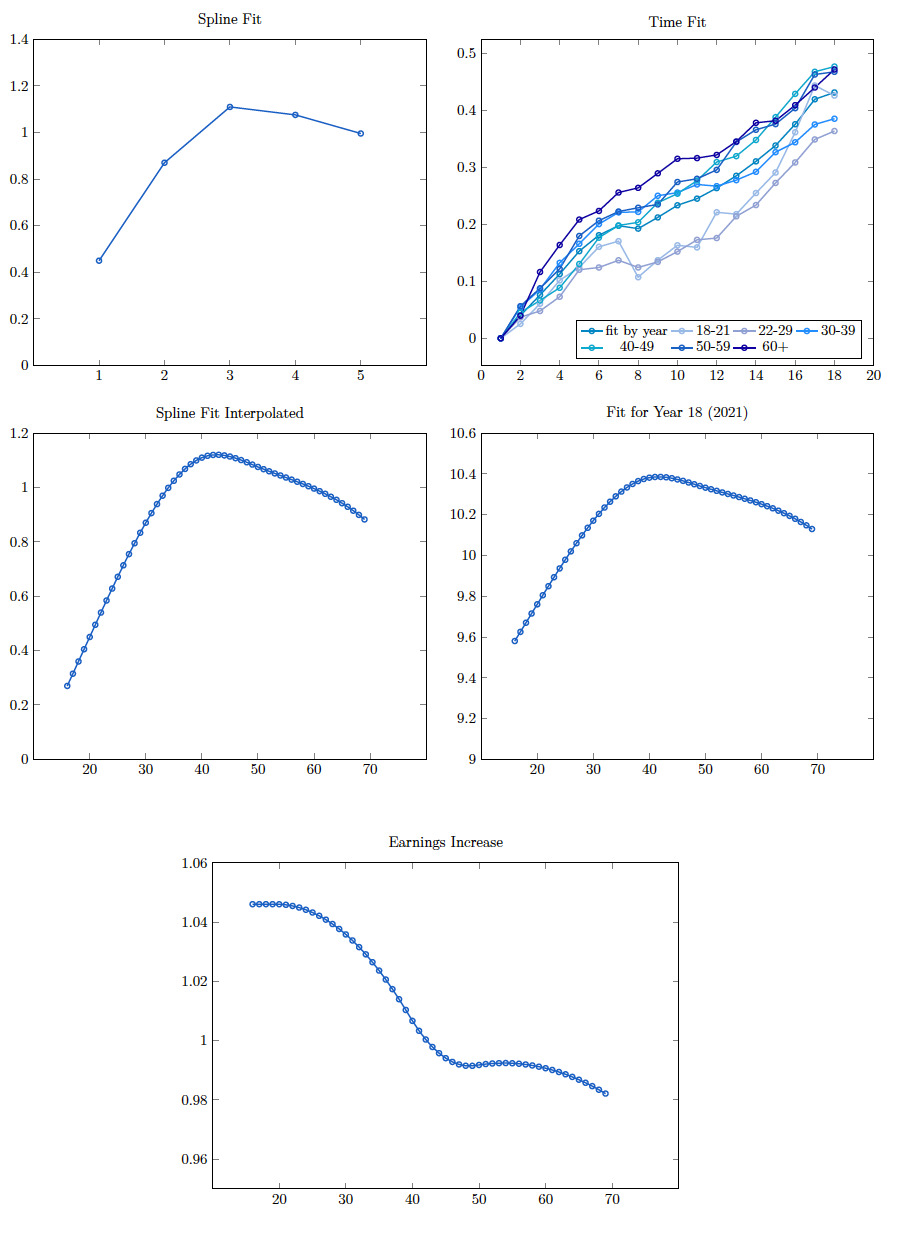
We use semiparametric regression and smoothing splines to construct the age-earnings profile tables for ASHE data. Figure 1 displays the average annual gross earnings for full-time and part-time employees, both male and female, over the period 2004 to 2021, for different age groups (18–21, 22–29, 30–39, 40–49, 50–59, 60+). The 18–21 age group has the lowest average earnings for men and women, both full- and part-time. The 30–39 age group has the highest average gross earnings for full-time and part-time females up through 2019, while the 40–49 age group has the highest for full-time male employees. Earnings data for part-time male employees is reported to be relatively low-quality data, based on the coefficient of variation. This might explain the slightly different patterns the average earnings display for this group. The steady increase in the earnings profiles over the years indicates stationary annual increments, although the effect of the COVID-19 pandemic on earnings can be observed as slight decreases, particularly in full-time male earnings, in 2021.^[3]

Figure 1.Average annual gross pay for full time and part time male and female employees

We fit age$\times$year models to the rectangles of median earnings for four sets of data—male full-time, male part-time, female full-time, and female part-time. This approach enables us to interpolate the ages, which display big lumps. We fit smoothing splines using ridge regression, and the design matrix is a simplified version of the proposed design matrix in Venter (2021) for mortality modeling for contagious events.

A design matrix is constructed presenting dummy variables in columns of each year and age group for each observation. The first age group is not included for specificity, as suggested in Venter and Şahin (2021) and Venter (2021), and a constant term is also added. The years and age groups are not independent of each other, and therefore further constraints are imposed. The design matrix has 17 columns for year variables and 5 columns for age variables. To fill out the design matrix, reference columns are created for each data observation to specify the year and age it comes from.

We fit our age$\times$year model by using a linear smoothing spline for year and a cubic spline for age. As for the linear splines in the model, the variables are the second differences of the final year parameters. The variable for year $i$ remains 1, as in the straight regression design matrix for observations with year $i,$ and 0 for earlier observations. For each cell from year $k$, the dummy for year $i$ is

$$(1+k-i)_+ \tag{2}$$

On the other hand, cubic splines have similar design matrices. Venter (2021) defines cubic spline design matrix entries by considering one direction of variables such as age, with spline segment variables $f_1$ to $f_n$. The design matrix value $f_i(z)$, for an observation at age $z$, is a function defined for any real number, $0\leq z \leq n$, so that the curves can be interpolated. They are defined as $f_1(z)=1, f_2(z)=z$, and for $i>2$,

$$\begin{align} f_i(z)&=(z-(i-2))^3_+ \\ &\quad - (n-(i-2))(z-(n-1))^3_+ \end{align} \tag{3}$$

The second term is nonzero only for $z>n-1$, and the design matrix has values only for integers. In our model, we use a simplified version of the cubic spline design matrix for the age variable, as proposed by Venter (2021), which is given as

$$f_i(z)=(z-(i-2))^3_+ \tag{4}$$

As seen from (4), the simplified version includes only the first part of (3), mainly because the last part is important to how the spline interpolates in the last interval and how it projects into the future. We will not use the spline model fitted here for projections. Thus, we prefer a simplified cubic spline design matrix for our earnings profiles model.

Smoothing splines are mainly used to increase smoothness of the splines by imposing constraints, as in ridge regression, which also improves accuracy (see Venter 2021 for details). We use a shrinkage methodology to reduce error variances, a method that has been used in credibility theory for more than a century and was extended into regression by Hoerl and Kennard (1970) with ridge regression. Ridge regression is used to estimate parameters $\beta_j$ by minimizing the negative log likelihood (NLL) plus a proportion, $\lambda$, of the sum of the squared parameters:

$$NLL+\lambda \sum \beta_{j}^{2} \tag{5}$$

The method is also called regularization. Ridge regression mainly shrinks the fitted means toward the grand mean. The choice of $\lambda$ is the main concern, as it is significant in the resulting parameter estimates. The selection is generally accomplished by cross validation. As described by Venter (2021), the data is separated into smaller subsets and the model is estimated by fitting the data several times for different values of $\lambda$, with each subset separately kept out. The NLL can then be calculated for each subset using the models that omitted it, and the results compared across $\lambda$s.

The matrix representation of the spline regression we use for the earnings profiles is given as

$$\small \begin{align} \left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right]_{n \times 1}=& {\overbrace{\left[\begin{array}{cc:c} 1 & x_{(y 2), 1} \ \ \ \ \ \ldots \ \ \ \ \ x_{(y 18), 1} & x_{(a 2), 1} \ \ \ \ \ \ldots \ \ \ \ \ x_{(a 6), 1} \\ 1 & x_{(y 2), 2} \ \ \ \ \ \ldots \ \ \ \ \ x_{(y 18), 2} & x_{(a 2), 2} \ \ \ \ \ \ldots \ \ \ \ \ x_{(a 6), 2} \\ \vdots & \vdots \ \ \ \ \ \ \ \ \ \ \ \ \vdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots & \vdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ 1 & \underbrace{x_{(y 2), n} \ \ \ \ \ \ldots \ \ \ \ \ x_{(y 18), n}}_{year\ variables} & \underbrace{x_{(a 2), n} \ \ \ \ \ \ldots \ \ \ \ \ x_{(a 6), n}}_{age\ variables} \end{array}\right]}^{Design\ matrix}}_{n \times 23} \\ &\times\left[\begin{array}{c} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_{23} \end{array}\right]_{23 \times 1}+\left[\begin{array}{c} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n \end{array}\right]_{n \times 1} \hspace{13em}{(6)} \end{align}$$

and the parameters, $\beta$, are estimated using ridge regression as

$$\widehat{\mathbf \beta}_{ridge}=(\mathbf X\mathbf X'+\lambda \mathbf{I})^{-1}\mathbf X'\mathbf Y\tag{7}$$

where $\mathbf Y$ represents log earnings for each year and age group, $\mathbf X$ is the design matrix including linear spline (2) for year and cubic spline (4) for age variables, and $\lambda > 0$.

Now we need to decide on the value of $\lambda$ to estimate the ridge regression parameters, $\beta$. We use a brute-force leave-one-out (loo) cross-validation to find the optimum $\lambda$. The nonlinear minimization, $nlm$, program in R is used to find the $\lambda$ with the lowest loo sum of squared errors (SSE), which is the cross-validation $\lambda$. The R code for the calculations is given in Appendix A.

The sum of squared error at the specified $\lambda$ is the output from $nlm$, which is given in Table 1 for four sets of data. Table 1 also presents the mean absolute percentage error (MAPE) for each data set to illustrate the goodness of fit of the ridge regression with given $\lambda$ values. MAPE expresses the mean or average of the absolute percentage errors of predicted values.^[4] The lower the value for MAPE, the better a model is able to predict values. Except for the male part-time data set, whose MAPE value is $4\%$, the MAPE values are around $2\%$, indicating a good fit.

Figures 2, 3, 4, and 5 present the linear spline (for years) and cubic spline (for age groups) fits; spline fits for interpolated ages; interpolated annual gross log earnings for year 2021; and the annual increase in earnings for male full-time, male part-time, female full-time, and female part-time gross earnings data. The cubic splines produce similar inverted U–shaped age-earnings profiles with slight differences for the four sets of data. Linear splines to capture the year effect indicate steadily increasing earnings over the years, with the 50+ age group displaying a higher overall trend, except for male part-time earnings. Annual gross earnings increases start at values between 1.04 and 1.06 and indicate an increase in earnings up through the early to mid-40s. Earnings level off for a couple of age groups, display a slight increase in the early 50s (apart from male full-time earnings), and decrease as age increases into the 60s.

Figure 2.Spline fit for male full-time annual gross earnings

Figure 3.Spline fit for male part-time annual gross earnings

Figure 4.Spline fit for female full-time annual gross earnings

Figure 5.Spline fit for female part-time annual gross earnings

Linear and cubic splines tend to have slightly different curve shapes and can provide fits that are subtly different. Tests can show which splines fit better, but often the measures are close and it becomes a matter of actuarial judgment. Linear splines often seem to fit slightly better and converge faster. Cubic splines give smoother interpolation, which sometimes is important. The details of those estimates are more extensive than needed here, where we present only the final models. Lasso is often used for spline estimates instead of ridge regression, but the latter is easier to include in your own code as well as in other software packages and is easier to optimize. Lasso does make some coefficients exactly zero, which is convenient, although which ones it does this to differs for different $\lambda$s. Popular R lasso software presents a few $\lambda$s chosen by cross-validation, and eliminating the zero variables from the smallest of these is usually helpful before applying more complex routines. However, cubic spline fits often need smaller $\lambda$s than the default settings of R lasso apps generally use. Ridge regression, being closed-form, does not have this problem.

Annual gross earnings and earnings increases obtained from the spline models for 2021 are presented in Table 2 for males and Table 3 for females, for interpolated ages starting at 16 and ending with 69. The purpose of the construction of the tables is threefold: First, these tables can be considered as a benchmark to decide the annual gross/net earnings to be used in the compensation calculations for different ages when the annual income is not known or the person is unemployed at the time of the injury. Second, the earnings increase can be used as a factor to consider the age-earnings profiles in the calculations. And finally, the interpolated earnings for part-time employment can be used as the earnings after the injury, since many injured people have to be included in part-time employment due to being disabled. We illustrate the use of the tables in the following examples.

4.2.1. Examples

The following examples are based on the Ogden tables, eighth edition (GAD 2022), and the loss of earnings calculations have been made considering the age-earnings profiles. The annuity values are computed for each year^[5] and multiplied by the relevant RFs presented in the Ogden tables (Tables A to D) as well as the annual gross income^[6] to illustrate the effect of the earnings profiles. The first two examples provide six tables in total for the details of the calculations, and two summary tables to illustrate the results for different discount rates. The third example presents several scenarios to illustrate how the age-earnings profiles affect the resulting loss of earnings.

Example 1

The claimant is female, age 35 at the date of the trial. She has a degree, she was not disabled, and she was in employment at the date of the accident (Table C in the Ogden tables to be used) at a gross annual income provided by the age-earnings profile table for all relevant ages (Table 3 to be used). As a result of her injuries, she is now disabled (Table D in the Ogden tables to be used) and lost her job but has found part-time employment at an annual gross income provided by Table 3. She expected to retire at age 65 pre-accident and still intends to retire at this age following her injuries. Her future loss of earnings is calculated based on the income at age 35 in Table 3, assuming no increase over the years, which is akin to the calculations using the Ogden tables. The loss of income is also calculated based on the age-earnings profiles table, which considers the change in annual earnings as age increases. We present the calculations as well as the percentage difference between the Ogden table approach and the age-earnings profiles approach. Discount rates are chosen as -0.75%, 1%, and 3% to illustrate the effect of positive and negative rates on the calculations. The percentage changes at the end of each table are calculated as the ratio of difference between the indemnities obtained from Ogden tables calculations and those from the age-earnings profiles approach, based on age 35 income for the Ogden table calculations. Table 4 (given here) and Tables 9 and 10 (in Appendix B) present the results as well as the percentage changes in the loss of earnings amounts based on the two different approaches.

Example 2

This example is very similar to Example 1, but this time the claimant is male and the annual gross income is given in Table 2 for all relevant ages. Table A and Table B from the Ogden tables are used to insert the RFs. With discount rates taken as -0.75% (Table 5), 1%, and 3% (Tables 11 and 12 in Appendix B), we present the results as well as the percentage changes in the loss of earnings amounts based on the two different approaches.

As seen from Tables 4 and 5 (and Tables 9, 10, 11, and 12 in Appendix B), the difference between the proposed approach and the Ogden table calculations highly depends on the age and sex of the claimant, the age-earnings profiles, and the RFs. Discount rates, on the other hand, though they significantly affect the indemnity amounts in both examples, have very similar effects on the compensation amounts calculated by the two approaches, leading to almost identical percentage changes. We generate different scenarios to explore the effects of those factors in Tables 6 and 7 below.

Tables 6 and 7 suggest that the percentage differences between the indemnity amounts calculated by the two approaches are negligible for females, a result that is mainly related to the age-earnings profiles. The use of beginning earnings for females age 35 does not significantly affect the results when using age-earnings profiles. On the other hand, for males, the indemnities under the Ogden tables approach are about 17% to 21% lower than those calculated using our proposed approach.

Example 3

This example illustrates the percentage differences between the calculated indemnities for claimants age 25 who cannot work after the accident due to their injuries and whose pre-injury incomes are not known. In this case, we use full-time earnings profiles—first beginning earnings and, second, average earnings—to determine the pre-injury earnings on which to base Ogden tables calculations. Calculated amounts represent the loss of earnings after the accident, due to claimants’ inability to work. Table 8 presents the percentage differences between the indemnities obtained from the Ogden tables and those from the age-earnings profile tables.

When we use the average earnings obtained from the age-earnings profile tables as the pre-injury earnings level and calculate the indemnities using both the Ogden tables approach and earnings increases from the age-earnings profiles, the discrepancies are insignificant. However, the use of beginning earnings in Ogden tables calculations leads to 45% to 53% lower compensation payments for males and 32% to 34% lower payments for females, compared with the age-earnings profiles approach, for different negative and positive discount rates. These differences would decrease as the age of the claimant increases.

On the other hand, based on comparing the results of the Ogden tables method with those of the age-earnings profiles method, both using beginning earnings, we can also comment on the impact of the compensation calculation on the typical motor insurance premium. Assuming that third-party bodily injury costs represent 15% of the motor insurance premium, the age-earnings profiles compensation methodology increases the premiums by about 7% to 8% for males and 5% for females. If the relevant costs represent 20% of the premium, then the age-earnings profiles compensation approach increases premiums by about 9% to 11% for males and about 7% for females. Furthermore, the analyses suggest that improved calculations by the age-earnings profiles would not be enough to substantially increase premium levels for females based on Tables 4, 9, and 10, while Tables 5, 11, and 12 indicate only a 2% to 4% increase in premiums for males.

4.2.2. Use of ASHE data and periodical payments for loss of earnings

The eighth edition of the Ogden tables (GAD 2022) introduces a new section that discusses the possible ways of calculating the loss of earnings as periodical payments. Once the periodical payments are considered, the discount rate, which is set by reference to real (being relative to price inflation) and net (after taxation, investment charges, and costs) returns, should be set. According to the Civil Liability Act 2018, in England and Wales the discount rate is based on the consumer price index plus 1%, while in Scotland, being set under the Damages (Investment Returns and Periodical Payments) (Scotland) Act 2019, it is based on the retail price index (RPI), which reflects inflation.

Wages have historically risen more than inflation, and annual payments are the most accurate way to closely balance adjustments in earnings-based losses and costs that could arise. In the case of loss of earnings claims being paid in the form of periodical payments, indexation and accounting for residual earnings capacity should be considered. Indexation is the process of escalating the periodical payments into the future under the Damages Act. The act set RPI as the default measure, but any other measure that satisfies the Mackay test, whose requirements are listed in the Ogden tables, may be used (see GAD 2022). The Ogden Working Party suggests that such periodical payments be indexed by reference to the ASHE standard occupational classification. It further recommends the use of ASHE data as a reliable and useful source to estimate individual earnings and earnings growth for specified occupations both pre- and post-injury.

In line with the above suggestions, we introduce a different set of ASHE data (ONS 2021, 2022), annual earnings for full-time and part-time employment, to improve the calculations for lump-sum payments. Although the method’s calculations can be considered to include the promotion by age factor, the spline fits indicate a decrease in annual earnings in all specified categories after a certain age. Clearly it is unlikely to find a decrease in salary scales as age increases in different industries or occupations. Perhaps the way the data is collected by ASHE might be the source of the inverted U–shaped age-earnings profiles. As explained at the beginning of this section, the data is provided by the employers. Thus, annual gross earnings may seem to decrease only because the industries reporting the data have relatively higher numbers of older employees—and employees with higher incomes might retire earlier than those with lower incomes. Another possible explanation might be young people who are employed by modern enterprises at higher incomes while older people may be employed by older industries, as well as have a higher probability of unemployment. ASHE uses median income rather than mean, since the distribution of earnings is skewed, with more people earning lower salaries than higher salaries (ONS 2021, 2022).

5. Discussion of the UK and U.S. systems

The U.S. forensic economics literature provides a well-developed research on calculating the future loss of earnings and on the dynamic multivariate modeling of employment decisions. Since the 1950s, the U.S. Bureau of Labor Statistics (BLS) has published work life tables of the U.S. population, as well as regular reviews of the tables’ methodologies and results. The first Markov chain increment-decrement work life tables introduced by the BLS were inspired by the research of Smith (1982), which was extended to allow for the effects of race, education, and gender in Smith (1986). These tables also made use of larger data sets based on population surveys (Butt et al. 2008).

Ward (2009) summarizes the U.S. methodology as follows. The U.S. tort system uses a multiple-state model and also allows for economic and individual productivity growth in the estimation process. Damages are generally calculated on the basis of gross earnings. All states require a discounting, but in some states that discounting can compensate for presumed future increases in costs or earnings. A few U.S. states legislate a discount rate, while the household services lost to plaintiffs as a result of a wrongful act are recoverable in all states. Moreover, collateral income sources are not permitted as deductions from earnings loss in general. Pre-judgment interest (past losses) is not allowed, and reductions for collateral payments from social security agencies are not made in the United States.

As mentioned earlier, the U.S. tort system relies more on expert-driven damages calculations than do the systems of the UK or most European countries. Ward (2009) reviews the Ogden tables approach and proposes economic loss tables (EL tables) for the United States that might be considered akin to the Ogden tables. The advantages of the Ogden tables can be listed as the simplicity and transparency of the calculations, the predictability and uniformity of the awarded damages, and the avoidance of expert testimony costs. On the other hand, the tables have been questioned for the accuracy of their calculations—that is, whether the multipliers are reasonable and reflect the true economic loss. In answer to these concerns, Ward (2009) introduces the EL tables—multiplier tables for the United States based on age, gender, race, and education level. The multipliers use the real net discount rate to consider future expected wage and compensation increases as well as interest rates. Two provided sets of tables consist of, respectively, the life cycle earnings pattern adjustment and the constant real wage rate growth that is embedded in the net discount rate.

Our proposed age-earnings profiles for the Ogden tables are inspired by the EL tables constructed by Ward (2009) for the United States. We provide an alternative way of including a life cycle earnings pattern in the compensation calculations, which is adaptable to the existing Ogden tables. The promotion tables proposed in this paper might be used for the U.S. system, although certain issues should be considered carefully. For instance, the data used to derive the promotion tables indicates a concave structure, which might reflect unemployment probabilities, particularly for older workers; thus, the use of the promotion tables and the RFs together might cause an unfair deduction for unemployment probabilities. Furthermore, the promotion tables might provide an alternative way to construct the EL tables.

As a last remark, the U.S. system is based on periodical payments, while lump-sum payments are more common in the UK. This discrepancy might be due to the different regulations and laws of the two countries, since the existence of periodical payments might require different assumptions and some sort of insurance to guarantee future payments. The UK system might need some alterations and modifications to introduce wide use of periodical payments.

6. Conclusions and future research

This paper has presented a methodology to improve the compensation calculations for personal injury and wrongful death cases. The approach can also be implemented in income protection insurance, which has become essential during the COVID-19 pandemic. We have introduced age-earnings profiles as promotion tables and illustrated the use of the tables as complementary to the UK’s Ogden tables.

The Ogden tables do not specifically consider promotions or wage increases in their calculations, although they do consider the RFs, such as unemployment probabilities based on education level, age, and sex. By constructing tables for age-earnings profiles, we present benchmark age- and sex-specific average earnings for both full-time and part-time employment. One can calculate the earnings increase from the tables to use as a factor to consider the age-earnings profiles in the compensation calculations. Additionally, since many injured people have to work part-time owing to their disabilities, the interpolated earnings for part-time employment can be utilized as earnings after the injury.

There are several paths for future research: One can explore the use of the cross-sectional data to construct industry- or occupation-specific age-earnings profiles, which might not display an inverted U–shaped structure. Another possible avenue for future investigation, to avoid the inverted U–shaped trend by age as retirement effects becomes important at older ages, is a cohort approach to construct age-earnings profiles, similar to longevity modeling. On the other hand, stochastic investment models designed for long-term actuarial applications, such as the model by Wilkie et al. (2011), can be used to forecast economy-wide earnings growth or overall wage increases in the age-earnings profiles. Those models can also be used to estimate the discount rates to be included in the compensation calculations.

Alternatively, one could construct salary scales based on the age-earnings profiles. Salary increases can be included in the compensation calculations by considering the distribution of salaries at each age or age group. Or one could discuss the use of the promotion tables in the calculation of actuarially fair pricing in compensation.

Acknowledgments

We would like to express our gratitude to A. D. Wilkie for his comments on the early version of the paper, Adrian Gallop for providing the UK mortality projections used in the Ogden tables, and the editor and anonymous referee for their valuable comments and suggestions. Their feedback substantially improved the paper.

Funding

The authors greatly acknowledge funding from the 2019 Individual Grants Competition of the Casualty Actuarial Society (CAS).”