Capital Tranching: A RAROC Approach to Assessing Reinsurance Cost Effectiveness

1. Introduction

The current industry standard approach (ISA) evaluates reinsurance effectiveness by calculating capital cost savings as the product of a fixed capital cost rate, the “hurdle rate,” and the theoretical required capital released by purchasing the reinsurance as measured by the change in a remote probability or “tail” metric. Reinsurance is deemed value-creating if the capital cost savings achieved through its purchase is greater than the ceded profit needed to support the reinsurance. This is usually defined as Expected Reinsurance Premium less Expected Recovery. The ISA reflects the change in portfolio risk from the reinsurance by changing the required capital amount—making the ISA an example of a Return On Risk-Adjusted Capital or RORAC approach. Despite the terminology used, insurers do not, in reality, release capital as a result of a reinsurance purchase. Capital amounts are largely fixed for the planning cycle, meaning a fundamental premise of the ISA is at odds with the way insurers operate. Furthermore, this decision process tends to make only high layer (catastrophe) covers appear to be worth purchasing.

However, the RORAC framework is not the only one available. Instead of risk-adjusting the capital amount, one can consider capital fixed and calculate a Risk-Adjusted Return On Capital—what is known as RAROC. Given an insurer’s distribution of expected losses, there are events for which collected premiums are insufficient to cover the liabilities incurred due to those losses. In those cases, some form of capital must be used to make up the difference. Following Mango (2003), we will refer to the distribution of the random variable representing this consumed capital as the capital consumption distribution, which can also be thought of as the distribution of downside earnings. In order to implement a RAROC framework, a means of calculating a risk-adjusted return as a function of this capital consumption distribution is needed. We will demonstrate one such method of doing this by replacing the capital with its reinsurance equivalent: a set of earnings stop-loss reinsurance covers, or what can be called Tranched Capital.

The paper proceeds as follows. Section 2 lays out the ISA. Section 3 assesses the comparability of RORAC and RAROC with insurer capital management. Section 4 discusses replacement of capital with a set of earnings stop-loss layers. Section 5 concludes by comparing the two approaches and the implications for indicated reinsurance cost effectiveness.

2. Industry standard approach

By “Industry Standard Approach” (ISA), we refer to the most commonly observed means of assessing the benefit of reinsurance. That this approach has entered the collective consciousness of the industry is evidenced by its appearance in a Wikipedia article.^[1] Despite its popularity, the literature on it is sparse. Venter, Gluck, Brehm, et al. (2007) sketch out its logic as part of a review of various assessment methods. Coutts and Thomas (1997) and Hürlimann (2003) provide formal models. Major (2011) defines and then critiques ISA from a different perspective than does this paper.

There is no definitive statement from a regulatory or standards-setting body. As an example, the International Actuarial Association (2009) has the following commentary:

Reinsurance programs: An [economic capital model] can be used to assess the capital required based on the risk profile of the organisation. The more risk that is on an organisation’s books the more capital is required to be set aside. Reinsurance is one of the main mechanisms available to insurers to pass on some of this risk to another party, therefore decreasing the amount of capital they are required to hold. Therefore in this instance, the value of reinsurance is derived from it acting as a proxy for capital. The cost of holding capital versus the cost of reinsurance can be considered by an organization . . . (p. 59)

ISA uses some type of portfolio or company internal risk model to follow these steps:

• Estimate the change in a portfolio-level or company-level required capital metric (e.g., 100-yr VaR of Net Income), with and without reinsurance;

• Call that change the “Capital Released”;

• Multiply Capital Released by some “Capital Cost Rate,” derived from one of a large number of sources—e.g., CAPM, Bloomberg, industry norms, investor expectations, etc.;

• Call the product the “Capital Cost Savings”;

• For the reinsurance, calculate the “Ceded Profit Margin” as Expected Reinsurance Premium less Expected Recovery;

• Purchase the reinsurance that maximizes the difference between Capital Cost Savings and Ceded Profit Margin.

To the extent the company-required capital tail metric is driven by other factors and risk sources not impacted by the reinsurance, the Capital Released will be less than the limit. For example, assume Company A is evaluating the benefit of $100MM of high-layer catastrophe coverage. The capital modeling team

• uses TVaR99 of earnings for its required capital metric;

• has run 100,000 trials of its capital model, meaning its TVaR99 uses the 1,000 worst trials as ranked by earnings (the “tail scenarios”); and

• finds that half the tail scenarios have major catastrophe losses which result in full limit reinsurance recoveries of $100MM, and the other half have no recovery because other risk sources are driving the adverse corporate outcome.

The resulting Capital Released will be $50MM—less than $1-for-$1 correspondence with the limit. If we assume the loss on line (expected ceded losses divided by limit) to be 1%, and the rate on line (expected reinsurance premium net of expenses divided by the limit) to be 6%, then the Ceded Profit Margin would be $100MM ∗ (6% − 1%) = $5MM. We are, in effect, paying $5MM to save a tail-expectation of $50MM, or a rate of 10%. In order for the cover to make sense under ISA, the Capital Cost Rate would have to be more than $5MM/$50MM or 10%. If we assume that indeed 10% is Company A’s Capital Cost Rate, then the ISA will not support purchasing any layer with either a higher Ceded Profit Margin on line or less Capital Released. Higher rates on line are generally associated with lower attachment points. Lower amounts of Capital Released are a function of the correlation between the reinsured lines of business and the modeled tail scenarios. Generally speaking, the more specific the reinsurance (e.g., individual business units or lines of business), the lower the Capital Released.

To demonstrate the ISA, we will simplify the company structure to help focus on the mechanics of reinsurance evaluation. These simplifications do not affect the main conclusion to be demonstrated: that the ISA is insensitive to how the reinsurance impacts the shape of the capital consumption distribution. Instead, the ISA implicitly assumes the impact of reinsurance is fully measured by the change in the required capital metric.

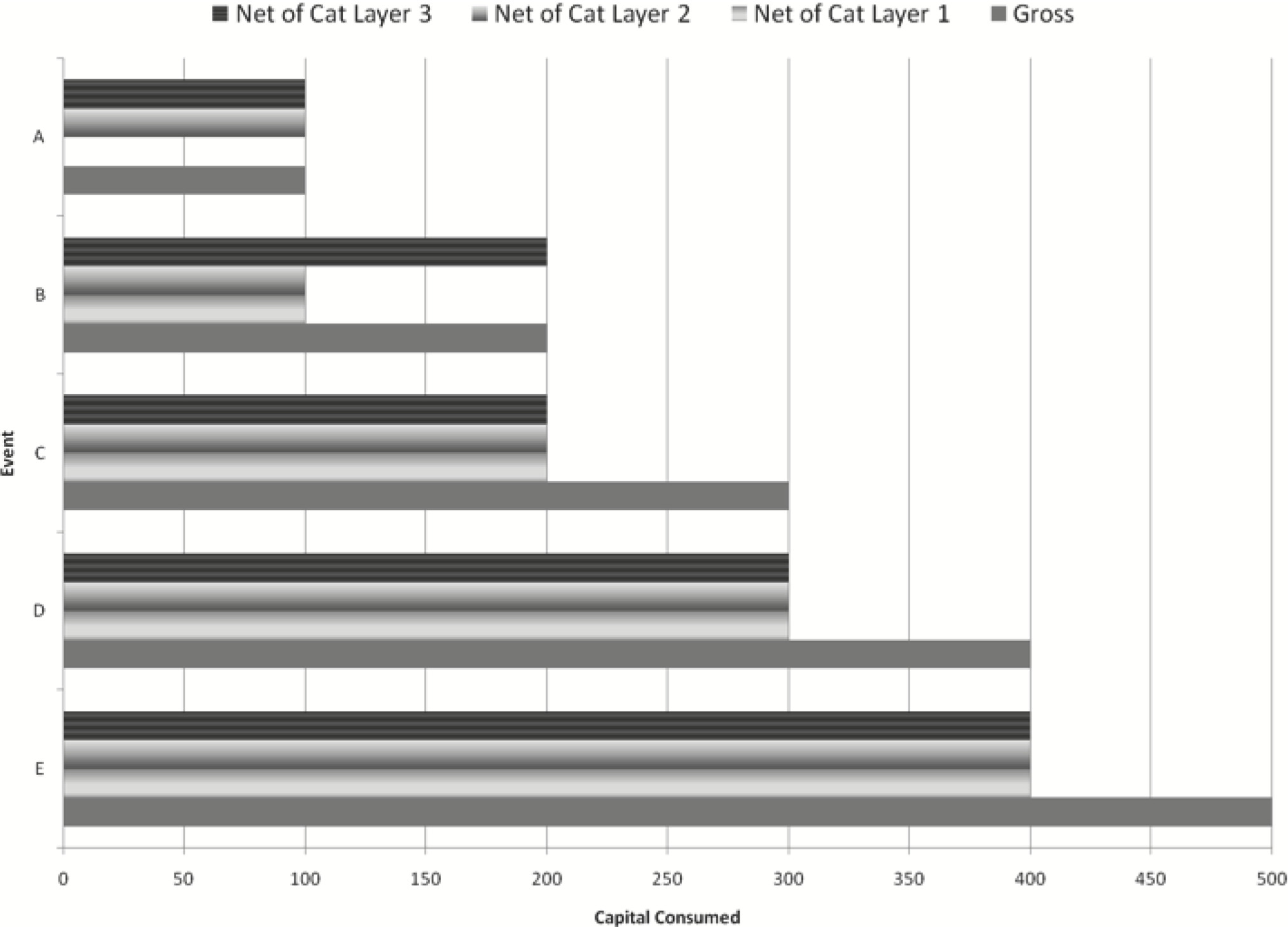
We will consider a collateralized sidecar, a special-purpose entity established to provide single-occurrence catastrophe protection for its parent company. We will assume no reserve or investment risk, and ignore accounting conventions. This will allow us to use the sidecar’s catastrophe occurrence distribution as the distribution of its negative earnings or what Mango (2003) calls the capital consumption. For simplicity, we will assume five possible cat events, labeled A through E, as shown on the Table 1 example capital consumption distribution.

We will assume the parent company uses the maximum loss (100th percentile VaR or VaR100) for capital requirement, giving a Gross Required Capital of $500MM.^[2] The parent will now use the ISA to evaluate purchasing $100MM of occurrence reinsurance protection, attaching (again for simplicity) every $100MM beginning at $0. We will call these options Cat Layer 1 through Cat Layer 5, and assume the company will purchase at most one of these. We will not reflect the cost of the cover in the capital consumption distribution (which would reduce the capital benefit), so the $100MM of catastrophe protection reduces the capital consumed by $100MM.

Table 2 shows the resulting capital consumption distribution net of each layer.

Using VaR100 for required capital, the ISA would show identical Capital Release of $100MM for all five alternatives—and therefore identical Capital Cost Savings. To see it graphically, Figure 1 plots Gross and Net of Cat Layer 1.

Figure 1.Capital consumption gross and net of cat layer 1

We can see Cat Layer 1 (attaching at $0) effectively shifts the entire Gross distribution to the left by $100MM. The VaR100 is $400MM Net of Cat Layer 1. Figure 2 adds the distribution Net of Cat Layer 2.

Figure 2.Capital consumption gross and net of cat layers 1 and 2

Net of Cat Layer 2 (attaching at $100MM) is the same as Net of Cat Layer 1 except for the top scenario, which is $100MM Net of Cat Layer 2 as opposed to $0 Net of Cat Layer 1. The VaR100 is still $400MM, however.

Figure 3 extends it to include Net of Cat Layer 3.

Figure 3.Capital consumption gross and net of cat layers 1–3

Net of Cat Layer 3 (attaching at $200MM) is the same as Net of Cat Layer 2 except for the second from the top scenario, which is $200MM Net of Cat Layer 3 as opposed to $100MM Net of Cat Layer 2. The VaR100 continues to be $400MM.

Based on typical reinsurance pricing practices, Cat Layer 5 would be the lowest cost. Since the ISA shows the same Capital Release for all five layers, it would indicate Cat Layer 5 to be the most valuable reinsurance purchase.

3. Comparability with insurer capital management

Despite its name, the ISA’s required capital is purely theoretical. No form is assumed—e.g., debt, common stock, preferred stock, surplus note, etc. Theory aside, the RORAC “Capital Released” framework suggests a liquid, back-and-forth relationship with the capital providers—quite far from the realities of insurer capital management. In fact, there are many supporting arguments to consider insurer capital to be fixed on an annual basis:

• Insurance companies typically plan one underwriting (or policy) year at a time, measure production and profitability based on that plan, and would not make capital decisions without comparing results to the most recent underwriting plan;

• As capital is assets less liabilities, and most insurers only perform a full reserve review on an annual basis, one could argue capital is only formally “evaluated” once a year;

• Rating agencies are often a binding constraint for held capital, and their required capital models are only run on an annual basis;

• Mutuals (and reciprocals) have limited means to release capital apart from paying policyholder dividends, and similarly have difficulty raising capital except through retaining earnings.

Clearly, we cannot risk-adjust the capital while keeping it fixed. All is not lost, however, because there is a perfectly valid alternative means to calculate capital cost savings—RAROC. Rather than treating the Capital Cost Rate as a constant, under RAROC this rate is a function of the amount of capital consumed. But what sort of function? We will demonstrate one way based on creating the “reinsurance-equivalent” of capital.

4. The reinsurance equivalent of capital

Recalling first that the ISA is based on theoretical required capital, we introduce a theoretical concept of an earnings stop-loss (ESL): an aggregate reinsurance cover that absorbs earnings downsides (capital consumed) up to a limit. Ignoring issues with credit risk and liquidity, an ESL with limit equal to required capital is the reinsurance-equivalent of that capital, in fact completely obviating the need for capital. We could conclude, assuming perfect information and efficient financial markets, that the cost of this “reinsurance capital” should be the same as actual capital. We will use this equivalence as a means of calculating the risk-adjusted return, as we have well known methods to price reinsurance. Following industry practice, and to facilitate understanding of the dynamics, we will divide the single ESL into a series of contiguous ESL layers. In the capital markets, similar layering is done in collateralized debt obligation (CDO) structures, with the layers referred to as tranches. Hence we coin the term capital tranching to refer to a layer-based approach to calculate the RAROC.

Reinsurance pricing methods for excess layers are primarily driven by the “probability of attaching” the layer or P(Att). For simplicity and without loss of generality, we will assume each layer to be binary: the layer either suffers no loss or a full limit loss. For a binary layer, the expected loss divided by limit (Loss on Line or LOL) equals P(Att), and the standard deviation as a percentage of limit is the square root of [P(Att) ∗ (1 − P(Att))]. The layer expected loss equals the product of the Loss on Line and the Limit. To convert Loss on Line into a Rate on Line (ROL) or price, for convenience we will use the formula from Kreps (1990) of Expected Loss plus the product of the Standard Deviation and a Reluctance Factor.

Returning to our example, we will replace the $500MM in Gross required capital with earnings stop losses (Capital Tranches) ESL 1 through ESL 5, each with $100MM limit, attaching every $100MM beginning with ESL 1 at $0. Table 3 shows the prices for these five ESL covers with a Reluctance Factor selected to produce an overall Capital Cost Rate of 10%.

The Total column for all five ESL Layers is the total cost of the $500MM of Capital Tranches—$50.0MM, for an average Capital Cost Rate of 10%.

We will now measure the change in risk-adjusted return due to the purchase of Cat Layers 1 through 5 (the same five covers evaluated earlier using the ISA). Table 4 shows the pricing Net of Cat Layer 1.

The highlighted ROL for ESL 5 is zero because there is no longer any chance of it attaching. We could also have assigned it a minimum rate on line of e.g., 3% as a capacity charge. We will stick with the free version for clarity and without loss of generality. ESL 1 to 4 on a Net basis are equivalent to ESL 2 to 5 on a Gross basis. The resulting total price is $35.7MM for an average Capital Cost Rate of about 7.2%. We could have calculated this price directly by realizing that Cat Layer 1 replaced ESL 1, resulting in a savings of $14.26MM. Subtracting that from the original Gross price of $50.0MM gives $35.74MM.

It is important to recognize how the Tranched Capital RAROC approach responds to changes in the capital consumption distribution because of Cat Layer 1.

Table 5 shows the impact on the Capital Tranches due to Cat Layer 2. Again, ESL 5 is at 0%. ESL 1 is unchanged Gross to Net, since Cat Layer 2 attaches above it. ESL 2 to 4 on a Net basis are equivalent to ESL 3 to 5 on a Gross basis. The resulting total price is $37.7MM for an average Capital Cost Rate of about 7.5%. This time, Cat Layer 2 replaced ESL 2 (original price of $12.3MM). We can go from Gross price of $50.0MM, subtract $12.3MM to get the Net price of $37.7MM.

Most importantly, however, the Capital Tranches clearly measure the difference in capital impact between Cat Layer 1 and Cat Layer 2—something the ISA did not do. The ISA measured the same capital release for all five Cat Layers, while Capital Tranches clearly differentiate among the five Cat Layers in the different RAROC.

Table 6 summarizes the Capital Tranching evaluation of the five Cat Layers.

The Total column shows the overall RAROC. Capital Cost Savings equals Price because we priced both the ESLs and Cat Layers using the same Reluctance Factor. Using a lower Reluctance for the Cat Layers—i.e., reinsurer capital costing less than insurer capital—would make the Price column less than the Capital Cost Savings, and the contract appear attractive. The opposite would be true for reinsurer capital costing more than insurer capital. In any event, the RAROC method differentiates itself from the ISA by explicitly demonstrating the difference in value to the insurer between various capital layers—something which the ISA is itself unable to do.

5. Conclusion

Table 7 provides a summary comparison of ISA and Capital Tranching.

As for commonalities, both are founded upon an internal capital model that produces a downside earnings distribution Gross and Net of the reinsurance program under consideration. Both also evaluate reinsurance effectiveness by comparing Ceded Profit Margin with Capital Cost Savings.

The main difference is in treatment of capital. The ISA’s RORAC approach, with its variable capital amount, is at odds with insurer realities. In contrast, Capital Tranching risk-adjusts the return on capital and while keeping the capital amount fixed. The risk-adjusted return is calculated from the capital consumption distribution and, in the example presented, standard reinsurance pricing techniques.

The implications for reinsurance purchasing are material. The ISA indicates that layers with the same limit, as long as they exhaust below the capital threshold, create the same value. As a result, lower layers with higher rates on line usually appear less attractive. The Capital Tranching framework instead evaluates the merits of every reinsurance purchase based on a comparison of the cost of supporting the risk with the insurer’s own capital to a reinsurance alternative. Depending on market pricing, any layer can potentially be worth purchasing.

Areas for future research include:

• Methodology for selecting an appropriate Capital Cost Rate, for both stock and mutual companies;

• Case studies using actual reinsurance programs;

• Assessment of consistency of the two approaches with risk aversion (both policyholder and shareholder);

• Consideration of other tranching pricing frameworks, including debt-equivalents and option pricing; and

• Integration into franchise-value models such as Major (2011).

Acknowledgments

The authors wish to thank Richard Goldfarb, Micah Woolstenhulme, and Joan Lamm-Tennant for their editorial feedback. We also wish to thank the many attendees at presentations of prior versions of this, whose feedback was instrumental in refining the message and greatly improving the final product.