Introduction
The loss development method (LDM) as described in the literature (Skurnick 1973; Friedland 2009), also known as the chain-ladder method, is easily the most commonly applied actuarial method for estimating the ultimate value of unpaid claims (Friedland 2009, Chapter 7). The customary way in which the LDM is applied produces a single ultimate value for all accident years, for each individual year separately and then for all years combined. The underlying historical loss development usually exhibits a degree of variability. The variability implicitly and inherently expressed in the loss development history, and therefore in the resulting outputs derived by the application of the LDM, can be quantified using the actual loss development history—and need not be based on a closed form of any particular mathematical function. In the course of quantifying this variability, one can derive a purely historically based[1] distribution of the potential outputs of the LDM. This paper presents such a method.
Literature
To date the actuarial literature has considered aggregate loss distributions predominantly in terms of distributions that can be expressed in closed form. That approach generally requires two categories of assumptions: the selection of a family of distributions thought to be applicable to the situation at hand, and the selection of the parameters that define the specific distribution based on the data associated with individual applications.[2] A limited amount of work has been done in producing non-formulaic, method-based, aggregate loss distributions that are not (or could not be) expressed in a closed form (Mack 1994; McClenahan 2003). The advantages of using formulaic distributions are that they (a) are easy to work with once the two categories of assumptions have been made and (b) can deal with variability from all sources, at least in theory. However, the disadvantage of using such distributions is that the potential error arising from selecting a particular family of distributions and from estimating parameters based on limited data can be great.
Non-formulaic distributions, on the other hand, also are easy to use but are difficult to contemplate directly because of the immense computing power needed to execute the necessary calculations. With the advent of powerful computers, the possibility of developing empirical method-based aggregate loss distributions keyed to specific methods can be considered and in this paper, a methodology for producing them is presented. A key argument in favor of method-based distributions is that once a particular method has been selected, the rest of the process of creating the conditional distribution of outputs can proceed without making any additional assumptions.[3] The principal drawback to using conditional loss distributions is that, when considered singly, they do not account for either (a) the “model risk” associated with the very choice of a particular method to calculate ultimate aggregate losses or (b) the effects of limited historical data (which can be thought of as a sample drawn out of some unknown distribution).
Objective
The objective of this paper is to describe and demonstrate a methodology for producing a deterministic approximation of the aggregate loss distribution of outputs, within a specified error tolerance, that can be generated by the application of the LDM[4] to a particular array of loss development data. More specifically, the approximation algorithm ensures that each point of the exact conditional distribution, if it were possible to construct, does not differ from its approximated value by more than the specified error tolerance. Extensions of this process to other commonly used development methods are briefly described but not developed.[5]
Organization
Section 2 presents the theoretical problem and the theoretical solution. Section 3 illustrates the practical impossibility of calculating the exact theoretical solution (i.e., producing an exact distribution of outputs) and establishes the usefulness of a methodology that can yield an approximation of the exact distribution of loss outputs. Section 4 describes the construction of the approximation distribution for a single accident year, including the process of meeting the error tolerance. Section 5 describes the construction of the convolution distribution that combines the various outputs for the individual accident years, thus producing a single distribution of outputs for all accident years combined. Section 6 demonstrates the methodology (with key exhibits provided in an appendix). Section 7 discusses a number of variations. Section 8 describes extensions to other commonly used loss projection methods. Finally, Section 9 discusses the scope of possibilities for this methodology as well as potential limitations.
The theoretical problem and the theoretical solution
This section describes the theoretical problem associated with using the LDM to develop a distribution of outputs. It also describes the theoretical solution to the problem.
The loss development method generally
The basic idea of the LDM is that the observed historical loss development experience provides a priori guidance with respect to the manner in which future loss development can be expected to emerge. In actual use, an actuary selects a loss development pattern based on observation and analysis of the historical patterns.[6] Once a future loss development pattern is selected, it is applied to the loss values that are not yet fully developed to their ultimate level. An important feature of this process is that the actuary makes a selection of a single loss development pattern that ultimately produces a single output for the entire body of claims, for all cohorts represented in the loss development history, as of the valuation date.
The theoretical problem
It is trivial to state that any single application of the LDM produces just one of many possible outputs. The challenge, and the objective of this paper, is that of identifying all possible outputs that can be produced by the LDM. If it were possible to do this, then the set of all outputs would provide a direct path to identifying measures of central tendency as well as of dispersion of the outputs produced by the LDM. In this regard, the reader should note that the language “all possible outputs” as used in this paper is intended to include all projections that can be produced using all possible combinations of the observed historical loss development factors for each period of development for every cohort of claims in the data set.[7] This convention will be used throughout the paper. Also, it is obvious that there are other possible outputs, both from the application of the LDM (using non-historical loss development patterns) and from the application of non-LDM methods, each requiring the use of judgment[8] and, as such, represents an alteration to the distribution of outputs that is produced purely on the basis of the observed history. Note: Although cohorts of claims can be defined in many different ways,[9] the working cohort used in this paper is the body of claims occurring during a single calendar year, normally referred to as an “accident year.”
The theoretical solution
The theoretical solution is rather straightforward and uncomplicated: calculate every possible combination of loss development patterns that can be formed using the set of observed loss development factors. In other words, the observed history contains within it an implied distribution of outputs that is waiting to be recognized. One of the key impediments to producing this set of outcomes is the vast number of calculations involved. What is described in this paper is the identification of an approximation of the implied universe of base line outputs that are present once the actuary has decided to use the LDM. Of course the actuary can continue to do what he always has done; select a specific loss development pattern and apply it to the undeveloped loss values. But now the actuary will also know the placement of this particular loss output along the continuum of all possible outputs (and their associated probabilities) that can be produced by using just the observed historical loss development factors.
The impossible task and the possible task
The size of the task of performing the calculations required to generate all possible outputs that can be produced using all different combinations of observed historical loss development factors can be gauged rather easily. Consider a typical loss development array of n accident years developed over a period of n years. For purposes of this illustration, let us assume that the array is in the shape of a parallelogram with each side consisting of n observations.[10] For this example, the number of possible outputs that can be produced using all different combinations of loss development factors is given by The values grow very rapidly as n increases. For example, when n is 10, the number of outputs is 8.7 ∗ 1042 and when n is 15 the number of outputs is 2.2 ∗ 10120. To put these values in perspective, if one had access to a computer that is able to produce one billion outputs per second, the time needed to execute the calculations is 2.8 ∗ 1026 years when n = 10 and 7.0 ∗ 10103 years when n = 15. There just is not enough time to calculate the results. This is the impossible task.
Given this practical impediment, it makes sense to consider approximating the exact distribution of outputs. This paper describes such an approximation algorithm. In other words, the target is to construct an approximation distribution of the outputs produced by the LDM such that every point in the true historical distribution, if it were possible to produce every single value, does not differ by more than a pre-established tolerance ε from the corresponding approximated value (which, in reality serves as a surrogate for the true value) in the approximation distribution. This is the possible task.
The construction of the approximation distribution
This presentation assumes the existence of a loss development history that captures the values, as of consecutive valuation dates, for a number of different accident years. This is commonly referred to as a loss development triangle or, more generally, a loss development array.
Given an error tolerance, ε, the idea is to construct a set of N contiguous intervals such that any given value produced by the LDM does not differ by more than ε from the midpoint of the interval which contains that value. The key steps in this construction are:
-
Specify an error tolerance, ε.
-
Identify the range of outputs: the overall maximum and minimum values produced by the LDM for all accident years combined using only the observed historical loss development factors.
-
Construct a set of intervals, the midpoints of which serve as the discrete values of the approximation distribution, and thus serve as the values to which frequencies can be attached. Perform this process separately for each accident year.[11]
-
Identify the optimal number N that can assure that the error tolerance ε is met for every output that can be produced by the LDM
-
Produce all outputs generated by the LDM, separately for each accident year.
-
Substitute the midpoint of the appropriate respective interval for each output generated by the LDM. Perform this process separately for each accident year. This step produces a series of distributions of all possible outputs, one for each accident year.
-
Identify the midpoints of the intervals which will serve as the discrete values for the final distribution of outputs; the convolution distribution of all possible outputs for all accident years combined.
-
Create the convolution distribution over the N final intervals to create the final distribution of outputs for all accident years combined.
Notation
The primary input that drives the LDM is the historical cumulative value of the claims that occurred during an accident year i, and valued at regular intervals. The jth observation of this cumulative value of the claims occurring during accident year i is denoted by Vi,j. For purposes of this presentation i ranges from accident year 1 to accident year I while j ranges from a valuation at the end of year 1 to a valuation at the end of year J, with I ≥ J.[12] J is the point beyond which loss development either ceases or reasonably can be expected to be immaterial.[13] It is also useful to set the indexing scheme such that the most recent (and least developed) accident year is designated as accident year 1, the second most recent accident year is designated as accident year 2, and continuing thus until the oldest (and most developed) accident year is designated as accident year I. The most recent valuation for each of the open accident years is then represented by Vi,i.
Also, the loss development factor (LDF) that provides a comparison of to is represented by
The error tolerance ε
Any approximation process necessarily generates estimation error. Whenever a true value is replaced by an approximated value, there will be a difference under all but the rarest of conditions. Different applications may require different levels of tolerance when considering the errors that can arise solely due to the approximation operation. For purposes of this presentation, the user is assumed to have identified a tolerance level that meets the needs of a specific application, denoted by ε, such that the true value of an output of the LDM, for each open year and for all open years combined, never differs from its approximated value by more than ε.[14] If, for example, ε is set at 0.01 (i.e., 1%) then the process would seek to produce a distribution of approximated outputs such that no individual output of the LDM can be more than 1% away from its surrogate value on the approximation distribution.
The range of outputs
This section focuses first on the construction of the range of outputs that can be produced by the LDM for a single accident year. Once a range is established for each accident year, the overall range, for all accident years combined, is constructed by (a) adding the maximum values for the various accident years to arrive at the maximum value for the overall distribution and (b) adding the minimum values for the various accident years to arrive at the minimum value of the overall distribution.
Therefore the problem of calculating the overall range of the distribution is reduced to the determination of the range of outputs for each individual accident year. For any single development period j, let {Li,j} denote the set of all observed historical LDFs that could apply to Vi,i in order to develop it through the particular development period j. When this notation is extended to all development periods, ranging from 1 to J – 1, a set of maxima and a set of minima of the form Max {Li,j} and Min {Li,j}, respectively, with i and j ranging over their respective domains, is generated.
Accordingly, the first loss development period would possess the maximum and minimum LDFs designated by and with i ranging from 2 to I; the second loss development period would possess the maximum and minimum LDFs designated by and with i ranging from 3 to I; the third loss development period would possess the maximum and minimum LDFs designated by and with i ranging from 4 to I, and so on.[15]
Having identified the maximum and minimum LDFs for each loss development period, it is now possible to identify the maximum (minimum) cumulative LDFs for a single accident year by multiplying together all maximum (minimum) LDFs for all the development periods yet to emerge. This process yields:
The maximum cumulative LDF for any given accident year is described by Π(Max {Li,j}), with the “Max function” ranging over i for every j and the “Π function” ranging over j for all the loss development periods which the subject accident year has yet to develop through in the future.
The minimum cumulative LDF for any given accident year is described by Π(Min {Li,j}), with the “Min function” ranging over i for every j and the “Π function” ranging over j for all the loss development periods which the subject accident year has yet to develop through in the future.
The maximum value of all outputs produced by the LDM for accident year i is given by the product Vi,i ∗ Π(Max {Li,j}). Similarly, the minimum value of all outputs produced by the LDM for accident year i is given by the product Vi,i ∗ Π(Min {Li,j}). Therefore, every ultimate output produced by the LDM for accident year i, after i – 1 development periods have elapsed, has to be in the interval [Vi,i ∗ Π(Min {Li,j}), Vi,i ∗ Π (Max {Li,j})].
As i ranges from 1 to J – 1, the respective maxima and minima for each accident year are generated and thus the overall range of the distribution of outputs produced by the LDM is generated, by adding the respective maxima and minima for all accident years.
Constructing the intervals
With the range of outputs for accident year i, after i – 1 periods of development have elapsed, already identified, the effort shifts to identifying the appropriate intervals, which midpoints will constitute the discrete values of the approximation distribution of all possible outputs for the subject accident year. The idea is that an output that can be produced by the LDM, using only the observed historical loss development factors, when slotted in the appropriate interval, can meet the overall error tolerance when compared to the midpoint of that interval. It is also obvious that the respective midpoints of the optimal intervals can be identified completely between the endpoints of the range of outputs if the optimal number of intervals, that would assure that the error tolerance is met, can be determined. First the focus will be on accident year i, to derive the number Ni, the optimal (i.e., minimum) number of intervals that would assure that no output of the LDM for this accident year differs by more than ε from the midpoint of one of the optimal intervals.
The method used in this paper to construct the Ni intervals starts with designating the leftmost (rightmost) boundary of the range of outputs for accident year i (after i – 1 periods of development have elapsed) as the midpoint of the first (last) interval. Thus the span of the midpoints, denoted by [Vi,i ∗ Π(Max {Li,j}) − Vi,i ∗ Π(Min {Li,j})] is equal to the sum of the widths of the remaining (Ni − 1) intervals. Therefore, the radius of each interval is set equal to the quantity [Vi,i ∗ Π(Max {Li,j}) − Vi,i ∗ Π(Min {Li,j})]/[2 ∗ (Ni − 1)]. The leftmost and rightmost intervals are then represented by the following expressions, respectively:
[Vi,i∗Π(Min{Li,j})−[Vi,i∗Π(Max{Li,j})−Vi,i∗Π(Min{Li,j})][2∗(Ni−1)],Vi,i∗Π(Min{Li,j})+[Vi,i∗Π(Max{Li,j})−Vi,i∗Π(Min{Li,j})][2∗(Ni−1)]]
[Vi,i∗Π(Max{Li,j})−[Vi,i∗Π(Max{Li,j})−Vi,i∗Π(Min{Li,j})][2∗(Ni−1)],Vi,i∗Π(Max{Li,j})+[Vi,i∗Π(Max{Li,j})−Vi,i∗Π(Min{Li,j})][2∗(Ni−1)]]
Finally, the remaining Ni − 2 intervals are constructed by spacing them equally and consecutively beginning with the rightmost point of the leftmost interval, previously constructed, and setting the width of each interval equal to: [Vi,i ∗ Π(Max{Li,j}) − Vi,i ∗ Π(Min{Li,j})]/[(Ni − 1)].
The goal is that the set of midpoints of the intervals thus constructed, if used as the surrogates for the outputs that can be produced by the LDM, meet the error tolerance ε specified at the outset. What remains to be done is to identify the conditions that Ni must meet in order to satisfy the specified error tolerance.
Note that with this particular construction, the interval, which was subtracted from Ni to arrive at the width of the optimal interval, is now restored in the interval construction proper, by means of adding the necessary half interval at each of the two boundaries of the range.
Meeting the ε tolerance standard for a single accident year
The overarching requirement the approximation distribution must meet is that the ratio of any output generated by an application of the LDM to the midpoint of the interval which contains such output is within the interval [1 − ε, 1 + ε]. More generally, based on the construction thus far, if the number of intervals Ni is appropriately chosen to meet the error tolerance, and given an output of the LDM designated by X, then there exists an interval within the range of outputs, having a midpoint Y such that 1 − ε ≤ X/Y ≤ 1 + ε. To continue this development, three cases are considered.
When X > Y
This case corresponds to the X/Y 1 + ε portion of the error tolerance that the approximation distribution must meet. This is equivalent to requiring that (X – Y)/Y ε. Also, since (X – Y) is not greater than the radius of the interval as constructed above, then the constraint denoted by (Radius of the Interval)/Y ε would be a more stringent constraint and that would ensure that the error tolerance (X – Y)/Y ε is met. Accordingly, the original error tolerance, for purposes of this construction, is replaced by the new, more stringent error tolerance represented by (Radius of the Interval)/Y ε.
Noting that Y can never be less than the lower bound of the overall range, as constructed above, the condition (Radius of the Interval)/Y ε can be replaced by an even more stringent condition if Y is replaced by the lower bound of the range for the subject accident year. Thus, for the remainder of this construction, the stronger error constraint, represented by (Radius of the Interval)/(Lower Bound of the Range) ε is used.
Using the notation from above, the new, more stringent error constraint, applicable to accident year i, can be stated as follows:
{[[Vi,i∗Π(Max{Li,j})−Vi,i∗Π(Min{Li,j})][2∗(Ni−1)]}Vi,i∗Π(Min{Li,j})<ε.
Solving for Ni yields
Ni>(1/2ε)∗[Vi,i∗Π(Max{Li,j})−Vi,i∗Π(Min{Li,j})]Vi,i∗Π(Min{Li,j})+1
Therefore, as long as Ni meets this condition, one can be certain that the approximation distribution meets the overall accuracy requirement for accident year i after i-1 periods of development have elapsed.
When X Y
Using parallel logic, the same result is produced yielding the same result as for the case when X > Y:
Ni>(1/2ε)∗[Vi,i∗Π(Max{Li,j})−Vi,i∗Π(Min{Li,j})]Vi,i∗Π(Min{Li,j})+1
When X = Y
Under this condition, the error constraint trivially is met.
The number of intervals for all accident years
Extending the result from Section 4.5 to all values of i produces a series of Ni values, one for each open accident year: This is a finite set of real numbers and thus possesses a maximum. For the purpose of the approximation that is the object of this paper, Max {Ni} would serve as the universal number of intervals that can be used for any accident year such that the approximation distribution associated with each accident year meets the original error tolerance ε. And for future reference, the value Max {Ni} is labeled N.
The output of the approximation distribution
The steps described thus far—(a) deriving the maximum and minimum outputs of the LDM for a single accident year; (b) deriving the optimal number of intervals, N, needed to make sure that the process of replacing an output of the LDM with the midpoint of the interval that contains the output meets the error tolerance ε; (c) creating the intervals that would serve as receptacles for holding the various outputs produced by the LDM, and (d) substituting the midpoints of the various intervals for the individual outputs of the LDM—combine to produce a frequency distribution for every open accident year. That frequency distribution could be represented by the contents of Table 1.
Deriving the distribution of outputs produced by the LDM for a single accident year, while involving considerable calculations, is quite manageable by today’s computers. For example, the largest number of outputs associated with a single year with a history array in the shape of an n × n parallelogram is Thus a ten-year history would generate about 387.4 million outputs. For an error tolerance that could be satisfied with one thousand intervals, a typical desktop computer can manage this number of calculations in a few minutes and certainly well within an hour.
The convolution distribution
The typical application of the LDM projects a single ultimate value for every open accident year and then combines the resulting values to produce the ultimate value for all open accident years combined. The typical application of the LDM employs a single loss development factor for each development period and applies that single factor to all the open accident years for which it is relevant.
On the other hand, as noted in the construction described above, the various historical LDFs are permuted and used in all possible combinations for every development period for every open accident year. The convolution distribution, in order to preserve the randomness required by the underlying idea of this construction, needs to combine all the different outputs, in all permutations, for all the open accident years. To that end, the process of combining the component distributions is best carried out iteratively: (a) create every combination of values that can be produced from the two distributions of all outputs associated with any two accident years to produce an interim convolution distribution, (b) combine the interim convolution distribution with the distribution of a third open accident year to create a new interim convolution distribution, and (c) continue this process until all component distributions have been combined into a single convolution distribution. Various elements of the convolution distribution and its compliance with the error tolerance are described in Section 5.4.
The range
The range of the convolution distribution was created in Section 4.3 above.
The midpoints of the intervals
Given two approximation distributions associated with two open accident years, with each distribution consisting of N midpoints, they can be arrayed as shown in Table 2, with Di serving as the label for the distribution associated with accident year i; with Xi,j denoting the midpoint of interval j.
The number of intervals, N, that was derived above in Section 4.6, was used in the construction of the distribution of outputs for each open accident year. For purposes of constructing the convolution distribution, it will be demonstrated that the same number N can be used to create the intervals (and the associated midpoints) used to describe the convolution distribution.
The midpoints of the intervals constituting the convolution distribution are set as the sum of the midpoints of the two component distributions. Those values are shown in the rightmost column of Table 2. Thus the width of each interval in the convolution distribution will be equal to the sum of the widths of the respective intervals in the component distributions.
The values of the convolution distribution and their frequencies
Each component distribution has N discrete midpoints of N intervals spanning the range of the component distribution. Each midpoint will have an associated frequency, f, as noted in Table 1. Thus the values of the convolution distribution, derived by adding various combinations of midpoints of the component distributions, will consist of N2 discrete values, with each such discrete value having a frequency equal to the product of the two component frequencies for the respective combination of values. More specifically, given two distributions, one for accident year p and one for accident year q, each of the form {X, f}, then the raw convolution distribution is given by {Xp,i, fp,i } ∗ {Xq,i, fq,i}, with i ranging from 1 to N. For example, midpoints and corresponding frequencies represented by (X6,4, f6,4) and (X22,17, f22,17) will produce a new discrete value equal to (X6,4 + X22,17, f6,4 ∗ f22,17). Each of the N2 values in turn can be replaced by a surrogate equal to the midpoint of the interval in the convolution distribution which contains the newly produced combined value. In the case of the example above, the value (X6,4 + X22,17) will be replaced by the midpoint of one of the N newly constructed intervals (as shown in Table 2) which contains (X6,4 + X22,17). Also, the frequency associated with this (X6,4 + X22,17), denoted by (f6,4 ∗ f22,17), will be added to the frequencies of all the other elements of the N2 discrete values in the convolution distribution that fall in the same interval as (X6,4 + X22,17). When every possible combination of the values in the two component distributions has been created, its respective frequency calculated, and it has been replaced by a surrogate midpoint of the convolution distribution, the construction of the interim convolution distribution of the two component distributions will have been completed.
Repeating the process, by combining this interim convolution distribution with another component distribution creates an updated interim convolution distribution made up of N intervals and their corresponding midpoints. Continuing this process until all component distributions have been utilized ultimately yields the final convolution distribution.
The error tolerance
It remains to be demonstrated that the particular construction of the convolution distribution described above does not violate the overarching requirement of meeting the error tolerance ε. Once again, the focus will be on demonstrating that the error tolerance is met when the convolution distribution combines just two component distributions. This is equivalent to demonstrating that the final convolution distribution also meets the error tolerance because it is created iteratively, by combining two component distributions to create an interim convolution distribution, then adding a third component distribution to the interim convolution distribution, and continuing in this manner until all component distributions are accounted for.
It was already established that, for every distribution of outputs for any given open accident year, any given individual output for that open accident year, x, produced by the LDM method does not differ from the midpoint, x′, of some interval such that the original error constraint is met, or, using inequalities: 1 + ε ≥ x/x′ ≥ 1 − ε or, equivalently, |x − x′|/x′ ≤ ε. Moreover, the number of intervals N was selected such that this condition was met. In the process of demonstrating that the error tolerance is met when N intervals are utilized, two substitutions were made such that a more stringent condition is met: (a) the amount equal to the radius of the interval was substituted for the amount |x − x′| and (b) the lower bound of the range was substituted for the amount x′. Thus the condition |x − x′|/x′ ≤ ε became the more stringent condition, which can be denoted by r/LB ≤ ε, where r is the radius of each of the N intervals and LB is the lower bound of the range of the distribution.
The problem now can be defined as follows, “Given two LDM outputs, x1 and x2, each drawn from a distinct component distributions of LDM outputs (i.e., distributions of outputs for two different accident years), with each distribution meeting the error tolerance ε, does the sum of the two outputs, (x1 + x2), also meet the error tolerance with respect to the convolution distribution that combines the two component distributions?”
Noting the convention of using the more stringent error tolerance discussed earlier, the question can be restated as: “Given that r1/LB1 ≤ ε and r2/LB2 ≤ ε, where r1 and r2 denote the radii of the intervals of the component distributions and LB1 and LB2 denote the lower bounds of the two component distributions, can one reach the conclusion that (r1 + r2)/(LB1 + LB2) ≤ ε?”
The answer is in the affirmative following the logic outlined below:
-
Given: r1/LB1 ≤ ε and r2/LB2 ≤ ε.
-
Rewrite the inequalities: r1 ≤ ε * LB1 and r2 ≤ ε * LB2.
-
Add the inequalities: (r1 + r2) ≤ ε * LB1 + ε * LB2.
-
Factor ε: (r1 + r2) ≤ ε * (LB1 + LB2).
-
Divide by (LB1 + LB2): (r1 + r2)/(LB1 + LB2) ≤ ε.
Thus the convolution distribution meets the overall error tolerance ε.
Demonstration
In this section a brief demonstration of the process described above is outlined. The demonstration is applied to the loss development history shown in Table 3, providing annual valuations for each of 13 accident years.
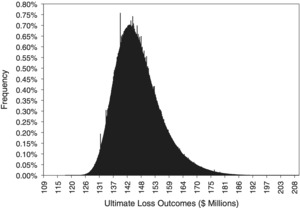
In this example up to 10 valuations are available for each accident year. Assume that 10 years is the length of time required for all claims to be closed and paid.[16] The data array is in the shape of a trapezoid. The user seeks to find the approximation distribution of outputs produced by the LDM with a maximum error tolerance of 1%. Table 4 shows a small segment of the full tabular distribution of outputs. The number of intervals necessary to meet the error tolerance for this array of data is 948.
Figure 1 shows the result as a bar graph showing the frequency distributions at the respective midpoints of the intervals. The number of intervals is sufficiently numerous to allow the various bars to appear to be adjacent and thus give the appearance of an actual distribution function. The key steps along with the key numerical markers that lead from the loss development history shown in Table 3 to the finished distribution are detailed in Appendix A.
Variations and other considerations
Given a particular loss development history and an error tolerance ε, the methodology described in this paper produces a unique distribution of outputs produced by the LDM. However, a number of variations on the manner of application of this methodology are possible that may be useful in certain circumstances. Out of the many possible variations, three basic types are presented in this section. It should be noted that each of these variations uses the same methodological scheme, with some slight adjustments to recognize the type of variation that is being used. No substantive changes in methodology are required to use these variations. Also, these variations can be used singly or in combination.
Weighting loss development factors
The basic methodology presented in this paper gives the observed loss development factors equal weight. In other words, the observed loss development factors for any one loss development period are considered to be equally likely. Absent any specific information to the contrary this is a reasonable way to approach the construction of the approximation loss distribution. In some cases the actuary may have sufficient reason to give some of the loss development factors more or less weight than others. There is virtually an unlimited number of ways in which one can assign weights: (a) weights equal to the associated values contained in the array of loss development data (i.e., use losses as weights), (b) an arithmetical progression that assigns the smallest weight to the oldest loss development factor and gradually increases the weight for the more recent development factors using a fixed additive increment, and (c) another type of progression (power, geometric) that assigns the smallest weight to the oldest loss development factor and gradually increases the weight for the more recent development factors using the increment dictated by the choice of the type of progression. Any of these types of weights can be used but it is the task of the actuary to rationalize the specific weighting procedure. When weights are used, each LDF produced by the historical data set would become a pair of values of the form (LDF, Weight). And every single output of the LDM that goes into the creation of the distribution is another pair of the form (specific output, product of the weights). In all other respects, the approximation process is identical.
In using this alternative, it is a good idea also to derive the unadjusted distribution of outputs for all years combined. In this manner the effect of the judgment the actuary chose to make in assigning the particular weights is quantified.
Outliers
Occasionally loss development histories include outliers. These are extreme values that stand out indicating something unusual had taken place. The methodology presented in this paper is not impeded in any way in such circumstances. The methodology, by its very construction, mainly confines the effect of such values to extending the overall range (and perhaps increasing the number of intervals needed to meet the error tolerance) but its actual effect on the “meat” of the distribution diminishes considerably as it is overwhelmed by the other, more “ordinary” values within the loss development history. All the same, the actuary may, in practice, choose to occasionally smooth such values using various smoothing techniques. In this manner the effect of the outlier on extending the overall range is mitigated. This variation should be used sparingly as it tends to negate the purpose of the exercise: quantifying the variability inherent in the source data. Once again, it is a good idea to also produce the uncapped, unadjusted distribution so as to be aware of the amount of variability that has been suppressed due to the use of this variation.
Tail factors
The methodology presented in this paper can be applied with or without a tail factor. The determination of the most appropriate tail factor(s) is beyond the scope of this paper. However, to the extent the actuary can identify suitable tail factors, those can be appended to the actual loss development history and the methodology can be applied as if the tail factors were the loss development factors associated with the last development period. Moreover, if the actuary is not certain which specific tail factor to use, a collection of tail factors can be appended to the loss development history (with or without weights) and thus the tail factor is allowed to vary as if it were just another loss development factor. Once again, it is a good idea to also produce the unadjusted distribution so as to assess the impact of introducing the tail factor distribution.
Applying the methodology to other loss development method
The basic methodology presented in this paper may be extended to related families of methods that are commonly used to project ultimate values. In this section two extensions are discussed: the Bornhuetter-Ferguson (B-F) family of methods and the Berquist-Sherman family of methods.
Bornhuetter-Ferguson family of methods
The original B-F method (Bornhuetter and Ferguson 1972), in its most basic form, starts with an assumed provisional ultimate value of an accident year (an Initial Expected Loss, or IEL), then combines two amounts: (a) the most recent valuation[17] and (b) the amount of expected additional development. In other words, the original expected additional development is gradually displaced by the emerging experience. The amount of expected remaining development is calculated by using factors derived from an assumed loss emergence pattern (usually based on some form of a prior loss development pattern or patterns) applied to an a priori expected loss. There are many variations on this theme that are well documented in the literature.
The remainder of this discussion will focus on developing the distribution of all outputs produced by the B-F method for a single accident year. From that point the convolution distribution will combine the various accident years’ distributions of outputs to produce the final distribution of outputs for all accident years combined, much as was already discussed and illustrated.
The extension of the methodology presented in this paper to the B-F family of methods will be discussed in two parts: one part that deals with a single selected IEL and one part that deals with an assumed distribution of IELs.
The IEL is a single value
This category consists of all those cases where the actuary makes use of an IEL that is a single value. Also, with respect to the loss development pattern that is used in the application of the B-F method, the pattern may be a prior pattern or a newly derived pattern based on the most current historical data. In all of these combinations, the application of the methodology is the same.
The construction of the distribution of outputs produced by the B-F method consists of the following two steps: (1) Construct the distribution of all outputs produced by the LDM, but instead of applying the various permutations of LDFs to the latest valuation of the accident year (previously denoted by Vi,i), apply the various permutations of LDFs to the portion of the IEL that is expected to have emerged (i.e., the assumed Vi,i); (2) for each point of this distribution, subtract the assumed Vi,i and add the actual Vi,i. This is the distribution of all outputs that can be produced by the B-F method when a single IEL is used.
A distribution of IELs
In this case the variability associated with the selection of the IEL is incorporated in the distribution of final outputs of the B-F method.
The process of creating the distribution of all outputs produced by the B-F method when the IEL is drawn from a distribution of IELs consists of the following steps: (1) Reconstitute the distribution of IELs into a discrete distribution consisting of ten[18] points, each representing one of the deciles of the distribution. (2) For each of the deciles, construct a distribution of all outputs as described in Section 8.1.1, thus producing 10 distinct distributions of outputs of the application of the B-F method, with one distribution associated with each of the deciles. Moreover, the distribution of all outputs associated with any one of the 10 values would have a probability of 10% of being the target distribution. (3) Take the union of all outputs that constitute the totality of the 10 different distributions thus producing the distribution of all outputs that can be produced by the application of the B-F method when the IEL is drawn from a distribution.
The Berquist-Sherman family of methods
The Berquist-Sherman (Berquist and Sherman 1977) family of methods, in the main, allows the actuary to review the historical data and, when appropriate, modify it to recognize information about operational changes that affected the emergence of loss experience. Various methods, such as the LDM or B-F, are then applied to the modified history. The distribution of all outputs produced by the LDM is applied to the modified historical loss experience. In this case, the distribution of all outputs produced by the LDM is exactly as described in this paper. Once again, it is essential that both the original distribution of outputs (using the original historical data) as well as the distribution of outputs using the modified historical data be produced so as to quantify the effect of making the changes to the historical data.
Closing remarks
This paper has dealt with a way to capture an approximation of the conditional distribution of outputs (empirical method-based distributions) that arise naturally in connection with the use of the LDM to make ultimate loss projections. As such the results produced by this methodology provide perspective, or a landscape, against which individual selections may be viewed. This is both useful as an end unto itself as well as an input to many other actuarial applications. The following notes deal with a number of related issues.
Statistics of the distribution
Given the approximation distribution of all outputs produced by the LDM (and all its extensions), the various statistics of the distribution can be produced using basic arithmetical functions that define each statistic of the distribution. Moreover, it is not difficult to demonstrate that the mean of the approximation distribution is approximately (within ε) equal to the single result produced by the LDM when the (arithmetic) average LDFs are used for every development period.
The reserve decision
Practice guidelines contains many references to the reserve decision in various ways, among them the following are noted: (a) The actuarial statement of principles[19] provides “An actuarially sound loss reserve . . . is . . . based on estimates derived from reasonable assumptions and appropriate actuarial methods . . .” and “. . . a range of reserves can be actuarially sound.”, (b) the Statement of Actuarial Opinion also calls for the actuary to identify a range of reasonableness for the reserve estimate, and (c) Actuarial Standard of Practice No. 43 speaks of “central estimate”.[20] The output produced by the methodology described in this paper, particularly measures of central tendency as well as measures of dispersion, can serve a useful purpose to the reserving actuary by providing important perspective in dealing with each of the three elements of guidance listed above: on arriving at the final reserve estimate, on the size and placement of a range of reasonableness, as well as assist with the derivation of a central estimate.[21] Note that there is no claim that the output produced by the methodology described in this paper is the main input to any of these items. Of course, the role of judgment remains a very important input to the final reserve decision and all associated requirements noted above. This paper describes just one item of input to guide the process of selecting the final estimate as well as the associated range.
Benchmarking
Although there are many potential uses of the type of output described in this paper, one particular use deserves specific mention: the use of the output in benchmarking reserves. Two particular methods of benchmarking will be discussed. One is the idea of “flash benchmarking.” This is simply the use of the output produced by the methodology described in this paper to perform quick benchmarking of the loss reserves of one or more entities; either in an absolute sense of in comparison to other similarly situated entities. The results, while obviously not dispositive, immediately can identify some situations, for example, where reserve estimates represent outlier values within the distributions derived in this paper that should be further studied and/or questioned. This type of benchmarking can be helpful to regulators and financial analysts. Another type of benchmarking is that performed over time: “longitudinal benchmarking.” In this type of benchmarking the results of a series of “flash benchmarking” results are viewed for any patterns that may be present. Persistent tendencies on either side of the mean can be fairly easy to spot, and in turn can be used to motivate further and more detailed study of the condition of reserves for the entity under review. This is a much more potent use of the benchmarking application for the outputs described in this paper.
The Impact on the Role of the Actuary
One of the potential implications of using the technology advanced in this paper is the concern that it can diminish the role of the actuary because a deterministic methodology is capable of producing ultimate loss estimates equal to the mean of the aggregate loss distribution associated with the historical data. This potential fails to materialize on at least two counts.
The role of judgment in arriving at ultimate loss estimates is not diminished in any way by the results of the processes described in this paper. The role of judgment remains a very important input into the final selection of the ultimate loss values. This fact alone can dispose of the potential diminution of the role of the actuary.
Moreover, having access to the outputs produced by the methodologies described in this paper creates an opportunity for the actuary to reconcile and rationalize the final reserve selection to the default values that are produced by this methodology. This process can only enhance the role of the actuary in the process of estimating ultimate loss costs.
Bootstrapping
The results produced by the methodology described in this paper are generally consistent with the results produced when using bootstrapping techniques in conjunction with applying the traditional LDM method. Several advantages over bootstrapping however, make it worthwhile to expend the additional effort required to produce the approximation distributions described in this paper. The general advantage of this methodology is that it makes it possible to extend and build on the raw results, namely the ability to: (a) extend the methodology to the B-F method (with a single IEL or a distribution of IELs) and the Berquist-Sherman families of methods, (b) apply a variety of weights to the historical LDFs, thus enabling the introduction of judgment directly into the process, (c) explain the approximation distribution to lay users of actuarial outputs without having to explain sampling, sampling error, and related issues required by bootstrapping techniques, and (d) make use of the outputs from the distributions of a variety of actuarial methods in order to aggregate various measures of central tendency and variability so as to define a single composite distribution.
Limitations
While the outputs that can be produced by the process described in this paper can be helpful, it is important to recognize a number of implicit limitations. The following list covers the main limitations associated with this methodology.
This methodology is not a reserving methodology per se. It can be used for that purpose (such as using the mean value of the distribution or the mean value + 10% of the standard deviation of the distribution) but that is a decision for the actuary to make and it is not the main purpose of deriving the conditional distribution of outputs.
The variability that can be derived from the use of the loss distribution produced by the methodology described in this paper reflects mainly the variability associated with the randomness that is inherent to the loss development process. It does not account for the increment of variability that is associated with the fact that the original data set containing the historical development is itself a sample out of numerous possible manifestations of historical loss development.
This methodology produces the conditional distribution of outputs that reflect actual historical experience. As such it does not recognize future changes in loss development patterns or in any other areas that may have an impact on the final output.
This methodology does not recognize or account for the model risk inherent in the very selection of the LDM (or any of the other methods used in this paper) as the proper method(s) for estimating ultimate loss values.
Applying the LDM to different samples of loss history (associated with the same cohort) necessarily produces different conditional aggregate loss distributions. No claim is made that the conditional aggregate loss distribution associated with a single sample history pertains to anything other than the specific sample used in the production of the approximation conditional aggregate distribution of outputs.
Typical application of the LDM generally relies on the use of various averages of LDFs. The outputs thus produced, while not exactly present in the loss distribution that is generated by the methodology outlined in this paper, can be expected to be close to actual values in the distribution. Thus any loss in the details of the description of the approximation distribution resulting from omitting the use of averages in the construction of the distribution is de minimus.
One also can think of the empirical distribution of the particular method as a type of “conditional” loss distribution, with the condition being ‘the method that is selected to produce the various ultimate loss outputs.’
The following sources illustrate the wide variety of ways in which closed form distributions can be constructed: Klugman, Panjer, and Willmot (1998), Heckman and Meyers (1983), Homer and Clark (2003), Keatinge (1999), Robertson (1992), and Venter (1983).
The set of assumptions is thus limited to the assumptions implicit in the operation of the selected method.
The classic LDM applies a single selected loss development factor (with respect to each loss development period) to all open years. The generalized version of LDM also applies a selected loss development factor (with respect to each development period) but allows this selection to be different for different open accident years. This type of LDM is a Generalized LDM and in this paper this is the version of the LDM that is used to develop the approximation methodology.
From this point forward, unless otherwise indicated, all distributions will refer to “method-based” distributions.
Often the selected value is a selected historical value (e.g., the latest observed value), some average of the observed loss development factors (e.g., the arithmetic average of the last three values), or some other average (e.g., the arithmetic average of the last five observations excluding the highest and lowest values). Moreover, any of these selections may be weighted by premiums, losses, or some other metric.
The issue of including outcomes that can be produced by using various averages or adjusted loss development factors is temporarily deferred and will be addressed later in this paper.
The reference to the use of “judgment” in connection with the application of the LDM speaks to introducing non-historical values into the process of calculating LDM outcomes (such as the use of averages for loss development factors). As such whatever is chosen, it is necessarily a reflection of the judgment of the user and is not a true observation of historical development. Therefore, any such outcomes technically are outside the scope of the methodology described in this paper.
Claims can be aggregated by accident year, report year, policy year, and by other types of time periods. The methodology presented in this paper applies equally to all such aggregations.
Data arrays come in many different shapes: triangles, trapezoids, parallelograms. And some arrays are irregular as some parts of some accident years histories may be missing. The methodology presented in this paper has equal application to virtually all possible shapes.
This step is necessary for purposes of this paper to demonstrate the theoretical foundation of the process. In actual practice this step is consolidated with step (4), into a single step for deriving N.
When I = J the array is a triangle and when I>J, the array is a trapezoid.
In actual practice a tail factor (or a set of tail factors) would be appended to the history. The issue of tail factors is addressed later in the paper. At this point, we only need to concern ourselves with the general condition of using the given historical values as the selection of a tail factor clearly invokes a judgment, which is beyond the immediate purposes of this paper.
For purposes of this paper ε is taken as a percentage value.
This construction assigns equal weight to each observed LDF. Weighted LDFs are addressed later in the paper.
In other words, the tail factor is taken to be 1.000. This is not a necessary assumption, merely a convenience for purposes of this particular demonstration. Tail factors other than 1.000 may be incorporated into this process. That discussion occurs in Section 7.3.
These valuations can be of either the paid or incurred variety.
Actually, any number of points can be used. Ten is used here as experience has shown that this is sufficient to capture the distribution of outcomes in all of its essential elements.
Property/Casualty Unpaid Claim Estimates, ASOP No. 43.
It should be kept in mind that in using the distribution produced by the methodology described in this paper, this distribution accounts mainly for the variability associated with the randomness of the loss development process and does not account for the increment of variability that is attributed to the fact that the original data set to which the methodology is applied is itself a sample that generates its own variability.