Optimal Growth for P&C Insurance Companies

1. Introduction

Long-term profitability and sustainable growth are important goals of property and casualty (P) insurers. Marketing plans such as segmentation penetration, new agency appointments, and new territory entries are all subject to the overall growth strategy of an insurer. For an insurer to grow, it must either explore new markets or attract new customers in existing markets. However, such new business generally produces both higher loss and expense ratios, and increases the overall operational risk of the company. Numerous case studies have shown that rapid growth rates can cause serious financial problems for a P insurer, reduce long-term value to its stakeholders, or even result in bankruptcy. According to A. M. Best (2004), 17.3% of P insolvencies from 1969 to 2002 were caused primarily by rapid growth.

D’Arcy and Doherty (1989, 1990) and Cohen (2005) discuss the “aging phenomenon” of P insurance markets in which new business usually generates a much higher loss ratio than renewal business, often resulting in an underwriting loss in the first year, but improving loss ratios in subsequent years for the retained portion of that cohort of business. Wu and Lin (2009) examine eight lines of business on 25 books with $28.7 billion of premium from 1995 to 2005 and demonstrate loss ratio improvements associated with this aging phenomenon. They find that renewal business produces loss ratios 7% to 18% lower than new business, with an average loss ratio difference of 13%. In addition to larger expected loss ratios, the expenses associated with acquiring new businesses (such as advertising, marketing, and underwriting) are higher than for renewal business. Feldblum (1996) suggests that an insurance company should price risks to take into account the expected profitability over the lifetime of the policy, including the loss ratio, expense ratio, and retention level at each renewal. An aggressive growth posture obviously means a higher proportion of a book of business is made up of new business, implying a higher combined ratio and greater underwriting risk. Therefore, an insurance company’s planned pace of growth should depend on whether the expected profit from insurance operations is high enough to support the growth. Without proper enterprise risk management, an aggressive growth strategy cannot be sustained over a long period, and may result in significant underwriting losses. P insurers may operate in the following cycle: reduce rates aggressively to be competitive; grow the book rapidly; see loss ratios deteriorate; increase the rates to alleviate underwriting losses; and watch sales go down because rates become less competitive.

Other academic researchers have found that increasing sales growth and improving per-unit profit margins can be conflicting goals. Aghion and Stein (2008) discuss that, given the constraints on management time and other resources, doing more in one dimension often implies doing less in the other. Harrington, Danzon, and Epstein (2008) investigate medical malpractice markets and show that insurance companies often sacrifice profit margins by cutting price excessively in the soft market to maintain sales volume. Ma (2009) shows that profitability will be eroded significantly when a high growth target is achieved by lowering underwriting standards.

Actuaries have long realized that growth rates influence an insurer’s loss, reserve, profit, and surplus, and have studied these effects using traditional actuarial and accounting methods. Muetterties (1979) presents an accounting model to calculate the necessary profit margin to keep pace with increasing premium growth. Based on rather conservative assumptions, he concludes that at least a 5% before-tax underwriting margin is necessary to maintain the relationship of premium to surplus. Niswander (1984) measures the trade-off between two conflicting goals: surplus growth based on profitability and exposure growth based on competitive rates. Because the average age of loss within an exposure period may change over time as a result of growth, McClenahan (1987) examines the impact of changes in exposure growth on loss development patterns, and proposes a method to adjust the development factors. To date, only D’Arcy and Gorvett (2004) have studied optimal growth from the perspective of the managers of insurance companies. They determine the optimal growth rate by maximizing the market value of a P insurance company. In their work, a three-factor econometric model is proposed in which an insurer’s market value is determined by its surplus, net written premium, and combined ratio. The model parameters are derived through linear regressions using data from fifteen publicly traded firms. They then run a series of dynamic financial analysis (DFA) simulations for a variety of growth rates using the Dynamo software.^[1] The D’Arcy and Gorvett (2004) study represents a significant milestone in pioneering the research on optimal growth for P insurers, but several aspects of their work may limit the benefit of their analysis for the entire P insurance industry. First, their method requires market values, which are only available for “stand-alone” P companies that are publicly traded. Mutual, reciprocal, subsidiary, and privately-held P companies do not have observable market values. As D’Arcy and Gorvett point out, very few of the more than 3,000 P insurers are both “stand-alone” and “publicly-traded.” Second, their approach is sensitive to stock prices of insurance companies, which can be very volatile. For example, excluding data from AIG, D’Arcy and Gorvett (2004) found that the optimal growth rate does not exist (negative growth will lead to higher market values); while including AIG data, the optimal solution is about 10%. Third, their study is based on sophisticated dynamic financial analysis (DFA), which requires significant resources and can be difficult to understand.

In this study we examine the numerical relationship between organic growth rates and the corresponding profitability and capital needs using an approach that requires less extensive data. Analytical models are derived based on an economic equilibrium model. In the optimization process, we incorporate practical constraints for the growth of P insurers. This paper extends and improves the previous study in three major aspects. First, it provides the maximum growth rate as well as the optimal growth rate under the predetermined constraints. Second, D’Arcy and Gorvett (2004) discuss that optimal positive growth may or may not exist, but they do not investigate the conditions for the existence of optimal growth. We investigate this issue and find that the existence of an optimal growth rate depends on the relative weighting assigned by a company’s management to their two goals of increasing surplus and increasing sales. When the weight on surplus is above a certain threshold, a positive optimal growth rate does not exist: an insurer can increase the expected value of the enterprise by increasing premium rates and improving profit margins while shrinking premium volume. Third, from the perspective of implementation, the models are developed using simpler assumptions and formulas than those deployed in Dynamo by D’Arcy and Gorvett (2004) and are therefore relatively easy to understand and apply. Additionally, all of the data required to use this method should be readily available from a P company’s actuarial database, and the calculations involved are easy to program in a spreadsheet, so that the proposed methods can be quickly implemented by P companies in their strategic financial planning.

This paper is organized in a straightforward manner. Section 2 discusses the relationship between growth rates and combined ratios, and introduces the concept of an equilibrium new business percentage (ENBP). Section 3 investigates the capital constraint on growth. Section 4 develops a conceptual framework for determining the optimal growth rate that maximizes the expected enterprise value. Section 5 provides a case study. The numerical relationship between growth rate and underwriting profit is presented. The constrained maximum growth rates and the optimal growth rates are calculated under various scenarios of market cycles, underwriting performances, and constraints. Section 6 offers a summary of the main conclusions drawn from this analysis. The appendix extends the model by subdividing the renewal book into multiple segments.

2. Growth rates and combined ratios

Let P_t^m be the market price at time t. If an insurance company does not deviate from the market price, its renewal business (RB) loss ratio would be L^m_r,t, where subscript r represents RB and superscript m represents market price. Let dp_t denote the percentage difference of a company’s price from P^m_t. The actual price of the insurer is P_t = P_t^m * (1 + dp_t). L_r,t is then the company’s actual RB loss ratio at time t and is given by L_r,t = L^m_r,t/(1 + dp_t). The company’s actual RB combined ratio is then C_r,t = L^m_r,t/(1 + dp_t) + E_r,t, where E_r,t is the expense ratio for renewal business.^[2] Using the same notation, the variables for loss, expense, and combined ratios for new business (NB) are denoted by L_n,t, E_n,t, and C_n,t = L^m_n,t/(1 + dp_t) + E_n,t, where L^m_n,t is the NB loss ratio if the company prices at the market level. As noted in the introduction, L_n,t > L_r,t, and E_n,t > E_r,t, meaning that C_n,t > C_r,t. Let G_t be the exposure growth rate. By the law of demand in economics, insurance demand decreases as the price increases. Therefore the growth rate G_t for an insurance company is a decreasing function of its price differential dp_t,

$$G_{t}=\alpha+\beta * d p_{t} \tag{2.1}$$

with β 0 to reflect decreasing demand with higher prices. Depending on market conditions, α can be positive or negative. In a hard market, α is positive, and an insurance company is able to rapidly grow its exposure at the market price. Even if it prices moderately above market (0 dp_t $-\frac{\alpha}{\beta}$), it can write more accounts and grow its exposures. In a soft market, α can be negative. Under this scenario, if an insurance company prices at the market rate level (dp_t = 0, G_t = α 0), it will reduce its exposure.

Let A_t and 1 − A_t denote the proportions of the overall book of business that NB and RB represent at time t, respectively. To grow in an absolute sense, an insurance company needs to attract more customers than those that fail to renew, so A_t is an increasing function of the growth rate G_t. Define R_r,t and R_n,t to be the retention ratios for renewal and new business.^[3] According to Wu and Lin (2009), R_r,t > R_n,t. Again, by the law of demand in economics, retention ratios are decreasing functions of a company’s price differential with market prices at time t,^[4] so

$$\begin{array}{l} R_{r, t}=\mu_{r}+\theta_{r} * d p_{t} \\ R_{n, t}=\mu_{n}+\theta_{n} * d p_{t} \end{array} \tag{2.2}$$

Let the written exposure in period $t-1$ be $Q_{t-1}$. The written exposure in period $t$ with annual growth $G_t$ is

$$Q_{t}=Q_{t-1}\left(1+G_{t}\right). \tag{2.3}$$

By expressing total exposures as the sum of NB and RB exposures, the following formulations will allow us to solve for the new business percentage, A_t, in terms of retention and growth rates. To start, the new business exposures written in period t can be expressed as

$$Q_{n, t}=Q_{t} A_{t}=Q_{t-1}\left(1+G_{t}\right) A_{t}. \tag{2.4}$$

The new business exposures written in underwriting period $t-1$ that are retained in period $t$ are $Q_{n, t-1} R_{n, t}=$ $Q_{t-1} A_{t-1} R_{n, t}$ and the renewal business exposures written in underwriting period $t-1$ that are retained in $t$ are $Q_{r, t-1} R_{r, t}=Q_{t-1}\left(1-A_{t-1}\right) R_{r, t}$. The total renewal business written in underwriting period $t$ is then

$$Q_{r, t}=Q_{t-1} A_{t-1} R_{n, t}+Q_{t-1}\left(1-A_{t-1}\right) R_{r, t}. \tag{2.5}$$

The total exposure at time t is the sum of both the NB and RB exposures:

$$Q_{t}=Q_{n, t}+Q_{r, t}. \tag{2.6}$$

Substituting (2.3), (2.4), and (2.5) into (2.6), we get

$$\begin{aligned} Q_{t-1}\left(1+G_{t}\right)= & Q_{t-1}\left(1+G_{t}\right) A_{t}+Q_{t-1} A_{t-1} R_{n, t} \\ & +Q_{t-1}\left(1-A_{t-1}\right) R_{r, t}. \end{aligned} \tag{2.7}$$

In a certain state with stable growth and retention, $\mathrm{NB}$ and $\mathrm{RB}$ exposures could achieve an equilibrium where $A_t$ will remain constant through time: $A_t=A_{t-1}$. In this situation, we name $A_t$ the Equilibrium New Business Percentage (ENBP). Substituting $A_t$ for $A_{t-1}$ in Equation (2.7) and canceling $Q_{t-1}$ from both sides, we can derive the percentage of $\mathrm{NB}$ required to gain a specific growth rate $G_t$ as

$$\begin{aligned} A_{t} & =\frac{1+G_{t}-R_{r, t}}{1+G_{t}+R_{n, t}-R_{r, t}} \\ & =1-\frac{R_{n, t}}{1+G_{t}+R_{n, t}-R_{r, t}}. \end{aligned} \tag{2.8}$$

The following example illustrates the ENBP concept. Consider a company whose current portfolio consists of 10% new business and that plans to grow its total written exposure by 15% annually. The annual retention rates for new and renewal business are 80% and 90%, respectively. The renewal business in the second year is 0.1 * 80% + 0.9 * 90% = 0.89. If the growth follows the plan, the total exposure in year two is 1.15, and new business needs to be 1.15 − 0.89 = 0.26. The NB percentage is 0.26/1.15 = 22.6%. The renewal business in the third year is 0.89 * 0.9 + 0.26 * 0.8 = 1.009. For 15% annual growth, the overall exposure is 1.15² = 1.323, and the volume of new business is 1.323 − 1.009 = 0.314. Following this procedure, Table 1 shows the required new business percentages for the next five years if the company wishes to grow its exposure by 15% annually.

Similarly, Table 2 reports the required new business percentages if the current NB percentage is 25% of the book. By comparing Table 1 and 2, it is clear that in equilibrium, A_t is determined by the planned growth rate and retention rates of NB and RB , and that it is independent of the current NB and RB composition of a book of business. However, this does not imply that the current mix of NB and RB is irrelevant to the growth plan.

When the current growth is slow (e.g., NB is 10% of total business), the required NB growth in the second year is 0.26/0.1−1 = 160%. The 15% growth plan is aggressive. On the other hand, when the current growth is rapid (e.g., NB is 25% of total business), the required NB growth in the second year is 0.275/0.25−1 = 10%. The 15% growth plan is relatively easy to achieve.

Now let us evaluate the impact of the growth pattern on the company’s combined ratio. Let b_t denote the difference between the NB and RB combined ratios,

$$b_{t}=C_{n, t}-C_{r, t}=\frac{L_{n, t}^{m}-L_{r, t}^{m}}{1+d p_{t}}+\left(E_{n, t}-E_{r, t}\right) . \tag{2.9}$$

Thus, b_t is a measure of the performance of new business relative to renewal business. The company’s combined ratio, C_t, can be written as

$$C_{t}=A_{t} C_{n, t}+\left(1-A_{t}\right) C_{r, t}=C_{r, t}+A_{t} b_{t}. \tag{2.10}$$

Substituting (2.8) into (2.10), the combined ratio C_t at growth rate G_t is

$$\begin{aligned} C_{t} & =\frac{\left(1+G_{t}-R_{r, t}\right) C_{n, t}+R_{n, t} C_{r, t}}{1+G_{t}+R_{n, t}-R_{r, t}} \\ & =C_{r, t}+\frac{\left(1+G_{t}-R_{r, t}\right) b_{t}}{1+G_{t}+R_{n, t}-R_{r, t}} . \end{aligned} \tag{2.11}$$

Equations (2.10) and (2.11) demonstrate the positive relationship between the combined ratio and the growth rate, which can be illustrated by the growth impact curve in Figure 1.

Figure 1.Growth impact curve

3. Capital constraint on growth

The growth of an insurance company is generally constrained by internal and external conditions such as surplus, stock market valuation, shareholder demands, and insurance market conditions. This implies that companies facing different constraints will have different growth strategies. Hagstrom (1981) discusses that the availability of surplus constrains the growth of an insurance company. Baker, Powell, and Veit (2003) show that firms follow stock market signals to adjust their business strategies. Wang et al. (2011) demonstrate that profitable growth is difficult to achieve in a soft market, and cycle management is a crucial consideration for an insurance company when determining its growth strategy.

Past studies have shown that surplus capacity can constrain the growth of an insurance company and that changes in insurance surplus affect the industry’s capacity for bearing risk (Davis 1979; Hagstrom 1981; Gron 1994; Winter 1994; Cummins and Danzon 1997). To support growth, regulators and rating agencies require the insurance company to hold additional capital to maintain its financial rating. In this section, we illustrate our methodology by assuming a simple capital constraint: to maintain a target premium-to-surplus ratio.^[5] Consider an insurance company in a growth equilibrium that has a target premium-to-surplus ratio K_t. It writes one unit of premium in underwriting year t and is growing its exposure at G_t annually. Assume the market price at year t is P^m_t = 1. dp_t is the company’s percentage price difference with the market. So its actual price at year t is P_t = 1 + dp_t. Written premium is the product of written exposure Q_t and price P_t, that is, 1 = Q_t * (1 + dp_t). Moving Q_t to the left side of the equation, the written exposure at year t is

$$Q_{t}=\frac{1}{1+d p_{t}}. \tag{3.1}$$

The written exposure at year $t+1$ is $Q_{t+1}=Q_t *(1+$ $\left.G_{t+1}\right)$. Substituting (3.1) into the equation,

$$Q_{t+1}=\frac{1+G_{t+1}}{1+d p_{t}}. \tag{3.2}$$

At time t+1, the market price is

$$P_{t+1}^{m}=P_{t}^{m} *\left(1+T_{t+1}\right), \tag{3.3}$$

where $T_{t+1}$ is the market rate change from year $t$ to $t+1$. To simplify the illustration, we assume $T_{t+1}=0$, which implies $P_{t+1}^m=P_t^m$. Let $d p_t$ be constant with time: $d p_t=d p_{t+1}=d p$. The insurer’s actual price at $t+1$ is then $P_{t+1}=P_{t+1}^m *\left(1+d p_{t+1}\right)=1+d p$. The total written premium in year $t+1$ is

$$\begin{aligned} W P_{t+1}=Q_{t+1} * P_{t+1} & =\frac{1+G_{t+1}}{1+d p_{t}} *\left(1+d p_{t+1}\right) \\ & =1+G_{t+1}. \end{aligned} \tag{3.4}$$

The written exposure at year t−1 is

$$Q_{t-1}=\frac{Q_{t}}{1+G_{t}}=\frac{1}{(1+d p)\left(1+G_{t}\right)}. \tag{3.5}$$

The written exposures at t and t+1 are$\frac{1}{1+d p}$and $\frac{1+G_{t+1}}{1+d p}$, respectively. The written premium at year t−1 is

$$\begin{aligned} W P_{t-1}=Q_{t-1} * P_{t-1} & =\frac{1}{(1+d p)\left(1+G_{t}\right)} *(1+d p) \\ & =\frac{1}{1+G_{t}} . \end{aligned} \tag{3.6}$$

The written premiums at $t$ and $t+1$ are 1 and $1+G_{t+1}$, respectively. Assuming annual policy terms and assuming uniform writing of policies throughout the year, the earned premium in calendar year $t$ is

$$\begin{aligned} E P_{t} & =0.5 *\left(W P_{t-1}+W P_{t}\right) \\ & =0.5 *\left(1+\frac{1}{1+G_{t}}\right), \end{aligned} \tag{3.7}$$

and the earned premium in calendar year t+1 is

$$\begin{aligned} E P_{t+1} & =0.5 *\left(W P_{t}+W P_{t+1}\right) \\ & =0.5 *\left(1+G_{t+1}+1\right). \end{aligned} \tag{3.8}$$

The underwriting profit in year t is EP_t * (1 − C_t). We assume that policyholder-provided funds (from unearned premium reserve and loss reserve) are proportional to written premium, and shareholder-provided funds are equal to surplus. Let S_t be the surplus at the beginning of year t. The total funds available for investment are

$$I_{t}=\lambda * W P_{t}+S_{t}, \tag{3.9}$$

where λ is the fund-generating coefficient. Let Y_t be the yield on investment, t_u and t_I be the tax rates on underwriting and investment profit, respectively, and D_t be the dividend payout ratio. The retained profit after taxes and dividends in year t is

$$\pi_{t}=\left[\begin{array}{l} E P_{t} *\left(1-C_{t}\right) *\left(1-t_{u}\right) \\ +I_{t} Y_{t} *\left(1-t_{I}\right) \end{array}\right] *\left(1-D_{t}\right). \tag{3.10}$$

The surplus at the beginning of year $t+1$ is $S_{t+1}=S_t$ $+\pi_t$. To maintain the target premium-to-surplus ratio in policy year $t+1$,

$$\frac{W P_{t+1}}{S_{t+1}}=\frac{W P_{t} *\left(1+G_{t+1}\right)}{S_{t}+\pi_{t}} \leq K_{t}. \tag{3.11}$$

Substitute (3.10) into (3.11) and solve for C_t:

$$\begin{array}{c} W P_{t} *\left(1+G_{t+1}\right)-K_{t} * S_{t} \\ C_{t} \leq 1-\frac{-K_{t} * I_{t} * Y_{t} *\left(1-t_{I}\right) *\left(1-D_{t}\right)}{E P_{t} *\left(1-t_{u}\right) *\left(1-D_{t}\right) * K_{t}}. \end{array} \tag{3.12}$$

Inequality (3.12) implies that in order to grow the business while maintaining the target premium-to-surplus ratio, an insurance company needs to achieve a profit rate better than a certain threshold to support the growth. Inequality (3.11) can also be rewritten as

$$G_{t+1} \leq \frac{K_{t} *\left(S_{t}+\pi_{t}\right)}{W P_{t}}-1. \tag{3.13}$$

Inequality (3.13) implies that there is a certain boundary that constrains an insurance company’s growth; beyond a certain growth rate, an insurer will not be able to maintain its target leverage ratio. The growth limit curve D in Figure 2 shows this constraint. In order to support growth, an insurer has to keep its combined ratio below curve D. The faster the growth, the higher the profitability that is required to support the growth. Recall from Figure 1 that the growth impact curve S indicates that faster growth will lead to a higher combined ratio. The intersection at point M between curves D and S is the maximum growth under the premium-surplus leverage constraint. All the points below M on curve S are below the growth limit curve D. If an insurer grows more slowly than M, its premium-to-surplus leverage ratio will remain under the target. All the points above M on curve S are also above the growth limit curve D. Therefore growth faster than M will make the expected premium-to-surplus ratio higher than the target level.

Figure 2.Maximum growth rate under the premium-to-surplus constraint

4. Optimal growth

In general, an insurance company’s value is an increasing function of its surplus, volume of sales, and profitability. In the stock market, ratios such as price-to-book, price-to-sales, and price-to-earnings are widely used parameters in a company’s valuation. Insurance companies’ combined ratios are often volatile, so any valuation based on earnings will also be unstable as a result. D’Arcy and Gorvett (2004) run multiple regressions using observed market values as the dependent variable and surplus, net written premium, and combined ratio as explanatory variables, and find that the coefficient for the combined ratio variable is significant for only one out of 15 companies (Acceptance). For the other 14 companies examined in the study, all 15 companies combined, and all companies excluding AIG, the coefficient of the combined ratio variable is not significant at the 5% level. However, as we all know, if the combined ratio is low, earnings will be high and the surplus will increase accordingly. From this aspect, the impact of the combined ratio on market value is correlated with surplus. After controlling for the effect of surplus, the combined ratio is no longer a significant variable in estimating the market value of the insurer. As a result, we assume that an insurance company’s expected enterprise value is a function of surplus and net written premium only, and exclude the combined ratio variable from D’Arcy and Gorvett’s (2004) formula^[6]

$$V_{t+n}=W * \phi * S_{t+n}+(1-W) * \eta * W P_{t+n}, \tag{4.1}$$

where $\phi$ is the expected price-to-book ratio, $\eta$ is the expected price-to-sales ratio, $n$ is the planning or evaluating horizon, and $W$ is the weight on surplusindicated enterprise value. To simplify the formulation, we assume the growth rate is constant with time, that is, $G_t=G$. In Equation (4.1), surplus at year $t+n, S_{t+n}$ is a decreasing function of the growth rate, $S_{t+n}=S(G, n)$; while written premium, $W P_{t+n}=(1+G)^n$, is increasing with $G$. The optimal growth rate is the one that maximizes the expected enterprise value at year-end $t+n$ :

$$\operatorname{Max}_{G} W * \phi * S(G, n)+(1-W) * \eta *(1+G)^{n}. \tag{4.2}$$

Market appetite to surplus and growth varies over time. Aghion and Stein (2008) find that the stock market pricing rule impacts management’s growth strategy. When the stock market is more interested in growth, managers may pay more attention to sales volume. When investors in the stock market prefer profit margins, managers take the cue and adapt their strategies accordingly by cutting costs. The study demonstrated that management’s tendency to give the stock market what it wants can lead to excess volatility in business operations. Ma (2009) examines Aghion and Stein’s catering theory on public P companies and confirms that insurers devote more effort to growth when the stock market places greater value on growth, and that the managerial “short-termism” from following stock market preferences can exert a destabilizing influence on insurance pricing and the insurance market cycle. Based on those studies, the authors do not attempt to estimate empirical weights implied by the stock market. We suggest that practitioners use a weight that represents management’s long-term view of the balance between exposure growth and surplus growth.

5. Numerical analysis

To illustrate the framework, we perform a case study on a hypothetical insurance company. Key parameters are selected based on the authors’ experience.

$$G_{t}=2 \%-1.5 * d p_{t}. \tag{5.1}$$

At the market price level, an insurance company will grow its exposure 2% annually, which is close to the average annual GDP (gross domestic product) growth.^[7] The retention rates of renewal and new business are^[8]

$$\begin{array}{l} R_{r, t}=84 \%-0.2 * d p_{t} \\ R_{n, t}=78 \%-0.3 * d p_{t}. \end{array} \tag{5.2}$$

At the market price level, the retention ratio of RB is 84%, 6% higher than that of NB. This retention difference between RB and NB is consistent with Wu and Lin (2009). At a 2% annual exposure growth rate, the equilibrium NB percentage by Equation (2.8) is $A=1-\frac{0.78}{1+0.02+0.78-0.84}=18.8 \%$. The NB loss ratio is assumed to be 75%, which is 13% higher than that of RB. The difference in loss ratios between NB and RB is also consistent with Wu and Lin (2009). The NB expense ratio is assumed to be 37%, while the RB expense ratio is 32%. At market price levels, NB, RB, and whole book combined ratios are 112%, 94%, and 97.4%, respectively. If the price is 4% below the market, the company will improve retention, attract more new business, and grow 8% a year. If it charges 4% above market, it will reduce retention, attract less new business, and shrink 4% annually. Table 3 exhibits ENBP, NB, and RB retention ratios, and NB and RB loss and combined ratios for dp_t values between −4% and 4% (with the corresponding growth assumptions). It is clear that lower prices will drive faster growth, higher retention, and higher combined ratios. This is consistent with the theoretical derivation in previous sections and with real-world observations.

The fund-generating coefficient is assumed to be 1.2. So investment funds available from the unearned premium and loss reserves are 120% of written premium. The investment yield is assumed to be 4%. The tax rate on investment and underwriting income is 35%.^[9] The dividend payout ratio is assumed to be 30%, which is close to the actual S 500 payout ratio in the 2000s.^[10] Year 0 written premium is 1. The target premium-to-surplus ratio is assumed to be 1.5. The surplus at the beginning of year 0 is 0.667, so that the premium-to-surplus ratio at the starting point is 1.5.

The target premium-to-surplus ratio can vary by time, and it may not be the initial ratio. For example, an insurer with a low premium-to-surplus ratio might be willing to increase its leverage for a period of time when it adopts a high growth plan in a hard market; it then slows down the growth and targets a lower premium-to-surplus ratio when the market turns soft. The case study can be easily adjusted to incorporate time-varying target leverage.

Tables 4 through 6 show five-year underwriting and investment profits, surplus, premium, and premium-to-surplus ratios if a company grows at 2%, −4%, and 8% (which correspond to scenarios that the insurer consistently prices at, 4% above, and 4% below the market). Table 7 shows the same statistics at the constrained maximum growth rate of 5.52%. If the growth is below the threshold, as shown in Tables 4 and 5, the company will generate more profit than is required to support the growth. Surplus will grow faster than premium; the expected premium-to-surplus ratio will go below 1.5 and decrease with time. Table 6 shows an example of what happens if the growth rate is faster than 5.52%. In this case, the company will generate less profit than is required to support the growth. Surplus levels cannot keep up with the pace of premium growth, and the expected premium-to-surplus ratio will go above 1.5 and continue to increase with time. Table 7 shows that if the insurer grows at 5.52%, the expected premium-to-surplus ratio will remain at 1.5, which is what we expect, as that is the growth solution to maintain a constant premium-to-surplus ratio, given our input assumptions.

Table 8 reports the combined ratios on the growth impact and growth limit curves. Figure 3 shows the two curves visually. To achieve faster growth, an insurance company needs to reduce prices and attract more NB. Both actions will result in a higher combined ratio. The combined ratios on the growth impact curve, as shown in Table 8 and Figure 3, represent this relationship. When the growth rate is zero, the combined ratio is 96.3%. When the growth rate is 9%, the combined ratio will increase 5.1% to 101.4%. The company will switch from an underwriting profit to an underwriting loss if it grows faster than 6.5%. When growth is zero, an insurer can maintain the target leverage ratio at a 7.5% underwriting loss. Under this scenario, the investment income offsets the underwriting loss, the net income is zero, and the surplus stays the same after one underwriting period. The premium does not change either, so that the insurer will maintain a stable leverage ratio. If the insurer plans to grow at 9% annually, it needs to increase its surplus at the same pace. The corresponding combined ratio on the growth limit curve is 94.0%, which implies that the company has to achieve a 6% underwriting profit so that it can retain a net profit (after tax and dividend) that is equal to 9% of its surplus. Unfortunately, a 9% growth in reality will result in an underwriting loss of 1.4%, according to the growth impact curve. At 5.52% growth, the combined ratios on the two curves are equal. If growth is faster than 5.52%, the growth impact curve is above the growth limit curve; that is, the actual combined ratios will be higher than those required to maintain the target leverage ratio. Following such aggressive growth, the premium-to-surplus ratio will penetrate the target leverage, as shown in Table 6. Therefore, 5.52% is the maximum allowable growth rate under the leverage constraint.

Figure 3.Empirical growth impact and limit curves

Insurance capital requirements vary by line of business. Volatile lines (such as coastal homeowners) in general require more economic capital to pay losses from worst-case scenarios, and the target premium-to-surplus ratios can be less than one. Alternatively, stable lines (such as standard personal auto) require less capital, and the target leverage ratios can be greater than two. Table 9 shows that, if the insurer’s target leverage ratio decreases from 1.5 to 1.0, its maximum growth under the constraint decreases from 5.52% to 4.54%. If the target leverage ratio increases to 3.0, it can grow 7.63% annually while still keeping its expected leverage ratio at the target level.

It is well known that companies with superior risk selection skills can outperform the industry in both profitability and growth. Assume an insurer can identify the most profitable segments and can write that business at a loss ratio significantly lower than the industry average. In this case, it can lower its price to be competitive while still being very profitable. As shown in Table 9, if the insurer can improve loss ratios by 5% at market price (NB LR = 70% and RB LR = 57%) through better risk selection, its maximum allowed growth rate increases from 5.52% to 8.00%. Alternatively, if the company is adversely selected against and loss ratios deteriorate by 5% (NB LR = 80% and RB LR = 67%), the constrained maximum growth declines from 5.52% to 3.07%. If the insurer can improve loss ratios by 10% (NB LR = 65% and RB LR = 52%), it can grow as fast as 10.51% without penetrating the target 1.5 premium-to-surplus ratio. Some personal auto insurers (such as Progressive) were able to achieve superior growth and profitability using advanced analytics in risk selection. Table 9 shows that if an insurer can produce a loss ratio 10% better than the industry average in the presence of a less restrictive capital requirement (with a target leverage ratio of 3), it can obtain a significant competitive advantage, grow at a stellar 15.55% annual rate, and achieve an outstanding combined ratio of 94.36% so that surplus can grow at the same rate as sales.

It is also well known that insurance companies can produce lower loss ratios and achieve faster growth in a hard market. Wang et al. (2011) shows that loss ratios in soft and hard markets can differ by as much as 25%. Consistent with Wang et al., we assume that the loss ratios in extreme soft/hard markets are 12% worse/better than that of the normal market. If the market is very hard, an insurer can grow its exposure by 6% while maintaining a market price level (α = 0.06 in Equation 2.1). In a very soft market, an insurer will shrink by 2% at the market price (α = −0.02). Table 10 illustrates the impacts of market cycles on loss performance and constrained maximum growth. In an extreme soft market, the maximum allowable growth rate is negative. The insurer has to reduce its size to maintain the target leverage ratio. In an extreme hard market, the insurer can grow by over 12% annually while still maintaining the leverage ratio.

Following D’Arcy and Gorvett (2004), we calculate the optimal growth rate that maximizes the expected enterprise value at the end of the fifth year. The expected price-to-book ratio and price-to-sales ratio are assumed to be 1.2 and 0.8,^[11] respectively. Table 11 shows the expected enterprise value at the end of the fifth year by various growth rates and weights on book value. If the weight on book value is high (W ≥ 77%), a company can increase its value through rate increases while shrinking its business. This is because the profit and surplus growth will create enough enterprise value to offset the reduction from the written premium loss. This case is equivalent to the regression scenario excluding AIG in D’Arcy and Gorvett (2004). Under this condition, there is no positive optimal growth and the insurance company would need to reduce its sales volume in order to increase its expected enterprise value. When the weight on book value is low (W ≤ 74%), the company can increase its value through aggressive growth and rate cuts. In this case, the expected enterprise value is increasing with growth, leading to an optimal exposure growth greater than 8%. An insurer can maximize its expected value through aggressive growth because the gain in premium will more than offset the loss in surplus and profit. This is equivalent to the regression scenario including AIG in D’Arcy and Gorvett (2004), in which the optimal growth rate is about 10%. When the weight on book value is between 74% and 76%, the optimal growth is between 0% and 8%. As shown in Table 11, when W = 76%, a 2% exposure growth provides the highest expected value of those reported scenarios. When W = 75%, 5% growth offers the highest value. When W > 76.5%, a positive optimal growth rate does not exist.

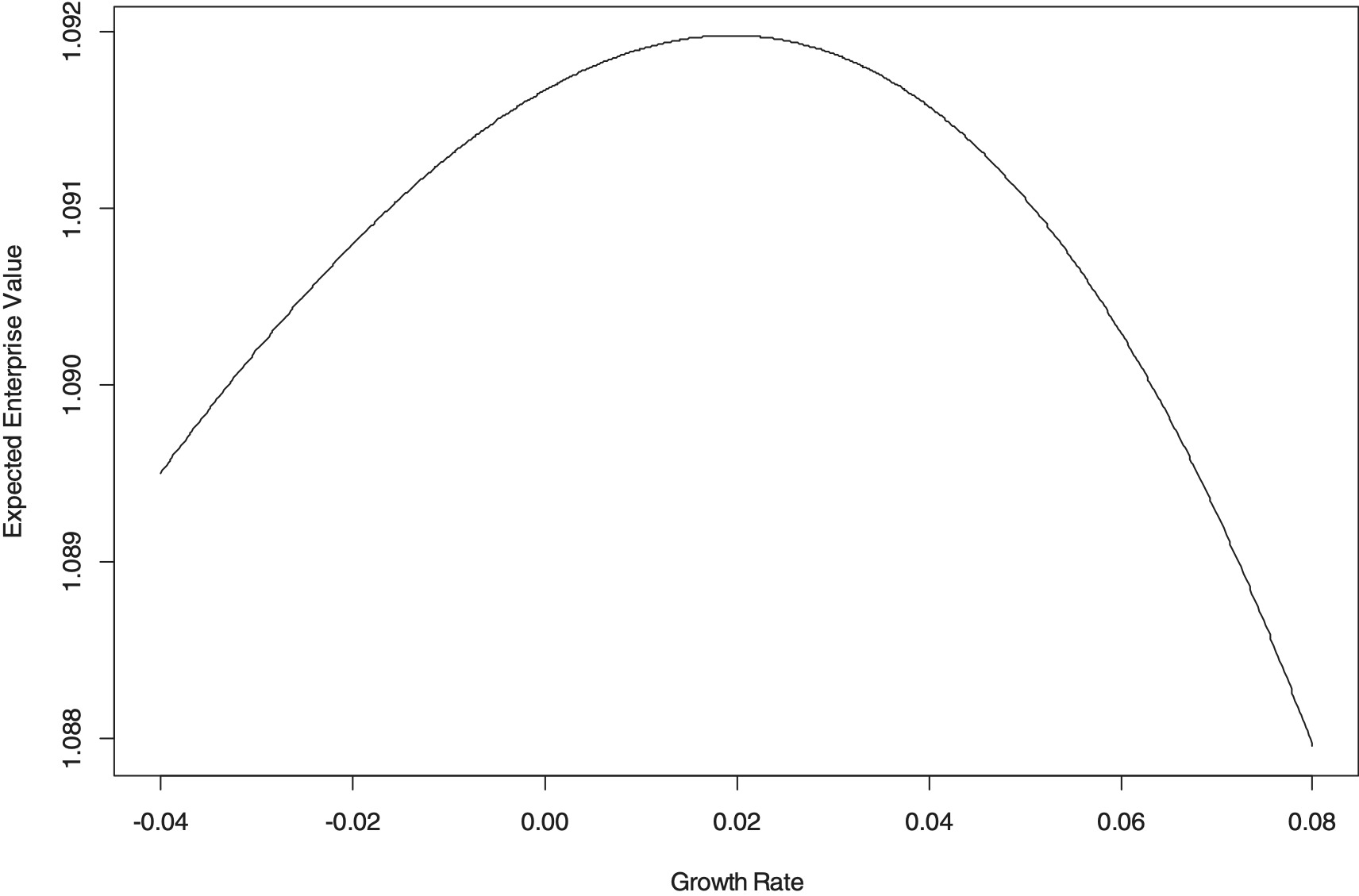
Table 12 shows the optimal growth rates for weights on book value between 74.5% and 77.5%. Two constraints are added in the optimization: the expected premium-to-surplus ratio is no larger than 1.5 and the exposure growth is not less than −3%. When W = 74.5%, the leverage constraint is enforced so that the optimal growth rate is the maximum allowable growth rate of 5.52%. When W = 77.5%, the minimum growth constraint is applied so that the optimal growth is −3%. When 75% ≤ W ≤ 77%, the constraints do not impact the optimization. Figure 4 demonstrates the optimal growth rate visually for W = 76%. As the growth rate increases from −4% to 1.94%, the growth creates more enterprise value than the loss from the reduction of book value. The expected enterprise value increases steadily until it reaches its peak value 1.092. When the growth is faster than 1.94%, the increase of enterprise value from growth cannot offset the loss from the reduction of book value, and so the expected enterprise value decreases with growth.

Figure 4.Optimal growth rate when W = 76%

6. Conclusions

Profit and growth are often two conflicting goals of insurance companies. It is common knowledge that profit and growth often move in opposite directions. Rapid growth may diminish underwriting performance, reduce profit, and even cause bankruptcy. When facing underwriting losses, management may have to slow down the rate of growth. Slow or negative growth may improve underwriting profit and increase surplus. A higher volume of surplus will reduce the premium-to-surplus ratio and result in a lower return on equity, which may give management incentives to grow the business and increase the leverage ratio.

Insurance companies need to grow rationally by balancing these two contradictory forces. On one hand, growth will drive up the combined ratio because new business generally produces higher loss and expense ratios. But on the other hand, rapid growth requires insurance companies to generate more underwriting profit and additional capital. The faster the growth, the lower the combined ratio needed to support such growth.

In this study, the author proposes a straightforward method to calculate a constrained maximum growth rate and optimal growth rate. Compared with the previous study (D’Arcy and Gorvett 2004), the proposed approach has three advantages: (1) it is easier to understand and implement; (2) all the required data is readily available in the actuarial database of insurance companies; (3) it discusses further the conditions for the existence of a positive optimal growth rate. The flip side of those advantages is that the approach is in a deterministic framework^[12] and therefore cannot provide valuable stochastic insights of DFA models, such as the risk frontier and distributional statistics in D’Arcy and Gorvett (2004).

Under growth equilibrium, the combined ratio is an increasing function of the growth rate. This is the growth impact curve. To maintain a target premium-to-surplus ratio, higher capital and underwriting profit is needed so that surplus can keep pace with premium growth. The faster the growth, the lower the combined ratio that is required. This is the growth limit curve where the combined ratio is a decreasing function of growth. The growth impact curve shows that the profit margin will decrease with growth from the perspective of underwriting performance. The growth limit curve represents the need for the profit margin to increase with growth from the perspective of capital management. The growth limit curve enforces a constraint on growth: the combined ratio needs to be below the curve so that the expected premium-to-surplus ratio will not penetrate a certain target level. The intersection of the growth impact and limit curves is the maximum growth rate under the leverage constraint.

To obtain the optimal growth rate, an insurance company is assumed to maximize its expected enterprise value, which is a weighted average of its book value and sales volume. The methodology and the results of our case study on optimal growth are consistent with D’Arcy and Gorvett (2004). When the weight on book value is beyond a certain threshold, the impact of surplus dominates that of written premium: an insurance company will increase its expected enterprise value by raising premium rates and reducing its exposure. In this case, positive optimal growth does not exist.

This paper studies the constrained maximum and optimal growth rates under certain market conditions for an insurer with a stable pricing strategy and a constant utility function. In practice, market conditions, pricing strategies and utility functions of insurance companies continuously change with time. While growth is approaching its equilibrium under a specific environment, the market condition changes. An insurance company may adjust its pricing strategy accordingly. This implies that growth may never reach equilibrium in the real world. Nevertheless, knowing the theoretical boundary (the maximum growth rate under the leverage constraint) for growth can help insurance companies to reduce enterprise risks due to irrational growth. Knowing the optimal growth rates conditional on management’s utility function can help management to make a growth plan that is consistent with their evaluations of the relative importance of surplus and sales volume. The calculations of constrained maximum and optimal growth rates are straightforward and can be effectively employed by property and casualty insurers in their strategic planning process.

Acknowledgments

The author thanks Professor Philip Garcia, Doug Pirtle, FCAS, MAAA, and C. K. “Stan” Khury, FCAS, MAAA for their valuable comments.

Appendix

Model Extension to Multiple Levels of Renewals

The proposed model in the main section of this paper simplifies the aging phenomenon into two classes: new and renewal books of business. The loss ratio of renewal business generally continues improving with policy age (D’Arcy and Doherty 1990). Retention also increases as renewal policies become older. A natural extension of the model is to subdivide renewals into multiple segments.

In the case study example, at the market price level, the NB and RB retentions are 78% and 84%, respectively, and the NB and RB loss ratios are 75% and 62%, respectively. Assume that an actuarial practitioner would like to further divide the RB book into two subgroups: first two renewals and the remainder. Let RB1 denote the first renewal, RB2 denote the second renewal, and RB3+ denote policies that are of age three years or older. Assume the retention ratios of RB1, RB2, and RB3+ are 82%, 82%, and 85%, respectively; and the loss ratios of RB1, RB2, and RB3+ are 65%, 65%, and 60%, respectively. To extend the model, we need the equilibrium percentages for NB, RB1, RB2, and RB3+.

Using the same logic as in the main section, suppose the exposures of NB, RB1, RB2, RB3+ are 0.10, 0.09, 0.08, and 0.73, respectively. Again, assuming the book would grow at 2% per year at the market price level, the convergences of equilibrium percentages are demonstrated in Table A1. In year 1, the RB1 exposure (0.078) is equal to the prior year’s NB exposure (0.1) multiplied by the new business retention ratio (78%); the RB2 exposure (0.074) is the prior year’s RB1 exposure (0.09) multiplied by the RB1 retention (82%); the RB3+ exposure (0.686) is the sum of the renewals from the prior year’s RB2 (0.08*82%) and RB3+(0.73*85%) books. The total RB exposure (0.838) is the sum of RB1, RB2, and RB3+. To grow the business by 2%, the NB exposure in year 1 (0.182) needs to be the exposure from the target growth (1.02) less the total RB exposure. Continuing the process, the percentages of NB, RB1, RB2, and RB3+ will converge at year 8. At equilibrium, NB is 18.7% of book, RB1 is 14.3%, RB2 is 11.5%, and RB3+ is 55.5% of book. If the starting exposures of NB, RB1, RB2, and RB3+ are 0.20, 0.15, 0.10, and 0.55, respectively, the convergence will be faster, and will arrive at the same equilibriums at year 6, as shown in Table A2.

Let A_NB, A₁, A₂, and A₃ be the equilibrium percentages of NB, RB1, RB2, and RB3+, respectively; and let R_NB, R₁, R₂, and R₃ be the respective renewal rates. RB1 is from the prior year’s new business:

$$A_{1}=A_{N B} * R_{N B} /(1+G) \tag{A.1}$$

RB2 is from the prior year’s RB1:

$$A_{2}=A_{1} * R_{1} /(1+G) \tag{A.2}$$

RB3+ is from the prior year’s RB2 and RB3+:

$$A_{3}=\left(A_{2} * R_{2}+A_{3} * R_{3}\right) /(1+G) \tag{A.3}$$

Finally, the sum of the percentages from various layers should be equal to one.

$$A_{N B}+A_{1}+A_{2}+A_{3}=1 . \tag{A.4}$$

The four equilibrium percentages can be obtained by solving the four equations above:^[13]

$$\small{ \left\{\begin{aligned} A_{N B}= & \frac{(1+G)^{2}\left(1+G-R_{3}\right)}{(1+G)^{2}\left(1+G-R_{3}\right)+(1+G)\left(1+G-R_{3}\right) R_{N B}} \\ & +\left(1+G-R_{3}\right) R_{N B} R_{1}+R_{N B} R_{1} * R_{2} \\ A_{1}= & \frac{A_{N B} R_{N B}}{1+G} \\ A_{2}= & \frac{A_{N B} R_{N B} R_{1}}{(1+G)^{2}} \\ A_{3}= & \frac{A_{N B} R_{N B} R_{1} R_{2}}{(1+G)^{2} *\left(1+G-R_{3}\right)} \end{aligned}\right. \tag{A5} }$$

Once the equilibrium exposure percentages for various layers of new and renewal business are derived, we can calculate the whole book’s combined ratio as a weighted average of the multiple layers. In this specific case, the equilibrium loss, expense, and combined ratios at 2% growth rate are 64.1%, 32.9%, and 97.0%, respectively. The new combined ratio formula will replace Equation (2.11) in the main section and the calculations after it will remain the same.