1. Introduction
Wildfires burn around 423 million hectares of the global land surface annually, which represents approximately 3% of the global vegetation land (Giglio et al. 2018). Under very dry conditions, such as extreme heat combined with very low precipitations, a natural spark or human activity can ignite a wildfire. The effect of climate on wildfire risk varies depending on the location and time due to the spatial and temporal climate diversity, spatial variation of vegetation, fire management and prevention policies, and the interaction between these variables. The 2016 wildfires in Alberta (Fort McMurray) and the 2017-2021 wildfires in California generated billions of dollars in insured losses and alerted the public and insurers to the threats caused by wildfires. Knowledge of the spatial likelihood of burning and the potential financial impact of wildfires can provide a great tool for wildfire risk management.
Although fire activity in North America fluctuates annually, recent years witnessed an increased annual number and size of forest fires in some locations compared to the past few decades. In fact, the 2017 and 2018 wildfires in British Columbia are the largest wildfires to be recorded in the area since the 1950s, with a total of 1.2 and 1.4 million hectares burned, respectively (Hanes et al. 2019). The Dixie fire in 2021 is the second-largest wildfire in the history of California, with around 0.4 million hectares burned (CALFIRE 2022).
Wildfire losses fluctuate considerably, depending on the location of events. Between 2000-2019, 26% of the world’s wildfires and 69% of the economic losses due to wildfires occurred in the United States of America (USA), with the most damage in California (Yaghmaei 2020). In California, numerous insurers have stopped writing homeowners’ insurance policies in fire-prone areas, resulting in a transfer of the insurance business to expensive specialty markets (Groom 2015). The Canadian Interagency Forest Fire Center (CIFFC) reports 6,317 wildfires across Canada in 2021, with more than 4.2 million hectares of burned land (CIFFC 2021). The International Disaster Database reports that North America suffered from $68.8 billion in total damages (adjusted to inflation) due to wildfires over the period between 2000-2019, with only 64% of those losses being insured (EM-DAT 2020).
Spatial wildfire risk assessment and fire spread models are growing fields with applications in fire-related decision making. Simulation-based fire spread algorithms were introduced to mitigate the damage caused by wildfires; see, for example, Van Wagtendonk (1996). Spatial wildfire models in the literature usually focus on a limited geographical study area; see, for example Finney et al. (2011) (continental USA), Atkinson et al. (2010) (Tasmania, Australia), Chuvieco et al. (2010) (Spain), Massada et al. (2009) (Northwestern Wisconsin, USA), and Van Wagtendonk (1996) (Sierra Nevada, USA), however, they are not created for actuarial purposes. Adequate estimation and prediction of future wildfire insured losses is challenging since it requires information on buildings. Moreover, constant developments in wildfire-prone areas may not be consistent with historical losses. As such, insurers are typically buying private complex wildfire insurance risk models, which may provide results that are difficult to interpret and replicate. Spatial modeling in the actuarial literature usually focuses on claims data; see, for example Shi and Shi (2017) for spatial frequency and severity modeling of auto-insurance claims, however, one may not always have sufficient claims data that covers the geographical region of interest. In the context of natural catastrophic events, such as wildfires, it is more suitable to follow a natural catastrophe risk modeling decomposition approach, i.e. identify the hazard, vulnerability and exposure; see Mitchell-Wallace et al. (2017) for details. There is wildfire risk at the intersection of those three components, such that a vulnerable property is subject to wildfire risk due to its location and characteristics.
This article provides a quantitative approach that considers the spatial variation in climate, land and demographic factors that drive wildfire occurrence in North America. We propose a wildfire risk model specifically tailored for USA and Canada, separately, splitting for each cause of ignition: man-made and natural. Our goal is to provide an open-source model, for pricing and underwriting P&C insurance policies. The model takes into account multiple types of wildfire risk features: continuous variables, categorical variables, and geographical coordinates. Several modeling techniques are used, such as GLMs and statistical learning algorithms that rely on decision trees. Combining numerous decision trees in an ensemble, such as a random forest, provides high predictive performance with an ability to discover interaction effects between the predictors. Tree-based machine learning models offer strong predictive capabilities, in addition to their interpretability and ease of explanation of the importance of the predictors, unlike neural network. They can also implicitly handle variable correlation, capture variable interactions and non-linear relationships between the predictors. Given the lack of publicly available wildfire claims data for each location in North America, we instead focus on modeling the annual burn probabilities by relying on publicly-available historical wildfire data. The goal of the article is to provide an interpretable model that predicts the annual burn probabilities for any location in North America and to compare how random forest models perform compared to more commonly used actuarial modeling techniques, such as GLMs. The best fit model is used in a downscaling exercise where we predict the annual burn probabilities at a high resolution, which is applicable for insurance purposes, such as pricing home insurance policies with coverage against wildfires.
Wildfire risk in North America is of great significance and over the past decade, insurers have been suffering annually from billions of dollars in losses. This article proposes a transparent and simple, yet powerful model that relies on random forests. It can be possibly used by actuaries to price, reserve or manage the financial risk from wildfires. Unlike wildfire models that were designed for a specific region, the models presented in this article cover a wide geographic area. They have high predictive capabilities with strong ability to classify locations into high/low risk zones. The random forest models are characterised by their ability to capture non-linearity and interaction in the model inputs. Occurrence of wildfire can be devastating, thus it is of utmost importance to measure wildfire risk by calculating the burn probabilities of wildfires in high-risk areas with densely populated communities. With sufficient property characteristics data obtained at the underwriting stage, our model can be used to compute the loss costs necessary for premium calculation, accordingly, complementing vendor catastrophe-loss models.
The remainder of the article is organized as follows. Section 2 explains the data used in the model, such as the historical wildfires data, vegetation information and land use, meteorological and population data. It also classifies the population of North America depending on the wildfire risk. Section 3 provides details on the methods proposed to fit the data. It also summarizes the results of the fitted models and compares their predictive capabilities. Section 4 provides a detailed analysis of the effect of each input variable. An insurance application is illustrated in Section 5 to underwrite and price insurance policies. Finally, Section 6 concludes the article.
2. Data
In this section, we discuss the data used to build our model. We explain the historical wildfires data and the wildfire risk factors such as climate, land cover, population census, and lightning frequency.
2.1. Wildfire occurrence and intensity
The area burned and the frequency of wildfires are relevant metrics to identify trends in wildfire risk and they are also of great importance to estimate insurance losses. Summaries of the historical wildfires in North America are provided in Figure 1, where the data is obtained from (CFS 2019; Short 2017). Data for Canadian wildfires range from 1975 until 2019. 2016 witnessed 1.3 million hectares burned - the Fort McMurray wildfire being responsible for 0.6 million. The last five years of data (2015-2019) had 29,000 wildfires causing a total of 13 million hectares burned, with an average fire size of 450 hectares. Data for the USA wildfires range from 1992 until 2015. The last five years of data (2011-2015) had 370,000 wildfires resulting in a total of 15 million hectares burned, with an average fire size of 40 hectares. The increase in the area burned can be attributed to the lengthening of fire seasons due to the increase in spring and summer temperatures, as explained by Westerling et al. (2006). Historical wildfires in the USA compared to Canada contain a substantial number of wildfires that are small in size, however, Canadian wildfires data contain relatively larger fires. This may be explained by the differences in reporting of wildfires by the fire agencies.
Lightning strikes are the leading cause of large wildfires, which is typically due to prolonged dry conditions, high temperatures, and excessive dry fuel. However, in densely populated areas, man-made sparks can be responsible for a large number of ignitions due to human-related activities, such as arson, campfires, equipment use, fireworks, smoking, etc. Figure 2 compares the annual number and size of wildfires of all sizes caused by lightning strikes and human ignitions, where we observe that natural wildfires are significantly less frequent compared to man-made wildfires, but they tend to burn more land and cause more damage.
Numerous small wildfires may not necessarily result in a significant increase in the area burned. Accordingly, it may be more appropriate to only consider large wildfires as they are more likely to cause material damage. The Canadian large wildfire database includes information on all wildfires larger than 200 hectares (Stocks et al. 2002). The large wildfires in Canada represent 4% of the count of all wildfires in Canada and 98.8% of the total area burned in the observed period. 84% of the Canadian large wildfires are ignited by lightning strikes and they contribute to 91% of the total area burned by all large wildfires in Canada. By applying the same threshold of 200 hectares, less than 1% of the count of wildfires in the USA is considered large and they correspond to 88.8% of the total area burned. 44.6% of the large wildfires in the USA are ignited by natural reasons and they contribute to 67.8% of the total area burned.
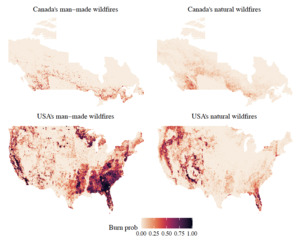
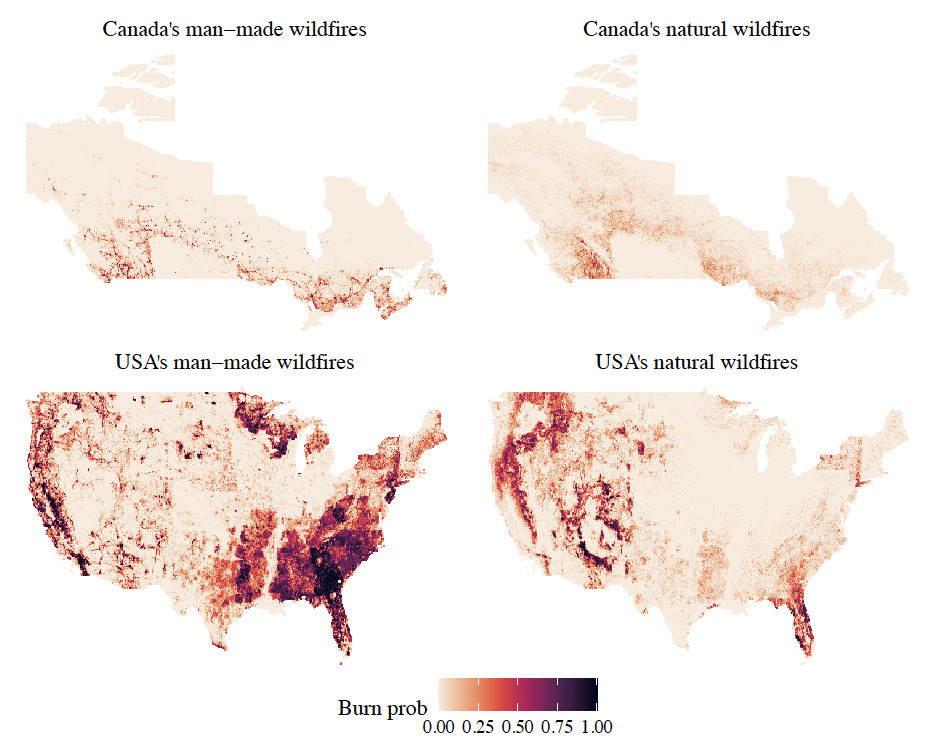
Figure 3 maps the historical annual burn probabilities for each cause per grid cell. The chosen resolution is where is approximately 111 km at the Equator, which is the resolution of the meteorological data. The count of wildfire origins that occurred in each cell is calculated for the entire duration of each dataset, 45 years for Canada and 24 years for the USA. Each year is coded as binary because only a few grid cells have more than one wildfire in a given year. The annual burn probability is obtained by dividing by the number of years of data. Due to the different natures of the maps, we choose to split our North American wildfire model by country and by cause. Wildfire risk is heterogeneous in space, which means that observations are not identically distributed, i.e. in each grid cell, there might be a different distribution. In addition, one could have spatial dependence in between the random variables, i.e. if there is a claim in a grid cell, then it is highly likely there is a claim in the neighbouring grid cell.
2.2. Predictors/Determinants of wildfires
Table 1 summarizes the wildfire risk predictors explained in this section and used throughout this paper. All meteorological data is obtained from the Copernicus Climate Change Service Climate Data Store (CDS) ERA5 reanalysis data at a spatial resolution of (CDS 2019). Monthly-mean averages for the observed period are obtained for the following variables: (1) the air temperature at 2m above the surface of the Earth, (2) the horizontal speed of air moving towards the east and the north at a height of 10m above the surface of the Earth, and (3) the total precipitation from the accumulated liquid and frozen water, including rain and snow that falls to the surface of the Earth. The data is then averaged by fire season, where fire season is defined to be March to September for the USA wildfires, May to September for Canada’s natural wildfires, and April to October for Canada’s man-made wildfires. The fire seasons are obtained from the historical wildfire data by observing the monthly seasonality for each wildfire cause. All other covariate information are aggregated/re-scaled to to unify the resolution and are stored as raster images, which are pixel-based files that contain unique information per cell.
We use the 2015 North American Land Cover 30m dataset (NALCMS 2020), which explains the material features of the Earth’s surface at a 30m spatial resolution based on Landsat-7 imagery. To unify the resolution with the other covariates, the percentage of each land type is calculated for each grid cell, hence, converting the 19 types of land cover from a categorical variable to 19 continuous variables that range from 0 to 1. The world digital elevation model, created from a digital database of land and sea-floor elevations on a resolution, is used as a predictor that represents elevation (NOAA 2016). The global map of lightning frequency contains the number of strikes/km2/year on a grid. In North America, Florida has the highest annual lightning strike rate, with an average of 59 strikes/km2/year (Cecil, Buechler, and Blakeslee 2014).
Population count data is obtained from the fourth version of the Gridded Population of the World collection, which provides a smoothed distribution of the human population on a continuous global raster surface at a resolution of km km (CIESIN 2017). The dataset is created from census data collected between 2005 and 2014 and then extrapolated to estimate the population count/density for the years 2000, 2005, 2010, 2015, and 2020. For this article, we use the raster for the population count in 2005 as a possible predictor and the population count in 2020 is used for predictions.
2.3. Population at risk
To analyze the population exposed to wildfire risk, we classify the population in each state and province into low, medium or high risk based on the observed burn probabilities of natural or man-made wildfires. We define low risk to be an annual likelihood medium risk is between and high risk are for grid cells above Table 2 summarizes the results. Overall, 8% of Canadian residents are at high risk of man-made wildfires, compared to 33% of US residents. While no Canadian residents are located in high risk zones for natural wildfires, 5% of the USA population resides in zones that are at high risk for natural wildfires.
3. Wildfire Occurrence Models
This section explains the models used in this paper and then provides the results of the fitted models and compares their predictive capabilities. We are interested in modeling the random number of wildfires for each location in North America over a grid of over a time period 45 years for Canada and 24 years for the USA. Due to the significant natural climate variability, we use as much available data over time as possible to cover most possible climate scenarios. The annual burn probability per grid cell is Following the discussion of determinants of wildfires in Section 2.2, the predictors of the models are: geographical location, percentage coverage over a grid cell by each land type, elevation, population count, lightning frequency, the mean temperature in fire season, the mean temperature other than fire season, the mean precipitation in fire season, the mean precipitation other than fire season, the mean eastward wind speed in fire season and the mean northward wind speed in fire season. See Table 1 for the definitions of the predictors.
Wildfire occurrence models are conditional on meteorological, topographical and socioeconomic variables, aiming to find the relationship between those sets of covariates and wildfire occurrence, as such, any trend in wildfire occurrence is implicitly captured by the trend in the covariates.
3.1. Methodology
We compare GLMs (McCullagh 1984), regression decision trees (Breiman et al. 2001) and random forests (Breiman 2001). Even though interpreting GLMs is quite simpler than tree-based models, yet the latter can capture interactions easily and model non-linear relationships between predictors. Decision trees provide predictions that are easily interpreted, however they are known to have high variance, where small changes in the data can generate different trees and hence different predictions for some observations. This limitation is taken care of by using random forests, which relies on numerous decision trees, thus minimizing the variance.
To fit the models and compare their predictive power, we first randomly partition the data into train (90%) and hold-out test (10%) datasets. We apply repeated 10-fold cross-validation (CV) with 5 repetitions to train the candidate models and tune the hyperparameters of the tree-based models. As a model validation technique, CV allows us to assess how the performance of our models can generalize to other independent datasets. In each iteration of the CV, we use 9 different folds out of the 10 folds to train our model, and we test on the remaining fold. We evaluate the performance of the tree-based models over an extensive grid search of possible values of the hyperparameters. The best set of hyperparameters are the ones that minimize the RMSE. See Bruce and Bruce (2017) for further details. The hold-out test dataset is later used to compare predictions with the actual observed values. The Caret (Kuhn 2021) R package is used to tune the hyperparameters, train the models and calculate variable importance.
In the next section, we present the details of the fitted models. First, we model the occurrences of wildfires of any size, split by country and cause of wildfire. Then, we consider large wildfires only and we model them by country.
3.2. Models for wildfires of any size
The wildfires are split by ignition cause; man-made or natural. Accordingly, we fit four models:
-
Canada man-made wildfires,
-
Canada natural wildfires,
-
USA man-made wildfires, and
-
USA natural wildfires.
Figure 4 displays the distribution of the response variable in each data set, representing generally balanced datasets. Canada man-made wildfires had a maximum of 44 wildfires in a grid cell over 45 years, i.e. almost a wildfire occurred in approximately the same location every year. However, Canada’s natural wildfires had a maximum of 32 wildfires in a grid cell over 45 years. The USA man-made and natural wildfires each had a maximum of 24 wildfires over 24 years.
We apply the algorithms discussed in Section 3.1 to train the data and tune the hyperparameters of the tree-based models. To assess the predictive accuracy of the models, we calculate the CV root mean squared prediction error (RMSE) and the CV mean absolute prediction error (MAE). To facilitate the comparision between the models for Canada and the USA, standardized versions of the RMSE and MAE, that account for the number of years in each model, are calculated. Thus, both measures are presented in terms of the annual burn probability. For model comparison purposes, we also compare the CV Pearson correlation coefficient between the observed values and the predictions, and we compute the RMSE on the hold-out test dataset. Additionally, we calculate the prediction error measures for a baseline model, which assumes that the country-wide mean is applied to all grid cells. Table 3 summarizes the discussed measures. As expected, the random forest models outperform the other fitted models. We also observe that the random forest models show around half the prediction error of the baseline model.
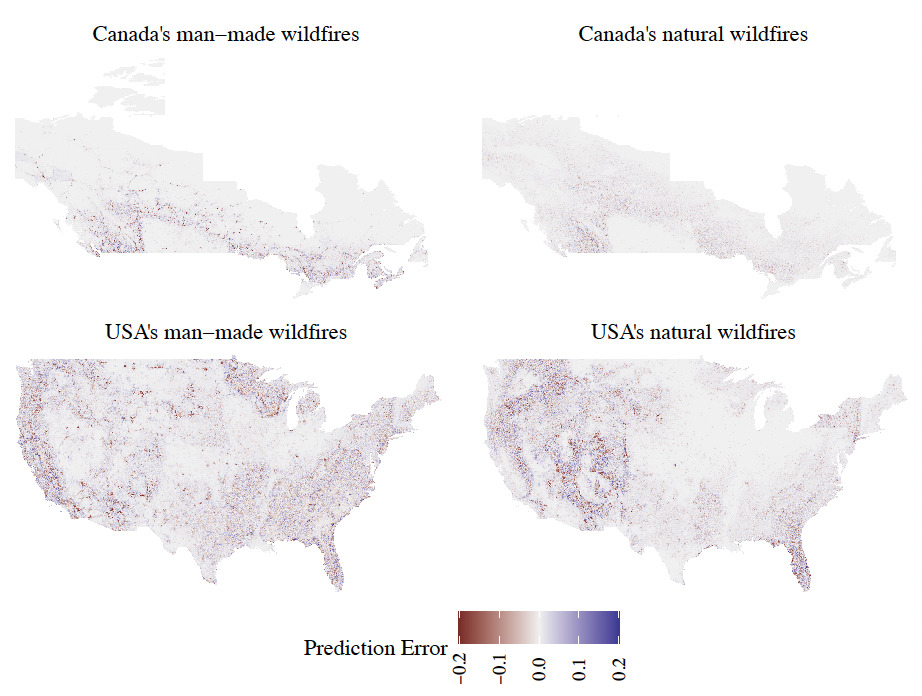
The random forest models have the strongest predictive power, and hence they are chosen as the optimal models such that all the analysis thereafter is performed on them. As a comparison tool against historical wildfire records, Figure 5 provides a visual representation of the differences between the predictions of the random forest models and the observed events for each grid cell to highlight zones where the model is lacking predictive power. To facilitate the comparison between the four maps, the differences are computed in terms of the annual burn probability.
Figure 6 displays the variable importance for each random forest model, which represents the percentage increase in the mean square error of the random forest model when the data for that variable are randomly permuted (Breiman et al. 2001). The analysis shows that for man-made wildfires in Canada and the USA, the most important predictors are population, urban land, water and northward wind speed. For natural wildfires, there are no common important predictors between the countries.
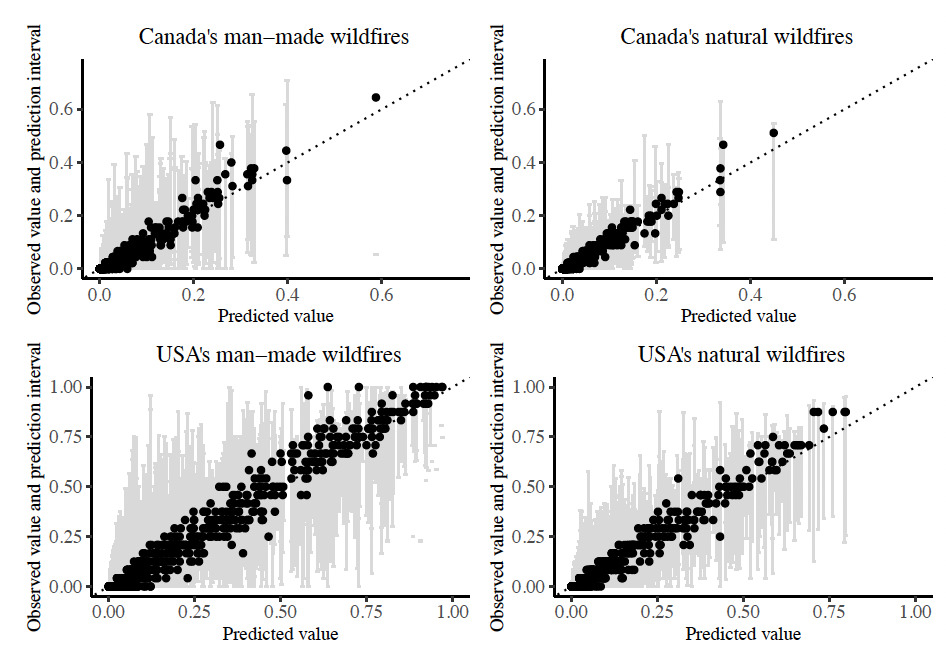
Figure 7 compares the predicted annual burn probabilities to the observed burn probabilities in the hold-out test dataset, where we notice a strong linear relationship close to the 45 line, except for slight under prediction of high-risks. This is generally acceptable due to the difficulty of any model in predicting outliers/extremes. For each observation, prediction intervals are plotted, which represent 95% of the individual predictions from the decision trees composing each random forest model. In fact, around 90% of the observed burn probabilities for the USA wildfires and 95% of the observed burn probabilities for Canadian wildfires fall within the 45 and 55 quantiles of the individual decision tree predictions.
3.3. Models for large wildfires
Even though large wildfires are small in number, they contribute significantly to the area burned and economic damage. Figure 8 displays the distribution of the response variable in each model. There was a maximum of 10 wildfires in a grid cell over 45 years in Canada, compared to 15 large wildfires in the USA over 24 years. We fit two models:
-
Canada large wildfires, and
-
USA large wildfires.
See Table 1 for the predictors of the models. We apply the methods discussed in Section 3.1 to train the data and tune the hyperparameters. Table 4 provides the CV RMSE, MAE and Pearson correlation coefficient of the fitted models, in addition to the RMSE computed on the hold-out test dataset. Both RMSE and MAE are presented in terms of the annual burn probability. Similar to the models in Section 3.2, the random forest models outperform the GLM and decision tree models. It is observed that the Pearson correlation coefficient of both models is low in comparison with the models for wildfires of any size, discussed in Section 3.2, which is attributed to the difficulty in predicting the large observation values.
As shown in Figure 8, where we have a large number of grids with no observed large wildfires, it is easier for the model to predict the zeros. Accordingly, we consider hurdle models, first introduced by Cragg 1971, which are pure mixtures of zero and non-zero outcomes. A logistic GLM is responsible for the binary component of whether the outcome is zero or positive. If the outcome is positive, the conditional distribution of the non-zeros is modeled by a zero-truncated count distribution. We apply the same methodology by using two-stages random forest model: the first stage is a classification model that categorizes the observations into “no large fire” vs “large fire” occurrence, while the second stage is a regression model to predict the number of occurrences should at least one large wildfire happens. In the first stage, we apply larger weights on the observations with “large fire” so that they have higher chances of selection in the bootstraps samples for the individual decision trees.
We assess the predictive strength of each model component separately: the hurdle component and the count component. For the hurdle component, we calculate the CV area under the receiver operating characteristic curve (AUC) and accuracy, i.e. the ratio of the correctly predicted observations to the total number of observations. While for the count component, we calculate the CV RMSE and Pearson correlation coefficient of the observed count of large wildfires and predicted count of large wildfires. The RMSE is presented in terms of the annual burn probability. Finally, we compute the same measures on the hold-out dataset. Table 5 summarizes the discussed measures. For the hurdle components, all attempted models perform similarly. By observing the AUC, the random forest models are slightly better, however by comparing the accuracy of the models, the GLM hurdle models seem to perform better. For the count components, the random forest models outperform the GLM hurdle models that fail to predict values in the tail of the distribution.
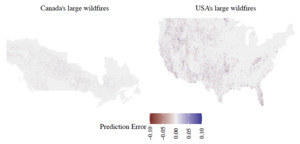
Overall, the two-stages random forest models have the strongest predictive power, and hence they are chosen as the optimal models for the occurrence of large wildfires in Canada and the USA. All the analysis thereafter for large wildfires is performed on the two-stages random forest models. Figure 9 illustrates the difference between the predictions of the random forest models for large wildfires and the observed events for each grid cell, where we observe minimal errors, comparable to the small RMSE values shown in Table 5. The values are computed in terms of the annual burn probability.
Figure 10 displays the variable importance for each model in the two-stages random forest models to help identify the most influential variables. The comparison between the variables shows that climate variables are the main drivers behind wildfires becoming large in size.
4. Sensitivity Analysis
The wildfire random forest models have a large number of input variables, with their importance ranked in Figures 6 and 10. Note that variable importance does not quantify the effect of changes in the predictors on wildfire risk. In this section, we compute that effect by performing sensitivity tests on some of the predictors, while keeping all other model components unchanged. Table 1 contains a list of the performed sensitivities. For each sensitivity, a shock is applied to one (or more) predictor(s), and predictions of the random forest models that are trained in Section 3 are calculated. The analyses are evaluated over British Columbia, Alberta and California, which are chosen because of their high level of wildfire risk.
Tables 7 and 8 provide some summary statistics of the predicted annual likelihood of a wildfire of any size and of large wildfires for each sensitivity, to be compared with the base scenario, where all predictors remain unchanged. The calculated statistics are the mean, standard deviation and percentiles of the burn probabilities over all grid cells in each state and province. More percentiles in the tail are provided for the sensitivities of large wildfires to reflect the behavior in the table. The burn probability of wildfires of any size is the sum of two components; the predicted likelihood of a wildfire due to natural causes multiplied by the historical probability of lightning-caused wildfires and the predicted likelihood of a fire due to man-made causes multiplied by the historical probability of man-made wildfires for each grid cell. The predicted annual likelihood of a wildfire of any size for each cause is obtained from the random forest models presented in Section 3.2. The results of the sensitivities are inline with the expectations; an increase in temperature, a decrease in total precipitation, an increase in lightning activity and human population are all factors that will increase the annual burn probabilities in the study regions. A change in the mean temperature has a stronger effect on the burn probabilities in British Columbia and Alberta compared to California. Even though a change in urban population affects the annual burn probabilities of wildfires of any size, it has a negligible effect on large wildfires because they are more commonly ignited from natural sparks.
We perform additional sensitivities to compare the distribution of the predicted annual burn probabilities of wildfires of any size over multiple scenarios of change in the mean temperature: and Figure 11 compares the densities of the sensitivities performed on the temperature predictor in the three chosen high-risk states and provinces. This figure complements the results from Table 7 by providing the full distribution across grid cells. One can see that across all study areas, an increase in temperature reduces the number of grid cells that have small predicted annual burn probabilities and increases the chances of medium and high wildfire risk, and vice versa. Additionally, higher volatility can be observed in Alberta and California, compared to British Columbia.
5. Insurance Application
In this section, we aim to illustrate how we can use the models to price and underwrite wildfire risk in an insurance portfolio. The goal is to estimate the expected losses due to wildfire risk, based on the geographical location of the homeowner. A typical catastrophe model is composed of hazard modeling, exposure collection, vulnerability assessment and expected losses calculation; see Mitchell-Wallace et al. (2017) for details. In this article, the hazard element is represented by the rate of wildfire occurrence, which varies across our chosen geographic region. This is reflected in the models built in Section 3 Collection of exposure requires the valuation of properties and/or infrastructures at risk. Vulnerability assessment helps in quantifying the relationship between the hazard and the damage by means of a metric, such as damage ratios. Finally, the annual pure premium is calculated in terms of the expected losses in each geographical location.
5.1. Hazard
A grid cell of size may be too large for some insurance applications, such as pricing exercises, due to the need to understand the risk at a household level. As such, we perform a downscaling exercise where we predict the burn probabilities of a wildfire in a year at a much higher resolution. The chosen resolution is that of the Gridded Population of the World dataset, i.e. km km grid cells, which is acceptable for insurers’ purposes to accurately reflect the location of the insureds. A new high-resolution dataset is created by changing the resolution of all predictors, defined in Table 1. For climate, elevation and lightning strikes predictors, all small grid cells of size within a large grid cell of size are assigned the same value. While for land cover predictors, the percentage of each land type is computed for each grid cell. The random forest models in Sections 3.2 and 3.3 are used to predict the annual burn probabilities of wildfires of any size and of large wildfires per grid cell, by using the new high-resolution dataset.
The left panel in Figure 12 shows the burn probabilities of wildfires for each location in British Columbia by using the original dataset of resolution and by using the high-resolution dataset of size Smaller grid cells indicate less number of predicted wildfires, and hence smaller burn probabilities. The annual burn probabilities in the small grid cells are scaled such that the overall likelihood of a wildfire is equivalent to that of the lower resolution model, while preserving the weights of the risk of the small grid cells. The right panel in Figure 12 shows a zoomed-in map on Lytton Creek and its surrounding region. As observed from the predictions of the original dataset and the downscaling exercise, the region has elevated burn probabilities compared to its surroundings and to other areas in British Columbia. This coincides with Lytton Creek’s large wildfire that occurred in 2021 in that area, which caused two fatalities and destroyed around 90% of Lytton village. The models were built on wildfires data up to the year 2019 in Canada, thus a 2021 wildfire is considered an out-of-sample prediction, hence confirming the appropriateness of the predictions of the models.
5.2. Vulnerability and exposure
The average claim cost of a wildfire is highly volatile, depending on the location of the wildfire, the construction material of the buildings affected, their location, the fire mitigation measures and the availability of firefighters. Table 9 summarizes the average claim cost of the most recent large wildfires that occurred in three high-risk regions, British Columbia, Alberta and California. Thus, relying on such limited values to generalize over the whole region can be problematic. The unit of currency throughout is the Canadian dollar for Canadian wildfires and the US dollar for USA wildfires.
Vulnerability assessment for wildfire risk usually requires the help of civil engineers to analyze the characteristics of the properties. Those details are not publicly available, however, such information is typically provided by the customers to their insurers and is used in the calculation of the insured exposure. In this article, we rely on insured exposure data that is provided by CatIQ, Canada’s Loss And Exposure Indices Provider (CatIQ 2021). They release annual updates of the Canadian insurance industry exposure database, which is developed from data from the Canadian P&C insurance companies. The 2020 year-end estimates of the personal properties sums insured and number of insured risks against fires is available for each Canada Post Forward Sortation Area (FSA). Depending on the population distribution in the FSA, the exposure value and the number of insured households in an FSA is distributed over each grid cell of size Accordingly, the average exposure value per household is calculated for each grid cell.
5.3. Insurance premiums
Pure premium computation requires hazard, vulnerability and exposure calculations to be performed at the homeowner’s level. This entails detailed information on the location of the household, to determine its subjection to wildfire risk, in addition to property value and characteristics to evaluate its vulnerability if a wildfire occurs. In this section, we illustrate how the model can be used in such process.
We rely on the downscaled annual burn probabilities, provided in Section 5.1, to be the measure of hazard for each geographical location. With no access to vulnerability, we assume complete destruction of buildings and infrastructure where a large wildfire occurs, which will likely overestimate premiums. We choose to use the burn probabilities of large wildfire because insurance claims are more likely to occur from wildfires that are large in size, which cause complete destruction of the area. Hence, by using the CatIQ industry exposure database, the annual pure premium for wildfire insurance can be computed as the product of the annual burn probabilities of large wildfire by the cost of household replacement.
As an illustration of the technique, we analyze the distribution of pure premiums over British Colubmia. The predicted insurance pure premium to cover wildfire risk in British Columbia is 0 for around 89% of the high resolution grid cells. This is because those cells have predicted annual burn probability of 0. Table 10 summarizes the quantiles of the insurance pure premium per household over all grid cells.
6. Discussion
Wildfire risk in North America is of great significance and over the past decade, insurers have been suffering annually from billions of dollars in losses. This article proposes a transparent and simple, yet powerful model that relies on random forests. It can be possibly used by actuaries to price, reserve or manage the financial risk from wildfires. Unlike wildfire models that were designed for a specific region, the models presented in this article cover a wide geographic area. They have high predictive capabilities with strong ability to classify locations into high/low risk zones. The random forest models are characterised by their ability to capture non-linearity and interaction in the model inputs. Occurrence of wildfire can be devastating, thus it is of utmost importance to measure wildfire risk by calculating the burn probabilities of wildfires in high-risk areas with densely populated communities.
Calculating insurance premiums is a very important task for actuaries, and it is a complex endeavor for emerging risks such as wildfires. The approach described in Section 5 along with the Leaflet maps provided (see Supplementary Material) can be used as a baseline description of the wildfire hazard. With extensive property characteristics data obtained at the underwriting stage and appropriate vulnerability curves, actuaries can therefore compute the loss costs necessary for premium determination and accurate underwriting. Moreover, some actuarial applications such as reserving or capital requirements might require a representation of spatial dependence. By construction, the wildfire models presented in Section 3 link occurrence to a set of covariates, and as such, borrows spatial dependence from e.g., temperature and precipitation dynamics. The actuary shall therefore make sure the inputs to the wildfire model are spatially consistent over the desired time horizon for the aforementioned applications.
Supplementary Material
Leaflet maps for the annual burn probabilities of wildfires of any size and of large wildfires are available in https://robabairakdar.shinyapps.io/WildfireLikelihood/, and https://robabairakdar.shinyapps.io/LargeWildfireLikelihood/, respectively. The maps are available for the three high-risk states and provinces: Alberta, British Columbia and California. They are desktop and mobile friendly interactive maps that provide the user with the flexibility to zoom on a certain location on a map. The leaflets can be used by insurers to obtain the burn probabilities for any location in the selected high-risk states and provinces.
Acknowledgements
This research was supported in part by the Casualty Actuarial Society. Roba Bairakdar recognizes the support of the Society of Actuaries’ James C. Hickman Scholar Program. Mathieu Boudreault acknowledges the support of the Natural Sciences and Engineering Research Council of Canada RGPIN-2021-03362. Mélina Mailhot recognizes the support of the Natural Sciences and Engineering Research Council of Canada RGPIN-2015-05447.
_and_area_burned_(bars)_in_north_america.png)
_and_area_burned_(bars)_by_cause_of_wildfire_in_north_am.png)


_of_the_random_forest_models_for.png)


_of_the_hurdle_and_count_compon.png)


_and_area_burned_(bars)_in_north_america.png)
_and_area_burned_(bars)_by_cause_of_wildfire_in_north_am.png)

_of_the_random_forest_models_for.png)


_of_the_hurdle_and_count_compon.png)

