Credibility for a Tower of Excess Layers

undefined

1. Introduction

This paper will address a particular problem in pricing excess reinsurance that can benefit from an application of credibility theory.

In reinsurance, an actuary or underwriter is required to estimate losses in a per-occurrence excess layer. For example, a treaty may cover loss occurrences that exceed a retention of $1,000,000 up to a limit of an additional $1,000,000; this would be referred to as a $1,000,000 xs $1,000,000 layer.

In order to estimate the expected losses in the excess layer, there may be several tools available. The first is a pure experience rating, sometimes called a “burn-cost” because of its use in rating fire policies. An experience rating looks at the actual historical losses for the ceding company that have penetrated the excess layer—including adjustments for trend and development—relative to the historical exposures.

In addition to the experience rating, there is usually an industry-based size-of-loss distribution available. This size-of-loss distribution gives the probability of a loss penetrating into the excess layer and the expected severity in the layer. It is the basis for an “exposure rating” estimate. More precisely, it is the basis for multiple exposure rating estimates because there are a variety of ways that the size-of-loss distribution can be used.

The exposure rating curve can be used to divide an overall (primary or ground-up) expected loss into the losses expected in various layers. The overall expected loss can be a permissible loss ratio (for example, 100% minus expenses) applied to manual premium. More often, it is calculated from the ceding company’s experience, in which case, the exposure rating is clearly not independent from the experience rating.

Alternatively, the size-of-loss curve can be applied to an estimate of total claim counts for the ceding company. It could also be applied to a lower excess layer; for example, we use the size-of-loss distribution to estimate the $1,000,000 xs $1,000,000 layer relative to the $500,000 xs $500,000 layer.

We see, therefore, that the analyst has a collection of estimators available. These estimators are not independent from one another but instead are related in many ways. Our goal is to select among these estimators, or combine them, in an optimal way.

Credibility theory can help us accomplish this goal.

1.1. Research context

This paper builds upon existing credibility theory. However, much of the past literature has been concerned with primary ratemaking, comparing loss experience in one class of business with others. For the reinsurance context, our concern will be “vertical” rather than “horizontal,” as we look at a tower of contiguous excess layers.

The excess reinsurance problem was taken up by Mashitz and Patrik (1990), who limited their discussion to the problem of layer counts. More recently, papers by Cockroft (2004); Goulet, Forgues, and Lu (2006); Parodi and Bonche (2008); and Marcus (2010) have included analyses that address severity as well as frequency. In general, these papers do not include methods that capture all the ways that exposure and experience ratings are interrelated.^[1]

The present paper will examine expected losses to excess layers, including some of the interrelationships between how exposure and experience rating are applied in practice. The focus will be on showing how the credibility procedure actually reduces the variance in the estimate of expected loss.

1.2. Objective

The goal is to outline a procedure that will produce an optimal, or best estimate, of expected loss for the excess layer being priced. “Best” will mean a minimum variance unbiased estimator.

Informally stated, the minimum variance criterion says that an estimate that incorporates all available information is more reliable than one that ignores some information (such as losses in lower excess layers).

1.3. Outline

The remainder of the paper proceeds as follows.

Section 2 will describe the basics of credibility theory supporting the proposed method.

Section 3 will show how this theory can be applied in practice as a recursive credibility method. In order to illustrate the technique, a simple example using a Pareto distribution will be traced throughout the paper.

The final result of this paper will be a very practical method for applying credibility that works recursively. It starts with a simple weighting of experience and exposure rates for a low layer and then uses a layer relativity from the exposure curve to provide an estimate for the next layer up. This practical implementation can be used even without direct reference to the theoretical model that is demonstrated.

2. Background and Methods

Our goal in setting up a credibility procedure is to find the best possible estimate of future expected losses, making use of all available relevant information. A best estimate will generally have two main properties:

• The estimate will be unbiased; meaning that its expected value will be equal to the true expected value.

• The estimate will have minimum variance; meaning informally that it will tend to be closer to the true expected value than other possible estimates.

We will assume that all of the estimators used in our discussion are unbiased. If some are biased, then they need to be adjusted to an unbiased basis before they are included in a credibility-weighted average.^[2]

The focus of this paper will be on the minimum variance criterion. The best combination of estimators will be one that minimizes the overall variance. For this reason, this approach is also known as “least squares” or “greatest accuracy” credibility (Boor 1992; Venter 2003; Marcus 2010).

If we have two or more estimates available that make use of different information, the best estimate may be some combination of those estimates. Credibility theory allows us to properly combine these different estimates so that we have a single, final estimate that makes the best use of all of the available information.

2.1. The two-factor model

We can begin with the familiar case in which credibility is applied as the weighted average of two estimators, $\widehat{\mu_1}$ and $\widehat{\mu_2}$, which are assumed to be unbiased estimators of a true value μ.

$$\widehat{\mu_{c w}}=w \cdot \widehat{\mu_{1}}+(1-w) \cdot \widehat{\mu_{2}} . \tag{2.1}$$

The assumption that these estimates are unbiased is expressed as follows:

$$E\left(\widehat{\mu_{1}}\right)=E\left(\widehat{\mu_{2}}\right)=\mu \tag{2.2}$$

The variance of the credibility-weighted (cw) average of the two estimators is a linear combination of the variances and covariances.

$$\begin{array}{l} {Var}\left(\widehat{\mu_{c w}}\right)=w^{2} \cdot {Var}\left(\widehat{\mu_{1}}\right)+2 w \cdot(1-w) \\ \cdot {Cov}\left(\widehat{\mu_{1}}, \widehat{\mu_{2}}\right)+(1-w)^{2} \cdot {Var}\left(\widehat{\mu_{2}}\right) . \end{array} \tag{2.3}$$

The optimal value of the credibility weight can be found by least squares by setting $\frac{\partial \operatorname{Var}\left(\widehat{\mu_{c w}}\right)}{\partial w}=0$. This produces the following weight:

$$\widehat{w}=\frac{{Var}\left(\widehat{\mu_{2}}\right)-{Cov}\left(\widehat{\mu_{1}}, \widehat{\mu_{2}}\right)}{{Var}\left(\widehat{\mu_{1}}\right)+{Var}\left(\widehat{\mu_{2}}\right)-2 \cdot {Cov}\left(\widehat{\mu_{1}}, \widehat{\mu_{2}}\right)} \tag{2.4}$$

The calculated weights can be substituted back into the formula for the variance of the credibility-weighted estimator (Formula 2.5). This form is instructive because it shows that the variance of the credibility-weighted estimator is less than either of the individual estimators’ variance. We can, therefore, see the value in a rigorous credibility formula as improving our ability to estimate an expected loss more accurately.

$${Var}\left(\widehat{\mu_{c w}}\right)=\frac{{Var}\left(\widehat{\mu_{1}}\right) \cdot {Var}\left(\widehat{\mu_{2}}\right) \cdot\left(1-\rho^{2}\right)}{{Var}\left(\widehat{\mu_{1}}\right)+{Var}\left(\widehat{\mu_{2}}\right)-2 \cdot {Cov}\left(\widehat{\mu_{1}}, \widehat{\mu_{2}}\right)} \tag{2.5}$$

In this expression, the correlation coefficient is defined as follows:

$$\rho=\frac{{Cov}\left(\widehat{\mu_{1}}, \widehat{\mu_{2}}\right)}{\sqrt{{Var}\left(\widehat{\mu_{1}}\right) \cdot {Var}\left(\widehat{\mu_{2}}\right)}} \tag{2.6}$$

2.2. Multifactor model

The multifactor theory can be expanded to include multiple estimators. In this case, we need to define a covariance matrix, Σ, which includes the variances and covariances between each pair of estimators.

$$\begin{array}{l} \mathbf{\Sigma}= \\ {\left[\begin{array}{cccc} {Var}\left(\widehat{\mu_{1}}\right) & {Cov}\left(\widehat{\mu_{1}}, \widehat{\mu_{2}}\right) & \cdots & {Cov}\left(\widehat{\mu_{1}}, \widehat{\mu_{n}}\right) \\ {Cov}\left(\widehat{\mu_{2}}, \widehat{\mu_{1}}\right) & {Var}\left(\widehat{\mu_{2}}\right) & \cdots & {Cov}\left(\widehat{\mu_{2}}, \widehat{\mu_{n}}\right) \\ \vdots & \vdots & \ddots & \vdots \\ {Cov}\left(\widehat{\mu_{n}}, \widehat{\mu_{1}}\right) & {Cov}\left(\widehat{\mu_{n}}, \widehat{\mu_{2}}\right) & \cdots & {Var}\left(\widehat{\mu_{n}}\right) \end{array}\right]} \end{array} \tag{2.7}$$

The credibility-weighted average of the n unbiased estimators is again a linear function of the individual estimators.

$$\widehat{\mu_{c w}}=w_1 \cdot \widehat{\mu_1}+w_2 \cdot \widehat{\mu_2}+\cdots+w_n \cdot \widehat{\mu_n} .\tag{2.8}$$

The set of these weights is defined as a vector of parameters.

$$\overrightarrow{\boldsymbol{W}}^{T}=\left(w_{1}, w_{2}, \ldots, w_{n}\right) \tag{2.9}$$

The constraint that these weights must add up to 1.00 (or 100%) can be written as$1=\overline{\boldsymbol{W}}^T \cdot 1_n$, where $\mathbf{1}_n$ is a column vector of ones.

The variance of the credibility-weighted estimator is then a weighted average of the variance and covariance terms in ∑.

$${Var}\left(\widehat{\boldsymbol{\mu}_{c w}}\right)=\overrightarrow{\boldsymbol{W}}^{T} \cdot \boldsymbol{\Sigma} \cdot \overrightarrow{\boldsymbol{W}} . \tag{2.10}$$

The least-squares estimate for these weights can be found by solving the equation above. The result is that the weights are proportional to the row (or column) totals of the inverse of the covariance matrix.^[3]

$$\overrightarrow{\boldsymbol{W}}=\left(\mathbf{1}_{n}^{T} \cdot \boldsymbol{\Sigma}^{-1} \cdot \mathbf{1}_{n}\right)^{-1} \cdot \boldsymbol{\Sigma}^{-1} \cdot \mathbf{1}_{n} \tag{2.11}$$

For the special case in which all of the estimators are independent, this reduces to having the weights proportional to the inverse of each estimator’s variance.^[4]

$$w_{i}=\frac{{Var}\left(\widehat{\mu_{1}}\right)^{-1}}{\sum_{k=1}^{n} {Var}\left(\widehat{\mu_{k}}\right)^{-1}} . \tag{2.12}$$

One final observation before showing how this applies to excess pricing is that the multivariate case can alternatively be written in a recursive form. For example, a three-variable case can be viewed as a weighted average between one variable and the weighted average of the other two variables.

$$\begin{gathered} \widehat{\mu_{c w}}=w_1 \cdot \widehat{\mu_1}+w_2 \cdot \widehat{\mu_2}+w_3 \cdot \widehat{\mu_3} \\ =z_1 \cdot \widehat{\mu_1}+\left(1-z_1\right) \cdot\left\{z_2 \cdot \widehat{\mu_2}+\left(1-z_2\right) \cdot \widehat{\mu_3}\right\} . \end{gathered}\tag{2.13}$$

3. Credibility applied to excess of loss reinsurance

The specific problem that we are examining is to find the best estimate of expected loss in an excess layer.

In order to make this discussion more practical, we will make an assumption that the true severity distribution is a single parameter Pareto, as defined in Section 3.1. In Section 3.2, we will then show how exposure and experience rating estimates are combined. Finally, in Section 3.3, we will show how lower excess layers can also be incorporated in the method using a recursive form of the multifactor credibility formula.

3.1. Defining the reinsurance problem

In order to describe the expected loss in the reinsurance application, we need to start with some definitions:

• X     random variable representing a single loss event

• F(x)     Cumulative Distribution Function; probability that a loss is x or less

• R     Retention taken by the ceding company

• L     Limit above the Retention covered by the reinsurer

• Layer     Function representing loss taken by the reinsurer

  Defined as:

  Layer = MIN{MAX(x – R, 0), L}

• N     Random variable representing the number of losses in the historical period

In order to make this discussion more realistic, we will define a simple curve form to use in the calculation of the credibility factors. For our example, we will use the single parameter Pareto distribution,^[5] defined as follows:

$$F(x)=1-\left(\frac{\theta}{x}\right)^{\alpha} \quad \text { for } x \geq \theta. \tag{3.1}$$

The value theta, θ, is known as the loss threshold, and represents the smallest loss amount that is part of the analysis. For example, in a reinsurance submission, we might ask for all losses of $500,000 and greater.

The expected loss in an excess layer is defined as E(Layer)

$$\begin{array}{l} \text { E(Layer }) \\ =\left\{\begin{array}{cc} \left(\frac{\theta}{\alpha-1}\right) \cdot\left[\left(\frac{\theta}{R}\right)^{\alpha-1}-\left(\frac{\theta}{R+L}\right)^{\alpha-1}\right] & \alpha \neq 1 \\ \theta \cdot \ln \left(1+\frac{L}{R}\right) & \alpha=1 \end{array} .\right. \end{array} \tag{3.2}$$

Similarly, the second moment of an excess layer is defined as follows:

$$\begin{array}{l} E\left(\text { Layer }^{2}\right) \\ =\left\{\begin{array}{cc} \left(\frac{2 \theta^{2}}{(\alpha-1) \cdot(\alpha-2)}\right) \\ \cdot\left[\left(\frac{\theta}{R}\right)^{\alpha-2}-\left(\frac{R+(\alpha-1) L}{R+L}\right) \cdot\left(\frac{\theta}{R+L}\right)^{\alpha-2}\right] & \alpha \neq 1,2 \\ 2 \theta \cdot\left\{L-R \cdot \ln \left(1+\frac{L}{R}\right)\right\} & \alpha=1 \\ 2 \theta^{2} \cdot\left\{\ln \left(1+\frac{L}{R}\right)-\left(\frac{L}{R+L}\right)\right\} & \alpha=2 \end{array}\right. \end{array} \tag{3.3}$$

For our example, we will have the following information available:

• All losses above a threshold θ = $500,000

• Experience rating for the $500,000 xs $500,000 (or $500xs$500) layer (Layer₁)

• Experience rating for the $1,000,000 xs $1,000,000 (or 1Mxs1M) layer (Layer₂)

• An insurance industry–based Pareto distribution, with parameter α₀

• An estimate of the expected number of losses above θ, denoted n₀ (This estimate, n₀, comes from manual rating, not from account experience.)

3.2. Combining exposure and experience rating estimates

We now proceed to define exposure and experience rating models and how they can be combined.

3.2.1. Exposure rating

An exposure rate is an estimate of expected losses in an excess layer based on external insurance data. It is sometimes called the “prior estimate” because it can be calculated prior to seeing the actual loss experience for the ceding company.

The exposure rate requires two pieces of information: a severity (size-of-loss) curve from industry wide data, and an expected number of total losses. Because we are assuming that the severity follows a Pareto distribution, we only need a single parameter, α₀, to describe it. For the expected number of losses in the prospective period, we likewise have a prior estimate n̂₀ .

In addition to our prior estimates, α₀ and n̂₀, we also need to have estimates of the variances around these estimates Var(α₀) and Var(n̂₀). The coefficient of variation (CV) related to the frequency is given below.

$$C V_{n_{0}}=\frac{\sqrt{{Var}\left(\hat{n}_{0}\right)}}{\hat{n}_{0}} \tag{3.4}$$

We can also approximate the variance of the severity using the “delta method”^[6] relative to the variance of the parameter α₀.

$${Var}\left(E\left( { Layer } \mid \alpha_{0}\right)\right) \approx {Var}\left(\alpha_{0}\right) \cdot\left[\frac{\partial E\left( { Layer } \mid \alpha_{0}\right)}{\partial \alpha_{0}}\right]^{2} \tag{3.5}$$

The derivative with respect to the Pareto alpha is easily calculated.

$$\begin{aligned} & \frac{\partial E\left( { Layer } \mid \alpha_0\right)}{\partial \alpha_0} \\ &= \frac{\theta}{\left(\alpha_0-1\right)} \\ & \quad\left\{\ln \left(\frac{\theta}{R}\right) \cdot\left(\frac{\theta}{R}\right)^{\alpha_0-1}-\ln \left(\frac{\theta}{R+L}\right) \cdot\left(\frac{\theta}{R+L}\right)^{\alpha_0-1}\right\} \\ &-\left.\frac{\theta}{\left(\alpha_0-1\right)^2}\right\} \\ & \cdot\left\{\left(\frac{\theta}{R}\right)^{\alpha_0-1}-\left(\frac{\theta}{R+L}\right)^{\alpha_0-1}\right\} . \end{aligned} \tag{3.6}$$

The exposure rate and the variance^[7] around the exposure rate are therefore estimated as follows.

$$\widehat{\mu_{{expos }}}=\hat{n}_{0} \cdot E\left({ Layer } \mid \alpha_{0}\right) \text {. } \tag{3.7}$$

$$\begin{array}{l} {Var}\left(\widehat{\mu_{ {expos }}}\right) \\ = \hat{n}_{0}^{2} \cdot C V_{n_{0}}^{2} \cdot {E}\left( { Layer } \mid \alpha_{0}\right)^{2}+\hat{n}_{0}^{2} \cdot\left(C V_{n_{0}}^{2}+1\right) \\ \cdot {Var}\left(E\left( { Layer } \mid \alpha_{0}\right)\right) . \end{array} \tag{3.8}$$

From these expressions for the exposure rate, we may observe that both the mean and standard deviation are proportional to the expected number of losses above the threshold θ. This allows us to scale the exposure rate for any change in subject premium.

Having defined the components of exposure rating, it is useful to show representative values^[8] for these calculations.

Following our earlier introduction, we will assume that the severity is a single parameter Pareto with a threshold θ of $500,000. For the parameter α, we will select a value of 1.500. The variance around this Pareto parameter can be roughly estimated by first selecting a range of possible values. For our example, we will assume that the variance is .05, with this amount selected by the user.

For expected counts n̂₀ above the threshold for the future period, we will select an average value of five losses. The variance around this number is more difficult to estimate, as it may be dependent on how much variance there is for risks within a manual rating classification. If the frequency is more judgmentally selected, then there may be even more uncertainty. To illustrate the calculations, we will assume a coefficient of variation (CV) of .300 or 30%.

From these selected values, we can estimate the severity for both excess layers, the exposure rate (frequency times severity), and the parameter variance around our estimated exposure rate, shown in Table 1.

3.2.2. Experience rating

An experience rate is an estimate of expected losses in an excess layer based on the actual loss experience for the ceding company. For our notation, this will be denoted a “burn-cost” with the subscript “bc.”

In our estimate of the experience rate, we need to adjust the sum of historical losses in the layer to the prospective period based on the relative exposure volumes (V).

$$\widehat{\mu_{b c}}=\frac{V_{ {prospective }}}{V_{ {historical }}} \cdot \sum_{k=1}^N { Layer }_{2, k} \text {. } \tag{3.9}$$

This expression is therefore simply the sum of the historical losses that penetrate into the second layer ($1,000,000 xs $1,000,000) adjusted to the volume of premium in the prospective period. It is assumed that these losses are trended to the future level and that the historical premium is likewise adjusted (“on-leveled”) to the future level.

The excess development can be built into this calculation by using as the historical exposure volume, the on-level premium divided by excess development:

$$V_{ {historical }}=\sum_{ {Years }=t} \frac{V_{t}}{L D F_{t}} \tag{3.10}$$

If we assume that the frequency distribution is Poisson, then we can estimate an expected variance around the experience rate.

$${Var}\left(\widehat{\mu_{b c}}\right)=\left(\frac{V_{\text {prospective }}}{V_{\text {historical }}}\right)^{2} \cdot E(N) \cdot E\left(\text { Layer }_{2}^{2} \mid \alpha_{0}\right) \tag{3.11}$$

This variance is based on the expected process variance^[9] of the severity from the exposure rating model. The relationship between the prospective expected counts and the expected counts for the historical period is based on the assumption that the claim frequency relative to the on-level average premium is unchanged.

$$\frac{E\left(\hat{n}_{0}\right)}{V_{\text {prospective }}}=\frac{E(N)}{V_{\text {historical }}} \tag{3.12}$$

We can estimate the expected losses in the historical period, E(N), by making use of the prospected expected losses from exposure rating, E(n̂₀ ), and Formula (3.12).

Table 2 shows the results of these calculations.

3.2.3. Credibility weighting these two estimates

The experience and exposure rating models produce estimates of the future expected loss to an excess layer. Because they are working with very different information, they can be considered independent.

$$\widehat{\mu_{c w}}=w \cdot \widehat{\mu_{b c}}+(1-w) \cdot \widehat{\mu_{\text {expos }}} . \tag{3.13}$$

The credibility weight for the experience rate is then written in a familiar form, based on the expected number of claims in the historical period (substituting in Formulas (3.8) and (3.11)).

$$w=\frac{{Var}\left(\widehat{\mu_{ {expos }}}\right)}{{Var}\left(\widehat{\mu_{b c}}\right)+{Var}\left(\widehat{\mu_{ {expos }}}\right)}=\frac{E(N)}{E(N)+k} \tag{3.14}$$

where

$$\begin{aligned} k=\frac{E\left( { Layer }_{2}^{2} \mid \alpha_{0}\right)}{C V_{n_{0}}^{2} \cdot E\left( { Layer } \mid \alpha_{0}\right)^{2}+\left(C V_{n_{0}}^{2}+1\right)} \\ \cdot {Var}\left(E\left( { Layer } \mid \alpha_{0}\right)\right) \end{aligned} \tag{3.15}$$

All of the elements of this credibility weight can be evaluated prior to actually estimating the experience rating. To illustrate, in Table 3 we continue with the numerical example.

As expected, the variance around the credibility-weighted rate is less than the variance of either of the individual estimates from exposure or experience rating. This is consistent with our goal of finding an estimator with minimum variance.

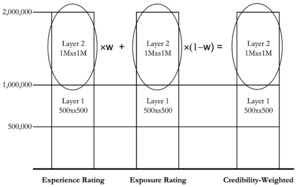
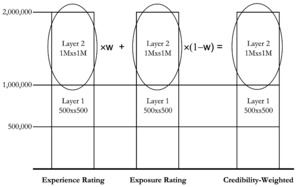
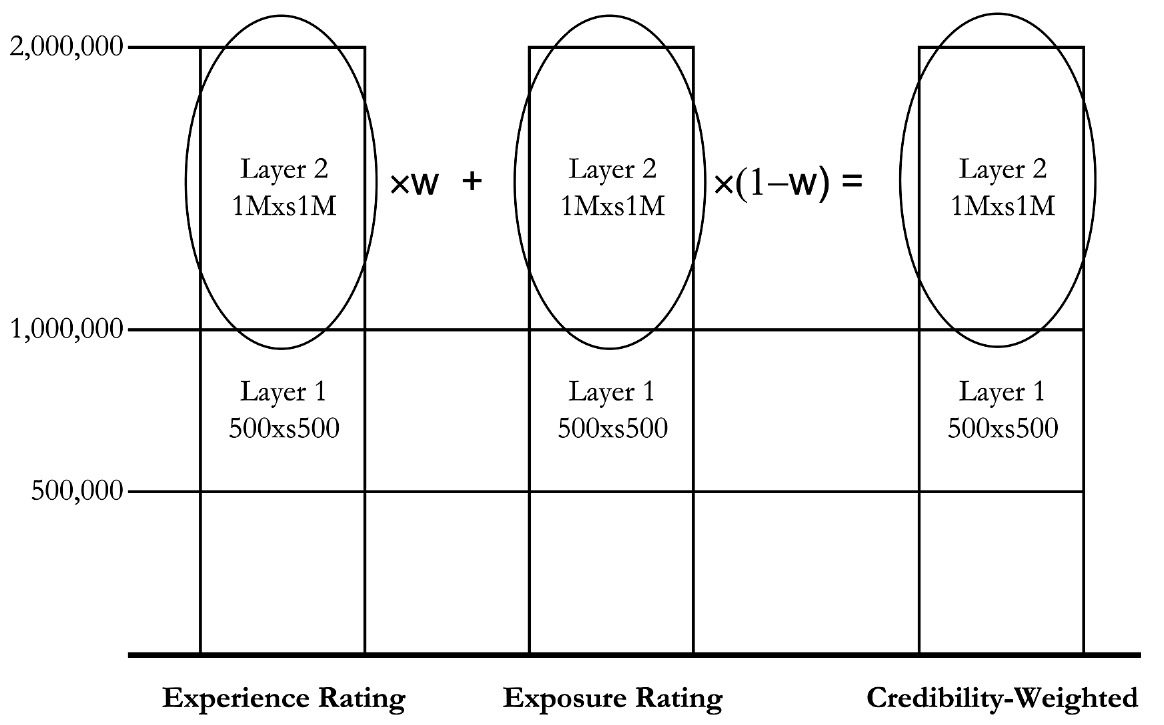
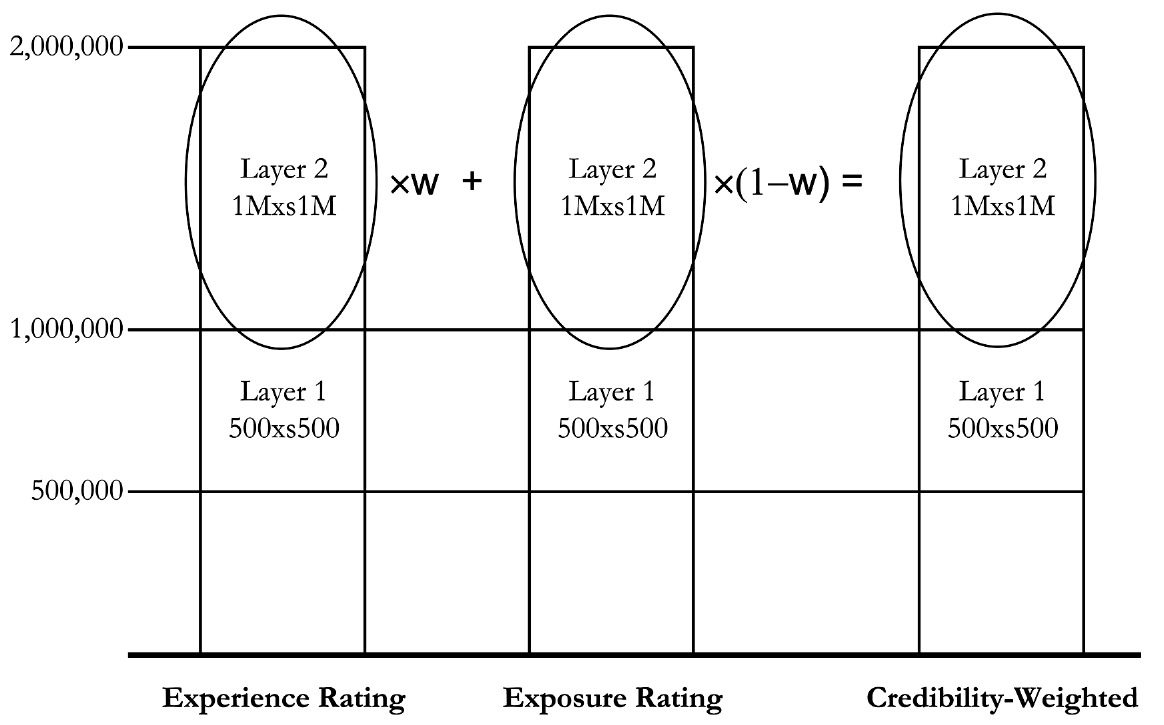
We can illustrate the concept of the credibility weighting of experience and exposure rates in Figure 1.

This illustrates the concept that the credibility weighting is based solely on the rates in the $1,000,000 xs $1,000,000 layer and makes no use of the information in the lower layer. We now proceed to show how the information in this lower layer can be used.

3.3. Including losses from a lower layer

As noted above, the experience and exposure rating models make use of different sources of information. However, they do not make use of all the information that is available to the analyst. We are also able to price layers of insurance below the layer being quoted.

An additional estimate of expected loss is made by applying relativities from the exposure rating model to the expected loss in the first layer $500,000 xs $500,000. This is our “relativity” (rel) method.

$$\widehat{\mu_{\text {rel }}}=\left\{\frac{V_{\text {prospective }}}{V_{\text {historical }}} \cdot \sum_{k=1}^{N} \text { Layer }_{1, k}\right\} \cdot \frac{E\left(\text { Layer }_{2} \mid \alpha_{0}\right)}{E\left(\text { Layer }_{1} \mid \alpha_{0}\right)} \tag{3.16}$$

In this formula, we continue to use the shorthand notation:

Layer $_{1, k}$
$$\qquad={MIN}\left\{{MAX}\left(x_k-500,000 ; 0\right) ; 500,000\right\}$$
for loss $k$

and Layer $_{2, k}$
$$\qquad={MIN}\left\{{MAX}\left(x_k-1,000,000 ; 0\right) ; 1,000,000\right\}$$

for loss $k$.

Figure 2 illustrates how the relativity method makes use of the experience in the lower layer.

This relativity-based estimate is not independent from either the pure exposure rate $\widehat{\mu_{\text {expos }}}$ or from the pure experience burn-cost $\widehat{\mu_{\text {bc}}}$. It shares dependence on the industry size-of-loss distribution with the exposure rate.^[10] The experience rates for first and second layers are also clearly related (for example, there can be no losses in the second layer without at least one loss in the first layer).

The remainder of this section will provide detailed formulas using the Pareto severity and Poisson frequency model. These formulas allow us to create a tractable numerical example that can be reproduced by the ambitious reader and may be helpful for gaining intuition about the sensitivity of the credibility weights to the variance assumptions.

However, the key result is not the Pareto/Poisson model itself but the recursive form of credibility that results. The more practical-minded reader can skip the detailed formulas and not miss this key result.

As a starting point, we may observe the covariance between the experience rates in the two layers.^[11]

$${Cov}\left(\sum_{k=1}^{N} \text { Layer }_{1}, \sum_{k=1}^{N} \text { Layer }_{2}\right)=E(N) \cdot L_{1} \cdot E\left(\text { Layer }_{2}\right) \tag{3.17}$$

The covariance of the relativity-based estimate and the experience rate for the second layer is given as follows:

$$\begin{aligned} {Cov}\left(\widehat{\mu_{ {rel }}}, \widehat{\mu_{b c}}\right)= & \left(\frac{V_{ {prospective }}}{V_{ {historical }}}\right)^{2} \cdot E(N) \cdot L_{1} \cdot E\left( { Layer }_{2}\right) \\ & \cdot \frac{E\left( { Layer }_{2} \mid \alpha_{0}\right)}{E\left( { Layer }_{1} \mid \alpha_{0}\right)} . \end{aligned} \tag{3.18}$$

The severity used in the exposure rate and the layer relativity are closely dependent and may be treated as perfectly correlated.

$$\begin{array}{l} {Cov}\left(E\left( { Layer }_{2} \mid \alpha_{0}\right), \frac{E\left( { Layer }_{2} \mid \alpha_{0}\right)}{E\left( { Layer }_{1} \mid \alpha_{0}\right)}\right) \\ =\sqrt{{Var}\left(E\left( { Layer }_{2} \mid \alpha_{0}\right)\right) \cdot {Var}\left(\frac{E\left( { Layer }_{2} \mid \alpha_{0}\right)}{E\left( { Layer }_{1} \mid \alpha_{0}\right)}\right)} \end{array} \tag{3.19}$$

The bases to which these exposure rating factors apply are independent, so that the covariance between the exposure rate and the relativity-based estimate is as follows:

$$\begin{aligned} {Cov}\left(\widehat{\mu_{ {expos }}}, \widehat{\mu_{ {rel }}}\right)=\hat{n}_{0}^{2} \cdot E\left( { Layer }_{1} \mid \alpha_{0}\right) \\ \cdot \sqrt{{Var}\left(E\left( { Layer }_{2} \mid \alpha_{0}\right)\right) \cdot {Var}\left(\frac{E\left( { Layer }_{2} \mid \alpha_{0}\right)}{E\left( { Layer }_{1} \mid \alpha_{0}\right)}\right)} . \end{aligned} \tag{3.20}$$

From the formulas given above, it is interesting to note that we can calculate all of the needed covariances without introducing any additional correlation assumptions into the model. Each correlation is implied directly by the structure of the layers themselves.

The variance around the relativity-based estimate can also be estimated.

$$\begin{aligned} & {Var}\left(\widehat{\mu_{ {rel }}}\right)=\left(\frac{V_{ {prospective }}}{V_{ {historical }}}\right)^2 \\ & \cdot\left\{E(N) \cdot E\left( { Layer }_1^2 \mid \alpha_0\right) \cdot\left(\frac{E\left( { Layer }_2 \mid \alpha_0\right)}{E\left( { Layer }_1 \mid \alpha_0\right)}\right)^2\right. \\ & +\left(E(N)^2 \cdot E\left( { Layer }_1 \mid \alpha_0\right)^2+E(N) \cdot E\left( { Layer }_1^2 \mid \alpha_0\right)\right) \\ & \left.\cdot {Var}\left(\frac{E\left( { Layer }_2 \mid \alpha_0\right)}{E\left( { Layer }_1 \mid \alpha_0\right)}\right)\right\} . \end{aligned}\tag{3.21}$$

As with the exposure rate, the variance of the relativity factor can be approximated via the “delta method.”

$$\begin{array}{l} {Var}\left(\frac{E\left( { Layer }_{2} \mid \alpha_{0}\right)}{E\left( { Layer }_{1} \mid \alpha_{0}\right)}\right) \\ \approx {Var}\left(\alpha_{0}\right) \cdot\left[\frac{\partial \frac{E\left( { Layer }_{2} \mid \alpha_{0}\right)}{E\left( { Layer }_{1} \mid \alpha_{0}\right)}}{\partial \alpha_{0}}\right]^{2} . \\ \end{array} \tag{3.22}$$

For the Pareto distribution, the relativity ratio is calculated as follows:

$$\frac{E\left( { Layer }_{2} \mid \alpha_{0}\right)}{E\left( { Layer }_{1} \mid \alpha_{0}\right)}=\left\{\frac{R_{2}^{1-\alpha_{0}}-\left(R_{2}+L_{2}\right)^{1-\alpha_{0}}}{R_{1}^{1-\alpha_{0}}-\left(R_{1}+L_{1}\right)^{1-\alpha_{0}}}\right\} \tag{3.23}$$

The derivative with respect to the Pareto alpha is calculated.

$$\begin{array}{l} \frac{\partial \frac{E\left( { Layer }_{2} \mid \alpha_{0}\right)}{E\left( { Layer }_{1} \mid \alpha_{0}\right)}}{\partial \alpha_{0}} \\ =\frac{E\left( { Layer }_{2} \mid \alpha_{0}\right)}{E\left( { Layer }_{1} \mid \alpha_{0}\right)} \\ \cdot\left\{\frac{\ln \left(R_{1}\right) \cdot R_{1}^{1-\alpha_{0}}-\ln \left(R_{1}+L_{1}\right) \cdot\left(R_{1}+L_{1}\right)^{1-\alpha_{0}}}{R_{1}^{1-\alpha_{0}}-\left(R_{1}+L_{1}\right)^{1-\alpha_{0}}}\right\} \\ \left.-\left\{\frac{\ln \left(R_{2}\right) \cdot R_{2}^{1-\alpha_{0}}-\ln \left(R_{2}+L_{2}\right) \cdot\left(R_{2}+L_{2}\right)^{1-\alpha_{0}}}{R_{2}^{1-\alpha_{0}}-\left(R_{2}+L_{2}\right)^{1-\alpha_{0}}}\right\}\right] . \\ \end{array} \tag{3.24}$$

The variance around the layer relativity is calculated in Table 4.

The covariance matrix for the three estimators is

$$\begin{array}{l} \boldsymbol{\Sigma}= \\ {\left[\begin{array}{ccc} {Var}\left(\widehat{\mu_{\text {expos }}}\right) & 0 & {Cov}\left(\widehat{\mu_{\text {expos }}}, \widehat{\mu_{r e l}}\right) \\ 0 & {Var}\left(\widehat{\mu_{b c}}\right) & {Cov}\left(\widehat{\mu_{b c}}, \widehat{\mu_{r e l}}\right) \\ {Cov}\left(\widehat{\mu_{r e l}}, \widehat{\mu_{\text {expos }}}\right) & {Cov}\left(\widehat{\mu_{r e l}}, \widehat{\mu_{b c}}\right) & {Var}\left(\widehat{\mu_{r e l}}\right) \end{array}\right] .} \end{array} \tag{3.25}$$

The inverse of this covariance matrix provides the credibility weights for the three estimates of expected loss. We calculate the inverse of the covariance matrix and then assign the credibility weights proportional to the row (or column) totals.

As Table 5 shows, this final three-factor credibility estimator has a smaller variance than any of the three individual variances. The resulting variance is also less than the variance from the two-factor credibility calculation that was shown in Table 3.

The credibility-weighted estimate is a weighted average of the three separate estimates.

$$\begin{aligned} \widehat{\mu_{c w}}= & w_1 \cdot \hat{n}_0 \cdot E\left( { Layer }_2 \mid \alpha_0\right) \\ & +w_2 \cdot \frac{V_{ {prospective }}}{V_{ {historical }}} \cdot \sum_{k=1}^N { Layer }_{2, k} \\ & +w_3 \cdot\left\{\frac{V_{ {prospective }}}{V_{ {historical }}} \cdot \sum_{k=1}^N { Layer }_{1, k}\right\} \cdot \frac{E\left( { Layer }_2 \mid \alpha_0\right)}{E\left( { Layer }_1 \mid \alpha_0\right)} . \end{aligned} \tag{3.26}$$

This can be rearranged in the recursive form discussed earlier. In this form, we see that a credibility weighting is performed between the exposure and experience rates for the first ($500,000 xs $500,000) layer. This credibility-weighted estimate for the first layer is then adjusted to the level of the second ($1,000,000 xs $1,000,000) layer using relativities, and that amount is weighted with the experience rate for the second layer.

$$\begin{aligned} \widehat{\mu_{c w}}= & \left(1-z_2\right) \cdot\left\{\left(1-z_1\right) \cdot \hat{n}_0 \cdot E\left( { Layer }_1 \mid \alpha_0\right)\right. \\ + & \left.z_1 \cdot \frac{V_{ {prospective }}}{V_{ {historical }}} \cdot \sum_{k=1}^N { Layer }_{1, k} w_2\right\} \\ & \cdot \frac{E\left( { Layer }_2 \mid \alpha_0\right)}{E\left( { Layer }_1 \mid \alpha_0\right)} \\ + & z_2 \cdot \frac{V_{ {prospective }}}{V_{ {historical }}} \cdot \sum_{k=1}^N { Layer }_{2, k} . \end{aligned}\tag{3.27}$$

If we had additional layers above the second layer, then this recursive procedure could be repeated.

As a practical matter, the variances needed for the rigorous multifactor model are not known with certainty. Further, the pricing analyst may want to modify the weights based on other considerations, such as data quality or potential changes in the underlying exposures that require expert judgment. The recursive form can still be used with judgmentally selected weights as a systematic way to incorporate all of the information from the lower layers.

4. Results and Discussion

We have seen that a minimum variance or “best” estimate of expected losses in an excess layer is one that makes use of all the available information from both experience and exposure rating models. The combination of estimates from simple methods is conveniently performed in a linear credibility framework.

The final procedure derived from this credibility framework starts with a lower excess layer, and credibility weights it with a complement from industry sources. The exposure distribution produces an expected layer relativity that can be applied to this lower layer to produce the complement for a second layer. Higher layers are likewise estimated by climbing recursively up the tower of excess layers.

This recursive procedure is grounded in credibility theory, but it also allows for a high degree of judgment as the analyst can adjust the credibility percentages for each step.

Some outstanding questions left from this research are:

• How can we improve on the estimate of the uncertainty in the exposure rating distribution?

• How can we include other sources of uncertainty, such as variability in trend, development, or on-level factors?

• Is there an optimal way of dividing the layers so that the best of all possible credibility-weighted averages is created?

5. Conclusions

The credibility procedure outlined in this paper should be useful for excess of loss reinsurance or other applications in which expected losses in excess layers need to be estimated. While this procedure was not invented by the author, the grounding in linear credibility theory provides a sound theory for systematically estimating expected losses.

---

Acknowledgment

The author gratefully acknowledges the helpful discussion with Michael Fackler, Ira Robbin, Jim Sandor, and Marc Shamula. Any errors remaining in the paper are, of course, solely the responsibility of the author.

Supplementary Material

An Excel example of the formulas in this paper is available from the author.

---

1. See, for example, the “Practical Considerations” (Section 6) in Cockroft (2004).

2. See Section 3 of Marcus (2010) for a good discussion on testing the validity of the unbiasedness assumption.

3. This result is well known in other branches of finance and represents the solution to the minimum variance or efficient portfolio weights. For example, see Theorem 17.1 in Hardle and Hlavka (2007).

4. This result is given as Theorem A.3 in Bühlmann and Gisler (2005), p. 280. It is also a standard feature of weighted regression theory.

5. This distribution, along with the formulas for capped moments related to (3.2) and (3.3) can be found in Appendix A.4.1.4 of Klugman, Panjer, and Willmot (2004).

6. A multivariate version of the delta method is described in Loss Models (Klugman, Panjer, and Willmot). For the single parameter Pareto, the variance approximation is much simpler.

   The univariate delta method is based on approximating a function using the first two terms of the Taylor series expansion, g(x) ≈ g(a) + g′ (a) · (x – a), which results in Var(g(x)) ≈ (g′ (a))² · Var(x). This method would provide an exact result if the Layer formula were a linear function of α; because is it not, our results are only approximate.

7. This formula assumes that the estimates for frequency and severity are independent, and then makes use of the relationship: Var(X · Y) = E(X)² · Var(Y) + Var(X) · E(Y)² + Var(X) · Var(Y).

8. For all of these numerical examples, the numbers are purely for illustration purposes and should not be taken as recommendations for pricing.

9. We are making an approximation in this paper that the expected process variance E~~[Var(Layer|)] can be approximated as Var(Layer|E()). Without this approximation, we would need to specify a complete prior distribution for the instead of just the variance. Alternatively, the process variance could be estimated from the empirical experience rating.

10. Here we deviate from Marcus (2010), who assumes independence of the exposure rating and the severity curve underlying the ILF. While that assumption avoids the need to calculate this additional covariance term, it does not lead to the practical implementation in a recursive form.

11. This formula is valid if the two layers are not overlapping—that is, the retention on the second layer is higher than the retention plus limit on the first layer.