1. Introduction
There are many actuarial methods for estimating expected losses, but how companies ultimately book their final loss reserves is a lot more complex: Actuaries first analyze data and make initial predictions. Next, various levels of management engage in discussions to consider the data and initial indications, impact of any potential changes, the current insurance environment and expectations of the future, and a host of other factors.
This paper is method agnostic and focuses instead on the end result of this entire process and on the corporate environment where loss reserving takes place. Data in the form of Schedule P filings from S&P Global was used to investigate and quantify the process. It was found that reserves are very slow to react to losses, both when updating current periods and when estimating new periods, significantly slower than the most accurate approach would dictate. This was found to be the case for both commercial and personal lines of business.
There are other concerns besides simple accuracy, however. Loss reserves are used to avoid default so having inadequate reserves may incur a greater cost relative to when reserves are redundant. Also, reacting too quickly to emerging losses can increase earnings volatility, which may lower the value of the firm. Such considerations are investigated but found to be unable to fully explain company practice. Drawing from behavioral economic theory, other explanations are offered to fill in the gap and explain reserving behavior.
1.1. Research context
The majority of the actuarial literature is focused on methods and their performance. Of those that utilize historical company data: Littman (2015) used Schedule P data to explore the responsiveness of reserves to emerging losses but the focus was more on how stakeholders form different views and how various methods differ from each other. Wang et al. (2011) analyzed public company data for the purpose of developing metrics for use in risk management. Forray (2012) also used Schedule P data to test the effectiveness of 30 different actuarial methods. Leong, Wang, and Chen (2014) performed a retrospective look using company data with the goal of testing the performance of a specific method. The Bornhuetter-Ferguson Initial Expected Loss Ratio Working Party Paper (2016) used historical data to judge the performance of various methods with much of the focus on changes due to underwriting cycles. And Jing, Lebens, and Lowe (2009) discussed the use of backtesting in general for evaluating different methods.
Wacek (2007) is probably the most similar to this paper and makes a retrospective comparison of booked reserves for Commercial Auto from 1995 through 2001 against those produced using common actuarial methods. Although more limited in scope, his conclusion that the latter would have resulted in greater accuracy is consistent with the results presented here. This theme is elaborated and expanded upon.
In this paper, methodology is essentially ignored (except for the purpose of quantifying tendencies), and the focus is on the end result – regardless of the techniques used to arrive at that result – and on the environment that influenced it. Most of the research is drawn from the field of behavioral economics with references given in their proper places.
1.2. Objective
The goal of this paper is to use company reserving data to gain better insight into how companies set and update their loss reserves and the rationale behind it.
1.3. Outline
The first half of the paper, consisting of Section 2, discusses how reserving responsiveness was quantified and the results of this exercise.
The second half seeks explanations for these findings: Section 3 draws from the behavioral economic literature and discusses several potential solutions but shows that they ultimately come up short on their own. Section 4 shows how the narrow framing principle can cause a multiplication of these effects and be used to fill in the gap.
2. Quantifying and analyzing the company process
This section describes how the loss reserving process was quantified and the results of this exercise. Most of the focus is on the reaction speed to the emerging losses when analyzing existing periods, but also of interest is the setting of loss ratio picks for newer periods.
2.1. The generalized method
It would be difficult and overly complex to build a model that explicitly accounts for the entire reserving operation. Instead, the goal was to find a simple method that can implicitly capture all of its behavior. This means constructing a method that closely mimics the reserve setting of an average company, even if it is an oversimplification of the step-by-step process that most companies use to set their reserves.
As a way of introduction, there are three commonly used, basic actuarial methods for selecting an ultimate loss projection for a given period: the loss ratio method, the chain-ladder method, and the Bornhuetter-Ferguson method. The loss ratio method effectively ignores the emerging experience and therefore is the least responsive; the chain-ladder method relies exclusively on the emerging experience and is the most responsive; and the Bornhuetter-Ferguson method lies somewhere in the middle. For a more thorough review of each of these methods, refer to Appendix A.
To generalize between these three methods, a simple method was used that takes a weighted average of the loss ratio and chain-ladder methods. The weight assigned to the chain-ladder method is calculated as the percentage of loss emergence (or equivalently, the inverse of the loss development factor) taken to a given power, and the weight assigned to the loss ratio method is set to one minus this quantity. In algebraic terms, the equation is as follows:
Ultimate=devR×CL+(1−devR)×ELR
where dev is the percentage developed (the inverse of the age-to-ultimate factor), CL is the chain-ladder method, ELR is the loss ratio method, and R is the selected power.
This method allows for a great deal of flexibility. If this power, R, is set to one, the indication will match the Bornhuetter-Ferguson method, as can be confirmed algebraically. If R is set to zero, then full weight is given to the chain ladder indication, and if R is set to infinity, full weight is given to the loss ratio method. So, R greater than one is more conservative than the Bornhuetter-Ferguson method since additional weight is being given to the a priori expectation, and R less than one would be more responsive.
This method will be referred to as the generalized method for the remainder of the paper, since it is able to generalize between the three most common actuarial methods. It was used to help quantify the level of responsiveness that reserves had to emerging losses.
2.2. Expected R values
Since the Bornhuetter-Ferguson method does not give any credibility to the emerged losses for predicting the remainder of the period – simply setting it to the a priori expectation – it would be expected that optimal R values should be less than one. After all, the losses seen thus far should give at least some indication as to how the remaining portion of the period will develop. This would mean that R values above one imply negative credibility to the experience and would seem counterintuitive at first glance.
This only holds if the expected development pattern is known with certainty, however. Volatility in the timing of loss emergence would increase the R value. For most reasonable cases this uncertainty should have a relatively minor effect, and values would still be expected to be below one.
This is all from the perspective of pure accuracy; stability and other considerations would increase the value of R at the cost of accuracy.
2.3. Tuning the method
The R parameter was optimized on Schedule P individual company triangles[1] for Workers Compensation (“WC”), General Liability (“GL”, Other Liability, Occurrence), Commercial Auto Liability (“AL”, Commercial Auto), Financial Lines (“FL”, Other Liability, Claims Made), and Private Passenger Auto (“PP”). Schedule P filings from 1991 to 2019 were used to analyze accident years 1991-2010 through 10 years of development.
Private Passenger Auto was included to show that this discussion pertains to personal lines as well as commercial, but the results should be viewed with caution due to the very short development time frame of this line, especially since only data from age 24 months was used, as mentioned later. The remaining amount of reported development at 24 months for Workers Compensation, General Liability, Commercial Auto Liability, and Financial Lines was 28%, 76%, 24%, and 72%, respectively, weighted by the square root of premium volume. For Private Passenger Auto, the average remaining development at 24 months was only 8.6%.
Table 1 shows the number of companies and accident year 2010 premiums by line of business after filtering.
The entire process ran as follows:
-
Age-to-age factors were selected (via weighted averages) by company for each line of business,[2] and age-to-ultimate factors were calculated by multiplication.
-
The a priori loss ratio was selected using each company’s booked ultimate loss ratio 12 months from the start of the accident year. This was done because rate change and trend information often used to derive these numbers was not available. Because of this, the method was only able to utilize the data for ages 24 months and later.
-
Ultimate losses were predicted for each accident year using the generalized method for a given value of R. (Only reported losses were used, since models trained on statutory data showed that the optimal weight to assign to paid losses was small.)
-
The squared difference between the predicted loss ratio and the booked loss ratio multiplied by the square root of premiums was calculated as the error. (The square root of premiums was used so that larger, more stable companies would receive more weight, but not disproportionately, so as not to overwhelm the smaller companies.)
This procedure was run on all companies and years together, for each line of business separately. The R value that produced the lowest sum of errors was taken as the value that best simulated average company behavior for each line of business.[3]
To facilitate comparison, this procedure was run again to determine the value of R that would result in the highest accuracy by optimizing against the true ultimate losses instead. These values were derived from the Schedule P filings 10 years after the start of each accident year and were calculated as the average of the company booked number and the chain-ladder prediction at that point in time. To keep the analysis simple, any company having more than 20% remaining development after this point was removed from the data.
2.4. Results
Both calculated R values are shown in Table 2 by line of business, along with the average biases of the initial a priori loss ratios relative to the eventual true ultimate, as described. The initial loss ratio biases varied by year but were generally upwards biased.[4]
As can be seen, the R values reflecting how reserves were booked are all significantly higher than the R values that achieved greatest accuracy. They are even greater than one, which, as mentioned, seems counterintuitive at first glance. All lines of business also show an upward bias in the initial loss ratio projections. This indicates that initial reserves are set conservatively, and that this initial conservatism is slow to come down in response to the emerging data.[5]
Errors against the true ultimate losses for all scenarios were calculated on out-of-sample data (using 5-fold cross validation at the company level). The mean square errors are shown in Table 3, in thousands of dollars.
The errors from the generalized method with R values for matching booked reserves are relatively close to the historical reserving errors, indicating that the method can effectively simulate how an average company sets reserves. It can be seen that both of these errors are significantly higher than those of the most accurate approach.[6]
A possible explanation for the high historical errors could be that companies are more concerned with estimating total reserves across all accident years combined, instead of each particular year – since reserves are all held together. To address this, errors were compared summing all accident years across each financial period, but the conclusions remained the same. As another test, to check if a few abnormal years could be skewing results, the process was run independently for the different 5-year periods within the analysis period. Despite some volatility, the differences between the R values that simulate company behavior are still all significantly higher than the most accurate R values. These tables are shown in Appendix B. The process was also run, perhaps more realistically, with taking the change in the historical loss ratios into account when setting the a priori for each age; this change (or a fraction of it) was used to modify the a priori loss ratio used each year. This caused errors to decrease slightly, but did not change the conclusions.
These results are surprising since companies have much more information at their disposal, including mix of business changes, rate changes, trend expectations, etc., all as mentioned. On the other hand, even though errors were calculated on out-of-sample data, the same group of years were used for each company; this allowed for a peek into the future as to the most appropriate R value for the line of business during the testing period. However, this argument becomes weaker when considering the consistently high company R values along with the large magnitude of the differences in the errors. The generalized method used was also extremely simple; a more sophisticated technique would be smarter in assigning credibilities by year.
This shows that the slowness to react causes reserves to be less accurate. Even though each accident year eventually catches up to its true value, since there are always accident years playing catch up, the result is that reserves are always less accurate than they could be. This causes earnings to be understated for most years and increases the uncertainty in the estimation of company liabilities.
However, when setting loss reserves, there are other concerns besides for accuracy. These are discussed in the next section.
2.5. Other considerations
As mentioned, there are considerations besides accuracy. Reacting too quickly to changes in the data can unnecessarily increase earnings volatility and cause investors to lose confidence in a company’s ability to accurately estimate its liabilities. Additionally, perhaps errors should be calculated asymmetrically: the cost of having reserves that are deficient is the increased probability of default, which may be more costly than the lower perceived earnings caused from redundant reserves.
To account for this, penalties for reserve changes were introduced, assuming that adverse changes are twice as costly as accuracy errors and that favorable changes are only half as costly; these penalties were judgmentally selected to serve as reasonable upper bounds for what the true values should be. This penalty accounts for both stability considerations as well as imposing asymmetric error costs, since having reserves set too low necessitates eventually having to make adverse changes and vice versa. And since the penalty for adverse changes is four times that of favorable changes, having reserves set too low will incur four times the cost as having reserves set too high.
The entire process was rerun using these penalties. These new R values can be described as being optimal from the company’s perspective (if these change costs were set correctly). Table 4 repeats the information shown previously with an added column for these “optimal” R values.
The “optimal” R values are all significantly higher and closer to one than the most accurate values, as expected. (Except for Private Passenger Auto, whose value approaches 2; One should not read too much into this, as it is likely caused by the difficulty in analyzing this line of business in this manner, as mentioned.) These “optimal” values help bridge some of the gap, but the average company R values are still significantly higher than even these values. Even with these added considerations, there are still significant gaps left to explain. It would require unrealistically high levels of risk aversion to be able to approach company behavior using this framework. Sections 3 and 4 make further attempts to explain this difference.
2.6. Loss ratio forecasts
The other item that was analyzed was the responsiveness of loss ratio forecasts. These were approximated by examining selected loss ratios 12 months from the start of each year. At this point, relatively little information is available for each year, and so selections should mostly rely on the loss ratio history.
The generalized Cape Cod method (Gluck 1997) was used to quantify the responsiveness. This method adapts the Cape Cod weights (premiums divided by the loss develop factor) to give additional weight to closer periods and less weight to more distant periods. This accounts for the possibility of loss ratio shifts, something that the original Cape Cod method does not consider.
Exponential decay is used to calculate the weights and control the responsiveness of the method. A parameter between zero and one determines the speed of decay, with lower values decaying faster and being more responsive, and the opposite for higher values. A value of one provides no decay and is identical to the original Cape Cod method while a value of zero would be ultra-responsive and gives full weight to the most recent period.
To run this method similar to how a company actuary would, past years need to be on-leveled for rate and trend changes. These changes were estimated by looking at the differences in company estimated ultimates at first evaluation. These values should be close to their initial values (especially given companies’ slow reaction speed).
This method was used to predict future accident years from 1995 to 2010 (using a maximum of 10 years of history). Optimizing the decay parameter yielded the results shown in Table 5.
As can be seen, the most accurate decay parameters are all significantly lower than the implied company values, which indicates that loss ratio forecasts are slow to adapt to year-to-year shifts in the data.
Errors were calculated on out-of-sample data (by holding out future years). Three size groups were used for estimation since values were highly dependent on the premium volume. The results are shown in Table 6.
The errors from the implied company approach are all relatively close to the historical, which indicates that the method provides a good approximation to company behavior. Interestingly, unlike in the above discussion concerning the reaction to the emerging losses, here, errors from the most accurate approach are only slightly lower than the company approach (and for Auto Liability, the most accurate approach is actually higher than the historical). Part of the reason for this is likely due to the increased uncertainty in estimating future years, but perhaps it may also be that mix of business and related considerations are more important for making forecasts than for adjusting current periods. Another possibility is that the estimated rate and trend changes used here were inaccurate.
For these predictions, unlike when making adjustments to historical years, there does not seem to be any outside considerations besides for accuracy (except for providing a slight bias, perhaps). These results are difficult to explain and will be elaborated on in the next sections as well.
3. Behavioral explanations
As almost anyone who has worked in a reserving department can attest to, loss reserve changes are closely scrutinized and generally discouraged, especially if those changes are adverse. This may cause actuaries to place an even greater emphasis on stability and avoiding increases in reserves than is strictly optimal from the overall company’s perspective. Not doing so can also lower management confidence by causing a loss in faith in the actuarial department’s ability to properly estimate the company’s liabilities.[7]
Just to be clear, this is not to suggest any wrongdoing by reserving departments themselves, since they are acting in accordance with the messages provided by their companies’ management. But just that, quite simply, corporate inefficiencies exist. As later examples demonstrate, the situation is not unique to the insurance industry, either.
The second half of this paper explores how the broader corporate environment affects loss reserving, drawing examples from behavioral economic theory. Essentially, behavioral economics diverges from traditional economic theory, which assumes that entities make perfect decisions using full information and realizes that decisions can sometimes be suboptimal. It investigates the reasons and economic consequences of these imperfect actions, with much of the focus on repeated behavioral patterns that are widespread and predictable. This theory is used to provide explanations and shed light on the discrepancies.
3.1. Visibility
If the corporate environment has a strong influence on reserving behavior, then it would be expected that with more company visibility – with decisions being subject to higher scrutiny – the more conservative the reserving will be.
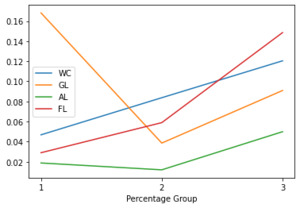
Company triangles were divided into three equal groups based on their line of business’ premium percentage relative to the entire company, which is a good proxy for visibility. The data shows that, as expected, higher visibility is correlated with both greater initial loss ratio picks and slower reaction to the emerging losses. As can be seen, Figures 1 and 2 display mostly increasing patterns, despite a couple exceptions in the pattern. This increase was most pronounced for the highest percentage group, which was the most different of the three groups.
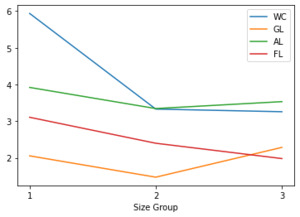
Note that this phenomenon is not related to the premium volume, which exhibits the opposite pattern with larger premium groups showing quicker reaction to the emerging losses and less conservatism, as shown in Figures 3 and 4. This is logical since with more volume and stability, there is less of a chance of being surprised by unexpected changes.
The complete tables for all of this data are shown in Appendix C. Note that Private Passenger Auto was left out of this comparison, which did not seem to show any pattern by percentage group. This could be due to the volatility related to the short development time frame, as mentioned. Another possibility is that private auto is considered distinct enough and so its results are evaluated independently, regardless of its relative size.[8] Note that the combined result was still meaningful even with including this line, as mentioned below.
To further test the assumption related to visibility, R values were calculated for each company and line of business, and a least squares regression was run. Parameters were included for the line of business, the (logarithmic) premium size and the (logarithmic) line of business premium percentage. (The logarithmic one plus R values were used as the response to stabilize values.) The results are shown in Table 7.
As can be seen from the bottom row of the table, visibility was positively correlated with higher R values, and the result was statistically significant at the 1.5% level. (Including Private Passenger Auto, the result was still significant at the 2.5% level.) This is strong support that the corporate environment has a strong influence and contributes to the observed patterns.
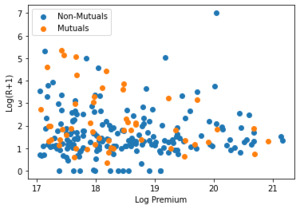
An alternative explanation is that this extra stability may be required for its favorable effect on company stock price. To test this assumption, mutual companies[9] were separated out and compared to all other companies, the majority of which were public. Figure 5 shows the R values by type of company. As can be seen, stock and non-stock companies appear to behave similarly (and in fact, mutual companies were slightly more conservative on average).
The question still remains as to how exactly the corporate environment affects the reserving process. The next two sections attempt to answer this question.
3.2. Managing expectations: Myopic loss aversion
An analogous situation can be found in the financial literature, in what is called the equity premium puzzle (Mehra and Prescott 1985). Using CCAPM,[10] the equity premium, which is the excess return of equities over the risk-free rate, was expected to have a maximum value of 0.35% for the period between 1889 and 1978. However, average stock returns over that period had an average annual return of 6.98% and average treasury yields were 0.8%, which means that the actual equity premium was 6.18%, significantly higher than predicted! Risk aversion can be used to close some of this gap, but the only way to fully support this high equity premium would be to assume risk aversion levels that are highly unrealistic.[11] Similar studies were repeated using different time periods and different assumptions (Siegel and Thaler 1997, for example), with the same overall conclusion: stock yields are much higher than expected.
One prominent solution to this puzzle was proposed by Benartzi and Thaler (1995) as the result of something they call myopic risk aversion. This consists of a greater sensitivity to losses than to gains coupled with the tendency to evaluate outcomes frequently, even for longer term investments. By polling subjects, they estimated that the period that would make one indifferent to stock returns versus bond returns was around 13 months, or roughly annual. Using this shorter timeframe, it was possible to explain the observed high stock returns using a realistic risk aversion parameter! The point is that when investors evaluate their returns frequently, they can be detered by short-term losses, which may not be offset by similar gains if one is risk averse. This short-term volatility scares off investors and causes them to withdraw their funds, and so the stock market needs to compensate with higher returns.
In a similar study, Thaler et al. (1997) found that investors who were given the most frequent feedback as to their returns took the least amount of risk and made the lowest returns. Conversely, investors who evaluated their investments less often were willing to take on greater risk. This gives rise to the popular investment advice of not checking one’s retirement balances too frequently.
Similarly, when reserving estimates are updated frequently, it has the same effect and raises the perceived riskiness. Being slower to make changes lowers the volatility, which can help management become more comfortable with the inherent uncertainty involved in loss reserve estimation. The data similarly shows that adverse prior deviations, which are the equivalent of losses, are minimized as a result of the conservatism and slower reaction. Across the five lines of business analyzed, only 33.7% of all calendar year changes were adverse[12] – in other words, favorable changes are roughly twice as common as adverse changes!
3.3. Avoiding errors: Hindsight bias
Another way to explain the corporate environment and the resulting conservatism may be related to a concept called hindsight bias, which is also known as the “knew-it-all-along” effect. This is an interesting psychological phenomena regarding how individuals can reinterpret their past opinions in the light of new information.
In Fischhoff (1975), a study was conducted where subjects were given narratives of historical events with four choices of possible outcomes and were asked to rate the probabilities of each. The subjects were divided into five groups and each was given a different version of the test: four of which indicated that one of the possible choices occurred, and the fifth where no outcome information was given. Comparing the estimated probabilities across the groups showed that being told of a resulting outcome doubled its estimated likelihood. The experiment was repeated with the added instructions to answer as if the reported outcomes were not known; this resulted in only slight reductions in the estimated likelihoods for the perceived true outcomes.
In a similar experiment (Fischhoff 1975), individuals were asked to assign probabilities to various scenarios shortly prior to President Nixon’s trip to China and the USSR in early 1972. (Would the trip be declared a success? Would he meet with Chairman Mao? Would he visit Lenin’s tomb?) When asked to recall their predictions several weeks after the trip, the probabilities of the realized outcomes were inflated while the probabilities of the unrealized ones were reduced!
Comparing the differences in the severities of judgements presented with and without outcome information shows the effect of the hindsight bias on potential jury awards. Casper, Benedict, and Perry (1989) studied its effect on judgements related to potentially illegal police searches; Hastie, Schkade, and Payne (1999) polled subjects on punitive damages related to environmental damages; and LaBine and LaBine (1996) studied cases involving the handling of potentially dangerous patients, to name a few. Other studies have similarly found that this bias can influence juries to form harsh judgments in determining legal liability and for medical malpractice cases based on an overestimated predictability of events, especially when severe outcomes like injury or death resulted (Harley 2007).
The lesson is that people often unintentionally reinterpret and even change their prior perceptions to fit later facts. To describe the hindsight bias succinctly: “People believe that others should have been able to anticipate events much better than was actually the case. They even misremember their own predictions so as to exaggerate in hindsight what they knew in foresight” (Kahneman, Slovic, and Tversky 1982).
Similarly, this makes life difficult for an actuary who does not want to be second-guessed for reserve changes that fail to materialize. It amounts to what is essentially a retroactive punishment for any later reversals, despite following best practices. This would incentivize an actuary to adapt to changes very slowly in order to minimize the chance of subsequent reversals, which can carry the perception of having acted incorrectly. From the company data, the slower reaction speed allowed for significant reductions in the standard deviation of wrong directional changes: by three quarters for Workers Compensation and General Liability, two thirds for both commercial and personal Auto Liability, and slightly less than half for Financial Lines.[13]
3.4. Not the full picture
In truth, there is likely a combination of both of the discussed incentive structures at play. Including both penalties (consistent with the above of assuming that adverse development is four times as costly as favorable development), which likely includes some double counting, was still not able to approach the company R values, as shown in Table 8.
Backing into the approximate implied penalties that would support company R values yielded the relative costs for each line of business, shown in Table 9.
For the change penalty, a value of 100, for example, meant that the cost of adverse development was 100 times as costly as a favorable change. For the retroactive penalties, the costs are for reversals relative to accuracy errors.
Given these high implied costs, it would be difficult to explain the company process using this framework alone. It would be unrealistic to assume that the implied costs are hundreds of times as costly as accuracy errors. Also, none of this helps with explaining the similar conservatism shown when setting initial loss ratios for new years.
The next section shows a possible solution to this riddle in a framework whereby the discussed theoretical costs would be magnified when working in a real company setting.
4. Narrow framing
4.1. A multiplication of costs
The entire discussion up until now has focused on line of business level reserves in total – but, in reality, smaller books of business are analyzed and managed as individual entities. Total reserves for the line of business are often analyzed, not at the overall level, but by looking at smaller divisions separately and then summing up the total reserves. And the impacts of reserve changes are evaluated at each business unit level – not just for the entire company or line of business. Analyzing results at finer levels can help with managing the various pieces of a corporation; the practice can be problematic, however, when it ignores the combined result.
The tendency to allow aggregate results to take a backseat to smaller divisions is called narrow framing.[14] Ideally, when an individual or company chooses whether to take on a new risk, it should merge its risk-reward distribution with the existing portfolio to ascertain whether the additional benefit outweighs the additional risk to their combined portfolio. When an entity fails to do so and evaluates each risk in isolation, it suffers from this principle. The tendency of ignoring the effects of aggregation can lead to excessive risk aversion (Kahneman and Lovallo 1993).
Interestingly, this principle has been used to explain why individuals purchase insurance that has a negative expected value even for instances where the potential loss being insured against would not cause any financial hardship and could easily be absorbed (Cicchetti and Dubin 1994). A study was conducted on an insurance policy covering faulty telephone wiring that carried a 0.5% chance of a possible loss of only $55! This loss amount would have an extremely insignificant effect on aggregate wealth (even in 1994 dollars). Only when viewed in isolation coupled with an aversion to loss would one think about purchasing such a policy, no matter how good the salesperson!
At the corporate level, Koller, Lovallo, and Williams (2011) (likely based on Swalm 1966), conducted a survey on behalf of McKinsey of 1,500 managers who were asked to evaluate an opportunity of an $100 million investment that could grow to $400 million in three years but that also had a chance of losing the entire principle. Most of the managers would only accept the risk only if the probability of loss was 18% or less, significantly lower than the risk neutral probability of 75%. What was puzzling was that little changed even if the investment amount was decreased by 90% to only $10 million – even though the risk to the overall firm was practically negligible at this point. Managers who were interviewed afterwards admitted that the investments might be positive for the company but were poor for their careers.
Another example is given by Thaler (2015) where he asked 22 managers if they would accept a 50-50 risk that would either result in a gain of $2 million or a loss of $1 million. Only three managers opted to accept the risk, while in contrast when the same question was posed to the CEO, he replied that he wished to accept all of them.
This tendency affects the environment in which loss reserving takes place. It causes the theoretical costs for reserve changes and reversals to be evaluated at smaller levels of detail and thus more attention is needed to stabilize the outcomes. Basically, it compounds all of the associated costs discussed. On its own, it would not be able to explain the findings of R values significantly above one. Only when combined with the first two frameworks does narrow framing have a significant effect.
The problem of narrow framing is also exacerbated by the fact that the profitability of an individual book of business may be only a few percentage points of total premiums, and so relatively small swings in the estimated loss ratios can completely change a book’s entire financial outlook. This would cause even more scrutiny to be put on individual reserving changes and cause further increases to the theoretical costs under either framework. This applies even to changes that are mostly meaningless from a statistical standpoint. And it can have an especially large impact when multiple periods are simultaneously affected, such as a trend adjustment or a slight increase in a tail development factor.
4.2. An illustration of narrow framing
In the S&P Global data, there is no way to break down results to analysis segments. But, as a thought experiment, the four commercial lines of business were combined together (after developing separately). When this was done, the differences between the company R values and accurate R values widened, which caused the implied penalties to increase substantially: the penalty for reversals became 3,000 – an increase of more than tenfold – and the implied penalty for adverse development to over 100,000!
The point is that attempting to explain aggregated results whose analysis was conducted at finer levels of detail can produce nonsensical levels of conservatism and lead to confusion. The only way to explain the results would be to examine the actual business units themselves.
4.3. Narrow framing for loss ratio forecasts
The story for being conservative when setting initial loss ratios is slightly different since the discussed costs related to managing expectations and avoiding errors do not apply. Instead, the issue relates to the tendency to make changes based on the volatility of the finer data segmentations instead of that of the overall company. When volatility is managed based on the individual analysis segments without considering the stabilizing effects that aggregation would provide, this is an example of narrow framing.
4.4. Narrow framing within narrow framing
It would be foolish to suggest that actuaries working within a corporate division ignore the business unit results and instead focus solely on the larger company, since this goes against how corporations are managed and will likely result in negative consequences. But where actuaries can have an impact is when additional analysis segments are created within the actuarial department for the sake of homogeneity or to help measure mix of business effects, for example. In this case, there is no need to over-manage the volatility of the individual segmentations since changes in one segment are likely to be canceled out by opposite changes in other segments – the same that would result as if the entire dataset were analyzed together.
A similar situation is cited in Kahneman and Lovallo (1993) regarding an investment manager who makes decisions on large investments while also managing a group of subordinates who decide on smaller investments. If the manager chooses to manage her subordinates the same way that she manages her own portfolio, the result will be that the subordinates combined aggregated portfolio will be more risk averse than the investment manager’s own portfolio. This occurs because the subordinates’ investments pass through another layer of management and so receive a double dose of narrow framing!
Returning to the insurance context, another way such a scenario can occur is when different analysts compute the reserves for separate subdivisions within a loose management structure. Blame for prior period development and reversals can trickle down to the responsible segment, and so each analyst has the incentive to be conservative and minimize changes. Once this starts happening, it lowers the combined volatility across the segments and makes changes in one segment less likely to be canceled out by changes in another, and thus even more likely to trigger blame. This has a snowballing effect and would cause each analyst to take an even more conservative approach to his or her reserving, and so on.
To counter the scenario of managed segments getting the double application of narrow framing, the following suggestion is given: “the counter-intuitive implication of this analysis is that … an executive should encourage subordinates to adopt a higher level of risk-acceptance than the level with which she feels comfortable.” In other words, since aggregation has the effect of lowering the overall volatility, with changes from one segment canceled out by opposite changes in another segment, less stability is needed for each individual segment. Viewing segmented numbers with the same eye as one would use for aggregated results causes the latter to be much more risk averse than is desirable.
5. Conclusions
This paper performed an empirical study of how loss reserves are set and updated, and it was shown that reserves are slow to react to loss information. The likely reasons for this were shown to be the need for increased stability and the avoidance of reversals. The theoretical costs for these considerations get multiplied with more subdivisions, an application of narrow framing, which necessitates the need to manage changes at finer levels of detail.
It is the author’s hope that a greater understanding of these effects will be beneficial to actuaries when managing the reserving process and the broader corporate environment in which it takes place.
Supplementary Material
The code used for the analysis can be found here: https://github.com/urikorn/behavioral-reserving
A special thanks to the reviewers: Derek Jones, Chandu Patel, John Karwath, Karl Goring, and another very helpful anonymous reviewer, and to Michael Wacek whose comments were helpful to further enhance this paper. All remaining errors are the author’s.