Risk Valuation for Property-Casualty Insurers

1. Introduction

The property-casualty (re)insurance industry has invested heavily in analytical modeling to estimate the effects that various management alternatives may have on the probability distribution of the firm’s future financial states—their risk transformations. Stochastic financial simulation embedded in enterprise risk management is now a high art. Specialized teams run massive simulations and produce detailed reports comparing the risk profiles of alternative management strategies. Yet these comparisons are necessarily multidimensional; the output of stochastic financial simulation—a probability distribution—is not just a single number, it is many, many numbers. In order to draw meaningful conclusions for enterprise risk management, that complexity must be reduced, often to a two-dimensional plot of (some one-dimensional measure of) risk versus expected return. Dominated strategies can be identified and discarded, leaving an efficient frontier of choices that span a risk-return tradeoff (Lowe and Stanard 1997). But how to adjudicate this tradeoff?

One approach is to evaluate risk-return tradeoffs by putting both on the same scale: shareholder value. Risk valuation is the process of assigning a value to a transformation of risk. Risk transformation can come about through changes in the operation of a business (line of business mix, investment mix), explicit risk transfer mechanisms (reinsurance, hedging), or financial changes (capital structure and amount). All else equal, an increase in expected profitability or a decrease in risk both lead to higher shareholder value. But what if profitability and risk increase or decrease together (which is of course the case with efficient frontiers)? Having a mathematical model of shareholder value allows one to determine which of several risk management alternatives—or capital strategies—brings higher value to the firm.^[1]

This paper reviews four classes of valuation models that have been applied to risk valuation questions. While some nuance is discussed, the models are stripped to their algebraic essentials in order to clarify what they do and do not do. We also do not delve into the distinctions between accounting capital, policyholder surplus, book value, or net assets and simply refer to shareholders’ residual claim on net assets as “surplus,” represented by W, and assume that if the firm were to go into runoff, W is the value of what shareholders ultimately receive. Unlike many “market consistent” valuation exercises (Wüthrich, Bühlmann, and Furrer 2008) that are focused on the balance sheet at one point in time, the goal here is valuing the firm as a going concern. In contrast to the liquidation value W, the symbol M is used to represent the value to shareholders of the firm as a going concern. M is what valuation attempts to measure.

Section 2 reviews the basic asset pricing theory that underlies all of the models. Section 3 discusses the traditional models used in actuarial appraisal/valuation, including the discounted dividends model, discounted cash flow model, and abnormal earnings model. Section 4 discusses the application of economic capital models to risk valuation and how that usage relates to the abnormal earnings model. Section 5 defines the firm life annuity model, an extension of discounted cash flow modeling that explicitly models the risk of losing franchise value. Section 6 discusses optimal dividends models. Section 7 illustrates the various methods by way of a simple example. Section 8 compares the key assumptions underlying the various models. Section 9 concludes.

2. Asset pricing theory

The fundamental determinant of the value of a financial asset is its set of cash flows. An asset may generate cash flows to (and from) the owner over time, or it may be held with no cash flows except at the time it is sold. Cash flows may be deterministic or stochastic. No-arbitrage asset pricing theory (Cochrane 2001) gives us the general pricing principle,

$$M_{t}=E\left[\sum_{i=1}^{\infty} d_{t+i} \cdot \Psi_{t, t+i}\right] \tag{2.1}$$

where $d_t$ is the cash flow at time $t, M$ represents the price or value of the asset generating those flows, and $\Psi_{s, t}$ is a “stochastic discount factor” representing market preferences. Sometimes $\Psi$ is derived from the marginal utility of consumption. In a market with no arbitrage, the stochastic discount factor exists; if the market is complete, it is unique (Panjer 1998).

This formula can be manipulated and reformulated in several ways. If expectation is taken with respect to the real-world probability distribution P for d, then Ψ must encompass a risk adjustment. This leads, for example, to the notion of a risk-adjusted cost of capital,

$$M_{t}=E_{P}\left[\sum_{i=1}^{\infty} \frac{d_{t+i}}{\left(1+r_{A}\right)^{i}}\right] \tag{2.2}$$

where the constant $r_A$ is greater than the risk-free rate $r_f$. On the other hand, $\Psi$ can be interpreted as proportional to a Radon-Nikodym derivative (ratio of probability densities) (Panjer 1998) so the expectation can be taken with respect to an altered probability distribution $Q$ and the equation becomes

$$M_{t}=E_{Q}\left[\sum_{i=1}^{\infty} \frac{d_{t+i}}{\left(1+z_{t, t+i}\right)^{i}}\right] \tag{2.3}$$

where $z$ is the risk-free zero-coupon yield. This is called “risk-neutral” valuation and is often used in pricing derivatives (e.g., stock options) in the “option pricing model” favored by finance academics.

Another set of equivalent formulations can be made by relating the values of M at two points in time:

$$M_{t}=E\left[\left(d_{t+1}+M_{t+1}\right) \cdot \Psi_{t, t+1}\right] \tag{2.4}$$

This emphasizes that from the perspective of time t, the value at time t + 1 is a random variable. This recursive formulation is often easier to deal with than an explicit infinite series. It also emphasizes that the return on the asset from time period t to t + 1 is composed of the actual cash flow in that period (d) plus the change in value (M) or capital gain.

This paper will also use continuous-time analogues of these equations where the summations are replaced by integrals.

The objective of risk valuation is to calculate the difference in shareholder value resulting from a risk transformation, usually in circumstances where market prices contribute at best indirect information. Therefore, risk valuation as presented in this paper consists of an idealized long-term “intrinsic value” calculation, with less concern about what the stock market might have to say at any particular point in time than it would be in other valuation exercises.

In a typical valuation engagement, specific cash flows are estimated for each of a few years into the future, and then a “terminal value” or “continuing value” covers all years beyond, using uniform assumptions. To illuminate the essentials, this paper focuses on terminal valuation and assumes a single discount rate rather than a yield curve.

Finance theory has for years inquired into the reasons a firm might engage in hedging or other risk management activities. The Modigliani-Miller theorems state that with frictionless capital markets and a fixed menu of business opportunities, a firm’s dividend policy, capital structure, and risk management do not affect firm value (Miller and Modigliani 1961). This is not observed in reality, however, and that fact spawned an extensive literature considering various market “frictions” to explain why capital structure and risk management do, indeed, matter (Doherty 2000). Froot (2007) summarizes the wider financial research into capital market frictions and the relevance of risk management to a financial firm. The key insight of Froot and Stein (1998) is that costly external capital makes risk management valuable. That insight underlies the differences between the models presented in this paper.

3. Actuarial appraisal/valuation

Formula (2.2) is the basis of several methods used in actuarial appraisal (Actuarial Standards Board 2005) or valuation (Goldfarb 2005). If the numerator d represents shareholder dividends, one gets the discounted dividends model. If d represents “free cash flow” (potentially distributable profits), one gets the discounted cash flow model. If those cash flows are separated into required and excess returns on capital, one gets the abnormal earnings^[2] model. Girard (2000) showed that if consistent assumptions are used, discounted cash flow and option pricing methods are equivalent. Abnormal earnings will be discussed in more detail in the next section.

It is important to remember that fundamentally, these are equivalent formulations. They merely differ by their algebraic structure and their emphasis on what fundamentals need to be estimated or assumed as inputs. Which one (among these or other variants) is chosen for a particular task depends in part on the relative difficulty of estimating, or reasonability of assuming, values for the particular parameters.

In its naïve form^[3] (and recalling the focus is on terminal valuation), the actuarial appraisal/valuation method assumes a perpetuity equal to the expected level of shareholder-distributable cash flows μ and computes its present value using a risk-adjusted discount rate r:

$$M=E\left[\int_{0}^{\infty} \mu \cdot e^{-r \cdot t} d t\right]=\frac{\mu}{r} \tag{3.1}$$

This rendition of the model does not reflect the profit stream growing over time. Assume that the scale of the insurer’s operations grows at a continuous rate of γ. This means that exposures, premiums, expenses, and losses are all bigger by a factor of exp(γt) at time s + t than they are at time s. As a result, the expected profit rate μ will grow at the same rate:

$$\mu_{t}=\mu_{0} \cdot e^{\gamma \cdot t} \tag{3.2}$$

However, there is one item that will not change “naturally” with the scale of operations-policyholder surplus (symbolized by W). In order to grow surplus, either capital has to be raised from shareholders, or earnings must be retained (i.e., not distributed). Algebraically, either alternative is represented the same way in the model by modifying the cash flow term:

$$\begin{align} \mu_{t}^{*} \equiv \mu_{0} \cdot e^{\gamma \cdot t}-\frac{d}{d t} W_{t}&=\mu_{0} \cdot e^{\gamma \cdot t}-\frac{d}{d t}\left(W_{0} \cdot e^{\gamma \cdot t}\right) \\ &=\left(\mu_{0}-\gamma \cdot W_{0}\right) \cdot e^{\gamma \cdot t} \end{align} \tag{3.3}$$

Taking constant growth into account, Equation (3.1) then becomes the Gordon Growth Model (Gordon 1959),

$$M=E\left[\int_{0}^{\infty}\left(\mu_{0}-\gamma \cdot W_{0}\right) \cdot e^{\gamma \cdot t} \cdot e^{-r \cdot t} d t\right]=\frac{\mu_{0}-\gamma \cdot W_{0}}{r-\gamma} \tag{3.4}$$

where the result is understood to apply only if $\gamma<r$; otherwise, the integral diverges. Note that this formula applies equally well to a discrete time model where $\mu_0$ is the annual expected profit (realized at the end of the year) and the scale of operations grows as $(1+\gamma)^t$.

Here, the retained earnings term is explicit in the numerator rather than having it left understood as part of the definition of μ. This is because stochastic financial simulation models that generate probability distributions of distributable earnings typically do not take growth into account.

How would the actuarial appraisal/valuation model in Equation (3.4) be used in risk valuation? In principle, all the necessary pieces are present, but practical advice is hard to come by. The terms “insolvency,” “bankruptcy,” “hedging,” and “risk management” do not appear in the CAS Part 8 study note (Goldfarb 2005) nor in the indices of the CFA textbook (Stowe et al. 2002) and EVA text (Young and O’Byrne 2001). Damodaran (2002) and Copeland, Koller, and Murrin (1995) spend a few pages each discussing the effects of hedging and its impact on bankruptcy costs, average tax rates, and other “costs of variability” (usually referred to by economists as “frictional costs”). Aside from saying that the expected cost of bankruptcy is the product of probability and severity, there is no clear modeling advice.

Given two risk management alternatives, stochastic financial simulation modeling would presumably produce different values of μ, but probably not γ. Changes in planned expansion, or entry into or exiting from markets, of course would change prospects for growth, but these would most likely be transient changes. The most appropriate long-term growth rate to assume in terminal valuation is something reflective of the long-term growth of the economy as a whole. Contemplating changes in W₀ resulting from each alternative is in the province of economic capital models discussed in the next section; in the basic application of actuarial appraisal/valuation, the current level of surplus is held fixed. The valuation rate r may differ, but only if the alternatives represent changes in systematic risk (derived from capital asset pricing model beta or multifactor market models). Thus, a change in investment hedges may result in a change of valuation rate but a change in underwriting practice typically will not.

As a result, the naïve application of actuarial appraisal/valuation concludes that the typical nonfinancial hedge (e.g., reinsurance) cannot bring value to the firm unless it carries a price lower than its actuarial expected value. In fact, it would also conclude that even financial hedges do not add value, as implementing these hedges incurs a small spread over their market values.

4. Economic capital

Economic capital models focus on the relation between risk and required surplus W. In effect, the infinite-dimensional distribution of outcomes is mapped to a single number: the economic capital. This is typically done through one of four risk metrics: default probability, expected policyholder deficit (expected value of negative surplus), value at risk (a specified quantile), or tail value at risk (conditional expectation beyond a quantile), although in principle there is an infinite array of candidate metrics. Economic capital is defined as that amount of capital that the firm needs to hold in order to avoid a specified condition on the risk metric. For example, the management of the firm may decide that it needs to keep its one-year risk of bankruptcy below the 1-in-200 year level. Stochastic financial simulation modeling then determines what level of surplus is necessary to achieve that goal (Exley and Smith 2006).

Economic capital models are often used to address value issues through the concept of “cost of capital,” represented by the parameter r in the previous equations.^[4]

This metaphorical usage of the term is understandable, but unfortunate.

The cost of equity is not a cash flow. Neither accounting standard setters nor taxation authorities recognize cost of equity as a cost. Even solvency regulators are not yet requiring firms to provide for future equity costs. Cost of equity does not accumulate arrears if you miss a payment, and cannot trigger default or bankruptcy. Nevertheless, describing required returns on equity as a cost has fallen into common usage (Exley and Smith 2006).

A more appropriate term for the valuation rate r is “hurdle rate.” Notice in Equation (3.4) that if μ₀ is less than rW₀, then M < W₀ and the firm would be worth more to shareholders in liquidation than as a going concern. Having expected earnings μ of at least rW is the “hurdle” for staying in business. Therefore, if a risk transformation causes a change ΔW in the amount that the firm needs to hold to meet its risk targets, then it thereby changes the elevation of the hurdle for μ. It will also, presumably, change μ itself by an amount Δμ, equal to the net of its cost (e.g., reinsurance premium) and expected benefit (e.g., recoveries).

In contemporary practice, if the net Δμ - rΔW is positive, the transformation is deemed to add value and should be considered; if not, it is deemed to destroy value and should not (Venter, Gluck, and Brehm 2007; IAA 2009; Hürlimann 2003). This can be seen to make sense in terms of valuation principles as follows. Let us assume that a given risk transformation, relative to the status quo, results in a one-time cash flow ΔW (algebraically positive or negative)^[5] to the firm from the shareholders and a change in ongoing flow rate Δμ with resulting change in market value of the firm given by Equation (3.4). Then the net value to the shareholders of making that transformation is given by

$$\begin{aligned} \Delta V=\Delta M-\Delta W&=\frac{\Delta \mu-\gamma \cdot \Delta W}{r-\gamma} -\Delta W \\ &= \frac{\Delta \mu-r \cdot \Delta W}{r-\gamma} \end{aligned} \tag{4.1}$$

as long as r does not change as a result of the transformation. The numerator in the final expression is the economic capital decision criterion.

This formulation hides an important detail, however. In a financial firm, most of the assets are financial assets, and so changes to assets caused by raising or disbursing capital will likely also change the level of investment income. If this is not already included in the definition of Δμ it needs to be represented explicitly. Using the symbol ι to represent the after-tax investment yield on assets liquidated for or invested as marginal surplus, Equation (4.1) becomes

$$\begin{aligned} \Delta V&=\frac{\Delta \mu-\gamma \cdot \Delta W+\iota \cdot \Delta W}{r-\gamma} -\Delta W \\ &= \frac{\Delta \mu-(r-\iota) \cdot \Delta W}{r-\gamma} \end{aligned} \tag{4.2}$$

Therefore the economic capital criterion for a risk transformation is not the cost of capital r, but the spread between the cost of capital and the after tax marginal investment yield. Making this explicit is important because stochastic financial simulation models used to inform economic capital calculations, being temporally prior, typically do not adjust investment earnings for changes in economic capital.

Economic capital valuation relates to the concept of abnormal earnings, a submodel of actuarial appraisal/valuation. Rewrite Equation (3.4) as

$$M=\frac{(\mu-r \cdot W)+(r-\gamma) \cdot W}{r-\gamma}=W+\frac{\mu-r \cdot W}{r-\gamma} \tag{4.3}$$

The numerator in the second term in the final expression is referred to as abnormal earnings, that is, earnings above the cost of capital, and the second term itself, the difference between market and book value, is referred to as franchise value (Exley and Smith 2006). It is sometimes incorrectly stated that market value is equal to book value plus the present value of earnings; the important qualifier “abnormal” is needed.

Given a theory of required capital (as a function of risk), the economic capital model presents an explicit method to value the tradeoff between risk (as measured by ΔW) and reward (as measured by Δμ). This is a marked improvement over naïve actuarial appraisal/valuation, which measures no value from risk management, focusing as it does on Δμ with nothing else changing.

Nonetheless, the economic capital method of risk valuation has its shortcomings.

As with actuarial appraisal/valuation, the connection between this model and the goal of maximizing shareholder value is tenuous. “Risk appetite” is the term of art for management consensus on the quantity of risk to which the firm ought to be exposed. Rather than determining from shareholder value principles the optimal level of risk the firm should hold, it is often simply assumed.

Additionally, the hurdle rate r is assumed constant, unaffected by risk transformation. However, only if there is precisely zero correlation between the risks being managed and the financial markets would a constant hurdle rate be theoretically correct.

Finally, the implicit abnormal earnings valuation assumes that abnormal earnings will continue to flow forever. Since the firm’s solvency is typically set at a 1-in-200-year risk appetite, and valuation rates are typically in excess of 10%, this does not at first seem an unreasonable approximation. It should be noted, however, that multiyear abnormal earnings valuations in the actuarial appraisal/valuation style tend to assume that franchise value will shrink at a “fade rate” and eventually disappear at the end of a “competitive advantage period” (Young and O’Byrne 2001). It is well known that for insurers, the loss of a relatively small portion of capital could be sufficient to materially hobble the firm’s ability to execute its business plan and continue to generate the abnormal earnings that yield franchise value (Exley and Smith 2006). This insight gives us the key to the next risk valuation method.

5. Firm life annuity

An obvious concern of enterprise risk management is the mortality of the firm; therefore it makes sense to model it. The firm life annuity model presented here can be viewed as an extension of the discounted cash flow model [Equation (2.2)].

5.1. The value of a life annuity with constant force of mortality

Consider again the case of an idealized insurer that holds surplus in the amount W and earns a continuous, constant stream of profits at the rate μ, which it immediately disburses to shareholders. This stream continues until a catastrophic event (a loss greater than surplus) occurs, at which time profits cease and surplus is lost (not given back to the shareholders). Catastrophic events occur at an annual rate of λ and follow a Poisson process. Assuming a constant (continuous) valuation rate of interest r, the value of this life annuity with constant force of interest and constant force of mortality is given by Bowers et al. (1997):

$$M_{t}=\int_{0}^{\infty} \lambda \cdot e^{-\lambda \cdot T} \cdot \int_{0}^{T} \mu \cdot e^{-r \cdot s} d s d T=\frac{\mu}{r+\lambda} \tag{5.1}$$

Remark 1. Note that the amount of surplus W does not appear explicitly in this equation; the risk is captured by the parameter λ. Presumably, the risk is related to the amount of surplus, and this will be made explicit later.

Remark 2. Discounted cash flow makes use of expected values of cash flows, substituting the expected value of “free cash flow to equity” (FCFE) for the constant μ. A risk-adjusted discount rate is therefore used in the denominator, reflecting the probabilistic nature of the cash flows (to be discussed later). Also, the existence of shareholder limited liability (insolvency put) means that μ cannot simply be equated with expected shareholder cash flows.

Remark 3. A key difference between this model and the previous models is that here, the firm is mortal. Post-catastrophe, investors cannot recapitalize the firm and continue operations.

An alternative, recursive derivation of Equation (5.1) is presented in Appendix A.

5.2. Financial distress and growth

While it is possible for a catastrophic event to consume all of an insurer’s surplus, it is more common for insurers to get into financial difficulties with positive, but inadequate, levels of surplus. Rather than having λ represent the risk of insolvency, let us redefine it to be the risk of encountering financial distress sufficient to drive the firm into runoff. When such an event occurs, the surplus of the firm may be greater than zero; we will assume the remaining surplus goes immediately to the shareholders. Equivalently, consider that, at that time, franchise value is lost and the market value M is equal to the remaining surplus, even if the firm does not go into runoff.

Notice we have not specified exactly how this distress comes about. One model for this is to specify a level of surplus representing a ratings or regulatory “cliff” (Major 2007) — if surplus should fall below W_C, then the firm loses its ability to continue operations. In that case, λ represents the probability (in continuous time, the Poisson rate) that surplus falls below W_C.

Here, introduce a new input variable, U, to represent risk transformation alternatives. For example, in considering a choice among several reinsurance alternatives, various terms are affected: First, there is a premium cost (negative impact on μ), which is offset by expected recoveries (positive impact on μ). Second, there is the impact on risk, affecting the probability—and perhaps even the definition—of distress, presumably reducing λ (at least compared to going bare). To the extent that risk transformation affects systematic risk, r could vary between choices for U as well.

Analogous to Equation (5.1), a finite-time valuation equation representing the “cliff” model and including constant growth in scale of operations γ is given by

$$M(W, U)=\frac{\mu^{*}(W, U)-\Gamma(W, U) \cdot W}{r(W, U)-\Gamma(W, U)} \tag{5.2}$$

where $\mu^*$ is the expected annual insolvency put-protected profit,^[6] $\Gamma=(1-\lambda) \gamma-\lambda$ is the “survival adjusted” growth rate, $W$ is the level of surplus, and $r$ is the valuation interest rate. This formula is derived in Appendix B.

The firm life annuity model provides an explicit valuation of the tradeoff between risk and reward through the effects of the μ and λ terms. However, it also provides a means to address capital questions such as, what is the impact on firm value of raising or disbursing capital? and, what is the optimum amount of capital to be held? Functional dependence is obvious in the λ term, where lowering W should increase the probability of encountering financial distress. Say an increase in surplus from W to W + ΔW could decrease λ, and that would imply an increase in value from M to M + ΔM. It would then be a matter of comparing the increase in shareholder value ΔM to the funds ΔW (plus costs) necessary to achieve that increase, to determine whether it would be advantageous to do so.

The firm life annuity model represents two levels of risk. On the first level, there is insolvency risk, controlled by risk management (transforming the probability distribution of financial outcomes) and by holding adequate levels of capital. Doing a “good job” of insolvency risk management means being in a position to execute profitable business strategies, collect abnormal earnings, and achieve positive franchise value. On the second level, there is the risk of losing one’s footing—of losing enough surplus (say) to undermine profitable operations and lose franchise value as well. This risk is much greater than insolvency risk, but it is controlled the same way: by risk transformation and by holding sufficient (additional) capital.

6. Optimal dividends models

Optimal dividends models have a history reaching as far back as discounted cash flow models. The first is credited to de Finetti (1957) but work continues on them to this day. See Gerber and Shiu (2004) or Major (2007) for an overview. In contrast to the early Miller and Modigliani (1961) discounted cash flow models which assumed frictionless recapitalization, early optimal dividends models assumed that recapitalization was impossible, thus optimal retained earnings strategies were the focus of the calculation. Later optimal dividends models allowed for costly capital inflows.

Given a probability model $P\left(W_{t+d t} \mid W_t, U\right)$ for the next-period level of surplus given the current level of surplus and choice of a risk transformation alternative for the period of operation, an optimal dividends model computes the market value through a version of Equation (2.4), as in the following example specification (Major 2007):

$$\begin{array}{r} M(w)=\max _{U, C, D}\left\{-(1+\kappa) \cdot d C+d D+e^{-(r-\gamma) d t}\right. \\ \left.\cdot E\left[M\left(W_{t+d t}\right) \mid W_{t}=w, U\right]\right\}, \end{array} \tag{6.1}$$

where market value $M$ is again explicitly modeled as a function of surplus $w$, as it was in Eq. (5.2). Having a functional relationship between $M$ and $w$ means we can peg a value for the firm at the current level of surplus it happens to be holding as well as inquire as to the optimal level it should be holding. $C$ and $D$ represent cumulative (nondecreasing) shareholder capital inflows and outflows, respectively (so $d C$ is an instantaneous inflow and $d D$ is an instantaneous outflow), $\boldsymbol{\kappa}$ is a cost load for external capital, and expectation is taken with respect to the conditional distribution $P$. Note the external cost load $\kappa$ is unrelated to the hurdle rate $r$—it represents the total of transaction costs [typically $3 \%$ to $5 \%$ (Butler, Grullon, and Weston 2002)] as well as dilution effects [which can easily exceed 20% (Insider Quarterly 2009)] arising from a seasoned equity issue. If information or reasonable assumptions support it, $\boldsymbol{\kappa}$ too could be made a function of $W$ and $U$.

Equation (6.1) is recognizable as an instance of a Bellman equation (Bellman 1954) in the theory of stochastic control. Analytically tractable models are typically solved by converting this to its first derivative form, the Hamilton-Jacobi-Bellman equation (Yong and Zhou 1999). Numerical methods (necessary for the empirical CDFs generated by stochastic financial simulation models) typically involve relaxation techniques similar to those applied in solving partial differential equations (Kushner and Dupuis 2001).

Because the usual stochastic financial simulation model is parameterized around a specific level of surplus (i.e., today’s), a number of downstream adjustments need to be made to properly represent the conditional distribution. These include adding investment income on marginal surplus and subtracting retained earnings to support surplus growth (both seen before) as well as an explicit dependence of profitability on the level of surplus. This profitability adjustment reflects customer risk aversion (Wakker, Thaler, and Tversky 1997) and is most simply implemented by a location shift in the distribution (“premium haircut”).

7. An example

In this section, a simple example is worked out in detail. Its purpose is to clarify the calculations and not to be representative of a realistic application of the valuation procedures.

Say the firm’s stochastic financial simulation results show its net income for the next year follows the baseline probability distribution given in Table 1; it has the opportunity to effect a risk transformation, also given in Table 1. Also assume no growth (γ = 0), distress coincides with bankruptcy (W_C = 0), no return on marginal surplus (ι = 0), a hurdle rate of r = 8.5%, and initial surplus of W₀ = 116.67. The initial surplus is chosen to meet an economic capital criterion described in Section 7.2.

7.1. Actuarial appraisal/valuation

The baseline expected cash flow is (-200)(0.012) + (-100)(0.138) + (0)(0.2) + (100)(0.65) = 48.8 and the value is 48.8/0.085 = 574.118. The corresponding expected cash flow if the transformation is effected is 46.91 and value is 551.882. The net change in value is 551.882 - 574.118 = -22.236. Thus a naïve actuarial appraisal/valuation concludes that transforming the risk results in a loss of 22.236 in shareholder value.

7.2. Economic capital valuation

The baseline distribution corresponds to an expected policyholder deficit (EPD) of (116.67 - 200) $(0.012)=-1$. If surplus is chosen to maintain this EPD after the risk transformation, then the required surplus would be 94.667 , because $(94.667-200)$ $(0.002)+(94.667-100)(0.148)=-1$. The economic capital criterion is to compare $\Delta \mu=46.91-48.8=$ -1.89 to $r \Delta W=(0.085)(94.667-116.67)=-1.87$. Because $\Delta \mu-r \Delta W$ is negative, the risk transformation is deemed value destroying.

Equivalently, in terms of abnormal earnings valuation [Equation (4.1)], the shareholder value change upon implementing the transformation is $(-1.89 / 0.085)-(94.667-116.67)=-0.232$.

7.3. Firm life annuity valuation

The previous calculations suggest that the “intrinsic” value of the firm, over 500, is much greater than the book value of equity, 116.67, indicating a substantial franchise value. The baseline probability of bankruptcy is 0.012, whereas after the transformation it is only 0.002. The transformation should therefore have considerable value when risk to franchise value is taken into account.

The baseline put-protected expected cash flow is $(-116.67)(0.012)+(-100)(0.138)+(0)(0.2)+(100)$ $(0.65)=49.8$; after transformation it is 47.077 . Plugging these values into the Equation (5.2), the baseline firm value is $(49.8+0.012 * 116.67) /(0.085+$ $0.012)=527.835$ versus transformed value $(47.077$ $+0.002 * 116.67) /(0.085+0.002)=543.797$, an increase of 15.962 .

The firm life annuity model can also assess the consequences of capital inflows or distributions. If, as the economic capital model suggests, surplus is drawn down to 94.667 , the post-transformation expected protected cash flow is $(-94.667)(0.002)+$ $(-94.667)(0.148)+(0)(0.2289)+(100)(0.6211)=$ 47.91 and the probability of bankruptcy is 0.15 . The firm value would then be $(47.91+0.15 * 94.667)$ / $(0.085+0.15)=264.298$, a value drop of $543.793-$ $264.298=279.495$, more than twelve times the 22.003 returned to the shareholders. According to firm life annuity, optimal capital, defined as the level that maximizes franchise value, is $100+\varepsilon$ (i.e., just enough to keep the risk of insolvency to the $\Delta W=$ -200 probability) in both the baseline and transformed alternatives, so there is no release of capital indicated.

7.4. Optimal dividends valuation

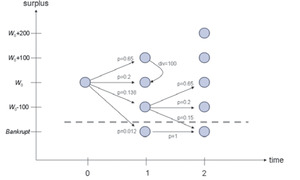
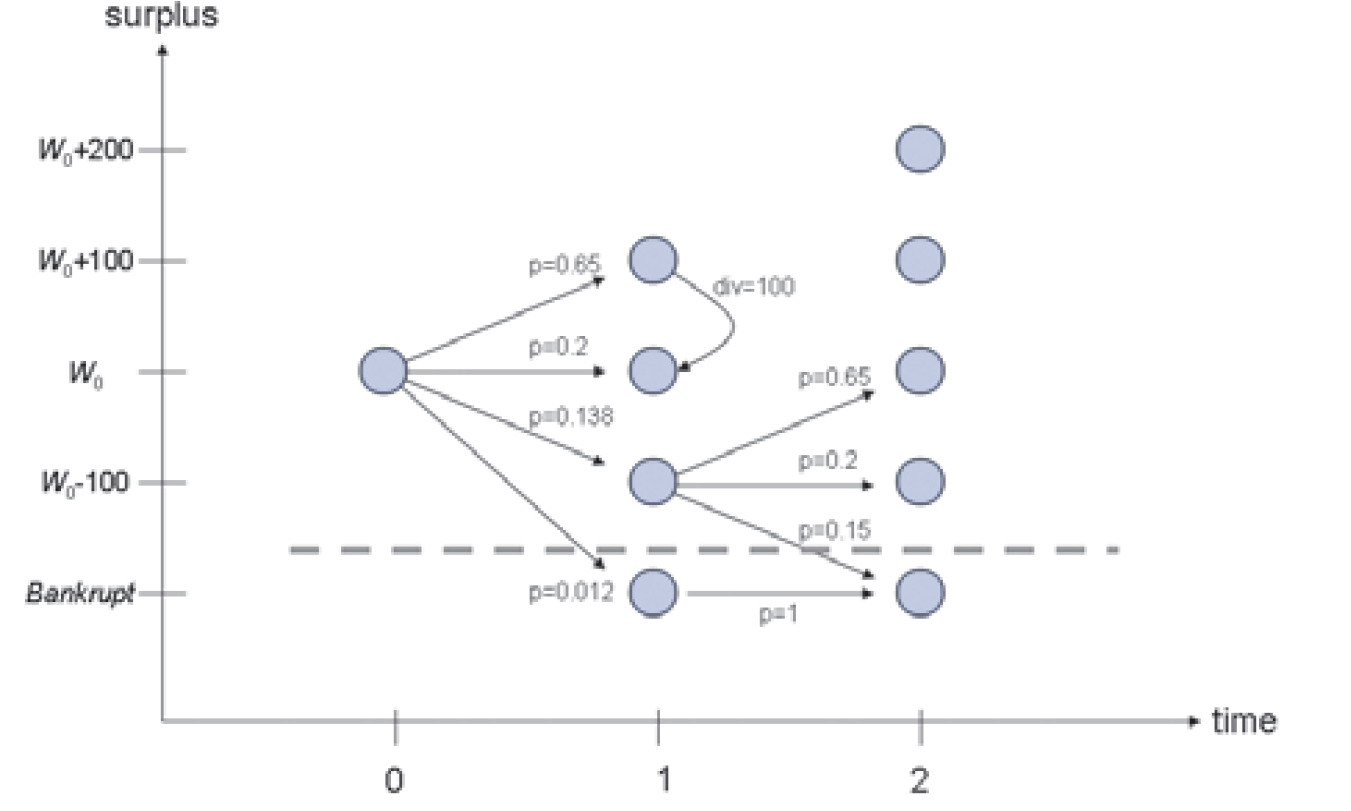
Starting at W₀ = 116.667, and barring capital inflows or distributions, future values can only vary by integer multiples of 100 due to the assumptions about the probability distribution of ΔW. To make the analysis tractable, assume inflows and outflows are similarly constrained; in a realistic example, the state space would be of much finer granularity. The random paths that surplus may take, (W₀, W₁, W₂, . . .), thus form a Markov chain (Kushner and Dupuis 2001). Specifically, they form a controlled Markov chain, because capital inflows and outflows constitute state changes that are under management control.

Transitions in the state space are illustrated in Figure 1. It shows surplus of W₀ at time t = 0 and the four possible transitions to W₁, each according to the probability given in Table 1. Say the worst occurs, ΔW = -200, and the firm goes bankrupt. No further transitions are possible. Say ΔW = -100; then the firm is at W₁ = W₀ - 100. If it chooses to stay there (no capital flows) then there are three possible future states for W₂, radiating out as shown. Note that the ΔW = -100 and ΔW = -200 produce bankruptcy, so their probabilities have been combined in Figure 1. For W₁ ≥ W₀, all four transitions are possible. The figure also illustrates an outward capital flow of 100 taking the firm from W₁ = W₀ + 100 to W₁ = W₀. Such capital flows are assumed to occur instantaneously.

Figure 1.A portion of the controlled Markov chain lattice for optimal dividends valuation

Further constrain the problem to assume that inflows are not possible. This is the extreme opposite of the actuarial appraisal/valuation assumption that costless inflows are available, even in bankruptcy. Allow two types of outflows by defining two control points or “barriers”: the target level of capital (B₁) and the runoff trigger point (B₀). The target level of capital is a barrier in that surplus is not allowed to exceed it. If a random transition from W_t leads to a state W_t+1 > B₁, then excess capital (W_t+1 - B₁) is immediately given back to the shareholders, leaving the firm in the state W_t+1 = B₁. The runoff trigger point defines when the firm goes out of business. If a random transition from W_t leads to a state 0 < W_t+1 ≤ B₀, then all capital W_t+1 is immediately given back to the shareholders, and the firm goes out of business.

Given barriers B₀ and B₁ we may define the Markov chain through its transition matrix P and its payoff vector D (dividends). Table 2 shows these for B₀ = 16.67 and B₁ = 216.67. An entry P_i,j (row i, column j) defines the probability that state i transitions to state j in the next time step. The instantaneous controlled jumps are implemented by redefining the transitions. Thus, the row corresponding to W = 16.67 has the same transition probabilities as for bankruptcy, and W = 316.67 has the same transitions as W = 216.67. The payoff vector D defines the outward flows to shareholders when a transition leads to a particular state. Thus a random jump to W = 16.67 brings with it a payoff of 16.67 to the shareholders (and going out of business, as no states with a payoff will be encountered again). A random jump to W = 316.67 brings a payoff of 100 to shareholders (and subsequent transitions that are identical to transitions from W = 216.67).

Given the payoff and transition probabilities, the value of the firm is defined recursively by a variant of Equation (6.1):

$$M\left(W_{t}\right)=D\left(W_{t}\right)+\frac{1}{1+r} \cdot E\left[M\left(W_{t+1}\right)\right] \tag{7.1}$$

With regard to the Markov chain model, M is a vector of the same size, and indexed the same way, as D. Writing in matrix-vector notation, this equation becomes

$$M=D+\frac{1}{1+r} \cdot P \cdot M \tag{7.2}$$

and its solution is

$$M=\left(I-\frac{1}{1+r} \cdot P\right)^{-1} \cdot D \tag{7.3}$$

where $I$ is the identity matrix and ()$^{-1}$ indicates matrix inversion. For the example laid out in Table 2, the solution is $M^{\prime}=(0,16.67,362.888,490.547$, 590.547).

By examining various combinations of (B₀, B₁) one can determine the optimal capital strategy. In this example, that turns out to be B₀ = bankrupt and B₁ = 116.67 in both the baseline and transformed alternatives. The transition matrices, payoff vectors, and consequent market value vectors are given in Table 3.

Optimal dividends analysis finds that maximum franchise value is also found at W = B₁ = 116.67 and that the transformed risk profile has market value 486.656 - 486.367 = 0.289 higher than the baseline.

A more sophisticated optimal dividends analysis would inquire as to which alternative—baseline or transformed—is the more appropriate at each level of surplus. The Table 3 results show that the baseline has more value at W = 16.67, whereas the transformed alternative has more value at W = 116.67, suggesting a mixed strategy. The corresponding results are shown in Table 4.

This again shows maximum franchise value at W = 116.67; firm value is 491.768 - 486.367 = 5.401 higher than the baseline. In order to guarantee that this is the optimal strategy, one would have to search over all combinations of dividend barriers and assignments of risk transformation alternatives to surplus levels.

7.5. Summary comparison

Table 5 summarizes the results of the four valuation methods.

The different valuation methods put the transformed distribution’s value anywhere from -3.9% (actuarial appraisal/valuation) to +3.0% (firm life annuity) of the baseline’s. They come to materially different conclusions; the next section discusses why that is the case.

8. Comparing model assumptions

The (naïve) actuarial appraisal/valuation approach to risk valuation can be conceptualized as describing a company that operates in the following manner:

1. A target level of surplus and risk transformation alternative are chosen initially and fixed.

2. Ensuing operations create gains or losses.

3. Gains are distributed to shareholders to reduce surplus back to the target level (which has been increased by an assumed growth rate).

4. Losses are made up by capital raised from shareholders to bring surplus back to its (growth-adjusted) target level.

5. The firm, finding itself in the same (growth adjusted) state as it started, continues again from step 2.

6. The firm never goes bankrupt.

Shareholder value is the net present value of expected earnings and franchise value is the difference between shareholder value and surplus. In such a model, risk management has no value beyond its expected impact on earnings. Unless reinsurance cover, for example, can be obtained at a price lower than actuarial expectation, it cannot add value. This is because the actuarial appraisal/valuation firm lives in a “Modigliani-Miller world” where capital flows freely, even into a bankrupt firm, to re-establish its initial position.

The abnormal earnings valuation implicit in economic capital models changes item #1 by linking the target surplus level and risk transformation through a theory of required capital. Other items are unchanged; though the firm may go bankrupt (item #6), this contingency has (exactly or approximately) the same probability across all risk transformation alternatives and so can be ignored. Here, risk management may have value if it can move the target level of surplus enough. Implicit in the economic capital method of accounting for the value of a risk transformation is the assumption that the firm value maximizing level of capital is some constant above the economic capital required level. However, this may not be the case. Unless the economic capital theory of required capital is closely aligned with a theory of firm value, its conclusions will not always serve to increase shareholder value.

The firm life annuity model keeps item #1 as it appears in the actuarial appraisal/valuation model, although the consequences of changing the target level can be assessed in a search for the optimal level. Items #2-3 are the same. In item #4, if losses are not so severe as to cause the firm to enter a distress state, they are made up from shareholders. Otherwise (item #5) the firm liquidates (contra item #6) and returns remaining surplus to the shareholders. The risk of entering the distress state is linked to the risk transformation alternative. In firm life annuity, firm mortality is a material risk, but short of that, capital flows freely to and from shareholders, Modigliani-Miller style, returning the firm to its starting state. Thus only the one-year risk of distress matters.

The optimal dividends model defines shareholder value in the same way, but differs in several other respects. Most importantly, while the firm may start out at a particular level of surplus, that level is not a target in the sense of #1. Surplus is dynamic and changes from time to time as a consequence of operations in item #2. Moreover, management controlled changes (distributions, infusions, retained earnings) contemplated in #3 and #4 are also variable, and are optimized to maximize franchise value, not set as input parameters. Risk management (item #1) is also a variable, with optimal risk transformation strategy being a mapping from surplus level W to risk transformation alternative U in such a way as to maximize value. With regard to items #5 and #6, the firm does not necessarily find itself in the same state it started, and could very well go bankrupt by small steps.

This last point explains why, in the example of Section 7, the firm life annuity valuation calculated a much higher improvement in shareholder value from the risk transformation (15.958) than did the optimal dividends valuation (0.289). The risk transformation took the one-year risk of bankruptcy (starting at original surplus) from 1.2% to 0.2%, a six-fold reduction. However, as can be verified by squaring the optimal dividends model transition matrices, the two-year risk went from 4.3% to 2.6%, only a 40% reduction. For the firm life annuity valuation, it is only the one-year risk that matters; recapitalization after the first year restores surplus to its target level. In the optimal dividends valuation example, a nonbankrupting loss in the first year puts the firm at serious risk of bankruptcy in the second year.

9. Conclusion

This paper shows how the basic principles of asset valuation could be applied to assign a value to a risk transformation. It presents four models, each differing in key assumptions, but all stemming from the arbitrage-free discounted cash flow approach. All start with the same probabilistic outputs that would be provided by a stochastic financial simulation exercise.

If a firm life annuity model is parameterized with no distress risk (λ = 0), it coincides with the traditional (naïve) actuarial appraisal/valuation model. If risk transformation alternatives are then mapped to required levels of capital, an economic capital-type valuation is obtained. It is also possible to parameterize an optimal dividends model (with variable cost of external capital) to cause it to coincide with a firm life annuity model. In this sense, the sequence Actuarial Appraisal/Valuation → Economic Capital → Firm Life Annuity → Optimal Dividends is from specific to general.

The key differences among the models are mortality and recapitalization. Mortality refers to the explicit treatment of the possibility of the firm experiencing a severe disruption (distress) or bankruptcy. Models also differ in their implied assumptions about how recapitalization works.

These two factors are interrelated because financial distress or bankruptcy are defined by inadequate surplus, and recapitalization is a method for increasing surplus. A firm with high earnings sees it reflected in an excess of market value over book value (franchise value) and so a loss of surplus leading to distress or bankruptcy causes an additional loss of franchise value—if the distress state is irreversible. To the extent that distress is reversible through recapitalization, distress is less of a concern, and efforts to avoid it (i.e., risk transformation) will therefore appear to be of lower value.

However, specific patterns of availability of recapitalization may complicate the picture. As shown in the numerical example, easy recapitalization in some financial states but not others (firm life annuity model) led to a higher value of risk transformation than did complete unavailability of recapitalization (optimal dividends model).

Acknowledgments

The author would like to thank Kenneth Froot, Anne Gron, Peter Hancock, Julian Cusack, Todd Bault, two anonymous referees, and many members of the NBER Insurance Project for their comments and stimulating discussions. Special thanks go to Don Mango, Joan Lamm-Tennant, Gary Venter, and Diane Major for their enduring support.

Appendix

Appendix A. Alternative derivation of Equation (5.1)

The recursive formulation of Equation (2.4) can be used to derive Equation (5.1) in a different way. While it is arguably not an easier derivation here, it does illustrate an alternative method that is easier in some cases, and is the basis for the derivation in Appendix B. Consider that the firm is in operation at time t. In the next short time interval Δt, if it survives catastrophe, it will have paid out μΔt to shareholders. If it fails in that interval, it will pay out something between 0 and μΔt. Failure occurs with probability λΔt (to first order). If it fails, its value at the end of the interval is 0. If it survives, its value will be $M_{t+\Delta t}$. Valuing the payout stream at its midpoint (also correct to first order), we can specialize Equation (2.4) to:

$$\begin{aligned} M_{t}=\mu \cdot \Delta t \cdot\left(1-\frac{\lambda \cdot \Delta t}{2}\right) \cdot e^{-r \frac{\Delta t}{2}} & +M_{t+\Delta t} \cdot(1-\lambda \cdot \Delta t) \cdot e^{-r \cdot \Delta t} \end{aligned} \tag{A.1}$$

Because the stochastic situation and financial assumptions the surviving firm faces at time $t+\Delta t$ are the same it faces at time $t$, it must be the case that $M_t=M_{t+\Delta t}=M$. Collecting $M$ terms, one obtains

$$\begin{align} M&=\frac{\mu \cdot \Delta t \cdot\left(1-\frac{\lambda \cdot \Delta t}{2}\right) \cdot e^{-r \frac{\Delta t}{2}}}{1-(1-\lambda \cdot \Delta t) \cdot e^{-r \cdot \Delta t}} \\ &=\frac{\mu \cdot\left(1-\frac{\lambda \cdot \Delta t}{2}\right) \cdot e^{-r \frac{\Delta t}{2}}}{\left(\frac{1-e^{-r \cdot \Delta t}}{\Delta t}\right)+\lambda \cdot e^{-r \cdot \Delta t}} \end{align} \tag{A.2}$$

and taking the limit as Δ t → 0, one obtains the same solution as in Equation (5.1).

Appendix B. Derivation of Equation (5.2)

We assume the firm starts with its desired level of surplus W and operations during the year cause a random net profit or loss in the amount of π, with probability density function f (π). Growth in scale of operations occurs at a rate γ, so the desired surplus at the beginning of the subsequent year, if operations are to continue at the same level of risk, is (1 + γ) W. Distress occurs if the sum of initial surplus and net profit falls below a critical threshold W_C; that is, distress is the event: W + π < W_C. Define λ as the probability of distress:

$$\lambda=\int_{-\infty}^{W_{C}-W} f(\pi) d \pi$$

At the beginning of the year, the value of the firm is M, the unknown for which we want to solve. At the end of the year, the payoff to shareholders is the sum of the net cash flow to them plus the value of the firm at the end of the year. The fundamental valuation principle is

$$M=\frac{1}{1+r} E[\text { Payoff }] \tag{B.1}$$

where $r$ is an exogenously given discount rate.

If distress does not occur, the cash flow to shareholders is the free cash flow to equity consisting of the net profit less a provision to bring surplus up to the desired level: π - γW. The value of the firm is (1 + γ) M because, adjusting for growth, the same stochastic environment and same initial conditions confront the firm and the investors. This payoff, the sum of cash flows and value, occurs with probability (1 - λ).

If distress does occur, the cash flow to investors is the remaining surplus (if any), max(0, W + π) and the firm value is zero. This occurs with probability λ.

Expanding Equation (B.1) with these particulars, we get

$$\begin{array}{l} M=\frac{1}{1+r} \\ \left(\begin{array}{l} (1-\lambda) \cdot\left\{E\left[\pi-\gamma \cdot W \mid \pi \geq W_{C}-W\right]+(1+\gamma) \cdot M\right\} \\ +\lambda \cdot E\left[\max (0, W+\pi) \mid \pi<W_{C}-W\right] \end{array}\right) \end{array} \tag{B.2}$$

Collecting M terms, noting that max(A, B) = A + max(0, B - A), and rearranging, we get

$$\begin{array}{l} (r-\gamma+\lambda+\lambda \cdot \gamma) \cdot M \\ =\left(\begin{array}{l} (1-\lambda) \cdot E\left[\pi \mid \pi \geq W_{C}-W\right]-((1-\lambda) \cdot \gamma-\lambda) \cdot W \\ +\lambda \cdot E\left[\max (-W, \pi) \mid \pi<W_{C}-W\right] \end{array}\right) \end{array} \tag{B.3}$$

Letting Г = (1 λ)γ - λ, moving the W term to the left-hand side, and rewriting expectations as integrals, we get

$$\begin{aligned} &(r-\Gamma) \cdot M+\Gamma \cdot W & \\ & \quad= \int_{W_{c}-W}^{\infty} \pi \cdot f(\pi) d \pi+\int_{-\infty}^{W_{C}-W} \max (-W, \pi) \cdot f(\pi) d \pi \\ & \quad= \int_{W_{c}-W}^{\infty} \pi \cdot f(\pi) d \pi+\int_{-\infty}^{-W}(-W) \cdot f(\pi) d \pi \\ & \qquad+\int_{-W}^{W_{c}-W} \pi \cdot f(\pi) d \pi \\ &\quad = \int_{-W}^{\infty} \pi \cdot f(\pi) d \pi+\int_{-\infty}^{-W}(-W) \cdot f(\pi) d \pi \\ &\quad = \int_{-\infty}^{\infty} \max (-W, \pi) \cdot f(\pi) d \pi=E[\max (-W, \pi)] \end{aligned} \tag{B.4}$$

Finally,

$$M=\frac{E[\max (-W, \pi)]-\Gamma \cdot W}{r-\Gamma} \tag{B.5}$$