Multi-Peril Frequency Credibility Premium via Shared Random Effects

1. Introduction

Usually, an auto insurance policy consists of various types of coverage against claims, such as collision, bodily injury liability, or property damage liability. Upon the presence of available covariates, their impacts for each type of claim could be different so that one needs to apply different regression coefficients for each claim type. Besides, it is natural to expect that various types of claims have different correlations with the unobserved heterogeneity in risk, such as driving habits. For example, an at-fault liability claim is usually at the control of a driver, so that the occurrence of such a claim is strongly related with driving habits. However, glass damage claims (for example, due to a heavy hail storm) are almost out of the driver’s control, so that association with driving habits is quite low. In the end, a company needs to develop a predictive model that utilizes the covariate information to calculate a presumptive premium as well as the unobserved heterogeneity in risks, which can be indirectly captured by past claims history of each policyholder.

The idea of capturing the unobserved heterogeneity via past claims history has been discussed under the name of credibility theory. Bailey (1950) and Bühlmann (1967) suggested the credibility procedure, which usually arrives at the following formula:

$$\begin{align} \text{Posterior premium} &= Z \times \text{Claim experience} \\ &\quad + (1-Z) \times \text{Prior premium}, \end{align}$$

where $Z$ is the so-called credibility weight. Since then, credibility theory has been developed and explored in the actuarial science literature. For example, Mayerson (1964) and Jewell (1974) analyzed credibility theory from a Bayesian perspective. While these researchers working on credibility theory provided a way to incorporate the unobservable heterogeneity, both the observed and unobserved heterogeneities need to be addressed in actuarial ratemaking practice, as shown in Norberg (1986). In this regard, Frees, Young, and Luo (1999) provided a general framework that integrated well-known credibility theory and regression analysis based on the use of linear mixed models. The linear mixed model is an extension of the linear model, whereby the response variable is affected by both the observed covariates via associated regression coefficients (fixed effects) and unobserved quantities (random effects). Upon the use of both fixed and random effects with a mixed model, it is noteworthy that credibility premiums have a close connection with bonus-malus systems, which reward or penalize a policyholder based on past claims history. Frangos and Vrontos (2001) showed that, upon the presence of fixed effects, credibility premium (or posterior premium) for claim takes the following form:

$$\begin{align} \text{Posterior premium} &= \frac{r+\text{Actual claim experience}}{r+\text{Expected claim experience}} \\ &\quad \times \text{Prior premium}, \end{align}$$

where $r$ denotes a smoothing factor in the bonus-malus system so that larger values of $r$ put less weight on past claims history. Similar results have been shown in the recent literature such as Jeong (2020) and Jeong and Valdez (2020a). Boucher and Denuit (2008) and Boucher, Denuit, and Guillen (2009) considered the use of a zero-inflated Poisson distribution in panel data to derive credibility premiums.

However, one should also consider possible dependence among the claims from either multiple lines of business or multiple coverages, in order to apply to ratemaking practices. Frees, Meyers, and Cummings (2010) proposed dependence modeling for multi-peril insurance under the individual risk model, which decomposes the compound loss into occurrence (a binary response whether there is a claim or not) and total amounts given a claim. To model dependence among the occurrence of claims in multiple coverages, they utilized multivariate binary regression via Gaussian copulas. On the other hand, Frees, Lee, and Yang (2016) proposed dependence modeling for multi-peril insurance under the collective risk model, which decomposes the compound loss into claim frequency and severity components. They applied copulas to describe possible dependence among the multivariate frequencies and severities, respectively. Andrade e Silva and Centeno (2017) suggested using various generalized bivariate frequency distributions to capture multi-peril dependence, which also allow capturing possible overdispersion in the observed claim counts. Quan and Valdez (2018) proposed the use of a multivariate decision tree in multi-peril claim amounts regression.

Interestingly, there are only a few research papers that incorporated such multi-peril dependence and longitudinal property simultaneously. For example, Frees (2003) proposed a way to calculate credibility premium of compound loss for multi-peril policy by specifying only the mean and covariance structures of claim frequencies and severities. While Frees took a non-parametric approach, Bermúdez and Karlis (2015) applied bivariate Poisson distributions for a posteriori ratemaking of two types of claims. However, these papers are limited to non-parametric or parametric setting without covariates, so that it is hard to incorporate both the observed and unobserved heterogeneities of a policyholder simultaneously with their models. Abdallah, Boucher, and Cossette (2016) provided a sophisticated approach to utilizing a bivariate Sarmanov distribution to account for the dependence between two lines of business with time weight for past claims, which is appropriate to deal with two types of claims but difficult to extend to the case where there are more than two types of claims. Recently, Pechon et al. (2018; 2019, 2020) proposed credibility premium formulas with multiple types of claims using correlated lognormal random effects. Although they provided a comprehensive framework that considers possible dependence among multi-peril claims in a longitudinal setting, their method requires high-dimensional integration (six or seven) in order to obtain credibility factors and marginal frequency distributions for every single policyholder, which may be burdensome in practice where the number of policyholders is usually large.

A novel method is proposed in this article that enables us to consider both the observed and unobserved heterogeneities of a policyholder in a longitudinal setting for multi-peril insurance via shared random effects. The proposed method can handle more than two types of claims and leads to a readily available closed-form formula for multi-peril credibility premiums. In short, the shared random effect for a policyholder is a latent variable that cannot be observed but affects the claims from multiple perils over time and induces a natural dependence structure among the claims. This article is organized as follows. In Section 2, the proposed method—a shared random effects model for multi-peril frequency—is specified in detail, and important characteristics of the model are provided including the multi-peril credibility premium formula. In Section 3, an empirical data analysis is conducted using a data set provided by the Wisconsin Local Government Property Insurance Fund (LGPIF). We conclude this article in Section 4 with some remarks and possible directions for future work.

2. Methodology

Let us consider a usual data structure for multi-peril frequency. For an insurance policy of $i^{th}$ policyholder where $i=1, 2, \ldots, I$, we may observe the multi-peril claim frequencies over time $t=1,2,\ldots, T$ for $j=1,\ldots, J$ types of coverage as follows:

$$\scriptsize{ \mathcal{D} = \left\{ \left(N^{(1)}_{it}, \, \ldots, N^{(j)}_{it}, \ldots, N^{(J)}_{it}, \mathbf{x}_{it} \right) \bigg| \, i=1, \ldots, I, \, t=1, \ldots, T \right\}, } \tag{2.1}$$

where $\mathbf{x}_{it}$ is a $p$-dimensional vector that captures the observable characteristics of the policy and $N_{it}^{(j)}$ is defined as the number of accident(s) from claim type $j\in \{1,2,\ldots, J\}$, for the $i^{th}$ policyholder in year $t$, respectively.

Based on the data structure, one can consider the following issues for multi-peril frequency modeling. Although the Poisson distribution is widely used for modeling frequency, it is often questionable whether it is valid due to possible overdispersion. In order to handle this issue, according to Wedderburn (1974), one can use a quasi-Poisson distribution to capture overdispersion in the observed data as follows:

$$N \sim \mathcal{QP}(\nu, w) \Longleftrightarrow wN \sim \mathcal{P}(w\nu),$$

for which ${\mathbb E}\left[N\right]=\nu$ and ${\mathrm{Var}}\left[N\right]=\nu/w$. Here $X \sim \mathcal{P}(\lambda)$ means $X$ follows a Poisson distribution with mean $\lambda$. In that regard, the Poisson distribution is a special case of the quasi-Poisson distribution where $w=1$. Due to this nested property, some research results enable to test

$$H_0: w=1 \text{ versus } H_1: w \ne 1.$$

For details, see Cameron and Trivedi (1990).

Secondly, recall that the data structure described in (2.1) has longitudinality, or repeated measurements of the same policyholder over time. Thus, it is natural to incorporate random effects, which may account for unobserved heterogeneity in risks of each policyholder. The following hypothetical example in Table 1 shows that one can capture the unobserved heterogeneity in risks by observing the residuals, after controlling for the effect of the observed covariates. The latter can be explained in terms of random effects for policyholders A and B. In Table 1, it is possible to observe that both policyholders have the same observable characteristics, whereas they exhibit quite different past claims experiences. In such a case, one may suspect that the observed covariates might not be sufficient to fully explain the heterogeneity in risks. Random effects can help capture such (unobserved) heterogeneity for both types of claims.

As we can see, the random effects model has connections with credibility theory and bonus-malus systems as well. Some papers have incorporated random effects in a ratemaking perspective, including but not limited to Gómez-Déniz and Vázquez-Polo (2005) and Jeong and Valdez (2020b).

Based on the observations from Table 1, let us assume that the number of claims is affected by both observable covariates via associated regression coefficients and the (common) unobserved heterogeneity factor $\theta_i$. It is shared for all types of coverages and every year of claims of policyholder $i$ as follows:

$$\scriptsize{ \begin{aligned} & N^{(j)}_{it}|\mathbf{x}_{it}, e_{it}, \theta_i \overset{indep}{\sim} \mathcal{QP}(\theta_i \nu^{(j)}_{it}, w^{(j)}) \\ &\quad \Longleftrightarrow \ w^{(j)} N^{(j)}_{it}|\mathbf{x}_{it}, e_{it}, \theta_i \overset{indep}{\sim} \mathcal{P}(\theta_i w^{(j)}\nu^{(j)}_{it}) \text{ and } {\mathbb E}\left[\theta_i\right]=1, \end{aligned} } \tag{2.2}$$

where $\nu^{(j)}_{it}=e_{it}\exp(\mathbf{x}_{it}\alpha^{(j)})$, $e_{it} \in (0,1]$ is the exposure, and $w^{(j)}$ is the (unknown) weight for each $j^{th}$ line of business or type of coverage. Here $\nu^{(j)}_{it}$ accounts for the observed heterogeneity in risks of policyholder $i$ at time $t$ for coverage $j$, while multiplicative random effect $\theta_i$ accounts for the unobserved heterogeneity in risks of policyholder $i$. One can also find a very comprehensive setup of the Poisson model with a shared random effect in Shi and Valdez (2014a), which is helpful to understand the proposed setup of the quasi-Poisson model with a shared random effect. Though $N$ does not necessarily have integer-valued quantities with quasi-Poisson distribution, the proposed framework allows for obtaining the posterior distribution of $wN$. Subsequently, distributional quantities of $N$ are easy to derive with the distribution, which are our main interest.

With the specification above, it is straightforward to derive that

$${\mathbb E}\left[w^{(j)} N_{it}^{(j)} | \theta_i \right]=w^{(j)}\nu_{it}^{(j)} \theta_i \text{ and } {\mathbb E}\left[N_{it}^{(j)} \right]=\nu_{it}^{(j)},$$

since ${\mathbb E}\left[\theta_i\right]=1$. Therefore, $\nu_{it}^{(j)}$ can be interpreted as a prior mean of the number of claims at time $t$, for policyholder $i$, without any information on her/his unobserved heterogeneity. For notational convenience, we suppress the subscript $i$ from now on when there is no confusion. Figure 1 provides a graphical description of the proposed model specified in (2.2). Although we assume that the common random effect affects multiple types of peril simultaneously, we also allow $w^{(j)}$ to vary so that the impacts of $\theta$ to $(N^{(1)}, \ldots, N^{(J)})$ are not necessarily identical.

Figure 1.Graphical description of the shared random effects model for multi-peril frequency

Note that the use of shared random effects is not the only way to capture possible dependence among multi-peril claims in a longitudinal setting. For example, one can utilize copulas to capture such dependence. For details, see Yang and Shi (2018).

The impact of the unobserved heterogeneity on the claim frequency is inherently unknown. Therefore, it needs to be described with a specified prior distribution. In a Bayesian analysis, it is usually recommended to use a noninformative prior or less informative prior on $\theta$ unless we have enough knowledge on the dynamics of the random parameter. In this sense, one can suggest to use Jeffreys’ prior, perhaps the most widely used noninformative prior in Bayesian analyses. According to Jeffreys (1946), Jeffreys’ prior is defined as the square root of the determinant of the Fisher information matrix. One can see that under the model specification in (2.2), Jeffreys’ prior of $\theta$ is given as $\theta^{-1/2}$ and the corresponding posterior distribution is proportional to $\theta^{N-1/2} \exp(-\nu\theta)$ so that $\theta|N \sim \mathcal{G}(N+0.5,\, \nu^{-1})$. Here $X \sim \mathcal{G}(\alpha, \lambda)$ means $X$ follows a gamma distribution with mean $\alpha\lambda$ and variance $\alpha\lambda^2$.

The corresponding posterior is proper although Jeffreys’ prior itself is improper. Nevertheless, there is an identifiability issue, unless we impose a condition on the mean of the random effects. For example, it is customary to set ${\mathbb E}\left[\theta\right]=0$ when $\theta$ is an additive random effect. Likewise, since $\theta$ is a multiplicative random effect in our specified model, we need to impose that ${\mathbb E}\left[\theta\right] = 1$. Therefore, in order to satisfy the identifiability condition as well as have a similar posterior as in the case of Jeffreys’ prior, one can propose the following prior on $\theta$:

$$\begin{aligned} &\pi(\theta) \propto \theta^{r-1}e^{-\theta r} \\ &\quad \text{ so that } \theta \sim \mathcal{G}(r,1/r) \\ &\quad \text{ and } {\mathbb E}\left[\theta\right]=1,{\mathrm{Var}}\left[\theta\right]=\frac{1}{r}. \end{aligned} \tag{2.3}$$

Here $\pi(\theta)$ is the so-called conjugate prior. This choice is not ad hoc but from the argument of prior elicitation, considering both informativeness of the prior and identifiability of the fixed effects. Based on the model specification in (2.2) and (2.3), it follows that

$$\small{ {\mathbb E}\left[N^{(j)}_{t}\right]=\nu^{(j)}_{t} \text{ and } {\mathrm{Var}}\left[N^{(j)}_{t}\right]=\nu^{(j)}_{t}/w^{(j)} + (\nu^{(j)}_{t})^2 /r, } \tag{2.4}$$

since $w^{(j)} N^{(j)}_{t} \sim \mathcal{NB}\left(r, \frac{w^{(j)}_t \nu^{(j)}_{t}}{r+ w^{(j)}_t \nu^{(j)}_{t}}\right)$ from Theorem 1. Here $X \sim \mathcal{NB}(r, p)$ means $X$ follows a negative binomial distribution with mean $\frac{pr}{1-p}$ and variance $\frac{pr}{(1-p)^2}$.

It is also shown that

$$\small{ \begin{aligned} {\mathrm{Cov}}\left(N^{(j)}_{t}, N^{(k)}_{t'}\right)&={\mathbb E}\left[{\mathrm{Cov}}\left(N^{(j)}_{t}, N^{(k)}_{t'}\bigg|\theta\right)\right]\\ &\quad +{\mathrm{Cov}}\left({\mathbb E}\left[N^{(j)}_{t}\bigg|\theta\right], {\mathbb E}\left[N^{(k)}_{t'}\bigg|\theta\right]\right) \\ &={\mathrm{Cov}}\left(\nu^{(j)}_{t}\theta, \nu^{(k)}_{t'}\theta\right)=\nu^{(j)}_{t}\nu^{(k)}_{t'}/r, \\ {\mathrm{Corr}}\left(N^{(j)}_{t}, N^{(k)}_{t'}\right)&=\frac{{\mathrm{Cov}}\left(N^{(j)}_{t}, N^{(k)}_{t'}\right)}{{\mathrm{Var}}\left[N^{(j)}_{t}\right]{\mathrm{Var}}\left[N^{(k)}_{t'}\right]}\\ &=\dfrac{1}{ \sqrt{1+r/w^{(j)}\nu^{(j)}_{t}} \sqrt{1+r/w^{(k)}\nu^{(k)}_{t'}}}, \end{aligned} \tag{2.5} }$$

for $t,t' = 1,\ldots, T$ and $j,k=1,\ldots, J$ due to conditional independence of $N^{(j)}_{t}$ and $N^{(k)}_{t'}$ given $\theta$. Therefore, the proposed model induces a natural dependence structure among the frequencies of the multiple insurance coverages over time. For example, if $r \rightarrow \infty$, then the proposed model is reduced to an independent quasi-Poisson model. Further, if $r \rightarrow \infty$ and $w^{(j)}=1$ for all $j=1, \ldots, J$, then the proposed model is reduced to an independent Poisson model.

Since ${\mathbb E}\left[N^{(j)}_{t}|\theta\right]=\theta\nu^{(j)}_{t}$, the multiplicative random effect $\theta$ can be understood as a bonus-malus factor on top of $\nu^{(j)}_{t}$ for determination of insurance premium. The value of hyperparameter $r$ can be determined by using either prior knowledge or the method of moments. For example, from $54\%$ to $200\%$ was once a common range of bonus-malus factors for the frequency premium according to Lemaire (1998). Therefore, one can incorporate this idea on choosing the hyperparameter $r$ for our proposed prior so that the $95\%$ highest posterior density (HPD) interval of $\theta$ can include $(0.54,2.00)$. One can also consistently estimate $r$ since the expectation of $\displaystyle\sum_{t \ne t', j \ne k} (N^{(j)}_{it} - \nu^{(j)}_{it})(N^{(k)}_{it'} - \nu^{(k)}_{it'})$ is $\dfrac{1}{r}\displaystyle\sum_{t \ne t', j \ne k} \nu^{(j)}_{it}\nu^{(k)}_{it'}$ for $i=1,\ldots, I$ (Sutradhar and Jowaheer 2003) so that

$$\hat{r} = \dfrac{\sum_{i=1}^I \sum_{t \ne t', j \ne k} \hat{\nu}^{(j)}_{it}\hat{\nu}^{(k)}_{it'}}{\sum_{i=1}^I \sum_{t \ne t', j \ne k} (N^{(j)}_{it} - \hat{\nu}^{(j)}_{it})(N^{(k)}_{it'} - \hat{\nu}^{(k)}_{it'})}, \tag{2.6}$$

where $\hat{\nu}$ is consistently estimated by solving generalized estimating equations (GEE) with a pre-specified mean structure (Liang and Zeger 1986; Purcaru, Guillén, and Denuit 2004; Denuit et al. 2007). According to this specification, one can easily observe that posterior density for $\theta$ as follows:

Lemma 1. Based on the model specification described in (2.2) and (2.3), we have

$$\small{ \theta|\mathbf{n}_T^{(1)},\ldots,\mathbf{n}_T^{(J)} \sim \mathcal{G}\left( \sum_{j=1}^J\sum_{t=1}^T w^{(j)}n^{(j)}_t +r ,\, \frac{1}{\sum_{j=1}^J \sum_{t=1}^T w^{(j)}\nu^{(j)}_t +r} \right), }$$

where $\mathbf{n}_T^{(j)}=(n_1^{(j)},\ldots,n_T^{(j)})$.

Proof. It is easy to show that

$$\scriptsize{ \begin{aligned} \pi(\theta|\mathbf{n}_T^{(1)},\ldots,\mathbf{n}_T^{(J)}) & \propto \pi(\theta) \prod_{j=1}^J \prod_{t=1}^T p(w^{(j)}n^{(j)}_t|\theta) \\ &\propto \theta^{r-1}e^{-\theta r} \prod_{j=1}^J\prod_{t=1}^T \theta^{w^{(j)}n_t} e^{-\nu^{(j)}_t\theta} \\ & = \theta^{ \sum_{j=1}^J\sum_{t=1}^T w^{(j)}n^{(j)}_t +r-1} \exp\left( -\theta \left(\sum_{j=1}^J\sum_{t=1}^T w^{(j)}\nu^{(j)}_t +r\right) \right), \end{aligned} }$$

which leads to

$$\scriptsize{ \theta|\mathbf{n}_T^{(1)},\ldots,\mathbf{n}_T^{(J)} \sim \mathcal{G}\left( \sum_{j=1}^J\sum_{t=1}^T w^{(j)}n^{(j)}_t +r ,\, \frac{1}{\sum_{j=1}^J \sum_{t=1}^T w^{(j)}\nu^{(j)}_t +r} \right). }$$

□

Further, it is not difficult to show that the predictive distribution of $N_{T+1}$ given $\mathbf{n}_T^{(1)},\ldots,\mathbf{n}_T^{(J)}$ follows a negative binomial distribution as follows:

Theorem 1. Suppose that $(w^{(1)}\mathbf{n}_T^{(1)},\ldots,w^{(J)}\mathbf{n}_T^{(J)})$ and $(w^{(j)}N^{(j)}_{T+1})$ follow the model specified in (2.2) and (2.3). Then we have

$$w^{(j)}N_{T+1}^{(j)} | \mathbf{n}_T^{(1)},\ldots,\mathbf{n}_T^{(J)} \sim \mathcal{NB}\left(r_T, \, \frac{ w^{(j)}\nu_{T+1}^{(j)} }{\tilde{r}_T+ w^{(j)}\nu_{T+1}^{(j)} }\right),$$

where $r_T=r + \sum_{j=1}^{J}\sum_{t=1}^T w^{(j)}n_t^{(j)}$, $\hat{r}_T=r + \sum_{j=1}^{J}\sum_{t=1}^T w^{(j)}\nu_t^{(j)}$, and

$$\scriptsize{ {\mathbb E}\left[N_{T+1}^{(j)} | \mathbf{n}_T^{(1)},\ldots,\mathbf{n}_T^{(J)}\right]=\frac{r + \sum_{j=1}^{J} (w^{(j)}\sum_{t=1}^T n_t^{(j)})}{r + \sum_{j=1}^{J} (w^{(j)}\sum_{t=1}^T \nu_t^{(j)})}\nu_{T+1}^{(j)}. \tag{2.7} }$$

Proof. It is sufficient to show that if $N|\theta \sim \mathcal{P}(\nu \theta)$ and $\theta \sim \mathcal{G}(r, 1/\beta)$, then

$$\begin{aligned} p(n)&=\int_0^\infty p(n|\theta)\pi(\theta)d\theta \\ &=\int_0^\infty \lambda^n \frac{\theta^n}{n!}e^{-\theta \lambda} \frac{\beta^r\theta^{r-1}}{\Gamma(r)} e^{-\theta\beta} \\ &=\frac{\nu^n\beta^r}{n!\Gamma(r)}\int_0^\infty \theta^{n+r-1} e^{-\theta(\beta+\nu)} \\ &=\frac{\nu^n\beta^r}{n!\Gamma(r)} \frac{\Gamma(n+r)}{(\beta+\nu)^{n+r}}\\ &=\frac{\Gamma(n+r)}{n!\Gamma(r)} \left(\frac{\nu}{\beta+\nu} \right)^n \left(\frac{\beta}{\beta+\nu}\right)^r, \end{aligned}$$

so that $N \sim \mathcal{NB} \left( r,\frac{\nu}{\beta+\nu} \right)$ and ${\mathbb E}\left[N\right]=\frac{r\nu}{\beta}$.

□

Therefore, the predictive premium of $N_{T+1}^{(j)}$, with the previous $T$ years’ information, is given in the form of a product of a prior premium that depends on regression coefficients associated with observable covariates, and with a pooled estimate of the credibility factor, which accounts for the unobserved (shared) heterogeneity on the claim frequency of a specific policyholder. Note that (2.7) is a natural extension of Frangos and Vrontos (2001), whereby $J=1$ and $w^{(1)}=1$. For example, if $J=2$, and $N^{(1)}$, $N^{(2)}$ denote the claim frequencies due to at-fault liability and glass damage, respectively, then the pooled estimate of unobserved heterogeneity is given as

$$\scriptsize{ \begin{aligned} &\mathbb{E}\left[\theta \mid \mathbf{n}_T^{(1)}, \mathbf{n}_T^{(2)}\right] \\&\quad =\frac{r+w^{(1)} \sum_{t=1}^T n_t^{(1)}+w^{(2)} \sum_{t=1}^T n_t^{(2)}}{r+w^{(1)} \sum_{t=1}^T \nu_t^{(1)}+w^{(2)} \sum_{t=1}^T \nu_t^{(2)}} \\ &\quad =\frac{\text { smoothing factor }+ \text { weighted sum of actual frequencies }}{\text { smoothing factor }+ \text { weighted sum of expected frequencies }} . \end{aligned} \tag{2.8} }$$

Therefore, the proposed model specification enables us to consider different levels of contribution to the credibility factor, ${\mathbb E}\left[\theta | \mathbf{n}_T^{(1)}, \ldots, \mathbf{n}_T^{(J)} \right]$, by allowing varying dispersions $w^{(j)}$ for multiple perils.

In (2.8), $r$, the hyperparameter of the prior distribution of $\theta$, is working as a smoothing factor. For example, if $r \rightarrow \infty$, then $\pi(\theta|\mathbf{n})$ converges to a Dirac delta function at 1, which implies that $\mathbb{P}(\theta=1)=1$ and ends up with a very informative point-mass prior. On the other hand, any choice of a smaller $r$ leads to use of a less informative prior.

In light of the empirical Bayes method, the estimation of parameters $\alpha^{(j)}$ for $j=1,2,\ldots, J$ can be done by maximizing the following joint loglikelihood:

$$\begin{align} &\ell\left(\alpha^{(1)}, \ldots, \alpha^{(J)} \mid \mathbf{n}_T^{(1)}, \ldots, \mathbf{n}_T^{(J)}\right)\\ &\quad =\sum_{i=1}^M \ln p\left(w^{(1)} \mathbf{n}_{i T}^{(1)}, \ldots, w^{(J)} \mathbf{n}_{i T}^{(J)}\right), \end{align} \tag{2.9}$$

where

$$\small{ \begin{aligned} &p(w^{(1)}\mathbf{n}_{iT}^{(1)},\ldots, w^{(J)}\mathbf{n}_{iT}^{(J)}) \\ &\quad =\int \prod\limits_{j=1}^{J} \prod\limits_{t=1}^{T} p(w^{(j)}n_{it}^{(j)}|\theta_i) \pi(\theta_i) d\theta_i \\ &\quad \propto \prod\limits_{j=1}^{J}\prod\limits_{t=1}^{T} \Biggl\lbrack \left( \frac{w^{(j)}\nu^{(j)}_{it} }{\sum_{j=1}^{J}\sum_{t=1}^{T} w^{(j)}\nu^{(j)}_{it} +r} \right)^{w^{(j)}n^{(j)}_{it}} \\ & \quad \quad \quad \quad \quad \times \left( \frac{r}{\sum_{j=1}^{J}\sum_{t=1}^{T} w^{(j)}\nu^{(j)}_{it}+r} \right)^r \Biggr\rbrack, \end{aligned} \tag{2.10} }$$

which follows a multivariate negative binomial (MVNB) distribution indeed.

3. Data Analysis

In this article, we use a public data set of insurance claims that has been provided by the Wisconsin Local Government Property Insurance Fund (LGPIF). The data set consists of six years of observations, from 2006 to 2011. We used a training set of 5,677 observations from 2006 to 2010 and a test set of 1,098 observations from 2011. Since there is a unique identifier that allows tracking of the claims of a policyholder over time, it is indeed longitudinal data. Furthermore, the data set contains the claims information for multiple lines of business so that one can try multivariate longitudinal frequency modeling. Here, information on inland marine claims (IM), collision claims from new vehicles (CN), and comprehensive claims from new vehicles (PN) is used with six categorical and four continuous explanatory variables. Table 2 provides a detailed summary of the observable policy characteristics of all lines of insurance business. Note that all of the categorical variables, which are dummy variables for location types, are commonly used for all types of coverage, but their impact is not necessarily identical.

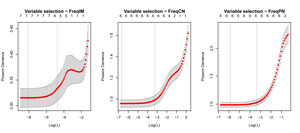
Before the fixed effects are incorporated in the marginal models of the coverages, a variable selection was performed by using penalized Poisson likelihood with elastic net, which considers both $L_1$ and $L_2$ penalties. Since the location parameters are correlated with each other, it is desirable to consider $L_2$ penalty for performing variable selection group-wise on top of $L_1$ penalty. The variable selection was implemented using glmnet (Friedman et al. 2021) by setting $\alpha = 0.5$ so that weights on $L_1$ and $L_2$ penalties are equal. As shown in Figure 2, it turns out that the validation errors measured by Poisson deviances are minimized with no variable selection in all three coverages. Therefore, all the available covariates were used for the calibration of marginal models eventually.

Figure 2.Variable selection via elastic net

Since the proposed model specified in (2.2) and (2.3) assumes the presence of both overdispersion and association among the numbers of claims from multiple coverages, one needs to investigate their effect in order to validate the application of more complicated models than the naive independent Poisson model. Table 3 shows the frequency tables for the number of IM, CN, and PN claims. By applying the usual measures to investigate the association between each pair of categorical responses, summarized in Table 4, one can observe that there are significant positive associations among the numbers of IM, CN, and PN claims, at least without controlling the possible impacts of common covariates. Note that these measures need to be used with precautions since they may not be appropriate for insurance claim counts with excessive zeros, due to possible ties in ranking. For discussions on effects of ties on the rank-based correlation, see Kendall (1945).

There has been some research on ways to estimate the dispersion parameter in a quasi-Poisson distribution. For example, McCullagh and Nelder (1989) proposed $\hat{\phi}= \dfrac{1}{m-p} \displaystyle \sum_{k=1}^m \dfrac{ (n_k - \hat{\nu}_k)^2 }{\hat{\nu}_k}$, while Cameron and Trivedi (1990) proposed $\tilde{\phi}= \dfrac{1}{m}\displaystyle\sum_{k=1}^m \tilde{R}_k$ where $\tilde{R}_k = \dfrac{(n_k - \hat{\nu}_k)^2-n_k}{ \hat{\nu}_k}$, $\hat{\nu}_k$ is expected value of $k^{th}$ frequency response depending on the estimated parameter(s) from the calibrated model, $p$ is the number of estimated parameter(s), and $m$ is the number of total observations. According to Table 5, for all types of coverages, we can observe that dispersion parameters are estimated to be quite above one. (Remember that the dispersion parameter should equal one under the Poisson assumption.)

Cameron and Trivedi (1990) also showed that

$$\tilde{Z} = \frac{\tilde{\phi}}{\sqrt{\frac{1}{n}\sum_{k=1}^m (\tilde{R}_k-\tilde{\phi})^2 }} \simeq \mathcal{N}(0,1) \text{ under } H_0: \phi=1,$$

when $m$ is large enough and $n_k$, for $k=1, \ldots, m$, are independent. For the given data, the values of $\hat{Z}$ for IM, CN, and PN claims are 2.7844, 4.1829, and 3.8956, respectively. Therefore, one can find significant evidence to reject the hypothesis that there is no overdispersion in all lines of business.

Since we have observed possible overdispersion from the data, it is natural to consider the following models that can capture overdispersion or possible dependence, except for the independent Poisson model:

• Poisson: Independent Poisson model as an industry benchmark. Note that it is a special case of the proposed model where $w^{(1)}=w^{(2)}=w^{(3)}=1$ and $r=\infty$.

• Poisson/gamma: Poisson random effects model where each coverage has unique unobserved heterogeneity as follows: $$\begin{aligned} N^{(j)}_{it}|\mathbf{x}_{it}, e_{it}, \theta_i \overset{indep}{\sim} \mathcal{P}(\theta^{(j)}_i \nu^{(j)}_{it}), \ \theta^{(j)} \sim \mathcal{G}(r_j, 1/r_j). \end{aligned}$$ Note that the marginal mean of ${\mathbb E}\left[N^{(j)}_{it}\right]$ under Poisson/gamma model is $\nu^{(j)}_{it}$, as in the independent Poisson model, so that we use the same regression coefficients of $\alpha^{(j)}$ as the independent Poisson model.

• ZI-Poisson: Zero-inflated Poisson model with the following density: $$\small{ p(n^{(j)}_{t}; \nu^{(j)}_{t}, \eta^{(j)}_{t}) = \begin{cases} \eta^{(j)}_{t} + (1-\eta^{(j)}_{t} )\exp(-\nu^{(j)}_{t}), \qquad n^{(j)}_{t}=0 \\ (1-\eta^{(j)}_{t} )\dfrac{ (\nu^{(j)}_{t})^{n^{(j)}_{t} } \exp(-\nu^{(j)}_{t}) }{n^{(j)}_{t}!}, \quad n^{(j)}_{t}\ne 0, \end{cases} }$$ which also assumes $n^{(j)}_{t} \perp n^{(j')}_{t'}$ for all $t \ne t'$ or $j \ne j'$. Since $\eta^{(j)}_{t}$ captures the zero-inflated probability, it is usual to model $\eta^{(j)}_{t}$ as $\eta^{(j)}_{t} = \dfrac{\exp(\mathbf{x}_t \gamma^{(j)})}{1+\exp(\mathbf{x}_t \gamma^{(j)})}$.

• Copula: While each marginal component is modeled with a Poisson distribution, possible dependence among the lines of business is captured by a copula, as proposed in Shi and Valdez (2014b), so that the joint probability of $n^{(1)}_{t}$ and $n^{(2)}_{t}$ is given as follows: $$\small{\begin{aligned} p(n^{(1)}_{t}, n^{(2)}_{t}, n^{(3)}_{t}; \nu^{(1)}_{t}, \nu^{(2)}_{t}, \nu^{(3)}_{t}, \phi) &= C_\phi(u^{(1)}_{t+}, u^{(2)}_{t+}, u^{(3)}_{t+})\\ &\quad-C_\phi(u^{(1)}_{t-}, u^{(2)}_{t+}, u^{(3)}_{t+})\\ &\quad-C_\phi(u^{(1)}_{t+}, u^{(2)}_{t-}, u^{(3)}_{t+})\\ &\quad+C_\phi(u^{(1)}_{t-}, u^{(2)}_{t-}, u^{(3)}_{t+}) \\ &\quad- C_\phi(u^{(1)}_{t+}, u^{(2)}_{t+}, u^{(3)}_{t-})\\ &\quad+C_\phi(u^{(1)}_{t-}, u^{(2)}_{t+}, u^{(3)}_{t-})\\ &\quad+C_\phi(u^{(1)}_{t+}, u^{(2)}_{t-}, u^{(3)}_{t-})\\ &\quad-C_\phi(u^{(1)}_{t-}, u^{(2)}_{t-}, u^{(3)}_{t-}), \\ \end{aligned}}$$
  where $C_\phi$ means a copula function parametrized by $\phi$, $u^{(j)}_{t+}=\mathbb{P}(N^{(j)}_t \leq n^{(j)}_t)$, and $u^{(j)}_{t-}=\mathbb{P}(N^{(j)}_t < n^{(j)}_t)$.

• Proposed model: The model specified in (2.2) and (2.3).

In the calibration of the Proposed model, values of $w^{(j)}$ should be determined either by prior knowledge of the characteristics of the multiple perils or by some statistics determined by observations. As mentioned in (2.8), a pooled estimate of the credibility factor is given as the ratio of weighted sum of actual frequencies to weighted sum of expected frequencies. Therfore, $w^{(j)}$ can be interpreted as a peril-specific factor that provides information about the association between the peril and the unobserved heterogeneity, such as driving habits. For instance, suppose there are two types of coverage: property damage (PD) liability and glass damage to the driver’s own car. In that case, claims from PD liability are more positively associated with the unobserved heterogeneity in risks than claims from glass damage, since claims from PD liability are at-fault of the policyholder, whereas claims from the driver’s own glass damage may be due to external factors such as a heavy hail storm. In this regard, it is natural to put more weight on the past claims experiences from PD liability than those from drivers’ own glass damage in calculating the pooled estimate of the credibility factor, or, equivalently, set $w^{(j)}$ for PD liability higher than $w^{(j)}$ for drivers’ own glass damage. Therefore, the proposed method enables practitioners to incorporate their prior knowledge about the characteristics of multiple perils in the modeling process with flexibility.

If there is no strong evidence to pre-specify the values of $w^{(j)}$ with prior knowledge, then one can directly use the estimated overdispersion parameters to determine $w^{(j)}$ by matching the moments. Recall that from (2.4) we have

$$\begin{align} \displaystyle\sum_{t=1}^{T_i} {\mathbb E}\left[(N^{(j)}_{it} - \nu^{(j)}_{it})^2\right]&=\displaystyle\sum_{t=1}^{T_i} {\mathrm{Var}}\left[N^{(j)}_{it}\right]\\ &=\displaystyle\sum_{t=1}^{T_i} \dfrac{\nu_{it}}{w^{(j)}} + \dfrac{(\nu_{it}^{(j)})^2}{r}, \end{align}$$

for $j=1,\ldots, J$ and $i=1,\ldots, I$ under the proposed model so that one can consistently estimate $w^{(j)}$ in a similar manner to (2.6):

$$\hat{w}^{(j)} = \dfrac{\sum_{i=1}^I \sum_{t=1}^{T_i} \hat{\nu}^{(j)}_{it}}{\sum_{i=1}^I \sum_{t=1}^{T_i} \left[(N^{(j)}_{it} - \hat{\nu}^{(j)}_{it})^2 -(\hat{\nu}^{(j)}_{it})^2/\hat{r} \right]}.$$

Once the overdispersion parameters $w^{(j)}$ for $j=1, 2, 3$ are specified, either from the prior knowledge or moment matching, one can estimate $\alpha^{(1)}$, $\alpha^{(2)}$, and $\alpha^{(3)}$ from the joint likelihood after integrating out the shared random effect, as given in (2.10). In our analysis, we used the moment matching approach so that $r$, $w^{(1)}$, $w^{(2)}$, and $w^{(3)}$ are estimated to be $2.256$, $0.7226$, $0.4828$, and $0.3732$, respectively. Since $w^{(1)}> w^{(2)}> w^{(3)}$ in our case, the relative contribution of IM frequencies to the proposed posterior ratemaking scheme is greater than those of CN and PN frequencies.

Tables 6, 7, and 8 provide the estimated regression coefficients for IM, CN, and PN frequencies, respectively. One can observe that the regression coefficients from the Poisson and Proposed models are similar while the coefficients from the other models are different. Further, as mentioned above, all types of frequencies share some dummy variables indicating location types, but their estimated coefficients are quite different from each other. This supports our model specification in that one can capture the fixed effects separately for each line of business while retaining a natural dependence structure by the shared random effects.

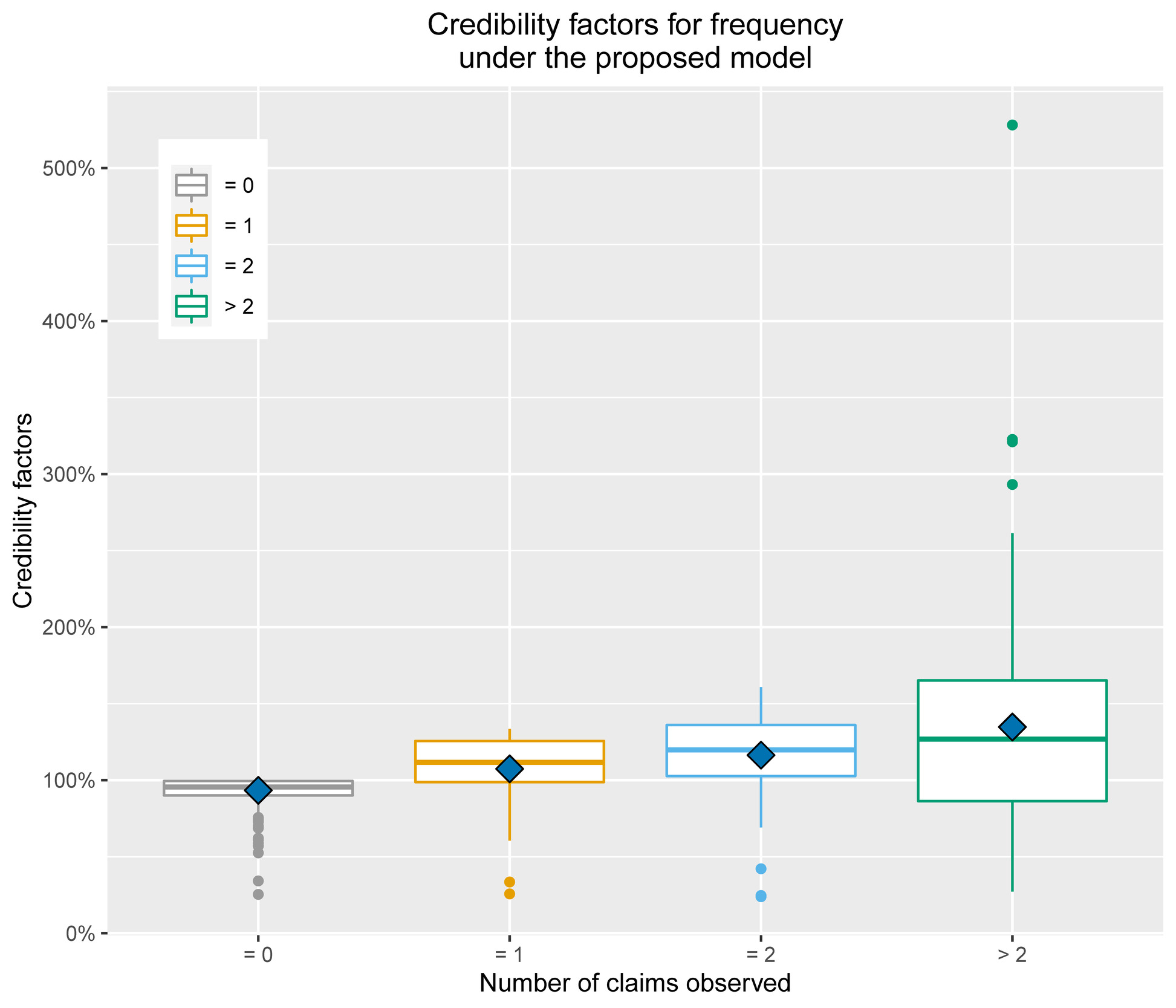
Figure 3 shows the distributions of the credibility factors under the proposed model, which are defined as the posterior expectations of $\theta$ given observations of past claims:

$$\small{ \begin{align} &{\mathbb E}\left[\theta|\mathbf{n}_T^{(1)}, \mathbf{n}_T^{(2)},\mathbf{n}_T^{(3)}\right] \\ &\quad =\frac{r + w^{(1)}\sum_{t=1}^T n_t^{(1)}+w^{(2)}\sum_{t=1}^T n_t^{(2)}+w^{(3)}\sum_{t=1}^T n_t^{(3)}}{r+ w^{(1)}\sum_{t=1}^T \nu_t^{(1)}+w^{(2)}\sum_{t=1}^T \nu_t^{(2)}+w^{(3)}\sum_{t=1}^T \nu_t^{(3)}}. \end{align} }$$

Figure 3.Credibility factors for multi-peril frequency

Blue squares mean the average of credibility factors for each group. From the figure, one can see that, if there are no past claims, then the insured can get a discount since $n_t^{(j)}=0$ while $\nu_t^{(j)}>0$ for all $j$ and $t$. It is also observed that, as a policyholder has more past claims, the credibility factor tends to rise on average. However, regardless of such general positive association between credibility factors and number of past claims, the latter varies because the proposed credibility premium formula utilizes both the actual claims and expected claims, which is based on the observable heterogeneity of risks. By doing so, an insurance company may avoid double discounts or surcharges due to segregating the impacts of the observable policy characteristics and unobservable heterogeneity in risks.

After all five models are calibrated, one can test the validity of each model by comparing the predicted performance via out-of-sample validation. In this case, it is natural to predict $N^{(j)}_{T+1}$ as $\hat{N}^{(j)}_{T+1}:={\mathbb E}\left[N_{T+1}^{(j)}|\mathbf{n}_T^{(1)},\mathbf{n}_T^{(2)} ,\mathbf{n}_T^{(3)} \right]$ under each model. Recall that

$$\begin{aligned} &{\mathbb E}\left[N_{T+1}^{(j)}|\mathbf{n}_T^{(1)},\mathbf{n}_T^{(2)}, \mathbf{n}_T^{(3)} \right]\\ &\quad= \frac{r + w^{(1)}\sum_{t=1}^T n_t^{(1)}+w^{(2)}\sum_{t=1}^T n_t^{(2)}+w^{(3)}\sum_{t=1}^T n_t^{(3)}}{r+ w^{(1)}\sum_{t=1}^T \nu_t^{(1)}+w^{(2)}\sum_{t=1}^T \nu_t^{(2)}+w^{(3)}\sum_{t=1}^T \nu_t^{(3)}} \\ &\qquad \cdot e^{\mathbf{x}_{T+1}\alpha^{(j)} } \end{aligned}$$

under the Proposed model from Theorem 1, whereas

$${\mathbb E}\left[N_{T+1}^{(j)}|\mathbf{n}_T^{(1)},\mathbf{n}_T^{(2)}, \mathbf{n}_T^{(3)} \right]={\mathbb E}\left[N_{T+1}^{(j)}\right]=e^{\mathbf{x}_{T+1}\alpha^{(j)} }$$

under the Poisson model.

To compare the out-of-sample validation performance, we use root-mean-square error (RMSE), mean absolute error (MAE), and Poisson deviance (PDEV) for each coverage that are defined as follows:

$$\small{ \begin{aligned} \text{RMSE}&: \sqrt{\frac{1}{I}\sum_{i=1}^I (N^{(j)}_{i,T_i+1}- \hat{N}^{(j)}_{i,T_i+1} )^2}, \\ \text{MAE}&: \frac{1}{I}\sum_{i=1}^I |N^{(j)}_{i,T_i+1}- \hat{N}^{(j)}_{i,T_i+1} |, \\ \text{PDEV}&: 2 \sum_{i=1}^I \left[ N^{(j)}_{i,T_i+1} \log (N^{(j)}_{i,T_i+1}/\hat{N}^{(j)}_{i,T_i+1}) - (N^{(j)}_{i,T_i+1}- \hat{N}^{(j)}_{i,T_i+1}) \right], \end{aligned} }$$

where $I$ means the number of observed policyholders in the validation set. We prefer a model with lower RMSE, MAE, and/or PDEV. As shown in Tables 9, 10, and 11, the Proposed model outperforms Poisson, ZI-Poisson, and Copula models in all validation measures. It is also shown that the Proposed model is comparable to Poisson-gamma model in RMSE and MAE while prediction performance of Poisson-gamma in PDEV is outstanding. Such empirical results show that the interdependence among the unobserved heterogeneities of coverages may exist but not be substantial in the given data set.

4. Conclusion

It is quite natural that an insurance company observes the same policyholder over many years with multiple coverages. Inspired by such characteristics, a new method is explored in this article that allows us to incorporate distinct fixed effects capturing inherent characteristics of each type of coverage (or line of business), while retaining a natural dependence structure among the claims from multiple perils over time, via the shared random effects. The proposed model has a good interpretation that can explain both overdispersion and serial/multi-peril dependence. The model is also easy to implement due to the presence of the closed form of joint likelihood and multi-peril premium formula. The proposed method is tested using a public property and casualty insurance data set provided by LGPIF. From the empirical study, it is observed that the proposed method outperforms many existing benchmarks but is less powerful than the model with unique heterogeneity for each coverage. Based on the results, one can consider a compromise between the complete shared random effects model (all coverages share the same random effect) and the unique random effects model (each coverage has its own unique random effect) by investigating underlying interdependence among the unobserved heterogeneities, as a future research topic.

Electronic Supplementary Material

The code for data analysis and out-of-sample validation is available at https://github.com/ssauljin/multi-peril_cred_premium/.