1. Introduction

Recent years have seen development in individual claim reserving techniques that model the actual claims process instead of using aggregated triangle data. Actuaries can use such models to generate point estimates for reserves or to incorporate simulation to develop a distribution of unpaid claim estimates. This paper develops a way to calculate policy-level unreported frequency distributions for use in such models. Those distributions can be used to simulate unreported claim counts at a policy level. The actuary can employ this method, combined with a close-with-pay probability model and a severity distribution, to simulate the pure incurred but not reported (IBNR) component of reserves.

Many existing methods for estimating unreported claim counts rely on applying development factors to reported claim counts. Those development factors can be calculated using chain-ladder techniques or using a report lag distribution. Such methods are relatively simple to implement, but they give no information on the variability around the estimate. In contrast, the method described herein has the following desirable characteristics at the cost of requiring more granular claim- and policy-level data:

• There is no need to develop the claim count data to ultimate.

  • Developing claim count data is difficult (especially for policy-level data).

  • Developing claim count data can mask some of the variability in the frequency distribution.

• An unreported frequency distribution for each individual policy is created.

  • Unlike aggregate distributions, this method controls for uneven policy writings throughout a year (e.g., due to growing or shrinking).

  • This also means that the output of this model is frequency at an individual policy level. This can feed other models that simulate closed-with-pay counts or severity and need policy characteristics.

• A Markov chain Monte Carlo (MCMC) process can be set up to incorporate parameter risk into the unreported claims simulation.

  • This allows the model to produce a full range of potential future payments, which is useful for developing confidence intervals or coefficient-of-variation estimates for reserves.

1.1. Note on Frequency Distribution Selections

Throughout the paper, we show results assuming that the ultimate frequency follows either a Poisson distribution or a negative binomial distribution. We show the Poisson case first because the derivations are simpler and usually easier to follow. However, the negative binomial distribution will likely be a better candidate for many lines of business.

The memoryless property of the Poisson distribution implies that the number of unreported claims for a policy is independent of claims that have been reported to date. In contrast, a negative binomial frequency distribution implies that a positive correlation exists between claims that have been reported to date and the number of unreported claims. This may be a more realistic assumption for many lines of business. We discuss this further in Section 5.

1.2. Close-with-Pay Probability and Pure IBNR Severity Models

In Section 6 we discuss a technique for simulating pure IBNR that requires a close-with-pay probability model and a pure IBNR severity model. A full discussion of these topics is outside the scope of this paper. Section 3.2 of Korn (2016) provides a framework the reader can use to model close-with-pay probability. In addition, the reader can turn to a number of sources to learn more about pure IBNR severity models. Goldburd et al. (2019) discusses fitting generalized linear models to insurance data, which can be useful in severity modeling. Meyers (2005) provides a framework by which to use Bayesian models to fit severity distributions by report lag. That author also discusses how to use Bayesian methodology to help mitigate both parameter and model uncertainty. McNulty (2017) provides examples of how mean loss amounts tend to shift with age and provides one model that attempts to address this. That author also provides a short survey of other approaches.

1.3. Outline

In Section 2 we discuss how to fit an ultimate frequency distribution to undeveloped policy-level claim count data based on the simplifying assumption that all policies have the same expected frequency. Section 3 modifies the method discussed in Section 2 to allow for the expected frequency of each policy to be proportional to some frequency exposure. In Section 4, we discuss why a report lag distribution is necessary to accurately model frequency and how to develop such a distribution. Section 5 shows how to transform the ultimate frequency distribution discussed in Sections 2 and 3 into an unreported frequency distribution for each policy. In Section 6, we explain how to use the unreported frequency distributions to help simulate pure IBNR dollars and discuss the Excel companion file that accompanies this paper. Section 7 develops methods that the actuary can use to evaluate how well the ultimate frequency distribution fits the data, and Section 8 discusses how to build an MCMC process to incorporate parameter risk. In the appendices we provide derivations of some of the important formulas as well as a summary of the notation we use in the paper.

2. Fitting a Frequency Distribution on Undeveloped Data

When modeling policy-level frequency, it is common to assume that ultimate claim counts for each policy follow some discrete parametric distribution (Poisson, negative binomial, etc.). Ideally, we would have a fully developed policy-level claim count data set with which to fit this distribution. However, in practice, data are available only as of some evaluation date and are therefore undeveloped. Using older, more developed policy years can sidestep this issue but may lead to results that are not relevant to newer and future policy years. Another method is to develop frequency data to ultimate before fitting the distribution, but that is challenging at a policy level and the uncertainty around development is lost. In this section, we discuss a method by which we can fit frequency distributions directly on undeveloped data.

2.1. Poisson Frequency on an Individual Policy

Let’s look at a single recently expired policy, policy $A,$ evaluated at time $T.$ At some future point, every claim on policy $A$ will be reported, but at evaluation time $T$ only a fraction of claims have been reported. The claims reported to date, then, can be thought of as a compounding of two distributions. Let

$$\begin{align} N &= \text{the ultimate number of claims on policy } A; \\ X &= \text{the number of claims reported by evaluation} \\ &\quad \text{ time } T \text{ on policy } A; \text{ and} \\ q &= \text{the probability that a claim on policy } A \text{ is} \\ &\quad \text{ reported by evaluation time } T. \end{align}$$

If $N$ and $q$ are known, $X$ follows a binomial distribution with parameters $N$ and $q.$ The rest of this section will show that if $N$ follows a Poisson or negative binomial distribution, it follows that the unconditional distribution of $X$ is the same distribution as $N$ with modified parameters.

Note that in this section the value of $q$ is assumed to be known. We can estimate this value using a report lag distribution, which we discuss in Section 4.

We start by looking at the case where $N$ is assumed to follow a Poisson distribution. Assume that $N$ follows a Poisson distribution with mean $\lambda.$ This implies that

$$\begin{align} N &\sim Poisson(\lambda), \text{ and} \\ X|N &\sim Binomial(N, q). \end{align}$$

Since $N$ is unknown, the conditional distribution of $X|N$ is not particularly useful. However, it can be shown that this relationship between $X$ and $N$ implies that

$$X \sim Poisson(\lambda * q) \text{ (Appendix A).}$$

This fact will allow the $\lambda$ parameter of the ultimate frequency distribution to be estimated using undeveloped claim count data.

2.2. Applying Poisson Frequency to Multiple Policies

Now this logic can be expanded to multiple policies in a data set. Assume that a data set contains policy-level claim count data for policies $A_{1}, A_{2}, \ldots, A_{M}.$ For each policy, the ultimate number of claim counts are represented by $N_{1}, N_{2}, \ldots, N_{M}.$ Assume that, for each policy $A_{i},$ there is a known value $q_{i}$ that represents the probability that a claim that occurred during the policy period would have been reported by the evaluation date. Now let $X_{1}, X_{2}, \ldots, X_{M}$ be the claims that have been reported for each policy as of the evaluation date. Assume that for $i$ in $(1, 2, \ldots, M),$ $N_{i}$ follows a Poisson distribution with mean $\lambda.$ Notice that

$$\begin{align} N_{i} &\sim Poisson(\lambda), \text{ and} \\ X_{i}|N_{i} &\sim Binomial(N_{i}, q_{i}). \end{align}$$

It follows that

$$X_{i} \sim Poisson(\lambda * q_{i}). \tag{2.1}$$

Since the $X_{i}$ and $q_{i}$ values are known, this allows a log-likelihood function to be derived for the parameter $\lambda.$ This log-likelihood function can be written as

$$LL(\lambda) = \sum_{i=1}^{M}ln(f_{\lambda*q_{i}}(X_{i})), \tag{2.2}$$

where $f_{\lambda*q_{i}}(X_{i})$ is the probability mass function (PMF) for a Poisson distribution with mean $\lambda*q_{i}.$ Using an optimization procedure on this equation, we can now calculate the maximum likelihood parameter estimate for $\lambda.$ This fitted Poisson distribution represents an estimate for the distribution of ultimate claim counts for a single policy.

2.3. Assuming a Negative Binomial Distribution

Next, we show how an ultimate claim count distribution can be estimated when frequency is assumed to follow a negative binomial distribution.

Assume now that the $N_{i}$ values in the policy-level data set discussed earlier follow a negative binomial distribution with common parameters $k$ and $p.$ Then

$$\begin{align} N_{i} &\sim Negative Binomial(k, p), \text{ and} \\ X_{i}|N_{i} &\sim Binomial(N_{i}, q_{i}). \end{align}$$

It can be shown that

$$\begin{align} X_{i} \sim Negative Binomial(k, \frac{p}{p + q_{i}-p * q_{i}}) \\ \text{ (Appendix A).} \end{align} \tag{2.3}$$

Similar to the Poisson case, this allows for the derivation of a log-likelihood function for the $k$ and $p$ parameters. This function can be written as

$$LL(k, p) = \sum_{i=1}^{M}ln(g_{k, p/(p+q_{i}-p*q_{i})}(X_{i})), \tag{2.4}$$

where $g_{k, p/(p+q_{i}-p*q_{i})}(X_{i})$ is the PMF for a negative binomial distribution with parameters $k$ and $\frac{p}{p + q_{i}-p * q_{i}}.$ The MLE (maximum likelihood estimation) estimates of the $k$ and $p$ parameters can be calculated using an optimization procedure on $LL(k, p).$

3. Adjusting for Nonhomogeneous Exposures

Notice that to derive the results in the previous section, we assumed that all policies in the data set share one common ultimate frequency distribution. That assumption is very strict and will likely not be reasonable when working with real-world data. An example of a violation of that assumption is when the data set contains policies that have been in force for different amounts of time. For instance, in general one would expect a two-year policy to have a higher frequency than a one-year policy.

To allow for different policies to have different expected frequencies we introduce the idea of a frequency exposure. A frequency exposure is defined such that the expected frequency for a policy is proportional to its frequency exposure. For example, if policy $A_{1}$ has a frequency exposure of 1 and policy $A_{2}$ has a frequency exposure of 2, the expected number of ultimate claim counts on policy $A_{2}$ would be twice that of policy $A_{1}.$ One can base the frequency exposure on a wide range of policy characteristics such as earned premium, exposure period length, or attachment point.

Continuing with the data set from the previous section, we now loosen the assumption that $N_{i}$ follows the same frequency distribution for all values of $i.$ We instead assume that each policy $A_{i}$ has a frequency exposure associated with it, denoted by $E_{i},$ that can be calculated based on policy-level characteristics.

Once the frequency exposure values are calculated for each policy in the data set, we can adjust the Poisson and negative binomial log-likelihood functions developed in Section 2 to incorporate the exposure differences. We can use the modified log-likelihood functions to fit a frequency distribution for a policy where $E_{i}=1.$

We start with the Poisson case:

Assume that the ultimate frequency for a policy that has a single unit of frequency exposure follows a Poisson distribution with mean $\lambda.$

We first look at policies where $E_{i} \leq 1.$ These policies can be thought of as risks that had a full frequency exposure, but the policy covered only $E_{i}\%$ of this exposure. Let $B_{i}$ be the ultimate number of claims that occurred for this full frequency exposure. Notice, the probability that each of the $B_{i}$ claims was covered by the policy is equal to $E_{i}.$ This implies that if $B_{i}$ were known, $N_{i}$ would follow a binomial distribution with parameters $B_{i}$ and $E_{i}.$ Thus,

$$\begin{align} B_{i} &\sim Poisson(\lambda), \text{ and} \\ N_{i}|B_{i} &\sim Binomial(B_{i}, E_{i}). \end{align}$$

This implies

$$N_{i} \sim Poisson(\lambda * E_{i}).$$

Now we look at the case when $E_{i}>1.$ Let $O_{i}$ be the ultimate number of claims that occurred for a single frequency exposure within the $E_{i}$ exposure. Notice, there is a $\frac{1}{E_{i}}\%$ chance that each of the $N_{i}$ claims occurred within this single frequency exposure. It follows that if $N_{i}$ were known, $O_{i}$ would follow a binomial distribution with parameters $N_{i}$ and $\frac{1}{E_{i}}.$ So,

$$O_{i}|N_{i} \sim Binomial(N_{i}, 1/E_{i}).$$

Notice that $O_{i}$ is the ultimate claim count for a single frequency exposure. So,

$$O_{i} \sim Poisson(\lambda).$$

This implies

$$N_{i} \sim Poisson(\lambda * E_{i}).$$

Notice that for both $E_{i} \leq 1$ and $E_{i}>1,$

$$N_{i} \sim Poisson(\lambda * E_{i}).$$

Now recall from the previous section that

$$X_{i}|N_{i} \sim Binomial(N_{i}, q_{i}).$$

So,

$$X_{i} \sim Poisson(\lambda * E_{i} * q_{i}). \tag{3.1}$$

The log-likelihood function for $\lambda$ can now be written as

$$LL(\lambda) = \sum_{i=1}^{M}ln(f_{\lambda*E_{i}*q_{i}}(Xi)). \tag{3.2}$$

Now assume that the ultimate frequency distribution for a policy that has a single unit of frequency exposure follows a negative binomial distribution with parameters $k$ and $p.$ Following the same process as the Poisson case, it can be shown that

$$N_{i} \sim Negative Binomial(k, \frac{p}{p + E_{i}-p * E_{i}}).$$

And since

$$X_{i}|N_{i} \sim Binomial(N_{i}, q_{i}),$$

this implies

$$\begin{align} X_{i} \sim &Negative Binomial(k, \\ &\frac{p}{p + E_{i} * q_{i}-p * E_{i} * q_{i}}). \end{align} \tag{3.3}$$

In this case, the log-likelihood for $k$ and $p$ can be written as

$$LL(k, p) = \sum_{i=1}^{M}ln(g_{k, p/(p+E_{i}*q_{i}-p*E_{i}*q_{i})}(X_{i})). \tag{3.4}$$

3.1. Examples of Exposure Adjustments

In the remainder of the section, we discuss methods of calculating the frequency exposure for each policy based on some common assumptions.

Assumption 1: Frequency is proportional to the length of the exposure period.

Notice that if we assume frequency is proportional to the exposure period length, then $E_{i}$ can be set equal to $V_{i}/365,$ where $V_{i}$ is the time in days the policy has been in force. In this case the frequency distribution represented by the fitted parameters would represent a policy that has been in force for 1 year $(V_{i}=365).$

Assumption 2: Frequency is proportional to earned premium.

If we assume frequency is proportional to premium, then $E_{i}$ should be proportional to the premium on the policy. Let $BP$ be some base-level premium and $P_{i}$ be the earned premium on policy $A_{i}.$ If $E_{i}=P_{i}/BP,$ then this will assume frequency is proportional to premium and the parameters being fit would represent the frequency distribution for a policy were $P_{i}=BP.$

Assumption 3: Frequency is dependent on the attachment point for a policy.

Sometimes frequency is assumed to differ for different attachment points. In general, frequency should decrease as the attachment point increases because it becomes less likely that a claim will breach the attachment. If a severity distribution is available, then this can be explicitly accounted for in the calculation of the frequency exposure. In this case, if $D_{i}$ is the attachment point on policy $A_{i}$ and $S(x)$ is the survival function of the ground-up severity distribution, then $E_{i}=S(D_{i}).$ This will reflect the fact that policies with higher attachments have lower frequencies. In this case the parameters being fit would represent the frequency distribution for a policy with no attachment since $S(0)=1.$

Assumption 4: Frequency is subject to a policy year frequency trend.

If the policy year frequency trend is equal to $g,$ then $E_{i}=(1+g)^{(py_{i}-yr)}$ where $py_{i}$ is the policy year for policy $A_{i}$ and $yr$ is the most recent policy year. The parameters being fit in this case would represent a policy that was written in the most recent policy year.

Assumption 5: Frequency is proportional to the length of the exposure period and dependent on the attachment point.

Many cases exist where we would expect frequency to be dependent on multiple factors simultaneously. Consider the case where frequency is proportional to exposure period length and is affected by attachment points. To adjust for this, we can simply combine the $E_{i}$ values calculated for Assumption 1 and Assumption 3. The appropriate frequency exposure in this case is $E_{i}= S(D_{i})*V_{i}/365.$ In this case the parameters being fit would represent the frequency distribution for a 1-year policy with no attachment.

4. Calculating $q_{i}$ Using a Report Lag Distribution

Recall that in the previous sections, $q_{i},$ the probability that a claim that occurred during policy $A_{i}$ has been reported by the evaluation date, was assumed to be known for each policy in the data set. In this section, we discuss how to calculate such probabilities using a report lag distribution and how to fit that distribution.

The report lag of a claim is calculated by subtracting the occurrence date from the report date of the claim. If we know the report lag distribution, then we can calculate the probability that a claim that occurred $w$ days ago has been reported to date as $R(w),$ where $R(x)$ is the cumulative distribution function (CDF) for the report lag distribution.

If we assume that accidents occur uniformly throughout a policy period, then we can use this report lag distribution to calculate the probability that a claim that occurred during the policy period has been reported by the evaluation date. For a claim on policy $A$ let

$$\begin{align} V &= \text{length of the earned policy period} \\ &= \text{min(evaluation date, policy expiration date)} \\ &\quad - \text{policy effective date;} \\ W &= \text{the occurrence date} - \text{the policy effective date;} \\ Y &= \text{the report lag for the claim = the report date} \\ &\quad - \text{the occurrence date; and} \\ Z &= \text{the evaluation date} - \text{the policy effective date.} \end{align}$$

Notice that the probability that a claim occurring on policy A is reported by the evaluation date can be written as $P(W + Y \le Z).$ If we assume that claims occur uniformly throughout the policy period, then

$$W \sim Uniform(0, V).$$

This implies

$$P(W + Y \le Z) = \int_{0}^{V}\int_{0}^{Z-W}r(y)*\frac{1}{V}dydw, \tag{4.1}$$

where $r(y)$ is the probability density function (PDF) for the report lag distribution.

Note that for many report lag distributions there is no closed-form solution for this double integral and it will need to be solved numerically. This probability will need to be calculated for every policy in the data set, so using numeric methods to solve for it can be cumbersome. Fortunately, if we make one additional simplifying assumption, the equation becomes much simpler to solve.

If we can instead assume that all claims on a policy occur at the midpoint of the policy period, then $W$ is no longer a random variable and can be set equal to $\frac{V}{2}.$^[1] Now notice,

$$\begin{align} P(W+Y\lt Z) &= P(Y\lt Z-W) \\ &= P(Y\lt Z-\frac{V}{2}) \\ &= R(Z-\frac{V}{2}). \end{align}$$

We can use this report lag method to calculate the $q_{i}$ values that were assumed to be known in the previous sections. Let

$$\begin{align} Vi &= \text{length of the earned policy period for} \\ &\quad \text{ policy } A_{i}, \text{ and} \\ Zi &= \text{the evaluation date} \\ &\quad - \text{the policy effective date for policy } A_{i}. \end{align}$$

Then

$$q_{i} = R(Z_{i}-\frac{V_{i}}{2}). \tag{4.2}$$

4.1. Fitting a Report Lag Distribution

Now that we have established that a report lag distribution is sufficient to calculate the $q_{i}$ values, let’s discuss how to fit this distribution. This will require a claim-level data set with three fields: occurrence date, report date, and evaluation date.

For each claim $C_{i}$ in this data set, let

$$\begin{align} Y_{i} &= \text{report lag, and} \\ G_{i} &= \text{evaluation date} - \text{report date.} \end{align}$$

It may be tempting to simply fit a distribution to the $Y_{i}$ values using standard MLE, but that method would be flawed. Fitting a distribution in such a way would assume that the data set is not subject to development, which is not the case. Since the data are available only as of the evaluation date, the data are right truncated. Specifically, the report lag of each claim in the data set is right truncated at $G_{i}.$ To handle right truncation, the likelihood function for each observation must be divided by the CDF at the truncation point.^[2] If there are $N$ claims in the claim-level data set, then the log-likelihood function for a specified report lag distribution is

$$\sum_{i=1}^{N}ln(\frac{r(Y_{i})}{R(G_{i})}). \tag{4.3}$$

We can use this log-likelihood function to calculate the MLE parameters for any specified distribution. Common choices for this distribution include exponential, gamma, and Weibull.

4.2. Piecewise Report Lag Distributions

For many lines of business, the probability is high that a claim will be reported relatively quickly (within a month). Often, however, a significant probability exists that a claim will take much longer to report (a year or two). If that is the case, then the standard distributions mentioned in the previous section will not fit the data well. These distributions cannot have a high point mass at early periods while simultaneously having a reasonable probability that claims will take much longer to report.

A solution to this is to model the report lag as a piecewise distribution that gives some weight to a uniform distribution and some weight to a shifted version of one of the standard distributions mentioned earlier. We can use the uniform portion of the distribution to assign a high point mass to early periods. The shifted exponential/gamma/Weibull portion of this distribution can allow for the possibility that a claim takes much longer to report.

Below, we show the general PDF and CDF for these piecewise distributions. In these functions, $h(x)$ and $H(x)$ represent the PDF and CDF, respectively, for either an exponential, gamma, or Weibull distribution. Notice that these distributions require the selection of a value, $s,$ that will dictate the range of the uniform distribution and the shift of the other selected distribution. Also, they require one additional parameter, $w,$ to be fit that indicates the probability that an observation comes from the uniform portion of the distribution.
PDF:

$$r(t)= \begin{cases} 0 & t \le 0 \\ w*\frac{1}{s} & 0 \lt t \le s \\ (1 - w) * h(t - s) & t>s \end{cases}$$
CDF:

$$R(t) = \begin{cases} 0 & t \le 0 \\ w*\frac{t}{s} & 0 \lt t \le s \\ w + (1 - w) * H(t - s) & t>s \\ \end{cases}$$

Notice that if $s$ is set to a relatively small value (around 1 month) and $w$ is sufficiently large, the uniform portion of the distribution allows there to be a high point mass at early periods. Simultaneously, the exponential/gamma/Weibull portion of the distribution allows for there to be a relatively high probability that claims will be reported at a much later date.

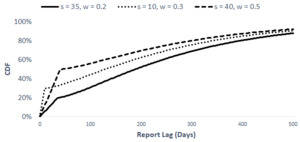
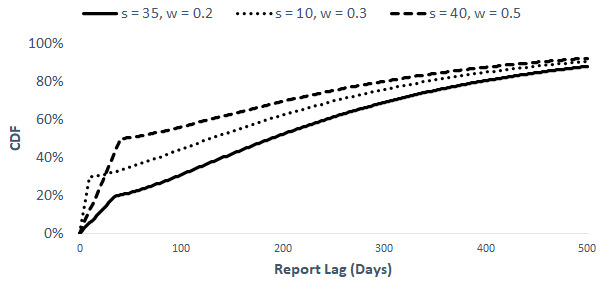
Figure 1 shows three examples of piecewise uniform-gamma distributions. The gamma portions of all three distributions are the same $(\alpha=1.5$ and $\theta=175).$ The $s$ and $w$ parameters differ for each distribution to illustrate how modifying those parameters affects the shape of the CDF. The values for the $s$ and $w$ parameters appear at the top of the chart.

Figure 1.Piecewise Uniform-Gamma Distributions

Notice that each of the CDFs begins with a steep line from $(0, 0)$ to $(s, w).$ This represents the uniform portion of the distributions. After the initial steep increase, a noticeable kink appears in each of the curves and the CDFs begin to increase more gradually. This represents the distributions shifting from the uniform portion to the gamma portion.

When fitting the piecewise report lag distributions, one must use judgment to select the value of $s.$ To aid in the selection process, we can compare fitted distributions based on different $s$ values. That comparison can be done by looking at the log-likelihood values and probability–probability (P-P) plots of the different fitted distributions.

Note that when looking at P-P plots for the report lag distributions, one needs to take into consideration the fact that the data are right truncated. To reflect the truncation, the predicted probabilities are set equal to $\frac{R(Y_{i})}{R(G_{i})}.$

5. Developing an Unreported Claims Distribution

So far, we have developed a framework for calculating ultimate frequency distributions based on undeveloped claim count data. We now look at how those distributions can be modified to represent the frequency of unreported claims for each policy.

To illustrate how to develop the unreported frequency distributions, we return to the policy-level data set that we discussed in Section 2. For simplicity, the first part of this section assumes that all policies in the data set have homogeneous frequency exposures. The formulas will be generalized in Section 5.1 to allow for nonhomogeneous frequency exposures.

Recall that the method in Section 2 allowed us to fit a distribution to ultimate frequency $(N_{i})$ for each policy. We now want to generate a distribution for the unreported frequency $(N_{i}-X_{i})$ for each policy. We start by looking at the case where $N_{i}$ is assumed to follow a Poisson distribution.

Recall

$$\begin{align} N_{i} &\sim Poisson(\lambda), \text{ and} \\ X_{i}|N_{i} &\sim Binomial(N_{i}, q_{i}). \end{align}$$

It can be shown that

$$\begin{align} N_{i}-X_{i}|X_{i} \sim Poisson(\lambda * (1-q_{i})) \\ \text{ (Appendix B).} \end{align} \tag{5.1}$$

Now we look at the case where $N_{i}$ follows a negative binomial distribution. Recall

$$\begin{align} N_{i} &\sim Negative Binomial(k, p), \text{ and} \\ X_{i}|N_{i} &\sim Binomial(N_{i}, q_{i}). \end{align}$$

It can be shown that

$$\begin{align} N_{i}-X_{i}|X_{i} \sim Negative Binomial(k + X_{i}, \\ p + q_{i}-p*q_{i}) \\ \text{ (Appendix B).} \end{align} \tag{5.2}$$

Since the $X_{i}$ values have already been observed, the parameters for the unreported frequency distributions can be directly calculated for both the Poisson and negative binomial cases.

Notice that the unreported frequency distributions differ for each policy based on the value of the $q_{i}$ parameter. As $q_{i}$ increases, the average unreported frequency implied by the distribution decreases. This makes intuitive sense because if $q_{i}$ is larger, we would expect a larger proportion of claims to already have been reported. This would imply that we would expect fewer claims to be reported in the future.

Also notice that in the Poisson case, $N_{i}-X_{i}$ is independent of $X_{i},$ but the same cannot be said for the negative binomial case. That is because the Poisson distribution is memoryless, so future frequency is assumed to be independent of the past. However, the negative binomial distribution is not memoryless, so reported frequency for each policy provides information about the unreported frequency. As $X_{i}$ increases, the expected unreported frequency increases.

5.1. Incorporating Nonhomogeneous Frequency Exposures

Recall that in Section 3 we generalized the ultimate frequency fit to allow for the possibility of nonhomogeneous frequency exposures. We can similarly generalize the calculations of the unreported frequency distribution parameters. We again start with the Poisson case.

Recall from Section 3 that

$$\begin{align} N_{i} &\sim Poisson(\lambda * E_{i}), \\ X_{i}|N_{i} &\sim Binomial(N_{i}, q_{i}), \text{ and} \\ X_{i} &\sim Poisson(\lambda * E_{i} * q_{i}). \end{align}$$

Now let

$$\lambda_{i} = \lambda * E_{i}.$$

Then

$$\begin{align} N_{i} &\sim Poisson(\lambda_{i}), \text{ and} \\ X_{i} &\sim Poisson(\lambda_{i} * q_{i}). \end{align}$$

This implies that

$$N_{i}-X_{i}|X_{i} \sim Poisson(\lambda_{i} * (1-q_{i})). \tag{5.3}$$

Similarly, for the negative binomial case it can be shown that

$$\begin{align} N_{i}-X_{i}|X_{i} \sim Negative Binomial(k + X_{i}, \\ p_{i} + q_{i}-p_{i}*q_{i}), \end{align} \tag{5.4}$$

where $p_{i} = \frac{p}{p + E_{i}-p * E_{i}}.$

6. Summarizing the Process and Simulating Pure IBNR

So far, we have discussed the steps necessary to develop policy-level unreported frequency distributions for each policy for a given line of business. In this section, we summarize that process and explain how to use the distributions, in combination with a close-with-pay probability model and a severity distribution, to simulate pure IBNR dollars.

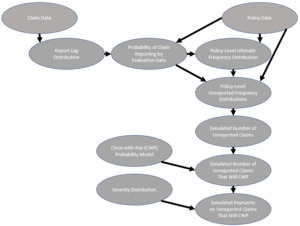
The following list outlines the steps necessary to use our frequency model to simulate pure IBNR loss dollars. Figure 2 shows a visual representation of this process.

1. The first step in the process is to gather the necessary claim- and policy-level data. Those data sets require the following fields:

   • Claim data fields: occurrence date, report date, evaluation date

   • Policy data fields: policy effective date, length of policy period, reported claim counts, evaluation date, frequency exposure

2. Next, we fit a report lag distribution based on the claim-level data using the process described in Section 4.

3. For each policy, the report lag distribution is then used to calculate the probability that a claim that occurred on the policy has been reported by the evaluation date.

4. We then use those probabilities, along with the policy-level data, to fit an ultimate frequency distribution for a policy with a frequency exposure of 1 using the process described in Sections 2 and 3.

5. With the method described in Section 5, we then estimate an unreported frequency distribution for each policy using the ultimate frequency distribution, the policy-level data, and the probabilities calculated from the report lag distribution.

6. Using the unreported frequency distributions, the number of unreported claims on each policy is then simulated.

7. Next, for each simulated claim, we calculate the probability that each claim will close with pay from the close-with-pay probability model.

8. Finally, for each claim that closes with payment, we can simulate the severity on the claim based on the severity distribution.

Figure 2.Diagram of Distribution Fitting and Simulation Process

The simulation portion of the process can be done multiple times to generate a distribution around the pure IBNR estimates. Such simulations can be used to generate a point estimate for pure IBNR by taking the mean of the simulated values. It can also help in understanding the variability around pure IBNR by looking at the distribution of the simulations.

Note that it may be useful to include policy-level predictive variables in the close-with-pay probability model and the severity distribution model. If that is the case, then simulating unreported claims at an individual policy level is particularly useful. That allows each simulated claim to be tied to a specific policy, which means that these policy-level predictive variables can be used in the simulation process.

6.1. Excel Companion File Discussion

The Excel file that accompanies the paper provides a worked example for the process shown in Figure 2 using simulated claim- and policy-level data. The file assumes that the report lag follows a gamma distribution and that policy-level frequency is proportional to the length of the policy period. In the tabs labeled (Poisson), policy-level frequency is assumed to follow a Poisson distribution. In the tabs labeled (Negative Binomial), policy-level frequency is assumed to follow a negative binomial distribution. The following is a more detailed description of each of the tabs in the Excel file:

• The CWP Prob & Severity Param tab provides inputs for the probability that a claim will close with payment and the lognormal severity distribution parameters for use in the pure IBNR simulation.

• The Report Lag Fit tab fits a gamma report lag distribution to a claim-level data set. This is done by solving for the parameters in cells A7 and B7, which maximize the log-likelihood in cell A3 (this is done using the Excel solver tool).

• The Freq Fit (Poisson) and Freq Fit (Negative Binomial) tabs show how the gamma report lag distribution, along with a policy-level data set, can be used to develop an unreported frequency distribution for each policy. The fitted parameters in cells A7 and B7 of these tabs are solved for by maximizing the log-likelihood in cell A3 (this is done using the Excel solver tool). The policy-level unreported frequency parameters are calculated in columns N and O.

• The Simulation (Poisson) and Simulation (Negative Binomial) tabs show how the pure IBNR is simulated based on the policy-level unreported frequency distributions, the close-with-pay probability, and the severity distribution. The simulated pure IBNR counts and dollars appear in cells A4 and B4 of these tabs.

• The Output (Poisson) and Output (Negative Binomial) tabs capture multiple iterations of the processes performed in the Simulation tabs. Columns D and E show the raw output from the simulations, the histograms in those tabs show the distributions implied by the simulations, and the table in cells H1:J4 provides some statistics from the simulations. The number of simulations can be modified by changing the value in cell A3 and pressing the button in cell A5. This runs a macro that copies cells A4:B4 from the Simulation tabs and pastes the result in columns D:E of this tab. For each simulation, the formulas are recalculated to get new random draws. Macros must be enabled in the Excel file for the simulation to work.

Note that the close-with-pay probability and the severity distribution used in this example are very simplistic. In practice, it may be more suitable to differ the close-with-pay probability and severity distribution based on report lag or some policy-level characteristics. It also may be necessary to take differing limits/attachments into account when simulating severity.

6.2. Simulating Pure IBNR Emergence in a Period

So far, we have discussed developing a model to simulate ultimate pure IBNR, but sometimes it is useful to model pure IBNR development over a finite period. For example, it may be beneficial to understand how much pure IBNR will emerge in the next 12 months.

If the goal is to model pure IBNR development over the next $L$ days, we need to modify the unreported frequency distributions to reflect only the emergence in that period.

For each policy $A_{i},$ let $j_{i}$ be the probability that an unreported claim will be reported in the next $L$ days. We can use the report lag distribution from Section 4 to estimate these $j_{i}$ values. Notice

$$\begin{align} j_{i} &= \text{Prob(Claim Reports between} \\ &\quad \text{ Evaluation Date and Evaluation} \\ &\quad \text{ Date + L Given Claim Reports} \\ &\quad \text{ after Evaluation Date)} \\ &= \bigl\lbrack R(\text{time since midpoint of policy} \\ &\quad \text{ period}+L) \\ &\quad - R(\text{time since midpoint of policy} \\ &\quad \text{ period}) \bigr\rbrack \div \bigl\lbrack 1-R(\text{time since} \\ &\quad \text{ midpoint of policy period}) \bigr\rbrack \\ &= \frac{R(Z_{i} - V_{i}/2 + L) - R(Z_{i}-V_{i}/2)}{1 - R(Z_{i}-V_{i}/2)}. \end{align} \tag{6.1}$$

Now let $U_{i}$ be the number of claims that will be reported in the next $L$ days for policy $A_{i}.$ Notice that

$$U_{i}|N_{i}-Xi \sim Binomial(N_{i}-X_{i}, j_{i}).$$

This implies that when frequency is assumed to follow a Poisson distribution,

$$U_{i}|X_{i} \sim Poisson(\lambda_{i} * (1-q_{i}) * j_{i}). \tag{6.2}$$

Similarly, when frequency is assumed to follow a negative binomial distribution,

$$\begin{align} U_{i}|X_{i} \sim Negative Binomial(k + X_{i}, \\ \frac{p_{i} + q_{i} -p_{i}*q_{i}}{p_{i} + q_{i} -p_{i}*q_{i} + j_{i}-j_{i}*(p_{i} + q_{i} -p_{i}*q_{i})}). \end{align} \tag{6.3}$$

Using these formulas for $U_{i},$ we can now develop a process for modeling the pure IBNR emergence over the next $L$ days. The process will be identical to the process described to simulate ultimate IBNR dollars, except instead of using the $N_{i}-X_{i}|X_{i}$ distributions to simulate frequency, we will use the $U_{i}|X_{i}$ distributions. Note that the close-with-pay probability model and the severity distribution will also need to be modified to reflect the fact that we are modeling development only over the next $L$ days.

7. Diagnostic Check on the Frequency Fit

After fitting a frequency distribution using the methods described in this paper, we need to run diagnostic checks to assess the adequacy of the fit. If we were working with developed claim count data with homogeneous frequency exposures, we could calculate the probability of different frequencies implied by the fitted distribution and compare that with the observed frequencies in the data. However, in our data set, the reported frequency for each policy follows a different distribution based on the time since the average accident date and the frequency exposure, so this test will not work.

To get around this issue, we will use the average probability of observing a particular reported frequency. Let $b_{x_{i}}(x)$ be the PMF for the reported frequency distribution for policy $A_{i}$ implied by the fitted frequency parameters. Recall that this PMF will differ for each policy based on the values of $E_{i}$ and $q_{i}.$ The average probability of observing a reported frequency $w$ can be written as

$$\mkern 1.5mu\overline{\mkern-1.5mub(w)\mkern-1.5mu}\mkern 1.5mu = \frac{1}{m}\sum_{i=1}^{m}b_{x_{i}}(w). \tag{7.1}$$

We can compare this value to the actual percentage of policies that had a reported frequency of $w.$ We denote this actual percentage as $A(w).$ If there are cases where $\mkern 1.5mu\overline{\mkern-1.5mub(w)\mkern-1.5mu}\mkern 1.5mu$ and $A(w)$ differ significantly, then that would indicate a poor fit and the distribution should be reevaluated.

Note that in many cases frequency distributions have a high point mass at 0. This means that $\mkern 1.5mu\overline{\mkern-1.5mub(w)\mkern-1.5mu}\mkern 1.5mu$ and $A(w)$ may be very small for values above 0 and therefore hard to compare. It may be useful to instead look at the $\mkern 1.5mu\overline{\mkern-1.5mub(w)\mkern-1.5mu}\mkern 1.5mu$ and $A(w)$ conditional on $w$ being nonzero. This can be done by comparing $\frac{\mkern 1.5mu\overline{\mkern-1.5mub(w)\mkern-1.5mu}\mkern 1.5mu}{(1-\mkern 1.5mu\overline{\mkern-1.5mub(0)\mkern-1.5mu}\mkern 1.5mu)}$ and $\frac{A(w)}{(1-A(0))}$ for values of $w$ greater than 0.

7.1. Historic Actual versus Expected Comparison

Recall that in Section 6.1, we developed a method for simulating the unreported claim counts that will emerge in a specified time period. We can use that method to retroactively test the performance of this unreported frequency model.

If the unreported frequency model described in this paper is fit on data that are evaluated as of 12 months ago, then one can use the method discussed in Section 6.1 to simulate the 12-month unreported claim count emergence. The actual claim count emergence can then be compared with these simulations. The further the observed emergence is from the mean of the simulations, the more likely it is that the parameters need to be revised. Note that this method is a good gut check to test model performance, but it should not be the only metric one uses to assess the model, as it relies on only one data point.

7.2. Other Diagnostic Checks

In Section 3 of a summary report, the Working Party on Quantifying Variability in Reserve Estimates (2005) lists several useful diagnostic tests. In the list that follows we present a few of the tests from that report as well as some examples of how one might apply them to the modeling framework we discuss in this paper:

• The coefficient of variation should generally be larger for older policy years than for more recent policy years.

  • Because our model produces pure IBNR at a policy level, the simulations can be aggregated by policy year. That allows the coefficient of variation to be calculated for each policy year separately to ensure that this relationship holds.

• The standard error should be larger for all policy years combined than for any individual year.

  • The policy-level output from our model allows the standard deviation to be calculated in aggregate and for each policy year to test whether this relationship holds.

• Model parameters should be checked for consistency with actuarially informed common sense.

  • Oftentimes actuaries have an a priori expectation about how long it should take for claim counts to be fully reported. If that is the case, then the report lag distribution used in this model should be compared against that expectation. For example, if an actuary expects the vast majority of claims to be reported within 10 years, then the report lag distribution should indicate that the probability of a claim being reported after 10 years is relatively small.

  • In addition, an actuary may have an a priori expectation about the average number of claim counts per policy. The implied mean frequency per policy coming out of this model can be compared against that expectation.

8. Incorporating Parameter Variance with MCMC

Throughout this paper, we developed log-likelihood functions for the frequency and report lag fits. We can use those log-likelihood functions to generate the MLE parameters for the fits. However, if we are interested in using those distributions to get an estimate for the variability of unreported claim counts, then using the MLE parameters to simulate will not be sufficient. That is because relying solely on the MLE parameters will ignore parameter risk.

One way to incorporate parameter risk into the simulations is to use MCMC techniques. MCMC methods take in a log-likelihood function and a prior distribution for each parameter that needs to be estimated and produce a list of parameter estimates. The parameter estimates are chosen according to their likelihood, which is determined by the log-likelihood function and selected prior distributions.^[3]

If we use an MCMC process to generate multiple parameter estimates, each simulation of unreported claim counts could be run using a different set of parameters. The distribution of unreported claims implied by those simulations would incorporate parameter risk as well as process risk.

Initially it would appear that if we wish to incorporate parameter risk for the report lag distribution and the frequency distribution, we could set up two MCMC processes (one for each distribution). However, that procedure would not appropriately reflect the parameter risk associated with the frequency distribution. Recall that the log-likelihood function for frequency is based on the values of $q_{i}$ for each policy, and $q_{i}$ is in turn based on the fitted report lag distribution. This implies that the log-likelihood function of the frequency distribution is affected by the selected parameters for the report lag distribution. This means that the parameter risk in the frequency distribution is affected by the parameter risk in the report lag distribution. One way to accurately account for this relationship is to create a single MCMC process that generates parameters for both distributions simultaneously. That will allow the log-likelihood function for the frequency distribution to be dependent on the selected parameters for the report lag distribution.

Of the many programs available to implement MCMC processes, we would recommend using Stan due to the seamless communication with R, the extensive documentation, and the efficient algorithm that is used. To learn more please refer to the documentation on Stan’s website: https://mc-stan.org/.

9. Conclusion

We present a method actuaries can use to predict unreported claim frequency at an individual policy level. It can be used in the estimation of pure IBNR and in the understanding of the variability around the pure IBNR estimate. It requires only some basic claim- and policy-level data and allows for frequency to be related to any policy characteristic through the frequency exposure component. This makes the model relatively simple to implement and flexible enough to adapt to different lines of business. This method of modeling unreported claim frequency can be a powerful tool for use in any reserving model that relies on individual claim- and policy-level data.

Addendum

In section 4 of our paper, formula 4.1 was derived which can be used to estimate the probability that a claim on policy $A_{i}$ has been reported by the evaluation date. Since publishing this paper, it has come to our attention that a similar formula was derived in section 4, formula 4.5 of Robbin (2004) and a similar idea was explored in Robbin (1988).

Also, it has come to our attention that there is a minor notational error in formula 4.1 of our paper. The W in the second integration limit was capitalized when it should have been lower case. The corrected formula is provided below:

$$P(W+Y \leq Z)=\int_0^V \int_0^{Z-w} r(y) * \frac{1}{V} d y d w$$

References

Robbin, Ira. 2018. “The Average Maturity of Loss Approximation of Loss.” CAS E-Forum, Spring, vol. 2, 1-22.

Robbin, I. 2004. “Exposure Dependent Modeling of Percent of Ultimate Loss Development Curves.” Casualty Actuarial Society Forum.

Robbin, I. and Homer, D., 1988. “Analysis of Loss Development Patterns Using Infinitely Decomposable Percent of Ultimate Curves.” CAS Discussion Paper Program, May, 503-538.

Appendices

Appendix A: Reported Frequency Distribution Derivations

Poisson Case

Let $n \sim Poisson(\lambda)$ and $x|n \sim Binomial(n, q).$

Recall that the probability mass functions for $n$ and $x|n$ are

$$\begin{align} f(n)&=\frac{e^{-\lambda}\lambda^{n}}{n!}, \text{ and} \\ f(x|n)&={n \choose x}q^x(1-q)^{n-x}. \end{align}$$

Notice that $f(x),$ the unconditional probability mass function for $x,$ is

$$\begin{align} f(x)&=\sum_{n=x}^{\infty}f(n)f(x|n) \\ &=\sum_{n=x}^{\infty}\frac{e^{-\lambda}\lambda^{n}}{n!}{n \choose x}q^{x}(1-q)^{n-x} \\ &=\sum_{n=x}^{\infty}\frac{e^{-\lambda}\lambda^{n}}{n!}\frac{n!}{(n-x)!x!}q^{x}(1-q)^{n-x} \\ &=\frac{q^{x}e^{-\lambda}}{x!} \sum_{n=x}^{\infty}\frac{\lambda^{n}(1-q)^{n-x}}{(n-x)!}. \end{align}$$

Let $a=n-x.$ Then

$$\begin{align} f(x)&=\frac{q^{x}e^{-\lambda}}{x!}\sum_{a=0}^{\infty}\frac{\lambda^{a+x}(1-q)^{a}}{a!} \\ &=\frac{(q\lambda)^{x}e^{-\lambda}}{x!}\sum_{a=0}^{\infty}\frac{(\lambda(1-q))^{a}}{a!} \\ &=e^{\lambda(1-q)}\frac{(q\lambda)^{x}e^{-\lambda}}{x!}\sum_{a=0}^{\infty}\frac{(\lambda(1-q))^{a}}{a!}e^{-\lambda(1-q)} \\ &=\frac{(q\lambda)^{x}e^{-q\lambda}}{x!}\sum_{a=0}^{\infty}\frac{(\lambda(1-q))^{a}}{a!}e^{-\lambda(1-q)}. \end{align}$$

Notice that $f(a)=\frac{(\lambda(1-q))^{a}}{a!}e^{-\lambda(1-q)}$ is the probability mass function for $a$ where $a \sim Poisson(\lambda(1-q))$ and since $\sum_{a=0}^{\infty}f(a)=1,$

$$f(x)=\frac{e^{-q\lambda}(q\lambda)^{x}}{x!}.$$

Notice that this is the probability mass function for a Poisson distribution. Thus,

$$x \sim Poisson(q\lambda).$$

Negative Binomial Case

Let $n \sim Negative Binomial(k, p)$ and $x|n \sim Binomial(n, q).$

Recall that the probability mass functions for $n$ and $x|n$ are

$$\begin{align} f(n)&=\frac{\Gamma(n+k)}{\Gamma(n+1)\Gamma(k)}p^k(1-p)^n, \text{ and} \\ f(x|n)&={n \choose x}q^x(1-q)^{n-x}. \end{align}$$

Notice that $f(x),$ the unconditional probability mass function for $x,$ is

$$\begin{align} f(x)&=\sum_{n=x}^{\infty}f(n)*f(x|n) \\ &=\sum_{n=x}^{\infty}\frac{\Gamma(n+k)}{\Gamma(n+1)\Gamma(k)}p^k(1-p)^n{n \choose x}q^x(1-q)^{n-x} \\ &=\sum_{n=x}^{\infty}\frac{\Gamma(n+k)}{\Gamma(n+1)\Gamma(k)}p^k(1-p)^n \\ &\quad \times \frac{\Gamma(n+1)}{\Gamma(x+1)\Gamma(n-x+1)}q^x(1-q)^{n-x} \\ &=\frac{p^kq^x}{\Gamma(k)\Gamma(x+1)} \\ &\quad \times \sum_{n=x}^{\infty}\frac{\Gamma(n+k)}{\Gamma(n-x+1)}(1-p)^n(1-q)^{n-x}. \end{align}$$

Let $a=n-x.$ Then

$$\begin{align} f(x)&=\frac{p^kq^x}{\Gamma(k)\Gamma(x+1)} \\ &\quad \times \sum_{a=0}^{\infty}\frac{\Gamma(a+x+k)}{\Gamma(a+1)}(1-p)^{a+x}(1-q)^a \\ &=\frac{p^kq^x(1-p)^x}{\Gamma(k)\Gamma(x+1)} \\ &\quad \times \sum_{a=0}^{\infty}\frac{\Gamma(a+x+k)}{\Gamma(a+1)}((1-p)(1-q))^a \\ &=\frac{p^kq^x(1-p)^x\Gamma(x+k)}{\Gamma(k)\Gamma(x+1)} \\ &\quad \times \sum_{a=0}^{\infty}\frac{\Gamma(a+x+k)}{\Gamma(a+1)\Gamma(x+k)}((1-p)(1-q))^a \\ &=\frac{\Gamma(x+k)}{\Gamma(x+1)\Gamma(k)}p^kq^x(1-p)^x \\ &\quad \times \sum_{a=0}^{\infty}\frac{\Gamma(a+x+k)}{\Gamma(a+1)\Gamma(x+k)}((1-p)(1-q))^a \\ &=\frac{\Gamma(x+k)}{\Gamma(x+1)\Gamma(k)}\frac{p^kq^x(1-p)^x}{(1-(1-p)(1-q))^{x+k}} \\ &\quad \times \sum_{a=0}^{\infty}\frac{\Gamma(a+x+k)}{\Gamma(a+1)\Gamma(x+k)} \\ &\quad \times ((1-p)(1-q))^a(1-(1-p)(1-q))^{x+k}. \end{align}$$

Notice that $f(a)$ $=$ $\frac{\Gamma(a+x+k)}{\Gamma(a+1)\Gamma(x+k)}((1-p)(1-q))^a$ $\cdot (1-(1-p)(1-q))^{x+k}$ is the probability mass function for $a$ where $a$ $\sim$ $Negative Binomial(x+k,$ $(1-p)(1-q))$ and since $\sum_{a=0}^{\infty}f(a)=1,$

$$\begin{align} f(x)&=\frac{\Gamma(x+k)}{\Gamma(x+1)\Gamma(k)}\frac{p^kq^x(1-p)^x}{(1-(1-p)(1-q))^{x+k}} \\ &=\frac{\Gamma(x+k)}{\Gamma(x+1)\Gamma(k)}(\frac{p}{p+q-pq})^k(\frac{q(1-p)}{p+q-pq})^x. \end{align}$$

Notice that this is the probability mass function for a negative binomial distribution. Thus, $x$ $\sim$ $Negative Binomial(k, \frac{p}{p+q-qp}).$

Appendix B: Unreported Frequency Distribution Derivations

Poisson Case

Let $n \sim Poisson(\lambda)$ and $x|n \sim Binomial(n, q).$

Recall from Appendix A that this implies $x \sim Poisson(\lambda)$ and the probability mass functions for $n,$ $x|n,$ and $x$ are

$$\begin{align} f(n)&=\frac{e^{-\lambda}\lambda^{n}}{n!}, \\ f(x|n)&={n \choose x}q^x(1-q)^{n-x}, \text{ and} \\ f(x)&=\frac{e^{-q\lambda}(q\lambda)^{x}}{x!}. \end{align}$$

Recall that Bayes’ theorem states that $P(A|B)=\frac{P(A \cap B)}{P(B)}.$ So,

$$\begin{align} f(n|x)&=\frac{P(n=n \cap x=x)}{f(x)} \\ &=\frac{f(n)f(x|n)}{f(x)} \\ &=\frac{\frac{e^{-\lambda}\lambda^{n}}{n!}{n \choose x}q^{x}(1-q)^{n-x}}{\frac{e^{-q\lambda}(q\lambda)^{x}}{x!}} \\ &=\frac{\frac{e^{-\lambda}\lambda^{n}}{n!}\frac{n!}{(n-x)!x!}q^{x}(1-q)^{n-x}}{\frac{e^{-q\lambda}(q\lambda)^{x}}{x!}} \\ &=e^{-\lambda+q\lambda}\lambda^{n-x}\frac{1}{(n-x)!}(1-q)^{n-x} \\ &=\frac{e^{-(1-q)\lambda}((1-q)\lambda)^{n-x}}{(n-x)!}. \end{align}$$

Let $a=n-x.$ The PMF for $a|x$ is

$$\begin{align} f(a|x)&=P(n-x=a|x) \\ &=P(n=a+x|x) \\ &=\frac{e^{-(1-q)\lambda}((1-q)\lambda)^{a}}{a!}. \end{align}$$

It follows that $a|x \sim Poisson((1-q)\lambda).$

Negative Binomial Case

Let $n \sim Negative Binomial(k, p)$ and $x|n \sim Binomial(n, q).$

Recall from Appendix A that this implies $x \sim Negative Binomial(k, \frac{p}{p+q-qp})$ and the probability mass functions for $n,$ $x|n,$ and $x$ are

$$\begin{align} f(n)&=\frac{\Gamma(n+k)}{\Gamma(n+1)\Gamma(k)}p^k(1-p)^n, \\ f(x|n)&={n \choose x}q^x(1-q)^{n-x}, \text{ and} \\ f(x)&=\frac{\Gamma(x+k)}{\Gamma(x+1)\Gamma(k)}(\frac{p}{p+q-pq})^k(\frac{q(1-p)}{p+q-pq})^x. \end{align}$$

Recall that Bayes’ theorem states that $P(A|B)=\frac{P(A \cap B)}{P(B)}.$ So,

$$\begin{align} f(n|x)&=\frac{P(n=n \cap x=x)}{f(x)} \\ &=\frac{f(n)f(x|n)}{f(x)} \\ &=\frac{\frac{\Gamma(n+k)}{\Gamma(n+1)\Gamma(k)}p^k(1-p)^n{n \choose x}q^x(1-q)^{n-x}}{\frac{\Gamma(x+k)}{\Gamma(x+1)\Gamma(k)}(\frac{p}{p+q-pq})^k(\frac{q-qp}{p+q-pq})^x} \\ &=\frac{\Gamma(n+k)\Gamma(n+1)\Gamma(x+1)\Gamma(k)}{\Gamma(n+1)\Gamma(k)\Gamma(x+1)\Gamma(n-x+1)\Gamma(x+k)} \\ &\quad \times \frac{p^k(1-p)^nq^x(1-q)^{n-x}}{\frac{p^kq^x(1-p)^x}{(p+q-pq)^{k+x}}} \\ &=\frac{\Gamma(n+k)}{\Gamma(n-x+1)\Gamma(x+k)}(p+q-pq)^{k+x} \\ &\quad \times (1-p)^{n-x}(1-q)^{n-x} \\ &=\frac{\Gamma(n+k)}{\Gamma(n-x+1)\Gamma(x+k)}(p+q-pq)^{k+x} \\ &\quad \times ((1-p)(1-q))^{n-x} \\ &=\frac{\Gamma((n-x)+(k+x))}{\Gamma(n-x+1)\Gamma(k+x)}(p+q-pq)^{k+x} \\ &\quad \times (1-p-q+pq)^{n-x}. \end{align}$$

Let $a=n-x.$ The PMF for $a|x$ is

$$\begin{align} f(a|x)&=P(n-x=a|x) \\ &=P(n=a+x|x) \\ &=\frac{\Gamma(a+(k+x))}{\Gamma(a+1)\Gamma(k+x)}(p+q-pq)^{k+x} \\ &\quad \times (1-p-q+pq)^{a}. \end{align}$$

It follows that $a|x \sim Negative Binomial(k+x, p+q-pq).$

Appendix C: Notation List

• $A_{i} =$ policy identifier

• $B_{i} / O_{i} =$ ultimate number of claims associated with policy $A_{i}$ if it was adjusted so that the frequency exposure equals 1 (used in Section 3)

• $BP =$ base-level premium (used in Assumption 2 of Section 3.1)

• $C_{i} =$ claim identifier

• $D_{i} =$ attachment point on policy $A_{i}$

• $E_{i} =$ frequency exposure on policy $A_{i}$

• $G_{i} =$ evaluation date $-$ report date for claim $C_{i}$

• $g =$ policy year frequency trend

• $j_{i} =$ probability that an unreported claim on policy $A_{i}$ will be reported in the next $L$ days

• $k, p =$ parameters for a negative binominal distribution

• $L =$ length in days of the simulated emergence period in Section 6.2

• $M =$ number of policies in the data set

• $N_{i} =$ ultimate number of claims on policy $A_{i}$

• $P_{i} =$ earned premium on policy $A_{i}$

• $py_{i} =$ policy year for policy $A_{i}$

• $q_{i} =$ probability that a claim on policy $A_{i}$ has been reported by the evaluation date

• $s =$ range of uniform portion of the piecewise report lag distribution discussed in Section 4.2

• $T =$ evaluation date

• $U_{i} =$ number of claims that will be reported in the next $L$ days for policy $A_{i}$

• $V_{i} =$ length of the earned policy period for policy $A_{i} =$ min(evaluation date, policy expiration date) $-$ policy effective date

• $W_{i} =$ the occurrence date for claim $C_{i} -$ policy effective date

• $w =$ probability that an observation comes from the uniform portion of the piecewise report lag distribution discussed in Section 4.2

• $X_{i} =$ number of claims that have been reported on policy $A_{i}$ by the evaluation date

• $Y_{i} =$ report lag for claim $C_{i} =$ report date $-$ occurrence date

• $yr =$ most recent policy year (used in Assumption 4 of Section 3.1)

• $Z_{i} =$ evaluation date $-$ policy effective date for policy $A_{i}$

• $\lambda =$ mean of a Poisson distribution

• $A(w) =$ actual percentage of policies that had a reported frequency of $w$

• $b_{x_{i}}(x) =$ PMF for the reported frequency distribution for policy $A_{i}$ implied by the fitted frequency parameters

• $\mkern 1.5mu\overline{\mkern-1.5mub(w)\mkern-1.5mu}\mkern 1.5mu =$ average probability of observing a reported frequency $w$ implied by the fitted frequency parameters

• $f(x) =$ PMF for a Poisson distribution

• $g(x) =$ PMF for a negative binomial

• $h(x) / H(x) =$ the PDF/CDF for either an exponential, gamma, or Weibull distribution used in the piecewise report lag distribution discussed in Section 4.2

• $LL(x) =$ log-likelihood function for parameter(s) $x$

• $r(x) / R(x) =$ PDF/CDF for the report lag distribution

• $S(x) =$ survival function for the severity distribution