1. Introduction

Traditional actuarial models are based on claim data which is widely used in risk assessment, loss reserving, and ratemaking. Many of these models focus on numerical or categorical variables originating from claim data and use traditional statistical techniques. For example, various regression models, such as linear, logistic, probit, tobit, mixed, and Bayesian credibility models, are used in frequency and severity modeling for claim data (Frees, Derrig, and Meyers 2014). In traditional insurance analytics, text information is utilized for descriptive purposes. It is difficult to use text data directly by traditional methods without preprocessing. However, these textual data may contain valuable hidden information that can significantly contribute to actuarial tasks, such as loss reserving and ratemaking. For example, in healthcare, medical record documentation such as doctor’s notes and patient medical histories provide crucial role in billing justification. In property and casualty insurance fields, claim descriptions may indicate claim reoccurrence(s) and loss-severity levels. However, many traditional actuarial models neglect such information (Wüthrich 2018). Hence, incorporating this information into actuarial models through machine learning (ML) techniques becomes a top priority. Natural language processing (NLP) can be used to incorporate text data and enhance the model’s predictive power. NLP is a branch of artificial intelligence with a focus on understanding, interpreting, and manipulating human language through machines.

NLP techniques and their use in insurance and actuarial science have been explored in several recent research articles. For example, Ly, Uthayasooriyar, and Wang (2020) survey NLP techniques and their applications in insurance. The article gives a general introduction to text mining, shares a background story of most techniques, and considers how to implement certain methods using open-source libraries and python codes. NLP methods are applied in Liao et al. (2020) to raw unstructured call data to identify latent topics among the calls, classify the calls, and process them more efficiently. The authors use R as computer language and Bayesian hierarchical modeling in their study. In Zappa et al. (2021), the authors discuss the possible use of NLP techniques and mention fraud detection as one of them; they propose a data-driven algorithm and use it to create a covariate that can be used for ratemaking and applied to the accident reports collected by the National Highway Traffic Safety Administration (NHTSA) between 2005 and 2007. The authors mention that text exploration would enrich the company database’s customer risk profile. Borba (2013) explains how crucial information related to auto accidents may be in accident text descriptions and how that can be used to predict an accident’s severity. However, none of the above-mentioned actuarial-related research explicitly applies the latest NLP model, Bidirectional Encoder Representations from Transformers (BERT), a (masked) language model published in 2018 by a Google team (Devlin et al. 2018) that achieved a high level of performance on multiple tasks, including question answering and language understanding to represent textual data. In this article, our focus is on how to use BERT, a (masked) language model, and machine-learning methods in claim loss modeling, especially for extended warranty, loss-frequency, and loss-severity predictions. Even though BERT was the leading NLP technique at the beginning of this research, recent progress in the NLP arena has brought more advanced models such as GPT-4 (Open 2023), Chinchilla (Hoffmann et al. 2022), and LaMDA (Thoppilan et al. 2022) to light. However, we would like to point out one of the main differences between BERT and GPT-4: BERT is a (masked) language model, which tries to predict masked words in a sentence, while GPT-4 tries to generate the next sentence based on previous inputs.

BERT is one of the most recent statistical language models to represent text for subsequent use in ML models. To understand a human language sentence, it is crucial to understand the content and the context. Therefore, reading a sentence sequentially from left to right or right to left is not sufficient. The key innovation of BERT is applying transformers, an attention mechanism that reads the entire sentence at once (bidirectional) and allows BERT to observe the relationship between words. Armed with bidirectional encoders as well as pretraining on a large English corpus and fine-tuning steps, BERT obtained new state-of-the-art results on many NLP tasks such as the General Language Understanding Evaluation (Wang et al. 2018), Natural Language Inference (MacCartney 2009), and Corpus of Language Acceptability (Warstadt, Singh, and Bowman 2019). Section 2 is devoted to a discussion of BERT in more detail.

Once BERT is used to read text input, the output is a machine-readable feature vector. These features can be used for the subsequent predictive task through ML techniques. Advances in the field of ML have allowed NLP to adopt new approaches with predictive models that learn directly from a set of texts. Machines and deep-learning methods also have enriched the predictive analytics procedure through automating various processes. In this article, we use the neural network (NN) regression model (Specht 1991) as our ML technique and aim at an automated procedure for predictive modeling by incorporating data-descriptive textual information. NN models have been used in many insurance- and actuarial-related tasks. For example, they have been used in general insurance pricing (Wüthrich 2020), insurance solvency predicting (Ibiwoye, Ajibola, and Sogunro 2012), health insurance claim predicting (Goundar et al. 2020), and claim count predicting (Yu et al. 2021), to name a few. To deal with its high-dimensional BERT feature vector and to better understand the extracted textual information, a deep-learning structure will be used to process its downstream tasks (Kaliyar, Goswami, and Narang 2021; Alatawi, Alhothali, and Moria 2021; Tang et al. 2019). Artificial NNs can aid the completion of NLP tasks, and a BERT-based deep-learning technique could be a powerful tool for predictive modeling.

In this article, we demonstrate how to use BERT-based models for claim-frequency and loss-severity predictions by incorporating textual information in the claim’s records based on 6,051 trucks’ 5-year extended warranty policies with 2,385 claims. Predictions are obtained by combining BERT with artificial NNs for regression. In addition, predictive distributions are investigated and estimated. The BERT-based frequency model is compared with traditional count models such as Poisson and negative binomial. For severity models, the BERT-based NN model is compared with the NN model directly. Real data analysis based on a data set of trucks’ extended warranty claims shows that the BERT-based model with suitable textual data available for modeling can provide a good possibility of outperforming those models that do not use textual descriptive information. This research gives an outline of BERT-based predictive modeling’s automated procedure, which incorporates claim-descriptive textual information with ML methods. Furthermore, statistical data plotting and predictive distribution curve fitting are included.

One of the major limitations of our research stems from the data set itself. The data set contains text information only for closed claims. For each closed claim, we have two types of text information available. One is DIAGNOSIS, which diagnoses the problem before the truck repair, and the other is REPAIR, which explains what is done during repair. Even though this text information should be available at different points in time, it is unclear when it was available to the insurer in our data set. If both types of text data were available after the claim was closed, then our model may contain signal bleed since any text information that was entered after closing of the claim may contain indirect information about target severity. Also, in this scenario, if text information were available only after the claim was reported, it would not be possible to use text data to predict the likelihood of a claim. When predicting severity using text data, we assumed DIAGNOSIS and REPAIR were known at the time of the prediction but that the severity was unknown. However, in real life, both would not be available to the insurance company at the first notice of claim. The same signal bleeding problem is present in frequency prediction. When predicting frequency, we concatenated text information, thus giving indirect information about the targeted number of claims. Regardless of these limitations or shortcomings, this research demonstrates how to incorporate text data by applying the BERT feature vectors into the NN regression for severity and frequency predictions, and it shows that it is possible to improve model performance when suitable textual data sets are available. We hope this research can be one of the first of many building blocks enabling actuaries to use text data in their models. In the future, by using text data sets that clearly identify the timing of text data that were available to the insurer, more rigorous models can be built. For example, finding data sets wherein text data were developed along with claim development (time series text data for each claim) may allow one to check (masked) language models’ predictive power more rigorously in actuarial settings.

The organization of this article is as follows. Section 2 gives a brief technical introduction to BERT. Section 3 describes the data set and data preprocessing. Frequency and severity modeling using BERT and NN methods are presented in the next two sections. Analysis results and comparisons, outlier treatment for extreme observations, conclusions, and final remarks are given in the final section.

2. NLP and BERT language model

This section gives a brief introduction, with some technical discussion, to BERT and, more broadly, current NLP techniques for reading text data. As we mentioned earlier, NLP enables computers to understand, interpret, and interact with human language in the same way a human being would do. NLP research has evolved from the era of punch cards and batch processing to the era of Google (Cambria and White 2014). Frequent challenges in NLP involve speech recognition, natural-language understanding, and natural-language generation. When processing textual data, some techniques are essential to preprocess the textual data before modeling. Once text data are preprocessed, the NLP techniques can help to represent words in numeric vectors so that computers can understand them.

2.1. Word representations and word embeddings

To understand the language, a proper word representation is needed. A word representation is a mathematical object associated with each word, often a vector. Word vectors, also called word embeddings, are one type of word representation. Word vectors are one of the most common types of word representation in the current NLP literature. The converted vectors contain not only information about each word but also its relations with the corresponding context.

In 2003, Bengio and colleagues developed a large-scale language model based on NNs. The model processed the text as an unsupervised learning task. The main idea of the model is the transformation of raw words into word vectors/word embeddings that represent words as numerical values through a mapping (Turian, Ratinov, and Bengio 2010). The input of the mapping is a set of nonduplicated words from the original text, called a dictionary. The output of the mapping is a vector representation of the corresponding words from the input. After the mapping is implemented, the textual data can be processed by ML models. The fundamental method of word embeddings is bag-of-words, introduced in 1954 by Harris (Harris 1954). The bag-of-words method represents the frequency of each word in each sentence in the given document. This representation is simple, but there is no semantic difference between each word. For example, the word “bank” has multiple meanings but has not in its embeddings. There are two general types of word embeddings (Baroni, Dinu, and Kruszewski 2014): (1) models that use word counts or frequency information are called count-based models, and (2) models based on the context information and usually incorporated with NNs are called prediction-based models.

Count-based models process words by collecting word counts or word-context co-occurrence counts in a corpus (a large and structured set of texts produced in a natural communicative setting that can be read by machines). The basic idea of early count-based models is to build count vectors that represent the frequencies of words from the dictionary of a given corpus. This idea is simple, but some common words such as “a” or “is” may have a very high frequency in those count vectors. To solve this issue, term weighting-based schemes were introduced by researchers, including term frequency (Luhn 1957), inverse document frequency (Jones 1972), and term frequency-inverse document frequency (Salton and Buckley 1988). Count-based models that leverage word context were introduced by Deerwester and colleagues in 1990 (Deerwester et al. 1990). These count-based models incorporated word context by implementing co-occurrence matrices used widely in NLP research. One of the more recent count-based word-embedding models is Global Vectors for Word Representation (GloVe), which was released by Pennington and colleagues in 2014 (Pennington, Socher, and Manning 2014). GloVe obtains vector representations of words by global word-word co-occurrence statistics, which tabulate how frequently a word co-occurs with another word in a given corpus via an unsupervised learning algorithm. The main idea of the GloVe model is that ratios of word-word co-occurrence probabilities can help to encode some form of meaning.

Prediction-based embedding models have become more popular with the development of ML algorithms. The first prediction-based model was introduced in 2003 (Bengio et al. 2003). The model applied word embeddings in its first layer of artificial NNs. An artificial NN is an information-gathering and -processing model that has a structure similar to a biological neural system’s. Therefore, artificial NNs can be learned through examples. Generally, artificial NNs have multiple layers to transmit and process information about inputs, including an input layer, several hidden layers, and an output layer. In 2010, Mikolov and colleagues (Mikolov et al. 2010) used a recurrent neural network (RNN) as an optimized way to train a language model. Due to their structures, RNNs have limitations when dealing with long sequences of words. One of the main tasks of prediction-based models is to speed up and improve the accuracy of training processes. Mikolov et al (2013) proposed two models for training embeddings called the continuous skip-gram and bag-of-words models in 2013 known as Word2Vec (Mikolov, Chen, et al. 2013; Mikolov, Sutskever, et al. 2013). The two models defined a context window C of size k on anywhere of a sentence of size n, where k ≤ n. The skip-gram model predicts the surrounding context from the central word in C. The continuous skip-gram and bag-of-words model predicts the central word based on its context in C. The two models used NNs in their training step and built relations between words and corresponding contexts (Mikolov et al. 2009). In 2014, Mikolov and Le extended the Word2Vec model to the Doc2Vec model by adding a new embedding that can map a paragraph to a vector (Le and Mikolov 2014). The vector is called a paragraph vector and represents information, such as the topic, about the paragraph from its context.

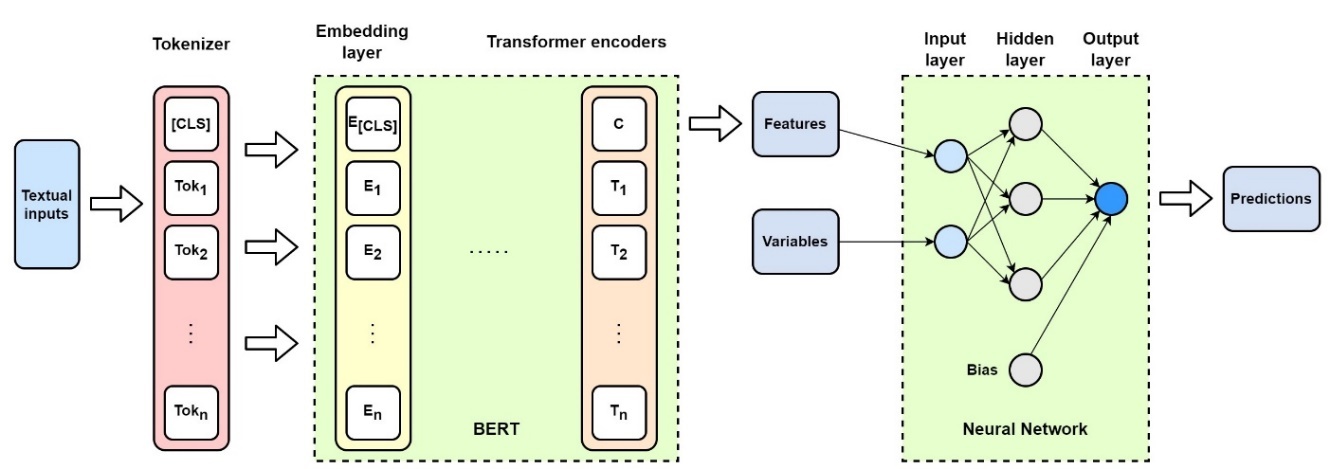
Another word representation technique called tokenization is a process used to split a document into several pieces of sentences or words. Many modern NLP techniques involve tokenization as the essential preprocessing step to analyze the textual data piece by piece. For example, the WordPiece tokenization method (Wu et al. 2016) was developed using ML techniques to split words into smaller pieces to retain suffixes. WordPiece tokenization is trained on a large-scale corpus to tokenize words and sentences efficiently. After the tokenization, textual data need to be transformed into numerical values to be used by mathematical or statistical models. BERT uses the WordPiece tokenization method to tokenize the text it reads.

2.2. Transformers and BERT

To obtain more complex relations, many traditional language models are based on NNs, such as RNNs and convolutional neural networks (CNNs), as their encoder-decoder mechanism. RNNs are a standard type of NNs that can be extended over time and are designed to process sequences such as texts through cycles in their structure that can pass the historical information from the sequences. The general idea of using RNNs is to store and pass information about earlier words in the text in the hidden layers, which can help the model to analyze texts among long sentences. A CNN is another type of NN that can extend across space through shared weights (Abiodun et al. 2018). However, RNNs have difficulties handling long sequences, and CNNs can be time-consuming when processing large-scale textual data. To improve efficiency, in 2017, Google researchers proposed the transformer model based on the attention mechanism (Vaswani et al. 2017). The transformer model can function like a human brain by giving attention to only the most important information. The model is designed to reduce the cost of the training stage and increase the accuracy of predictions without either traditional RNN or CNN structures. BERT is a transformer-based NLP tool that was released by Google in late 2018 (Devlin et al. 2018). Many researchers have shown that BERT can process product review data with high accuracy, working alongside reading comprehension and aspect-based sentiment analysis (Polignano et al. 2019; Gao et al. 2019; Peters et al. 2018; Howard and Ruder 2018; Alsentzer et al. 2019).

BERT (Devlin et al. 2018) is a language model trained on a large corpus that allows fine-tuning for specific tasks. The general idea of BERT is to pretrain the language model by using large-scale corpora in a transformer model (Vaswani et al. 2017). Pretrained representations can be either contextual or context free. The contextual representation can be bidirectional and unidirectional. Context-free models such as GloVe and Word2Vec create a single word-embedding representation for each word from the document, regardless of its context. Contextual models, on the other hand, create a representation of each word based on the context. The bidirectional representation uses both the left and the right context for each word, and the unidirectional representation uses only the left or the right context. The BERT model is trained bidirectionally through multiple layers using transformer NNs. The BERT model learns the words and their contexts during pretraining. Then it can be used to learn some specific details for the given textual task during fine-tuning. The model tokenizes its input using WordPiece as its word embedding. The WordPiece tokenization is applied before pretraining and fine-tuning for the model: (1) A special token (CLS) is added before each sequence. Another special token (SEP) is used for sentence separation. (2) All inputs are tokenized based on a large vocabulary using WordPiece tokenization (Wu et al. 2016) as token embeddings. The WordPiece tokenization can split a sentence or a word into small pieces. (3) To represent that a word belongs to a specific sentence in the text, a segment embedding is applied to each token.

During pretraining, BERT is trained using a large plain-text corpus such as Wikipedia and is structured by combining several encoders extracted from transformers. The bidirectional encoder architecture is pretrained with two main tasks (Devlin et al. 2018). Masked language modeling is a process that replaces about 15% of the original words with (MASK) tokens. The model can then be trained to predict the masked words. Next sentence prediction, as a classification problem, is used to train a model to predict whether one sentence will follow another, given two sentences. Pretraining aims to learn the language by minimizing the loss functions for these two tasks. The pretrained BERT can go through fine-tuning to solve downstream tasks using its learned language. The input and output of fine-tuning are specific to the downstream task. In this article, the inputs are textual descriptions from the data sets, and the outputs are the extracted vector representations that can be exploited using NN models. BERT has shown its adaptivity for multiple end tasks by optimizing different fine-tuning processes (Peters et al. 2018; Howard and Ruder 2018). BERT is useful for various downstream tasks without changing its pretrained language model. Compared to other language methods, BERT has better prediction accuracy for many downstream tasks, especially those that feature extraction-related tasks. BERT has shown state-of-the-art performance on natural language understanding tasks such as the General Language Understanding Evaluation, Stanford Question Answering Dataset, and Situations with Adversarial Generations. The number of studies applying the NLP techniques to address industrial problems has been increasing (Baker, Hallowell, and Tixier 2020; Moon, Chi, and Im 2022). In S. Xu, Barbosa, and Hong (2020), a predictive model for determining helpfulness scores of customer reviews based on the incorporation of BERT features with deep-learning techniques is proposed. It becomes natural to extend the application of BERT to insurance data as the authors in Ly, Uthayasooriyar, and Wang (2020) already emphasize that BERT is a potential tool for insurance data analysis. Very recently, BERT-based NLP techniques for severity modeling via portfolio classification and loss prediction have been investigated in Shuzhe Xu, Zhang, and Hong (2022). In this investigation, the severity prediction model is based on a 2-year basic warranty policy with 11,639 claim records, and the data-driven model is featured with the models for classification of claim loss types and prediction of severity amount in each type of loss, respectively.

BERT has two primary model sizes that were released in 2018: the $\text{BERT}_{Large}$ model and the $\text{BERT}_{Base}$ model. In 2019, 24 pretrained miniature BERT models were released (Turc et al. 2019). The releases of smaller BERT models were intended for some environments with limited computational resources. The model sizes of some released BERT models are listed in Table 1. In this article, the $\text{BERT}_{Base}$ model will be used in a study of trucks’ extended warranty data.

3. Description of data and data preprocessing

The data set contains a sample of claims for trucks in the years between 2009 and 2013 under extended warranty coverage from a U.S. company. The data set comprises two tables: one contains information about warranty contracts, and the other contains information pertaining to claims related to those contracts. Each truck is assigned a unique vehicle identification number. Contract files give warranty contracts attached to particular vehicle identification numbers, and claim files give records about warranty claims under those contracts. Usually, a warranty contract can be categorized as the base warranty, basic warranty, and extended warranty. The warranty cycle progresses from base to basic to extended. The base warranty comes as default coverage. Usually, this coverage depends on age and accumulated hours of the vehicle, for example, “12 months/2,000 hrs.” For this particular dataset, the basic and extended warranties do not come as default, and customers can purchase those if they prefer. For example, basic warranty is “12 months/no limit on hrs,” and the extended warranty lists as “60 months/10,000 hrs” or “60 months/6,000 hrs” depending on the vehicle type. A claim in this study from this set of policies belongs to only the extended warranty. Also, as mentioned in Musakwa (2015), an extended warranty may be purchased by the customer on preowned vehicles. In our case, we assume that all trucks are still with the first owner and all warranties were purchased at the time of vehicle purchase. We chose claims related to extended warranty (without extended powertrain) listed as “60 months/10,000 hrs” for our analysis.

The observational period runs from 2009 to 2013. The data contain 6,051 unique extended warranty policies in the period. The data set was collected based on a 5-year extended warranty policy that is extracted from a raw data set for actuarial modeling, especially with textual descriptive information in claim records. The data set, collected during a 5-year period, contains each truck’s warranty contract policy information and claim details for warranted trucks. The data set contains information about contracts and claims. Several attributes in the contract table are listed in Table A.1 in Appendix A. This includes the truck’s vehicle identification number, brand, model, coverage type, coverage begin date, coverage end date, deductibles, and more. The claim table contains information about each claim including textual descriptions of the causes of truck failure and repair. Several attributes in the claim table are listed in Table A.2 in Appendix A. Some extra preprocessing steps are added to the contract and the claim tables for ML. Claim records with censored textual data have been removed, and extreme cases with abnormal values such as multiple repairs in one claim also have been removed. For our analysis, we counted no claims, denied claims, and rejected claims as zero claims.

There are 6,051 extended warranty policies in the data set. The frequency diagram for coverage months for extended warranties is given in Table B.1 in Appendix B.1. Out of 5,342 extended warranties, which are listed at “60 months” of coverage, we removed 4 warranty policies since hours were listed as “6,000.” This resulted in 5,338 extended warranty policies listed as “60 months/10,000 hrs” being selected for frequency modeling. For each nonzero claim, there is a corresponding claim record in the claim table. Thus, there are 2,402 claim records in the claim table. In the claim table, DIAGNOSIS and REPAIR attributes contain textual descriptions with large sentences or paragraphs. However, some of these claim records contain no text descriptions in the DIAGNOSIS and REPAIR columns. Since our focus is using text descriptions of severity and frequency modeling, we removed those and used 2,385 records for severity analysis. As we mentioned, our focus is demonstrating how to incorporate text data into frequency and severity modeling using BERT. Therefore, we put less focus on other variables in the contract and claim tables. The analysis was done using open-source statistical software tool R.

4. Frequency modeling

In this study, the data are split randomly into 60% for training and 40% for testing using base R. In R, a seed is set at 123 for frequency analysis to make sure the results are reproducible. This results in 3,202 records for training and 2,136 records for testing in frequency modeling. There are no overlapping data between the two data sets. We assume independence among each warranty policy as well as independence between frequency and severity. Therefore, for a given extended warranty policy, the joint distribution of claim severity can be written as

$$f(N, X)=f(N) \times f(X), \tag{4.1}$$

where N denotes the frequency of claims per policy and X denotes the severity of loss amount per claim.

The frequency table for the number of claims stemming from the selected extended warranty policies of “60 months/10,000 hrs” is given in Table B.2 in Appendix B.1. The mean and standard deviation of the count data for coverage type given as “60 months/10,000 hrs” are 0.4499813 and 1.154793, respectively. The mode is 0 counts. Five number summaries of the number of claims can be found in Table 2.

Even though our emphasis is on BERT-based frequency modeling, we need at least one traditional frequency modeling approach for comparison purposes. We use Poisson and negative binomial NB-2 as traditional approaches. These results are compared with the BERT-based frequency modeling approach. We use the following covariates to model the frequency N for the extended warranty data set: BRAND, MODEL, DIAGNOSIS, and REPAIR.

The reason for using BRAND and MODEL is simplicity as well as interpretability. In Table A.1, for example, DEALER contains more than 422 dealers. By using BRAND and MODEL, one can interpret the effect of BRAND and MODEL on the number of failures/breakdowns. The Cramer V statistic between BRAND and MODEL is 0.5768, thus indicating strong (but not perfect) association between two variables. Hence we did not use both variables at the same time. Instead, we developed models that use BRAND and MODEL as explanatory variables in the Poisson and NB-2 approaches. DIAGNOSIS and REPAIR contain the concatenated text description of claims. Thus, DIAGNOSIS and REPAIR along with BRAND and MODEL have been used in BERT-based frequency modeling.

4.1. Poisson model

The Poisson regression model can be defined as follows:

$$P\left(Y=y_i \mid X_i\right)=\frac{e^{-\mu_i} \mu_i^{y_i}}{y_{i} !}$$

$$\begin{align} \ln \left(E\left[Y \mid X_i\right]\right)&=\ln \left(\mu_i\right)\\ &=\beta_0+\beta_1 X_{1 i}+\beta_2 X_{2 i}\\ &\quad +\cdots+\beta_k X_{k i}\\ &=X_i^T \beta, \end{align}$$

where $X_{i}\ = \ \left( 1,X_{1i},X_{2i}, \cdot \cdot \cdot ,X_{ki} \right)$ are the explanatory variables and $\beta\ = \ (\beta_{0},\beta_{1}, \cdot \cdot \cdot \ ,\beta_{k})$ is the vector of the corresponding coefficients. Observe that when there are no predictors, we get a model that does not depend on covariates, which we call the “null” model (or fitted Poisson model to count data without any predictors).

Observe that the proportion of zero in the full data set is 78.96%. If we use the standard Poisson model, then the probability of zero counts with a mean of 0.4499813 is 63.76%, which is somewhat close to observed zeros. We do not plan to use zero-inflated models in this article. The Poisson regression is done using the following variables: BRAND and MODEL. Fit statistics for this model on the training data set are given in Table B.3 in Appendix B.2. Based on the analysis we would recommend using MODEL as the predictor if the Poisson model were going to be used. This decision depends on the low Pearson dispersion chi-square, Akaike information criterion (AIC), and Bayesian information criterion (BIC), and model simplicity. The observed versus predicted values for these models on the testing data set are given in Figure B.1 in Appendix B.2. Based on Figure B.1, the Poisson model fits best when the number of claims is more than 1. However, when the number of claims is 0 or 1, fitted models display deviation from predicted versus observed. This dispersion is shown in the Pearson dispersion parameter. Under the Poisson model, we expect it to be 1. Since for each model, Pearson dispersion statistics are around 3, we consider the negative binomial model next.

4.2. Negative binomial model

As we mentioned above, we observed that data show Poisson overdispersion. Hence, we need a model that can account for this extra dispersion in the model. In this section, we consider an NB-2 model. The NB-2 model is defined as follows:

$$P\left(Y=y_i \mid X_i\right)=\frac{\Gamma\left(y_i+v\right)}{y_{i} ! \Gamma(v)}\left(\frac{v}{v+\mu_i}\right)^v\left(\frac{\mu_i}{v+\mu_i}\right)^{y_i}$$

$$\begin{align} \ln \left(E\left[Y \mid X_i\right]\right)&=\ln \left(\mu_i\right)\\ &=\beta_0+\beta_1 X_{1 i}+\beta_2 X_{2 i}\\ &\quad +\cdots+\beta_k X_{k i}\\ &=X_i^T \beta \end{align}$$

where $X_{i} = (1,X_{1i},X_{2i}, \cdot \cdot \cdot ,X_{ki})$ are the explanatory variables and $\beta\ = \ (\beta_{0},\beta_{1}, \cdot \cdot \cdot \ ,\beta_{k})$ is the vector of the corresponding coefficients. Observe that under the NB-2 model,

$$\begin{align} E\left[Y \mid X_i\right]&=\mu_i, \operatorname{Var}\left(Y \mid X_i\right)\\ &=\mu_i\left(1+\alpha \mu_i\right), \\ \text { where } \alpha&=\frac{1}{v}. \end{align}$$

Fit statistics for the NB-2 model on the training data set are given in Table B.4 in Appendix B.3. Here we can see that the Pearson dispersion parameter is close to 1 for all three models, which indicates the NB-2 model fits very well. Other fit statistics indicate a better fitting compared to the Poisson model. Finally, observed versus predicted values for the NB-2 model on the testing data set are given in Figure B.2 in Appendix B.3, confirming that the NB-2 model is the better fit compared to the Poisson model.

Mean squared error (MSE) is not an appropriate measurement of the performance of these traditional count models on the testing data set. Therefore, we use the Pearson goodness-of-fit statistic to measure the performance when Poisson and NB-2 models are applied to the testing data set. The results are given in Table 3. The null hypothesis is that there is no significant difference between the observed and predicted values. Thus, this shows that other than the Poisson model, NB-2 performs very well on the testing data set. We do not plan to build more complex frequency models with more predictors since our aim is to demonstrate that BERT models can predict the frequency in a sufficiently accurate manner.

4.3. BERT and frequency modeling

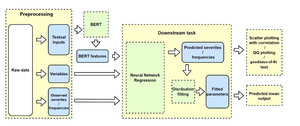
The BERT-based frequency modeling method is discussed in this section. The proposed model, called BERT&NN, is based on Figure 1. Textual input for the frequency modeling is from DIAGNOSIS and REPAIR. Observe that each claim has a separate DIAGNOSIS and REPAIR text description. To predict frequency, when there are multiple claims for a given policy during the 5-year periods, we concatenated text description of DIAGNOSIS for those claims with REPAIR separately. This resulted in only one text description in DIAGNOSIS and one in REPAIR for a given policy for claim-frequency modeling. Some combined textual descriptive information could be in pages and thus increase processing complexity.

Figure 1.BERT&NN model

The device we used for this study is NVIDIA GeForce RTX 2080 Ti graphic card with 11 gigabyte memory size. To keep the model simple and within the limits of computational power, we used only the DIAGNOSIS column in our BERT-based frequency model. BERT extracted features, and BRAND and MODEL were used as input to the NN. Thus, in Figure 1, the variables for the NN when predicting frequency are BRAND and MODEL, along with the BERT features extracted from the DIAGNOSIS column. We use one hidden layer NN with the output as predicted frequency. The NN is trained using the following loss function on the training data set:

$$M S E=\frac{1}{n} \sum_{i=1}^n\left(O_i-E_i\right)^2, \tag{4.2}$$

where $O_{i}$ is the observed frequency and $E_{i}$ is the expected frequency. A natural question to ask at this point is, What is the effect of the NN on the prediction? What happens if one tries to use BRAND and MODEL in the NN while discarding text data features coming through BERT? This approach resulted in zero as the predicted frequency for every testing data entry. Hence, one can argue that without text data, this model is not able to predict the frequency. We use Pearson goodness-of-fit statistics to measure the performance of the BERT&NN model. The Pearson goodness-of-fit test statistic under the BERT&NN model is 7.7786, and the p-value is 0.3525. Thus, there is no significant difference between the BERT-predicted frequencies and observed frequencies. The results are summarized in Table 4.

Since MSE is used as the loss function for BERT-based frequency models, the MSE for each model is given in Table B.5 in Appendix B.4. Several hyperparameters are used in the BERT model and the NNs to achieve the best result. These parameters are given in Table B.6 in Appendix B.4. To optimize the model with limited computational resources, max seq length = 512 and train batch size = 4 are selected.

5. Severity modeling

In this section, we discuss severity modeling using NLP techniques, more specifically a BERT-based technique. At the first stage, we use a BERT-based model to predict the loss amount for each testing datum directly through a regression model that uses features extracted by BERT. Under this method, we predict original severities using BERT. Then we use these predicted severities to calculate the empirical expected loss amount per claim per policy for the policy coverage period. In the second stage, we try to understand the distribution of predicted severities. For this, we fit a parametric distribution on BERT-predicted severities and then use the distributional expected value as the prediction for the expected loss amount per claim per policy for the policy coverage period. For severity modeling, we used 2,385 claim records. Five number summaries of severity of claims are given in Table 5.

5.1. BERT and pointwise severity prediction

For BERT severity modeling, we use the following four variables in claims (see Table A.2 in Appendix A). The variables are REPAIR, which includes the textual description of repairing; DIAGNOSIS, a detailed text description of diagnosis of the cause of troubles and failures; DCAT, a categorical variable for the failure; and GCAT, a categorical variable that indicates in which part of the vehicle the failure occurred. For example, “Short Circuit” is coded in DCAT, while “Horn” is coded where the short circuit occurred as categorized in GCAT. Noticing that the descriptive texts are of reasonable size for each claim, we can include both variables—REPAIR and DIAGNOSIS—in our loss-severity modeling.

The BERT severity-modeling procedure is shown in Figure 1, and the pseudocode is listed in Algorithm 1 in Appendix D.1. The textual data are tokenized as the inputs of the BERT model. An NN for regression model is followed by the BERT model. The output features of BERT and other explanatory variables are then fed into the NNs for predicting severity. The output of the NNs is the predicted severity. The BERT model can help to extract hidden features from text with its contexts. The dimension of these extracted features is high and maybe useless without the NNs. Also, the extracted features are difficult for humans to read. Thus, NNs or other approaches are required to handle BERT-extracted features. In this article, BERT-based NNs are used as the strategy.

To gauge the effect of textual data on the prediction, we run a model using only DCAT, GCAT, and NNs named NN, a model not using BERT for including textual information. Thus, we have two models to compare: Model 1 (BERT&NN model) and Model 2 (NN model).

The BERT&NN model uses all four variables as input, i.e., two categorical variables, DCAT and GCAT, together with the textual data variables REPAIR and DIAGNOSIS. The NN model uses only two categorical variables—DCAT and GCAT—and hence no textual data. Under the BERT&NN model, BERT is used to extract hidden features in text descriptions of DIAGNOSIS and REPAIR variables. Then these BERT-extracted BERT features/BERT vectors, along with DCAT and GCAT, are used to form one layer of NNs. The model is trained on the training data set while minimizing MSE. The NNs are formed by incorporating the BERT pretrained model with one additional output layer to predict severity by regression. A general regression from NNs is designed as

$$\widehat{X} = f(W^{T}X + b).\tag{5.1}$$

The input of the NN model is a vector that contains the extracted features of the textual information (DIAGNOSIS and REPAIR columns) from the claim table by BERT algorithms; the DCAT column, which categorizes the cause of failure/defect; and the GCAT, which classifies where the failure occurred. The textual information should be tokenized before feeding into the BERT model. The output of the NN model is the predicted severity. The model can be discussed in more detail as

$$\widehat{X} = f({w_{1}}^{T}x_{1} + {w_{2}}^{T}x_{2} + {w_{3}}^{T}x_{3} + b), \tag{5.2}$$

where $\widehat{X}$ is the predicted severity; f is an activation function; and w₁, w₂, and w₃ are vectors of the weights of specific terms x₁, x₂, and x₃. The length of w₁, w₂, and w₃ are determined by the length of the corresponding input x₁, x₂, and x₃. Here, x₁ is the output from textual information (DIAGNOSIS and REPAIR) by BERT, which has a size of 768 dimensions; x₂ is the DCAT column, x₃ is the GCAT column, and b is bias. Bias is a single value since there is only one output, which is the predicted severity. The inputs of the NN are elements in x = [x₁, x₂, x₃]. Each element in x is multiplied by the corresponding weight in the hidden layer, and then the bias b is added. The output of the NNs is the summation of outputs that come from the activation function. The NN model is trained on the training data set using MSE as the loss function.

$$MSE = \frac{1}{n}\sum_{i = 1}^{n}{(X_{i} - {\widehat{X}}_{i})}^{2}.\tag{5.3}$$

Here n denotes the size of the training data set, $X_{i}$ observed severities, and $\widehat{X}$^ˆ_i the predicted severities. Fine-tuning parameters used for each model are given in Table C.1 in Appendix C. We would like to point out that any other suitable criteria can be used instead of MSE as the loss function. Once the model is trained, predictions on the testing data set are obtained. Results for each model are listed in Table 6.

To test whether the populations of BERT&NN and NN are identical without assuming differences are normally distributed, we use the Wilcoxon signed rank test. Data samples are paired since these are two differently predicted values for the same testing data set. The null hypothesis for the test is no median difference. The alternative hypothesis is that the median difference is not zero. The resulting p-value is 0.03211, thus rejecting the null hypothesis at the 5% significance level and accepting the two distributions are nonidentical. We can use explained variance to see how much each model explains the variation in data. Explained variance is defined as follows:

$$explained\ variance\ = \ 1 - \frac{var(y - \widehat{y)}}{var(y)}, \tag{5.4}$$

where $var(y - \widehat{y)}$ is the variance of prediction error and $var(y)$ is the variance of actual testing values. According to Table 6, explained variance changed from 19.13% to 28.50% when the model was changed to the BERT&NN model. Scatter plots of predictive results from the NN model and the BERT&NN model are shown in Figures 2a and 2b. We also calculated the Pearson correlation coefficient for both predictions against actual. The result shows that BERT&NN-predicted values are more correlated with actual loss amounts than are the NN model–predicted values.

Figure 2a.Scatter plot for neural network (NN) model prediction values versus actual

Figure 2b.Scatter plot for BERT&NN model prediction values versus actual

5.2. Predictive distribution and parametric models

The purpose of this section is to understand the shape and behavior of BERT-predicted values through parametric distributions. To that end, we fit several common parametric distributions to predictive values in the BERT&NN model. Our choices are lognormal, gamma, Weibull, and normal distributions. Even though it is known that severity distributions are skewed, we used the normal distribution for comparison purposes. We implemented two approaches to fit distributions to predicted values:

1. Calculate distribution parameters using complete individual data.

2. Calculate distribution parameters based on complete grouped data.

The 10-fold cross-validation method is used to calculate distributional parameters and test each model fit. Under this approach, BERT-predicted severities are divided randomly into 10 subsets, and 9 of them are used to calculate distributional parameters. The remaining subset is used to test the model fit. For both approaches, the maximum likelihood method is used to estimate parameters. The Kolmogorov Smirnov (KS) test, Anderson Darling (AD) test, Cramer Von Mises (CVM) test, and information criteria such as AIC, BIC, and log-likelihood are used to compare the fitted model using complete individual data. For complete grouped data, the Pearson chi-square goodness-of-fit test is used. Once the distributional parameters are calculated, we use distributional expected values as predicted average severity per claim per policy.

5.2.1. Distribution fitting on complete individual BERT&NN model predicted values

Table C.2 in Appendix C summarizes fitted statistics for KS, AD, CVM, and expected severities for distributional fits on complete individual BERT&NN model predicted values. Informational criteria values for each model are given in Table C.3 of Appendix C. In Table C.2, $\overline{X}$_test stands for the observed average severity on the testing data set, E[X]_dist stands for the distributional expected value based on parameters calculated using the training data set, and $\widehat{X}$_BRT stands for the average of the BERT&NN model–predicted values before fitting a distribution. Based on KS, AD, and CVM statistics in Table C.2, it is clear that the lognormal model fit well to the individual BERT&NN model–predicted severities under the 0.01 significance level. Also, according to Table C.3, information criteria values such as AIC and BIC reached minimum for the lognormal model. We used the following loss function to find the best model:

$$MSE = \frac{1}{10}\sum_{i = 1}^{10}\left( {\overline{X}}_{test,i} - E\lbrack X\rbrack_{dist,i} \right)^{2},$$

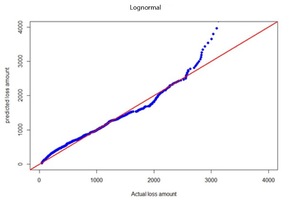
where ${\overline{X}}_{test,i}$ is the average severity of the $i^{th}$ test fold and $E\lbrack X\rbrack_{dist,i}$ is the distributional expected value based on parameters calculated using training data (remaining nine folds). Results are given in Table E.1 in Appendix E. The lognormal model had the smallest MSE. Therefore, we conclude that the lognormal model better fits for BERT-predicted severities. Quantile-quantile (QQ) plots for BERT&NN versus actual, NN versus actual, fitted gamma versus actual, and lognormal versus actual are given in Figures 3a through 3d.

Figure 3a.Quantile-quantile plot for actual versus neural network (NN)–predicted severities

Figure 3b.Quantile-quantile plot for actual versus Bidirectional Encoder Representations from Transformers–predicted severities

Figure 3c.Quantile-quantile plot for actual versus gamma-predicted severities

Figure 3d.Quantile-quantile plot for actual versus lognormal-predicted severities

5.2.2. Distribution fitting on grouped BERT&NN model–predicted values

Next, we fit distributions to the group BERT&NN-predicted values. One of the key questions to ask is how one should do the grouping of the data. This can be done either by calculating the number of bins based on a rule such as in Sturges (1926) and Larson (1975) or by optimizing the bin width based on a rule such as in Shimazaki and Shinomoto (2007) and Scott (1979). A bin width can be optimized to fit a specific distribution. A short survey of these methods can be found in Dogan and Dogan (2010). It is worthwhile noticing that there is no general consensus on which method is better for selecting the number of bins or the bin width. Therefore, for our training data set, we calculated bin width based on Sturges (1926), Larson (1975), Scott (1979), and Shimazaki and Shinomoto (2007) and used Shimazaki and Shinomoto’s bin width as the optimal bin width. The bandwidth from other methods is also used for comparison purposes. The results are given in Table 7. It should be noted that we must add one more bin to each group above, with the interval being the endpoint of the last interval and infinity.

Since there is no standard selection procedure, or “correct” answer for the bin width or the number of bins, we decided to fit models for the number of bins in Table 7. The results are given in Table C.4. As we mentioned earlier, fit statistics are calculated using the Pearson chi-square goodness-of-fit test. The parameters are calculated using the maximum likelihood estimate for complete grouped data (Klugman, Panjer, and Willmot 2013). According to Table 6 and Table C.4 in Appendix C, the lognormal model is significant under 0.01 on more test folds than are other models. This concurs with the result we obtained for individual BERT-predicted values. The grouped data set, when the number of bins is nine, is given in Table 8. We calculated the average MSE under the cross-validation. The result under the Shimazaki and Shinomoto (2007) grouping method is given in Table E.2 in Appendix E.

5.2.3. Outlier adjustment with corresponding analysis results

From the scatter plots, we see that there are data points that differ significantly from other observations. These are outliers, and they can cause serious problems in predictions and statistical analyses, since many ML models such as regression, NN, and K-means are sensitive to outliers, and the analysis results would be affected. Therefore, we expand our discussion a little more in the direction of the treatment of outliers and corresponding analysis based on the extended warranty loss claim data.

Basic approaches for outlier detection include implementing mathematical formulas, using statistical distributions and tests, and using visualization tools. An outlier can be determined simply by using the interquartile (IQR) range, which is equal to the difference between quartile 3 (Q3) and quartile 1 (Q1). All the data points below Q1 – 1.5 $\times$ IQR and above Q3 + 1.5 $\times$ IQR are considered outliers. The z-score indicates how far the data point is from the mean point in terms of the standard deviation. An outlier can be defined as the observation whose z-score is greater than or less than three times the standard deviation, i.e., mean + 3 $\times$ standard deviation or mean – 3 $\times$ standard deviation. The percentile can be used to define outliers quantitatively if the box plot or scatter plot clearly shows visible outliers. For instance, an outlier can be defined as a value at the 99th percentile or beyond. Alternatively, a more advanced method of determining an outlier is by its distance from a regression curve. If the difference is greater than 1.96 times the standard deviation of the data set, then this data point is considered an outlier.

There is no standard method in treatment/adjustment of outliers for data preprocessing. The following are common methods to treat outliers:

• Deletion—Deleting outlier values simply removes outliers from the data set.

• Mean/Median/Mode Imputation—Imputation of outliers is similar to handling missing values. We can use mean, median, mode imputation methods to replace the outliers.

• Quantile-Based Flooring and Capping—In this technique, the outliers are capped at a certain value above the 95th percentile or floored at a factor below the 5th percentile. The data points less than the 5th percentile are replaced with the 5th percentile value, and the data points greater than the 95th percentile are replaced with the 95th percentile value.

In this study, we define the outliers by using an upper 99th percentile observation, which is 3314.29, larger than Q3 + 1.5 $\times$ IQR = 1467.78 and also larger than mean + 3 $\times$ (standard deviation) = 2874.07, and treat the outliers using the following method: 60% of the data points with a severity value greater than the 99th percentile are replaced by the mean severity value, and 40% of them are capped by the 99th percentile severity value by randomly picking. The corresponding scatter plots of predictive results from the BERT&NN and NN models are shown in Figures 4a and 4b. Similarly, QQ plots for BERT&NN versus actual, NN versus actual, fitted gamma versus actual, and lognormal versus actual when outliers are adjusted from severity data are given in Figures 5a and 5b and Figures 6a and 6b, respectively. Clearly, both QQ plots and scatter plots show that the BERT&NN model fits the original claim loss data well.

Figure 4a.Scatter plot for BERT&NN versus actual with outlier treatment from the original data set

Figure 4b.Scatter plot for neural network (NN) versus actual with outlier treatment from the original data set

Figure 5a.Quantile-quantile plot for BERT&NN with outlier treatment from the original data set

Figure 5b.Quantile-quantile plot for neural network (NN) versus actual with outlier treatment from the original data set

Figure 6a.Quantile-quantile plot for fitted gamma versus actual with outlier treatment from the original data set

Figure 6b.Quantile-quantile plot for fitted lognormal versus actual with outlier treatment from the original data set

Five testing samples with outlier treatment were carried out for data analysis. The average normalized root mean squared errors (NRMSEs) of the BERT&NN and NN models were calculated. NRMSE is calculated using root MSE of predicted values divided by the mean of the original observed values. Both values, 0.747 and 0.844, are smaller than the corresponding values of the models using the raw data. Also, the BERT&NN model has smaller average NRMSE than do the NN model and the models for the raw data. The average prediction values from the BERT&NN and NN models are 498.00 and 496.00, respectively. Accordingly, the gamma and lognormal fitted distributions generate prediction values of 496.29 and 498.01, respectively. Noticing that the method of outlier treatment will affect the distributions due to the tails’ adjustment, further justification analysis should be studied. This is a common issue in data-driven modeling and is a good topic for future research.

6. Conclusion

Our goal in this article is to introduce a framework for using text data for loss-frequency and severity prediction through BERT-based NLP models. Our data set contained two textual variables called DIAGNOSIS and REPAIR. In this study, we have shown how to use these variables for frequency and severity predictions. For frequency analysis, we used two traditional approaches, Poisson and negative binomial, as well as a BERT-based model. Traditional approaches are not able to use textual input. Chi-square goodness-of-fit tests show that the BERT-based model is better than the traditional models in terms of the MSE since the BERT-based model has smaller MSE than any other model. The expected claim frequency, E[N], and variance, VAR[N], for all frequency models tested in this article are summarized in Table 9. All models’ expected frequencies are close to the observed frequency in the testing data set: 0.45 per claim per policy.

For severity prediction, we used the BERT&NN model. To compare the true effect of BERT, we ran an NN model without BERT. For the BERT&NN model, we used two textual variables as well as two categorical variables as input. For the NN without BERT, we used two categorical variables but no text input. A summary of these two severity models is given in Table 6. We show through the hypothesis tests that two predictive populations are not identical. The Pearson correlation results show that BERT&NN-predicted values are more closely correlated with the actual loss amount than are NN model–predicted values. We also tried to investigate the shape and the behavior of the BERT-based predictive distribution by fitting several common parametric distributions. We used two approaches: calculating maximum likelihood estimated parameters from individual predicted values and grouping predicted values. Using 10-fold cross-validation, we concluded the lognormal model better fits the BERT-predicted values. We observed a heavy tail in severity histograms, and models we used do not accommodate thick tails very well. Therefore, composite models such as lognormal-Pareto (Cooray and Ananda 2005) and Weibull-Pareto (Scollnik and Sun 2012) should be considered. These are deferred as future research topics. The explained variance of the BERT&NN model is around 28.80% compared to 19.13% in the NN model. This confirms that adding text data to a model reasonably improves the explained variation. It should be noted that we did not use many variables in our model—thus the low overall explained variation. The average severity for the testing data set is $559.37 per claim per policy; the individual BERT-predicted severity is $538.92, close to the observed value.

Note: STD.DEV = standard deviation.

In Table 10, the means and variances have been calculated on five randomized sample sets using different random seeds. For each randomization, we split the data into a training set and a testing set as we did in previous sections. The result in the table demonstrates that the BERT&NN model has the smaller standard deviation of 5 samples compared to the NN model not using textual data. This smaller standard deviation shows the robustness of the BERT&NN model when dealing with different data sets.

We set out to see whether NLP techniques can be used to predict frequency and severity in actuarial science applications. We used one of the prominent NLP techniques, BERT, then demonstrated how to extract information from text columns and use that information to predict frequency and severity. Also, we concluded that using just NN without BERT would not improve the predictions. In this article, we used a few of the existing count models to compare to the BERT model. In the future, we would like to investigate BERT-based model performance against other existing models, specifically existing severity models. We conclude that these results encourage BERT as an NLP tool to be incorporated with traditional actuarial models for loss prediction. This research outlines an automated procedure of BERT-based modeling for insurance claim frequency and severity. A flowchart is provided in Figure D.1 in Appendix D.2.

Acknowledgment

The authors would like to acknowledge funding from the Casualty Actuarial Society under the 2021 individual grant competition (C22-0005) and gratefully thank the editor and anonymous referees for their constructive comments and suggestions, which helped improve the quality of the article. Don Hong would also like to express his thanks for his 2022 Non-Instructional Assignment Award support from Middle Tennessee State University.

Appendices

Appendix A. Attributes of the contract and policy tables

Appendix B. Results from frequency modeling

Appendix B.1. Frequency tables

Appendix B.2. Poisson regression results

Figure B.1.Observed versus predicted distribution for Poisson regression on the testing data set

Appendix B.3. NB-2 regression results

Figure B.2.Observed versus predicted distribution for NB-2 regression on the testing data set

Appendix B.4. Frequency model comparision and hyperparameters

Appendix C. Tables from severity modeling

Appendix D. Algorithm and flowchart

Appendix D.1. BERT&NN algorithm for severity modeling

Appendix D.2. Automated procedure flowchart of BERT-based models for frequency/severity prediction

Figure D.1.Flowchart for an automated procedure of BERT-based frequency/severity prediction models

Note: BERT = Bidirectional Encoder Representations from Transformers; QQ = quantile-quantile. Python source codes are available at https://capone.mtsu.edu/dhong/BERT4LossPrediction.htm.

Appendix E. Average mean squared errors for models’ cross-validations

Appendix E.1. Average mean squared error for each individual model under cross-validation

Appendix E.2. Average mean squared error for each grouped model under cross-validation